Юмашев. Интегралы и производные в физике
Вместо предисловия
Дорогой читатель! Ты держишь в своих руках не совсем обычное пособие по физике. Основное место в нем занимает разговор о физическом приложении одного из самых интересных и загадочных разделов математики дифференциального исчисления. Центральными понятиями дифференциального исчисления являются производная и интеграл, и эти понятия тесно связаны с физикой, с законами окружающей нас природы. Созданное впервые И. Ньютоном и Г. Лейбницем во второй половине XVII в., новое направление математики на протяжении двух последующих столетий получило бурное развитие, будучи в центре внимания величайших ученых: Эйлера, Гаусса, Лагранжа, Лапласа, Коши, Римана, Вейерштрасса, Пуанкаре и многих, многих других. Современное дифференциальное исчисление включает в себя огромное количество направлений, которым посвящены сотни книг. Несомненно, оно стоит в ряду наиболее значительных разделов математики.
Однако не нужно забывать, что основы дифференциального исчисления были разработаны Ньютоном при исследовании именно физической задачи о движении планет вокруг Солнца. Впоследствии многие вопросы из математического анализа и теории дифференциальных уравнений также были сформулированы и разрешены физиками, которые пытались построить адекватное описание природных явлений. Поэтому попытка опереться в изучении производных на их физическое приложение продиктована историей математики и, если хотите, самой сущностью дифференциального исчисления. Именно это автор и попробовал сделать в настоящем пособии, предложив читателю знакомство с рядом интересных физических задач, подразумевающих использование производных.
Ни для кого не секрет, что начала математического анализа очень тяжело даются многим ребятам. Усвоив формальные правила дифференцирования степенных функций и синусоид, они зачастую не отдают себе отчет, что за этими правилами стоит. В подобном случае производные кажутся школьникам (а также и некоторым студентам) ÷åì-òîсовершенно абстрактным, и они чувствуют естественную неприязнь к новому математическому языку. Сходные проблемы испытывал и сам автор.
С другой стороны, всем хорошо известна некоторая ограниченность школьного курса физики, которая естественным образом проистекает из необходимости использовать в нем только элементарную мaтематику. Автор ни в коем случае не хочет этим сказать, что элементарную физику изучать не нужно; более того, она является фундаментом, без которого почти невозможно построить понимание общей и теоретической физики и заниматься впоследствии собственной научной работой. В рамках элементарного курса рассматривается масса интересных и красивых задач, направленных на тренировку физической интуиции, физического чутья. В приложе-
studfiles.net
Применение интегралов в физике и математике
1. Перемещение материальной точки
Пусть точка движется по прямой (по оси ) и известна скорость движения этой точки. Пусть скорость меняется и задан закон этого изменения на некотором отрезке . Тогда перемещение равно
2. Зависимость между работой и силой
Зависимость между работой и силой при перемещение материальной точки от значения к значению устанавливается соотношением:
Работа за промежуток времени от до , если задан закон изменения мощности , вычисляется по формуле:
3. Масса тонкого стержня
Масса тонкого стержня, если известна его линейная плотность вычисляется по формуле:
4. Количество электричества (электрический заряд)
Количество электричества (электрический заряд) за промежуток времени при известной силе тока вычисляется по формуле:
5. Количество теплоты за время
Если задана теплоемкость , то количество теплоты за время вычисляется по формуле:
6. Зависимость магнитного потока и ЭДС
Математическая зависимость между
7. Площадь криволинейной трапеции
Площадь криволинейной трапеции – фигура, ограниченная графиком непрерывной положительной на интервале функции , осью абсцисс и вертикальными прямыми и (рис. 1) – вычисляется по формуле:
8. Вычисление длины дуги плоской кривой
Пусть в прямоугольных координатах дана плоская кривая , заданная уравнением (рис. 3).
Если функция и ее производная непрерывны на отрезке , то кривая имеет длину, которая вычисляется по формуле:
9. Вычисление объема тела вращения
Пусть вокруг оси вращается криволинейная трапеция, ограниченная непрерывной линией , прямыми и (рис. 4). Полученная от вращения фигура называется
Если криволинейная трапеция ограничена графиком не прерывной функции и прямыми и , то объем тела, образованного вращением этой трапеции вокруг оси , равен
10. Вычисление площади поверхности вращения
Пусть кривая задана функцией , которая является непрерывной вместе со своей производной на этом отрезке. Площадь поверхности, образованной вращением кривой вокруг оси (рис. 4) равна
ru.solverbook.com
4.3.2 Примеры применения интеграла в физике и геометрии
Видеоурок: Применение интегралов в физике и математике
Лекция: Примеры применения интеграла в физике и геометрии
Процесс нахождение первообразной называется интегрированием.
Как и производная, интегралы используются и в физике, и в геометрии, а также в других областях знаний.
Сегодня же мы рассмотрим, каким образом используется интегрирование в физике и геометрии.
Итак, начнем сначала. Мы помним, что скорость – это первая производная перемещения. Но так как мы знаем, что интегрирование и нахождение производной – это два взаимообратных процесса, то мы можем предполагать, что, если для нахождения скорости, нужно было найти производную от перемещения, то для нахождения перемещения по скорости, необходимо произвести интегрирование заданной функции.
Отсюда можно сделать вывод, что перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:
Пример: Итак, предположим, что некоторое тело двигается со скоростью, заданной функцией:
V(t) = t2 +1.
По условию задачи мы должны определить путь, который пройдет тело за промежуток времени [0;1].
Итак, найдем определенный интеграл данной функции:
Это означает, что за данный промежуток времени, тело прошло 1,3(3) м.
Точно так же можно найти скорость по заданной функции ускорения.
Еще одной физической величиной, которая находится с помощью интегрирования, является работа.
Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:
Пример: Предположим, что к некоторому телу для его передвижения прикладывают силу, которая изменяется по закону F(x) = x +3. Необходимо найти работу, которую при этом совершает сила для перемещения тела с 1 м до 2 м.
Для нахождения работы следует найти определенный интеграл заданной функции по известным пределам интегрирования:
Это значит, что для передвижения тела потребовалось совершить работу, равную 4,5 Дж энергии.
Кроме рассматриваемых задач, интегрирование в физике используется для нахождения работы по мощности, массы по плотности, заряда по силе тока, количества теплоты по известной теплоемкости, а также многое другое.
Что же касается геометрии, то геометрическим смыслом интегрирования считается нахождение площади фигуры под графиком.
Итак, чтобы найти площадь фигуры, которая ограничена с двух сторон пределами интегрирования и с одной стороны графиком функции, то необходимо найти интеграл данной функции:
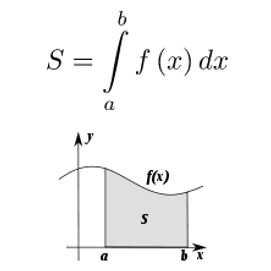
Пример: Вычислим площадь фигуры, ограниченной графиком функции у = 4х – х
Итак, найдем интеграл данной функции в заданных пределах и построим полученный график:

cknow.ru
Юмашев. Интегралы и производные в физике
кета мгновенно выбрасывает малую порцию газа
Переходные процессы в электрических цепях | 21 |
и т.д. Надеюсь, после рассмотренных примеров вам понятно, откуда в физике возникает понятие мгновенной скорости, подразумевающее использование производных. Должен быть также понятен основной путь при работе с дифференциалами непрерывное суммирование , или, как его называют, интегрирование.
А пока давайте задумаемся вот над чем. Если мы еще толком не знаем, что такое производная и интеграл, и как и с чем их едят, то, может быть, мы попытаемся решать некоторые из перечисленных задач, не переходя к бесконечно малым вели- чинам? Так, применимо к движению ракеты вместо непрерывного истечения газа можно рассмотреть порционные выбросы: через равные промежутки времени t ðà-
m0. Понятно, что такое движение
после N выбросов будет описываться системойN алгебраических уравнений, вы-
ражающих собой закон сохранения импульса на каждой стадии. Худо бедно, после решения мы получим v(N) скорость ракеты наN-îìшаге , а с ней и зависимость
v(m) скорости от текущей массы ракеты (т.к.m = m | 0 | ¡ | N m0). Но что произой- | |
дет, если в этом решении мы начнем уменьшать t è |
| , сохраняя их отношение | ||
| m0 |
| ||
¹ = m0= t (массовый расход газа) постоянным? Придем ли мы таким образом к
решению уже рассмотренной задачи о полете ракеты с непрерывным истечением топлива, в которой потребовалось использовать дифференциалы и вычислять площадь под гиперболой? Обсуждению этой проблемы посвящена следующая глава пособия.
Глава 2
Предельный переход от дискретной модели к непрерывной
Рассмотренная в самом конце предыдущей главы модель движения ракеты может быть названа дискретной. Дискретное это нечто, состоящее из отдельных звеньев, этапов. К примеру, лестница в доме позволяет подняться на строго определенные высоты hN = N h (ãäåh высота ступеньки), т.е. является дискретной . Горка
же для вкатывания колясок позволяет подняться на любую высоту в своих пределах, т.е. является непрерывной. Остановимся на конкретных примерах.
Пример 2.1. Движение ракеты с дискретными выбросами топлива.
Опишем движение ракеты с дискретными выбросами0 топлива. При этом будем счи- тать, что после выброса небольшой порцииm скорость ракеты меняется наv;
влиянием же этого изменения на скорость газов относительно неподвижной системы в силу малости v пренебрежем. Закон сохранения импульса для выбросаN-îé
порции имеет вид
(m0 ¡ N m0) vN¡1 + m0 vN¡1 = (m0 ¡ N m0) vN + m0 (vN¡1 ¡ u)
ракета без N-îé | N-àÿпорция | ракета без N-îé | N- ая порция; |
порции |
| порции |
|
здесь vk скорость ракеты послеk-ãîвыброса. Из данного уравнения находим связь скоростей до и послеN-ãîвыброса:
|
|
| m0 | |
vN= vN¡1 + u |
|
|
| : |
m0 | ¡ | N m0 | ||
|
|
|
| |
Такое соотношение называется рекуррентным оно связывает величины на двух соседних шагах между собой. Понятно, что это соотношение справедливо для любого N. В частности, приN = 1 (1-ûéвыброс)
v1= v0+ u |
| m0 |
| ; |
m0 | ¡ | m0 | ||
|
|
|
|
ïðè N = 2
m0
v2 = v1 + um0 ¡ 2Δm0 ;

оставался неизменным.11)
Движение ракеты с дискретными выбросами топлива | 23 |
и т.д. Когда мы запишем все подобные уравнения вплоть до N-ãîодно под другим, то
сразу обратим внимание на любопытное обстоятельство. Если их просуммировать, все промежуточные значения скорости сократятся, и мы получим связь vN ñv0:
| N |
| ¡ |
|
|
|
| X |
|
|
|
| |
vN = v0 | + u m0 |
| 1 | : | (2.1) | |
m0 |
| n m0 | ||||
| n=1 |
|
|
| ||
|
|
|
|
|
| |
Теперь начнем уменьшать m0 таким образом, чтобы массовый расход топлива
¹ =
m0
t
Рассматриваемые начальное и текущее (спустя N выбросов) значения массы ракеты (m0 èM =m0 ¡ N m0, соответственно) при этом не меняются, а вот количество выбросовN, приходящееся на то же самое уменьшение массы ракеты, возрастает. В пределеm0 ! 0
N = m0 ¡ M ! 1 ;m0
и сумма в (2.1) состоит из бесконечного количества слагаемых, непрерывным образом переходящих друг в друга.12) ÏðèN ! 1 вместо зависимости скорости ракеты от
числа выбросов (vN ) имеет смысл ввести зависимость скорости от текущей массы ракеты:v(M). ВеличиныM èv теперь изменяются непрерывным образом. С учетом этих замечаний уравнение (2.1) можно переписать в виде
v(M) =v0 | + umZ0 | m 0 | ; |
| M | dm |
|
причем дифференциал dm0 | получается из конечной величины m0 в результате пре- | ||||||||||
|
|
|
|
| M |
|
|
|
|
| |
дельного перехода. Символом | m | обозначена непрерывная сумма (интеграл) по всем | |||||||||
значениям |
|
|
|
|
|
|
|
|
|
| |
| m массы ракеты отR0ее первоначального значения m0 и до интересующе- | ||||||||||
го нас текущего значения M. Особое внимание обращаю на то, что в знаменателе | |||||||||||
стоит произвольное значение массы ракеты m = m0 |
| n m0, которое по совершении | |||||||||
предельного перехода m0 | ! dm0 изменяется в | процессе суммирования (интегриро- | |||||||||
|
|
| ¡ |
| |||||||
вания) непрерывным образом от m0 äîM. |
|
|
|
|
| ||||||
Заменяя dm0 íà | ¡ | dm (dmизменение массы ракеты), найдем: | |||||||||
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| M |
|
|
|
|
|
|
|
|
|
|
| v(M) = v0 ¡ umZ0 |
| dm | : |
| |
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| m |
| |||
11)t суть время между двумя последовательными выбросами.
12)Расстояние между соседними слагаемыми m0 при совершении предельного перехода стано-
вится исчезающе малым и может быть заменено дифференциалом dm0. Малая величина каждого слагаемого в сумме компенсируется большим их количеством.
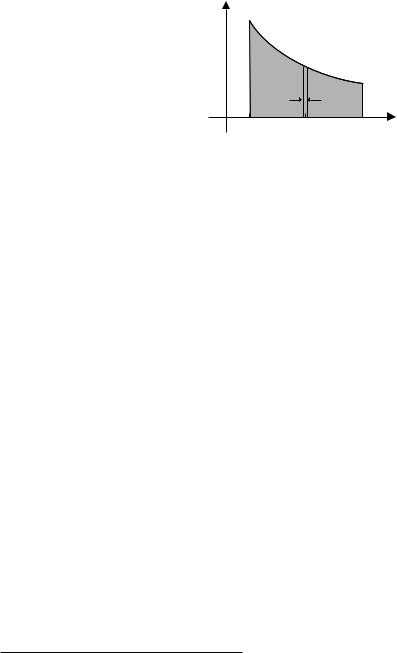
24 | Предельный переход от дискретной модели к непрерывной |
Такой же результат, как легко убедиться, непосредственно вытекает из дифференциального соотношения Мещерского mdv = ¡udm, описывающего полет ракеты с
непрерывным выбросом топлива.13) Мы опять приходим к необходимости вычисле-
ния площади под гиперболой (рис. 10), только несколько иным путем после предельного перехода в дискретной модели. Окончательное решение задачи о полете ракеты придется пока отложить.14)
Чтобы, наконец, научиться считать площадь под гиперболой, рассмотрим еще один пример перехода от дискретной модели к непрерывной.
1/m
dm
m
M m m0
Рис. 10. Увеличение скорости ракеты пропорционально площади под графиком гиперболы
Пример 2.2. Изотермическая откачка газа из баллона.
Пусть у нас есть баллон объема V, в котором заключеноº0 моль идеального газа при температуреT . Будем при постоянной температуре (изотермически) откачивать из
баллона небольшие порции газа, подсоединяя маленький пустой резервуар объемом v ¿ V . Организовав изотермическое перетекание части газа в объемv, отсоеди-
ним его, удалим из него весь газ и снова подсоединим к баллону. Вопрос: каково будет давление и количество вещества в баллоне после N подобных операций?
Íà N-îìøàãå â ñèëóT = const имеем:
pN¡1V= pN (V+ v)
до заполн. после заполн.
(давление в объединенном сосуде V + v, очевидно, всюду одинаково после установ-
ления динамического равновесия). Кроме того, запишем уравнение состояния для газа в малом объеме v:
pN v= ºN RT;
здесь ºN количество вещества, откаченное наN-îìøàãå.pN , таким образом, пропорциональноºN . Полученные соотношения справедливы для любогоN, è ìû
13)См. главу 1, пример 1.4.
14)См. главу 4, задачу 4.6.
Изотермическая откачка газа из баллона |
|
|
|
|
|
| 25 | ||
опять приходим к системе рекуррентных уравнений: | |||||||||
2 p1= p0 |
| V |
|
|
| ||||
|
|
|
|
| |||||
V + | v |
| |||||||
6 | 2 | 1 |
|
|
|
|
|
| |
6 |
|
|
| V |
|
|
| ||
6 p= p |
|
|
|
|
| ||||
6 |
|
|
|
|
|
|
|
| |
6 |
|
| V + | v |
| ||||
6 |
|
|
|
|
|
|
|
| |
6 |
|
|
|
|
|
|
|
| |
6 |
|
|
|
|
| V |
| ||
6 |
|
|
|
|
|
| |||
6 | ::::::::::::::::::::::::: |
| |||||||
4 |
|
|
|
|
|
|
|
| |
6 pN= pN | 1 |
|
|
| : | ||||
V + v | |||||||||
6 |
|
|
| ¡ |
| ||||
На сей раз путем их перемножения, все промежуточные значения p удается сократить, что позволяет установить связь давления наN-îìшаге откачки с начальным
давлением: | µV+ v | ¶ | N | ; ºN = RT | µV+ v¶ | : | |||||||||||
pN = p0 | |||||||||||||||||
|
| V |
|
|
|
|
| p0 v |
|
|
| V |
| N | |||
|
|
|
|
|
|
|
|
|
|
|
| ||||||
С использованием уравнения состояния несложно найти, что после N-ãîøàãà â áàë- | |||||||||||||||||
лоне осталось количество вещества |
|
| = RTµV+ v | ¶ | : |
|
| ||||||||||
| ºN = RT |
|
|
|
| ||||||||||||
|
|
| pNV |
|
| p0V |
|
| V |
| N |
| |||||
Величину ºN можно посчитать иначе, просуммировав все откаченные порцииºk è вычтя их из первоначального количества веществаº0:
ºN = º0 ¡ | º1¡ | º2¡ ::: ¡ ºN | = | RT | ¡ RT | n=1 | µV+ | v | ¶ | = | |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| p0V | p0 v |
| N |
| V |
| n |
| |||
|
|
|
|
| ¡ |
| ¢¡¡ |
|
| ¢ |
|
|
|
|
| X |
|
|
|
|
| ||||
|
|
|
|
| V | V | N+1 |
|
|
|
|
| µ |
|
| ¶ |
|
| |||||||
= | p0 |
| V |
| v |
| V +Δv | ¡ |
| V +Δv |
| = :::= | p0V |
|
| V |
| : |
| ||||||
RT “ |
| ¡ |
|
|
| 1 |
|
| V |
|
|
| # |
|
| RT V + v |
|
|
| ||||||
|
|
|
|
| V +Δv |
|
|
|
|
|
|
| |||||||||||||
Как ни странно, результат получился тот же самый, однако мы отвлеклись от сути. | ||||
Пусть порции откачиваются за время | t каждая; тогда tN = N tвремя откачки | |||
N порций. Теперь будем устремлять | t è | v к нулю так, чтобы объемная скорость | ||
откачки (л/сек) оставалась постоянной: |
| |||
q = | v |
| = const ; | |
t | ||||
|
| |||
в результате мы будем иметь непрерывный процесс откачки. При такой откачке зна- чение давления в любой момент времени t åñòü
|
| t; v!0 0 | µ |
|
| V |
| ¶ | ¡N(t) | = | ½ Níà t= t | ¾ | = | |||||
p(t) = |
| lim p |
| V + | v |
|
| заменим v íàq | t ; |
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
| µ1 + | q | t | ¶ | ¡ | t |
|
|
|
|
|
|
| ||
|
|
|
| t |
|
|
|
|
|
|
| |||||||
= | lim p | 0 |
|
|
|
|
|
| : |
|
|
|
|
|
| |||
|
| V |
|
|
|
|
|
|
|
|
| |||||||
t!0 |
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
26 | Предельный переход от дискретной модели к непрерывной | |
В любом курсе высшей математики доказывается, что |
| |
| lim (1 + ®x)1=x =e® ; | (2.2) |
| x!0 |
|
где число e = 2; 718:::, подобно числу¼, суть фундаментальная математическая
константа. Данное число является иррациональным и трансцендентным. Исходя из двух последний уравнений, получим:15)
( ) = |
| 0 | t!0 · µ¡ t |
| ¶µ¡V | ¶¸ | t | = | ½ | = ¡V | ¾ | ||||
p t | p |
| lim | 1 + |
| t | qt | ¡ | t |
| в данном случае ® |
| qt | = | |
|
|
|
|
|
|
|
|
| |||||||
= p0 expµ¡V | ¶: |
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
| qt |
|
|
|
|
|
|
|
|
| ||
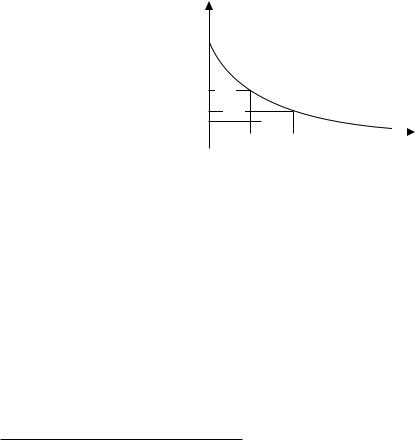
Мы установили зависимость давления в баллоне от времени при непрерывной изотермической откачке с постоянным объемным расходом q (q объем, проходящий
через насос за единицу времени). Характерный вид этой функции, называемой экспонентой (или экспоненциальной функцией), показан на рис. 11. Экспонента есть частный случай показательной функции y(x) =ax и имеет огромное значение для
описания физических явлений.
p(t)
p0
1/2
1/4
| 1/8 |
|
|
|
| t | |
|
|
|
| 1/16 |
|
|
|
τ 2τ3τ4τ
Рис. 11. Изменение давления в баллоне при непрерывной изотермической откачке
Такой же результат, разумеется, должен получиться, если сразу написать дифференциальное соотношение для бесконечно малого объема dv =qdt откачиваемого
за время dt ãàçà:
pV = (p+ dp)(V+ dv) :
Это есть условие изотермичности перетекания газа в подсоединенный к баллону малый резервуар dv. Как и в случае с ракетой, после раскрытия скобок величинойdpdv
можно с математической строгостью пренебречь (она имеет другой порядок малости по сравнению с величинами dp èdv). Следовательно,
V dp = ¡pdv;
15)Записьexp(¡qt=V ) означает то же самое, что иe¡qt=V (числоe в степени¡qt=V ).

p(t) p0
Изотермическая откачка газа из баллона | 27 |
dp < 0, т.к. давление при откачке непрерывно уменьшается. Деля это уравнение наpV и вспоминая определение объемного расходаq, приведем его к виду
Чтобы из данного уравнения определить зависимость p(t), нужно вновь считать пло-
щадь под гиперболой. Действительно, при суммировании (2.3) по ходу откачки от самого начала (t = 0) до интересующего моментаt â ñèëóq = const получим:
pZo | p | = ¡V : | (2.4) | |
p(t) |
|
|
|
|
| dp |
| qt |
|
Возведение числа e в степень, равную левой и правой частям равенства (2.4),16)
приведет к соотношению | 2Z | p | 3 | = exp µ¡V ¶ : | (2.5) | ||
exp | |||||||
| p(t) |
|
|
|
|
|
|
| 4p0 | dp | 5 | qt |
| ||
|
|
|
|
|
| ||
Отметим сразу, что площадь под гиперболой в данном случае равна стоящему в (2.5) интегралу, взятому со знаком минус. Объясняется это тем, что p(t)< p0, è
при интегрировании получатся dp < 0; площадь же должна быть положительной
величиной. Ну а теперь вспомним, что из рассмотрения дискретной откачки мы уже установили искомую зависимость p(t):
p(t) =p0 exp | µ¡V ¶ | : | |
|
| qt |
|
Сравнивая последние две формулы, найдем:
2Zp(t)
= exp 4
p0
Введем операцию ln , обратную возведению числаe в любою степень:
ln (e®) =® ; | (2.7) |
следовательно, exp (ln e®) = e®. Обозначаяx = e®, получим важное свойство: |
|
elnx = x : | (2.8) |
Функция ln x носит название натурального логарифма; она является обратной функцией для экспоненты.17) Здесь мы не будем перечислять все ее свойства, поскольку
16)Такая операция называется потенциированием.
17)Рекомендую вам самостоятельно построить график логарифмической функции, найдя предва-
рительно область ее определения, множество значений, нули и т.п. Исходите из того, что экспонента и натуральный логарифм есть взаимно обратные функции (см. (2.7), (2.8)).

28 Предельный переход от дискретной модели к непрерывной
сейчас важно другое. Применим операцию ln к перевернутому уравнению (2.6):
ln µp(t)¶ = ln | 0exp | 2¡Z | p | 31 | = ¡Z | p | ´ Z | p = Sïîä ãèï.18) | |||
|
|
|
| p(t) |
|
| p(t) |
| p0dp | ||
| p0 | @ 4 p0 | dp | 5A |
| dp | |||||
|
|
|
| p0 |
| p(t) |
|
| |||
В результате долгожданная площадь под гиперболой в общем случае определяется следующим образом (рис. 12):
Sïîä ãèï.= | pZ1 | p | = ln | µp1 | ¶ | : | |
| p2>p1 dp |
|
| p2 |
|
| |
Отсюда легко установить геометрический смысл числа e. Полагаяp1 = 1 èp2 =e (e = 2:718::: > 1), получим, что площадь под графиком гиперболы на отрезке [1; e]
равна ln(e) = 1 (последнее равенство вытекает из формулы (2.7) при® = 1).
Элементарно выводится также правило дифференцирования логарифмической функции. Одним из важнейших свойств логарифма является его аддитивность:
ln a + lnb = ln (ab); lna ¡ lnb = ln³ab ´:
С учетом второго свойства перепишем выражение для площади под графиком ги-
перболы в виде | p2dp |
| |
| pZ1 |
| = ln p2 ¡ lnp1 : |
| p | ||
Отсюда заключаем, что | dp |
|
| = d(lnp); | |
| p | |
|
|
поскольку только при интегрировании (суммировании) дифференциалов от логарифма на отрезке [p1; p2] получается разность его конечного и начального значений. Деля
последнее равенство на dp, найдем искомое правило:
d(lnp)= 1: dp p
Его легко установить непосредственным дифференцированием формулы (2.8), однако такой путь основан на знании правил взятия производной от сложной функции и от экспоненты, которые могут быть еще незнакомы читателю. О них речь пойдет в главах 4 и 5 (производная от экспоненты упоминается также в конце примера 2.6 настоящей главы).
Пример 2.3. Веревка в поле тяжести.
18)Здесь мы использовали важное свойство интеграла: при взаимной перестановке пределов перед интегралом появляется знак¡ . Попробуйте самостоятельно это доказать.
= TB. Запишем последовательно уравнения для вертикальной
Веревка в поле тяжести | 29 |
| 1/p |
ln(p2/p1)p
Рис. 12. Выражение для площади под гиперболой
Рассмотрим типичную олимпиадную задачу: в поле тяжести висит однородная веревка массой m и длинойl, конецA которой подвешен на высотеh ниже концаB
(рис. 13). Спрашивается, на сколько сила натяжения веревки в точке B больше силы
натяжения в точке A, и чему равна сила натяженияT (y) на произвольной высотеy от нижней точки веревки? Давайте подробно в этом разберемся.
B
h
A
y
Рис. 13. Провисание веревки под действием тяжести
Представим веревку в виде цепочки, состоящей из точечных масс m, соединенных невесомыми нерастяжимыми стержнями длинойl. Таким образом, мы рассматриваем дискретную модель веревки. Если в цепочкеN грузиков, тоm = m=N;l = l=(N + 1) (количество стержней равноN + 1). Теперь рассмотримn-ûéãðó-
зик. Помимо силы тяжести, на него действуют также силы Tn èTn+1 со стороны стержней, направленные под углами®n è®n+1 к горизонту, соответственно (рис. 14). Условия равновесияn-ãîгрузика записываются в виде системы:
8 Tn cos®n =Tn+1 cos®n+1 |
| 8 | n = 1;2; :::; N : | ||
: | ¡ | Tn sin®n | = g m |
| |
< Tn+1sin ®n+1 |
|
| |||
Из первого уравнения следует, что горизонтальная составляющая Tn cos ®n одинако- ва всюду вдоль цепочки. В частности,T1 cos ®1 = TN+1 cos ®N+1 = Tk+1, ãäåTk+1 сила натяжения низшего звена, которая направлена горизонтально (®k+1 = 0); ïðè ýòîìT1 = TA,TN+1
30 | Предельный переход от дискретной модели к непрерывной | |||
|
| n | Tn+1 | |
|
| αn+1 | ||
| αn |
|
| |
|
|
|
| |
| Tn | g m |
| |
Рис. 14. Силы, действующие на звено цепочки
компоненты силы, начиная от k-ãîгрузика и заканчивая1-ûì:
8 | ¡Tk+1 sin®k+1 +Tk sin®k =g | |||||
> | ¡ |
|
| ¡ |
| ¡ |
> |
|
|
|
|
| |
> |
|
|
|
|
|
|
> |
|
|
|
|
|
|
> |
|
|
|
|
|
|
> |
| Tksin ®k+ Tk1 sin ®k1 = g | ||||
> |
| |||||
< |
|
|
|
|
|
|
> | ::::::::::::::::::::::::::::::::::::::::::::: | |||||
> | ||||||
> | ¡ |
|
|
|
|
|
> |
|
|
|
|
| |
> |
|
|
|
|
|
|
> |
|
|
|
|
|
|
> |
|
|
|
|
|
|
: |
| T | sin ® +T | sin ® |
| = g m : |
> |
| 1 | ||||
> |
| 2 | 2 1 |
|
| |
Производя суммирование и принимая во внимание, что
T1 sin ®1 = (k ¡1) g m :
m
m
®k+1 = 0, будем иметь:
Аналогично, записывая уравнения для вертикальной компоненты силы от k + 1-ãî
грузика до N-ãîи складывая их, получим, чтоTN+1 sin®N+1 = (N + 1¡ k)g m. Из последних двух уравнений вытекает соотношение
T1 sin®1 +TN+1 sin®N+1 =Ng m =mg :
Вес цепочки, как и должно быть, уравновешивается силами натяжения на концах. Изменим нумерацию. Нижнее звено (горизонтальное) назовем нулевым и пойдем, скажем, по правой части цепочки (рис. 15). Левую часть можно отдельно не рассматривать, поскольку до уровня точки A цепочка симметрична относительно вертикали
(рис. 13). В самом деле, если мы на данном уровне мысленно закрепим правую часть, форма цепочки не изменится; ниже точки A при этом получится кусок цепочки, кон-
цы которого подвешены на одинаковой высоте. Симметрия такого куска очевидна. Запишем еще раз условия равновесия для n-ãîгруза:
8 Tn cos®n =Tn+1 cos®n+1 |
|
| (2.9) | ||
: | ¡ | Tn sin®n | = g | m : |
|
< Tn+1sin ®n+1 |
|
| |||
Возводя определенным образом в квадрат и складывая уравнения (2.9), получим:
Tn2+1 ¡ Tn2 = (g m)2 + 2g mTn sin ®n :
Из цепного характера уравнений (2.9) следует, что
Tn sin ®n = T0 sin ®0 + n ¢ g m :
studfiles.net
Юмашев. Интегралы и производные в физике
Переход от дискретной среды к сплошной | 39 |
В большинстве протекающих в гидросфере и нижних слоях атмосферы гидромеханических явлений, заключающихся в разнообразных перемещениях воды и воздуха, движение происходит на масштабах L, которые много больше среднего расстоя-
ния между молекулами среды (длины свободного пробега l). Представьте себе плы-
вущего дельфина или летящую в небе птицу с точки зрения их обтекания встречным потоком среды. Понятно, что картина такого обтекания формируется вблизи движущихся в среде тел, и параметры потока (скорость, плотность, температура) меняются на масштабах порядка 10¡4 ¥ 102 м в зависимости от конкретного случая. То же ка-
сается и неживой природы, например волн на поверхности жидкости или торнадо, а также искусственных (созданных человеком) явлений, например обтекания самолета или катера. Во всех указанных примерах масштаб развития и перестройки течения на много порядков превосходит длину свободного пробега молекул. Поэтому зернистость среды никак не влияет на характер потока газ или жидкость с нашей точки зрения движутся как непрерывная масса, т.е. ведут себя как сплошная среда.
Итак, модель сплошной среды работает в тех гидродинамических явлениях, в которых l=L ¿ 1. Может ли случиться так, что это условие не выполняется? Оче-
видно, например, что обтекание спутника потоком разреженного воздуха в верхних слоях атмосферы нельзя рассматривать как сплошносредное там расстояния между молекулами являются величинами порядка и даже много больше размеров самого аппарата и, соответственно, масштабов изменения течения. Однако в нашей повседневной жизни в основном встречаются как раз сплошносредные явления.
Что дает переход от дискретной среды к сплошной? Допустим, мы захотели описать механику потока воздуха около обтекаемого тела, проследив за движением каждой отдельно взятой молекулы. Задача эта совершенно нереальная ведь мы с вами прекрасно знаем, что в 1 литре воздуха при нормальных условиях содержится » NA
молекул. А при переходе к сплошной среде у нас появляется шанс. В сплошной среде можно говорить о плотности вещества в данной точке пространства в данный момент времени, т.е. определить функцию ½(~r; t),~r = (x; y; z). Можно также ввести импульс
единицы массы газа ~v(~r; t),26) давлениеp(~r; t) и температуруT (~r; t). Тут к механи-
ке присоединяется термодинамика, которая также рассматривает газ как целое, а не как набор отдельных молекул (что делается в МКТ). В результате для описания движения среды достаточно найти функции ½(~r; t),p(~r; t),~v(~r; t); температуру в
каждой точке можно выразить через p è½ посредством уравнения состояния. Ука-
занные функции полностью определяют картину течения: по ним можно построить линии тока (вдоль которых движутся частицы жидкости), изобары, линии постоянной плотности и температуры. Кроме того, с помощью этих функций можно найти характеристики, описывающие воздействие потока на тело, например, силу сопротивления, нагрев, и т.д.
Откуда берутся указанные функции? Оказывается, что из рассмотрения законов сохранения массы, импульса и энергии в произвольном объемчике внутри сплошносредного потока выводятся уравнения, описывающие изменение ½,p,~v в пространстве
и во времени. Такие уравнения ÷åì-òîпохожи на волновое уравнение они содержат частные производные от рассматриваемых функций по пространственным коорди-
studfiles.net
сборник задач по физике. Производная и интеграл при решении задач.
Мини – сборник задач по физике.
Производная и интеграл при решении задач.
1. Применение производной для решения задач по физике
Задача 1
Тело массой 4 кг движется прямолинейно по закону х(t) = t2 +t + 1. Какова кинетическая энергия тела в конце третьей секунды движения после начала движения и сила, действующая на тело?
Дано:
m =4 кг
х(t) = t2 +t + 1
t=3 с
Wк ? F?
Решение: Скорость есть функция времени, поэтому
= х’(t)
= 2t + 1
(3) = 7 м/с
В физике скорость изменения скорости называется ускорением.
a(t) = ’(t)
a(t) =2м/с2
Операция нахождения производной функции называется дифференцированием. С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х. Последняя не обязана иметь физический смысл времени.
W =
W = 98 Дж
F = ma
F = 8 Н
Ответ: 98 Дж; 8 Н.
Задача 2
Зависимость между массой вещества М, получаемого в химической реакции и временем t выражается уравнением: М(t) = Аt2 +Bt, где А и В – постоянные. Какова скорость реакции?
Дано:
М(t) = Аt2 +Bt
Скорость химической реакции определяется: = М’(t)
= 2 At+ B
Ответ: 2 At+ B
Задача 3
Конденсатор ёмкостью C и зарядом q0 разряжается через резистор R по закону: q = q0 Найти скорость изменения заряда конденсатора. Какова скорость в начале разряда (t = 0)?
Дано:
q = q0
q’(t) ? q’(0) ?
Решение:
q’(t) = (q0’ = q0 (’·(- )’ = q0 = –
q’(0)= –
Ответ: – ; – .
Задача 4
Концентрация некоторого вещества в крови человека вследствие его выведения из организма изменяется по закону: n(t) = 2. Как изменяется скорость выведения вещества из организма с течением времени? Какой смысл имеет знак скорости?
Дано:
n(t) = 2
n’(t) ?
Решение:
n’(t) = (2 = 2 ( · (- 0,05t)’ = 2 · (- 0,05) = -0,1
Ответ: -0,1; знак (-) означает убывание концентрации вещества с течением времени.
Задача 5
В двухэлектродной лампе сила анодного тока зависит от анодного напряжения по закону: I(U) = , где – постоянная, зависящая от формы, размеров, расположения электродов. Получить формулу прироста тока на каждую единицу изменения напряжения.
Дано:
I(U) =
I’(U)?
Решение:
I’(U) = )’ =
Исходя из определения производной I’(U) = tg
I’(U) = lim
Ответ: .
Задача 6
Каково изменение периода колебаний математического маятника при изменении его длины?
Решение:
Период колебаний математического маятника определяется по формуле:
T = 2.
T’(l) = (2)’ = 2(()’ ·( )’ = 2 · (· = · = .
Ответ:
Задача 7
Заряд на пластинах конденсатора колебательного контура с течением времени изменяется по закону: q = 10-6. Записать уравнение зависимости силы тока от времени.
Дано:
q = 10-6
I(t) ?
Решение:
I(t) = q’(t) = 10-6· 104 = 10-2
Ответ: 10-2
Применение интеграла для решения задач по физике
Задача 1
Уравнение скорости материальной точки имеет вид: Напишите уравнение движения x = x(t).
Дано:
x = x(t)?
Решение:
x = = = 6· – 3· = 2t3 –t2.
Ответ: 2t3 –t2
Задача 2
По закону Гука сила упругости пропорциональна растяжению пружины. Сила в 100 Н растягивает пружину на 2 см. Какую работу она при этом совершает?
Дано:
F = 100 H
x = 0,02 м
А?
Решение:
По закону Гука: F = kx, k = .
K = 500
А =
A = = k·
A = 0,1 Дж
Ответ: 0,1 Дж
Задача 3
ЭДС изменяется по закону: = – 0,01 . Как изменяется магнитный поток?
Дано:
= – 0,01
Ф = Ф(t)?
Решение:
Ф = = = – 0,01 · (- =
0,01 .
Ответ: 0,01 .
Задача 4
Электрические заряды q1 = 1 нКл, q2 = 4 нКл расположены на расстоянии 20 см друг от друга. Найти работу по перемещению зарядов, если расстояние увеличилось до 40 см.
Дано:
q1 = 1 нКл
q2 = 4 нКл
r1 = 20 см
r2 = 40 см
А?
Решение:
По закону Кулона F =k .
A = = dr = kq1q2 = kq1q2 dr = kq1q2 ( =
= kq1q2(
A = 90·10-9 Дж = 90 нДж.
Ответ: 90 нДж.
Задача 5
Из шахты глубиной 200 м равномерно поднимают клеть весом 15 кН с помощью каната, намотанного на барабан. Вес каждого метра каната 30 Н. Какова работа, необходимая для поднятия клети.
Дано:
h = 200 м
P = 15 000Н
P0 = 30 Н
А?
Решение:
Работа, необходимая для поднятия клети, равна сумме работ для поднятия самой клети и каната.
А =А1 + А2
Работа по поднятию клети А1 = P h
Работа по поднятию каната А2 = = = P0· = P0· .
А = P h + P0· .
А = 3,6 · 106 Дж
Ответ: 6,6 МДж
Задача 6
На оси ОХ закреплено тело массой 10 кг. В точке с координатой 10 м находится тело массой 20 кг. Найти работу силу тяготения, если тело массой 20 кг перемещается в точку с координатой 20 м.
Дано:
m1 = 10 кг
m2 = 20 кг
r1 = 10 м
r2 = 20 м
А?
Решение:
Так как сила тяготения будет направлена к началу координат, поэтому
F = – .
A = = – = – = – G(- r)– 1 = G( – ).
A =
Задача 7
Найти работу изотермического расширения идеального газа под поршнем цилиндра, если площадь цилиндра S, объём изменяется от V1 до V2, а высота столба газа от L1 до L2.
Дано:
S, V1 ,V2
L1 ,L2
A?
Решение:
Работа силы давления газа равна
A = .
Cилы давления газа равна: F = PS
Из уравнения Менделеева-Клапейрона получается:
P = Обозначим как С. V = SL. Тогда А = = = = c .
dV = SdL, A = C ln = C(ln) = C·ln.
Ответ: C·ln
infourok.ru
Интегралы. Историческая справка. Применение интегралов на практике – Математический анализ. Интегральное исчисление
Имеется несколько типов интегралов: неопределенный и определенный интегралы, интеграл Римана и Римана-Стилтьеса, интеграл Лебега и Лебега-Стилтьеса, интеграл Даниэля. По области интегрирования интегралы подразделяются на кратные, криволинейные и поверхностные интегралы.Интеграл — одно из важнейших понятий математического анализа, которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по её производной (неопределённый интеграл). Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых.
Историческая справка
Основные понятия интегрального исчисления введены в работах Ньютона и Лейбница в конце XVII века. Лейбницу принадлежит обозначение интеграла , напоминающее об интегральной сумме, как и сам символ , от буквы («длинная s») — первой буквы в латинском слове summa (тогда ſumma, сумма)[1]. Сам термин «интеграл» предложен Иоганном Бернулли, учеником Лейбница. Обозначение пределов интегрирования в виде введено Фурье в 1820 году.
Строгое определение интеграла для случая непрерывных функций сформулировано Коши в 1823 году, а для произвольных функций — Риманом в 1853 году. Определение интеграла в смысле Лебега впервые дано Лебегом в 1902 году (для случая функции одной переменной и меры Лебега).
Интегрирование берет свое начало ещё в древнем Египте примерно с 1800 года до н. э., о чем свидетельствует Московский математический папирус (или математический папирус Голенищева). Первым известным методом для расчёта интегралов является метод для исследования площади или объёма криволинейных фигур – метод исчерпывания Евдокса (Евдокс Книдский (ок. 408 г. до н.э. – ок. 355 г. до н.э.) – древнегреческий математик, механик и астроном), который был предложен примерно в 370 до н. э. Суть этого метода заключается в следующем: фигура, площадь или объем которой пытались найти, разбивалась на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод получил свое дальнейшее развитие в работах древнегреческого математика, физика и инженера Архимеда (287 до н.э. – 212 до н.э.) для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны в Китае в третьем веке нашей эры китайским математиком Лю Хуэйем (ок. 220 – ок. 280), который с их помощью находил площадь круга. Для нахождения объёма шара этот метод использовали китайский математик, астроном, механик, писатель Цзу Чунчжи (429 – 500) вместе со своим сыном, также математиком и астрономом, правителем области и государственным казначеем, Цзу Гэном.
Далее большой шаг вперед в развитии интегрального исчисления был предпринят в 11 веке в Ираке арабским ученым-универсалом, математиком, механиком, физиком и астрономом Абу Али аль-Хасан ибн аль-Хасан ибн аль-Хайсам аль-Басри (965-1039) (или Ибн ал-Хайсамом, в Европе известном как Alhazen), который в своей работе “Об измерении параболического тела” приводит формулы для суммы последовательных квадратов, кубов и четвёртых степеней, и ряд других формул для сумм рядов. С помощью этих формул он проводит вычисление, равносильное вычислению определённого интеграла:
Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвёртой степени. Таким образом, он был близок к поиску общей формулы для интегралов от полиномов не выше четвёртой степени.
Следующий значительный толчок в исчислении интегралов состоялся лишь в 16 веке в работах итальянского математика Бонавентура Франческо Кавальери (1598 – 1647), в которых описывался предложенный им метод неделимых, а также в работах французского математика Пьера де Ферма (1601 – 1665). Этими учеными были заложены основы современного интегрального исчисления. Дальнейшее развитие связано с деятельностью английского математика, физика и богослова Исаака Барроу (1630 – 1677) и итальянского математика и физика, ученика Галилея Эванджелиста Торричелли (1608 – 1647), которые представили первые намеки на связь между интегрированием и дифференцированием.
За время становления интегрального исчисления менялось и обозначение интеграла. Английский физик, механик, математик и астроном Исаак Ньютон (1643 – 1727) использовал, правда не во всех своих работах, в качестве символа интегрирования значок квадрата перед обозначением функции или вокруг него, а также вертикальную черту над функцией, но эти обозначения не получили широкого распространения. Современное обозначение неопределённого интеграла было введено немецким философом, логиком, математиком, механиком, физиком, юристом, историком, дипломатом, изобретателем и языковедом Готфридом Вильгельмом Лейбницем (1646 – 1716) в 1675 году. Он образовал символ интеграла из буквы “длинная s” (от первой буквы слова Summa – сумма) Современное обозначение определённого интеграла, с указанием пределов интегрирования, было впервые предложено французским математиком и физиком Жаном Батистом Жозефом Фурье (1768 – 1830) в 1819-20 годах. Сам термин “интеграл” придумал швейцарский математик Якоб Бернулли (1654 – 1705) в 1690 году.
Применение интегралов на практике
Основной задачей дифференциального исчисления является определение для заданной функции ее производной или ее дифференциала . Обратная задача, состоящая в определении функции по ее известным производной или дифференциалу , представляет собой основную задачу интегрального исчисления.
Применение определенного интеграла математике
- Вычисление площади плоской фигуры в прямоугольных координатах.
- Вычисление площади плоской фигуры в полярных координатах.
- Вычисление объема тела вращения.
- Вычисление длины дуги кривой.
- Вычисление площади поверхности тела вращения. и т.д.
Применение определенного интеграла в физике
- Работа А переменной силы.
- S – (путь) перемещения пройденные телом.
- Вычисление массы.
- Вычисление момента инерции линии, круга, цилиндра.
- Вычисление координаты центра тяжести.
- Количество теплоты
- Давление жидкости на вертикальную пластинку и т.д.
Применение определенного интеграла в биологии
- Численность популяции.
- Биомасса популяции.
- Средняя длина пролета(пробега) животного и т.д.
Применение определенного интеграла в экономике
- дисконтированной стоимости денежного потока
- определение функции издержек
- прогнозирование материальных затрат,
- нахождение потребительского излишка
- определение объема выпуска продукции,
- определение экономической эффективности капитальных вложений (задача дисконтирования) и т.д.
intellect.ml
