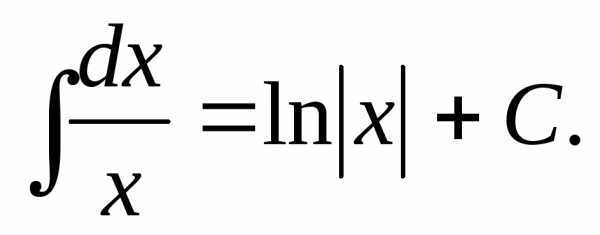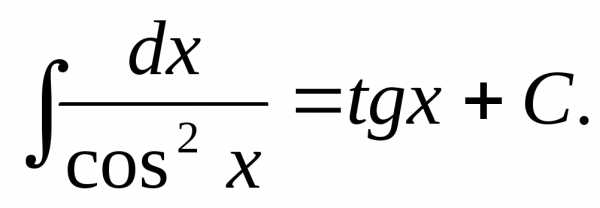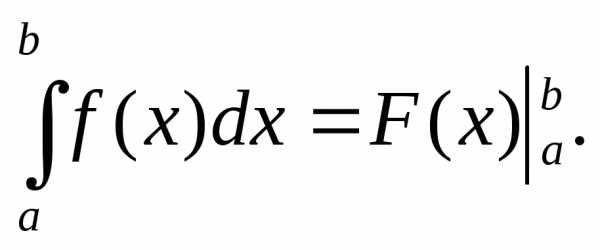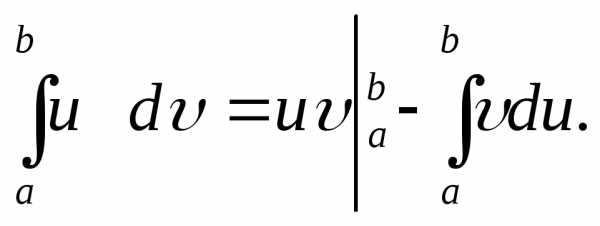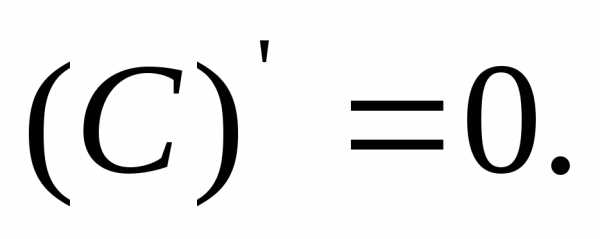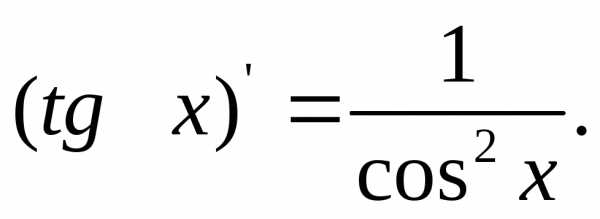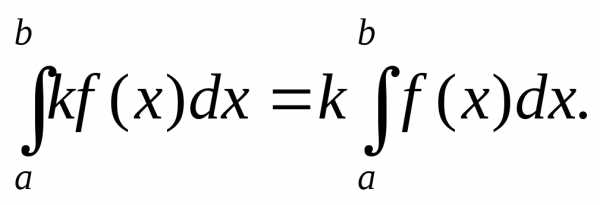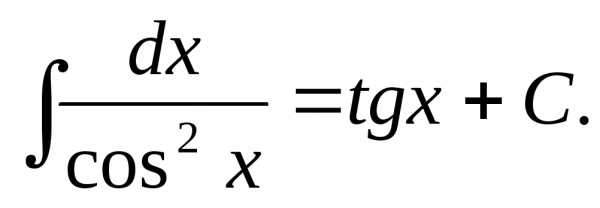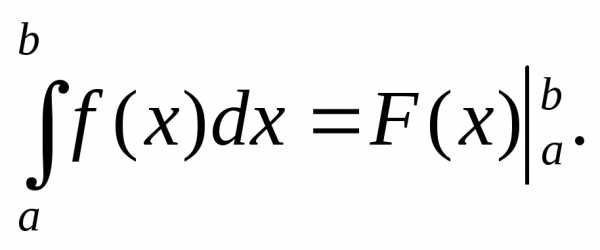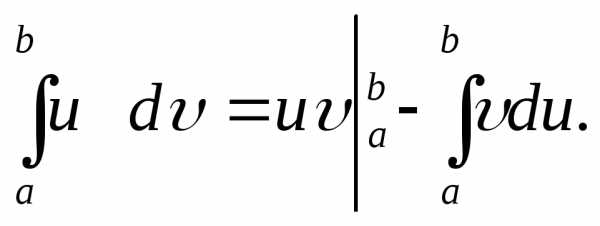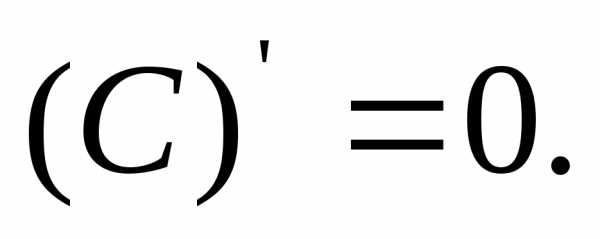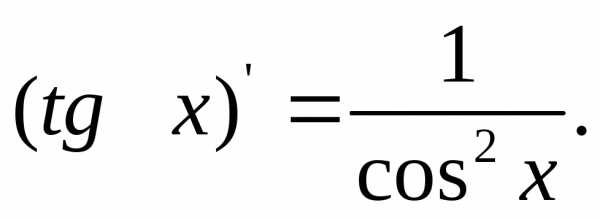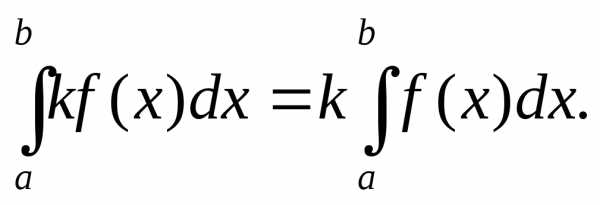Таблица производных и интегралов
Таблица производных. Табличные производные.
Производная степенной функции
Производная степенной функции
Производная экспоненциальной функции
Производная экспоненты
Производная сложной экспоненциальной функции
Производная экспоненциальной функции
Производная логарифмической функции
Производная натурального логарифма
Производная натурального логарифма функции
Производная синуса
Производная косинуса
Производная косеканса
Производная секанса
Производная арксинуса
Производная арккосинуса
Производная арксинуса
Производная арккосинуса
Производная тангенса
Производная котангенса
Производная арктангенса
Производная арккотангенса
Производная арктангенса
Производная арккотангенса
Производная арксеканса
Производная арккосеканса
Производная арксеканса
Производная арккосеканса
Производная гиперболического синуса
Производная гиперболического косинуса
Производная гиперболического тангенса
Производная гиперболического котангенса
Производная гиперболического секанса
Производная гиперболического косеканса
Таблица первообразных (“интегралов”). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром).
Интеграл степенной функции.
Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
Интеграл экспоненциальной функции.
Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.
Интеграл экспоненциальной функции.
Интеграл, равняющийся натуральному логорифму.
Интеграл : “Длинный логарифм”.
Интеграл : “Длинный логарифм”.
Интеграл : “Высокий логарифм”.
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму.
Интеграл : “Высокий логарифм”.
Интеграл косинуса.
Интеграл синуса.
Интеграл, равный тангенсу.
Интеграл, равный котангенсу.
Интеграл, равный как арксинусу, так и арккосинусу
Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арксинусу, так и арккосинусу.
Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл равный косекансу.
Интеграл, равный секансу.
Интеграл, равный арксекансу.
Интеграл, равный арккосекансу.
Интеграл, равный арксекансу.
Интеграл, равный арксекансу.
Интеграл, равный гиперболическому синусу.
Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому секансу.
Интеграл, равный гиперболическому косекансу.
Таблица основных интегралов: | Основные св-ва неопределённого интеграла: | ||
| |||
|
| ||
Основные методы интегрирования: | |||
Метод подстановки: формула замены переменной в неопределённом интеграле. | Метод интегрирования по частям: формула интегрирования по частям в неопределённом интеграле. | ||
Формула Ньюто-Лейбица(для определённого интеграла): тогда | Замена переменной в определённом интеграле: | ||
Интегрирование по частям в определённом интеграле:
| |||
Простейшие производные: | Основные св-ва определённого интеграла: | ||
|
|
| |
| |||
studfiles.net
Таблица основных интегралов: | Основные св-ва неопределённого интеграла: | ||
| |||
|
| ||
Основные методы интегрирования: | |||
Метод подстановки: формула замены переменной в неопределённом интеграле. | Метод интегрирования по частям: формула интегрирования по частям в неопределённом интеграле. | ||
Формула Ньюто-Лейбица(для определённого интеграла): тогда | Замена переменной в определённом интеграле: | ||
Интегрирование по частям в определённом интеграле:
| |||
Простейшие производные: | Основные св-ва определённого интеграла: | ||
|
|
| |
| |||
studfiles.net