Таблица производных простых функций
Пояснение:При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение:
В данном случае, при каждом изменении аргумента функции (х) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.
Откуда следует, что
(cx + b)’ = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю
|x|’ = x / |x| при условии, что х ≠ 0
Пояснение:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
( xc )’= cxc-1, при условии, что xc и сxc-1,определены а с ≠ 0
Пример:
(x2 )’ = 2x
(x3)’ = 3x2
Для запоминания формулы:
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу. Например, для x2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x
6. Производная дроби 1/х
(1/х)’ = – 1 / x2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)’ = (x-1 )’ , тогда можно применить формулу из правила 5 таблицы производных
(x-1 )’ = -1x-2 = – 1 / х2
7. Производная дроби с переменной произвольной степени в знаменателе
( 1 / xc )’ = – c / xc+1
Пример:
( 1 / x2 )’ = – 2 / x3
8. Производная корня (производная переменной под квадратным корнем)
( √x )’ = 1 / ( 2√x ) или 1/2 х-1/2
Пример:
( √x )’ = ( х1/2 )’ значит можно применить формулу из правила 5
( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
( n√x )’ = 1 / ( n n√xn-1 )
.
Приведенная здесь таблица производных простых функций содержит только основные преобразования, которые (по большому счету) следует запомнить наизусть. Нахождение более сложных производных приведены в соответствующих таблицах других уроков:
profmeter.com.ua
Что такое производная
Производная – главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
То есть,
(1)
Наиболее употребительны следующие обозначения производной:
Пример 1. Пользуясь определением производной, найти производную функции
.
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
.
Найдём отношение приращения функции к приращению аргумента:
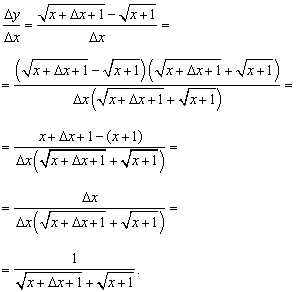
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле – задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения
постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути.
Такая характеристика тем точнее, чем меньше промежуток времени .
Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени
(при условии, что этот предел существует и конечен).
Так выясняется, что мгновенная скорость есть предел отношения приращения функции s(t) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.
.
Решение обозначенной задачи представляет собой физический смысл производной. Итак, производной функции y=f
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при , то есть производную:
Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .
Из определения следует, что для существования касательной достаточно, чтобы существовал предел
,
причём предел равен углу наклона касательной к оси .
Теперь дадим точное определение касательной.
Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x
где – угол наклона касательной к оси абсцисс, т.е. угловой коэффициент касательной.
Пример 3. Найти производную функции и значение этой производной при .
Решение. Воспользуемся схемой, приведённой в примере 1.
Шаг 1.
Шаг 2.
Шаг 3.
Шаг 4.
Выражение под знаком предела не определено при (неопределённость вида 0/0), поэтому преобразуем его, избавившись от иррациональности в числителе и затем сократив дробь:
Найдём значение производной при :
Весь блок “Производная”
function-x.ru
Производная, таблица производных. Нравственное воспитание
Дополнительные сочиненияНа этом уроке мы повторим определение производной и таблицу производных.
В начале урока мы определим понятие приращения функции и приращения аргумента и их отношения, дадим геометрическую интерпретацию этого отношения. Далее мы дадим определение производной через отношение приращений и рассмотрим геометрический смысл производной. Повторим таблицу основных производных и вспомним правила дифференцирования и производную сложной функции.
В конце урока мы решим несколько примеров на нахождение производной сложной функции.
Тема: Повторение курса алгебры 10 класса
Урок: Производная. Таблица производных
1. Определение производной, ее физический и геометрический смысл
Рассмотрим функцию и ее график (Рис. 1). Для наглядности будем использовать физическую интерпретацию производной.
Рис. 1.
Аргументом пусть будет время . Зависимой переменной пусть будет – расстояние до дома. График функции показывает путь до дома в каждый момент времени.
– момент времени. В этот момент времени мы находимся на расстоянии от дома.
Через некоторое время мы будем находиться на расстоянии от дома. Мы имеем приращение аргумента – , и приращение функции – .
Получим треугольник, у которого катеты равны приращению аргумента, приращению функции, а гипотенуза АВ – секущая, где – тангенс угла наклона этой секущей.
Нас интересует отношение приращения функции к приращению аргумента.
Во-первых, мы получим среднюю скорость. Таков физический смысл.
А геометрический смысл состоит в том, что мы получим тангенс угла наклона секущей.
За конечное время может произойти множество событий, и все их надо уловить, отразить. Для этого устремим к 0. То есть мы будем рассматривать ближайшие точки к точке . Но если приращение аргумента стремится к 0, то приращение функции также стремится к 0. Тогда секущая АВ будет стремиться занять положение касательной к графику в точке А. Рассмотрим, что произойдет с отношением:
Более строгое определение
Такой предел называется производной функции и обозначается .
Каков физический и геометрический смысл производной?
– это мгновенная скорость в момент . Таков физический смысл производной.
Геометрический смысл: – тангенс угла наклона касательной в точке .
Мы вспомнили определение производной, ее физический и геометрический смысл.
Следующей нашей целью будет вспомнить технику дифференцирования, то есть технику нахождения производных.
2. Таблица производных
1. (производная от постоянной величины является нулем)
Например: , поскольку тангенс – величина постоянная и от не зависит.
2. Следующая функция линейная:
То есть производной от линейной функции является ее угловой коэффициент.
Например:
3.
4.
5.
6.
7.
8.
3. Правила нахождения производных
1.
То есть производная суммы равна сумме производных
.
2.
То есть константу можно выносить за знак производной.
.
3. Производная произведения:
4. Производная частного:
4. Производные сложных функций
Тогда:
1.
а.
б.
2.
а.
б.
3.
а.
б.
4.
5.
а.
б.
6.
а.
б.
Мы повторили определение производной и таблицу производной. Следующий урок посвятим исследованию функций с помощью производных.
Список литературы
1. Мордкович А. Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Mathprofi. ru .
2. Math34.ru .
3. Википедия .
Домашнее задание
1. Найдите производные функций:
2. Найдите значения производной в точках
.
3. Найдите производную функции .
4. Алгебра и начала анализа, Мордкович А. Г.: № 750-752, 760, 761.
dp-adilet.kz
Решение производных
Для того чтобы понять определение производной рассмотрим следующий график функции.
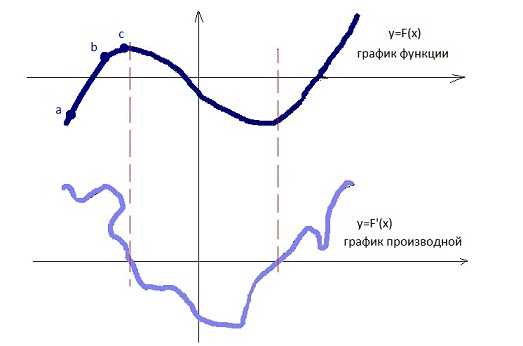
Рис.1. Пример функции и ее производной.
Глядя на рисунок можно увидеть места, где функция растет быстрее, а где убывает. Например, с точки a до точки b график поднимается стремительнее, чем с точки b до точки c.
Если перенести точки с графика функции на новую систему координат таким образом, чтобы точки возрастания располагались выше по оси x, а точки убывания ниже оси x (соблюдая масштаб) и соединить эти точки, то получится новый график новой функции (нижний график на рис. 1). Данная функция и есть производная от основной функции. Данный график есть не что иное, как показатель скорости изменения функции. Другими словами, производная – показатель скорости изменения функции. На практике производные применяются для определения скорости изменения каких-нибудь процессов: физических, химических, экономических и т.д.
Если говорить более сложным языком, то производная – это предел, к которому стремится отношение приращения x к приращению y. В общем виде производная функция выглядит и определяется следующим образом:
Процесс вычисления производной функции называется дифференцированием.
Функций на практике встречается великое множество, но есть простые функции (элементарные), такие как, F(x)=sinx, F(x)=C (где С-константа), F(x)=lnx и т.д. Для этих элементарных функций уже определены производные, и достаточно выучить их наизусть. Производные простых (элементарных) функций приведены в таблице ниже.
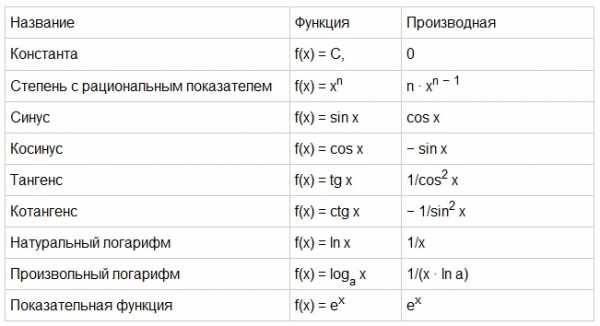
Рис.2. Таблица производных простых (элементарных) функций.
Решение производных, говоря простым языком, заключается в превращении одной функции в другую, следуя определенным правилам (исключением, является экспоненциальная функция F(x)=e^x, которая не меняется).
Рассмотрим пример. Необходимо найти производную функции F(x)=х^3 + 3x^2 – 72x + 90
Для решения производной достаточно воспользоваться таблицей производных простых (элементарных) функций. В соответствии с данными из таблицы получим производную:
F’(x)= (х^3 + 3x^2 – 72x + 90)’=3x^2+6x-72
Решение сложных производных
На практике с решением производных сложных функций приходится сталкиваться значительно чаще, чем с простыми.
Правило определения производной сложной функции выглядит следующим образом:
(a(b))’=a’(b)*b’, где a-внешняя функция, b-внутренняя функция.
Рассмотрим пример
Необходимо найти производную функции F(x)=sin(3x-5)
Найти производную данной функции, воспользовавшись таблицей простых (элементарных) функций, не получится, так как под sin находится целое выражение, т.е. функция состоит из двух функций a=sin(x)(внешняя функция) и b=3x-5 (внутренняя функция).
Воспользуемся правилом определения производной сложной функции и получим:
F’(x)=(sin(3x-5))’=cos(3x-5)*(3x-5)’=3cos(3x-5).
заметка: деревянные окна (http://www.woodlan.ru/) и Продвижение товара и услуг в интернете недорого от частного специалиста подробнее на http://seoshnig.ru.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Как брать производную? Высшая математика, производная.
На самом деле брать производную не так уж и трудно, главное хорошенько проработать алгоритм.
Кстати если после просмотра материала у вас будут трудности пишите МНЕ, я дешево помогу вам решить примеры.
Итак, без чего мы не сможем обойтись? Конечно же таблица производных!
Таблица производных
в данной таблице указаны значения производной простейших функций, внимательно изучите таблицу производных, после чего можно приступать к решению заданий.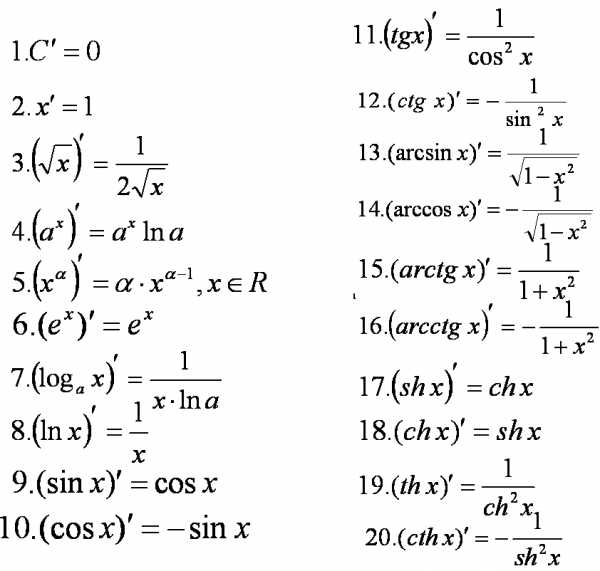
Данная таблица поможет нам брать производные от тригонометрических и логарифмических функций.
Теперь разберем поэтапно как брать производную, начиная с самых простых и элементарных функций.
Сперва разберем самые простые производные.
Если вы еще не поняли смотрим более легкие уроки.
matematikaprosta.ru
Производные простых тригонометрических функций
Для нахождения производной тригонометрической функции нужно пользоваться таблицей производных, а именно производными 6-13.
При нахождении производных простых тригонометрических функций во избежание распространённых ошибок следует обращать внимание на следующие моменты:
- в выражении функции часто одно из слагаемых представляет собой синус, косинус или другую тригонометрическую функцию не от аргумента функции, а от числа (константы), поэтому производная этого слагаемого равна нулю;
- почти всегда нужно упростить выражение, полученное в результате дифференцирования, а для этого нужно уверенно пользоваться знаниями по действиям с дробями;
- для упрощения выражения почти всегда нужно знать тригонометрические тождества, например, формулу двойного угла и формулу единицы как сумму квадратов синуса и косинуса.
Пример 1. Найти производную функции
.
Решение. Допустим, с производной косинуса всё понятно, скажут многие, начинающие изучать производные. А как быть с производной синуса двенадцати, делённых на пи? Ответ: считать равной нулю! Здесь синус (функция всё-таки!) – ловушка, потому что аргумент – не переменная икс или любая другая переменная, а просто число. То есть, синус этого числа – тоже число. А производная числа (константы), как мы знаем из таблицы производных, равна нулю. Итак, оставляем только минус синус икса и находим его производную, не забывая про знак:
.
Ответ:
.
Пример 2. Найти производную функции
.
Решение. Второе слагаемое – тот же случай, что и первое слагаемое в предыдущем примере. То есть, число, а производная числа равна нулю. Находим производную второго слагаемого как производную частного:
Ответ:
Пример 3. Найти производную функции
.
Решение. Это уже другая задача: здесь в первом слагаемом нет ни арксинуса, ни другой тригонометической функции, но есть икс, а значит, это функция от икса. Следовательно, дифференцируем её как слагаемое в сумме функций:

Здесь потребовались навыки в действиях с дробями, а именно – в ликвидации трёхэтажности дроби.
Пример 4. Найти производную функции
.
Решение. Здесь буква “фи” играет ту же роль, что “икс” в предыдущих случаях (и в большинстве других, но не во всех) – независимой переменной. Поэтому, когда будем искать производную произведения функций, не будем спешить объявлять равной нулю производную корня от “фи”. Итак:
Но на этом решение не заканчивается. Так как в двух скобках собраны подобные члены, от нас ещё требуется преобразовать (упростить) выражение. Поэтому умножаем скобки на вынесенные за них множители, а далее приводим слагаемые к общему знаменателю и выполняем другие элементарные преобразования:

Пример 5. Найти производную функции
.
Решение. В этом примере от нас потребуется знание того факта, что существует такая тригонометрическая функция – секанс – и её формулы через косинус. Дифференцируем:
Пример 6. Найти производную функции
.
Решение. В этом примере от нас потребуется помнить из школьного курса формулу двойного угла. Но сначала дифференцируем:
Далее применяем следующие тригонометрические тождества:
,
(это и есть формула двойного угла)
и получаем:
.
Пример 7. Найти производную функции
.
Решение. В этом примере от нас потребуется всего-то лишь умение сокращать дроби. И внимание – не забыть, что дробь нужно сократить. Это сделано на последнем шаге решения:
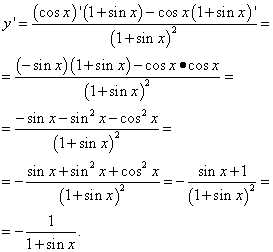
В решении применено тригонометрическое тождество:
.
Поделиться с друзьями
Весь блок “Производная”
function-x.ru
|
|
|
|
Производная экспоненциальной функции |
Производная экспоненты |
|
Производная сложной экспоненциальной функции |
Производная экспоненциальной функции |
|
|
|
|
|
Производная натурального логарифма функции |
|
|
Производная косинуса |
|
Производная косеканса |
Производная секанса |
|
|
|
|
Производная арксинуса |
Производная арккосинуса |
|
|
|
|
|
|
|
|
|
|
Производная арксеканса |
Производная арккосеканса |
|
Производная арксеканса |
Производная арккосеканса |
|
|
|
|
|
Производная гиперболического котангенса |
|
Производная гиперболического секанса |
Производная гиперболического косеканса |
tehtab.ru
