Разделы механики в физике – Основные разделы механики конспект лекций и задачи для 9 класса

Основные разделы механики конспект лекций и задачи для 9 класса

ФЕДЕРАЛЬНОЕ АГЕНТСТВО

ПО ОБРАЗОВАНИЮ

МОСКОВСКИЙ

ИНЖЕНЕРНО‑ФИЗИЧЕСКИЙ ИНСТИТУТ

(ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)

Для физико-математического лицея

Москва 2008

УДК 531(075)

ББК 22.251я7

О-75

Основные разделы механики. Конспект лекций и задачи для 9 класса/ М.М. Астахов, А.Б. Батеев, С.Н. Борисов, В.И. Кондарь, Л.А. Корнеева, В.Н. Маскалец, О.М. Сторожук. М.: МИФИ, 2009.-116 с.

Учебно-методическое пособие структурно состоит из трех частей. Первая часть содержит теоретический материал, включающий в себя основные положения, определения и законы кинематики, динамики, законов сохранения в соответствии с программой по физике лицея при МИФИ.

В приложениях, которые являются второй частью пособия, даны необходимые математические определения и формулы, а также приведена методика решения задач.

Третья часть содержит задачи по вышеприведенным разделам физики.

Пособие предназначено для учеников 9-х классов физико-ма-тематических лицеев.

Рекомендовано редсоветом института

в качестве учебно-методического пособия

Isbn 978-5-7262-0952-4

© Астахов М.М., Батеев А.Б., Борисов С.Н., В.И. Кондарь,

Л.А. Корнеева, Маскалец В.Н.,О.М. Сторожук , 2008, 2009

© Московский инженерно‑физический институт

(государственный университет), 2008, 2009

Тема 1. Кинематика

Механика  раздел физики, в котором изучается движение тел или их частей относительно друг друга.

Кинематика  раздел механики, в котором движение тел изучается без рассмотрения причин, его вызывающих.

§1. Скорость материальной точки

Движение (механическое)  изменение положения тела в пространстве относительно другого тела (других тел) с течением времени.

Для описания движения тела необходима система отсчета.

Система отсчета  система, состоящая из тела отсчета, связанной с ним системы координат и счетчика времени (например, часов).

Время t  скалярная физическая величина (СФВ), служащая для определения последовательности событий и длительности процессов.

Единица времени  секунда: [ t ] = с.

Промежуток времени t  СФВ, равная разности между конечным (t_к) и начальным (t_н) моментами времени:

(1.1)

Промежуток времени является приращением (изменением) времени.

Промежуток времени  величина положительная:

t > 0. (1.2)

Материальная точка (м.т.)  тело, размерами которого можно пренебречь в данной задаче.

Траектория  непрерывная линия, образованная совокупностью точек пространства, последовательно проходимых движущейся материальной точкой.

Траектории подразделяются на прямолинейные и криволинейные. Траектория и ее вид зависят от системы отсчета.

Кинематическое уравнение (закон) движения материальной точки  зависимость радиус-вектора м.т. от времени:

(1.3)

или эквивалентная ей система зависимостей координат м.т. от времени (при движении в одной плоскости):

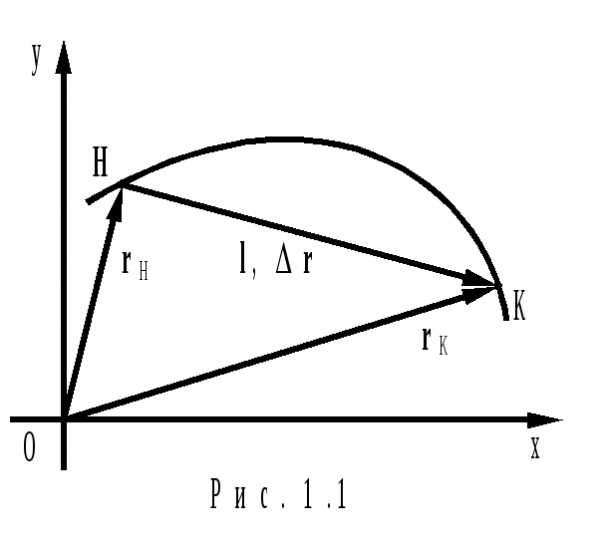
(1.4)

На рис.1.1 показана траектория материальной точки, являющаяся графиком зависимости y(х), которая может быть получена исключением времени t из зависимостей x(t) и y(t).

Длина пути (путь) S, S  СФВ, равная длине траектории от начального (при t = t_н) до конечного (при t = t_к) положений материальной точки.

Путь  неотрицательная и неубывающая величина.

На показанной траектории (см. рис.1.1) путь м.т. за промежуток времени от t_н до t_к равен длине линии НК.

Перемещение l  вектор, начало и конец которого совпадают с начальным (t = t

н) и конечным (t = t_к) положениями м.т. соответственно.

Перемещение равно приращению радиус-вектора м.т.:

(1.5)

где r_к и r_н  радиус-векторы конечного и начального положений м.т. соответственно (рис.1.1).

Единица пути и перемещения — метр: [S = l] = м.

Средняя путевая скорость <v_s>  СФВ, равная отношению пути S к промежутку времени t, за который пройден этот путь:

(1.6)

Если известны пути S_i (рис.1.2) за соответствующие им промежутки времени t_i (i = 1,2,…,n), такие, что выполняются равенства:

(1.7)

(1.8)

то средняя путевая скорость за весь промежуток времени t может быть найдена по формуле:

(1.9)

Путевая скорость (мгновенная) v_s  СФВ, равная пределу отношения пути S к промежутку времени t, за который этот путь был пройден, при бесконечном уменьшении промежутка времени:

(1.10)

Средняя скорость <v>  векторная физическая величина (ВФВ), равная отношению перемещения r к промежутку времени t, за который это перемещение произошло:

(1.11)

Направление средней скорости за некоторый промежуток времени t совпадает с направлением перемещения м.т. за этот же промежуток времени (см. рис.1.2).

Скорость (мгновенная) v  ВФВ, равная пределу отношения перемещения r к промежутку времени t, за который это перемещение произошло, при бесконечном уменьшении промежутка времени:

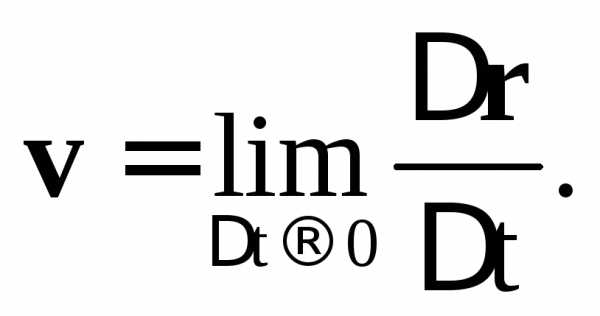(1.12)

Скорость направлена по касательной к траектории в данной точке (на рис.1.3 — в т.Н).

Единица скорости — метр в секунду: [v] = м/с.

Модуль скорости равен путевой скорости:

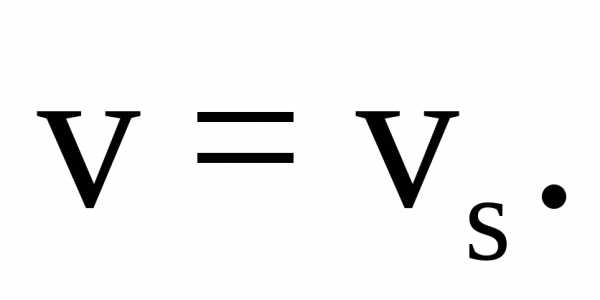(1.13)

studfiles.net

Механика | Наука | FANDOM powered by Wikia

Меха́ника (греч. μηχανική — искусство построения машин) — техническая наука, выделившаяся из прикладной физики; наука о движении и силах, вызывающих движение. Предельными случаями механики являются небесная механика (механика движения небесных тел и гравитации) и квантовая механика (механика элементарных частиц и электромагнитного взаимодействия).

Механическая система Править

Объекты, изучаемые механикой, называются механическими системами. Механическая система обладает определённым числом k степеней свободы и описывается с помощью обобщённых координат q₁, … q_k. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.

Наиболее важными механическими системами, в порядке увеличения сложности, являются:

Разделы механики Править

Стандартные («школьные») разделы механики:

кинематика, статика, динамика. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:

Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идет не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошной среды.

Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. В классической формулировке, механика строится на трёх законах Ньютона. Решение многих задач механики упрощается, если ограничиться только потенциальным взаимодействием тел, поскольку в этом случае интегрирование уравнений движения приводит к закону сохранения энергии.

Лагранжева механика Править

Все три закона Ньютона можно вывести из экстремального принципа. В этой формулировке, механика строится как следствие одного-единственного утверждения: все тела движутся так, чтобы обеспечить минимальность действия. Такая формулировка называется лагранжевой механикой.

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.

Границы применимости классической механики Править

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

• Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
• При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
• Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

---

---

ru.science.wikia.com

Физика. – Механика

Меха́ника (греч.μηχανική — искусство построения машин) — наука о движении материальных объектов и взаимодействии между ними; в узком смысле — техническая наука, выделившаяся из прикладной физики. Предельными случаями механики являются небесная механика (механика движения небесных тел и гравитации) и квантовая механика (механика элементарных частиц и других малых тел). Механическая система Объекты, изучаемые механикой, называются механическими системами. Механическая система обладает определённым числом kстепеней свободы и описывается с помощью обобщённых координат q1, … qk. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени. Наиболее важными механическими системами, в порядке увеличения сложности, являются: материальная точка математический маятник крутильный маятник абсолютно твердое тело деформируемое тело абсолютно упругое тело сплошная среда Разделы механики Стандартные («школьные») разделы механики: кинематика, статика, динамика. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы: теоретическая механика небесная механика квантовая механика классическая механика сопротивление материалов строительная механика теория колебаний (аналитическая динамика) теория упругости теория пластичности теория устойчивости и катастроф стохастическая динамика. нелинейная динамика вычислительная механика Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идет не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошной среды. Основной математический аппарат классической механики:дифференциальное и интегральное исчисление, разработанное специальнодля этого Ньютоном и Лейбницем. В классической формулировке, механикастроится на трёх законах Ньютона.Решение многих задач механики упрощается, если ограничиться толькопотенциальным взаимодействием тел, поскольку в этом случаеинтегрирование уравнений движения приводит к закону сохранения энергии. Различные формулировки механики Все три закона Ньютона для широкого класса механических систем можно вывести из экстремального принципа. В этой формулировке механика строится как следствие одного-единственного утверждения — принципа наименьшего действия: все тела движутся так, чтобы обеспечить минимальность действия. Такая формулировка называется лагранжевой механикой. Уравнения движения в ней — уравнения Эйлера — Лагранжа. Аналогично, если считать независимыми переменными, описывающими состояние системы, обобщённые координаты и импульсы, а не обобщённые координаты и их производные по времени, то можно придти к гамильтоновой механике. Уравнения движения в ней — уравнения Гамильтона. Наконец, если отталкиваться от функции действия, определённой какдействие по реальной траектории системы, соединяющей некую начальнуюточку с произвольной конечной, то возникает механика Гамильтона — Якоби, аналогом уравения движения в которой является уравнения Гамильтона — Якоби. Следует отметить, что все эти формулировки несколько менее общие,чем классическая формулировка механики, основанная на силах, иногданазываемая собственно ньютоновой механикой. Не все механическиесистемы, движение которых может быть описано в её рамках, имеютуравнения движения, выводимые как уравнения Эйлера — Лагранжа,уравенения Гамильтона или сводимые к уравнению Гамильтона — Якоби. Темне менее, все формулировки являются как полезными с практической точкизрения, так и плодотворными с теоретической. Лагранжева формулировкаоказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике. Классическая механика Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта. Границы применимости классической механики В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность. Свойства микромира не могут быть поняты в рамках классическоймеханики. В частности, в сочетании с термодинамикой она порождает рядпротиворечий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика.Подчеркнём, что переход от классической к квантовой механике — это непросто замена уравнений движения, а полная перестройка всейсовокупности понятий (что такое физическая величина, наблюдаемое,процесс измерения и т. д.) При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности.Опять же, этот переход подразумевает полный пересмотр парадигмы, а непростое видоизменение уравнений движения. Если же, пренебрегая новымвзглядом на реальность, попытаться всё же привести уравнение движения квиду F = ma, то придётся вводить тензор масс, компонентыкоторого растут с ростом скорости. Эта конструкция уже долгое времяслужит источником многочисленных заблуждений, поэтому пользоваться ейне рекомендуется. Классическая механика становится неэффективной при рассмотрениисистем с очень большим числом частиц (или же большим числом степенейсвободы). В этом случае практически целесообразно переходить к статистической физике.

fizika.my1.ru

Механика – это… Что такое Механика?

Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве^[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика.

Механическая система

Механика занимается изучением так называемых механических систем.

Механическая система обладает определённым числом степеней свободы, а её состояние описывается с помощью обобщённых координат и соответствующих им обобщённых импульсов . Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.

Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.

Наиболее важными механическими системами являются:

Разделы механики

Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:


Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.

Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).

Различные формулировки механики

Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.

Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.

Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.

Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.

Классическая механика

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.

Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

• Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
• При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду , то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
• Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

См. также

Примечания

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.

biograf.academic.ru

Механика – это… Что такое Механика?

Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве^[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика.

Механическая система

Механика занимается изучением так называемых механических систем.

Механическая система обладает определённым числом степеней свободы, а её состояние описывается с помощью обобщённых координат и соответствующих им обобщённых импульсов . Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.

Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.

Наиболее важными механическими системами являются:

Разделы механики

Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:


Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.

Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).

Различные формулировки механики

Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.

Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.

Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.

Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.

Классическая механика

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.

Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

• Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
• При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду , то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
• Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

См. также

Примечания

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.

dik.academic.ru

Механика — Википедия

Меха́ника (греч. μηχανική — искусство построения машин) — раздел физики, наука, изучающая движение материальных тел и взаимодействие между ними; при этом движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве^[1].

Предмет механики и её разделы

По поводу предмета механики уместно сослаться на слова авторитетного учёного-механика С. М. Тарга из введения к 4-му изданию его широко известного учебника^[2] теоретической механики: «Механикой в широком смысле этого слова называется наука, посвящённая решению любых задач, связанных с изучением движения или равновесия тех или иных материальных тел и происходящих при этом взаимодействий между телами. Теоретическая механика представляет собою часть механики, в которой изучаются общие законы движения и взаимодействия материальных тел, то есть те законы, которые, например, справедливы и для движения Земли вокруг Солнца, и для полёта ракеты или артиллерийского снаряда и т. п. Другую часть механики составляют различные общие и специальные технические дисциплины, посвящённые проектированию и расчёту всевозможных конкретных сооружений, двигателей, механизмов и машин или их частей (деталей)»^[3].

В приведённом высказывании упущен из виду тот факт, что изучением общих законов движения и взаимодействия материальных тел занимается также и механика сплошных сред (или механика сплошной среды) — обширная часть механики, посвящённая движению газообразных, жидких и твёрдых деформируемых тел. В этой связи академик Л. И. Седов отмечал: «В теоретической механике изучаются движения материальной точки, дискретных систем материальных точек и абсолютно твёрдого тела. В механике сплошной среды … рассматриваются движения таких материальных тел, которые заполняют пространство непрерывно, сплошным образом, и расстояния между точками которых во время движения меняются»^[4].

Таким образом, по предмету изучения механика подразделяется на:

Другой важнейший признак, используемый при подразделении механики на отдельные разделы, основан на тех представлениях о свойствах пространства, времени и материи, на которые опирается та или иная конкретная механическая теория. По данному признаку в рамках механики выделяют такие разделы:

Видео по теме

Механическая система

Механика занимается изучением так называемых механических систем.

Механическая система обладает определённым числом k{\displaystyle k} степеней свободы, а её состояние описывается с помощью обобщённых координат q1,…qk{\displaystyle q_{1},\dots q_{k}} и соответствующих им обобщённых импульсов p1,…pk{\displaystyle p_{1},\dots p_{k}}. Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.

Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.

Наиболее важными механическими системами являются:

Важнейшие механические дисциплины

Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся по содержанию) механические дисциплины:

Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.

Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).

Различные формулировки механики

Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.

Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.

Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.

Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.

Классическая механика

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.

Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

• Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см. Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
• При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F=ma{\displaystyle F=ma}, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
• Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

См. также

Примечания

1. ↑ Механика  — Статья в Физической энциклопедии
2. ↑ На конец 2012 г. выдержал 18 изданий на русском языке и издан в переводах не менее, чем на 14 языках.
3. ↑ Тарг С. М. Краткий курс теоретической механики. 4-е изд. — М.: Наука, 1966. — С. 11.
4. ↑ Седов, т. 1, 1970, с. 9.

Литература

• Билимович Б. Ф.  Законы механики в технике. — М.: Просвещение, 1975. — 175 с.
• Голубев Ю. Ф.  Основы теоретической механики. 2-е изд. — М.: Изд-во МГУ, 2000. — 720 с. — ISBN 5-211-04244-1.
• Киттель Ч., Найт У., Рудерман М.  Механика. Берклеевский курс физики. — М.: Лань, 2005. — 480 с. — ISBN 5-8114-0644-4.
• Ландау Л. Д., Лифшиц Е. М.  Теоретическая физика. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2004. — 224 с. — ISBN 5-9221-0055-6.
• Маркеев А. П.  Теоретическая механика: Учебник для университетов. 3-е изд. — М.; Ижевск: РХД, 2007. — 592 с. — ISBN 978-5-93972-604-7.
• Матвеев А. Н.  Механика и теория относительности. 3-е изд.. — М.: ОНИКС 21 век: Мир и Образование, 2003. — 432 с. — ISBN 5-329-00742-9.
• Седов Л. И.  Механика сплошной среды. Том 1.. — М.: Наука, 1970. — 492 с.
• Седов Л. И.  Механика сплошной среды. Том 2.. — М.: Наука, 1970. — 568 с.
• Сивухин Д. В.  Общий курс физики. Т. 1. Механика. 5-е изд. — М.: Физматлит, 2006. — 560 с. — ISBN 5-9221-0715-1.
• С.П. Стрелков. Механика. — Москва : Наука, 1975. — 560 с. — (Общий курс физики). — 60 000 экз.
• ред. Григорьян А. Т., Погребысский И. Б. История механики с древнейших времен до конца XVIII века. — М.: Наука, 1971. — 296 с. — 3600 экз. (в пер., суперобл.)
• ред. Григорьян А. Т., Погребысский И. Б. История механики с конца XVIII века до середины XX века. — М.: Наука, 1972. — 412 с.
• Хайкин С.Э. Физические основы механики. — 2. — Москва : Наука, 1971. — 752 с. — (Общий курс физики). — 49 000 экз.

wikipedia.green

Механика – это… Что такое Механика?

Меха́ника (греч. μηχανική — искусство построения машин) — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве^[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика.

Механическая система

Механика занимается изучением так называемых механических систем.

Механическая система обладает определённым числом степеней свободы, а её состояние описывается с помощью обобщённых координат и соответствующих им обобщённых импульсов . Задача механики состоит в изучении свойств механических систем, и, в частности, в выяснении их эволюции во времени.

Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на изолированные (замкнутые), закрытые и открытые, по принципу изменения свойств во времени — на статические и динамические.

Наиболее важными механическими системами являются:

Разделы механики

Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся) разделы:


Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.

Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).

Различные формулировки механики

Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.

Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.

Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.

Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.

Классическая механика

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта.

Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

• Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)
• При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду , то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
• Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

См. также

Примечания

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.

dikc.academic.ru