Вычисление определителя методом Гаусса
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
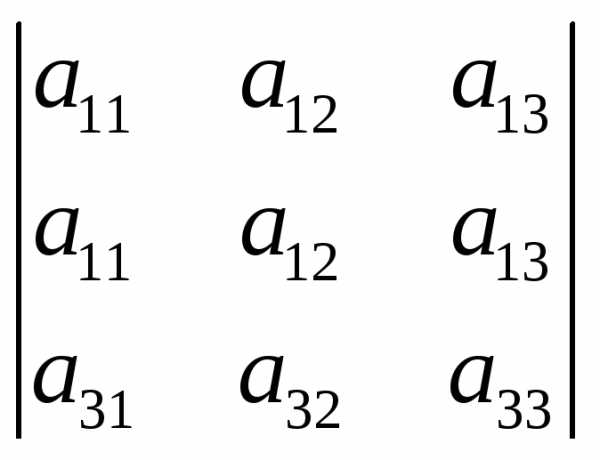 (1)
(1)
элемент должен быть равен
должен быть равен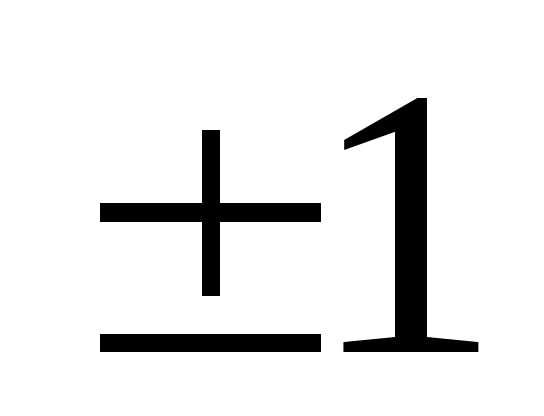 ,
для этого первую строку разделим на
,
для этого первую строку разделим на .
.
Получим определитель вида  (2)
(2)
 ,
далее из третьей строки вычтем первую,
умноженную на
,
далее из третьей строки вычтем первую,
умноженную на .
Получим определитель вида
.
Получим определитель вида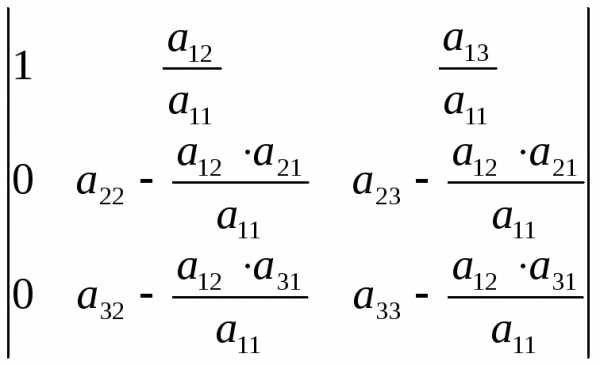 .
.Обозначим его элементы буквой с, тогда
 (3)
(3)
Теперь надо обнулить элемент  .
Элемент
.
Элемент
 ,
для этого вторую строку разделим на
,
для этого вторую строку разделим на .
Получим определитель вида
.
Получим определитель вида .
. Далее из третьей строки вычтем вторую,
умноженную на  .
.
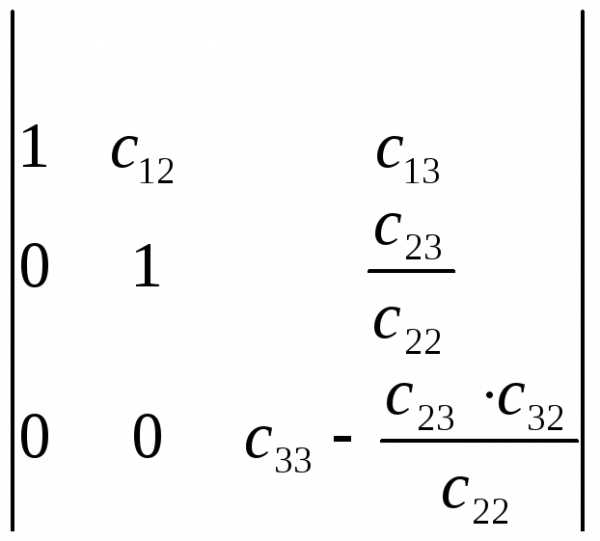 .
.
Обозначим его элементы буквой t, тогда
 (4)
(4)
Вот мы привели определитель к треугольному виду, теперь он равен .
Разберем теперь это на конкретном примере.
Пример 4:Вычислить определитель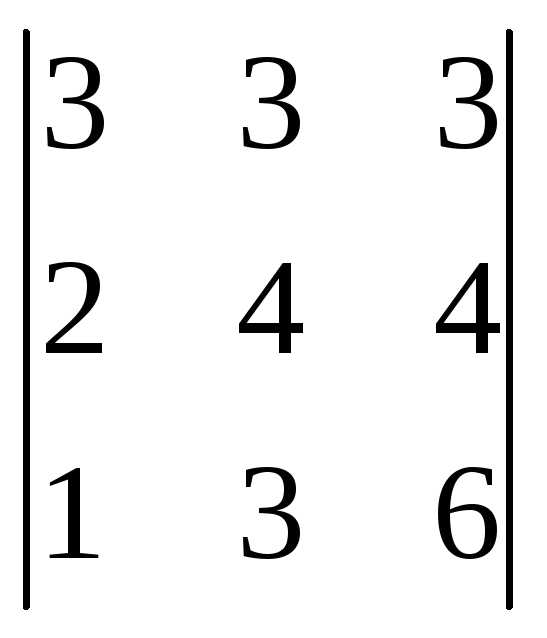 методом Гаусса.
методом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили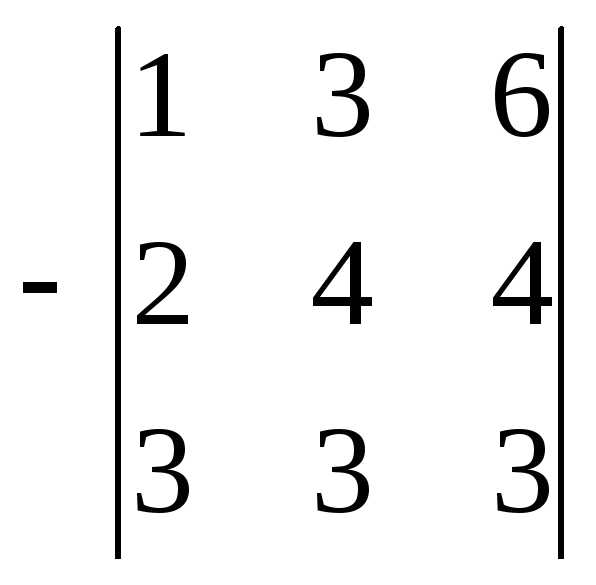
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили 
Далее из третьей строки вычтем вторую, умноженную на 3.
Получили – 
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностьюm nи пишут
nи пишут .
.
Определение 8: Если ,
то матрица называется квадратной.
,
то матрица называется квадратной.
Определение 9:Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10:Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11:Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12:Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.
Определение 13:Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е. 
Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен.
Пример 6: Найти матрицу, если
Решение:
Cвойства сложения
 А+В=В+А(переместительное)
А+В=В+А(переместительное)
20А+О=А, где О-нулевая матрица
30 А+(В+С)=(А+В)+С (дистрибутивное)
40А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число
 .
.Пример 7:
Умножение матиц
Это действие распространяется на так называемые согласованные матрицы.
Определение 17: Матрица А называется согласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8: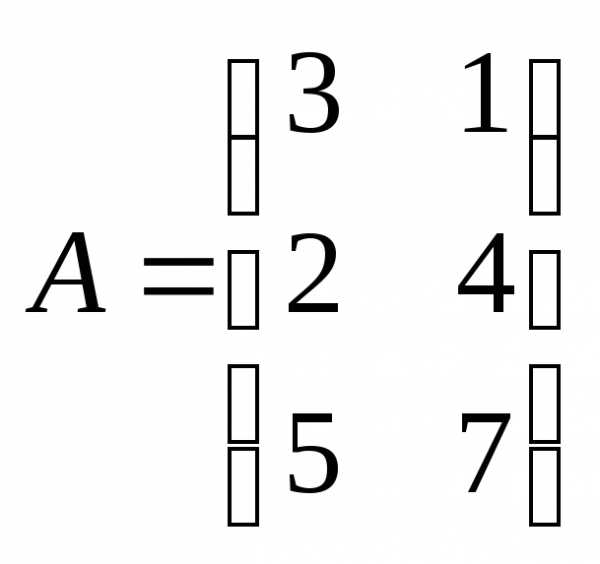 и
и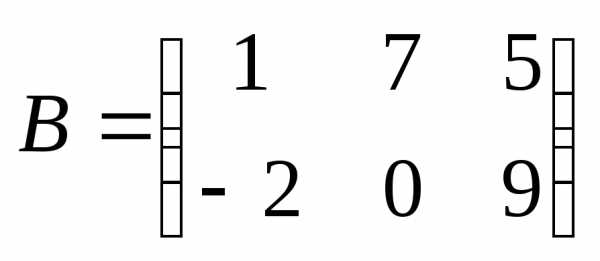
 и- несогласованные
и- несогласованные
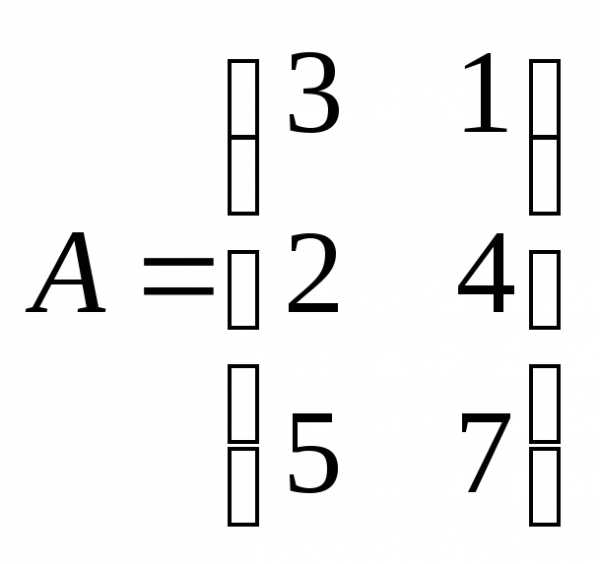 и
и несогласованные
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность  ,
а матрица В
,
а матрица В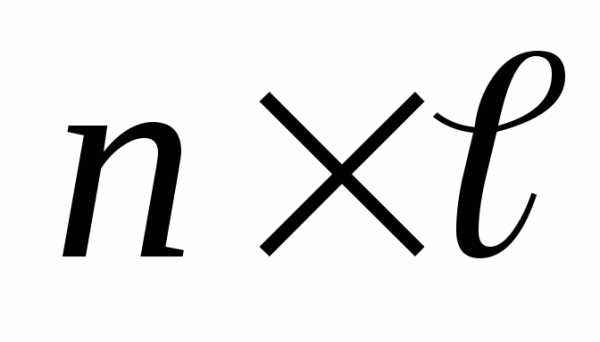
Пример 9: Умножить матрицы
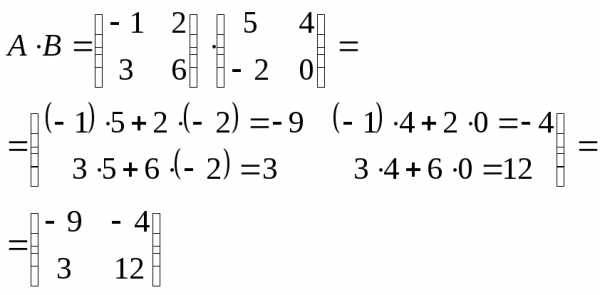
studfiles.net
Матрицы Метод Гаусса
КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ
Кафедра «Автоматизации управления войсками»
Только для преподавателей
“Утверждаю”
Начальник кафедры № 9
полковник ЯКОВЛЕВ А.Б.
«____»______________ 2004 г.
доцент СМИРНОВА А.И.
“МАТРИЦЫ. МЕТОД ГАУССА”
Обсуждено на заседании кафедры № 9
«____»___________ 2003г.
Протокол № ___________
Кострома, 2003
C одержание
Введение
1. Действия над матрицами.
2. Решение систем линейных уравнений методом Гаусса.
Заключение
Литература
1. В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.
2. В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.
ВВЕДЕНИЕ
На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.
1-ый учебный вопрос ДЕЙСТВИЯ НАД МАТРИЦАМИ
ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m , n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m ´ n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента а i j
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т.е. m = n , называется квадратной.
Число строк (столбцов) квадратной матрицы называется порядком матрицы.
ПРИМЕР.
ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.
ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.
ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n , состоящая из одной строки, называется матрицей – строкой.
Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.
ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.
Рассмотрим квадратную матрицу порядка n :
побочная диагональглавная диагональ
Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а i i ).
Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы .
Рассмотрим некоторые частные виды квадратных матриц.
1) Квадратная матрица называется диагональной , если все элементы, не стоящие на главной диагонали, равны нулю.
2) Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной . Обозначается:
3) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:
верхняя нижняя
треугольная матрица треугольная матрица
Для квадратной матрицы вводится понятие: определитель матрицы . Это определитель, составленный из элементов матрицы. Обозначается:
Ясно, что определитель единичной матрицы равен 1: ½Е ½ = 1
ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.
Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной , если определитель равен нулю, то матрица называется вырожденной.
ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.
Матрицу, транспонированную к А , обозначают АТ .
ПРИМЕР.
2
3 3 2ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.
Рассмотрим действия над матрицами.
СЛОЖЕНИЕ МАТРИЦ.
Операция сложения вводится только для матриц одинакового размера.
ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (а i j ) и В = ( bi j ) одинакового размера называется матрица С = (с i j ) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с i j = a i j + b i j
Обозначается сумма матриц А + В.
ПРИМЕР.
УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k , надо умножить на это число каждый элемент матрицы :
если А= (а i j ), то k · A = (k · a i j )
ПРИМЕР.
СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО
1. Переместительное свойство: А + В = В + А
2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )
3. Распределительное свойство: k · ( A + B ) = k A + k B , где k – число
УМНОЖЕНИЕ МАТРИЦ
Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.
ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k , элемент которой а i j , расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.
c i j = a i 1 b 1 j + a i 2 b 2 j +……+ a i n b n j
Обозначим: С = А · В.
Если
тоПроизведение В ´ А не имеет смысла, т.к. матрицы
не согласованы.ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А , то, вообще говоря
А ´ В ¹ В ´ А , т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А .
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ . Найти , если можно, А ´ В и В ´ А .
1.
Решение : Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.
2.
Решение : Матрицы А и В согласованы
mirznanii.com
1.8. Метод Гаусса
Выпишем расширенную матрицу системы: .
1 – ый шаг. Получим в верхнем левом углу матрицы единицу. Для этого поменяем местами первую и вторую строки: . Умножим первую строку на и прибавим ее ко второй строке, затем умножим первую строку на и прибавим ее к третьей строке. После выполнения указанных операций все элементы первого столбца матрицы, кроме , окажутся равными нулю: .
Чтобы упростить дальнейшие вычисления, мы еще разделим третью строку на общий множитель всех ее элементов – : .
2 – ой шаг. Теперь сделаем элемент равным единице, а остальные элементы второго столбца “обнулим”. Для этого поменяем местами вторую и третью строки: . Умножим вторую строку на и прибавим ее к первой строке, затем к третьей строке прибавим вторую строку: .
3 – ий шаг. Разделим третью строку на , после этого элемент будет равен единице: .
Умножим третью строку на и прибавим ее ко второй строке, затем умножим третью строку на и прибавим ее к первой строке, тогда все элементы третьего столбца матрицы, кроме , окажутся равными нулю: .
В итоге получаем единственное решение системы: .
nww13.narod.ru
