Разностные уравнения решить онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Разностное уравнение представляет собой уравнение, связывающее значение некоторой неизвестной функции в любой точке с её значением в одной или нескольких точках, отстоящих от данной на определенный интервал. Пример:
\[Г (z+1) = zГ(z)\]
Для разностных уравнений с постоянными коэффициентами существуют детально разработанные методы нахождения решения в замкнутой форме. Неоднородное и однородное разностные уравнения n-го порядка задаются соответственно уравнениями, где \[a\] постоянные коэффициенты.
Однородные разностные уравнения.

Так же читайте нашу статью “Решить уравнения с дискриминантом онлайн”
Рассмотрим уравнение n-го порядка
\[(a_nE^n +a{n-1}E^n1 + \cdots +a_1Е + a_1)y(k) = 0 \]
Предлагаемое решение следует искать в виде:
\[y(k)=e^rk\]
где \[r\] – подлежащая определению постоянная величина. Вид предполагаемого решения, задаваемый уравнением, не является наиболее распространенным. Допустимые значения \[r\] служат корнями многочлена от \[ е^r.\] При\[ \beta = е^r \]предполагаемое решение становится таким:
\[y(k)= \beta ^k \]
где \[\beta\] – подлежащая определению постоянная величина. Подставляя уравнение и учитывая \[E^m \beta ^k= \beta ^mm \beta ^k\], получим следующее характеристическое уравнение:
\[a_n \beta ^n+a_{n-1} \beta ^n-1+\cdots + a_1 \beta + a_0=0 \]
Неоднородные разностные уравнения. Метод неопределенных коэффициентов. Рассмотрим разностное уравнение n-го порядка
\[ (a_nЕn +а_{n-1}Еn^-1+\cdots+ а_1Е +a_1)y(k) =F(k) \]
Ответ имеет следующий вид:
\[y(k) =y_n+ у_p\]
Где можно решить разностное уравнение онлайн?
Решить уравнение вы можете на нашем сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
pocketteacher.ru
Решение уравнения разности к определяется наиболее просто если уравнение разрешимо относительно функции .
Зададим к начальных условий при 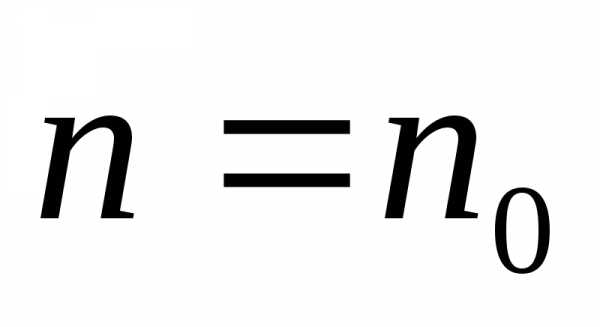
Используя 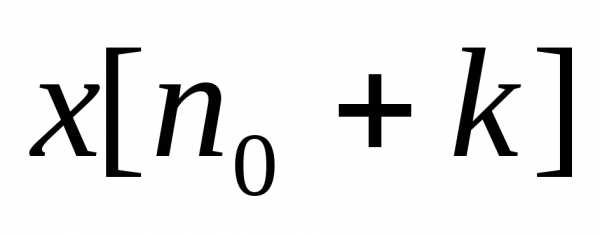 вычислим последовательно
и все остальные значения
вычислим последовательно
и все остальные значения 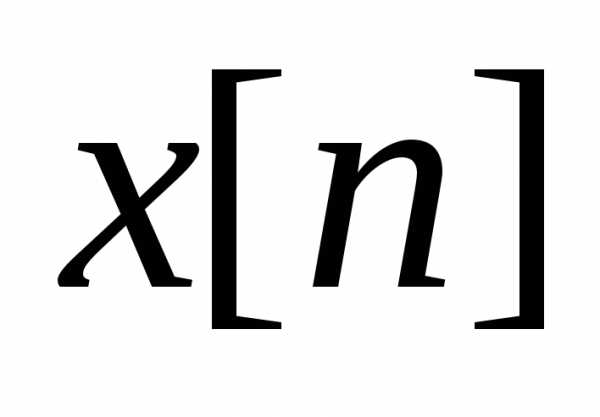 при
при 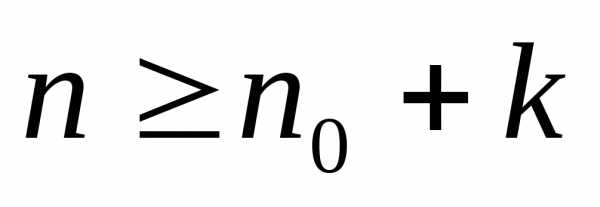 .
Пологая
,
вычисляем
.
Пологая
,
вычисляем 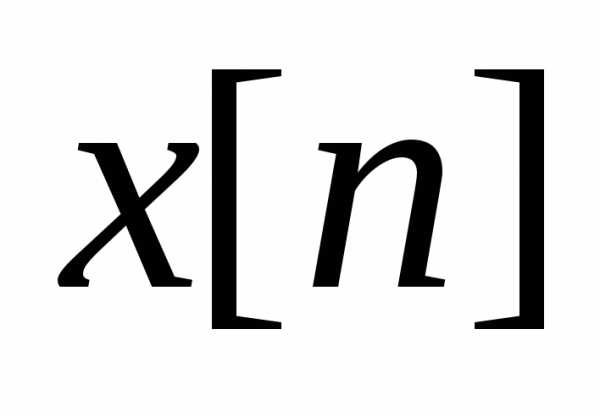 при
при 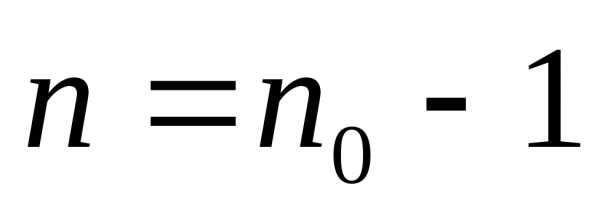 ,
т.е
,
т.е 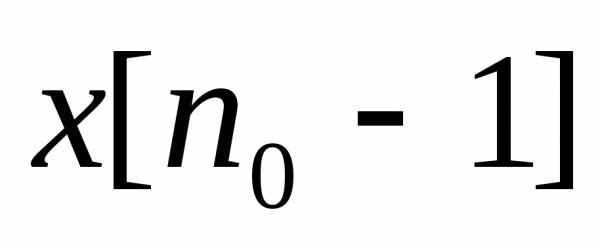 ,
, 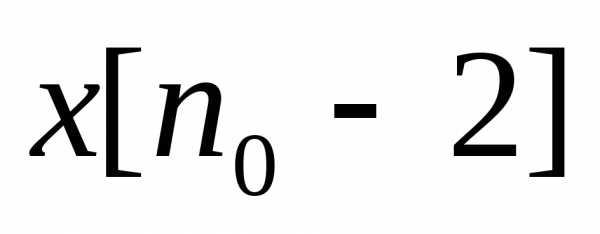
т.е.
или
Решение является общим в том же смысле как решение линейного дифференциального уравнения.
Наряду с разностным уравнением
относительно решетчатых функций 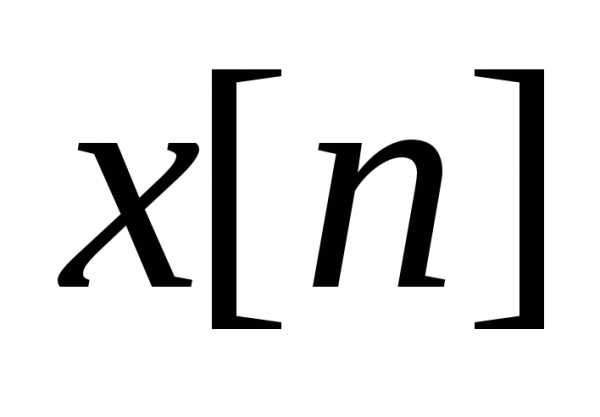
Линейные разностные уравнения
1. – неоднородное разностное уравнение.
Будем считать, что функции определены
при 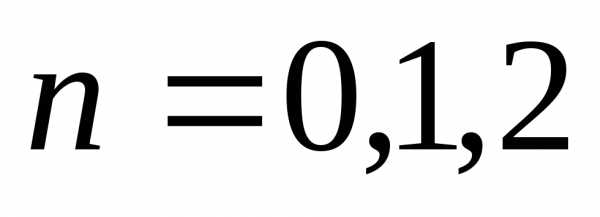 и ограничены.
и ограничены.
Уравнение 1 можно преобразовать к виду
где
Коэффициент 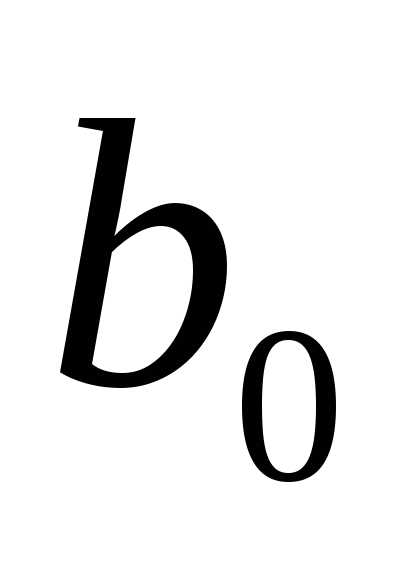 без ограничения общности можно считать
равным 1, а
без ограничения общности можно считать
равным 1, а 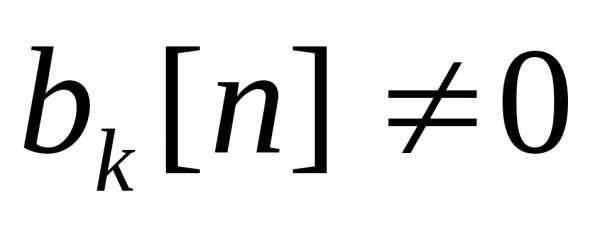
Теорема
1.Если решетчатые функции
являются решениями линейного однородного
уравнения
то функции 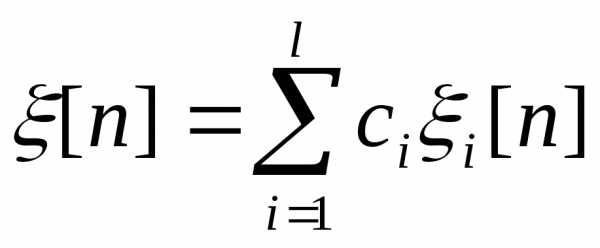 где
где 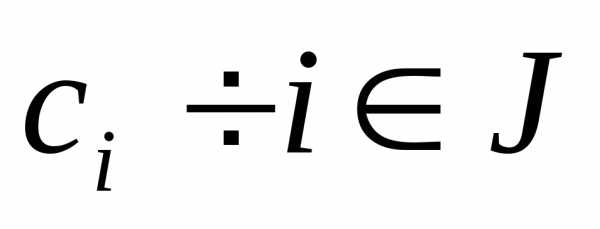 производные постоянные также являются
его решениями.
производные постоянные также являются
его решениями.
Теорема 2.Если решетчатые функции
линейно-зависимы,то при всех значениях 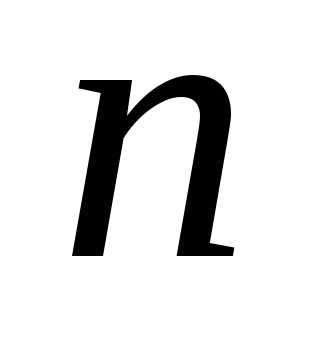 ,при
которых они определены обращаются в
ноль.
,при
которых они определены обращаются в
ноль.
Теорема 3.Если решетчатые функции
линейно независимые решения однородного
разностного уравнения при 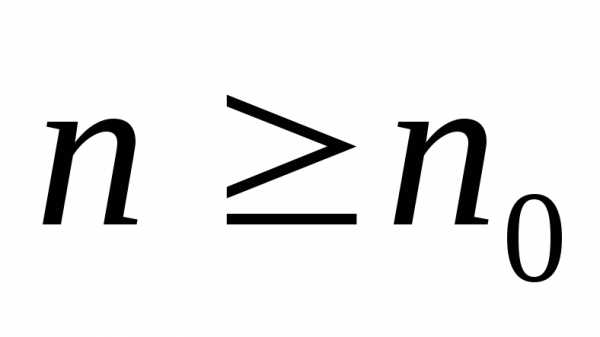
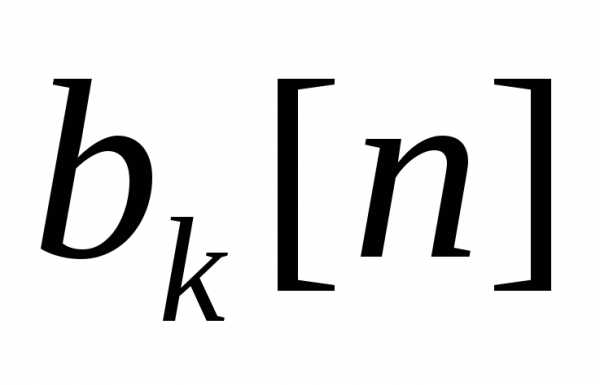 не обращается в ноль ни при одном
не обращается в ноль ни при одном 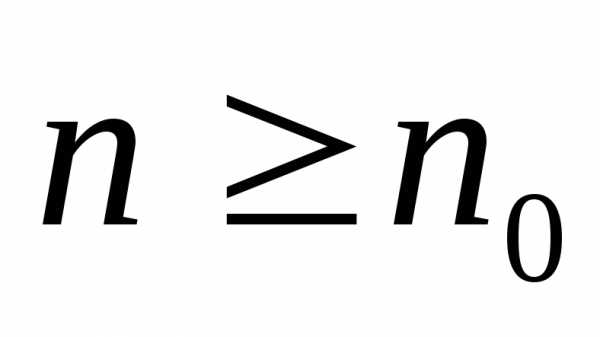 ,
то определитель
не обращается в ноль ни при одном
,
то определитель
не обращается в ноль ни при одном 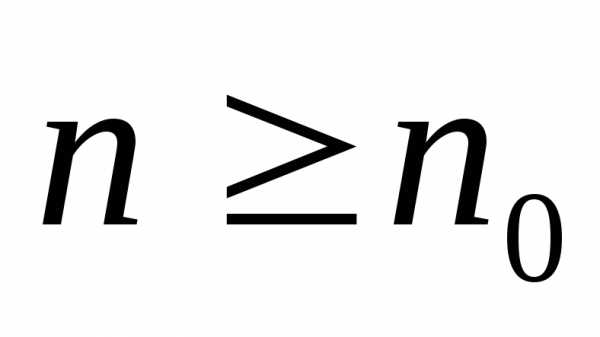 .
.Линейные неоднородные разностные уравнения.
Общее решение линейного неоднородного
разностного уравнения
равно сумме
частного решения 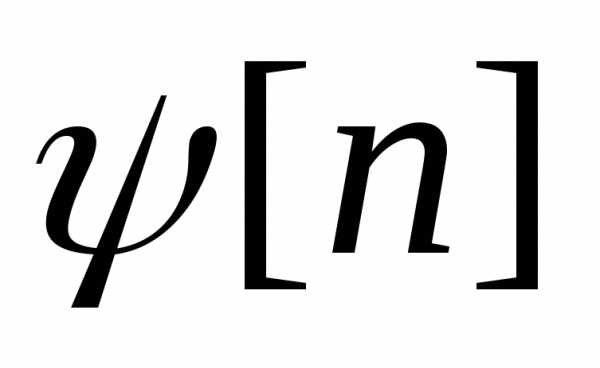 и общего решения
и общего решения  однородного уравнения
однородного уравнения
где 
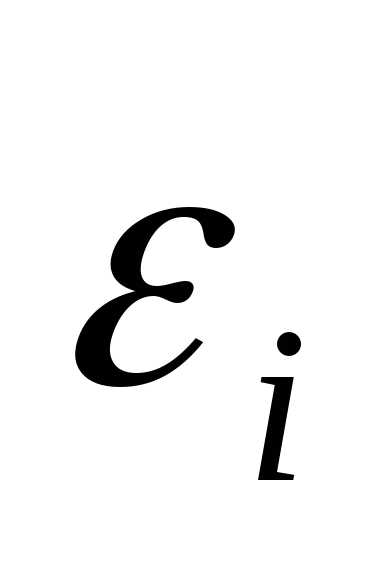 -решения однородного уравнения для
которого
-решения однородного уравнения для
которогоДоказательство:

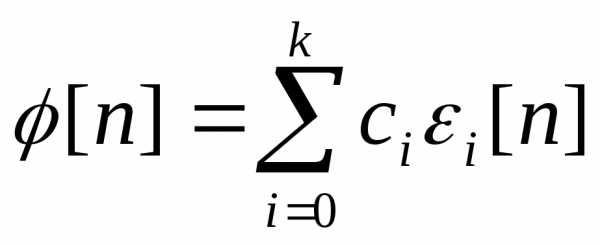
если 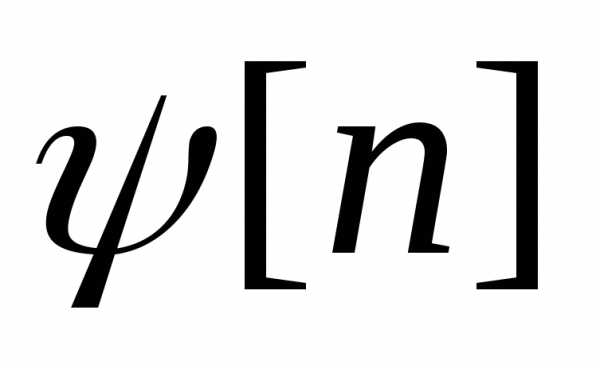 -решение неоднородных уравнений, то
,
тогда
–
однородное уравнение, а
-решение неоднородных уравнений, то
,
тогда
–
однородное уравнение, а 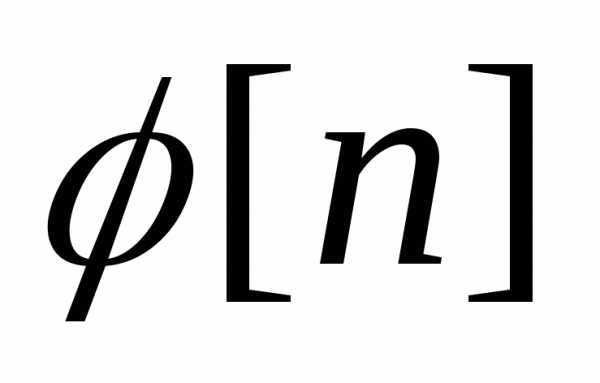 его решение.
его решение.
Пример:
:
тогда
или
Разностные уравнения с постоянными коэффициентами.
Будем искать решение 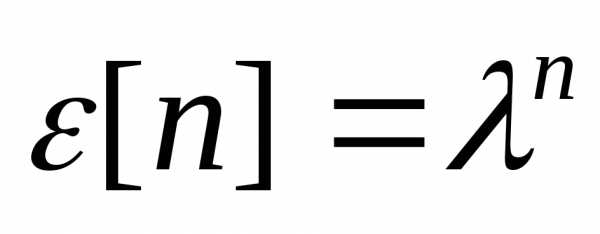
– хапрактеристическое уравнение разностного уравнения.
Найдем корни  – характеристического уравнения.
– характеристического уравнения.
Если корни простые, то – ре6шения разностного уравнения.

Если корни различны, то определитель не равен нулю и решетчатые функции независимы и решение имеет вид:

Если 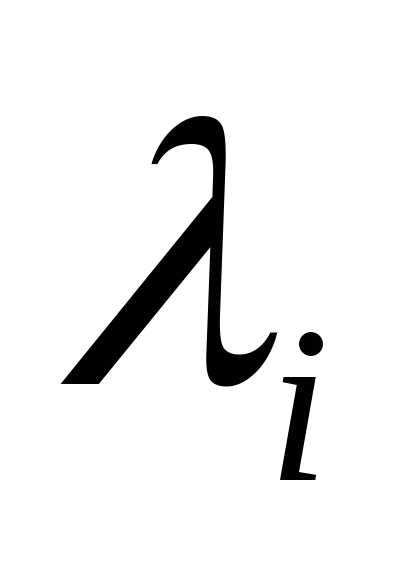 и
и  – сопряженные комплексные корни
– сопряженные комплексные корни
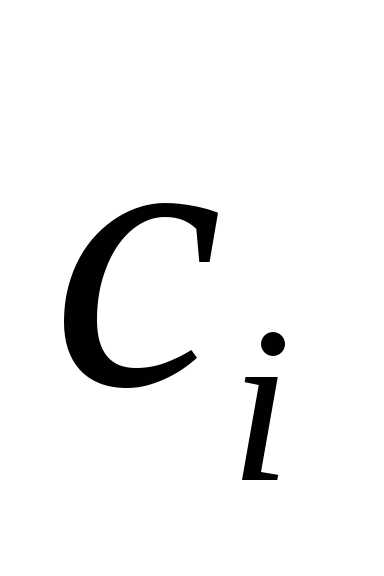 и
и 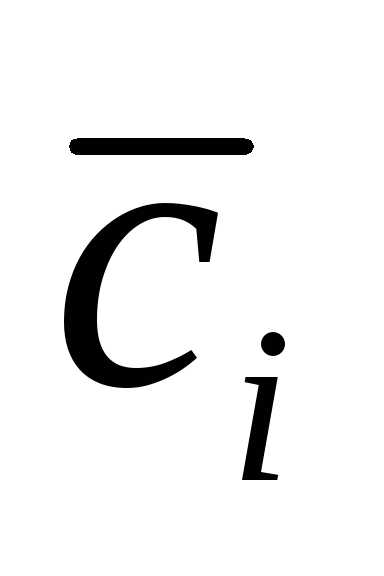 – сопряженные комплексные константы
– сопряженные комплексные константы
Системы разностных уравнений
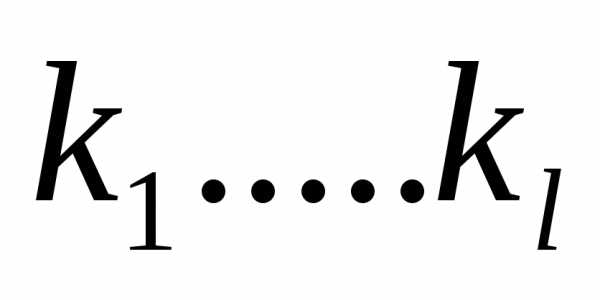 соответственно
соответственно 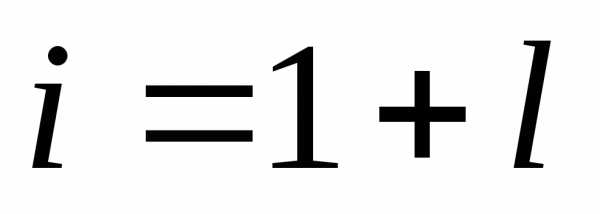
Переходя к разности будем иметь:
Линейноя система разностных уравнений:
Уравнение импульсных систем автоматического регулирования
Системы автоматического управления в которых применяются импульсная модуляция называются импульсными системами автоматического управления.
А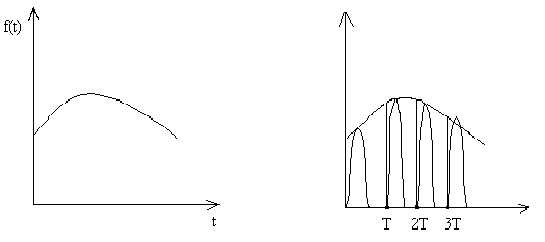 мплитудно
импульсная модуляция – замена непрерывного
сигнала
мплитудно
импульсная модуляция – замена непрерывного
сигнала 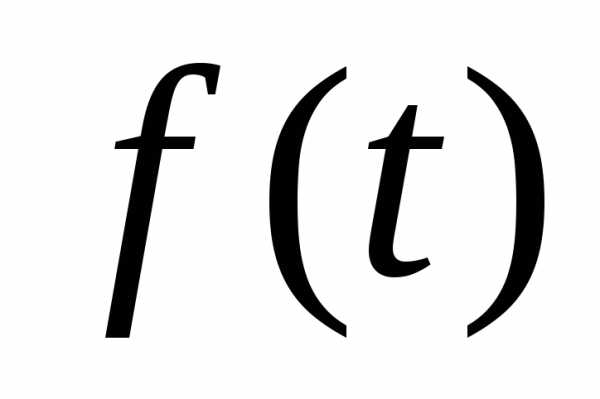 последовательностью импульсов с
постоянным интервалом времени Т.
последовательностью импульсов с
постоянным интервалом времени Т.
Пусть 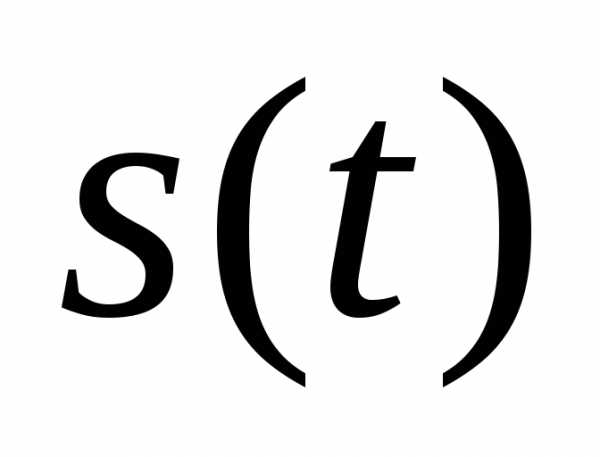 – функция описывающая форму импульса,
тогда
– функция описывающая форму импульса,
тогда
Устройство, в котором осуществляется модуляция называют импульсными элементами.
Одномерная импульсная система:
Н.Ч – непрерывная часть
Замкнутая импульсная система:
Многомерная импульсная система:
Синхронная система– система с совпадающими периодами импульсов.
Синфазная система– синхронная система, у которой совпадают моменты возникновения импульсов.
Составление уравнений импульсных систем:
Описание дифференциальными уравнениями.
Описание интегральным преобразованием:
В дальнейшем, полагая будем иметь
Для описания импульсных систем применяют два вида уравнений:
Описание с помощью разностных уравнений
Уравнения импульсной системы с одним импульсным элементом:
– импульсное описание непрерывное части.
– описание импульсного элемента.

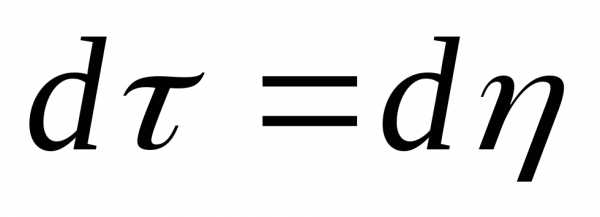
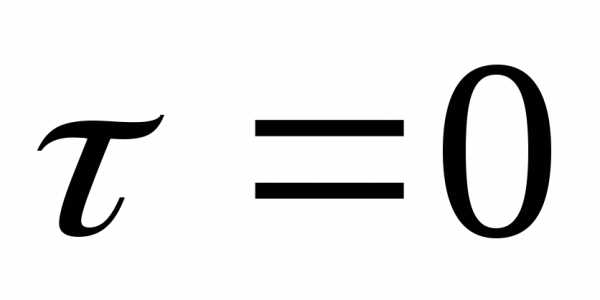
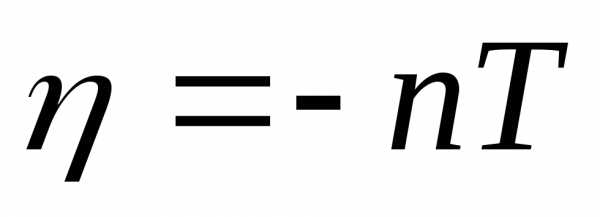
Здесь
Примем во внимание , что
,
а функция 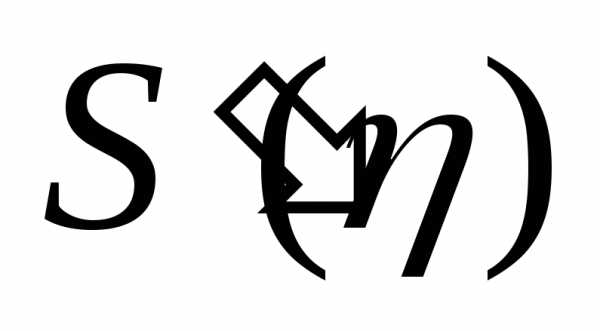 обращается в 0 при
обращается в 0 при 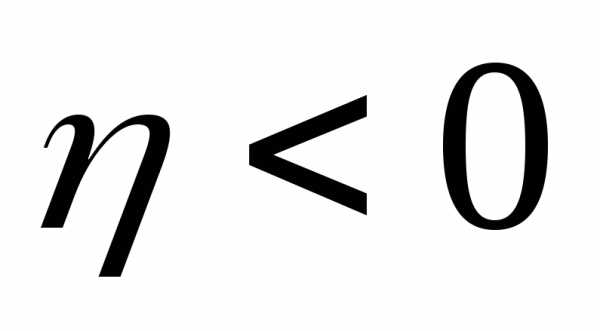 т.е. при
т.е. при
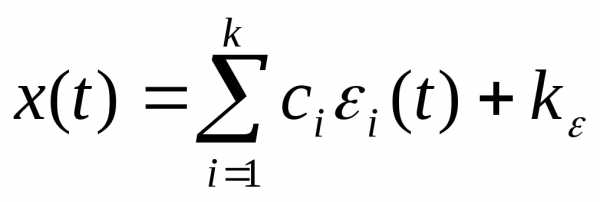
Но функция 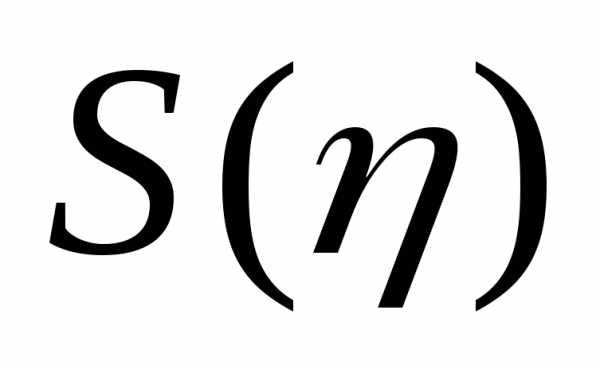 обращается
в 0 также при
обращается
в 0 также при 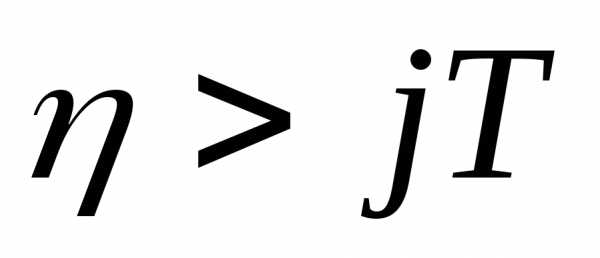 ,
где
,
где 

Уравнение разомкнутой импульсной системы можно записать:
Функции  можно придать определенный физический
смысл, если ввести понятие о простейшем
импульсном элементе.
можно придать определенный физический
смысл, если ввести понятие о простейшем
импульсном элементе.
Простейший импульсный элемент описывается
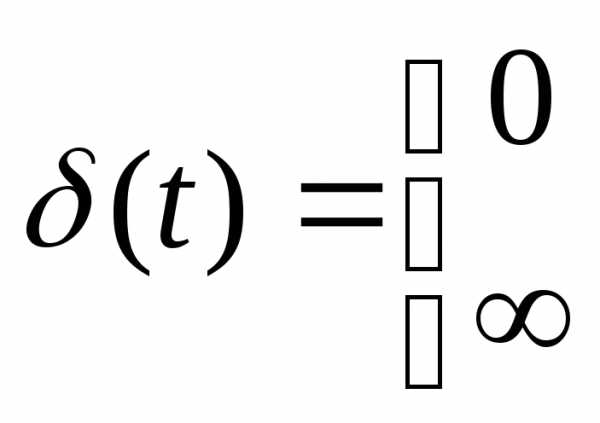
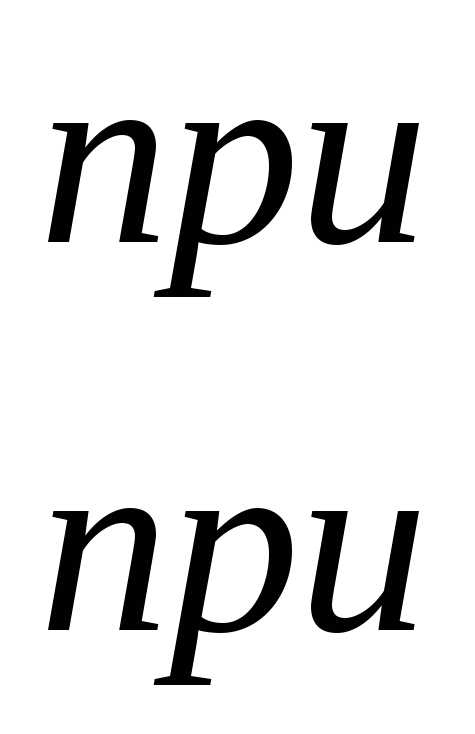
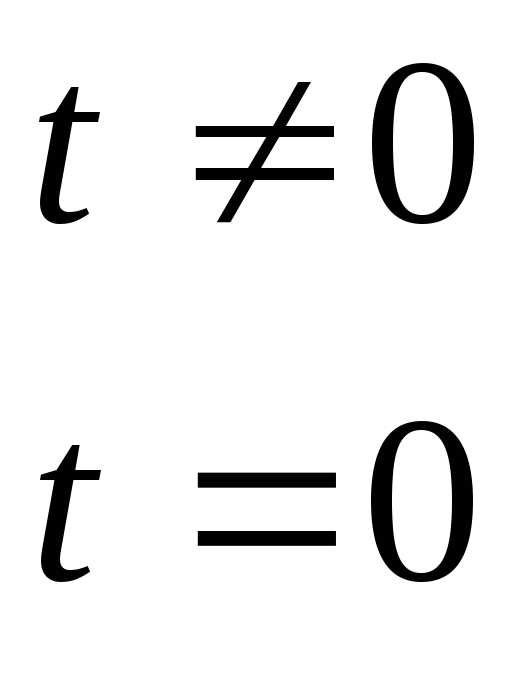

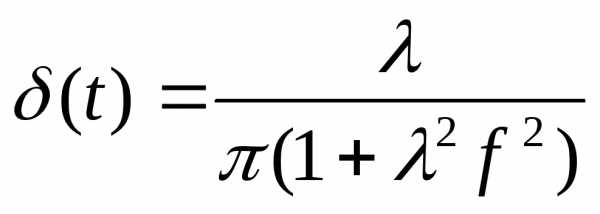
Единичная ступенчатая функция.
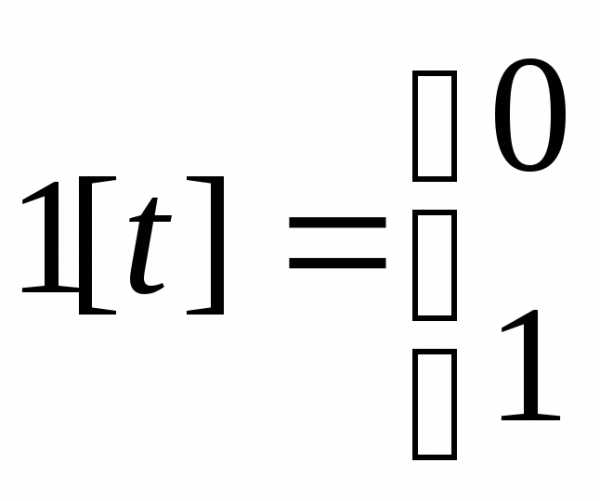
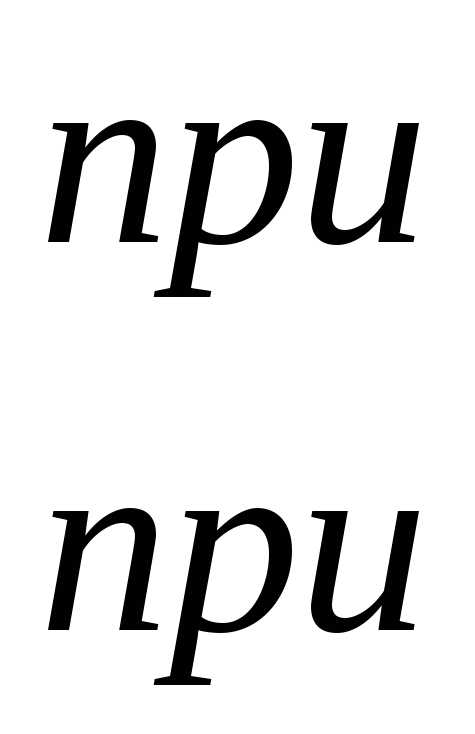
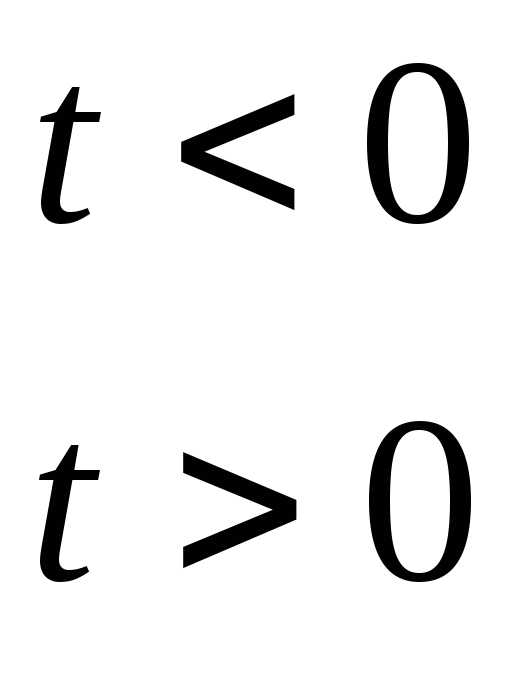
Смещенная единичная ступенчатая функция
1). 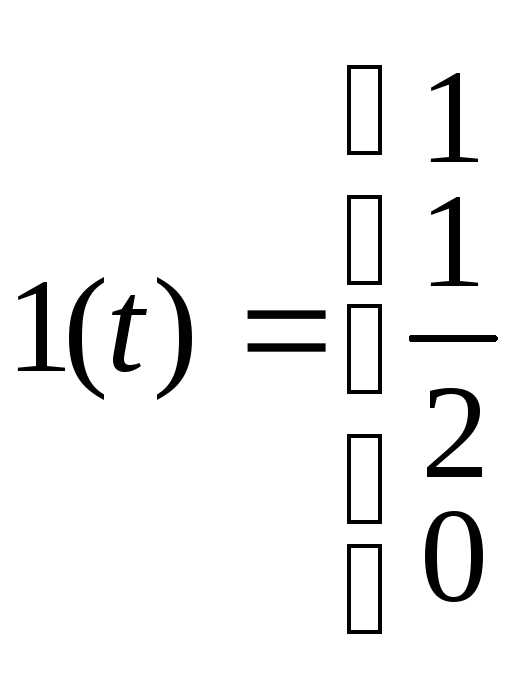
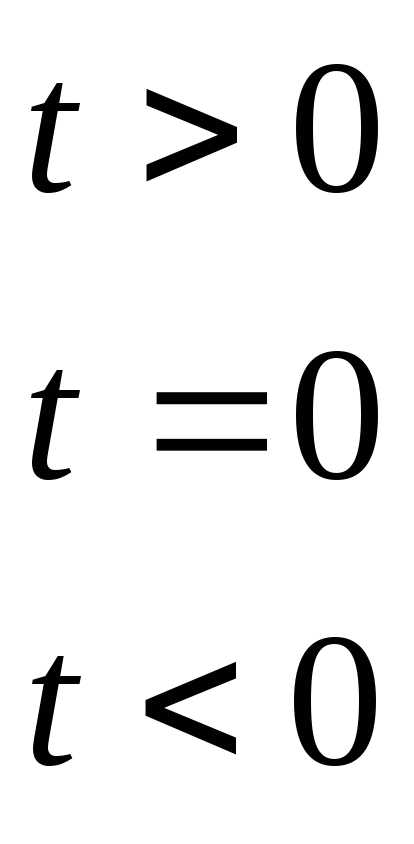 2).
2). 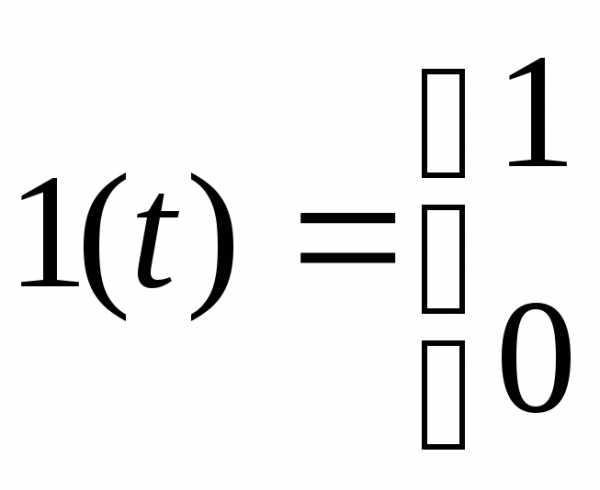
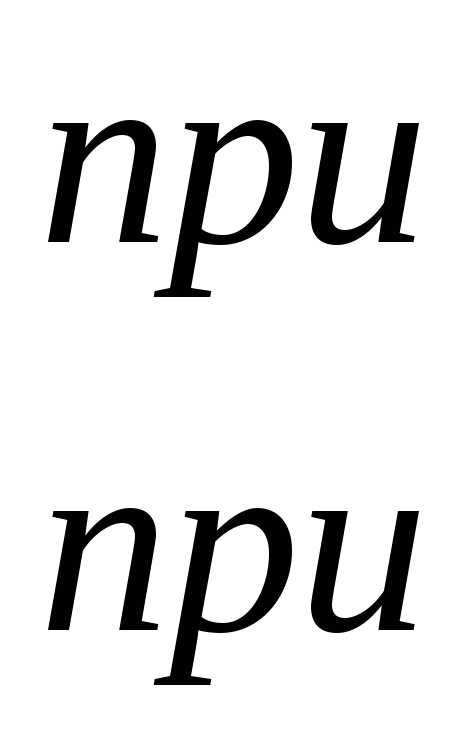
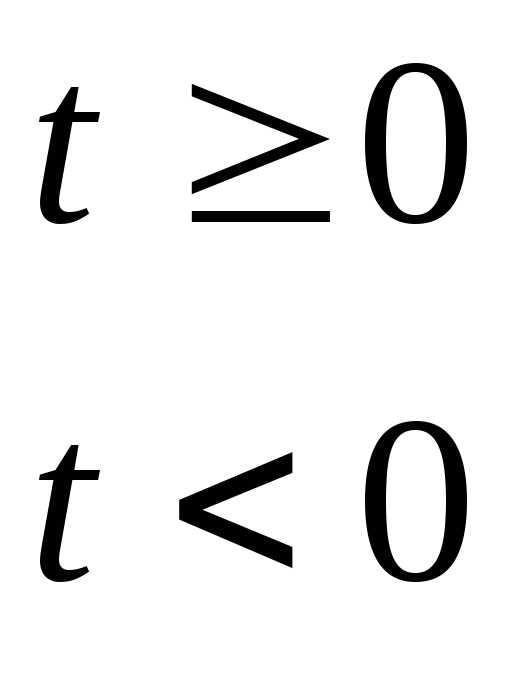 3).
3). 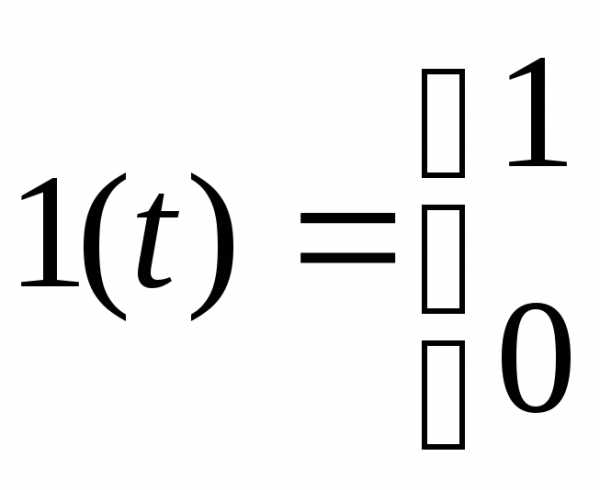
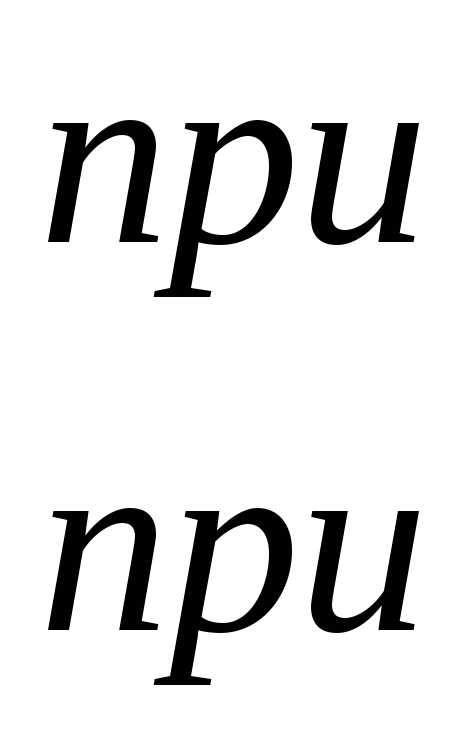
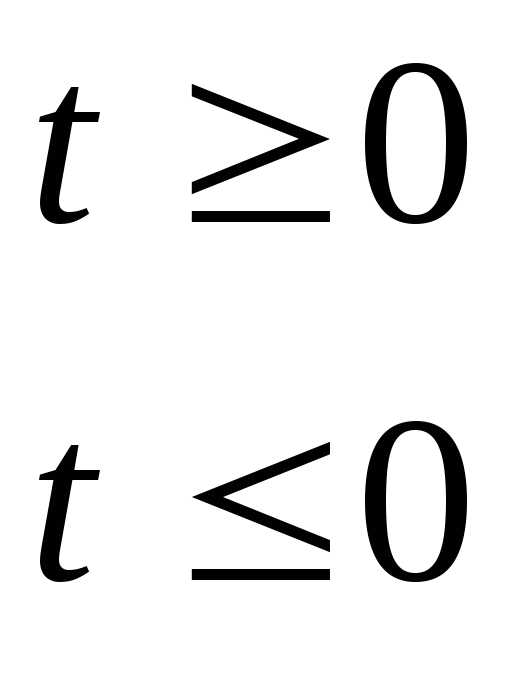
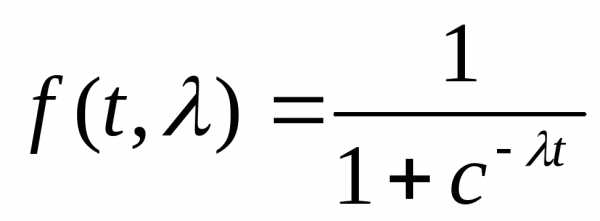
Основное и важное фильтрующее свойство
Это уравнение имеет тот же вид, что и уравнение исходного импульсного элемента, но не может быть воспроизведен никаким реальным устройством.
Реальный импульсный элемент можно представить в вид:
Непрерывный элемент с весовой функцией s(t) называют формирующим элементом.
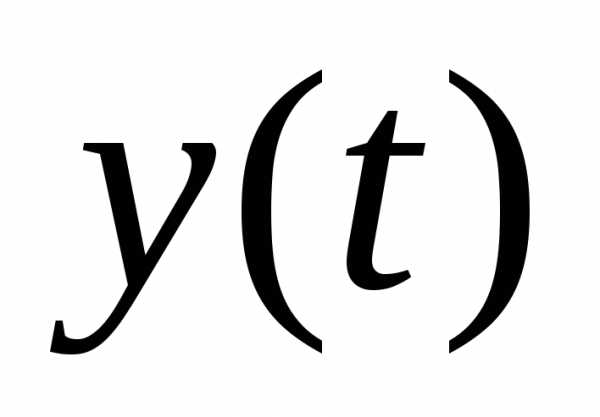
Простейший Формирующий элемент
импульсный элемент
Структурная схема разомкнутой импульсной системы
Импульсная система – последовательное соединение простейшего импульсного элемента, формирующего элемента и непрерывной части.
Непрерывная часть + формирующий элемент = приведенная непрерывная часть.
Если продолжительность импульса 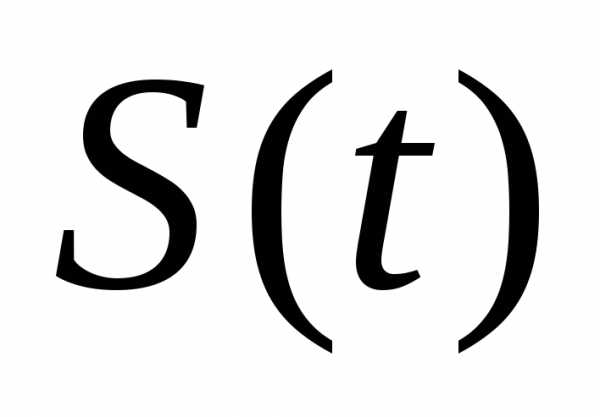 мала , весовая функция приведенной
непрерывной части
мала , весовая функция приведенной
непрерывной части 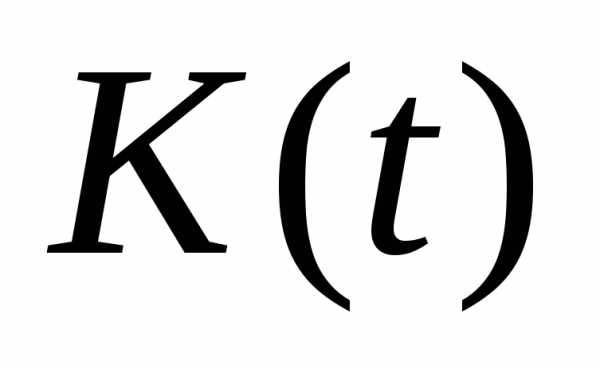 приближенно может быть заменена весовой
функцией непрерывной части
у-жимой
на постоянных коэффициентах.
приближенно может быть заменена весовой
функцией непрерывной части
у-жимой
на постоянных коэффициентах.
Вернемся к уравнению разомкнутой системы :
при нулевых начальных условиях
.
Введем относительное время 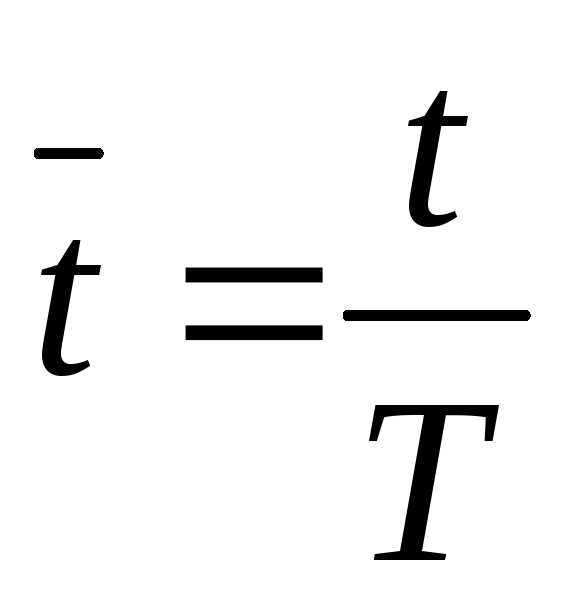 .
.
Введем обозначения:
, , .
Выражение импульсной переходной функции
Введем новую переменную 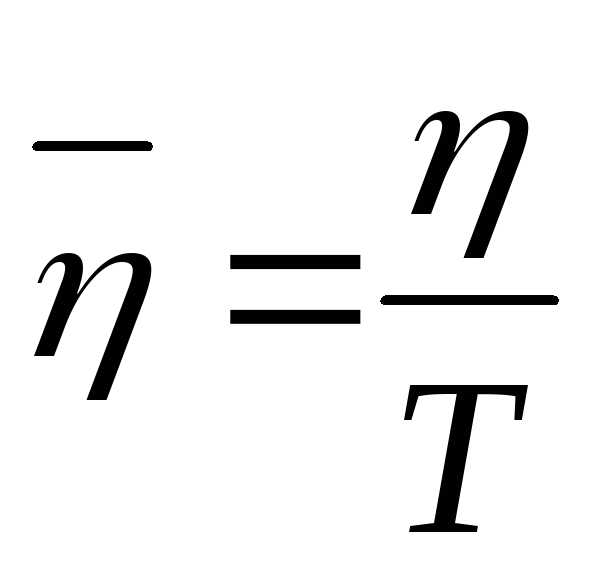
Уравнение 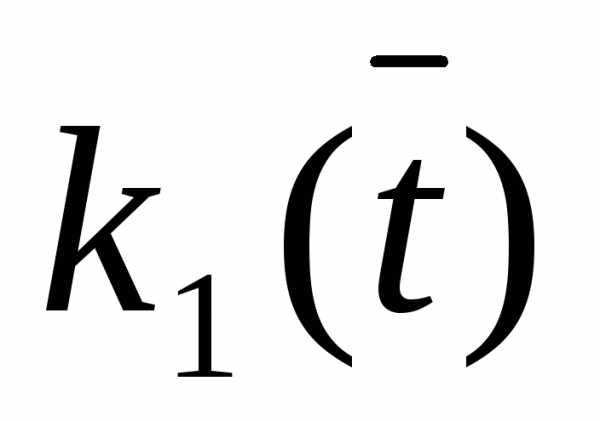 равно
свертке функций
равно
свертке функций 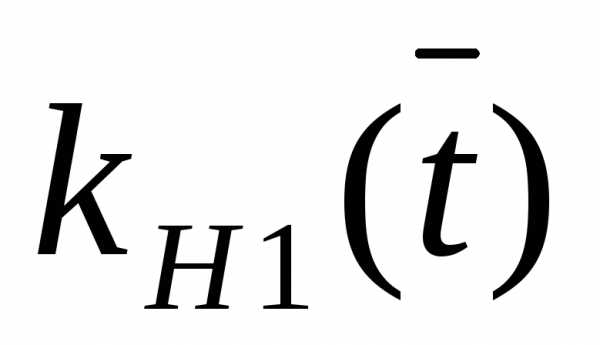 и
и 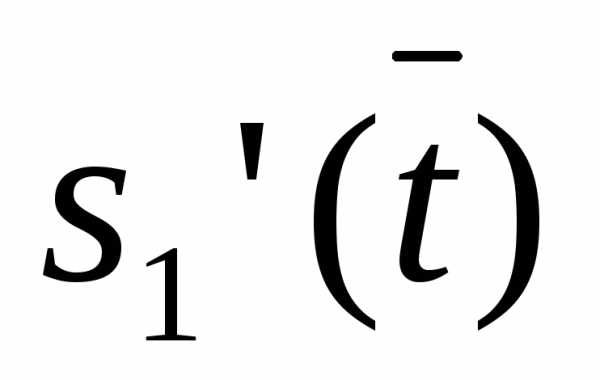 умноженной
наT.
умноженной
наT.
Уравнение разомкнутой импульсной системы можно записать в виде:
Учитывая, что  =0
при
=0
при  можно записать:
можно записать:
Пример:
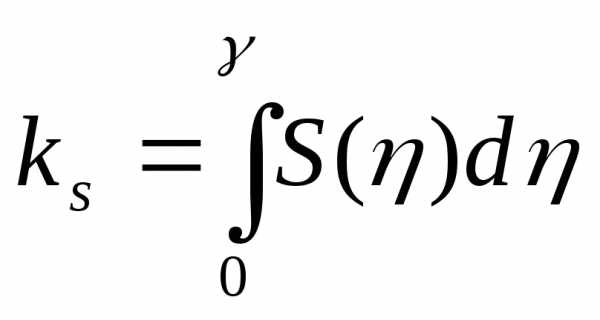
Вход системы:
где
, 
studfiles.net
Решение обыкновенных линейных разностных уравнений с постоянными коэффициентами
Решение обыкновенных линейных разностных уравнений
с постоянными коэффициентами
Связь выхода и входа линейной дискретной системы может быть описана обыкновенным линейным разностным уравнением с постоянными коэффициентами
,
где y[n]– выходной сигнал в момент n,
x[n] – входной сигнал в момент n,
ai, bk – постоянные коэффициенты.
Для решения таких уравнений могут использоваться два метода
- Прямой метод,
- Метод Z – преобразования.
Вначале рассмотрим решение линейного разностного уравнения с помощью прямого метода.
Общее решение неоднородного (с отличной от нуля правой частью) линейного разностного уравнения равно сумме общего решения линейного однородного разностного уравнения и частного решения неоднородного уравнения
Общее решение однородного разностного уравнения (zero-input response) yh[n]
определяется в виде
.
Подставляя это решение в однородное уравнение, получаем
или .
Такой полином называют характеристическим полиномом системы. Он имеет N корней . Корни могут быть действительными или комплексными и некоторые корни – совпадающими (кратными).
Если корни являются действительными и разными, то решение однородного уравнения имеет вид
,
где коэффициенты определяются по начальным условиям.
Если некоторый корень, например, λ1 имеет кратность m, то соответствующий ему член решения приобретает форму
.
Если все коэффициенты однородного уравнения и соответственно характеристического многочлена действительны, то два члена решения, соответствующие простым комплексно сопряженным корням можно представить (записать) в виде , при этом коэффициенты A, B определяются по начальным условиям.
Вид частного решения yp[n] уравнения зависит от правой части (входного сигнала) и определяется согласно нижеприведенной таблице
Таблица 1. Вид частного решения для различного характера правой части
Входной сигнал x[n] | Частное решение yp[n] |
A (константа) AMn AnM | K KMn |
Решение линейного разностного уравнения методом Z – преобразования заключается в применении Z – преобразования к уравнению с использованием свойств линейности и временного сдвига. В результате получается линейное алгебраическое уравнение относительно Z – изображения искомой функции. Обратное Z – преобразование дает искомое решение во временной области. Для получения обратного Z – преобразования чаще всего используется разложение рационального выражения на простые (элементарные) дроби, так как обратное преобразование от отдельной элементарной дроби имеет простой вид.
Заметим, что для перехода во временную область могут использоваться и другие методы вычисления обратного Z – преобразования.
Пример. Определим отклик (выходной сигнал) системы, описываемой линейным разностным уравнением , на входной сигнал
Решение.
1. Прямой метод решения уравнения.
Однородное уравнение . Его характеристический полином .
Корни полинома .
Решение однородного уравнения .
Поскольку ,то частное решение определяем в виде .
Подставляем его в уравнение
.
Для нахождения константы К примем n = 2. Тогда
, или , К=2,33
Отсюда частное решение и общее решение разностного уравнения (1)
Найдем константы С1 и С2. Для этого положим n = 0, тогда из исходного разностного уравнения получаем . Для данного уравнения
, поэтому . Из выражения (1)
, следовательно,
.
Далее положим n = 1, при этом из уравнения следует . Поскольку , то
. Из выражения (1) для n = 1 имеем .
Получаем следующие два уравнения для С1 и С2
.
Решение этой системы дает следующие значения: С1 =0,486 и С2 = -0,816.
Следовательно, общее решение данного уравнения
2. Решение методом Z – преобразования.
Возьмем Z – преобразование от исходного разностного уравнения , учитывая свойство (теорему) временного сдвига . Получаем
Для данного уравнения , в связи с этим
. Разрешая это уравнение относительно Y(z), имеем
.
Для данного случая его Z
– преобразование .
Подставляя его в предыдущее выражение, получаем решение уравнения в Z – области
.
Найдем корни полинома
.
Для получения решения уравнения во временной области представим Y(z) в виде суммы элементарных дробей
.
Определим коэффициенты A, B, C
, ,
.
Поэтому представление Y(z) как суммы элементарных дробей имеет вид
.
Обратное Z – преобразование от равно
Следовательно, решение уравнения во временной области имеет вид
Составил: доц. Щетинин Ю.И.
vunivere.ru
Методика решения разностных уравнений — Мегаобучалка
Способы квантования непрерывных (аналоговых) сигналов.
Основные способы квантования:
а) Квантование по уровню. Значение непрерывной ф-ции фиксируются при достижении опред. уровня.
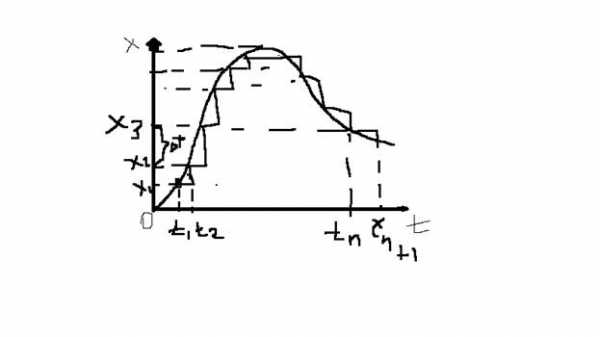 Релейные АС
Релейные АС
б)Квантование по времени
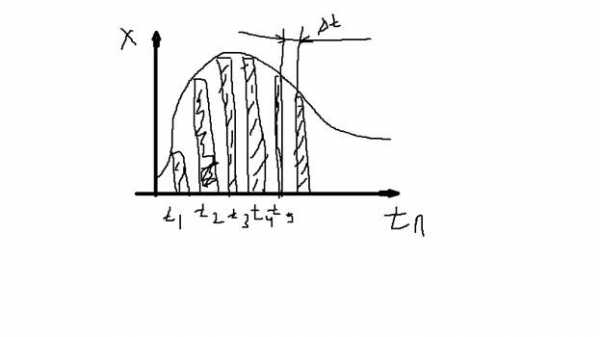
Фиксируется в равновноостающие моменты времени дельтаt=const
При таком способе квантования изменяется амплитуда по импульсному моделированию.
б)Комбинированное квантование(т.е. Квантование по времени и уровню). Цифровые автоматические системы 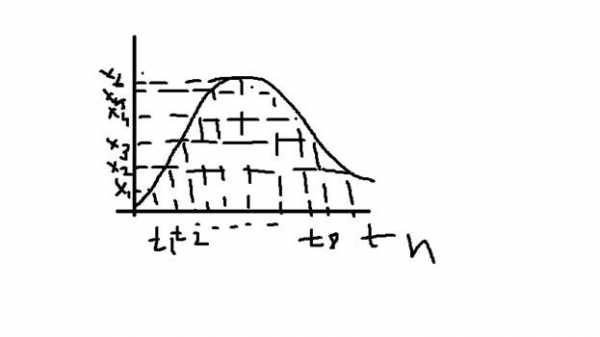
∆ t=Const
∆x=const
Амплитудно–импульсная и широтно–импульсная модуляция дискретных сигналов.
А)Амплитудно-импульсная модуляция ( АИМ) – вид импульсной модуляции .при которой от воздействия передаваемых сигналов изменяется величина ( амплитуда) импульсов. В лекции( АИМ- Система, которая содержит хоть один такой элемент.
Б)Широкоимпульсное моделирование.
При ШИМ амплитуда импульсов не изменяется
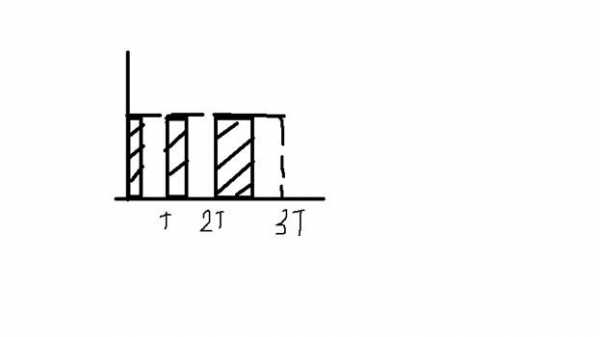
дельтаt=const T= дельтаt=const-Период квантования
Относительная ширина импульсов
S=ț/Y-скважность сигнала( не уверен, лучше не писать)
Импульсная система АУ
Классификация дискретных систем по способу квантования.
Существует три вида квантования: по времени, по уровню и по времени и уровню одновременно. При квантовании по времени это аим-системы
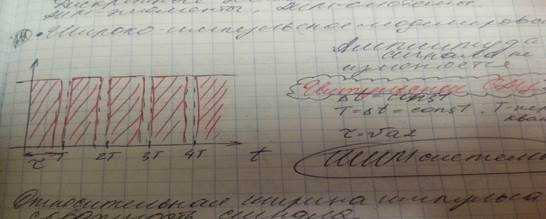
При таком способе квантования для каждого момента времени меняется амплитуда ->амплитудо-импульсное моделирование. ШИМ-системы 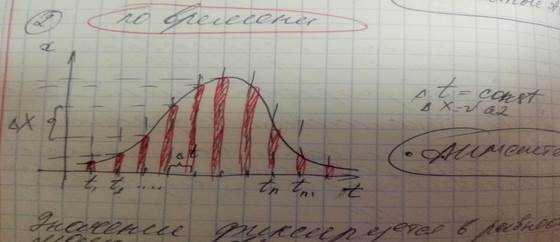
 |
По уровню.Значения непрерывной функции фиксируются при достижении определённого уровня. Уровни поднимаются равноотстоящими друг от друга. где фотки, не обязательно писать. Релейные АС

Комбинированное квантование.По времени и по уровню. Значения функции берутся не текущие, а равное ближайшему уровню. Цифровые АС
Решетчатые функции
5) Разностные уравнения 
Постановка задачи
Требуется найти решение разностного уравнения с заданными начальными условиями
y(0)=y0; y(1)=y1 ;….y(n-1)=yn-1 – начальные условия
Известно: общее решение неоднородного разностного уравнения ищется как сумма общего решения однородного дифференциального уравнения при не нулевых начальных условиях и частного решения неоднородного уравнения при нулевых начальных условиях
y(k)=yобщ (k)+yчасн (k)=yсвобод (k)+yвынужден (k)
Общее решение при ненулевых начальных значениях условно называют свободным движением системы
Частное решение называется вынужденное движение
Т.о. y(k)= yсвобод (k)+yвынужден (k)
Продолжение в 6 ответе
Методика решения разностных уравнений.
Общее решение содержит 3 этапа.
any(k+n)+an-1(k+n-1)+…+a1y(k-1)+a0y(k)=0
1)Составить характеристическое уравнение.
anλn+an-1λn-1+…+a1λ+a0=0
2)В зависимости от типа корней записать общее решение однородного уравнения.
Возможны 4 случая, в зависимости от типа корней:
а)корни действительные, разные.
y(k)=C1λk+C2λk+…+Cnλk
б)пара комплексных сопряженных корней:
α±iβ i2=-1
Решение ищется в виде
y(k)= rk(C1*Cosφk+C2*Sinφk)
в) действительные кратные корни
λi кратность m
y(k)=(C1+C2k+…+Cmkm-1)λik
г)кратные комплексные корни.
Пара комплексных сопряженных кратностей.
y(k)= rm[(C1+C2k+…+Cmkm-1)Cosφk+(B1+B2k+…+Bmkm-1)Sinφk]
3)Найти произвольные константы из заданных начальных условий.
Методика нахождения решения общего решения разностного уравнения (4 этапа)
1) Найти общее решение однородного уравнения.
2) Найти частное решение неоднородного уравнения с нелувыми начальными условиями.
y=k/a0
a2*d2y/dt2+a1*dy/dt+a0y=k
Общим методом нахождения частного решения является метод вариации произвольных постоянных.
3) Найти общее решение неоднородного уравнения как сумму общего решения однородного и частного решения неоднородного.
4) Найти произвольную константу, исходя из начальных условий.
megaobuchalka.ru
Основные свойства линейных разностных уравнений
Линейное разностное уравнение n-го порядка можно записать в форме:
(anEn+an-lEn-1 +… + a1E + a0)y(k) = F(k) (73)
где an≠0, a0≠0 и аi определены для всех интересующих нас целых значений k. В отличие от дифференциального уравнения, порядок разностного уравнения определяется как разность между высшей и низшей степенями Е. При использовании оператора ∆, например, в уравнении
[cn∆n+cn-1∆n-1+…+c1∆+c0]y(k) = [dm∆m+…+d1∆+d0]v(k). (74)
установить порядок уравнения непосредственно по его виду не представляется возможным. Так, уравнение
(∆2+З∆+2)у(k)=0
эквивалентно
(E2 + E)y(k) = 0,
являющемуся уравнением первого, а не второго порядка. Уравнение (73) называют неоднородным разностным уравнением, в отличие от однородного разностного уравнения n-го порядка.
(anEn+an-lEn-1 +… + a1E + a0)y(k) = 0 (75)
Разностные уравнения называют также рекуррентными формулами. Уравнение (73) можно переписать в виде
y(k+n)=-1/an[an-1y(k + n-1) + … + a1y(k + 1) + a0y(k) + F(k)] (76)
В
отличие от дифференциальных уравнений,
непосредственно по разностному
уравнению можно определить y(k) для любых
значений k; решение дается в виде первых
n
значений y(k) . Величины у(0)  у(n-1)
или эквивалентная информация
необходимы для единственности решения
уравнения (73).
у(n-1)
или эквивалентная информация
необходимы для единственности решения
уравнения (73).
Однородное дифференциальное уравнение n-го порядка содержит n линейно независимых решений. Если аn≠0 и а0≠0. то независимые уравнения (75) можно обозначить через y1(k), y2(k),…,yn(k). Необходимое и достаточное условие линейной независимости решении имеет вид
 (77)
(77)
В общем виде решение уравнения (75) представляется как
un=C1y1(k)+ C2y2(k)+ …+Cnyn(k), (78) где Ci -произвольные постоянные не зависящие от k. Общее решение уравнения (73) имеет вид
y = yн + yp,
где ун задается уравнением (78), а ур – произвольное решение, удовлетворяющее уравнению (73). Составляющие ун и ур называют соответственно вспомогательным и частным решениями. Так как ур не содержит произвольных постоянных, то в решении у содержатся n произвольных постоянных, которые должны определяться по начальным или граничным условиям.
Решение разностных уравнений с постоянными коэффициентами.
Для разностных уравнений с постоянными коэффициентами существуют детально разработанные методы нахождения решения в замкнутой форме. Неоднородное и однородное разностные уравнения n-го порядка задаются соответственно уравнениями (73) и
(75), где аi постоянные коэффициенты.
Однородные разностные уравнения.
Рассмотрим уравнение n-го порядка
(anЕn +аn-1Еn-1 + … + а1Е + a0)y(k) = 0 (79)
Предлагаемое решение следует искать в виде
y(k)=erk, (80)
где r- подлежащая определению постоянная величина. Вид предполагаемого решения, задаваемый уравнением (80), не является наиболее распространенным. Допустимые значения r служат корнями многочлена от еr. При β = еr предполагаемое решение становится таким:
y(k)=βk, (81)
где β – подлежащая определению постоянная величина. Подставляя уравнение (81) в (79) и учитывая Emβk=βmβk, получим следующее характеристическое уравнение:
аnβn+аn-1βn-1+… + а1β + а0 =0 (82)
Если n корней характеристического уравнения различны и обозначаются β1, β2,…, βn, общее решение однородного разностного уравнения имеет вид
(83)
Неоднородные разностные уравнения. Метод неопределенных коэффициентов. Рассмотрим разностное уравнение n-го порядка
(anЕn +аn-1Еn-1 + … + а1Е + a0)y(k) = F(k), (84)
решение которого имеет вид:
y(k) = yн + ур . (85)
Вспомогательное решение ун находится из решения соответствующего однородного уравнения. Частное решение ур находится на основе тех же самых двух методов, как и в случае дифференциальных уравнений, а именно: методов неопределенных коэффициентов и вариации параметров. Метод неопределенных коэффициентов применим лишь в том случае, если в результате последовательного воздействия оператором Е на возмущающую функцию F(k) получаем конечное число линейно независимых членов. F(k) может быть многочленом, экспоненциальной, синусоидальной или гиперболической функцией или содержать линейную комбинацию указанных функций. Решение ищут в виде линейной комбинации составляющих F(k), F(k+1), F(k+2),…, причем каждая из составляющих входит с неопределенным постоянным коэффициентом.
Неоднородные разностные уравнения. Вариация параметров.
При известном решении вспомогательного уравнения метод вариации параметров позволяет получить выражение для ур вне зависимости от характера функции F(k). Если применение этого метода к дифференциальным уравнениям сводится в конечном счете к интегрированию некоторой известной функции t, то применительно к разностным уравнениям приходим к суммированию некоторой известной функции k. Рассмотрим уравнение первого порядка:
(a1E + a0)y(k) = F(k) (86)
Вспомогательное решение содержит лишь один член yn=Cy1(k).
Предполагаем, что частное решение имеет вид
Ур = μ(k)у1. (87)
Подстановка уравнения (87) в (86) дает
a1μ(k+1)у1(k+1) + a0μ(k)y1(k) = F(k).
Преобразуем его к виду
al[μ(k+1)y1(К+1)-μ(k)y1(k+1)]+μ(k)[a1y1(k+1)+a0y1(k)]=F(k)
Выражение в первых скобках равно y1(k+1)∆μ(k), а выражение во вторых скобках равно нулю, так как y1(k) является решением соответствующего однородного уравнения. Следовательно, a1y1(k+1)∆μ(k)=F(k).
Рассмотрим разностное уравнение n-го порядка (84), вспомогательное решение которого имеет вид
yн=C1yl(k) + C2y2(k) + … +Cnyn(k).
Частное решение ищем в виде
yp = μ1(k)y1(k) + μ2(k)y2(k) + … + μn(k)yn(k). (88)
Следующие n-1 условий выбираются произвольно с целью упрощения решения:
y1(k+1)∆μ1(k) + y2(k+1)∆μ2(k) +…+ yn(k+1)∆μ0(k) = 0,
y1(k+2)∆μ1(k) + y2(k+2)∆μ2(k) +…+ yn(k+2)∆μ0(k) = 0,
………………………………………………………………
y1(k+n-1)∆μ1(k) + y2(k+n-1)∆μ2(k) +…+ yn(k+n-1)∆μ0(k) = 0, (89)
Подставив уравнение (88) в уравнение (84) и используя (89), получим
y1(k+n)∆μ1(k) + y2(k+n)∆μ2(k) +…+ yn(k+n)∆μn(k) = F(k)/an (90)
Получение импульсной характеристики на основе разностного уравнения.
Реакция на дельта-функцию (импульсная характеристика), обозначаемая через d(k), представляет собой реакцию предварительно невозбужденной дискретной системы на сигнал
При рассмотрении разностных уравнений масштаб времени предполагается таким, что Т=1.
studfiles.net
Разностные уравнения 1 порядка. Разностные уравнения 2 порядка
Тема: Разностные уравнения 1 порядка
Контрольные вопросы:
1. Какая функция называется сеточной?
2. Какое уравнение называется разностным?
3. Какие уравнения называются разностными уравнениями 1-го порядка?
4. Как находится общее решение неоднородного разностного уравнения 1-го порядка?
5. Какое решение разностного уравнения называется фундаментальным?
6. Почему общее решение однородного уравнения с постоянными коэффициентами имеет вид геометрической прогрессии?
Задания.
1. Написать процедуру решения разностного уравнения первого порядка с начальным условием .
2. Для заданного уравнения найти общее и частное решение аналитически.
3. Сравнить результаты вычислений по рекуррентной формуле с аналитическим решением.
4. Выяснить, как влияет на результат возмущение начального условия, коэффициентов уравнения, правой части.
А | В | Указания | ||
1 | 2 | |||
2 | 0 | 2 | ||
3 | 1 | 1 | 2 | |
4 | n | 1 | 2 | |
5 | 3 | 2 | ||
6 | 1 | |||
7 | 0 | 1 | ||
8 | 1 | 1 | 1 | |
9 | n | 1 | 1 | |
10 | 3 | 1 | ||
11 | ||||
12 | 0 | |||
13 | 1 | 1 | ||
14 | n | 1 | ||
15 | 3 |
Рекомендации к выполнению задания.
Найдем общее решение разностного уравнения 1-го порядка
. (1)
Частное решение однородного уравнения при получим, используя рекуррентную формулу: . Поскольку значение Y в каждом следующем узле сетки удваивается, получается геометрическая прогрессия со знаменателем q=2:
.
Частное решение неоднородного уравнения найдем в виде:, где А – неопределенный коэффициент. Тогда , , и, приравняв полученное значение к заданной правой части, найдем неопределенный коэффициент A=. Окончательно, общее решение: .
Используя начальное условие , находим константу: . Окончательно, частное решение при заданном начальном условии:
.
Для исследования устойчивости решения к возмущению самого решения и начального условия рассмотрим следующее уравнение:
с возмущенным начальным условием
(здесь – величина возмущения). Вычитая исходное уравнение (1), получим разностное уравнение для возмущения:
с начальным условием . Решение этого уравнения имеет вид: , т.е. даже малое возмущение в каком-либо узле экспоненциально растет с увеличением номера узла.
Студенту необходимо проиллюстрировать сказанное выше: исследовать влияние возмущений начального условия, правых частей и коэффициентов уравнения, изменив рекуррентную формулу.
Вариант, в соответствии с номером студента по списку в журнале, необходимо решить на языке программирования C++ (допускается использование среды Builder) или Pascal (допускается использование среды Delphi).
Содержание отчета должно быть следующим:
- Постановка задачи. Исходное разностное уравнение и граничные условия.
- Рекуррентная формула для получения численного решения.
- Аналитическое решение разностного уравнения. Общее решение и частное решение, удовлетворяющее заданным начальным условиям.
- Графики численного решения и аналитического решения (в одних осях).
- График разности численного и аналитического решения.
- Исследовать устойчивость решения к возмущению начального условия и решения аналитически.
- Графики возмущенных численных решений и разности возмущенного и невозмущенного решений:
а) при возмущении начального условия;
б) при возмущении коэффициентов уравнения;
в) при возмущении правой части.
Тема :Разностные уравнения 2 порядка
Контрольные вопросы:
1. Какие уравнения называются разностными уравнениями 2-го порядка?
2. Что такое характеристическое уравнение?
3. Как выглядит частное решение однородного разностного уравнения 2-го порядка с действительными корнями характеристического уравнения?
4. Как выглядит частное решение однородного разностного уравнения 2-го порядка с комплексными корнями характеристического уравнения?
5. Как находится общее решение неоднородного разностного уравнения 2-го порядка?
6. Что такое численное и аналитическое решение разностного уравнения 2-го порядка?
7. Какие задачи называются хорошо обусловленными?
Задания
1. Написать процедуру решения разностной краевой задачи для уравнения второго порядка с граничными условиями , .
2. Для заданного уравнения найти общее и частное решение аналитически и проверить критерий обусловленности.
3. Сравнить результаты вычислений по рекуррентной формуле с аналитическим решением.
4. Выяснить, как влияет на результат возмущение граничных условий и правой части.
№ | А | В | a | b | c | |
1 | 2 | 1 | -2 | 1 | ||
2 | 0 | 2 | 2 | 4 | 1 | |
3 | 1 | 1 | 2 | 1 | 3 | 1 |
4 | n | 1 | 2 | 5 | -26 | 5 |
5 | 3 | 2 | 2 | 5 | 2 | |
6 | 1 | 2 | 5 | 2 | ||
7 | 0 | 1 | 5 | -26 | 5 | |
8 | 1 | 1 | 1 | 2 | 5 | 2 |
9 | n | 1 | 1 | 1 | 3 | 1 |
10 | 3 | 1 | 1 | 3 | 1 | |
11 | 2 | 4 | 1 | |||
12 | 0 | 1 | -2 | 1 | ||
13 | 1 | 1 | 2 | 5 | 2 | |
14 | n | 1 | 2 | 5 | 2 | |
15 | 3 | 1 | 3 | 1 |
Рекомендации к выполнению задания
Найдем общее решение разностного уравнения 2-го порядка
. (1)
Запишем характеристическое уравнение:
.
Поскольку корни совпали, то частные решения однородного уравнения имеют вид (8), (9):
,.
Частное решение неоднородного уравнения найдем в виде: , где А – неопределенный коэффициент. Подставив это выражение в исходное уравнение, получим:
,
откуда , , и окончательно, общее решение:
.
Теперь любое частное решение при заданных начальных условиях можно найти выбором произвольных постоянных .
Наряду с задачами Коши, для уравнений 2-го порядка рассматриваются также двухточечные краевые задачи, в которых заданы значения сеточной функции в двух узлах, расположенных не подряд, а на концах некоторого конечного отрезка: (граничные условия). Аналитическое решение такой задачи можно получить подходящим выбором произвольных постоянных в общем решении. Однако, в отличие от задачи с начальными условиями, краевая задача не обязательно будет однозначно разрешимой. Поэтому большое значение имеет выяснение класса краевых задач, которые обладают однозначной разрешимостью и слабой чувствительностью к возмущению (вследствие ошибок округления) правых частей и граничных условий. Такие задачи будем называть хорошо обусловленными
Рассмотрим пример плохо обусловленной краевой задачи
, (2)
и придадим правым частям малые приращения:
.
Тогда решение получит приращение, определяемое из вспомогательной краевой задачи
, . (3) Решение задачи (3) несложно получить аналитически:
В частности, при n=N-1 имеем: , т.е. возмущение решения быстро растет с увеличением числа узлов N. Оценка хорошей обусловленности задачи, которая рассматривается в курсе лекций, не выполняется (проверьте!).
Один вариант, в соответствии с заданием, полученным от преподавателя, необходимо решить на языке программирования C++ (допускается использование среды Builder) или Pascal (допускается использование среды Delphi).
Содержание отчета должно выглядеть следующим образом:
- Постановка задачи. Исходное разностное уравнение и граничные условия.
- Процедура для получения численного решения.
- Аналитическое решение разностной краевой задачи. Общее решение и частное решение, удовлетворяющее заданным граничным условиям. Проверка критерия обусловленности.
- Графики численного решения и аналитического решения (в одних осях).
- График разности численного и аналитического решения.
- Графики возмущенных численных решений и разности возмущенного и невозмущенного решений:
а) при возмущении начального условия;
б) при возмущении правой части.
- Вывод об обусловленности краевой задачи.
vunivere.ru
4. Основные теоремы о решениях линейных разностных уравнений с постоянными коэффициентами. Решение методом неопределенных коэффициентов.
Теорема 1: Если решетчатые функции E1[n], … , El[n] являются решениями линейного однородного разностного уравнения f[n+k]+b1[n]f[n+k-1]+…+bk[n]f[n]=0 (3), то функция E[n]=, где Сi(i=1,1,…,l) – произвольные постоянные, также является его решением.
Теорема 2(о линейности зависимости решетчатых функций): Если решетчатые функции f1[n],..,fk[n] линейно зависимы, то при всех щначениях аргумента n, при которых они определены, обращается в ноль определитель. W[f1[n], f2[n],…,fk[n]]=
Теорема 3: Если решетчатые функции E1[n], E2[n],…,Ek[n] являются линейно независимыми решениями однородного разностного уравнения (3) при n>=n0, то определитель W[E1[n],…Ek[n]] не обращается в ноль ни при одном значении n>=n0.
Теорема 4: Если при n>=n0 существует фундаментальная система решений E1[n],..,Ek[n] однородного разностного уравнения(3), то общее решение этого уравнения выражается формулой E[n]=, где Ci (i=1,2,…,k)- произвольные постоянные.
Для решения линейных неоднородных разностных уравнений также необходима Теорема 5: Общее решение линейного неоднородного разностного уравнения f[n+k]+b1[n]f[n+k-1]+..+bk[n]f[n]=g[n] равно сумме его частного решения x[n] и общего решения соответствующего однородного уравнения (3), т.е. f[n]=x[n]+, дге Сi- произвольные постоянные, Ei[n]= решения однородного уравнения (3), удовлетворяющие условию W[E1[n0],…Ek[n0]]=/=0
Решение разностных уравнений (однородных).
b0f[n+m]+b1f[n+m-1]+…+bmf[n]=0. Ищем решение в виде f[n]=λn. Составим характеристическое уравнение: b0 λm+ b1 λm-1+…+ bm-1 λ+bm=0. λi-корень, i=1,..,m.
f[0]=C1+C2+…+Cm f[1]=C1λ1+C2λ2+…+Cmλm ….. f[m-1]=C1 λ1m-1+C2 λ2m-1+…+Cm λmm-1 -определитель Вандермонда.
Пример: x[n+2]+5x[n+1]-0.5x[n]=0 x[0]=1, x[1]=0
λ2+5 λ-0.5=0 => λ1=0.5 ; λ2=-1.
x[n]=C1(0.5)n+(-1)nC2 – общее решение.
1=С1+С2 => 0=C1*0.5-C2 => C2=0.5 C1 C1=2/3; C2=1/3.
Решение разностных уравнений (неоднородных).
]
первое слагаемое- общее решение однор. второе- частное неоднор.
x[n+1]+2x[n]=5+6n
Будем искать x^[n]=a+bn –частное a+b(n+1)+2(a+bn)=5+6n => a=1 b=2
Общее однородное: λ+2=0 =>λ=-2 x[n]=C(-2)nНайдём С: пусть x[0]=4. 4=1+0+C => C=3.
5. Дискретное преобразование Лапласа(d-преобразование):
D-изображение всегда является функцией от ,поэтому
используют Z-преобразование,в котором
1) Линейность (следует из определения Z-образования)
2) Смещение в области оригиналов
3) Изображения конечных разностей и конечных сумм дискретных
функций:
если дискретная функция является оригиналом,то её первая и все
последующие конечные разности также являются оригиналами
4) Свертка оригиналов и изображений:
если дискретные функции являются оригиналами, то свертка этих
функций также является оригиналом
Обратное Z-преобразование:
Вычисление оригинала методом вычетов:
при
6. Решение разностных уравнений с помощью z-преобразования
Дискретная функция описывается уравнением:
,
Известны начальные условия:
Преобразуем обе части с помощью Z- преобразования:
,
решение разностного уравнения:
передаточная функция
studfiles.net
