Решение однородных систем линейных уравнений
Однородная
система
всегда совместна и имеет тривиальное
решение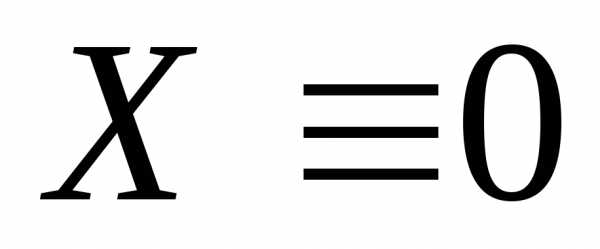 .
Для существования нетривиального
решения необходимо, чтобы ранг матрицы
.
Для существования нетривиального
решения необходимо, чтобы ранг матрицы был меньше числа неизвестных:
был меньше числа неизвестных:
.
Фундаментальной системой решений однородной системы называют систему решений в виде векторов-столбцов, которые соответствуют каноническому базису, т.е. базису, в котором произвольные постоянныепоочередно полагаются равными единице, тогда как остальные приравниваются нулю.
Тогда общее решение однородной системы имеет вид:
,
где – произвольные постоянные. Другими словами, общее решение есть линейная комбинация фундаментальной системы решений.
Таким образом, базисные решения могут быть получены из общего решения, если свободным неизвестным поочередно придавать значение единицы, полагая все остальные равные нулю.
Пример. Найдем решение системы
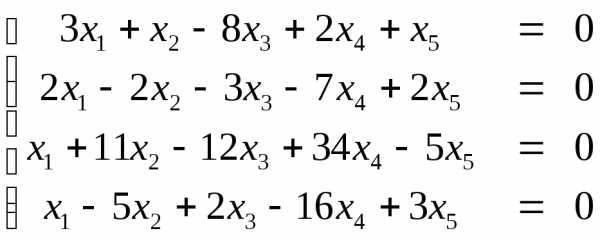
Примем , тогда получим решение в виде:
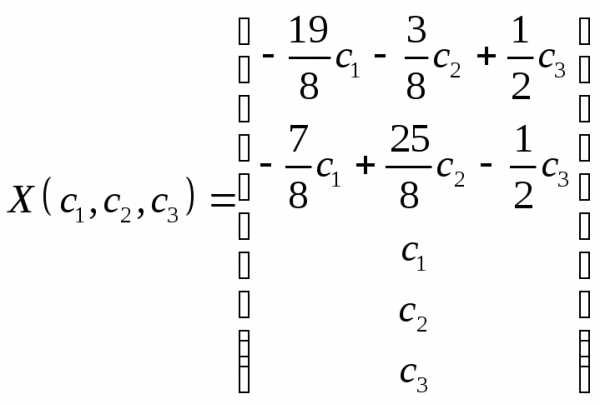
Построим теперь фундаментальную систему решений:
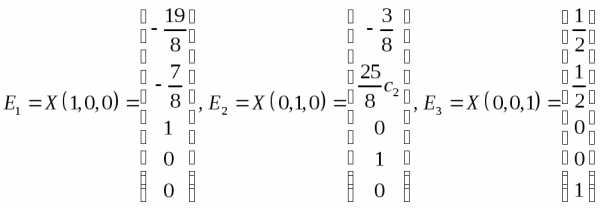 .
.Общее решение запишется в виде:
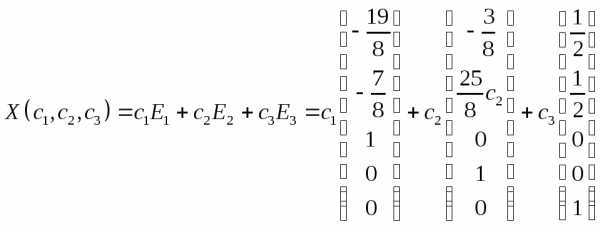
Решения системы однородных линейных уравнений имеют свойства:
Если
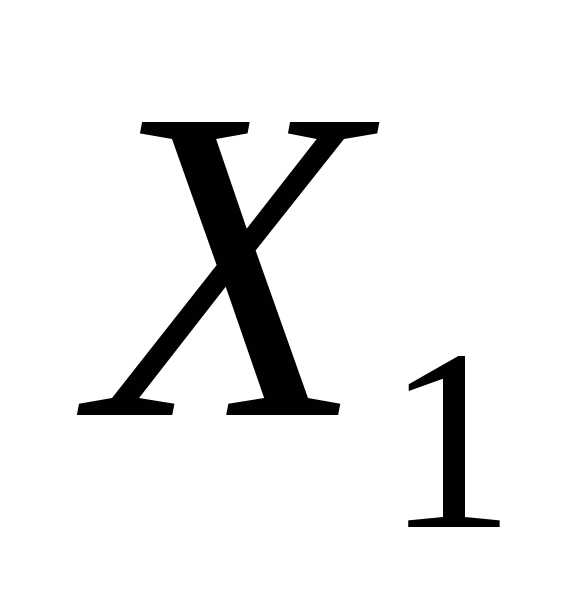 – решение системы, то и
– решение системы, то и – также решение.
– также решение.Если

 – решения системы, то и- также решение.
– решения системы, то и- также решение.
Другими словами, любая линейная комбинация решений однородной системы есть опять решение.
Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений интересует математиков несколько столетий. Первые результаты были получены в XVIII веке. В 1750 г. Г.Крамер (1704 –1752) опубликовал свои труды по детерминантам квадратных матриц и предложил алгоритм нахождения обратной матрицы. В 1809 г. Гаусс изложил новый метод решения, известный как метод исключения.
Метод Гаусса, или метод последовательного исключения неизвестных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида. Такие системы позволяют последовательно находить все неизвестные в определенном порядке.
Предположим,
что в системе (1)  (что всегда возможно).
(что всегда возможно).
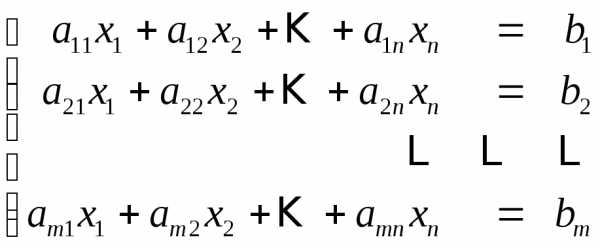 (1)
(1)
Умножая поочередно первое уравнение на так называемые
и складывая результат умножения с соответствующими уравнениями системы, мы получим эквивалентную систему, в которой во всех уравнениях, кроме первого, будет отсутствовать неизвестная х1
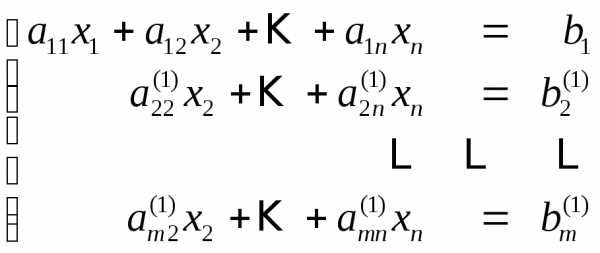 (2)
(2)
Умножим
теперь второе уравнение системы (2) на
подходящие числа, полагая, что 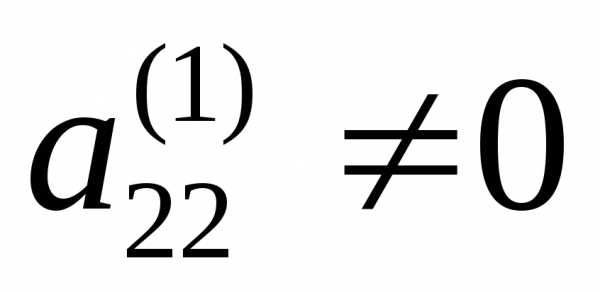
,
и
складывая его с нижестоящими, исключим
переменную 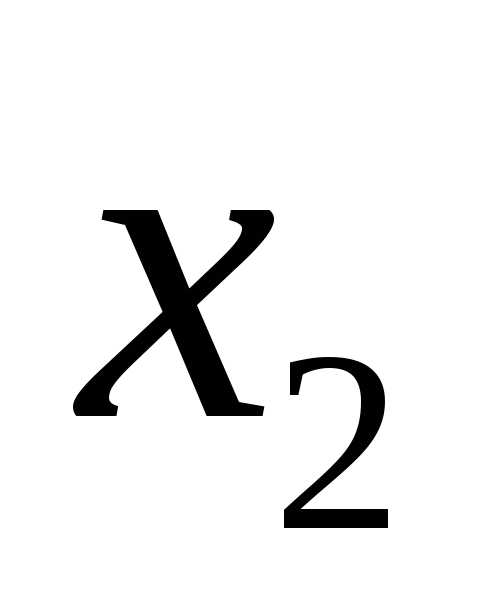
Продолжая
этот процесс, после 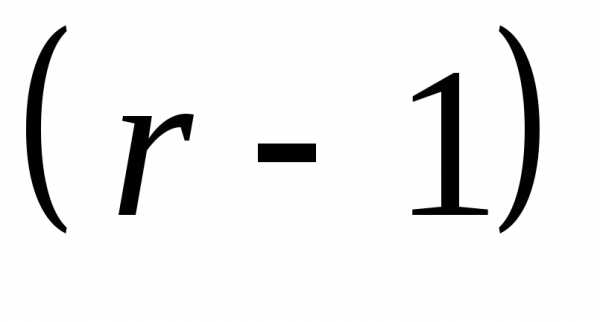 шага мы получим:
шага мы получим:
(3)
Если
хотя бы одно из чисел
не равно нулю, то соответствующее
равенство противоречиво и система (1)
несовместна. Обратно, для любой совместной
системы числаравны нулю. Число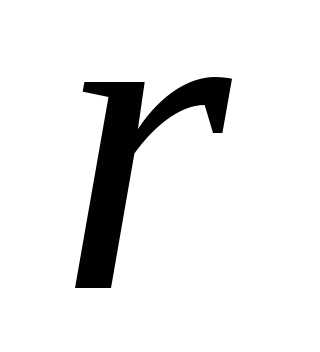 – это ни что иное, как ранг матрицы системы
(1).
– это ни что иное, как ранг матрицы системы
(1).
Переход от системы (1) к (3) называется прямым ходом
Замечание: Преобразования удобнее производить не с самими уравнениями, а с расширенной матрицей системы (1).
Пример. Найдем решение системы
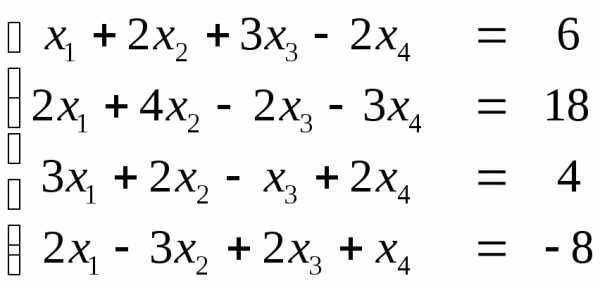 .
.
Запишем расширенную матрицу системы:
 .
.
Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:
 .
. Поменяем
строки 2 и 3 местами, затем в получившейся
матрице добавим к строке 4 строку 2,
умноженную на 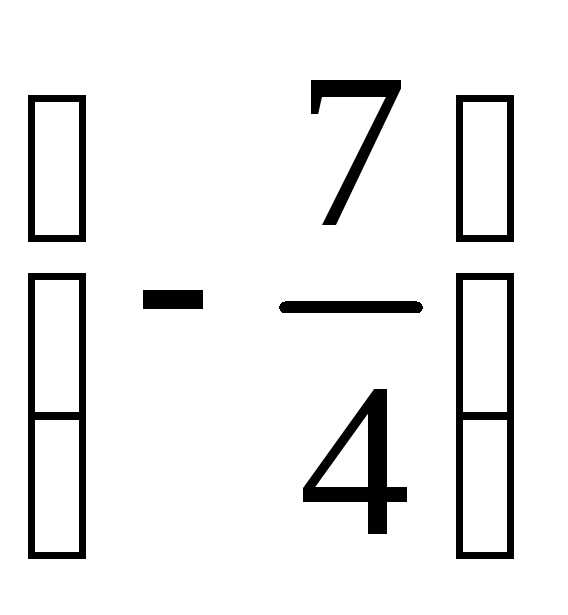 :
:
 .
.
Прибавим
к строке 4 строку 3, умноженную на 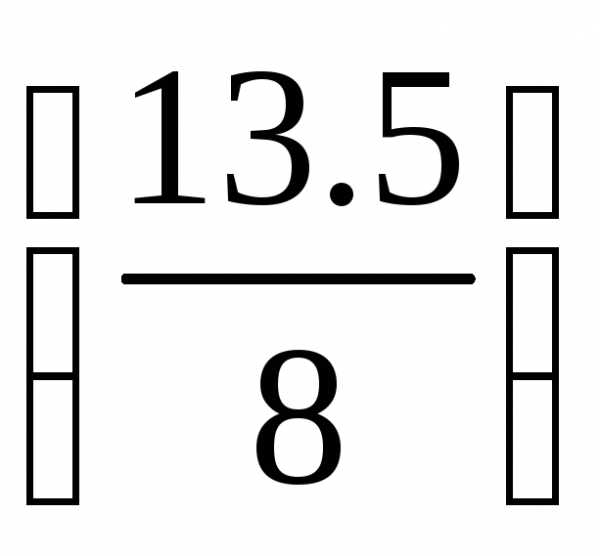 :
:

Очевидно, что , следовательно, система совместна. Из полученной системы уравнений

находим решение обратной подстановкой:
 ,
, 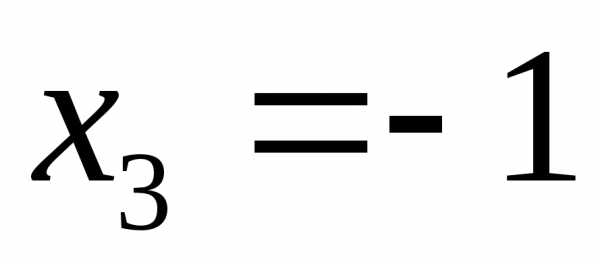 ,
,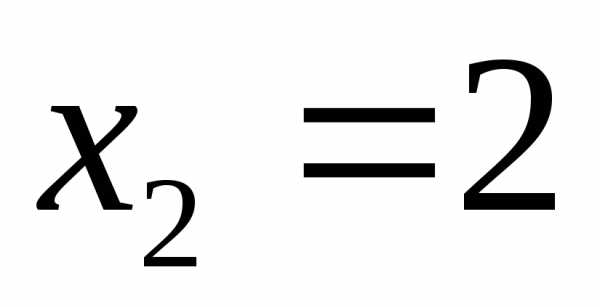 ,
,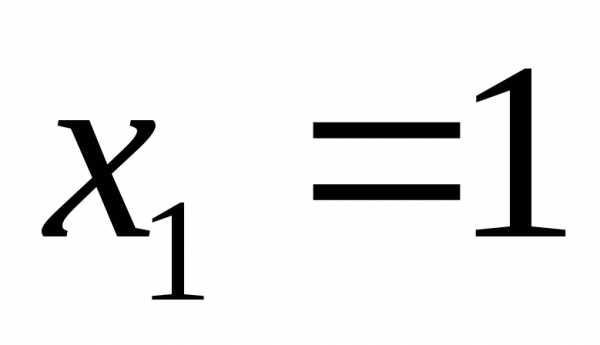
Пример 2. Найти решение системы:
 .
.
Очевидно,
что система несовместна, т.к.
,
а .
.
Достоинства метода Гаусса:
Менее трудоемкий, чем метод Крамера.
Однозначно устанавливает совместность системы и позволяет найти решение.
Дает возможность определить ранг любых матриц.
studfiles.net
Решение однородных систем линейных уравнений
Однородная
система
всегда совместна и имеет тривиальное
решение .
Для существования нетривиального
решения необходимо, чтобы ранг матрицы
.
Для существования нетривиального
решения необходимо, чтобы ранг матрицы был меньше числа неизвестных:
был меньше числа неизвестных:
.
Тогда общее решение однородной системы имеет вид:
,
где – произвольные постоянные. Другими словами, общее решение есть линейная комбинация фундаментальной системы решений.
Таким образом, базисные решения могут быть получены из общего решения, если свободным неизвестным поочередно придавать значение единицы, полагая все остальные равные нулю.
Пример. Найдем решение системы

Примем , тогда получим решение в виде:
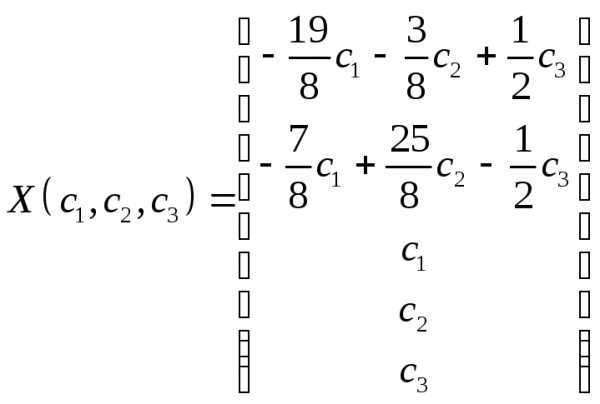
Построим теперь фундаментальную систему решений:
 .
.
Общее решение запишется в виде:
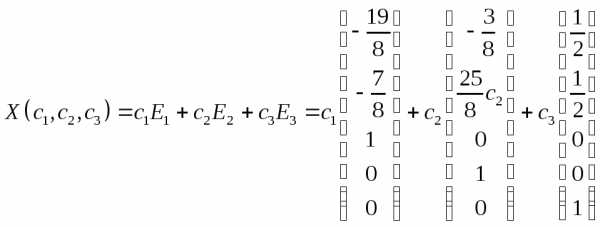
Решения системы однородных линейных уравнений имеют свойства:
Если
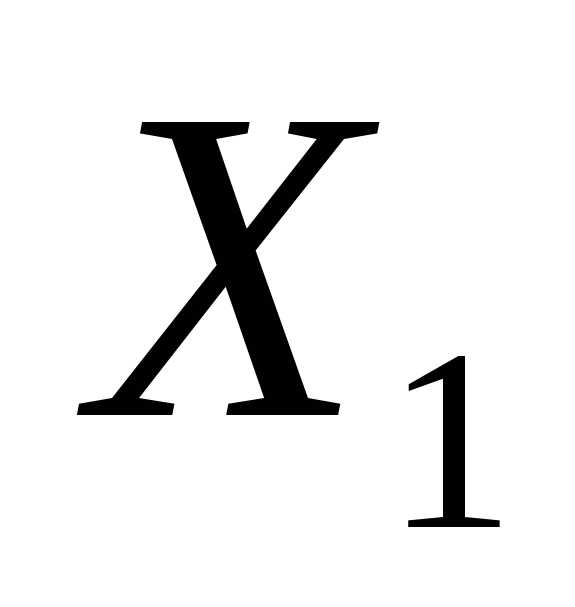 – решение системы, то и
– решение системы, то и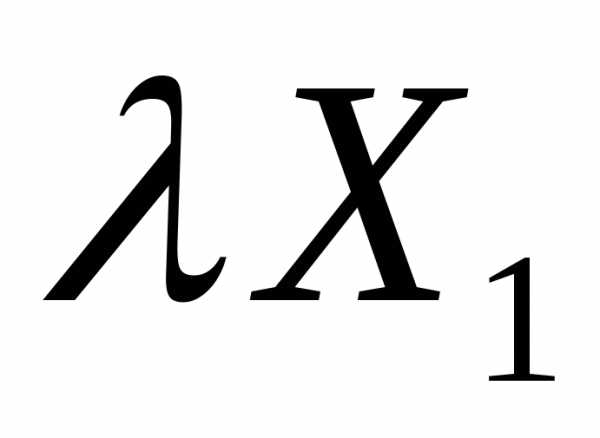 – также решение.
– также решение.Если
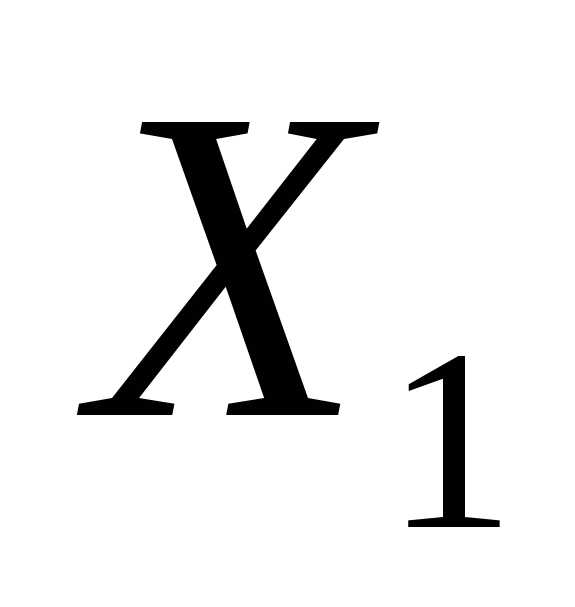 и
и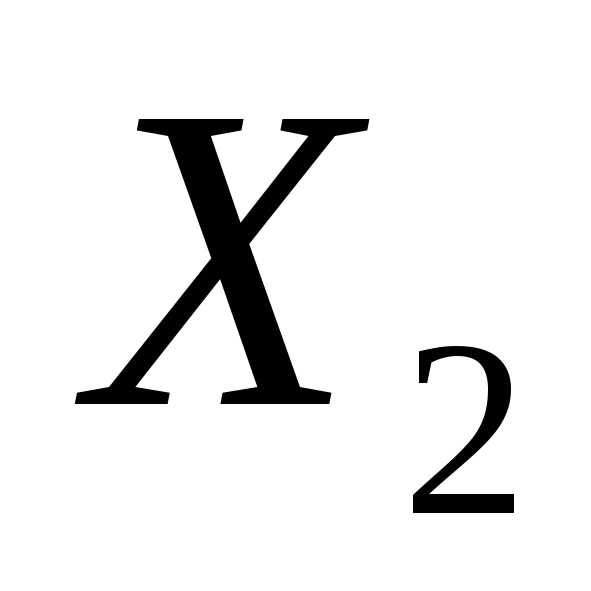 – решения системы, то и- также решение.
– решения системы, то и- также решение.
Другими словами, любая линейная комбинация решений однородной системы есть опять решение.
Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений интересует математиков несколько столетий. Первые результаты были получены в XVIII веке. В 1750 г. Г.Крамер (1704 –1752) опубликовал свои труды по детерминантам квадратных матриц и предложил алгоритм нахождения обратной матрицы. В 1809 г. Гаусс изложил новый метод решения, известный как метод исключения.
Метод Гаусса, или метод последовательного исключения неизвестных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида. Такие системы позволяют последовательно находить все неизвестные в определенном порядке.
Предположим,
что в системе (1)  (что всегда возможно).
(что всегда возможно).
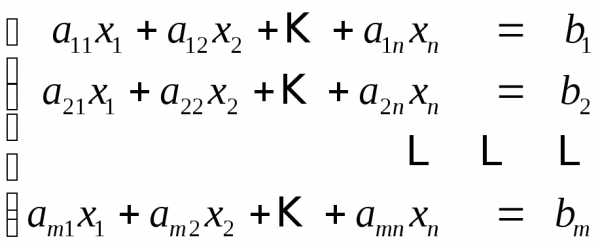 (1)
(1)
Умножая поочередно первое уравнение на так называемые подходящие числа
и складывая результат умножения с соответствующими уравнениями системы, мы получим эквивалентную систему, в которой во всех уравнениях, кроме первого, будет отсутствовать неизвестная х1
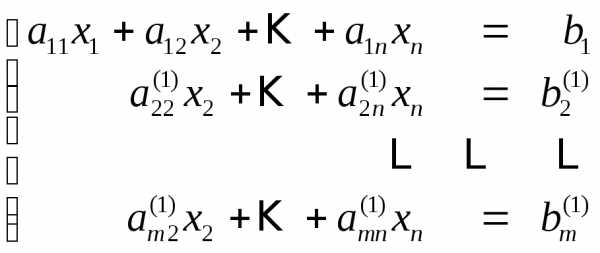 (2)
(2)
Умножим
теперь второе уравнение системы (2) на
подходящие числа, полагая, что 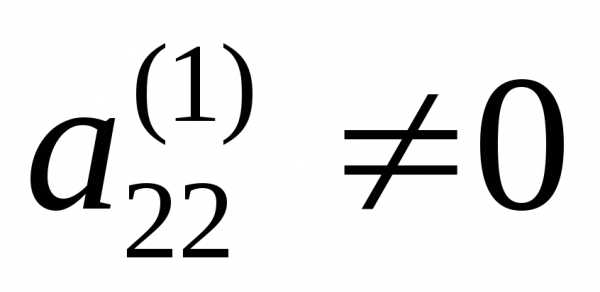
, 
и
складывая его с нижестоящими, исключим
переменную  из всех уравнений, начиная с третьего.
из всех уравнений, начиная с третьего.
Продолжая
этот процесс, после 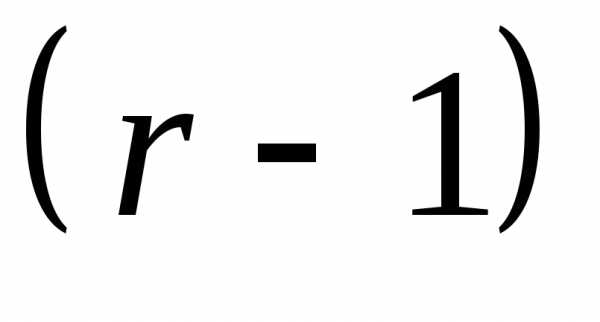 шага мы получим:
шага мы получим:
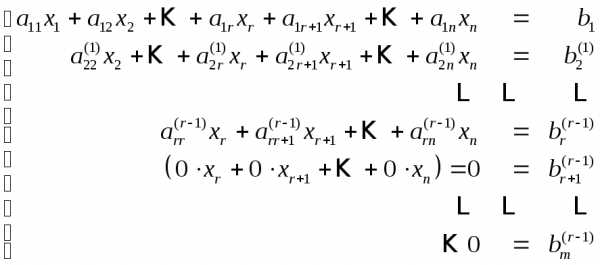 (3)
(3)
Если
хотя бы одно из чисел
не равно нулю, то соответствующее
равенство противоречиво и система (1)
несовместна. Обратно, для любой совместной
системы числаравны нулю. Число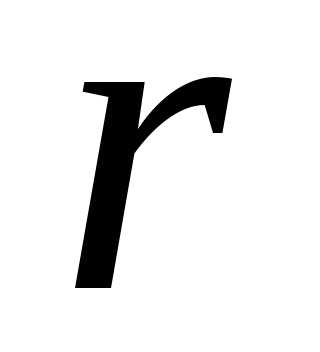 – это ни что иное, как ранг матрицы системы
(1).
– это ни что иное, как ранг матрицы системы
(1).
Переход от системы (1) к (3) называется прямым ходом метода Гаусса, а нахождение неизвестных из (3) – обратным ходом.
Замечание: Преобразования удобнее производить не с самими уравнениями, а с расширенной матрицей системы (1).
Пример. Найдем решение системы
 .
.
Запишем расширенную матрицу системы:
 .
.
Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:
 .
.
Поменяем
строки 2 и 3 местами, затем в получившейся
матрице добавим к строке 4 строку 2,
умноженную на 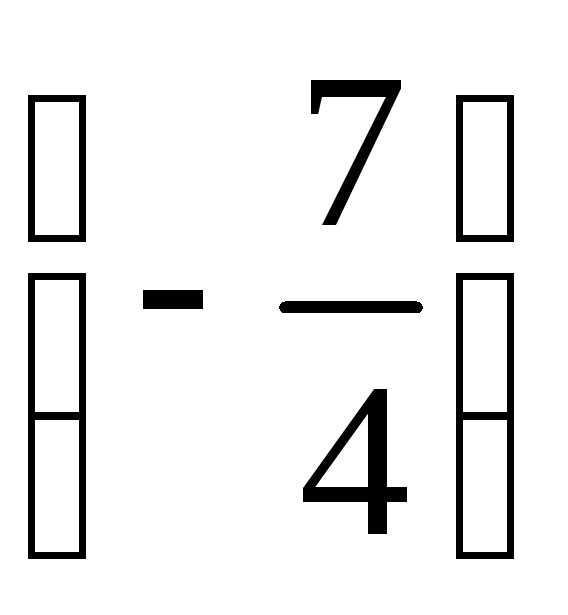 :
:
 .
.
Прибавим
к строке 4 строку 3, умноженную на  :
:
 .
.
Очевидно, что , следовательно, система совместна. Из полученной системы уравнений
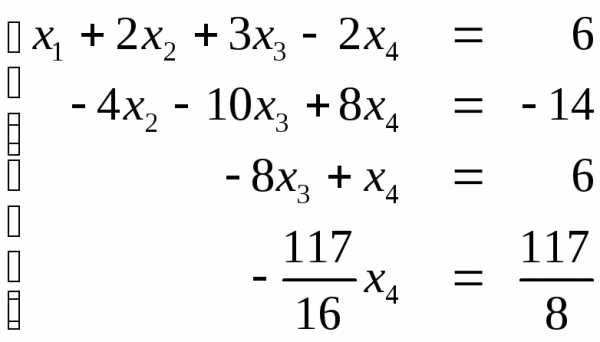
находим решение обратной подстановкой:
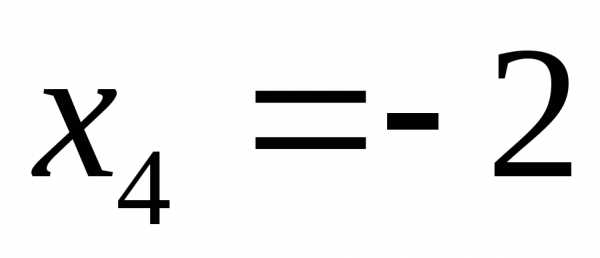 ,
, 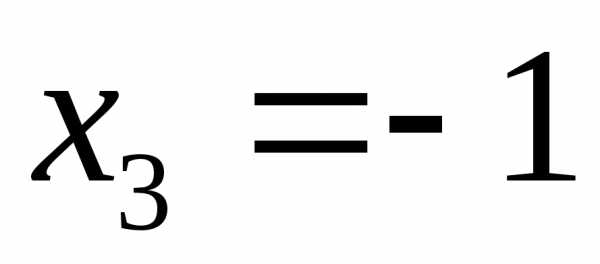 ,
,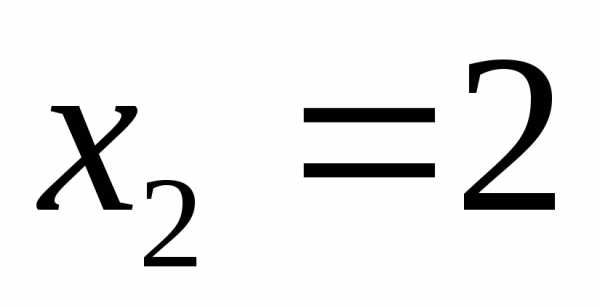 ,
, .
.
Пример 2. Найти решение системы:
 .
.
Очевидно,
что система несовместна, т.к.
,
а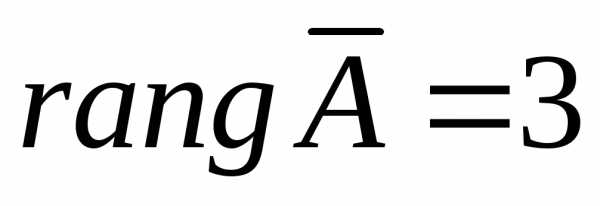 .
.
Достоинства метода Гаусса:
Менее трудоемкий, чем метод Крамера.
Однозначно устанавливает совместность системы и позволяет найти решение.
Дает возможность определить ранг любых матриц.
studfiles.net
17.Решение систем линейных алгебраических уравнений прямым методом Гаусса.
Пусть исходная система выглядит следующим образом
Матрица называется основной матрицей системы, — столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных [3].
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число , где , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть для любых .
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где — номер строки):
, где
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
18. Методы, используемые при решении систем линейных алгебраических уравнений
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
-На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
-На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
19. К какому виду методов относится метод Гаусса для решения системы линейных
алгебраических уравнений ( СЛАУ) ?
20. Из каких основных частей состоит метод Гаусса для решения системы линейных
алгебраических уравнений ( СЛАУ) ?
21. Основные действия в прямом ходе при решении системы линейных
алгебраических уравнений ( СЛАУ) методом Гаусса?
22. Основные действия в обратном ходе при решении системы линейных
алгебраических уравнений ( СЛАУ) методом Гаусса
23. Вектор внешних усилий ( вектор правых частей) СЛАУ.
24. Перемещения, рассматриваемые на концах стержня в местной системе координат
25. Реакции, рассматриваемые на концах стержня в местной системе координат
26. Физический смысл произвольного элемента матрица жесткости
27. Для чего используется таблица реакций отдельного стержня ?
28. Расчет составной балки . МЖЭ элементов балки .
29. МЖС составной балки .
30. Узловые перемещения составной балки .
31.Отличие местной системы координат от общей системе координат
studfiles.net
Решение однородных систем методом Гаусса
Однородная система всегда совместна, так как она всегда имеет нулевое решение x1 = x2 = … = xn = 0. Для нее справедливо, что .
Теорема Кронекера–Капелли для однородной системы: 1) если , то система имеет единственное решение – нулевое, 2) если , то система имеет бесконечное множество решений, среди которых есть и ненулевые.
Определение.Линейно независимая совокупность решений однородной системы называется фундаментальной системой решений, если каждое решение является линейной комбинацией остальных.
Идея метода Гаусса: матрица системы приводится к трапециевидной или к треугольной форме, затем все получившиеся базисные переменные выражаются через свободные переменные и находится фундаментальное решение системы.
Пример. Решить систему линейных уравнений: .
Решение.Запишемматрицу системы: ,
отсюда т.к. три ненулевые строки. Количество неизвестных n = 4, т.е. , следовательно, по теореме Кронекера – Капелли система имеет бесконечное множество решений. Найдем его. Запишем полученную матрицу в виде системы уравнений:
. Система имеет три базисные неизвестные: х1, х2, х3 и одну свободную х4. Выразим базисные неизвестные через свободную переменную, начиная с последнего уравнения:
,
,
.
Ответ: Фундаментальная система решений: .
Похожие статьи:
poznayka.org
6Вопрос Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
Где Коэффициенты aii называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Опишем метод Гаусса подробнее.
Будем считать, что элемент (если a11=0 , то первым в системе запишем уравнение, в котором коэффициент при х1 отличен от нуля).
Преобразуем систему (4.3), исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения наи сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
Здесь — новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом , исключим неизвестное х2из всех уравнений системы, кроме первого я второго, и так далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 0=0, их отбрасывают Если же появится уравнение вида то это свидетельствует о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений, В последнем уравнении этой системы выражаем первое неизвестное xkчерез остальные неизвестные (xk+1,…,xn). Затем подставляем значение xk в предпоследнее уравнение системы и выражаем xk-1 через (xk+1,…,xn). , затем находим xk-2,…,x1.. Придавая свободным неизвестным (xk+1,…,xn). произвольные значения, получим бесчисленное множество решений системы.
Замечания:
1. Если ступенчатая система оказывается треугольной, т. е. k=n, то исходная система имеет единственное решение. Из последнего уравнения находим xn из предпоследнего уравнения xn-1, далее поднимаясь по системе вверх, найдем все остальные неизвестные (xn-1,…,x1).
2. На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11¹1).
Пример 4.4.
Решить систему методом Гаусса:
Решение: В результате элементарных преобразований над расширенной матрицейсистемы
исходная система свелась к ступенчатой:
Поэтому общее решение системы: x2=5x4-13x3-3;x1=5x4-8x3-1 Если положить, например, x3=0,x4=0, то найдем одно из частных решений этой системы x1=-1,x2=-3,x3=0,x4=0.
studfiles.net
Решение систем линейных уравнений методом Гаусса — МегаЛекции
Одним из наиболее универсальных и эффективных методов решений систем линейных алгебраических уравнений является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
(4.3)
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где . Коэффициенты называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных этой ступенчатой системы.
Опишем метод Гаусса подробнее.
Прямой ход.
Будем считать, что элемент (если , то первым в системе запишем уравнение, в котором коэффициент при отличен от нуля).
Преобразуем систему (4.3), исключив неизвестное во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
Здесь – новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом , исключим неизвестное из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида , то их отбрасывают. Если же появится уравнение вида , а , то это свидетельствует о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное через остальные неизвестные ; затем находим . Придавая свободным неизвестным произвольные значения, получим бесчисленное множество решений системы.
Замечания: 1. Если ступенчатая система оказывается треугольной, т.е. , то исходная система имеет единственное решение. Из последнего уравнения находим , из предпоследнего уравнения , далее поднимаясь по системе вверх, найдем все остальные неизвестные .
2. На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).
Пример 4.4. Решить систему методом Гаусса:
Решение: В результате преобразований над расширенной матрицей системы
~ ~
~ ~
исходная система свелась к ступенчатой:
Поэтому, общее решение системы: Если положить, например, , то найдем одно из частных решений этой системы
Пример 4.5. Решить систему методом Гаусса:
Решение: Произведем элементарные преобразования над строчками расширенной матрицы системы:
~ ~ ~ .
Полученная матрица соответствует системе:
Осуществляя обратный ход, находим
Системы однородных линейных уравнений
Пусть дана система линейных однородных уравнений
Очевидно, что однородная система всегда совместна , она имеет нулевое (тривиальное) решение
При каких условиях однородная система имеет и ненулевые решения?
Необходимость.
Так как ранг не может превосходить размера матрицы, то, очевидно, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то .
Достаточность.
Пусть . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.
Пусть дана однородная система линейных уравнений с неизвестными
Если система имеет ненулевые решения, то . Ибо при система имеет единственное, нулевое решение. Если же , то ранг основной матрицы системы меньше числа неизвестных, т.е. . И, значит, система имеет бесконечное множество (ненулевых) решений.
Пример 4.6. Решить систему
Решение: Так как , то система имеет бесчисленное множество решений. Найдем их
Стало быть – общее решение. Положив получим одно частное решение: Положив получаем второе частное решение: и т.д.
Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
ВЕКТОРЫ
Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина изображается с помощью вектора.
Вектор– это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А – начало вектора, а В – его конец, то вектор обозначается символом или . Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .
Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, дина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается через . Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .
Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || .
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору.
Два вектора и называются равными ( = ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.
На рисунке 1 векторы образуют прямоугольник. Справедливо равенство = , но . Векторы и – противоположные, . Равные векторы также называют свободными.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие векторы компланарны.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
