Решение системы уравнений по формулам Крамера.
Исходная система уравнений имеет вид:
Из коэффициентов при неизвестных составляем главный определитель системы:

По правилу Сарруса находим значение этого определителя:
 =5∙2∙2+3∙6∙1+2∙4∙4-3∙2∙4-2∙6∙2-5∙4∙1=
20+18+32-24-24-20=2≠0
=5∙2∙2+3∙6∙1+2∙4∙4-3∙2∙4-2∙6∙2-5∙4∙1=
20+18+32-24-24-20=2≠0
Заменяя столбцы коэффициентов при каждом из неизвестных в главном определителе системы столбцом свободных членов, мы находим соответствующие вспомогательные определители системы:
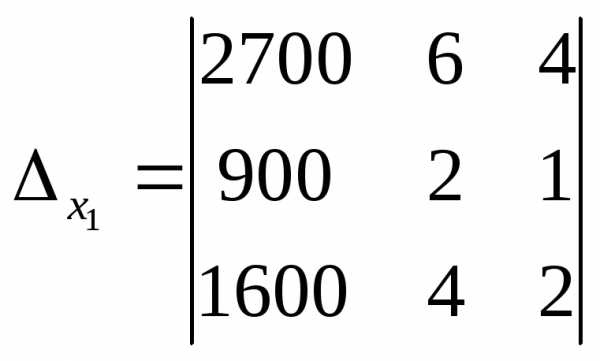
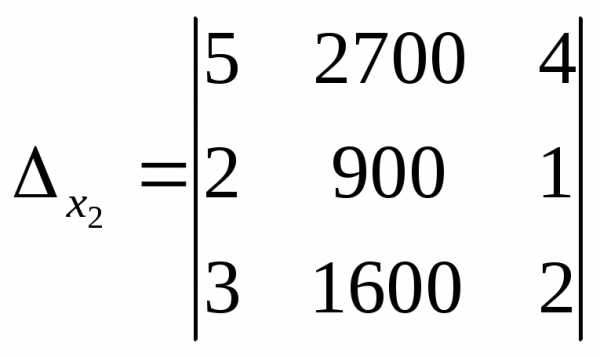

4. В целях рациональности вычисления находим вспомогательные определители, применяя теорему Лапласа к первому, второму, третьему столбцу, соответственно:
4.1
4.2
4.3
По формулам Крамера находим неизвестные:
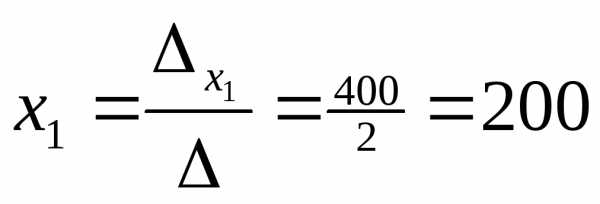

Решение окончено.
Проверка:
Ответ:ежедневный выпуск продукции составляет200 шт.изделияS
Задача № 2
Определить, имеет ли матрица Aобратную, и если имеет, то вычислить ее:

Решение
1)Вычисляем определитель матрицыА, применяя теорему Лапласа к первой строке:
2)Выписываем транспонированную матрицуАТ:

3)Строим присоединенную матрицу
Выписываем присоединенную матрицу: 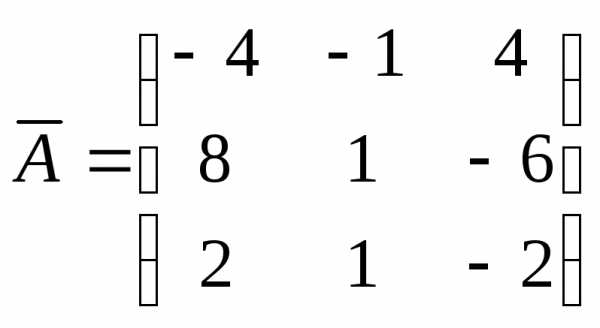
4)Находим обратную матрицу по
формуле: 
Проверка.Воспользуемся определением обратной матрицы :


Задача № 3
В таблице приведены данные об исполнении баланса. Используя модель Леонтьевамногоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной в 1,2 раза.
Вариант №1. | ||||||
№ | Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
Энергетическая | 100 | 160 | 240 | 500 | ||
Машиностроение | 275 | 40 | 85 | |||
Решение
1)Вычисляем коэффициенты прямых затратaij, показывающие, какой объем продукцииi-ой отрасли идет на производство одной единицы продукцииj-ой отрасли:
2)Выписываем столбец валового выпускаX, столбец нового конечного выпускаY, а также матрицу прямых затратА.
3)Вычисляем матрицуE–A
4)Вычисляем матрицу полных затратS=(E–A)-1.Каждый элементsijэтой матрицы показывает величину валового выпускаi-ой отрасли, необходимого для обеспечения выпуска одной единицы конечного продукта
4.1.Вычисляем определитель
4.2.Находим транспонированную матрицу
4.3.Строим присоединенную матрицу:
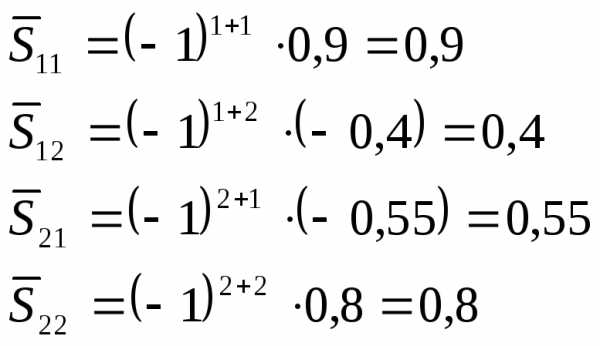

4.4.Находим обратную матрицу:
5)Вычисляем новый вектор валового выпуска:
6)Строим новую балансовую таблицу, предварительно вычисляя недостающие величины:

№ | Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
Энергетическая | 186,4 | 265,6 | 480 | |||
Машиностроение | 512,6 | 66,4 | 85 | 664 | ||
Проверка:
studfiles.net
Решение системы уравнений по формулам Крамера.
Исходная система уравнений имеет вид:
Из коэффициентов при неизвестных составляем главный определитель системы:

По правилу Сарруса находим значение этого определителя:
 =5∙2∙2+3∙6∙1+2∙4∙4-3∙2∙4-2∙6∙2-5∙4∙1=
20+18+32-24-24-20=2≠0
=5∙2∙2+3∙6∙1+2∙4∙4-3∙2∙4-2∙6∙2-5∙4∙1=
20+18+32-24-24-20=2≠0
Заменяя столбцы коэффициентов при каждом из неизвестных в главном определителе системы столбцом свободных членов, мы находим соответствующие вспомогательные определители системы:

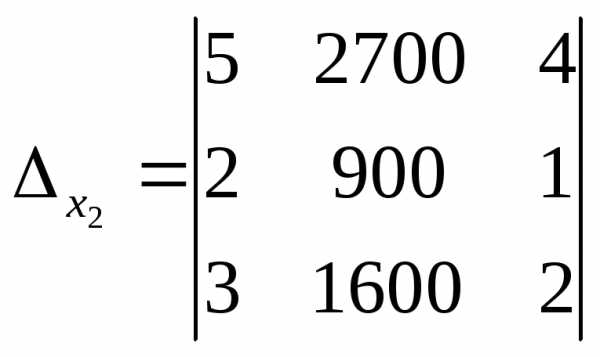

4. В целях рациональности вычисления находим вспомогательные определители, применяя теорему Лапласа к первому, второму, третьему столбцу, соответственно:
4.1
4.2
4.3
По формулам Крамера находим неизвестные:
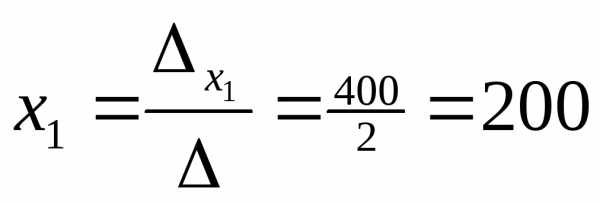

Решение окончено.
Проверка:
Задача № 2
Определить, имеет ли матрица Aобратную, и если имеет, то вычислить ее:
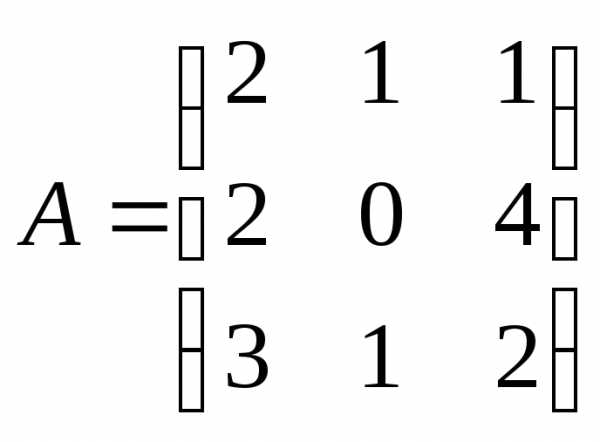
Решение
1)Вычисляем определитель матрицыА, применяя теорему Лапласа к первой строке:
2)Выписываем транспонированную матрицуАТ:
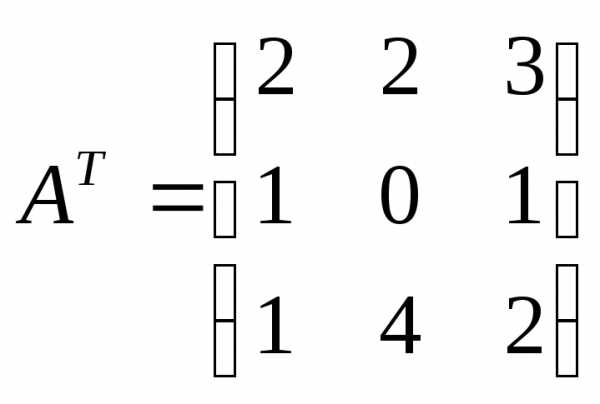
3)Строим присоединенную матрицу .
Ее элементы представляют собой
алгебраические дополнения соответствующих
элементов транспонированной матрицыАТ.
.
Ее элементы представляют собой
алгебраические дополнения соответствующих
элементов транспонированной матрицыАТ.
Выписываем присоединенную матрицу: 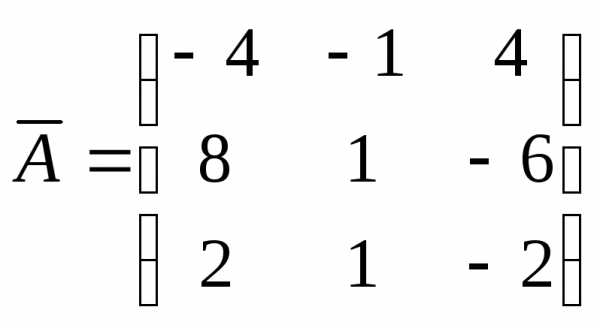
4)Находим обратную матрицу по
формуле: 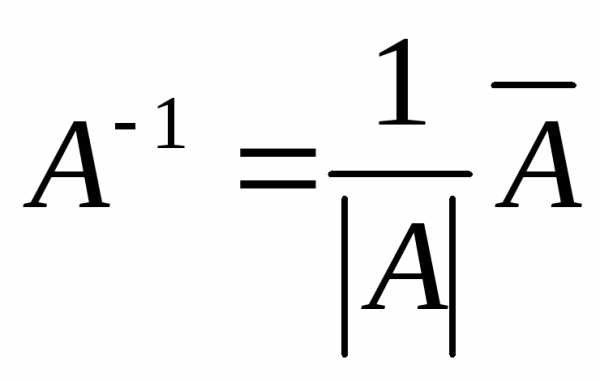
Проверка.Воспользуемся определением обратной матрицы :
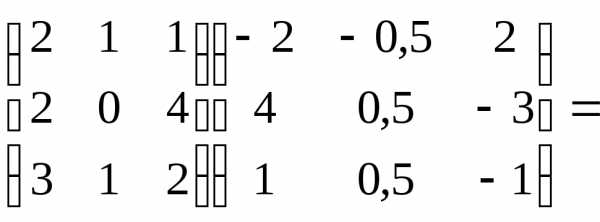

Задача № 3
В таблице приведены данные об исполнении баланса. Используя модель Леонтьевамногоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной в 1,2 раза.
Вариант №1. | ||||||
№ | Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
Энергетическая | 100 | 160 | 240 | 500 | ||
Машиностроение | 275 | 40 | 85 | 400 | ||
Решение
1)Вычисляем коэффициенты прямых затратaij, показывающие, какой объем продукцииi-ой отрасли идет на производство одной единицы продукцииj-ой отрасли:
2)Выписываем столбец валового выпускаX, столбец нового конечного выпускаY, а также матрицу прямых затратА.
3)Вычисляем матрицуE–A
4)Вычисляем матрицу полных затратS=(E–A)-1.Каждый элементsijэтой матрицы показывает величину валового выпускаi-ой отрасли, необходимого для обеспечения выпуска одной единицы конечного продуктаj-ой отрасли.
4.1.Вычисляем определитель
4.2.Находим транспонированную матрицу
4.3.Строим присоединенную матрицу:

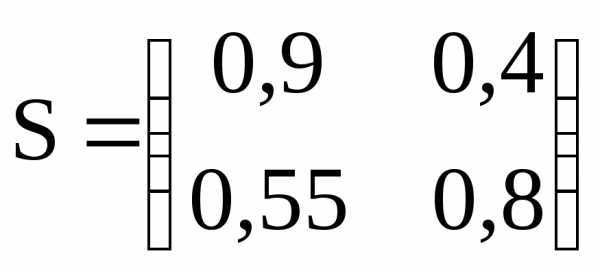
4.4.Находим обратную матрицу:
5)Вычисляем новый вектор валового выпуска:
6)Строим новую балансовую таблицу, предварительно вычисляя недостающие величины:

№ | Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
Энергетическая | 186,4 | 265,6 | 480 | 932 | ||
Машиностроение | 512,6 | 66,4 | 85 | 664 | ||
Проверка:
studfiles.net
Решение систем линейных уравнений по формулам Крамера
Время проведения –2 часа.
Цель работы:научиться решать системы линейных уравнений методом Крамера;
Вопросы для подготовки к работе:
1. Понятие системы линейных уравнений;
2. Совместные и несовместные системы линейных уравнений;
3. Понятие матрицы;
4. Понятие определителя матрицы;
5. Формула определителя второго порядка;
6. Формула определителя третьего порядка;
7. Свойства определителя n-го порядка;
8. Решение систем линейных уравнений методом Крамера;
Содержание работы:
1. Нахождение определителя матрицы;
2. Решение систем линейных уравнений методом Крамера.
Порядок выполнения задания:
При выполнении первого задания используются формулы для вычисления определителей первого и второго порядка, а также правило разложения определителя n-го порядка по строке или столбцу.
Пусть задана квадратная матрица второго порядка . Определитель этой матрицы (определитель второго порядка) вычисляется следующим образом:
Пример: Вычислить определитель
Решение:
Имеем определитель второго порядка. Используем формулу, указанную выше.
Ответ:
Пусть задана квадратная матрица третьего порядка . Определитель этой матрицы (определитель третьего порядка) вычисляется следующим образом:
Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Это правило называют правилом треугольников.
Пример: Вычислить определитель
Решение:
Имеем определитель третьего порядка, для его вычисления воспользуемся правилом треугольников:
Ответ:
Для определителей четвертого и более высоких порядков обычно применяют разложение по элементам строки или столбца. Определитель равен сумме произведений элементов строки определителя на их алгебраическое дополнение (число , где – минор к элементу определителя порядка, то есть определитель порядка, полученный из исходного вычеркиванием строки и столбца). Обычно выбирают ту строку/столбец, в которой/ом есть нули.
Пример: Вычислить определитель
Решение:
Используем формулу разложения по элементам второй строки:
Ответ:
При решении второго задания используется метод Крамера – способ решения квадратных систем линейных уравнений, который основан на следующей теореме Крамера: если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера: , где – определитель матрицы системы, – определитель матрицы системы, где вместо столбца стоит столбец правых частей.
Пример: Найдите решение системы линейных уравнений при помощи метода Крамера.
Решение:
Вычисляем определитель матрицы системы по формуле:
Имеем,
Так как , то по Теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель получим из определителя заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:
Аналогично, определитель получается из определителя матрицы системы путем замены второго столбца столбцом свободных коэффициентов6
Тогда получаем:
Ответ:
Пример: Найдите решение системы линейных уравнений методом Крамера
Решение:
Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле:
Имеем,
Определитель основной матрицы отличен от нуля, следовательно. система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители .
Таким образом,
Ответ:
Пример: Найдите решение системы линейных уравнений методом Крамера
Решение:
Вычислим определитель основной матрицы системы, разложив его по элементам второй строки:
Определитель основной матрицы системы отличен от нуля, поэтому для решения системы можно воспользоваться методом Крамера. Найдем .
Аналогично вычисляются:
Таким образом,
Ответ:
Практическая работа № 9
infopedia.su
