Блоки. Условие равновесия блоков
«Кто овладел творениями Архимеда,
будет меньше удивляться открытиям
самых великих людей нашего времени»
Г.В. Лейбниц
Данная тема посвящена решению задач на тему «Блоки. Условие равновесия блоков».
Задача 1. Какую минимальную силу нужно приложить к концу веревки для подъема мешка цемента массой 50 кг с помощью данной системы блоков? На какую высоту будет поднят мешок при совершении этой силой работы в 2500 Дж? Считать блоки идеальными.
|
ДАНО: |
РЕШЕНИЕ: Подвижный блок, позволяет получить выигрыш в силе в два раза. Значит, минимальная сила, которую нужно приложить к концу веревки для подъема мешка цемента, равна половине веса этого мешка Вес мешка цемента: Тогда минимальная сила Работа силы определяется по формуле Согласно «Золотому правилу механики», если мы выигрываем в силе, то во столько же раз проигрываем в пути. Так как подвижный блок дает нам выигрыш в силе в два раза, то в пути мы проиграем также в два раза, то есть высота подъема мешка цемента будет в два раза меньше высоты подъема точки приложения силы Высоту подъема точки приложения силы определим как отношение работы, совершенной силой, к модулю этой силы Тогда искомая высота |
Ответ: 250 Н; 5 м.
Задача 2. В системе, изображенной на рисунке, масса самого правого груза равна 1,5 кг, а массы всех блоков одинаковы и равны 0,4 кг. Система уравновешена и неподвижна. Определите массы остальных грузов, если массой троса и трением в блоках можно пренебречь.
|
ДАНО: |
РЕШЕНИЕ: Если трос является невесомым и нерастяжимым, а так же при отсутствии трения в блоках, силы натяжения троса должны быть равны между собой Поскольку система уравновешена, то: С другой стороны, трос передает производимое на него воздействие равномерно по всей своей длине. Так как на блоки с обеих сторон действуют силы натяжения T, а на ось каждого блока действует вес подвешенного на него груза и вес самого блока, то получаем, что в равновесии сила тяжести, действующая на каждый из блоков с грузом, уравновешивается удвоенной силой натяжения троса Поскольку система уравновешена, то: |
Ответ: 2,6 кг.
Задача 3. Плита массой 120 кг была равномерно поднята с помощью подвижного блока на высоту 16 м за 40 с. Считая КПД механизма 80%, а массу блока — 10 кг, определите полную работу и развиваемую мощность. Считать, что в блоке отсутствуют силы трения.
|
ДАНО: |
РЕШЕНИЕ: Коэффициента полезного действия механизма определяется отношением полезной работы механизма ко всей затраченной им работе Полезная работа: Сила тяжести плиты и блока: Тогда Затраченная работа: Затраченная мощность: |
Ответ: 26 кДж; 650 Вт.
Задача 4. На рисунке изображена система грузов. Массы тел соответственно равны 0,2 кг и 0,4 кг. Определите силу натяжения нити. Считать нить и блоки идеальными?
|
ДАНО: |
РЕШЕНИЕ: Так как нить и блоки идеальны, то: На основании II закона Ньютона: Так как блок 2 подвижный: Тогда получаем Выразим из второго уравнения ускорение a2, подставим полученное выражение в первое уравнение Преобразуем полученное уравнение и выразим из него искомую силу натяжения нити
|
Ответ: 2 Н.
Неподвижный блок, все формулы и примеры задач
Общие сведения о неподвижном блоке
Неподвижный блок относят к простым механизмам (рис.1). Будем считать, что блок вращается без трения. Если веревка натянута и не скользит по блоку, то на блок действуют две силы натяжения веревки ( и ). Точки приложения этих сил на рис. 1 обозначены как A и B, которые расположены на окружности блока.
Условия равновесия блока определяют из условия равновесия моментов сил, которые к нему приложены. Блок на рис.1 будет находиться в равновесии, если силы , так как плечи этих сил одинаковы (ОА=ОВ). Блок – это рычаг, который имеет равные плечи. Блок, который представлен на рис.1 не дает выигрыша в силе, однако он позволяет изменять направление действия силы. Тянуть за веревку, которая идет сверху обычно удобнее, чем за веревку, которая идет снизу.
Вместо блока можно использовать гладкую неподвижную опору. При этом через нее перекидывают веревку или канат, скользящие по опоре, однако при этом существенно увеличивается сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, значит, равны работы.
Комбинация блоков
Для получения выигрыша в силе используют комбинации блоков, например, двойной блок. При этом используют блоки разного радиуса, которые соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку крепится веревка таким образом, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в данном случае неодинаковы. Двойной блок работает как неравноплечный рычаг. На рис.2 представлена схема двойного блока.
Условием равновесия такого рычага является выражение:
Двойной блок можно считать преобразователем силы. Прикладывая меньшую силу к веревке, приложенной к блоку большего радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Золотое правило механики
Формулировка «Золотого правила»: Отношение перемещений точек, к которым приложены силы в блоке всегда обратно отношению сил, которые приложены к этим точкам.
Для двойного блока, если для равновесия блока сила должна быть в n раз больше по величине, чем сила , то при вращении блока путь, который пройдет точка приложения силы будет в n раз меньше, чем путь который проходит точка приложения силы .
Золотое правило было сформулировано в древности как: «То, что выиграно в силе, проиграно в пути». В математическом виде это правило представим как:
Золотое правило стало первой самой простой формулировкой закона сохранения энергии. Золотое правило механики выполняется для случаев, когда движения простых механизмов равномерно или почти равномерно. Так, при вращении двойного блока концы веревок переместятся на расстояния, которые связаны с радиусами блоков как:
Следовательно, для того чтобы выполнялось золотое правило для двойного блока должно выполняться условие:
Когда силы и будут уравновешены, то блок должен покоиться или двигаться равномерно.
Примеры решения задач на неподвижный блок
ru.solverbook.com
Задачи по динамике с подробными решениями
Задачи по динамике с решениями
Сила, импульс, законы Ньютона
2.1.1 Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени
2.1.2 Тело массой 3 кг движется горизонтально с ускорением 4 м/с2. Определить
2.1.4 Под действием какой силы прямолинейное движение частицы массой 100 г
2.1.5 Под действием горизонтальной силы, равной 12 Н, тело движется по горизонтальной
2.1.6 Определить плотность тела массой 100 г и объемом
2.1.7 Определить вес человека массой 70 кг в лифте, опускающемся равнозамедленно
2.1.8 С какой силой давит человек массой 70 кг на вертикальную спинку сиденья
2.1.9 К нити подвешен груз массой 1 кг. Определить силу натяжения нити, если нить
2.1.10 К нити подвешен груз массой 1 кг, который опускается с ускорением 5 м/с2
2.1.11 Поезд, подъезжая к станции со скоростью 72 км/ч, начинает тормозить. Каково
2.1.13 При каком ускорении разорвется трос, прочность которого на разрыв равна
2.1.14 Груз массой 2 кг подвешен на динамометре. Снизу груз тянут с силой 10 Н
2.1.15 Автомобиль массой 1,2 т движется с места с ускорением 0,8 м/с2. Какую силу тяги
2.1.16 Под действием силы 30 Н тело поднимается вверх с ускорением 10 м/с2. Определить
2.1.17 Тело массой 3 кг падает в воздухе вертикально вниз с ускорением 8 м/с2
2.1.18 С какой силой давит тело массой 2 кг на пол лифта, поднимающегося с ускорением
2.1.19 Шар массой 0,1 кг движется со скоростью 5 м/с. После удара о стенку шар стал
2.1.20 Автомобиль массой 2 т, двигаясь равноускоренно, через 4 с достиг скорости 2 м/с
2.1.21 На тело массой 15 кг, лежащее на земле, действует направленная вверх сила 45 Н
2.1.22 Автомобиль массой 2 т, трогаясь с места, прошел путь 100 м за 10 с. Найти
2.1.23 Тело массой 50 г, падающее со скоростью 2 м/с, упруго соударяется с горизонтальной
2.1.24 Из орудия вылетает снаряд массой 10 кг со скоростью 500 м/с. Найти силу давления
2.1.25 Скорость автомобиля изменяется по закону v=10+0,5t. Найдите результирующую
2.1.26 Два автомобиля массами m и 2m движутся в одном направлении с одинаковыми
2.1.27 Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см
2.1.28 Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы
2.1.30 На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч
2.1.31 Найти модуль изменения импульса шарика массой 20 г за 3 с свободного падения
2.1.32 Определить натяжение каната, к которому подвешена клеть подъемной машины
2.1.33 Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют
2.1.34 Канат может выдержать нагрузку 2,5 кН. С каким максимальным ускорением можно
2.1.35 Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.37 Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30 градусов к ней
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
2.1.40 Две стальные проволоки одинаковой длины, диаметр первой в 3 раза больше
2.1.41 Ракета на старте с поверхности Земли движется вертикально вверх с ускорением
2.1.42 С каким ускорением будет опускаться груз на нити, если сила натяжения нити в 1,25
2.1.43 С какой минимальной силой, направленной горизонтально, нужно прижать плоский
2.1.44 С какой силой давит человек массой 70 кг на пол лифта, движущегося вниз с ускорением
2.1.45 С какой силой следует придавить тело массой 4,5 кг к вертикальной стене, чтобы
2.1.46 Автомобиль идет по горизонтальной дороге со скоростью 72 км/ч. Найти тормозной
2.1.47 Тело массой 5 кг покоится на горизонтальной поверхности. К телу приложена сила
2.1.48 Тело, брошенное вертикально вверх с начальной скоростью 30 м/с, достигло высшей
2.1.49 Три бруска, массы которых 0,5, 0,3 и 0,1 кг, связаны нитями и лежат на столе
2.1.50 Тело массой 1,5 кг движется вверх по вертикальной стенке под действием силы 20 Н
2.1.51 Тело массой 100 кг движется по горизонтальной поверхности под действием силы
2.1.52 Тело массой 200 кг упало на грунт со скоростью 100 м/с и погрузилось в него
2.1.53 Брусок массой 50 кг прижимается к вертикальной стенке с силой 100 Н. Какая сила
2.1.54 Троллейбус, масса которого 12 т, трогаясь с места, за 5 с проходит по горизонтальному
2.1.55 Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8 м/с
2.1.56 Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н
2.1.57 На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой
2.1.58 Человек везет двое связанных между собой саней, прикладывая к веревке силу 120 Н
2.1.59 Тело массой 100 г движется вверх по вертикальной стенке под действием силы 2 Н
2.1.60 Груз массой 1 кг падает с высоты 240 м и углубляется в землю на 0,2 м. Определить
2.1.61 Дождевая капля массой 0,02 г под влиянием горизонтально дующего ветра падает
2.1.62 Материальная точка массой 1 кг движется со скоростью, которая изменяется по закону
2.1.63 Канат лежит на плоской горизонтальной крыше так, что часть его свешивается
2.1.64 Мяч массой 0,2 кг движется к стене под углом 30 градусов к ней со скоростью 6 м/с
2.1.65 Пуля массой 0,3 г, выпущенная из пневматической винтовки вертикально вверх, упала
2.1.66 Стержень длиной 0,9 м движется с ускорением под действием приложенной к его
2.1.67 Тело массой 2 кг начинает движение под действием постоянной по направлению
2.1.68 Что покажут пружинные весы в лифте при измерении веса груза массой 1 кг
2.1.69 Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки
2.1.70 Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут
2.1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
2.1.72 К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг
2.1.74 Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60 градусов к нормали
2.1.75 На скользкой дороге коэффициент трения между дорогой и колесами мотоцикла
2.1.76 Груз массой 10 кг привязан к свободно свисающему концу веревки, намотанной
2.1.77 Координаты тела массы m=1 кг, движущегося прямолинейно вдоль оси x, меняются
2.1.78 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.1.79 Молекула массы m, летящая со скоростью v, ударяется о стенку сосуда под углом a
2.1.80 К невесомой нити подвешен груз массы 1 кг. Точка подвеса нити движется
2.1.81 Четыре одинаковых кубика, связанные невесомыми нитями, движутся по гладкому
2.1.82 Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной
2.1.83 Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
2.1.84 Тело массы 10 кг движется по горизонтальной плоскости под действием силы
2.1.85 В кузове автомобиля лежит груз. При каком минимальном ускорении автомобиля груз
2.1.86 На шероховатой горизонтальной поверхности лежит тело массы 1 кг. Коэффициент
2.1.87 Тело массы m движется под действием силы F. Как изменится модуль ускорения тела
2.1.88 Тело массы m движется под действием двух равных по модулю взаимно
2.1.89 Тело массы 2 кг движется с результирующим ускорением 5 м/с2 под воздействием
2.1.90 На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные
Неподвижный блок
2.2.1 Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2.2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
2.2.4 Два грузика массами m1=0,3 кг и m2=0,2 кг соединены нитью, перекинутой через блок
2.2.5 Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой
2.2.6 Две гири неравной массы висят на концах нити, перекинутой через невесомый блок
2.2.7 Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой
2.2.8 К концам нерастянутой нити, перекинутой через застопоренный блок, подвешенный
2.2.9 К одному концу невесомой и нерастяжимой нити, перекинутой через невесомый блок
Наклонная плоскость
2.3.1 Тело скользит с постоянной скоростью вниз по наклонной плоскости с углом наклона
2.3.2 Льдинка скользит по инерции вверх по наклонной плоскости с углом наклона
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.4 По наклонной плоскости с углом наклона 30 градусов к горизонту скользит вниз тело
2.3.5 Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с
2.3.7 Тело скользит равномерно по наклонной плоскости, угол наклона которой 30 градусов
2.3.8 Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона
2.3.9 Автомобиль при полностью включенных тормозах (колеса не вращаются) может
2.3.10 С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов
2.3.12 Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной
2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами
2.3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень
2.3.20 По наклонной плоскости с углом наклона 60 градусов соскальзывает без трения клин
2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
2.3.22 На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском
Центростремительное ускорение
2.4.1 Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой
2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
2.4.4 Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
2.4.6 Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси
2.4.7 Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно
2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
2.4.9 Определить силу, действующую на летчика, выводящего самолет из пикирования
2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить
2.4.11 Трактор массой 8 т проходит по мосту со скоростью 36 км/ч. Какова сила давления
2.4.12 Конькобежец движется по закруглению ледяной дорожки радиусом 2,5 м со скоростью
2.4.13 Шоссе имеет вираж с уклоном 10 градусов при радиусе закругления дороги в 100 м
2.4.14 Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости
2.4.15 В желобе, наклоненном под углом 30 градусов к горизонту и вращающемся с частотой
2.4.16 Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность
2.4.17 Груз массой 1 кг, привязанный к нити, отклоняют на 90 градусов от положения
2.4.18 Груз, подвешенный на нити длиной 5 м, равномерно движется по окружности
2.4.19 Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
2.4.21 Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол
2.4.22 На легкой нерастяжимой нити подвешен тяжелый шарик. На какой угол нужно отвести
2.4.23 Нить может выдержать силу натяжения 25,4 Н. На нити подвесили тело массой 2 кг
2.4.24 По гладкому столу вращается груз, прикрепленный к центру вращения пружиной
2.4.25 Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне
2.4.26 Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно
2.4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
2.4.32 Мотоциклист движется по цилиндрической стенке диаметра 12 м. При каком коэффициенте
2.4.33 Спортивный молот — ядро на тросике длиной L, бросают, раскрутив вокруг себя
2.4.34 Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной
2.4.35 Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение
2.4.40 Бусинка может скользить вдоль гладкого кольца радиуса R, расположенного
2.4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
2.4.42 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси с постоянной
2.4.43 В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна
Закон всемирного тяготения
2.5.1 Во сколько раз уменьшится сила тяготения тела к Земле при удалении его
2.5.2 Определить силу взаимодействия тела массой 2 кг и Земли, если тело удалено от
2.5.3 Во сколько раз ускорение свободного падения около поверхности Земли больше
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения
2.5.5 Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.7 Определить первую космическую скорость для планеты, масса и радиус которой в два
2.5.8 На некоторой планете сила тяжести, действующая на тело массой 4 кг, равна 8 Н. Найти
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе
2.5.10 Сколько метров пройдет тело, свободно падая без начальной скорости в течение трех
2.5.11 Чему равно ускорение свободного падения на высоте, равной половине радиуса
2.5.12 Определить, с каким ускорением падают тела на поверхность Луны, зная, что радиус
2.5.13 Человек на Земле прыгает на высоту 1 м. На какую высоту, совершив ту же работу, он
2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение
2.5.15 Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
2.5.18 Тело поднялось на высоту 1600 км над поверхностью Земли. На сколько процентов
2.5.19 Определить минимальный период обращения спутника нейтронной звезды. Её плотность
2.5.20 Радиус Земли равен 6400 км. Какую скорость имеют точки земной поверхности на широте
2.5.21 На каком расстоянии от центра Земли (в долях радиуса Земли R) ускорение свободного
2.5.22 Радиус Земли равен 6400 км. На каком расстоянии от поверхности Земли сила притяжения
Упругая сила
2.6.1 Для сжатия пружины на 2 см надо приложить силу 10 Н. Определить энергию упругой
2.6.2 Какую работу надо совершить, чтобы удлинить на 0,1 м резиновый шнур с коэффициентом
2.6.3 Под действием силы 4 Н пружина удлинилась на 2 см. Чему равна при этом
2.6.4 Какова начальная скорость шарика массой 1 г, которым выстрелили из пружинного
2.6.5 При вращении шарика, прикрепленного к пружине длиной 20 см, с частотой вращения
2.6.6 Груз массой 1 кг, прикрепленный к пружине, равномерно тянут по горизонтальной
2.6.7 Каков коэффициент жесткости буксировочного троса, если при буксировке автомобиля
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.9 Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины
2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
2.6.11 Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы
2.6.12 К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки
2.6.13 Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную
2.6.14 Какую минимальную работу необходимо совершить, чтобы передвинуть по
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью
Работа, мощность, энергия
2.7.1 Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м
2.7.2 Какую работу совершает постоянная сила по перемещению на 5 м тела массой 3 кг
2.7.3 Определить работу, необходимую для поднятия груза массой 3 кг на высоту 10 м
2.7.4 Автомобиль поднимается в гору со скоростью 36 км/ч. Определить силу тяги мотора
2.7.5 Пуля массой 10 г вылетает из винтовки со скоростью 600 м/с. Определить работу
2.7.6 Автомобиль массой 1800 кг, двигаясь с ускорением 2 м/с2, прошел 100 м пути
2.7.7 Найти кинетическую энергию стрелы массой 0,5 кг, пущенную вертикально вверх
2.7.8 Мальчик везет санки, прилагая к веревке силу 10 Н, которая образует угол 30 градусов
2.7.9 При подъеме тела массой 10 кг на высоту 2 м совершена работа 230 Дж
2.7.10 Санки тянут на пути 100 м с силой 80 Н за веревку, составляющую угол 30 градусов
2.7.11 Во сколько раз изменится запас потенциальной энергии упруго деформированного тела
2.7.12 При торможении автомобиля массой 1 т скорость уменьшилась от 72 км/ч до 36 км/ч
2.7.13 Автомобиль массой 1500 кг, двигаясь равноускоренно, проходит путь 20 м за 2 с
2.7.14 На какой высоте над поверхностью Луны тело будет обладать такой же потенциальной
2.7.15 Определить работу, которую нужно произвести для того, чтобы сжать пружину на 10 см
2.7.16 Определить массу тела, имеющего кинетическую энергию 16 Дж, а импульс
2.7.17 Тело массой 1 кг начинает свободно падать. Определить мощность силы тяжести
2.7.18 Автомобиль массой 1,5 т едет со стоянки с постоянным ускорением 2 м/с2. Коэффициент
2.7.19 Автомобиль движется со скоростью 72 км/ч. Мощность двигателя 60 кВт, его КПД 30%
2.7.20 Вертолет весит 3 т. На его подъем тратится 30% мощности мотора. Определить
2.7.21 Двигатели электровоза при движении со скоростью 72 км/ч потребляют мощность
2.7.22 Какая работа совершается внешней силой при поднятии тела массой 5 кг на высоту
2.7.23 Какую работу должен совершить двигатель, чтобы разогнать по горизонтальной
2.7.24 Какую работу надо совершить, чтобы поднять груз массой 30 кг на высоту 10 м
2.7.25 Какую работу надо совершить, чтобы поднять груз массой 3000 кг на высоту 10 м
2.7.26 Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой
2.7.27 Камень брошен под углом 30 градусов к горизонту. Кинетическая энергия камня в верхней
2.7.28 Камень массой 100 г бросили под углом 60 градусов к горизонту со скоростью 15 м/с
2.7.29 На тело массой 10 кг действует постоянная сила 5 Н. Определить кинетическую энергию
2.7.30 Подъемный кран поднимает груз массой 5 т на высоту 15 м. За какое время поднимется
2.7.31 Поезд массой 1000 т начинает двигаться с места равноускоренно и достигает скорости
2.7.32 Резец токарного станка мощностью 3 кВт снимает в минуту стружку длиной 500 мм
2.7.33 Самолет для взлета должен иметь скорость 25 м/с. Длина пробега перед взлетом 100 м
2.7.34 Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью
2.7.35 Тепловоз за 5 мин набирает скорость 72 км/ч. Определить среднюю мощность
2.7.36 Укажите график зависимости потенциальной энергии свободно падающего тела
2.7.37 Уравнение движения материальной точки имеет вид: x=t^2-2t^3 (м). Определите
2.7.38 Футбольный мяч весом 8 Н летит со скоростью 15 м/с. Вратарь ловит мяч и за 0,1 с
2.7.39 Пуля летит со скоростью v0. Она пробивает доску толщиной 3,6 см и продолжает полет
2.7.40 Максимальная высота подъема тела массой 2 кг, брошенного с поверхности Земли
2.7.41 На рисунке приведена зависимость потенциальной энергии от времени движения
2.7.42 Начальная скорость пули 600 м/с, её масса 10 г. Под каким углом к горизонту она
2.7.43 Самолет массой 2 т летит со скоростью 50 м/с. На высоте 420 м он переходит на снижение
2.7.44 Тело массой 3 кг падает вертикально вниз с начальной скоростью 2 м/с. Найти работу
2.7.45 Трактор имеет тяговую мощность на крюке, равную 72 кВт. С какой скоростью может
2.7.46 Трактор массой 10 т и мощностью 150 кВт поднимается в гору со скоростью 5 м/с
2.7.47 Ядро массой 8 кг, выпущенное метателем под углом 45 градусов к горизонту с высоты
2.7.48 Допустим, что сила, которая заставляет баржу двигаться по каналу, прямо пропорциональна
2.7.49 Конькобежец движется по горизонтальному пути равномерно, а затем с разгона проезжает
2.7.50 Для растяжения недеформированной пружины на 1 см требуется сила, равная 30 Н
2.7.51 Шайба массы 0,1 кг, пущенная по льду с начальной скоростью 0,5 м/с, остановилась
2.7.52 На тело массы 5 кг действует постоянная сила 10 Н. Чему будет равна кинетическая
2.7.53 Какой кинетической энергией обладает свободно падающее тело массой 0,1 кг
2.7.54 Чему равна кинетическая энергия тела массы 0,2 кг, брошенного вертикально вверх
2.7.55 Камень брошен под углом 60 градусов к горизонту. Как соотносятся между собой
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.7.57 Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения
Законы сохранения энергии и импульса
2.8.1 Камень массой 1 кг бросили вертикально вверх с начальной скоростью 2 м/с
2.8.2 Найти скорость винтовки при отдаче, если её масса в 500 раз больше массы пули
2.8.3 Снаряд массой 20 кг, летевший горизонтально, попадает в платформу с песком массой
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости
2.8.5 Какую скорость приобретает ракета массой 2 кг, если продукты горения массой
2.8.6 Тело массой 2 кг падает с высоты 10 м и углубляется в песок на глубину 0,5 м
2.8.7 Брусок массой 1 кг первоначально покоился на вершине наклонной плоскости
2.8.8 Велосипедист движется со скоростью 8 м/с. Определить расстояние, пройденное
2.8.9 Мальчик, стреляя из рогатки, натянул резиновый шнур так, что шнур растянулся
2.8.10 Винтовка массой 2,8 кг подвешена горизонтально на двух параллельных нитях
2.8.11 Во сколько раз изменится потенциальная энергия пружины при увеличении
2.8.12 Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара
2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия
2.8.14 Маленький шарик массой m, закрепленный на нерастяжимой нити в поле силы
2.8.15 Мальчик раскачивается на качелях. При максимальном отклонении от положения
2.8.16 Оконная штора массой 1 кг и длиной 2 м навертывается на валик, расположенный
2.8.17 Под каким углом к горизонту нужно бросить камень, чтобы в верхней точке траектории
2.8.18 При выстреле из орудия снаряд получил начальную скорость 300 м/с и летит
2.8.19 Телеграфный столб длиной 7 м и массой 140 кг при установке перемещается
2.8.20 Укажите график зависимости кинетической энергии свободно падающего тела
2.8.21 Чему равна работа по подъему лежащей цепи массой 50 кг и длиной 2 м, если
2.8.22 Подъемный кран поднимает груз массой 8 т на высоту 15 м. Определить время
2.8.23 Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча
2.8.24 Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий
2.8.27 Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
2.8.29 Камень бросили под углом 60 градусов к горизонту со скоростью 15 м/с. Найдите
2.8.30 На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
2.8.32 С какой начальной скоростью v0 нужно бросить вниз мяч с высоты h, чтобы он
2.8.33 Шарик массой m, подвешенный на нити, отклонен от положения равновесия на угол
2.8.34 Шарик подбросили вверх, сообщив ему кинетическую энергию 20 Дж. Через
2.8.35 Мяч падает с высоты 7,5 м на гладкий пол. Какую скорость нужно сообщить мячу
2.8.36 Тело, брошенное с вышки высотой 10 м, упало на землю со скоростью 15 м/с
2.8.37 Мяч скатился с горы высотой 20 м и после короткого горизонтального участка упал
2.8.38 Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила
2.8.39 Горизонтально летящая пуля массой 10 г насквозь пробивает первоначально
2.8.40 На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка
2.8.41 Определите время подъема камня массой 1 кг, брошенного под углом к горизонту
2.8.42 Пуля массой 10 г подлетает к доске массой 1 кг со скоростью 600 м/с и, пробив ее
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.44 В школьном опыте с «мертвой петлей» шарик массой 0,1 кг отпущен с высоты h=3R
2.8.45 Вертикальный невесомый стержень длиной 6 м подвешен одним концом к оси
2.8.46 Колодец, имеющий глубину 5 м, площадь дна 0,5 м2, наполовину заполнен водой
2.8.47 Небольшое тело скользит с вершины полусферы вниз. На какой высоте h от вершины
2.8.48 Небольшое тело соскальзывает вниз по наклонному скату, переходящему в мертвую
2.8.49 Небольшое тело соскальзывает по наклонной плоскости, переходящей в мертвую
2.8.50 Плавательный бассейн площадью 100 м2 заполнен водой до глубины 2 м. Требуется
2.8.51 Подвешенному на нити длиной 1 м шарику сообщили начальную скорость такую
2.8.52 При ударе шарика об идеально гладкую горизонтальную поверхность теряется третья
2.8.53 Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной
Абсолютно упругий удар
2.9.1 Тело массой 1 кг упруго ударяется о покоящееся тело массой 3 кг и летит обратно
2.9.2 Шарик массой 100 г упал с высоты 2,5 м на горизонтальную плиту, масса которой
2.9.3 Во сколько раз уменьшится энергия нейтрона n при столкновении с ядром углерода C
2.9.4 Гранату бросают от поверхности земли под углом 30 градусов к горизонту
2.9.5 Два упругих стальных шара массами m1=0,2 кг и m2=0,1 кг подвешены рядом
2.9.6 Шарик подлетает к неподвижной вертикальной стенке сверху со скоростью 10 м/с
2.9.7 На горизонтальной поверхности в 3 м от вертикальной стенки находится шар массой
Абсолютно неупругий удар
2.10.1 По абсолютно гладкой поверхности движется со скоростью 6 м/с ящик с песком
2.10.2 Тележка массой 100 кг движется со скоростью 2 м/с. Когда она проезжает мимо
2.10.3 Найти количество теплоты, выделившееся при лобовом абсолютно неупругом ударе
2.10.4 Охотник стреляет из ружья. Определить силу отдачи, если масса дроби 35 г
2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
2.10.6 Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара
2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость
2.10.8 Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную
2.10.9 Масса пушки 800 кг. Пушка выстреливает ядро массой 10 кг с начальной скоростью
2.10.10 На вагонетку массой 800 кг, катящуюся по горизонтальным рельсам со скоростью
2.10.11 На тележку с песком массой 49 кг, движущуюся по прямой со скоростью 1 м/с, падает
2.10.12 Пушка, стоящая на горизонтальной поверхности, стреляет под углом 30 градусов
2.10.13 Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется
2.10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
2.10.15 Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет
2.10.16 Конькобежец, стоя на льду, бросил вперед гирю массой 5 кг и вследствие отдачи
2.10.17 Два мальчика играют в мяч, стоя на льду на расстоянии 10 м друг от друга
2.10.18 Вагон массой 50 т движется со скоростью 12 км/ч и встречает стоящую на пути
2.10.19 Конькобежец, стоя на льду, бросает горизонтально с высоты 1,5 м груз массой 10 кг
2.10.20 Кусок пластилина массой m=32 г попадает в брусок массой 6m, двигавшийся
2.10.21 На горизонтальном столе лежит деревянный брусок массой 5 кг. В брусок попадает
2.10.22 По горизонтальной поверхности стола скользит брусок массой m и сталкивается
2.10.23 Пуля массой 10 г застревает в первоначально покоящемся бруске, масса которого 0,1 кг
2.10.24 Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с
2.10.25 В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой
2.10.26 Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового
2.10.27 Два груза массами 0,04 и 0,01 кг соединены невесомой нитью, переброшенной
2.10.28 В шар массой 1,5 кг, подвешенный на нерастяжимой нити длиной 55 см, попадает
2.10.29 Какая доля кинетической энергии перейдет в теплоту при неупругом столкновении
2.10.30 Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой
2.10.31 Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно
2.10.32 Два шарика массами 2 и 3 г движутся в горизонтальной плоскости со скоростями
2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
2.10.34 На горизонтальной плоскости сделан выстрел из винтовки, ствол которой направлен
2.10.35 С незакрепленной горки (клина) массой 1 кг соскальзывает тело массой 500 г. Угол
2.10.36 Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается
2.10.37 Человек, сидящий в лодке, бросает камень под углом 60 градусов к горизонту. Масса
easyfizika.ru
Динамика: сложные задачи
Предлагаю решение нескольких задач из книги “Отличник ЕГЭ. Физика. Решение сложных задач”. Возможно, в дальнейшем на сайте появятся и решения других задач из этой книги. Задачи интересные, и все как одна “решабельные”, то есть никаких подвохов в них нет.
Задача 1. Шайба, брошенная вдоль наклонной плоскости, скользит по ней, двигаясь вверх, а затем движется вниз. График зависимости модуля скорости шайбы от времени дан на рисунке. Найти угол наклона плоскости к горизонту.
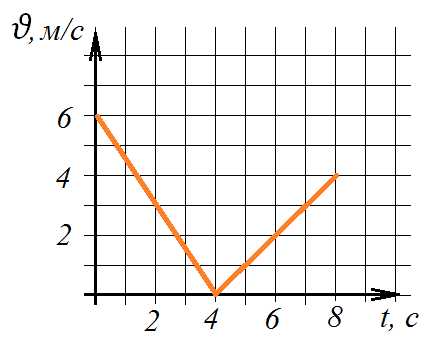
К задаче 1
Так как график составлен из двух отрезков прямых, то ускорение шайбы постоянно на обоих отрезках. Определим его. При движении вверх скорость шайбы изменилась с 6 м/с до 0 за 4 с, следовательно, ускорение равно м/с. На пути вниз скорость шайбы с нуля доросла до 4 м/с за 4 с, следовательно, ускорение равно м/с.
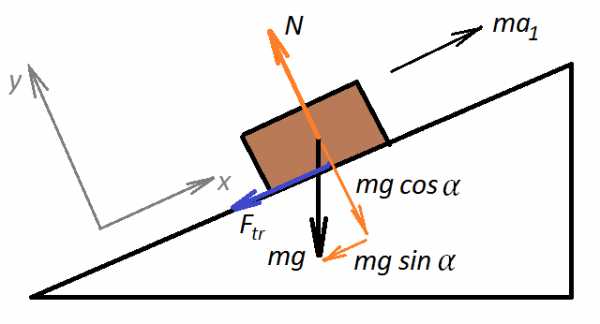
К задаче 1 – движение вверх
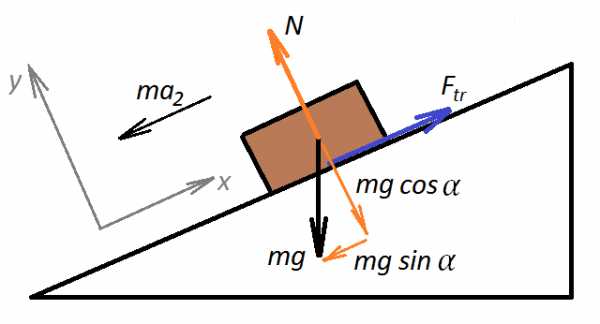
К задаче 1 – движение вниз
Реакция опоры при движении шайбы равна
От реакции опоры напрямую зависит сила трения. Запишем уравнение по второму закону Ньютона для движения шайбы вверх (сразу учтем, что ускорение отрицательно, поскольку шайба тормозит):
Запишем уравнение по второму закону Ньютона для движения шайбы вниз:
Складывая уравнения, имеем:
Откуда
Ответ: .
Задача 2. Два шарика одинакового диаметра, имеющие массы г и г, связаны между собой легкой нерастяжимой нитью, длина которой значительно превышает диаметр шариков. Шарики сбросили с достаточно большой высоты. Спустя некоторое время после этого вследствие сопротивления воздуха скорость падения шариков стала постоянной. Найти натяжение нити Т при установившемся падении шариков. Ускорение свободного падения м/с .
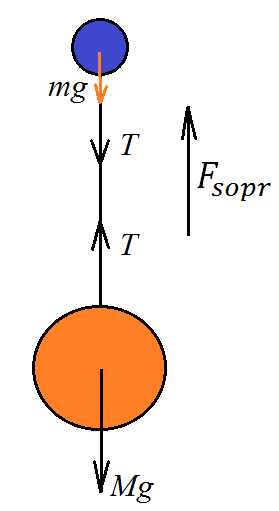
К задаче 2
Шарики при падении «выстроятся»: снизу расположится более тяжелый, за ним «потянется» более легкий. «Потянется» в прямом смысле, посредством нити.
Для первого шарика уравнение для установившегося движения:
Для второго шарика:
Складывая, имеем:
Подставим в любое уравнение полученную силу сопротивления:
Ответ: Н.
Задача 3. Два одинаковых груза массой кг связаны между собой нитью, перекинутой через блок с неподвижной осью. На один из грузов кладут перегрузок массой кг. С какой силой Р будет давить перегрузок на груз ? Массой блока и нити, а также трением в оси блока пренебречь, нить считать нерастяжимой‚ ускорение свободного падения принять равным м/с.
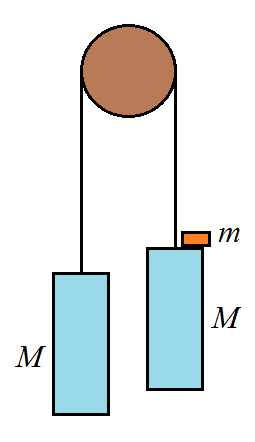
К задаче 3
Запишем уравнение по второму закону для груза с перегрузком:
Для груза без перегрузка:
Из второго уравнения имеем :
Подставим в первое:
Теперь, зная ускорение, легко отыщем силу давления перегрузка на груз:
Ответ: .
Задача 4. В системе, показанной на рисунке, грузы массами кг и кг прикреплены к концам невесомой нерастяжимой нити. На такой же нити, один конец которой закреплен, а другой прикреплен к грузу массой , висит подвижный блок. К оси этого блока на легких нерастяжимых нитях подвешен груз массой кг. Отрезки нитей, не лежащие на блоках, вертикальны. Пренебрегая трением и массой блоков, найти модуль и направление ускорения груза . Ускорение свободного падения принять равным м/с.
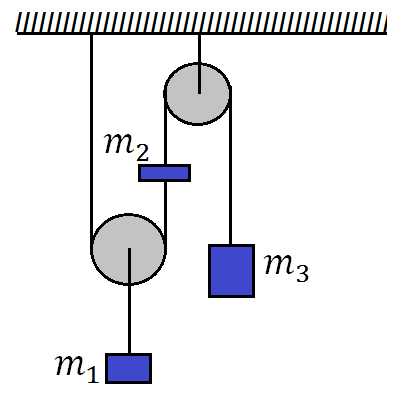
К задаче 4
Это одна из задач, решение которых строится на факте нерастяжимости нити. Именно этот факт будет важен, так как решение будем основывать на том, что сумма путей, пройденных грузами, постоянна, и максимально равна длине нити. Пусть координаты грузов по оси , и соответственно. Пусть в некоторый момент времени их координаты стали , и . Путь, пройденный телом 1:
А нить при этом «сократилась» на .
Путь, пройденный телом 2:
А нить при этом «сократилась» на .
Путь, пройденный телом 3:
А нить при этом «удлинилась» на .
Запишем пути, пройденные телами, через их ускорения:
Можно записать, что
Следовательно, ускорения тел 2 и 3 одинаковы, , а у тела 1 тогда .
Теперь можно перейти к динамике. Запишем уравнения по второму закону Ньютона для всех тел. При этом обратим внимание, что разные участки нити будут по-разному натянуты. Это происходит из-за наличия груза 2, он является своеобразным «перегрузком»:

Силы
Перейдем везде к ускорению , ведь оно – искомое:
Из последнего уравнения
А из первого
Тогда, подставляя все во второе, получим:
«Минус» указывает направление ускорения: оно направлено вверх, против .
Ответ: м/с, направлено вверх.
Задача 5. Через гладкий блок, закрепленный на гладкой неподвижной наклонной плоскости, составляющей с горизонтом угол , перекинута легкая нерастяжимая нить. Один конец нити прикреплен к бруску массой кг, лежащему на плоскости, а свисающий конец пропущен через узкое отверстие в грузе массой кг, как показано на рисунке. Если одновременно отпустить брусок и груз, нить будет проскальзывать через отверстие с постоянным ускорением м/с относительно груза. Найти силу натяжения нити. Ускорение свободного падения принять равным м/с.
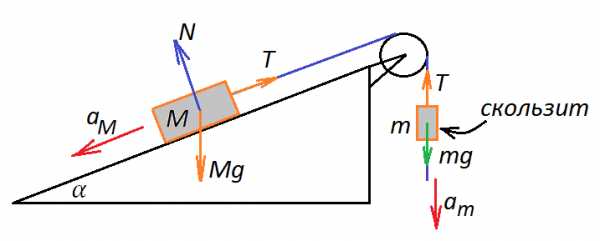
К задаче 5
Запишем уравнение по второму закону для обоих грузов:
Теперь определимся с ускорениями: так как нить проскальзывает относительно груза , то
Тогда, подставляя силу натяжения нити, имеем:
Теперь можно определять силу натяжения:
Ответ: Н
Задача 6. Маленькую шайбу массой г запустили со скоростью м/с в направлении по касательной к внутренней поверхности находящейся в невесомости сферы массой г и радиусом м. Найдите модуль силы, действующей на шайбу со стороны сферы. Трение отсутствует, сфера вначале покоилась.
По закону сохранения импульса
Если перейти в систему отсчета «сфера», то скорость шайбы в ней будет равна
Известно, что при движении по окружности угловая скорость такого движения равна , следовательно,
Угловая скорость через период:
Период – время одного оборота:
Следовательно,
Аналогично
Теперь можем найти, с какой силой шайба будет давить на сферу:
Ответ: Н.
Задача 7. На горизонтальном диске на расстоянии см от оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время с после начала раскручивания шайба начала скользить по диску. Найти коэффициент трения шайбы о диск, если за время диск сделал оборотов.
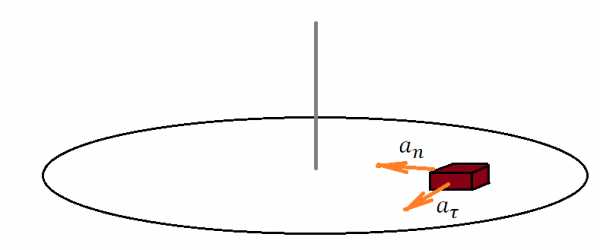
К задаче 7
Сила трения удерживает шайбу от соскальзывания. Однако диск разгоняется, следовательно, есть тангенциальное ускорение, и скорость шайбы растет, что вызывает рост нормального ускорения. Наконец, общее ускорение становится столь большим, что сила, им обусловленная, превышает силу трения, и шайба соскальзывает.
Условие соскальзывания
Где .
Выясним, каковы нормальное и тангенциальное ускорения.
Скорость шайбы растет и становится равной к моменту соскальзывания. Угловая скорость становится равной за то же время. Тогда
Путь, пройденный телом – пять кругов – равен .
Угловая скорость определяет, какой угол преодолело тело за промежуток времени. У нас пять кругов, следовательно, тело прошло радиан за время , тогда
Нормальное ускорение тела
В свою очередь, полное ускорение равно
Тогда
Ответ: .
easy-physic.ru
ФИЗИКА: Задачи на простые механизмы – Ответы и решения
Задачи на простые механизмы с решениями
Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».
Название величины | Обозначение | Единица измерения | Формула |
Сила | F | Н | F1l1 = F2l2 |
Плечо силы | l | м | |
Момент силы | M | Нм | M = Fl |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?

Задача № 2. На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.
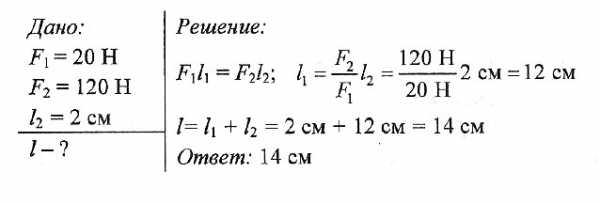
Задача № 3. На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?
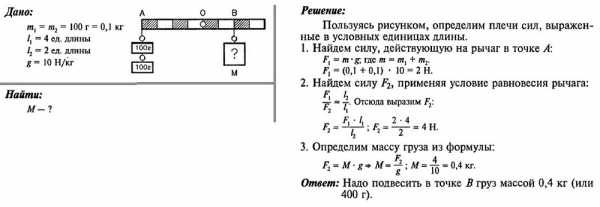
Задача № 4. На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.

Задача № 5. Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?
Задача № 6. Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.
Задача № 7. Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).
Задача № 8. Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).
Задача № 9. При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.

Задача № 10. ОГЭ Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти его центр тяжести. Плотность свинца p1 = 11,4 г/см3, плотность железа p2 = 7,8 г/см3.
Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P.
У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра.
Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня.
Задача № 11. ЕГЭ Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?

Краткая теория для решения задачи на простые механизмы.

Конспект урока «Задачи на простые механизмы с решениями».
Следующая тема: «Задачи на КПД простых механизмов».
ЗАДАЧИ на простые механизмы с решениями
5 (100%) 2 votesuchitel.pro
Решение задач по физике №20. Физические основы механики. Динамика.
2.31. Невесомым блок укреплен на конце стола. Гири 1 и 2 одинаковой массы m1, = m2 = 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол k – 0,1. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением в блоке пренебречь.Решение:
2.32. Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол а = 30°. Гири 1 и 2 одинаковой массы m1, = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гири о наклонную плоскость и трением в блоке пренебречь.
Решение:
2.33. Решить предыдущую задачу при условии, что коэффициент трения гири 2 о наклонную плоскость k = 0,1.
Решение:
2.34. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы а =30° и Р = 45°. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
Решение:
2.35. Решить предыдущую задачу при условии, что коэффициенты трения гирь 1 и 2 о наклонные плоскости k1 = k2 = 0,1 . Показать, что из формул, дающих решение этой задачи, можно получить, как частные случаи, решения задач 2.30 — 2.34.
Решение:
egain.ru
Подвижный и неподвижный блок, с примерами задач
Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.
Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:
так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.
Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
Комбинация неподвижных блоков
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.
Условие равновесия для рычага на рис.2 станет формула:
Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .
Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы и уравновешены, то блок покоится или движется равномерно.
Примеры решения задач
ru.solverbook.com
