Шифр “Решетка Кардано”
Автор: КТОН
©, 2012 г.,
мастерская “Фантазеры”,
ГБОУ ЦО № 1811 “Измайлово”
Решетка Кардано — инструмент кодирования и декодирования, представляющий собой специальную прямоугольную (в частном случае — квадратную) таблицу-карточку, часть ячеек которой вырезана.
Решетка не имеет жесткого шаблона, она сделана из листа картона или пергамента, или же из тонкого металла. Чтобы обозначить линии письма, бумагу разлиновывают, и между этими линиями вырезают прямоугольные области через интервалы произвольной длины.
Шифратор помещает решетку на лист бумаги и пишет сообщение в прямоугольных отверстиях, в которых помещается отдельный символ, слог или целое слово. Исходное сообщение оказывается разделенным на большое число маленьких фрагментов. Затем решетка убирается, и пустые места на бумаге заполняются посторонним текстом так, чтобы скрываемый текст стал частью другого текста. Такое заполнение требует известного литературного таланта.
Для расшифровки у получателя сообщения должна быть такая же решетка.

Текст записки: Сэр Джон высоко ценит Вас и снова повторяет, что все, что доступно ему, теперь ваше, навсегда. Может ли он заслужить прощение за свои прежние промедления посредством своего обаяния.
Шифрованное послание: В мае Испания направит свои корабли на войну.
Одна из разновидностей решетки Кардано — вращающаяся решетка или сетка.
Вращающиеся решетки бывают квадратными и прямоугольными.


Такие решетки не предполагают, что вписанный текст будет дополняться и дописываться.
Чтобы зашифровать текст таким образом, необходимо приложить решетку к листу бумаги и вписать текст сообщения в вырезанные ячейки, затем повернуть решетку по часовой стрелке и продолжить запись сообщения, потом снова повернуть решетку и т.д.
В итоге мы получаем такого вида таблицу, полностью заполненную буквами:
|
к |
н |
с |
а |
а |
я |
с |
о |
|
м |
ж |
ы |
к |
п |
д |
е |
т |
|
р |
о |
е |
ы |
щ |
м |
д |
й |
|
о |
е |
с |
а |
ж |
в |
а |
е |
|
с |
л |
т |
т |
м |
и |
т |
р |
|
с |
з |
е |
е |
п |
а |
т |
с |
|
и |
п |
а |
е |
м |
е |
с |
р |
|
ь |
б |
с |
а |
я |
я |
н |
й |
Для шифрования можно использовать также и прямоугольные решетки, в которые вписываются не отдельные буквы, а части слов или даже небольшие слова. В таком случае шифровальщик не может просто все четыре раза поворачивать решетку по часовой стрелке, поэтому он вначале прикладывает решетку к листу, вписывает слоги, потом поворачивает ее на 180
Преимущество такого вида шифрования заключается в том, что решетка вращения может иметь множество различных шаблонов. В одном квадрате 8Х8 умещается более 4-х миллиардов секретных решеток.
 Для того, чтобы составить свою собственную решетку необходимо обратиться к «Квадрату для составления решеток». Он расчерчен на 64 клетки, внутри него также присутствует деление на четыре более крупных квадрата 4Х4. В качестве вырезанных ячеек Вы можете выбрать любые 16 клеток, лишь бы их номера не повторялись дважды.
Для того, чтобы составить свою собственную решетку необходимо обратиться к «Квадрату для составления решеток». Он расчерчен на 64 клетки, внутри него также присутствует деление на четыре более крупных квадрата 4Х4. В качестве вырезанных ячеек Вы можете выбрать любые 16 клеток, лишь бы их номера не повторялись дважды.
Важно чтобы при повороте решетки по часовой стрелке вырезанные ячейки не перекрывали друг друга и при этом все поля в итоге должны быть заполнены.
Более наглядно познакомиться с этим и другими шифрами Вы можете здесь: КТОН: Таинственное послание или КТОН разгадывает шифр (1 серия)
В этом фильме героиня по имени Афортунада (Форта) предлагала прочитать сообщение, написанное ее герою по имени Áртур.




www.terrakid.ru
3 Шифр поворотной решетки
Для использования шифра, названного поворотная решетка, изготавливают трафарет из прямоугольного листа в клетку (размер 2m х 2k клеток). В этом трафарете вырезают mk клеток так, чтобы при наложении его на чистый лист бумаги того же размера четырмя возможными способами (лицевой и обратной сторонами каждая с поворотом на 180 градусов) вырезы без наложений полностью покрывали бы всю площадь чистого листа. Буквы исходного текста последовательно вписывают в вырезы трафарета по строкам слева направо при каждом из четырех его возможных положений в предварительно установленном порядке. Затем для получения шифротекста считывают полученную таблицу последовательно по строкам или столбцам.
Ключом для прочтения (востановления) исходного текста должен быть сам трафарет (или его описание), информация о последовательности(порядке) его поворотов и особенностей считывания таблицы. Количество возможных трафаретов (решеток) составляет T = 4(mk)!, а длина исходного текста составит n=4mk. Число всех перестановок в тексте такой длины составит (4mk)!, что существенно больше числа ключей T.
4 Шифры с использованием магичных квадратов
Магичный квадрат – квадратная таблица с вписаными в клетки последовательными натуральными числами, начиная с 1, которые при суммировании по столбцам, строкам и диагоналям дают одно и то же число. Исходный текст вписывают в магический квадрат в соответствии с нумерацией его клеток. Для получения шифротекста таблицу считывают по строкам или столбцам. В качестве ключа для востановления исходного текста может быть ссылка на номер магического квадрата в некоторой базе, которая известна отправителю и получателю шифротекста.
16
3
2
13
5
10
11
8
9
6
7
12
4
15
14
1
Рис 1а
13
8
12
1
2
11
7
14
3
10
6
15
16
5
9
4
Рис 1б
4
15
14
1
9
6
7
12
5
10
11
8
16
3
2
13
Рис 1в
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
Рис 1г
На рисунке выше приведены примеры магических квадратов размера 4х4 (из 880 возможных). Количество магических квадратов размера 5х5 – около 25 тыс.
5 Перестановка бит
Использование компьютеров для выполнения шифрования породило такой метод как перестановка бит в каждом символе исходного текста. К примеру, ключ для такого шифрования может выглядеть так (3,5,7,1,4,2,8,6). Это означает, что исходное сообщение, представленное в бинарной форме разбивается на блоки по 8 бит и в каждом таком блоке происходит перестановка в соответствии с заданнын ключом: на первое место переставляется 3-й бит, на второе–5-й, на третье–7-й и т.д. Возможна разбивка на блоки, содержащие другое число бит.
studfiles.net
Cybern.ru » Шифрование с помощью решеток
Шифрование с помощью решеток применяется для защиты информации, представляющую ценность в течение ограниченного времени(несколько часов). Этот шифр также является перестановочным, т.е. криптограммы этого шифра представляют собой анаграммы открытого текста. Данный метод шифрования активно применялся во время второй мировой войны, и до сих пор используется в качестве армейского шифра.
Алгоритм шифрования
Выбирается число k. Строим квадрат со стороной длины k и заполняем его клетки числами от 1 до :
Поворачиваем квадрат на 90 градус по часовой стрелке и приписываем справа от исходного квадрата:
Поворачивая на 90 градусов по часовой стрелки и добавляя полученный квадрат сначала снизу, а затем слева от предыдущего, получим следующий квадрат со стороной 2k:
В этом квадрате закрасим произвольным образом все цифры, причем каждая цифра может быть закрашена только один раз. Вот например:
Это и будет решеткой для шифрования. Код для шифрования представляет последовательность k цифр от 1 до 4, i-тая цифра обозначает в каком подквадрате (нумеруются в порядке создания) закрашивать число i(например, для этой таблицы код решетки имеет вид: 242431134). Асимптотическая сложность шифра — (для этой решетки — 262144).
Открытый текст разбивается на блоки длины . Каждый блок разбивается на подстроки длины . Решетка накладывается на пустой лист бумаги, закрашиваемые клетки вырезаются. Для первой подстроки ее i-ый символ записывается в вырезанное i-ое число решетки. Повторяем процесс еще 3 раза, поворачивая перед этим решетку на 90 градусов по часовой стрелке. В результате получаем таблицу, составляющую из символов открытого текста. Криптограмма из этой таблицы получается путем построчного выписывания символов или применения приемов маршрутного шифрования.
Пример
Пусть задан открытый текст: ТЕКСТ ПОСЛЕ ШИФРОВАНИЯ СТАНЕТ НЕПОНЯТНЫМ
В качестве кодирующей решетки возьмем выше взятый пример. В результате запись первого блока(ТЕКСТПОСЛ) запишется с помощью решетки так:
Повторив эту операцию для других трех блоков, повернув перед каждой операции решетку на 90 градусов по часовой стрелки, получим итоговую таблицу:
Из этой таблицы криптограмма получается выписыванием символов по любому маршруту.
cybern.ru
Решетка Кардано – NIGHTQUESTS
Решетка Кардано — это ключ к секретному посланию, как правило, специальная карточка, в которой в определенных местах имеются прорези — ячейки. Чтение зашифрованного послания происходит при наложении на кодированный текст.
Данный метод придуман в 16 веке итальянским математиком Джероламо Кардано.
Решетка Кардано — процесс шифрования с использованием
Решетка Кардано изготавливается из плотной бумаги или картона, в редких случаях из металлических пластин (тонких и легких). Заготовка для ключа разлиновывается, чтобы впоследствии текст письма выглядел естественно. Затем вырезаются прорези в произвольных местах заготовки, абсолютно рандомно.
Шифрующий закрепляет решетку поверх бумаги и вписывает в прорези буквы или даже целые слова того самого секретного сообщения, которое необходимо передать. Таким образом оно раскидывается фрагментарно по всему пространству листа.
После этого, все пространство заполняется произвольным открытым письмом, тем самым, наше скрытое послание становится органичной его частью. Безусловно, придется постараться, чтобы все выглядело естественно.
Тот, кому предназначалось послание, используя копию использованной решетки Кардано, читает скрытое послание.
Основные особенности решетки Кардано
Данный способ сокрытия информации имеет три отличительные особенности:
очень легко применить на практике
при попадании не в те руки произвести расшифровку практически невозможно
очень сложно не зная наверняка заподозрить в имеющемся тексте наличие скрытого послания
Имея на руках всего лишь одну решетку можно 8 разными способами размещения и вращения трафарета зашифровать сообщение.
Можно также попытаться вписать ложное послание повернув сетку, но потом будет вдвойне сложнее создать связный открытый текст, не вызывающий подозрений.
Квадратная форма трафарета
Особый вариант решетки Кардано у нее имеется всего 4 способа расположения. В ней как и положено прорезаются отверстия такого размера, чтобы поместилась ровно одна буква.
Одно правило — ячейки нельзя вырезать так, чтобы при поворотах какие-либо 2 не оказывались в таком же месте во время вращения.
Шифрование с использованием «Мусора»
Процесс шифрования происходит следующим образом:
прикладываем квадрат к бумаге и вписываем часть текста в прорези
вращаем на 90 градусов и повторяем процедуру
в пустые места вписываем произвольные буквы, желательно, того же алфавита
Получается в итоге вот такое послание:

Шифрование без «Мусора»
Разница с предыдущим способом в том, что ячейки вырезаются таким образом, что при поворотах буквы заполняют все пространство квадрата и, по окончанию шифрования, не остается пустого пространства. Требование про отсутствие пар совпадающих прорезей сохраняется.
Как изготовить решетку Кардано?
Для этого можно воспользоваться конструктором например для создания варианта «без мусора» необходимо вырезать цифры по порядку (1,2,3 — ит.д), но только одну из 4х.

Если нужно сделать шаблон с «мусором», то некоторые клетки можно вообще не вырезать.
Минимальное стойкое число стороны квадрата — 8 ячеек, но чем она больше, тем большее число возможных конфигураций решеток появляется и, следовательно, подобрать ключ становится практически невозможно.
Как обнаружить в письме признаки шифрования решеткой Кардано?
Как правило, если шифровальщик не очень добросовестно отнесся к составлению текста сообщения, то текст выглядит достаточно странно и неестественно. Имея достаточное количество образцов переписки можно попытаться восстановить и вырезать аналогичный ключ.
В реальности, самое лучшее решение — это заполучить заветный кусок картона с прорезями.
В случае, если шифрование проведено «без мусора», — то это становится простым шифром перестановки и дешифровка может быть произведена путем частотного криптоанализа.
nightquests.ru
тайнопись и загадки докомпьютерной эпохи / Offсянка
Теоретически можно разгадать любой шифр. Для успешной расшифровки необходимо научиться пользоваться логикой — простейшие примеры логических выводов могут выглядеть так. Если текст засекречен с помощью подстановочного шифра, а первые шесть букв послания стоят перед восклицательным знаком, логично предположить, что это обращение “Привет!”. Если в тексте есть слово из двух букв, то почти наверняка это предлог. И так далее. Конечно, это логика простейшего примера. При более сложных вариантах шифрования важна собственная интуиция, чтобы с помощью шестого чувства догадаться, какой же метод был применен. Проблема в том, что алгоритмов шифрования существует бесчисленное множество, к тому же могут применяться комбинации подходов, что значительно усложняет задачу.
Современные компьютерные системы многократно усложнили расшифровку данных. Часто разработчики какого-нибудь известного проекта, чтобы закрыть все дыры в собственном программном обеспечении, предлагают всем желающим попробовать свои силы в дешифровке. Так, например, в 2013 году основатель «ВКонтакте» Павел Дуров предложил всем желающим принять участие в расшифровке его переписки с братом Николаем в новом мессенджере Telegram.

В качестве вознаграждения победителю сулился приличный приз — 200 тысяч долларов. Спустя год никто так и не выполнил эту задачу (по крайней мере так говорится в официальном блоге проекта), а конкурс продолжили, увеличив награду до 300 тысяч за взлом протокола. Любопытной была реакция некоторых членов сообщества, которые сожалели о такой строгой формулировке задания и предлагали взломать сам сервер.
Безусловно, работа такого уровня стоит больших денег. Но не стоит думать, что в современных условиях дешифрованием могут заниматься только программисты и хакеры. К счастью, прошлый век оставил нам уйму загадок и полезной пищи для того, чтобы размять “серые клеточки”. В этом материале мы собрали самые интересные методы шифрования докомпьютерной эпохи, а также неразгаданные послания от наших предков.
Появление письменности стало одним из переломных моментов в истории человечества, дало мощный импульс к развитию знаний в самых разных областях. Но как только человек понял, что может передавать свои мысли в виде графических символов, он тут же начал искать способы делать это тайно, чтобы лишь избранные могли прочесть написанное. Родились первые алгоритмы шифрования, а вместе с ними стали появляться и диковинные приспособления, которые служили ключом к пониманию зашифрованного текста.
⇡#Скитала: древнегреческая палочка-шифровалочка
В Древней Спарте использовали вот такую вот палицу, которая называется скитала (если верить сотрудникам музея Сен-Сир, где выставлена такая штука, она сделана приблизительно в пятом веке до нашей эры).

На этот посох наматывалась по спирали полоска пергамента с зашифрованным посланием. Смысл такого “гаджета” был в том, что прочитать эту полоску мог лишь обладатель скиталы аналогичного размера. При правильном размере витка буквы послания совпадали, и получался связный текст. Устройство было очень простым и практичным, хотя особо надежным его назвать никак нельзя.
Согласно легенде, этот “шифр” сумел разгадать еще Аристотель, а в 1841 году в июльском журнале Graham’s Magazine его редактор Эдгар Аллан По опубликовал статью «Несколько слов о тайнописи» (A FEW WORDS ON SECRET WRITING), в которой рассказал про скиталу и поведал об остроумном методе дешифровки скиталы любого диаметра.

По словам родоначальника детективного жанра, для “взлома” скиталы нужно взять, скажем, шестифутовый конус и намотать на него ленту с текстом, а затем перемещать вдоль длины конуса, пока текст не станет читаемым. Страсть Эдгара По к различным головоломкам и шифрам нашла свое отражение не только в его бессмертных произведениях. Будучи редактором журнала, он вел активное общение с читателями, призывая присылать ему ребусы и зашифрованные послания, которые он старался разгадывать совместно с подписчиками издания, совершенствуя тем самым свои навыки в криптологии.
⇡#Линейка Сен-Сира: шифруем на коленках
На следующей фотографии вы можете наблюдать вещь, которая имеет определенное сходство с логарифмической линейкой (простое механическое устройство для математических расчетов).

Эта вещь и есть линейка, только шифровальная. Её название — “Линейка Сен-Сира” — произошло от названия военного училища, которое в свое время организовал Наполеон Бонапарт.

Это высшее учебное заведение выпустило немало известных личностей — маршалов и военачальников. Военному искусству здесь обучался сам Шарль де Голль, а некоторое время в ней учился и Жорж Шарль Дантес, кавалергард, чья пуля на дуэли оборвала жизнь известного поэта Александра Сергеевича Пушкина.
В военной академии Сен-Сир придумали простое и оригинальное устройство, состоящее из двух частей — алфавитной линейки и подвижного бегунка с написанным алфавитом и прорезью. Принцип шифрования этой линейкой был очень простым и основывался на замещении букв алфавита. Но, в отличие от шифра Цезаря, где общий сдвиг букв при письме был одним и тем же (например, вместо А — Б, вместо В — Г и так далее), в линейке Сен-Сира был реализован шифр замещения с переменным сдвигом, так называемый шифр Блеза де Виженера, французского дипломата, жившего в шестнадцатом столетии.

Блез де Виженер
Обычное замещение текста — слишком слабый способ шифрования, который очень просто разгадывается с помощью банальной логики и статистики употребления тех или иных букв в языке. Помните, как лихо расшифровал подобный шифр сыщик Шерлок Холмс в рассказе “Пляшущие человечки” Артура Конан Дойля? Аналогично можно было бы расшифровать шифр Цезаря. Но с шифром Виженера у великого сыщика не вышло бы так просто разгадать загадку, ведь одна и та же буква в кодируемом сообщении могла иметь разные подстановки.

Джованни Батиста Беллазо
Интересно, что человек, давший имя этому шифру, никакого отношения к нему не имел. На самом деле его автором был итальянский математик Джованни Батиста Беллазо. Его труды и изучил Блез де Виженер во время своей двухлетней дипломатической миссии в Риме. Вникнув в простой, но эффективный принцип шифрования, дипломат сумел преподнести эту идею, показав ее комиссии Генриха III во Франции.
Суть нового принципа шифрования заключалась в том, что величина сдвига для замещения букв была переменной и определялась ключевым словом или фразой. Долгое время этот метод считался неуязвимым для разгадывания, и даже авторитеты в области математики признавали его надежность. Так, легендарный автор приключений “Алисы в зазеркалье” и “Алисы в стране чудес”, писатель-математик Льюис Кэрролл в своей статье «Алфавитный шифр» прямо и категорично называет шифр Виженера “невзламываемым”. Эта статья вышла в детском журнале в 1868 году, но даже спустя полвека после статьи Чарльза Латуиджа Доджсона (это настоящее имя автора сказок про Алису) научно-популярный американский журнал Scientific American продолжал утверждать, что шифр Виженера невозможно взломать.
Для расшифровки шифра Виженера использовалась специальная таблица, которая называлась tabula recta.

Линейка Сен-Сира — это своего рода механическая таблица Виженера. Пользоваться линейкой Сен-Сира несложно. Предположим, вы хотите закодировать текст MORTALENEMY ключевым словом POST. Многократно пишем это ключевое слово, чтобы получившееся выражение было по длине таким же, как шифруемый текст. Получается так:
MORTALENEMY
POSTPOSTPOS
На линейке подбираем положение бегунка, чтобы начало алфавита совпадало с буквой P и смотрим, какая буква соответствует первой букве шифруемого текста М. Это — буква B. Аналогичным образом букве O соответствует буква С, R меняется на J и так далее. В результате мы получаем зашифрованное слово: BCJMPZWGTAQ.
Проверить свое понимание принципов работы с шифром Виженера можно с помощью онлайнового сервиса — шифратора, кодировщика и декодировщика данного метода.
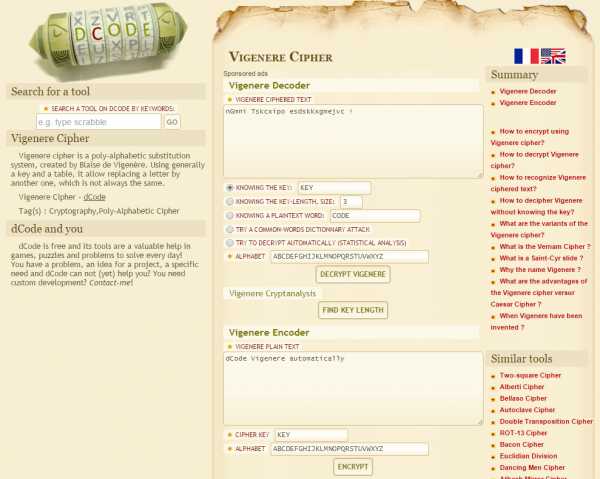
Помимо скиталы, на основе таблицы Виженера (tabula recta) было создано множество карманных “склерозников” разных форм, которые упрощали тайнопись. Наряду с линейкой Сен-Сира, большой популярностью пользовались шифровальные круги, идею которых подсказал в своих трудах Леон Баттиста Альберти — итальянский учёный середины XV столетия.

Леон Баттиста Альберти
Во время войны Севера и Юга в США (1861–1865 годов) диск Альберти (иногда можно встретить название “колеса Альберти”) — кружок диаметром девять с половиной сантиметров — лежал в кармане у разведчиков и связистов. Шифровальный диск был сделан из плотной светло-желтой картонки и состоял из двух концентрических кругов, скрепленных посередине. Внутренний диск содержал буквы и окончания, а внешний включал в себя группу сигнальных цифр. Секретное устройство украшали буквы A.J.M. — инициалы главного начальника связи, генерала Альберта Дж. Майера.

Для отчетности каждый такой круг имел порядковый номер, который был закреплен за владельцем.
⇡#Решетка Кардано и как ее сделать самому
Часто так бывает, что талантливый человек входит в историю как автор какого-то одного открытия, а прочие его заслуги при этом остаются в тени. Наверное, то же самое можно сказать про Джероламо Кардано.

Джероламо Кардано
Даже если вы не разбираетесь в автомобилестроении, то наверняка слышали о каком-то карданном вале. Это такая деталь, которая передает крутящий момент от коробки передач или раздаточной коробки к редуктору переднего или заднего моста. Джероламо придумал этот шарнирный механизм, но, помимо “автомобильного” изобретения, у Кардано было много других блестящих идей, например о пользе переливания крови. Еще одно изобретение Кардано — шифрование по трафарету или решетке.

Решетка Кардано знакома каждому, кто хоть раз смотрел бессмертный советский сериал с Василием Ливановым в роли Шерлока Холмса. В заглавных титрах одной из серий этого фильма показана идея шифрования решеткой Кардано — из массы бессмысленных символов сквозь прорези в нужных местах решетки как будто проступал осмысленный текст.
Решетка Кардано может быть двух видов — простая и симметрично-поворотная. В первом случае для шифрования применяется трафарет с отверстиями, через которые “фильтруется” полезный текст. Другой вариант решетки, более интересный, состоит в том, чтобы использовать симметричный (квадратный) трафарет, который можно применять несколько раз, просто поворачивая его вокруг центра. Поворотная решетка Кардано позволяет записать текст массивом символов так, что результат будет выглядеть совершенно нечитаемым, например:

Решетка Кардано была очень практичной и удобной. Чтобы прочитать секретный текст, не нужно было “решать кроссворд” или тратить время на обучение секретному языку. Этим шифром предпочитали пользоваться многие известные личности, например кардинал Ришелье и русский драматург и дипломат Александр Грибоедов.
Сделать решетку Кардано очень легко даже за несколько минут. Возьмите тетрадный лист в клетку или разлинуйте квадрат, например со стороной в восемь клеток.

По центру квадрата проведите две перпендикулярные черты, отделив четыре зоны. Затем заполните каждую из зон номерами клеток. Нумерацию клеток следует начинать из угла и вести ее так, чтобы направление нумерации каждый раз было по часовой стрелке.
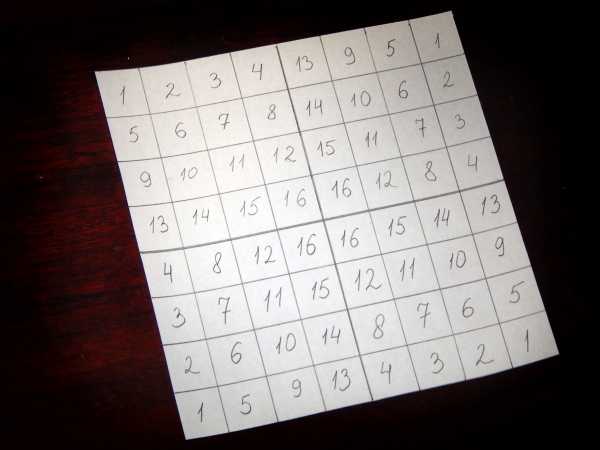
В каждой части квадрата есть набор цифр. Необходимо в произвольном порядке закрасить цифры от 1 до 16 так, чтобы числа не повторялись в разных частях решетки (например, если в первой зоне закрашена двойка, то в других зонах ее закрашивать уже не нужно).

Закрашенные клетки — это отверстия, которые необходимо вырезать. Квадратная решетка Кардано готова.

Приложите ее к листу и впишите текст. Затем поверните ее на 90 градусов и продолжайте писать текст, затем снова поверните и так до тех пор, пока весь квадрат под решеткой не будет заполнен текстом.
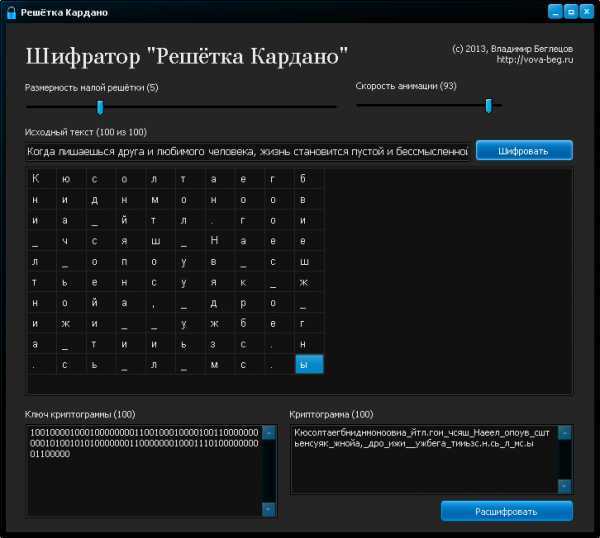
Чтобы вам было легче разобраться с принципом построения решетки, скачайте бесплатное приложение Владимира Беглецова “Шифратор решетки Кардано”. С помощью этой программы можно генерировать решетку разной размерности, а также кодировать и расшифровывать текстовое сообщение.
Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.
3dnews.ru
Перестановочный шифр — WiKi
Точное время появления шифра перестановки не известно. Вполне возможно, что писцы в древности переставляли буквы в имени своего царя ради того, чтобы скрыть его подлинное имя или в ритуальных целях[1].
Одно из древнейших известных нам шифровальных устройств — Скитала. Бесспорно известно, что скитала использовалась в войне Спарты против Афин в конце V века до н. э.[2][3]
Прародителем анаграммы считают поэта и грамматика Ликофрона, который жил в Древней Греции в III веке до н. э. Как сообщал византийский автор Иоанн Цец, из имени царя Птоломея он составил первую из известных нам анаграмм: Ptolemaios — Аро Melitos, что в переводе означает «из мёда», а из имени царицы Арсинои — как «Ion Eras» (фиалка Геры)[4].
Как правило, при шифровании и дешифровании шифра простой перестановки используется таблица перестановок:
Первая строка — позиция символа в открытом тексте, вторая строка — позиция в шифрограмме. Таким образом, при длине сообщения n{\displaystyle n} символов существует ровно n! {\displaystyle n!\ } ключей.
Шифры маршрутной перестановки
Широкое распространение получили так называемые маршрутные перестановки, использующие некоторую геометрическую фигуру (плоскую или объемную). Преобразования состоят в том, что отрезок открытого текста записывается в такую фигуру по некоторой траектории, а выписывается по другой траектории. Пример данного шифра — шифр Скиталы.
Шифр табличной маршрутной перестановки
Наибольшее распространение получили маршрутные шифры перестановки, основанные на прямоугольниках (таблицах). Например, можно записать сообщение в прямоугольную таблицу по маршруту: по горизонтали, начиная с верхнего левого угла, поочередно слева направо. Сообщение будем списывать по маршруту: по вертикалям, начиная с верхнего правого угла, поочередно сверху вниз.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки
| п | р | и | м | е |
| р | м | а | р | ш |
| р | у | т | н | о |
| й | п | е | р | е |
| с | т | а | н | о |
| в | к | и |
КРИПТОГРАММА: ешоеомрнрниатеаирмупткпррйсв
Обращение описанных шагов не представит труда при расшифровании[5].
Шифр вертикальной перестановки
Широкое распространение получила разновидность маршрутной перестановки — вертикальная перестановка. В этом шифре также используется прямоугольная таблица, в которую сообщение записывается по строкам слева направо. Выписывается шифрограмма по вертикалям, при этом столбцы выбираются в порядке, определяемом ключом.
ОТКРЫТЫЙ ТЕКСТ: пример маршрутной перестановки КЛЮЧ: (3, 1, 4, 2, 5)
| 3 | 1 | 4 | 2 | 5 |
| п | р | и | м | е |
| р | м | а | р | ш |
| р | у | т | н | о |
| й | п | е | р | е |
| с | т | а | н | о |
| в | к | и |
КРИПТОГРАММА: рмупткмрнрнпррйсвиатеаиешоео
Заполнять последнюю строку таблицы «нерабочими» буквами нецелесообразно, так как криптоаналитик, получивший данную криптограмму, получает сведения о длине числового ключа[6].
Шифр «поворотная решётка»
Решётка КарданоВ 1550 году итальянский математик Джероламо Кардано (1501—1576) в книге «О тонкостях» предложил новую технику шифрования сообщений — решётку.
Изначально решётка Кардано представляла собой трафарет с отверстиями, в которые записывали буквы, слоги или слова сообщения. Затем трафарет убирали, а свободное место заполняли более или менее осмысленным текстом. Такой метод сокрытия информации относится к стеганографии.
Позднее был предложен шифр «поворотная решётка» — первый транспозиционный (геометрический) шифр. Несмотря на то, что существует большая разница между изначальным предложением Кардано и шифром «поворотная решётка», методы шифрования, основанные на трафаретах, принято называть «решётками Кардано».
Четыре позиции решётки
Для шифрования и дешифрования с помощью данного шифра изготовляется трафарет с вырезанными ячейками. При наложении трафарета на таблицу того же размера четырьмя возможными способами, его вырезы полностью должны покрывать все клетки таблицы ровно по одному разу.
При шифровании трафарет накладывают на таблицу. В видимые ячейки по определённому маршруту вписывают буквы открытого текста. Далее трафарет переворачивают три раза, каждый раз проделывая операцию заполнения.
Шифрограмму выписывают из получившейся таблицы по определённому маршруту. Ключом являются трафарет, маршрут вписывания и порядок поворотов.
Данный метод шифрования использовался для передачи секретной информации нидерландскими правителями в 1740-х годах. Во время Первой мировой войны армия кайзера Вильгельма использовала шифр «поворотная решётка». Немцы использовали решётки разных размеров, однако очень недолго (четыре месяца), к огромному разочарованию французских криптоаналитиков, которые только-только начали подбирать к ним ключи. Для решёток разных размеров французы придумали собственные кодовые имена: Анна (25 букв), Берта (36 букв), Дора (64 буквы) и Эмиль (81 буква)[1][7].
В данном классе шифров перестановки используется идея многократной перестановки символов или повторного шифрования уже зашифрованного сообщения.
Шифр двойной перестановки
При шифровании шифром двойной перестановки в таблицу по определённому маршруту записывается текст, затем переставляются столбцы и строки. Далее по определённому маршруту выписывается шифрограмма.
Ключом к шифру являются размер таблицы, маршруты вписывания и выписывания, порядки перестановки столбцов и строк. Если маршруты являются фиксированными величинами, то количество ключей равно n!m!{\displaystyle n!m!} , где n{\displaystyle n} и m{\displaystyle m} — количество строк и столбцов в таблице[8].
ОТКРЫТЫЙ ТЕКСТ: двойная перестановка МАРШРУТ ВПИСЫВАНИЯ: слева - направо МАРШРУТ ВЫПИСЫВАНИЯ: сверху - вниз СТОЛБЦЫ: ( 3, 1, 4, 2) СТРОКИ: ( 3, 2, 4, 1, 5)
|
|
|
КРИПТОГРАММА: аавркопйстндевняоеа
ru-wiki.org
3 Шифр поворотной решетки
Для использования шифра, названного поворотная решетка, изготавливают трафарет из прямоугольного листа в клетку (размер 2m х 2k клеток). В этом трафарете вырезают mk клеток так, чтобы при наложении его на чистый лист бумаги того же размера четырмя возможными способами (лицевой и обратной сторонами каждая с поворотом на 180 градусов) вырезы без наложений полностью покрывали бы всю площадь чистого листа. Буквы исходного текста последовательно вписывают в вырезы трафарета по строкам слева направо при каждом из четырех его возможных положений в предварительно установленном порядке. Затем для получения шифротекста считывают полученную таблицу последовательно по строкам или столбцам.
Ключом для прочтения (востановления) исходного текста должен быть сам трафарет (или его описание), информация о последовательности(порядке) его поворотов и особенностей считывания таблицы. Количество возможных трафаретов (решеток) составляет T = 4(mk)!, а длина исходного текста составит n=4mk. Число всех перестановок в тексте такой длины составит (4mk)!, что существенно больше числа ключей T.
4 Шифры с использованием магичных квадратов
Магичный квадрат – квадратная таблица с вписаными в клетки последовательными натуральными числами, начиная с 1, которые при суммировании по столбцам, строкам и диагоналям дают одно и то же число. Исходный текст вписывают в магический квадрат в соответствии с нумерацией его клеток. Для получения шифротекста таблицу считывают по строкам или столбцам. В качестве ключа для востановления исходного текста может быть ссылка на номер магического квадрата в некоторой базе, которая известна отправителю и получателю шифротекста.
16
3
2
13
5
10
11
8
9
6
7
12
4
15
14
1
Рис 1а
13
8
12
1
2
11
7
14
3
10
6
15
16
5
9
4
Рис 1б
4
15
14
1
9
6
7
12
5
10
11
8
16
3
2
13
Рис 1в
1
12
8
13
14
7
11
2
15
6
10
3
4
9
5
16
Рис 1г
На рисунке выше приведены примеры магических квадратов размера 4х4 (из 880 возможных). Количество магических квадратов размера 5х5 – около 25 тыс.
5 Перестановка бит
Использование компьютеров для выполнения шифрования породило такой метод как перестановка бит в каждом символе исходного текста. К примеру, ключ для такого шифрования может выглядеть так (3,5,7,1,4,2,8,6). Это означает, что исходное сообщение, представленное в бинарной форме разбивается на блоки по 8 бит и в каждом таком блоке происходит перестановка в соответствии с заданнын ключом: на первое место переставляется 3-й бит, на второе–5-й, на третье–7-й и т.д. Возможна разбивка на блоки, содержащие другое число бит.
studfiles.net
