6.Решение линейных систем по формулам Крамера
Теорема Крамера.
Дана система, в которой число уравнений совпадает с числом неизвестных
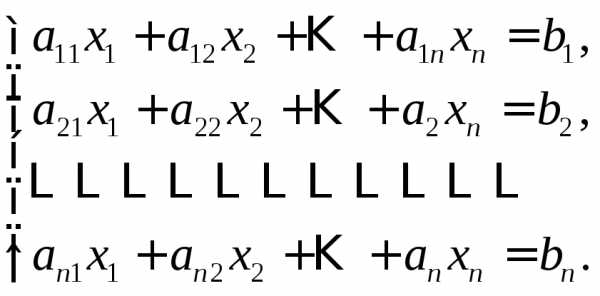 (10)
(10)
Определитель, составленный из коэффициентов системы
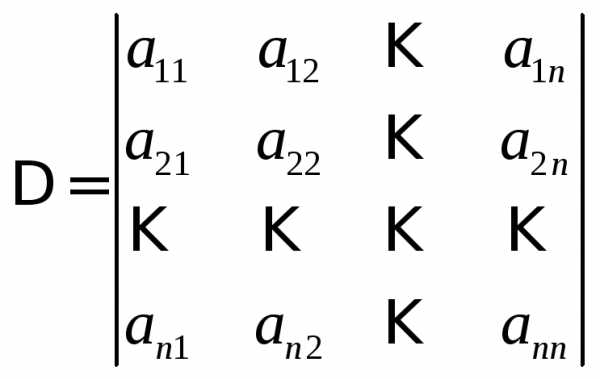 ,
,
называется главным определителем системы.
Если главный
определитель системы не равен нулю, то
система имеет единственное решение и 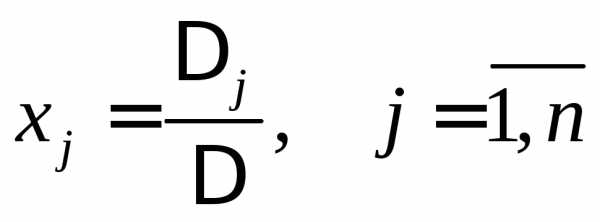 ,
где
,
где
Определители , получены из главного определителя заменой соответствующего столбца на столбец свободных членов.
►Пример 8. По
формулам Крамера найти решение системы
уравнений 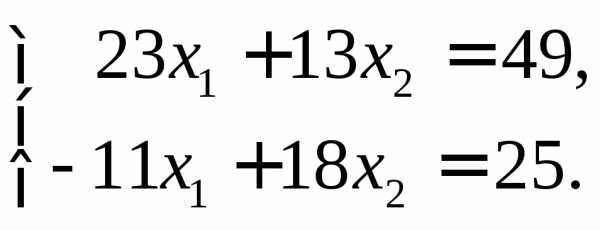
Решение.
Вычислим определители и найдем решение
Ответ:  .◄
.◄
Упражнения.
Решить системы по формулам Крамера.
1) 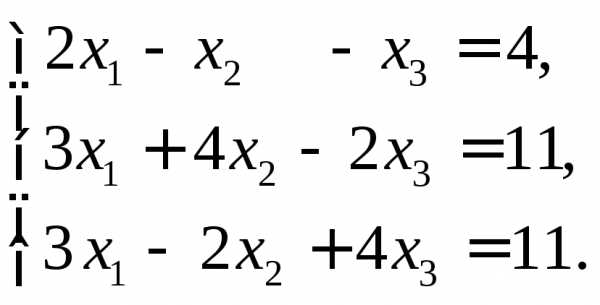
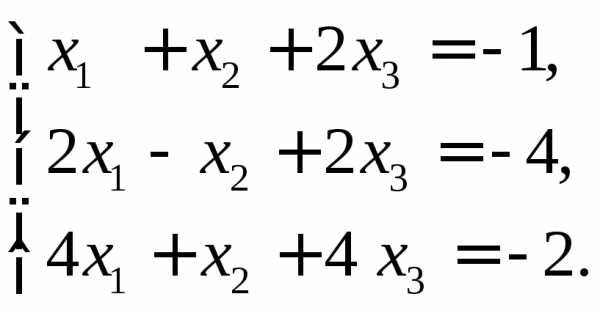 3)
3)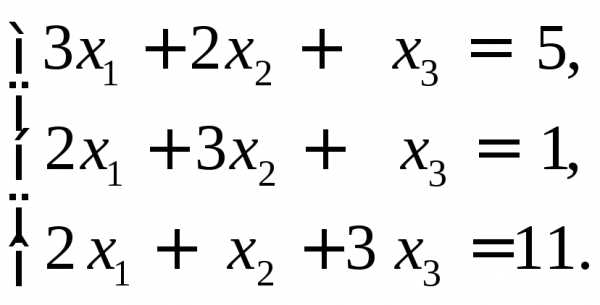
Ответы:
1)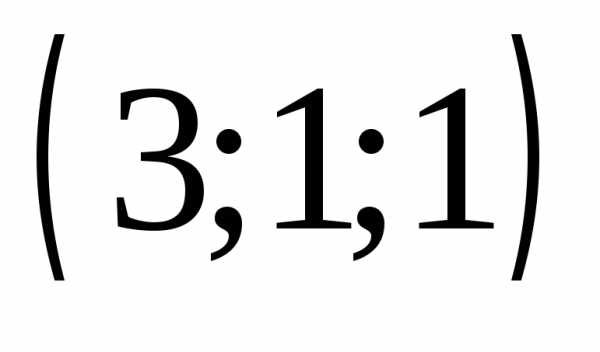 ,
2)
,
2)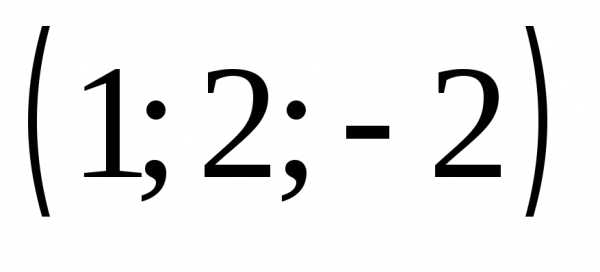 ,
3)
,
3)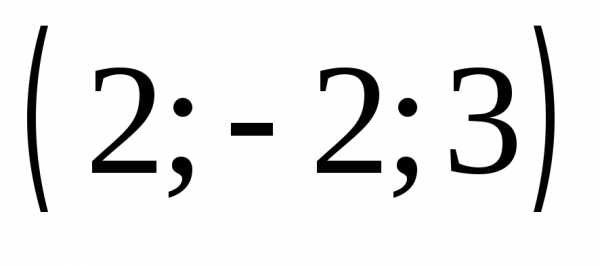 .
.
7. Решение систем с помощью обратной матрицы
Система из 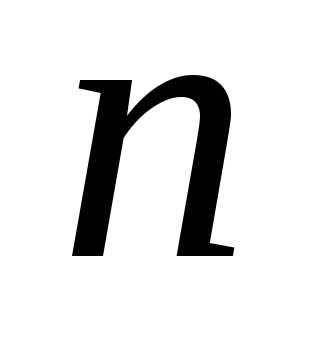 уравнений с
уравнений с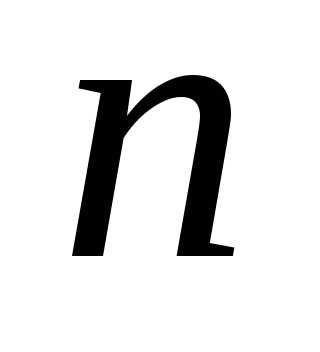
,
где 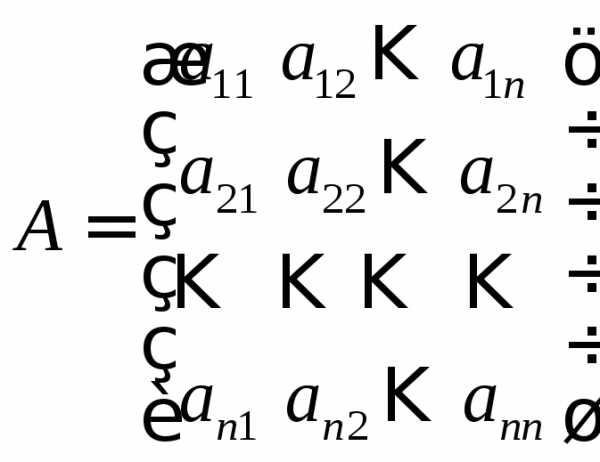 ,
,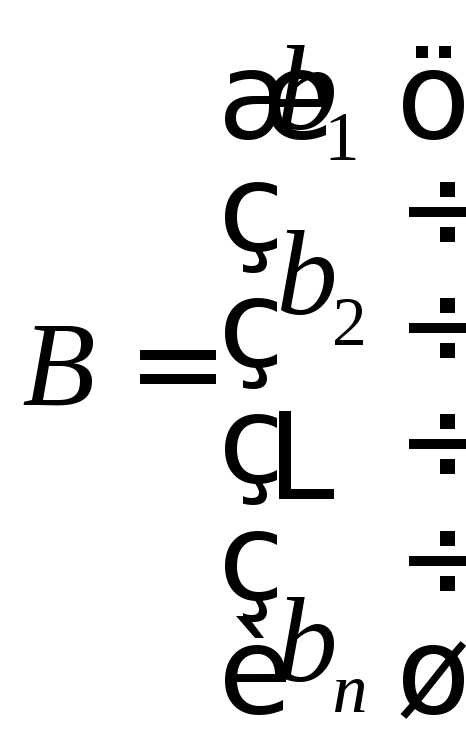 ,
,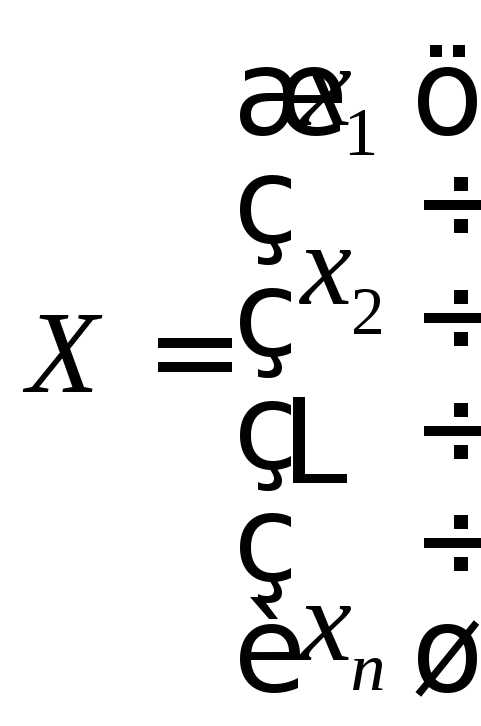 .
.
Если матрица  невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
►Пример 9.
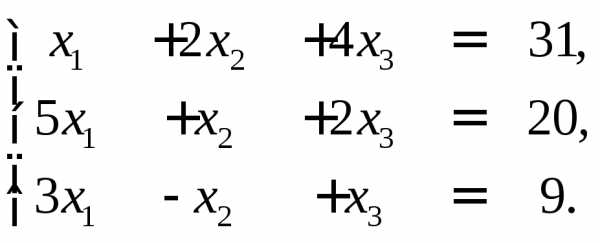
Решение.
Проведем необходимые вычисления
.
Ответ: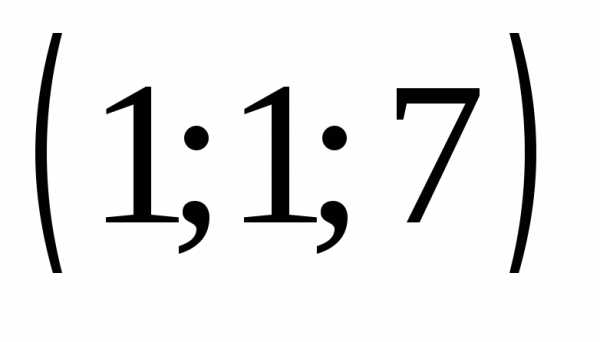 .
◄
.
◄
Упражнения.
Найти решение систем с помощью обратной матрицы.
а) 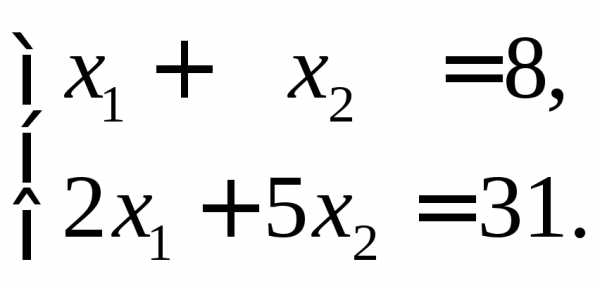
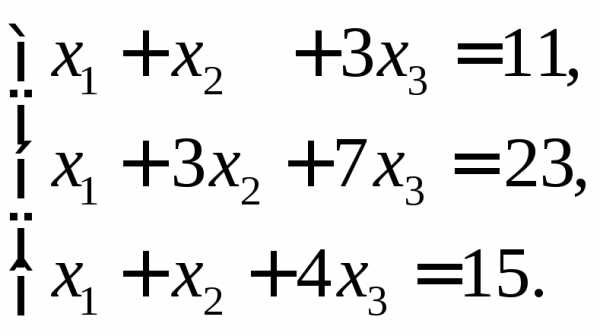 в)
в)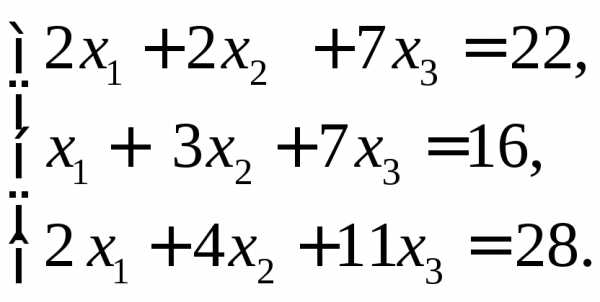
г) 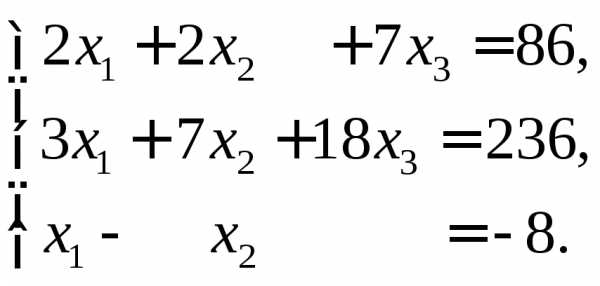 Ответы: а)
Ответы: а) 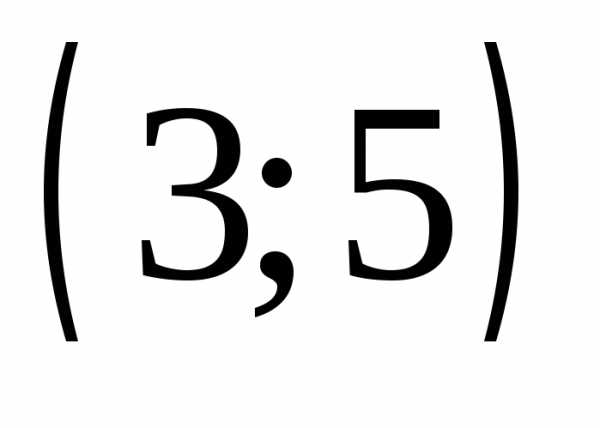 ;
б)
;
б)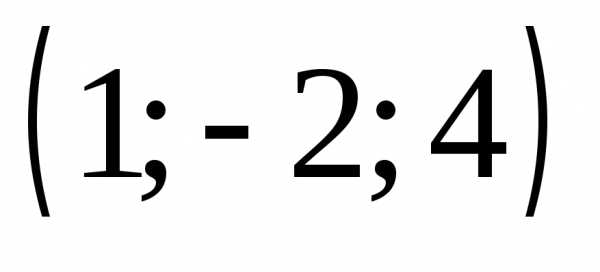 ;
в)
;
в)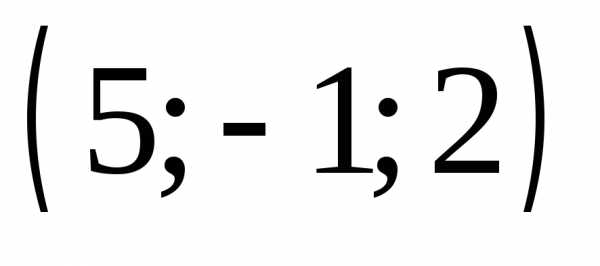 4
г)
4
г)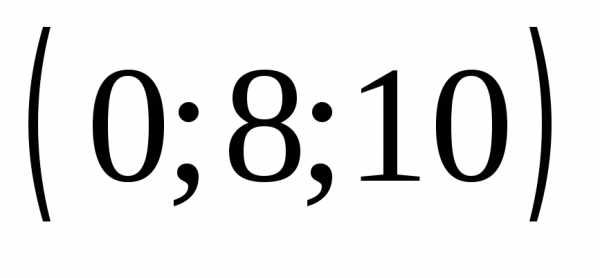 .
.
8. Исследование систем линейных уравнений. Метод Гаусса.
Рассмотрим линейную систему общего вида:
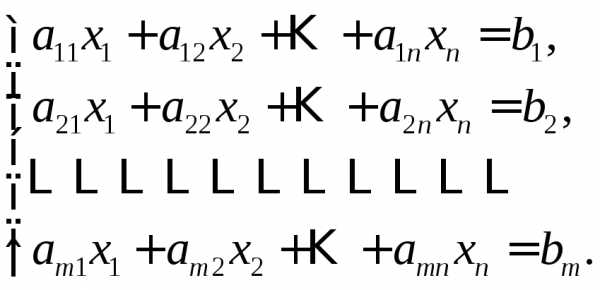
Теорема (Кронекера-Капелли).
Для совместности
системы линейных уравнений необходимо
и достаточно, чтобы ранг ее основной
матрицы (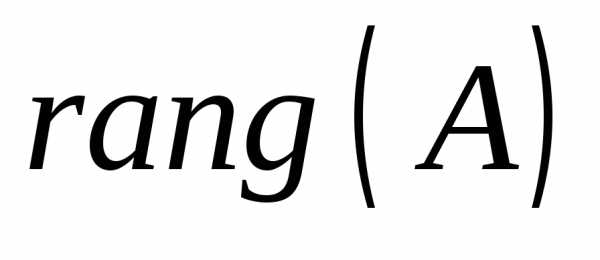 )
был равен рангу расширенной матрицы
(
)
был равен рангу расширенной матрицы
(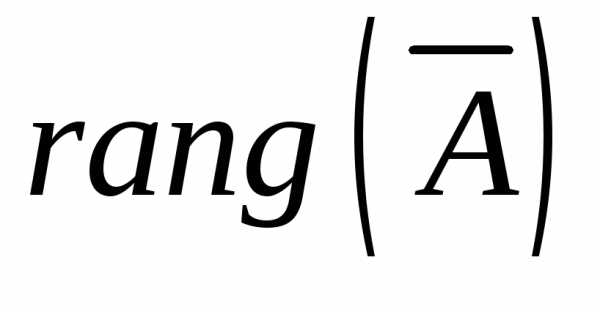 ).
).
Пусть 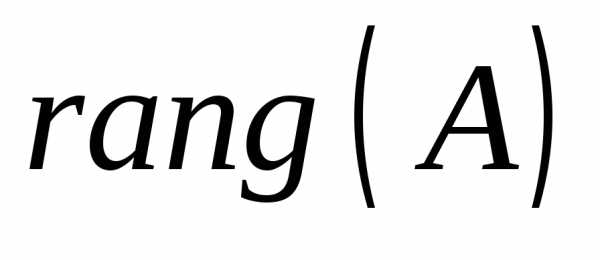 =
=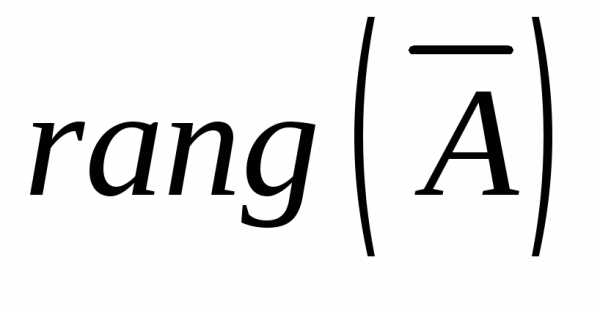 =
=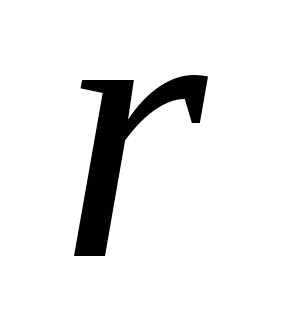 .
Тогда верны следующие утверждения.
.
Тогда верны следующие утверждения.
Следствие
1. Если ранг
матрицы 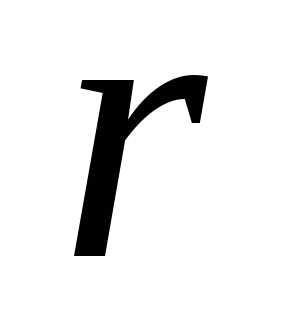 равен числу неизвестных
равен числу неизвестных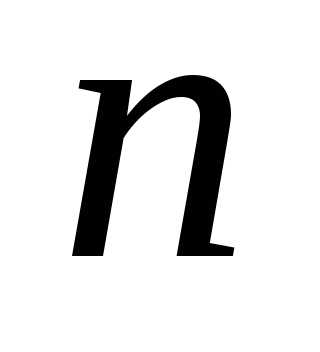 ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Следствие
2. Если ранг
матрицы 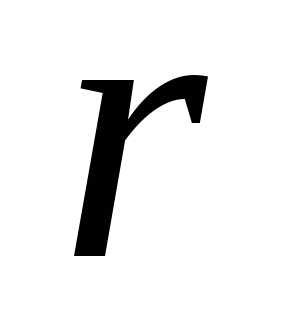 меньше числа неизвестных, то система
имеет бесконечное множество решений.
При этом
меньше числа неизвестных, то система
имеет бесконечное множество решений.
При этом неизвестных, которые называются
свободными, принимают произвольные
значения. Говорят, что система имеет
неизвестных, которые называются
свободными, принимают произвольные
значения. Говорят, что система имеет
Метод Гаусса (исключение неизвестных) состоит в том, что с помощью умножения уравнений на ненулевые числа и сложения в первом уравнении оставляем все неизвестные, во втором на одно меньше, в третьем на два меньше и т.д. Эту операцию (назовем ее процедурой Гаусса) удобно проводить, используя матрицы.
Составим расширенную матрицу систему и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк.
Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной.
Рассмотрим три ситуации, возникающие при исследовании линейных систем.
1) .Система несовместна.
►Пример 10.
Решить систему уравнений методом Гаусса.
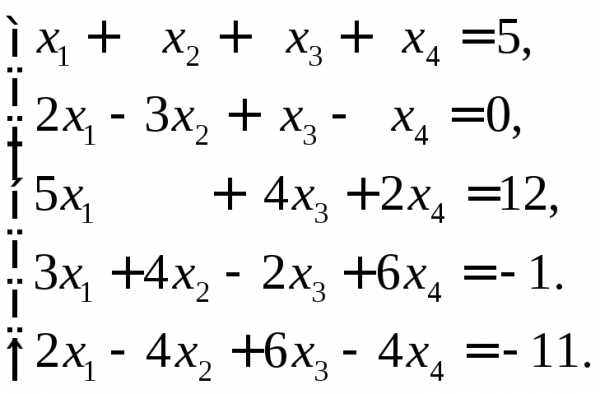
Решение.
Составим расширенную матрицу и преобразуем ее
.
Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки – в третьем столбце.
В четвертой строке легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой. Мы не упрощали вычислений, чтобы сохранить алгоритм получения нулей в нижележащих строках за один шаг.
По преобразованной матрице определяем ранги: ,, следовательно, данная система уравнений несовместна.
Ответ: система не имеет решений. ◄
2) .Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.
►Пример 11. Решить систему уравнений методом Гаусса
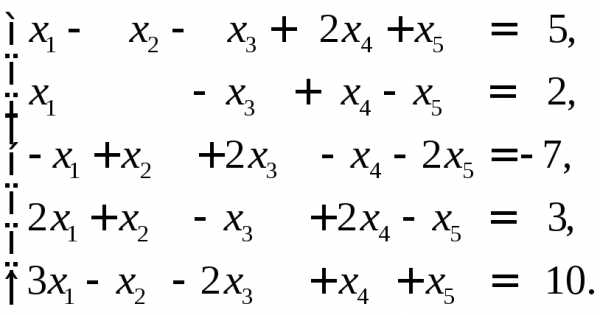
Решение.

Ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной
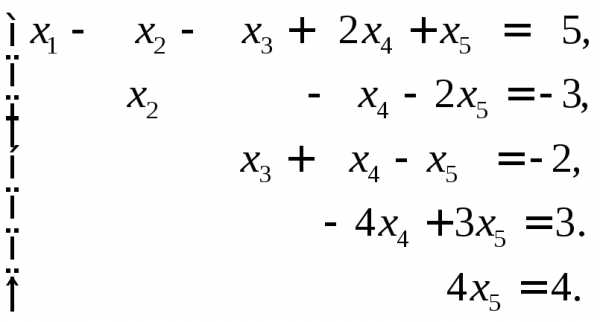
Полученная система имеет ступенчатый вид и легко решается.
Ответ: .◄
3) .Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося члены со свободными неизвестными в правую часть уравнений.
Рассмотрим запись решения таких систем в матричной форме.
Пусть дана система
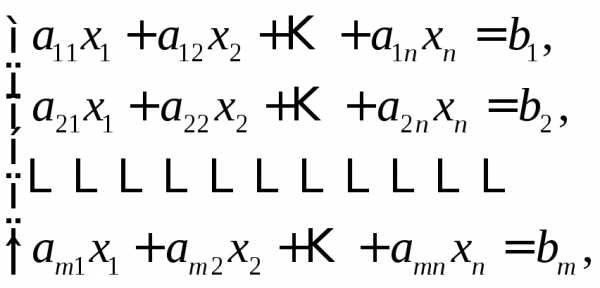
и известно, что
.
Тогда система имеет степеней свободы, т.е.
степеней свободы, т.е. неизвестных принимают произвольные
значения, а
неизвестных принимают произвольные
значения, а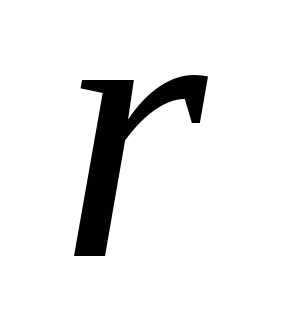 неизвестных выражаются через них.
Минор, не равный нулю, напоминаем,
называетсябазисным.
Не уменьшая общности, будем считать,
что базисный минор системы занимает в
ней верхний левый угол. Обозначим этот
минор
неизвестных выражаются через них.
Минор, не равный нулю, напоминаем,
называетсябазисным.
Не уменьшая общности, будем считать,
что базисный минор системы занимает в
ней верхний левый угол. Обозначим этот
минор 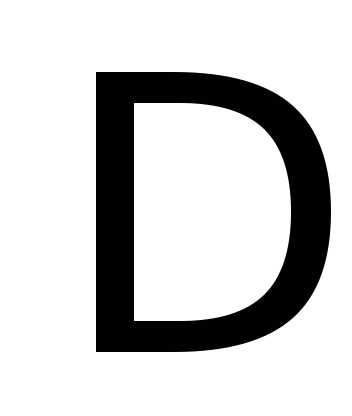 :
:
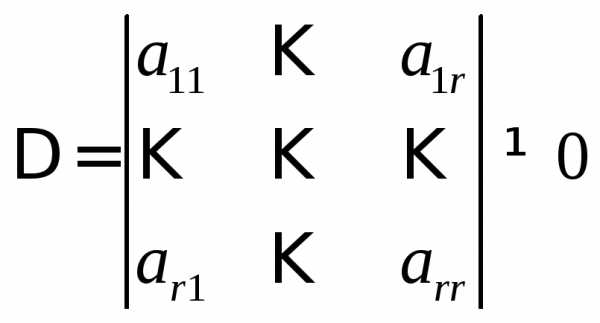 .
.
Минор 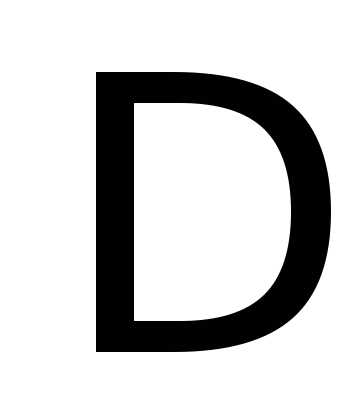 является базисным и для матрицы
является базисным и для матрицы ,
поэтому строки с номерами
,
поэтому строки с номерами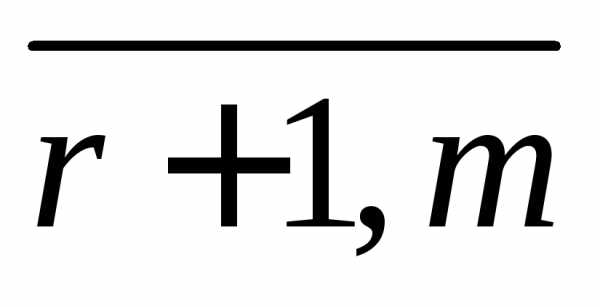 являются линейными комбинациями первых
являются линейными комбинациями первых строк и система эквивалентна системе
из
строк и система эквивалентна системе
из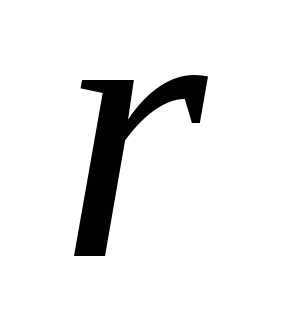 уравнений (свободные неизвестные
перенесены в правую часть)
уравнений (свободные неизвестные
перенесены в правую часть)
Решая эту систему по методу Крамера, имеем
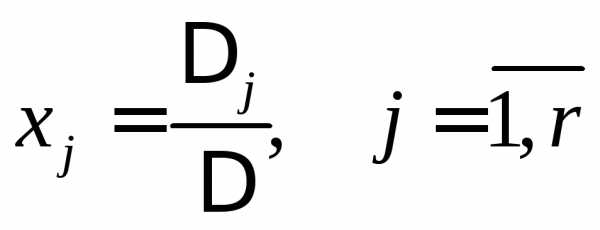 ,
,
где
– определитель,
полученный из базисного заменой 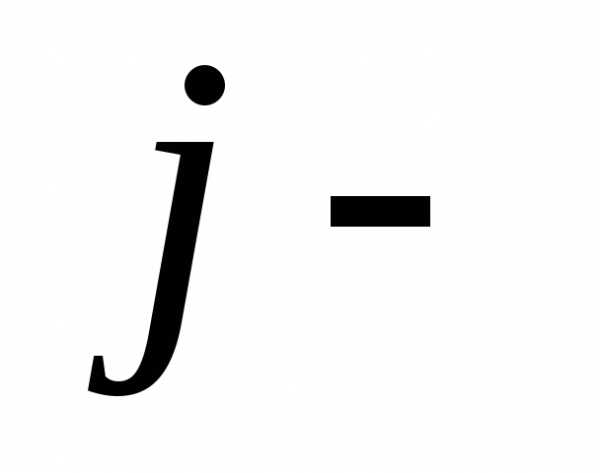 го
столбца на столбец правой части системы.
Пользуясь свойствами определителей,
имеем
го
столбца на столбец правой части системы.
Пользуясь свойствами определителей,
имеем
. (11)
Символ: 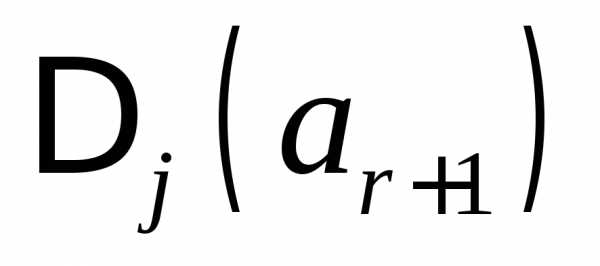 ,-
означает, что
,-
означает, что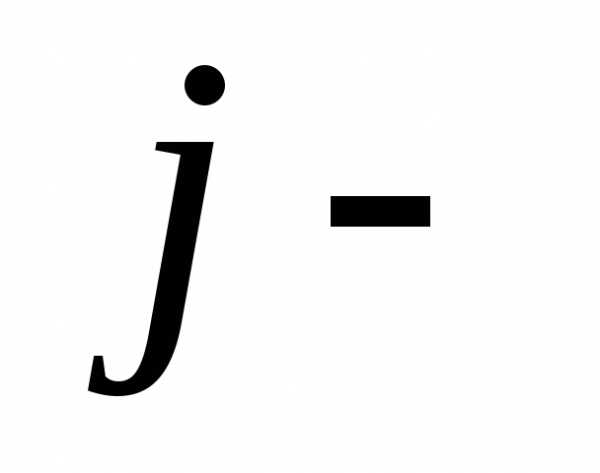 й
столбец базисного минора заменен на
столбец коэффициентов при неизвестном
й
столбец базисного минора заменен на
столбец коэффициентов при неизвестном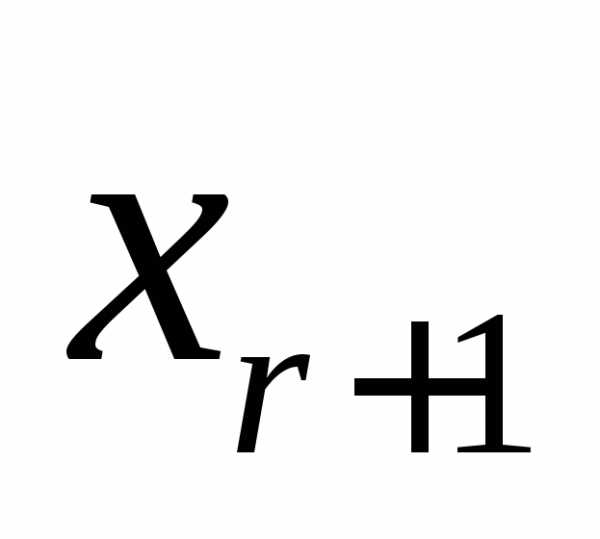 .
Вектор,
является решением системы, Главный
определитель системы совпадает с
базисным минором, а свободные члены
равны коэффициентам при неизвестном
.
Вектор,
является решением системы, Главный
определитель системы совпадает с
базисным минором, а свободные члены
равны коэффициентам при неизвестном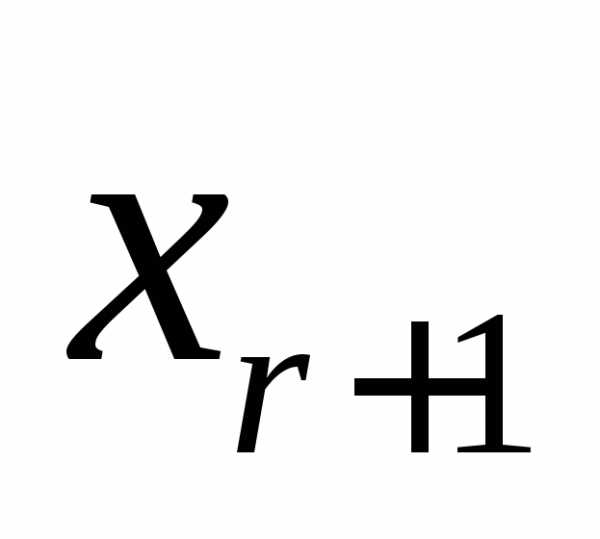 .
Введем обозначения
.
Введем обозначения
.
Тогда множество решений системы можно записать в виде
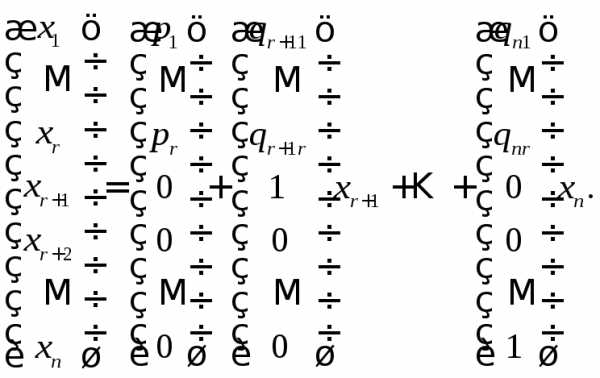 (12)
(12)
Для вычисления
полагаем свободные неизвестные равными
нулю. Для вычисленияполагаем свободные члены равными нулю,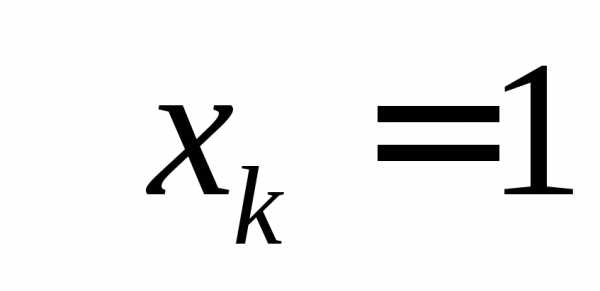 ,
а остальные свободные неизвестные
равными нулю.
,
а остальные свободные неизвестные
равными нулю.
. Выбор свободных
неизвестных, вообще говоря, можно делать
по-разному. Однако не всякие  неизвестных можно принять за свободные.
Необходимо, чтобы коэффициенты при
остальных
неизвестных можно принять за свободные.
Необходимо, чтобы коэффициенты при
остальных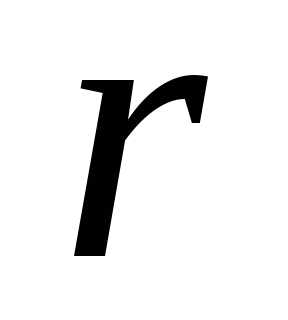 неизвестных составили базисный минор.
неизвестных составили базисный минор.
►Пример 12. Решить систему уравнений
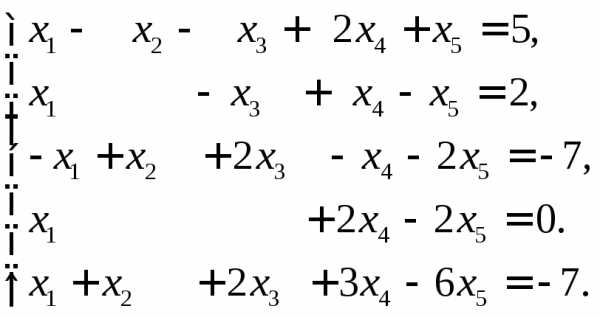
Решение.
Преобразуем расширенную матрицу системы
.
Ранг основной
матрицы равен рангу расширенной матрицы
,
но меньше числа неизвестных. Следовательно,
система совместна, но имеет бесконечное
множество решений. Число степеней
свободы равно двум. Выберем свободными
неизвестными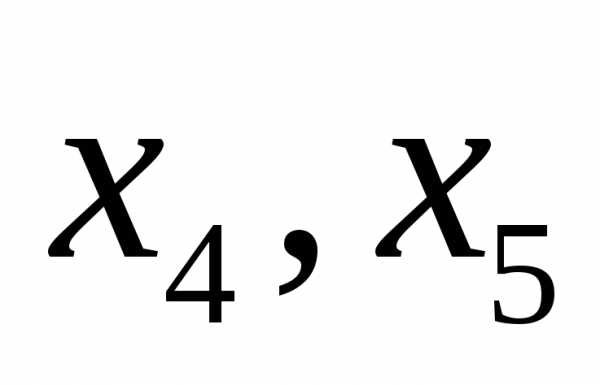 и выразим
и выразим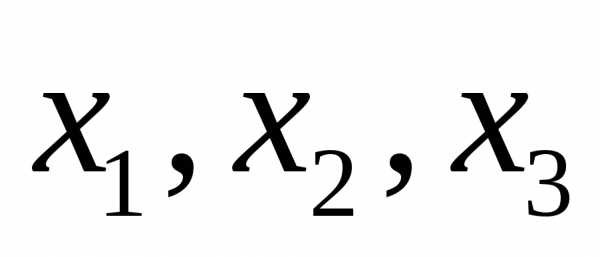 через них.
через них.

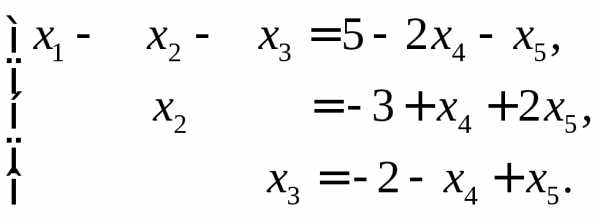 отсюда получаем
отсюда получаем 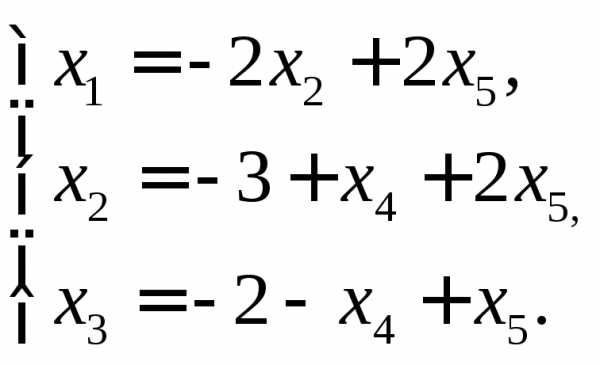
Ответ запишем в виде вектора-столбца.
Ответ: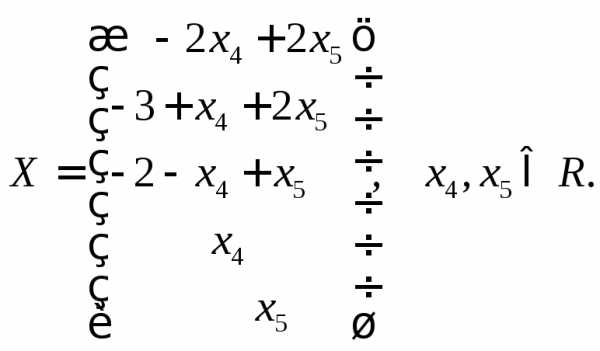 .
◄
.
◄
Получим также
решение заданной системы, используя
формулу (11). Положим
.
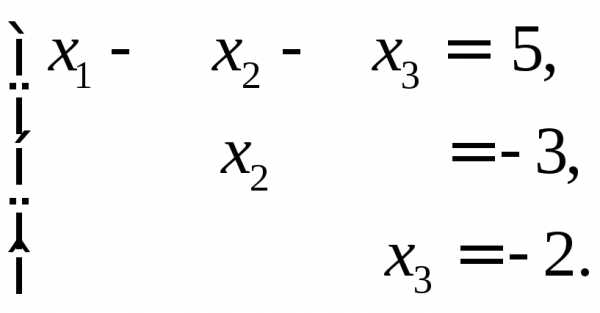 Получаем вектор
Получаем вектор 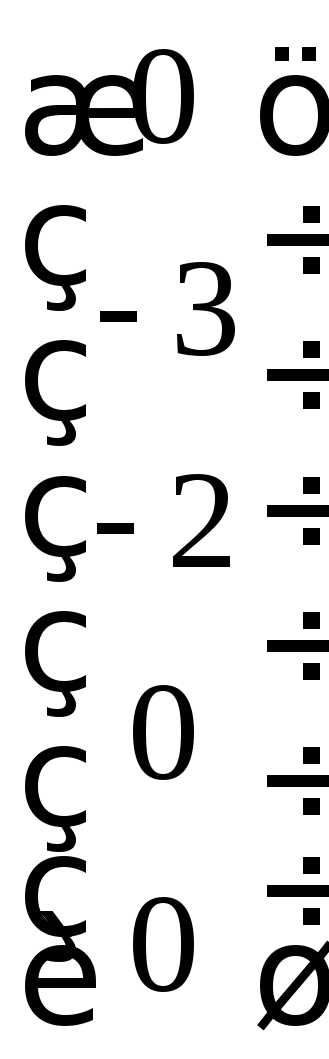 .
.
Положим .
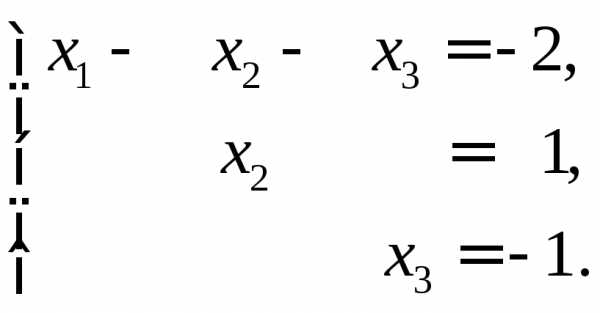 Получаем вектор
Получаем вектор 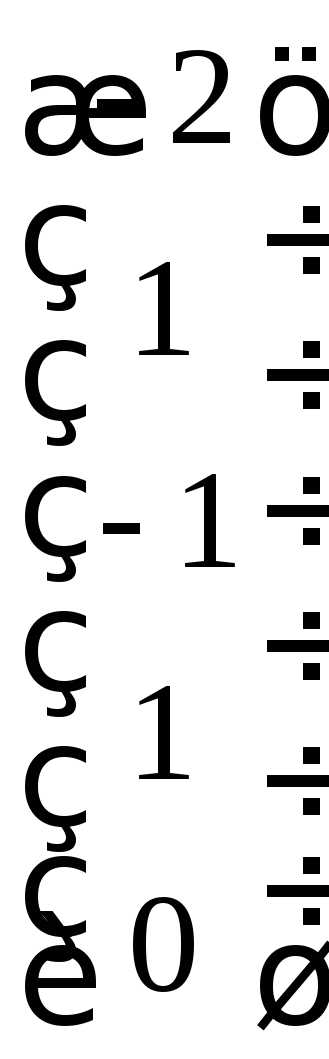 .
.
Положим .
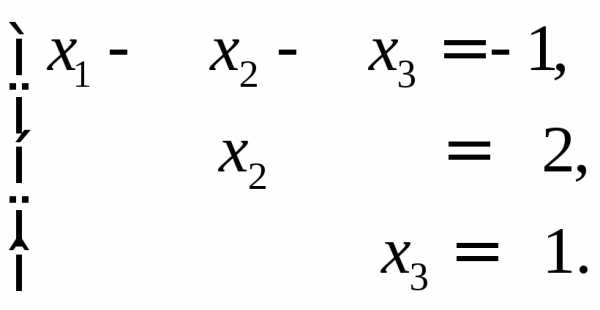 Получаем вектор
Получаем вектор 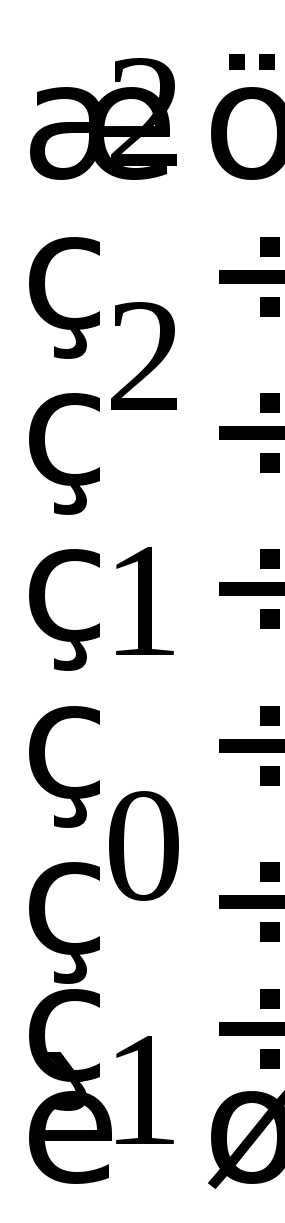 .
.
Окончательное
решение: 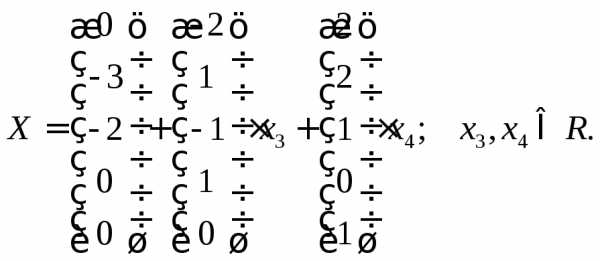 ◄
◄
Упражнения.
Исследовать и решить системы уравнений.
1. 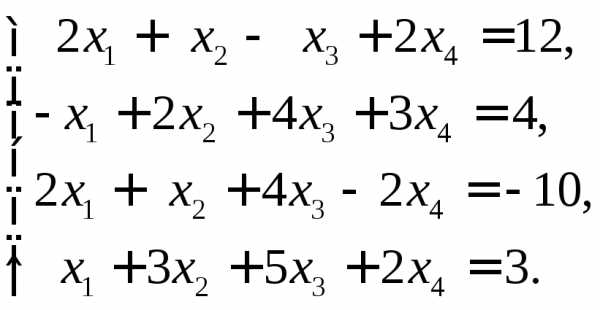 Ответ:
Ответ: 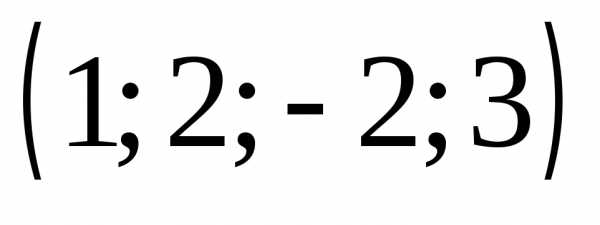 .
.
2. 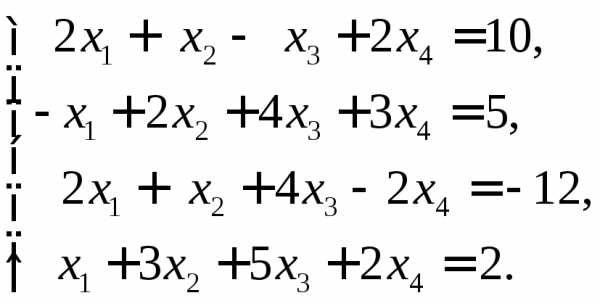 Ответ:
Ответ: 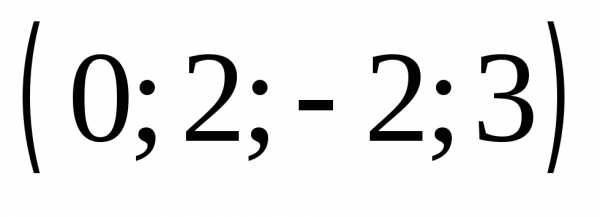 .
.
3. 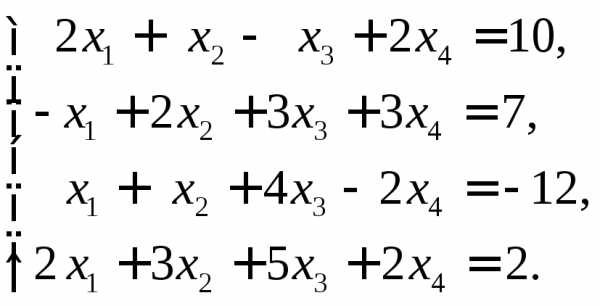 Ответ:
Ответ: 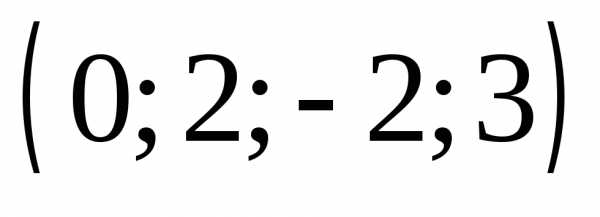 .
.
4. 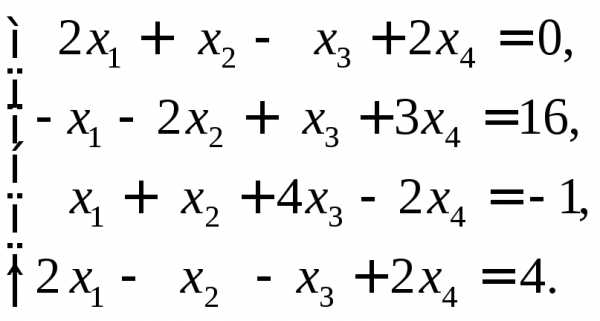 Ответ: .
Ответ: .
5. 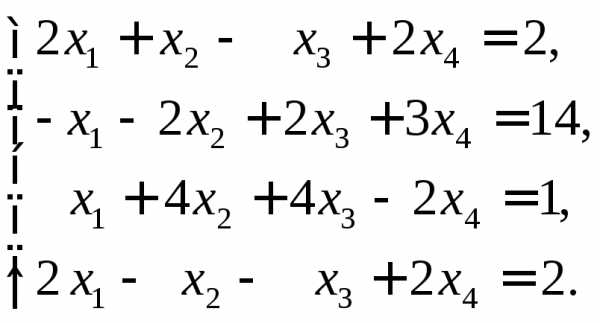 Ответ:
Ответ: 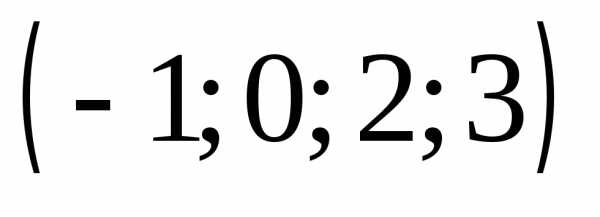 .
.
6. 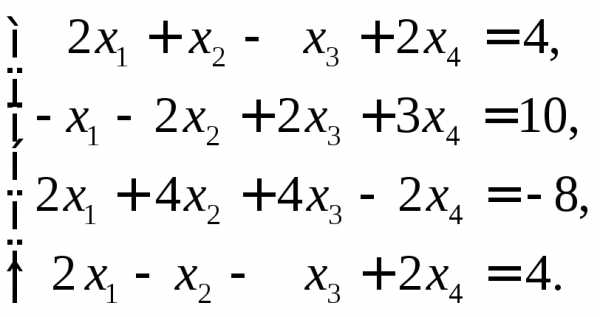 Ответ:
Ответ: 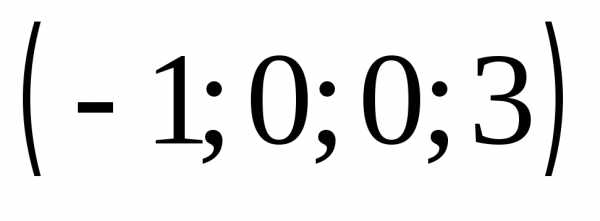 .
.
7. 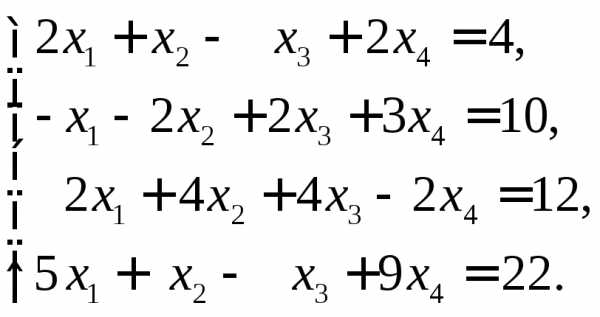 Ответ:
Ответ: 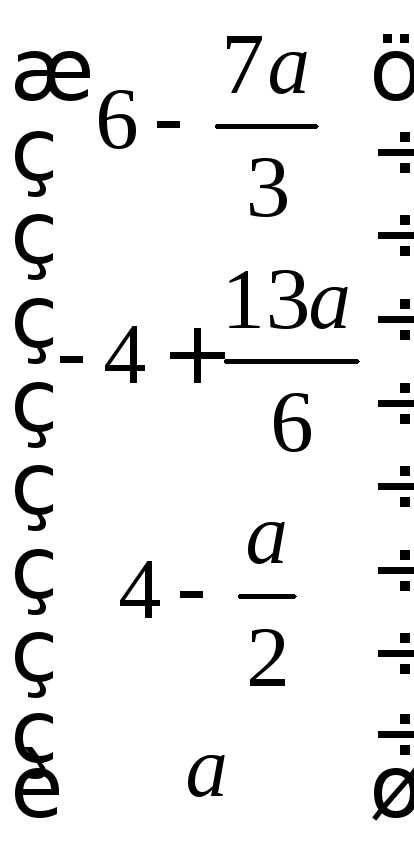 .
.
8. 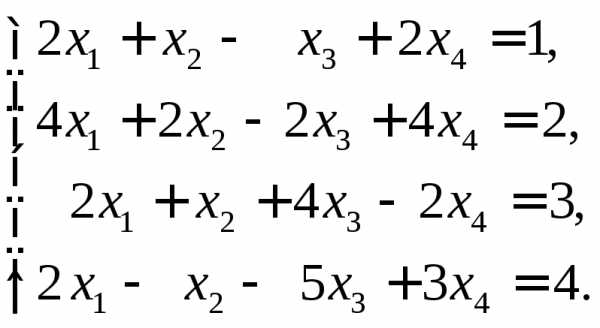 Ответ:
Ответ:  .
.
9.  Ответ:
Ответ:  .
.
10. 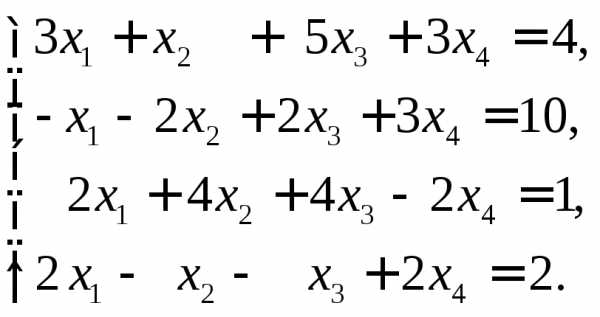 Ответ:
Ответ: 
studfiles.net
Система уравнений по формулам Крамера
Задание № 1
Решить систему уравнений:
1) по формулам Крамера
2) с помощью обратной матрицы
3) методом Гаусса
Решение
найдем определитель матрицы
1) методом Крамера
найдем определители
найдем значения ; ;
2) метод обратной матрицы
транспонированная матрица
найдем алгебраические дополнения
; ; ;
; ; ;
; ; ;
матрица из дополнений
3) методом Гаусса
построим расширенную матрицу
приведем матрицу к треугольному виду
разделим первое уравнение на 3 и вычтем второе
умножим первое уравнение на 5/3 вычтем третье
Второе уравнение умножим на 3, третье уравнение умножим на 3
второе уравнение умножаем на 4/11 вычитаем третье.
Первое уравнение разделим на 3
Второе уравнение разделим на -11
третье уравнение разделим на 159/11
полученной матрице соответствует система уравнений
решаем уравнение снизу вверх
решение системы
Задание № 2
Координаты вершин пирамиды А(1, -4, 0), В(5, 0, -2), С(3, 7, -10), Д(1, -2, 1) – вершины пирамиды. Найти:
1) записать векторы АВ, АС, АД в системе орт и найти их длины
2) найти угол между векторами АВ и АС
3) найти проекцию вектора АД на вектор АВ
4) найти площадь грани АВС
5) найти объем пирамиды АВСД
Решение
1. записать векторы в системе орт и найти их длины.
Произвольный вектор может быть представлен в системе орт i, j, k следующей формулой , где – проекции вектора а на соответствующие координатные оси. Если даны точки и , то проекции вектора на координатные оси находятся по формулам
; ;
расстояние между двумя точками и определяется по формуле
запишем вектор
; ; ;
длина АВ будет равна
запишем вектор
; ; ;
длина АС будет равна
запишем вектор
; ; ;
длина АД будет равна
2. найти угол между векторами ;
косинус угла между двумя векторами равен скалярному произведению этих векторов, деленному на произведение их модулей.
модуль вектора равен
модуль вектора равен
скалярное произведение векторов
Таким образом, , угол А=36,86°
3. найти проекцию вектора на вектор ;
Проекция вектора на вектор равна скалярному произведению этих векторов, деленному на модуль вектора
скалярное произведение векторов
4. найти объем пирамиды ABCД
Объем пирамиды равен 1/6 объема параллелепипеда, построенного на ребрах
Объем параллелепипеда, построенного на трех некомпланарных векторах , , , равен абсолютной величине их смешанного произведения
Объем пирамиды равен
Задание № 3
Найти указанные пределы
а)
б)
– бесконечно малые
в)
tgα(x)~α(x) эквивалентные бесконечно малые при α(x)→0
г)
– бесконечно малые
Задание № 4
Найти производные функции
а)
б)
в)
г)
д)
Задание № 5
Найти производную указанного порядка
Задание № 6
Найти дифференциал функции
Задание № 7
Найти неопределенные интегралы и результат проверить дифееренцированием
а)
проверка
б)
проверка
в)
проверка
Задание № 8
Найти площадь фигуры, ограниченной линиями. Сделать схематический чертеж
Вычислить объем тела, образованного вращением вокруг оси ох фигуры, ограниченной указанными линиями. Сделать схематический чертеж
Объем фигуры образованной вращением вокруг оси ох ограниченной линиями
coolreferat.com
Решение системы по формулам Крамера
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы.
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение: Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
, значит, система имеет единственное решение.
;
;
Ответ: ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательнымфрагментом оформления задания является следующий фрагмент: « , значит, система имеет единственное решение». В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение: Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ: .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
infopedia.su
Решение системы по формулам Крамера
Стр 1 из 2Следующая ⇒Правило Крамера. Метод обратной матрицы
Представляю Вашему вниманию вторую часть урока Как решить систему линейных уравнений? В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Настоятельно рекомендую скачать программу для автоматизированного решения систем по формулам Крамера и с помощью обратной матрицы. Всегда приятно знать правильный ответ заранее, более того, программа позволит сразу обнаружить ошибку по ходу решения задачи, что значительно сэкономит время!
Решение системы по формулам Крамера
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы.
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение: Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
, значит, система имеет единственное решение.
;
;
Ответ: ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательнымфрагментом оформления задания является следующий фрагмент: « , значит, система имеет единственное решение». В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение: Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ: .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru
