Шифр хилла онлайн – Онлайн калькулятор: Шифр Хилла

Онлайн калькулятор: Шифр Хилла

Шифр Хилла — полиграммный шифр подстановки, основанный на линейной алгебре. Лестер С. Хилл изобрел этот шифр в 1929. Калькулятор ниже позволяет зашифровать и расшифровать текст методом Хилла. Подробности о шифре для интересующихся приведены под калькулятором.

Все символы, подвергающиеся шифрованию, должны входить в алфавит

никогда еще штирлиц не был так близок к провалуТекстПреобразование

Преобразованный текст

 

Сохранить share extension

Как работает шифр

Для начала символы используемого алфавита (в широком смысле этого слова, например, алфавит может включать в себя пробел и некоторые знаки пунктуации, как в калькуляторе выше) кодируются числами, то есть каждому символу алфавита сопоставляется некоторое число, например, порядковый номер. Выбирается матрица размера n x n, которая будет являться ключом шифра. Весь текст разбивается на блоки из из n букв, числовые значения которых рассматриваются как вектор размерности n. Каждый вектор умножается на матрицу шифрования n × n. Результирующий блок (вектор) размерности n — соответствующий исходному блоку зашифрованный текст. Операции сложения и умножения при этом выполняются в кольце вычетов по модулю m, где m — размерность алфавита. Очевидно, это делается для того, чтобы значения результирующего блока тоже принадлежали исходному алфавиту.

Ключ, в принципе, можно сразу задавать матрицей, но для удобства еще чаще задают кодовой фразой, числовое представление которой трансформируют в матрицу. Понятно, что для того, чтобы получить квадратную матрицу n x n, длина кодовой фразы должна являться квадратом целого числа, то есть, 4, 9, 16, 25, и т. д.

Дополнительные ограничения на ключ шифра накладывает необходимость осуществления расшифровки зашифрованного текста 🙂

Предположим, что мы зашифровали исходный вектор B матрицей шифрования А и получили вектор С — соответствующий зашифрованному тексту. Для того, чтобы восстановить исходный вектор B по вектору C (расшифровать текст), вектор С надо умножить на матрицу, обратную к матрице А.

Таким образом, чтобы операция расшифрования была возможна, матрица шифрования должна быть обратима в — кольце вычетов по модулю m.

Отсюда вытекают два условия: детерминант матрицы не должен быть равен 0, и, дополнительно, детерминант матрицы должен иметь обратный элемент в кольце вычетов по модулю m.
Второе следует из формулы
.
где операция деления на детерминант заменена на операцию умножения на обратный элемент.

Чтобы иметь обратный элемент, детерминант и модуль (длина алфавита) должны быть взаимнопростыми числами. См. Обратный элемент в кольце по модулю. Для того, чтобы повысить вероятность этого, обычно составляют алфавит, длина которого является простым числом. Поэтому русский алфавит в данном примере был расширен пробелом и символами пунктуации до 37 символов.

Не каждая матрица подойдет для шифра Хилла (и не каждое кодовое слово), но тем менее, подходящих более чем достаточно. Кстати, когда я писал калькулятор, я случайно с первого раза выбрал неподходящее кодовое слово — «абыр валг».

Дополнительно можно почитать в википедии

planetcalc.ru

Шифр Хила. Подробный разбор / Хабр

В этой публикации я попытаюсь максимально подробно описать шифрования и дешифрование по алгоритму Хилла. Итак, без лишних слов сразу к делу.

Шифрование

Для того, чтобы зашифровать какой-либо текст по алгоритму Хилла необходимо проделать следующие шаги:

1. Создаем кодированный алфавит. Допустим мы хотим шифровать русский текст. Тогда длина алфавита будет 33 буквы. Целесообразно добавить к алфавиту еще 4 символа на выбор, я добавлю такие: “?”, “.”, “,”,” “. Это делается для того, чтобы длина алфавита была простым числом, т.е. числом, которое делится нацело только на себя и на 1. Это, конечно, не обязательно, но очень удобно, потому что для расшифровки необходимо, чтобы детерминант ключа и длина алфавита были взаимно простыми, т.е. не имели общих делителей кроме 1. Если длина алфавита – простое число, то таких ключей, для которых выполняется это условие значительно больше. Каждому символу нашего алфавита ставим в соответствие целочисленный код. Удобнее всего использовать просто номера букв. Таким образом получаем кодированный алфавит:
   

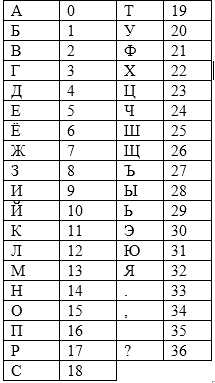
2. Теперь берем текст, который хотим зашифровать и кодируем его с помощью нашего алфавита. Возьмем для примера слово «ШИФР», его код будет таким: 25 9 21 17 .
3. Теперь выбираем ключевое слово, или просто набор букв, который будем использовать в качестве ключа. Тут важно, чтобы длина этого ключевого слова была равна квадрату целого числа, т.е. 4, 9, 16, 25 и т.д. Только тогда мы сможем сделать из него квадратную матрицу, необходимую для шифрования. Я выбрал слово «АЛЬПИНИЗМ». Кодируем его с помощью нашего алфавита. Получаем: 0 12 29 16 9 14 9 8 13. Запишем ключ в виде матрицы 3х3:

   Ключ можно задавать сразу матрицей, если вам так удобней. Я же использовал ключевое слово.

4. Теперь надо разбить текст на блоки по n символов в каждом, где n-размерность матрицы, в моем случае – 3. Начнем разбивать:

   Первый блок: (25 9 21)

   На второй блок у нас осталось всего одно число – 17. Самое простое решение в таком случае: добавить столько символов, чтобы образовать целый блок. Я решил добавить пробелы.

   Тогда второй блок: (17 35 35)

5. Теперь шифруем наш текст. Для шифрования текста требуется провести матричное умножение каждого блока на матрицу ключа. Тут стоит заметить, что блоки можно было бы записывать не в строки, а в столбцы. Тогда мы бы умножали ключ на столбец, это не существенное различие.

   Также важным фактором для данного шифра является определитель матрицы ключа: он должен быть отличным от нуля, иначе расшифровку зашифрованного текста будет невозможно осуществить.

   Итак, умножаем первый блок на ключ:

   Умножаем второй блок на ключ:

   Матричное умножение — это не сложная операция, поэтому расписывать его подробно я не стал.
   Теперь нам нужно получившиеся матрицы разделить по модулю на 37, т.е. взять остаток от деления на 37.

   Делим первую матрицу:

   Делим вторую матрицу:

   Почему делим на 37? Потому что это длина нашего алфавита, будь у вас алфавит другой длины, вы бы делили на другое число. Например, для английского алфавита делим на 26, или 29, если вы добавили какие-то символы.

6. Теперь декодируем полученные матрицы с помощью нашего алфавита.

   Первая матрица: АЮН
   Вторая матрица: ЧХЯ

   Склеиваем две матрицы и получаем зашифрованный текст: АЮНЧХЯ
   

Дешифрование

Теперь переходим к дешифрованию. Дешифрование производим по следующему алгоритму:

1. Обратно кодируем шифротекст в цифры и разбиваем на блоки.
2. Находим определитель матрицы ключа:

   Нахождение определителя тоже очень простая операция, так что я ее не расписывал.

3. Теперь по расширенному алгоритму Евклида находим d, x, y.

   Описание и сам алгоритм я расписывать не буду. Информацию об этом алгоритме легко можно найти в Интернете. На вход алгоритма подаем det K и длину нашего алфавита. На выходе мы получим d=1

   , x=-4, y=41. Нас интересует только x.

4. Теперь сложная и важная вещь. Нам надо найти обратный детерминанту элемент в кольце по модулю 37. Для этого делаем следующее:

   • Если детерминант отрицательный, а x – положительный, то обратный элемент детерминанта будет равен x.
   • Если детерминант положительный, а x – отрицательный, то обратный элемент детерминанта будет равен 37+x.
   • Если детерминант положительный, и x – положительный, то обратный детерминанту элемент будет равен x.
   • Если детерминант и x – отрицательные, то обратный элемент будет равен -x.

   Этот алгоритм поиска обратного элемента я подобрал экспериментальным путем, т.к. не мог найти ровным счетом ничего полезного по этой теме. В любом случае, даже если этот алгоритм примитивный, он работает.

   Итак, наш детерминант равен 379, он положительный, а x равен -4 – отрицательный. Тогда обратный детерминанту элемент находим по формуле 37+x=37+(-4)=37-4=33.

5. Теперь еще один момент, с которым я долго мучился, потому что никакой полезной информации в Интернете найти не удалось. Надо найти матрицу обратную матрице ключа по модулю 37. Для того чтобы найти эту матрицу нам необходимо найти матрицу алгебраических дополнений ключа и обратный детерминант матрицы ключа (уже нашли в предыдущем пункте). Матрица алгебраических дополнений ищется тоже очень просто, это я расписывать не буду. В нашем случае она выглядит так:

   Теперь эту матрицу делим по модулю на 37, это я уже расписывал в шифровании. Получаем такую матрицу, тут важно не терять знаки у элементов (некоторые выполняют деление по модулю с потерей минусов, в данном алгоритме это недопустимо):

   Умножаем матрицу алгебраических дополнений на обратный детерминанту элемент. Получаем такую матрицу:

   Делим данну матрицу по модулю на 37:

   Транспонируем ее (меняем строки и столбцы местами):

   Теперь если элемент матрицы отрицательный, меняем его на другой, вычисленный по формуле 37+<элемент>:

   Последняя полученная матрица является обратной по модулю к матрице ключа. Если перемножить матрицу ключа и эту матрицу, а потом результат разделить по модулю на 37, мы получим единичную матрицу, т.е. матрицу вида:

6. Для дешифровки шифротекста умножаем строки шифротекста на матрицу обратную ключу.
   Умножаем первую строку:

   Умножаем вторую строку:

   Делим полученные строки на 37 по модулю:

   Склеиваем матрицы (25 9 21 13 35 35) и декодируем с помощью нашего алфавита: ШИФР.

   В итоге мы получили исходный текст с двумя лишними пробелами в конце, которые никакой роли не играют.
   

Спасибо за внимание!

habr.com

Онлайн калькулятор: Шифр Хилла

Шифр Хилла — полиграммный шифр подстановки, основанный на линейной алгебре. Лестер С. Хилл изобрел этот шифр в 1929. Калькулятор ниже позволяет зашифровать и расшифровать текст методом Хилла. Подробности о шифре для интересующихся приведены под калькулятором.

Все символы, подвергающиеся шифрованию, должны входить в алфавит

никогда еще штирлиц не был так близок к провалуТекстПреобразование

Преобразованный текст

 

Сохранить share extension

Как работает шифр

Для начала символы используемого алфавита (в широком смысле этого слова, например, алфавит может включать в себя пробел и некоторые знаки пунктуации, как в калькуляторе выше) кодируются числами, то есть каждому символу алфавита сопоставляется некоторое число, например, порядковый номер. Выбирается матрица размера n x n, которая будет являться ключом шифра. Весь текст разбивается на блоки из из n букв, числовые значения которых рассматриваются как вектор размерности n. Каждый вектор умножается на матрицу шифрования n × n. Результирующий блок (вектор) размерности n — соответствующий исходному блоку зашифрованный текст. Операции сложения и умножения при этом выполняются в кольце вычетов по модулю m, где m — размерность алфавита. Очевидно, это делается для того, чтобы значения результирующего блока тоже принадлежали исходному алфавиту.

Ключ, в принципе, можно сразу задавать матрицей, но для удобства еще чаще задают кодовой фразой, числовое представление которой трансформируют в матрицу. Понятно, что для того, чтобы получить квадратную матрицу n x n, длина кодовой фразы должна являться квадратом целого числа, то есть, 4, 9, 16, 25, и т. д.

Дополнительные ограничения на ключ шифра накладывает необходимость осуществления расшифровки зашифрованного текста 🙂
Предположим, что мы зашифровали исходный вектор B матрицей шифрования А и получили вектор С — соответствующий зашифрованному тексту. Для того, чтобы восстановить исходный вектор B по вектору C (расшифровать текст), вектор С надо умножить на матрицу, обратную к матрице А.

Таким образом, чтобы операция расшифрования была возможна, матрица шифрования должна быть обратима в — кольце вычетов по модулю m.

Отсюда вытекают два условия: детерминант матрицы не должен быть равен 0, и, дополнительно, детерминант матрицы должен иметь обратный элемент в кольце вычетов по модулю m.
Второе следует из формулы
.
где операция деления на детерминант заменена на операцию умножения на обратный элемент.

Чтобы иметь обратный элемент, детерминант и модуль (длина алфавита) должны быть взаимнопростыми числами. См. Обратный элемент в кольце по модулю. Для того, чтобы повысить вероятность этого, обычно составляют алфавит, длина которого является простым числом. Поэтому русский алфавит в данном примере был расширен пробелом и символами пунктуации до 37 символов.

Не каждая матрица подойдет для шифра Хилла (и не каждое кодовое слово), но тем менее, подходящих более чем достаточно. Кстати, когда я писал калькулятор, я случайно с первого раза выбрал неподходящее кодовое слово — «абыр валг».

Дополнительно можно почитать в википедии

skokaskoka.ru

Онлайн калькулятор: Шифр Виженера

Так как Шифр Цезаря у нас уже есть, было бы логично дополнить его калькулятором, который шифрует/расшифровывает текст используя шифр Виженера.

Суть алгоритма шифрования проста. Шифр Виженера — это последовательность шифров Цезаря с различными значениями сдвига (ROTX — см. Шифр Цезаря). То есть к первой букве текста применяется преобразование, например, ROT5, ко второй, например, ROT17, и так далее. Последовательность применяемых преобразований определяется ключевой фразой, в которой каждая буква слова обозначает требуемый сдвиг, например, фраза ГДЕ ОН задает такую последовательность шифров Цезаря: ROT3-ROT4-ROT5-ROT15-ROT14, которая повторяется, пока не будет зашифрован весь текст сообщения.

Как повествует Википедия, шифр Виженера является шифром подстановки, то есть шифром, в котором каждая буква исходного текста заменяется буквой шифр-текста. Для вскрытия подобных шифров используется частотный криптоанализ.

Еще там можно прочитать про вариант шифра с бегущим ключом (running key), который был когда-то был невзламываемым. Этот вариант заключается в использовании в качестве ключа блока текста, равного по длине исходному тексту. Впрочем, и этот вариант, как оказалось, успешно поддается взлому. Проблема с бегущим ключом шифра Виженера состоит в том, что криптоаналитик имеет статистическую информацию о ключе (учитывая, что блок текста написан на известном языке) и эта информация будет отражаться в шифрованном тексте. Если ключ действительно случайный, его длина равна длине сообщения и он использовался единожды, то шифр Виженера теоретически будет невзламываемым, но такие системы уже относятся к классу систем одноразового кода, или одноразового шифр-блокнота (one-time pad). Они действительно не поддаются взлому, однако их практическое применение довольно затруднительно.

АлфавитАнглийскийИспанскийРусскийРусский (без ё)

Квадрат Виженера начинается сROT0 (“a” преобразуется в “а”)ROT1 (“а” преобразуется в “б”) Карл у Клары украл кораллыТекстПреобразование

Преобразованный текст

 

Сохранить share extension

planetcalc.ru

Шифр Хилла

шифр хиллари, шифр хилла
Шифр Хилла — полиграммный шифр подстановки, основанный на линейной алгебре и модульной арифметике Изобретён американским математиком Лестером Хиллом в 1929 году Это был первый шифр, который позволил на практике хотя и с трудом одновременно оперировать более чем с тремя символами Шифр Хилла не нашёл практического применения в криптографии из-за слабой устойчивости ко взлому и отсутствия описания алгоритмов генерации прямых и обратных матриц большого размера

Содержание

• 1 История
• 2 Описание шифра Хилла
• 3 Пример
• 4 Криптостойкость
• 5 Механическая реализация
• 6 Примечания
• 7 Литература

Историяправить

Впервые шифр Хилла был описан в статье «Cryptography in an Algebraic Alphabet»1, опубликованной в журнале «The American Mathematical Monthly» в июне-июле 1929 года В августе того же года Хилл расширил тему и выступил с речью о криптографии перед Американским математическим обществом в Боулдере, штат Колорадо2 Позднее его лекция привела ко второй статье «Concerning Certain Linear Transformation Apparatus of Cryptography»3, которая была опубликована в журнале «The American Mathematical Monthly» в марте 1931 года Дэвид Кан в своем труде «Взломщики кодов» так описал шифр Хилла и его место в истории криптографии4:

Хилл был одним из тех, кто разработал общий и мощный метод К тому же шифр Хилла впервые перевёл криптографию с использованием полиграмм в разряд практических дисциплин

Оригинальный текст англ   But Hill alone devised a method of power and generality In addition, his procedure made polygraphic cryptography practical for the first time

Описание шифра Хиллаправить

Шифр Хилла является полиграммным шифром, который может использовать большие блоки с помощью линейной алгебры Каждой букве алфавита сопоставляется число по модулю 26 Для латинского алфавита часто используется простейшая схема: A = 0, B = 1, …, Z = 25, но это не является существенным свойством шифра Блок из n букв рассматривается как n-мерный вектор и умножается по модулю 26 на матрицу размера n × n Если в качестве основания модуля используется число больше чем 26, то можно использовать другую числовую схему для сопоставления буквам чисел и добавить пробелы и знаки пунктуации5 Элементы матрицы являются ключом Матрица должна быть обратима в Z 26 n _^ , чтобы была возможна операция расшифрования67

Для n = 3 система может быть описана так:

c_=k_p_+k_p_+k_p_,\\c_=k_p_+k_p_+k_p_,\\c_=k_p_+k_p_+k_p_,\\\end

или в матричной форме:

c 1 c 2 c 3 = k 11 k 12 k 13 k 21 k 22 k 23 k 31 k 32 k 33 p 1 p 2 p 3 mod 26 , c_\\c_\\c_\end=k_&k_&k_\\k_&k_&k_\\k_&k_&k_\endp_\\p_\\p_\end,

или

C = K P mod 26 , ,

где P и C  — векторы-столбцы высоты 3, представляющие открытый и зашифрованный текст соответственно, K  — матрица 3 × 3, представляющая ключ шифрования Операции выполняются по модулю 26

Для того, чтобы расшифровать сообщение, требуется получить обратную матрицу ключа K − 1 Существуют стандартные методы вычисления обратных матриц см способы нахождения обратной матрицы, но не все матрицы имеют обратную см обратная матрица Матрица будет иметь обратную в том и только в том случае, когда её детерминант не равен нулю и не имеет общих делителей с основанием модуля8 Если детерминант матрицы равен нулю или имеет общие делители с основанием модуля, то такая матрица не может использоваться в шифре Хилла, и должна быть выбрана другая матрица в противном случае шифротекст будет невозможно расшифровать Тем не менее, матрицы, которые удовлетворяют вышеприведенным условиям, существуют в изобилии6

В общем случае, алгоритм шифрования может быть выражен в следующем виде69:

Шифрование: C = E K , P = K P mod 26

Расшифрование: P = D K , C = K − 1 C mod 26 = K − 1 K P mod 26 = P C=K^KP=P

Примерправить

В следующем примере7 используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25

Шифрование

Рассмотрим сообщение «ACT» и представленный ниже ключ GYBNQKURP в буквенном виде:

K = 6 24 1 13 16 10 20 17 15 6&24&1\\13&16&10\\20&17&15\end

Данная матрица обратима, так как её детерминант не равен нулю и не имеет общих делителей с основанием модуля Опасность того, что детерминант матрицы ключа будет иметь общие делители с основанием модуля, может быть устранена путём выбора простого числа в качестве основания модуля Например, в более удобном варианте шифра Хилла в алфавит добавляют 3 дополнительных символа пробел, точка и знак вопроса, чтобы увеличить основание модуля до 295

Так как букве «A» соответствует число 0, «C» — 2, «T» — 19, то сообщение — это вектор

P 1 = 0 2 19 =0\\2\\19\end

Тогда зашифрованный вектор будет

C 1 = K P 1 mod 26 = 6 24 1 13 16 10 20 17 15 0 2 19 mod 26 = 15 14 7 =KP_=6&24&1\\13&16&10\\20&17&15\end0\\2\\19\end=15\\14\\7\end

Вектор соответствует зашифрованному тексту «POH» Теперь предположим, что наше сообщение было «CAT»:

P 2 = 2 0 19 =2\\0\\19\end

Теперь зашифрованный вектор будет

C 2 = K P 2 mod 26 = 6 24 1 13 16 10 20 17 15 2 0 19 mod 26 = 5 8 13 =KP_=6&24&1\\13&16&10\\20&17&15\end2\\0\\19\end=5\\8\\13\end

Этот вектор соответствует зашифрованному тексту «FIN» Видно, что каждая буква шифротекста сменилась Шифр Хилла достиг диффузииen по Шеннону, и n-размерный шифр Хилла может достигать диффузии n символов за раз

Расшифрование

Обратная матрица ключа:

K − 1 mod 26 = 8 5 10 21 8 21 21 12 8 =8&5&10\\21&8&21\\21&12&8\end

Возьмём зашифрованный текст из предыдущего примера «POH»:

P 1 = K − 1 C 1 mod 26 = 8 5 10 21 8 21 21 12 8 15 14 7 mod 26 = 0 2 19 =K^C_=8&5&10\\21&8&21\\21&12&8\end15\\14\\7\end=0\\2\\19\end

Этот вектор соответствует сообщению «ACT»

Криптостойкостьправить

Стандартный шифр Хилла уязвим к атаке по выбранному открытому тексту, потому что в нём используются линейные операции Криптоаналитик, который перехватит n 2 пар символ сообщения/символ шифротекста сможет составить систему линейных уравнений, которую обычно несложно решить Если окажется, что система не решаема, то необходимо всего лишь добавить ещё несколько пар символ сообщения/символ шифротекста Такого рода расчёты средствами обычных алгоритмов линейной алгебры требует совсем немного времени В связи с этим для увеличения криптостойкости в него должны быть добавлены какие-либо нелинейные операции Комбинирование линейных операций, как в шифре Хилла, и нелинейных шагов привело к созданию подстановочно-перестановочной сети например, сеть Фейстеля Поэтому с определённой точки зрения можно рассматривать современные блочные шифры как вид полиграммных шифров78

Длина ключаправить

Длина ключа — это двоичный логарифм от количества всех возможных ключей Существует 26 n 2 матриц размера n × n Значит, log 2 ⁡ 26 n 2 ≈ 4 , 7 n 2 26^\approx 47n^  — верхняя грань длины ключа для шифра Хилла, использующего матрицы n × n Это только верхняя грань, поскольку не каждая матрица обратима, а только такие матрицы могут быть ключом Количество обратимых матриц может быть рассчитано при помощи Китайской теоремы об остатках Матрица обратима по модулю 26 тогда и только тогда, когда она обратима и по модулю 2 и по модулю 138

Количество обратимых по модулю 2 и 13 матриц размера n × n равно порядку линейной группы GLn, Z2 и GLn, Z13 соответственно:

| K 1 | = 2 n 2 1 − 1 / 2 1 − 1 / 2 2 … 1 − 1 / 2 n , |=2^1-1/21-1/2^\dots 1-1/2^, | K 2 | = 13 n 2 1 − 1 / 13 1 − 1 / 13 2 … 1 − 1 / 13 n |=13^1-1/131-1/13^\dots 1-1/13^

Количество обратимых по модулю 26 матриц равно произведению этих чисел:

| K | = 26 n 2 1 − 1 / 2 1 − 1 / 2 2 … 1 − 1 / 2 n 1 − 1 / 13 1 − 1 / 13 2 … 1 − 1 / 13 n 1-1/21-1/2^\dots 1-1/2^1-1/131-1/13^\dots 1-1/13^

Кроме того, будет разумно избегать слишком большого количества нулей в матрице-ключе, так как они уменьшают диффузию В итоге получается, что эффективное пространство ключей стандартного шифра Хилла составляет около 4 , 64 n 2 − 1 , 7 64n^-17 Для шифра Хилла 5 × 5 это составит приблизительно 114 бит Очевидно, полный перебор — не самая эффективная атака на шифр Хилла7

Механическая реализацияправить

Шифровальная машина Хилла

При работе с двумя символами за раз шифр Хилла не предоставляет никаких конкретных преимуществ перед шифром Плэйфера и даже уступает ему по криптостойкости и простоте вычислений на бумаге По мере увеличения размерности ключа шифр быстро становится недоступным для расчётов на бумаге человеком Шифр Хилла размерности 6 был реализован механически Хилл с партнёром получили патент на устройство US Patent 1 845 947, которое выполняло умножение матрицы 6 × 6 по модулю 26 при помощи системы шестерёнок и цепей Расположение шестерёнок а значит, и ключ нельзя было изменять для конкретного устройства, поэтому в целях безопасности рекомендовалось тройное шифрование Такая комбинация была очень сильной для 1929 года, и она показывает, что Хилл несомненно понимал концепции конфузии и диффузии Однако устройство было довольно медленное, поэтому во Второй мировой войне машины Хилла были использованы только для шифрования трёхсимвольного кода радиосигналов10

Примечанияправить

1. ↑ Lester S Hill Cryptography in an Algebraic Alphabet англ : Article — 1929 — С 7
2. ↑ Chris Christensen Lester Hill Revisited англ // Taylor & Francis Group, LLC : Article — 2014 — С 297 — ISSN 0161-1194
3. ↑ Lester S Hill Concerning Certain Linear Transformation Apparatus of Cryptography англ // The American Mathematical Monthly — 1931 — Март — С 135-154
4. ↑ David Kahn The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet — Simon and Schuster — New York: Scribner, 1996 — С 405 — 723 с — ISBN 0-684-83130-9
5. ↑ 1 2 Murray Eisenberg Hill Ciphers: A Linear Algebra Project with Mathematica англ
6. ↑ 1 2 3 William Stallings Cryptography and Network Security: Principles and Practice — 5 — Pearson Education, 2011 — С 46—49 — ISBN 978-0-13-609704-4
7. ↑ 1 2 3 4 A V N Krishna, Dr A Vinaya Babu A Modified Hill Cipher Algorithm for Encryption of Data In Data Transmission англ // Computer Science and Telecommunications : Georgian Electronic Scientific Journal — 2007 — № 314 — С 78—83 — ISSN 1512-1232
8. ↑ 1 2 3 А П Алферов, А Ю Зубов, А С Кузьмин, А В Черёмушкин Основы криптографии — 2-е изд — Гелиос АРВ, 2002 — С 115-119 — 480 с — ISBN 5-85438-137-0
9. ↑ Dorothy Elizabeth Robling Denning Cryptography and Data Security — London: Addison-Wesley Publishing Company, 1982 — С 88-89 — 400 с — ISBN 0-201-10150-5
10. ↑ Friedrich L Bauer Decrypted Secrets: Methods and Maxims of Cryptology — Springer, 2002 — С 85 — 474 с — ISBN 978-3-662-04738-5

Литератураправить

• William Stallings Cryptography and Network Security: Principles and Practice — Pearson, 2011 — P 46-49 — 711 p — ISBN 978-0-13-609704-4
• David Kahn The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet — Simon and Schuster, 1996 — P 405 — 723 p — ISBN 978-0-13-609704-4
• Jeffrey Overbey, William Traves, Jerzy Wojdylo On the Keyspace of the Hill Cipher — 2005 — Т 29 — P 59–72 — DOI:101080/0161-110591893771
• Wade Trappe, Lawrence C Washington Introduction to Cryptography: With Coding Theory — Pearson Prentice Hall, 2006 — P 34-38 — 577 p — ISBN 0-13-198199-5
• Craig P Bauer Secret History: The Story of Cryptology — CRC Press, 2013 — P 227-228 — 575 p — ISBN 978-1-4665-6187-8

шифр хилла, шифр хиллак, шифр хиллари

---

Шифр Хилла Информацию О

---

---

Шифр Хилла Комментарии

Шифр Хилла
Шифр Хилла
Шифр Хилла Вы просматриваете субъект

Шифр Хилла что, Шифр Хилла кто, Шифр Хилла описание

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com

Нововведения: шифр Хилла – КОДИРОВАНИЕ И КРИПТОГРАФИЯ – МИР МАТЕМАТИКИ – Каталог файлов

Шифры, обсуждавшиеся прежде, в которых один символ заменялся другим по некоторому заранее установленному правилу, как мы уже видели, всегда уязвимы для криптоанализа.

В 1929 г. американский математик Лестер Хилл придумал, запатентовал и выставил на продажу — правда, без особого успеха — новую систему шифрования, в которой использовались и модульная арифметика, и линейная алгебра.

Как мы увидим ниже, матрицы являются очень полезным инструментом для шифрования сообщений, когда текст разбивается на пары букв и каждой букве ставится в соответствие числовое значение.

Чтобы зашифровать сообщение, мы будем использовать следующие матрицы:

с определителем, равным единице, то есть ad — Ьс = 1. Для расшифровки мы будем использовать обратную матрицу:

* * *

НЕМНОГО ЛИНЕЙНОЙ АЛГЕБРЫ

Матрица может быть определена как таблица, представляющая собой совокупность строк и столбцов. Например, матрица 2×2 имеет вид:

а матрица 2×1 записывается как:

Произведение этих двух матриц дает нам новую матрицу 2×1, называемую вектор-столбцом:

В случае матрицы 2×2 число (аd — Ьс) называется определителем матрицы.

* * *

Ограничение на значение определителя установлено для того, чтобы обратная матрица работала как инструмент расшифровки. Как правило, для алфавита из n символов необходимо, чтобы НОД определителя матрицы и числа n равнялся единице. Иначе нельзя гарантировать существование обратного элемента в модульной арифметике.

Продолжая пример, возьмем алфавит из 26 букв с символом пробела, который мы обозначим как @. Каждой букве мы поставим в соответствие число, как показано в следующей таблице:

Для получения значений от 0 до 26 мы будем работать по модулю 27.

Процесс шифрования и расшифровки текста происходит следующим образом: сначала мы определяем шифровальную матрицу с определителем 1.

Например,

Матрицей для расшифровки будет обратная матрица

Таким образом, А будет ключом шифра, А^-1 — ключом для расшифровки.

Например, зашифруем сообщение BOY («мальчик»). Буквы сообщения группируются в пары: ВО У@. Их численными эквивалентами, согласно таблице, являются пары чисел (1, 14) и (24, 26). Умножим матрицу А на каждую пару чисел.

Зашифрованное

что, согласно таблице, соответствует буквам (Q, Т).

Зашифрованное

что соответствует буквам (V, О).

Сообщение BOY будет зашифровано как QTVO.

Обратная операция расшифровки выполняется при помощи матрицы:

Возьмем пару букв (Q, Т) и найдем их числовые эквиваленты из таблицы: (16, 19). Затем умножим их на A^-1 и получим:

то же со второй парой (V, О) и ее численными значениями (21, 14) и получаем:

Таким образом, мы доказали, что расшифровка работает.

В этом примере мы рассматривали пары символов. Для большей безопасности можно группировать буквы по три или даже по четыре. Тогда расчеты будут проводиться с матрицами порядка 3 х 3 и 4 х 4 соответственно, что было бы чрезвычайно трудоемким процессом для вычислений вручную. Современные компьютеры позволяют работать с огромными матрицами и с обратными к ним.

У шифра Хилла есть существенный недостаток: имея даже небольшой фрагмент исходного текста, можно расшифровать все сообщение. Поиск идеального шифра был еще далек от завершения.

xn—-7sbbao2ali0aghq2c8b.xn--p1ai