Сила гравитационная формула – Гравитационная сила формула. Ссылки и примечания. Весомость как фундаментальное понятие механики - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

понятие и особенности применения формулы для их расчета

Гравитационные силы являются одним из четырех основных видов сил, которые проявляются во всем своем многообразии между различными телами как на Земле, так и за ее пределами. Кроме них еще выделяют электромагнитные, слабые и ядерные (сильные). Вероятно, именно их существование человечество осознало в первую очередь. О силе притяжения со стороны Земли было известно еще с самых древних времен. Однако прошли целые столетия, прежде чем человек догадался, что взаимодействие подобного рода происходит не только между Землей и любым телом, но и между разными объектами. Первым, кто понял, как работают гравитационные силы, был английский физик И. Ньютон. Именно он и вывел всем известный сейчас закон всемирного тяготения.

Формула гравитационной силы

Ньютон решил проанализировать законы, по которым происходит движение планет в системе. В результате он пришел к выводу, что вращение небесных тел вокруг Солнца возможно лишь в том случае, если между ним и самими планетами действуют гравитационные силы. Понимая, что небесные тела от других предметов отличаются всего лишь своими размерами и массой, ученый вывел следующую формулу:

F = f x (m₁x m₂) / r², где:

m₁, m₂ – это массы двух тел;
r – расстояние между ними по прямой;
f – гравитационная постоянная, значение которой равно 6,668 х 10^-8 см³/г х сек².

Таким образом, можно утверждать, что любые два объекта притягиваются друг к другу. Работа гравитационной силы по своей величине прямо пропорциональна массам данных тел и обратно пропорциональна расстоянию между ними, возведенному в квадрат.

Особенности применения формулы

На первый взгляд, кажется, что пользоваться математическим описанием закона притяжения довольно просто. Однако если поразмыслить, данная формула имеет смысл лишь для двух масс, размеры которых по сравнению с расстоянием между ними ничтожно малы. Причем настолько, что их можно принять за две точки. А как же тогда быть, когда расстояние сопоставимо с размерами тел, а сами они имеют неправильную форму? Разделить их на части, определить гравитационные силы между ними и вычислить равнодействующую? Если так, то сколько точек нужно брать для расчета? Как видите, не все так просто. А если учесть (с точки зрения математики), что точка размеров не имеет, то такое положение и вовсе кажется безвыходным. К счастью, ученые придумали способ, как производить расчеты в таком случае. Они используют аппарат интегрального и дифференциального исчислений. Суть метода в том, что объект разбивается на бесконечное число малых кубиков, массы которых сосредоточены в их центрах. Затем составляется формула для нахождения равнодействующей силы и применяется предельный переход, посредством которого объем каждого составляющего элемента сводится к точке (нулю), а количество таких элементов устремляется в бесконечность. Благодаря данному приему удалось получить некоторые важные выводы.

Если тело представляет собой шар (сферу), плотность которого однородна, то оно притягивает к себе любой другой объект так, словно вся его масса сосредоточена в его центре. Поэтому с некоторой погрешностью можно применять этот вывод и для планет.
Когда для плотности предмета характерна центральная сферическая симметрия, он взаимодействует с другими объектами так, как будто в точке симметрии находится вся его масса. Таким образом, если взять пустотелый шар (например, футбольный мяч) или несколько вложенных друг в друга шаров (как куклы-матрешки), то они будут притягивать другие тела подобно тому, как это делала бы материальная точка, имеющая их общую массу и расположенная в центре.

fb.ru

определение, формула, роль в природе и космосе

Абсолютно все тела, которые обладают конечной массой, взаимодействуют друг с другом благодаря так называемой силе притяжения или гравитации. Дадим в статье определение силы тяжести, а также рассмотрим, какую роль она играет в природе и космосе.

Что такое сила тяжести или гравитациия?

В физике определение силы тяжести или гравитации дают следующее: это сила, с которой два тела, имеющие массу, притягиваются друг к другу. Это означает, что каждый человек притягивается к любому предмету, который встречает в своей жизни. Однако эта сила является настолько маленькой, что она не ощущается.

Проявление гравитации заметно, когда среди взаимодействующих тел имеется объект с огромной массой, например, наша планета. Во многих задачах по физике определение силы тяжести сводят до понятия притяжения объектов к Земле. В последнем случае говорят о весе тела, который вычисляют по формуле P = m*g. Здесь m и g – масса тела и ускорение свободного падения, которое приблизительно равно 9,81 м/с².

Сэр Исаак Ньютон и всемирное тяготение

Впервые исчерпывающее определение силы тяжести дал в конце XVII века великий английский ученый Исаак Ньютон. Он смог объединить существовавшие на то время разрозненные знания и эмпирические наблюдения (понятие Галилея об инерции тел и законы Кеплера) и оформить их в виде стройной теории, получившей название «Небесная механика».

Согласно Ньютону, все тела притягиваются друг к другу с силой, которая записывается следующей формулой

F = G*m₁*m₂/R², где
m₁и m₂– массы тел,
R – расстояние между ними,
G=6,674*10^-11 Н*м²/кг² – универсальная гравитационная постоянная.

Сила тяжести (гравитации) F действует на абсолютно любых расстояниях, направлена к центру масс тел и быстро убывает с увеличением дистанции между ними.

Если в отмеченную формулу подставить значение для массы и радиуса Земли, то можно получить названное выше ускорение g.

Эффекты, обусловленные существованием гравитации

Выше было дано определение силы тяжести, но не было сказано, какую роль она играет в нашей жизни. Во-первых, благодаря ее существованию мы не парим в воздухе, а твердо стоим на поверхности, и сам воздух не улетает в космическое пространство. Во-вторых, любое подброшенное тело падает обратно на землю. В-третьих, при расчете траекторий полета свободных тел учет влияния этой силы является принципиальным. Наконец, сила всемирного тяготения является главным фактором, который определяет особенности движения нашей планеты вокруг Солнца, и вообще движение любых космических тел.

В настоящее время ученые всего мира пытаются объединить гравитацию с другими фундаментальными взаимодействиями, чтобы создать единую физическую теорию нашей Вселенной.

fb.ru

понятие и особенности применения формулы для их расчета

Образование 9 ноября 2013

Формула гравитационной силы

F = f x (m₁x m₂) / r², где:

m₁, m₂ – это массы двух тел;
r – расстояние между ними по прямой;
f – гравитационная постоянная, значение которой равно 6,668 х 10^-8 см³/г х сек².

Особенности применения формулы

А если учесть (с точки зрения математики), что точка размеров не имеет, то такое положение и вовсе кажется безвыходным. К счастью, ученые придумали способ, как производить расчеты в таком случае. Они используют аппарат интегрального и дифференциального исчислений. Суть метода в том, что объект разбивается на бесконечное число малых кубиков, массы которых сосредоточены в их центрах. Затем составляется формула для нахождения равнодействующей силы и применяется предельный переход, посредством которого объем каждого составляющего элемента сводится к точке (нулю), а количество таких элементов устремляется в бесконечность. Благодаря данному приему удалось получить некоторые важные выводы.

Если тело представляет собой шар (сферу), плотность которого однородна, то оно притягивает к себе любой другой объект так, словно вся его масса сосредоточена в его центре. Поэтому с некоторой погрешностью можно применять этот вывод и для планет.
Когда для плотности предмета характерна центральная сферическая симметрия, он взаимодействует с другими объектами так, как будто в точке симметрии находится вся его масса. Таким образом, если взять пустотелый шар (например, футбольный мяч) или несколько вложенных друг в друга шаров (как куклы-матрешки), то они будут притягивать другие тела подобно тому, как это делала бы материальная точка, имеющая их общую массу и расположенная в центре.

Источник: fb.ru

Гравитационные силы. Закон всемирного тяготения. Вес тела

В природе существуют различные силы, которые характеризуют взаимодействие тел. Рассмотрим те силы, которые встречаются в механике.

Гравитационные силы. Вероятно, самой первой силой, существование которой осознал человек, являлась сила притяжения, действующая на тела со стороны Земли.

И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. Первым этот факт понял английский физик Ньютон. Анализируя законы, которым подчиняется движение планет (законы Кеплера), он пришёл к выводу, что наблюдаемые законы движения планет могут выполняться только в том случае, если между ними действует сила притяжения, прямо пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними.

Ньютон сформулировал закон всемирного тяготения. Любые два тела притягиваются друг к другу. Сила притяжения между точечными телами направлена по прямой, их соединяющей, прямо пропорциональна массам обоих и обратно пропорциональна квадрату расстояния между ними:

Под точечными телами в данном случае понимают тела, размеры которых во много раз меньше расстояния между ними.

Силы всемирного тяготения называют гравитационными силами. Коэффициент пропорциональности G называют гравитационной постоянной. Его значение было определено экспериментально: G = 6,7 • 10¯¹¹ Н•м² / кг².

Сила тяготения действующая вблизи поверхности Земли, направлена к её центру и вычисляется по формуле:

F = m • g,

где g – ускорение свободного падения (g = 9,8 м/с²).

Роль силы тяготения в живой природе очень значительна, так как от её величины во многом зависят размеры, формы и пропорции живых существ.

Вес тела. Рассмотрим, что происходит, когда некоторый груз кладут на горизонтальную плоскость (опору). В первый момент после того, как груз опустили, он начинает двигаться вниз под действием силы тяжести (рис. 8).

Плоскость прогибается и возникает сила упругости (реакция опоры), направленная вверх. После того как сила упругости (Fу) уравновесит силу тяжести, опускание тела и прогиб опоры прекратятся.

Прогиб опоры возник под действием тела, следовательно, со стороны тела на опору действует некоторая сила (Р), которую называют весом тела (рис. 8, б). По третьему закону Ньютона вес тела равен по величине силе реакции опоры и направлен в противоположную сторону.

Р = – Fу = Fтяж.

Весом тела называют силу Р, с которой тело действует на неподвижную относительно него горизонтальную опору.

Поскольку сила тяжести (вес) приложены к опоре, она деформируется и за счёт упругости оказывает противодействие силе тяжести. Силы, развиваемые при этом со стороны опоры называются силами реакции опоры, а само явление развития противодействия – реакцией опоры. По третьему закону Ньютона сила реакции опоры равна по величине силе тяжести тела и противоположна ему по направлению.

Если человек на опоре движется с ускорением звеньев его тела, направленных от опоры, то сила реакции опоры возрастает на величину ma, где m – масса человека, а – ускорения с которыми движутся звенья его тела. Эти динамические воздействия можно фиксировать с помощью тензометрических устройств (динамограммы).

Вес не следует путать с массой тела. Масса тела характеризует его инертные свойства и не зависит ни от силы тяготения, ни от ускорения, с которым оно движется.

Вес тела характеризует силу, с которой оно действует на опору и зависит как от силы тяготения, так и от ускорения движения.

Например, на Луне вес тела примерно в 6 раз меньше, чем вес тела на Земле, Масса же в обоих случаях одинакова и определяется количеством вещества в теле.

В быту, технике, спорте вес часто указывают не в ньютонах (Н), а в килограммах силы (кгс). Переход от одной единицы к другой осуществляется по формуле: 1 кгс = 9,8 Н.

Когда опора и тело неподвижны, то масса тела равна силе тяжести этого тела. Когда же опора и тело движутся с некоторым ускорением, то в зависимости от его направления тело может испытывать или невесомость или перегрузку. Когда ускорение совпадает по направлению и равно ускорению свободного падения, вес тела будет равен нулю, поэтому возникает состояние невесомости (МКС, скоростной лифт при опускании вниз). Когда же ускорение движения опоры противоположно ускорению свободного падения, человек испытывает перегрузку (старт с поверхности Земли пилотируемого космического корабля, Скоростной лифт, поднимающийся вверх).

opace.ru

понятие и особенности применения формулы для их расчета

Особенности применения формулы

Если тело представляет собой шар (сферу), плотность которого однородна, то оно притягивает к себе любой другой объект так, словно вся его масса сосредоточена в его центре. Поэтому с некоторой погрешностью можно применять этот вывод и для планет.
Когда для плотности предмета характерна центральная сферическая симметрия, он взаимодействует с другими объектами так, как будто в точке симметрии находится вся его масса. Таким образом, если взять пустотелый шар (например, футбольный мяч) или несколько вложенных друг в друга шаров (как куклы-матрешки), то они будут притягивать другие тела подобно тому, как это делала бы материальная точка, имеющая их общую массу и расположенная в центре.

autogear.ru

Гравитационные силы

Как указывалось, гравитационные силы (или силы тяготения) в громадном большинстве случаев целиком определяют свободное движение космического аппарата. Гравитационные силы определяются законом всемирного тяготения:всякое точечное материальное тело притягивает каждое другое точечное материальное тело с силой, пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними. Честь открытия закона всемирного тяготения принадлежит знаменитому английскому ученому – математику, физику и астроному Исааку Ньютону (1643 – 1727).

Говорят, что открытие Ньютоном великого закона объясняется случайностью. Якобы произошло это примерно так: молодой 23-летний ученый, погруженный в глубокое раздумье, сидел в саду и, наблюдая падение с дерева яблок, пришел к мысли, что тяготение есть мировая сила. Так ли это было на самом деле – трудно сказать. Однако можно наверняка утверждать, что о силе тяжести люди знали и до Ньютона. Вполне возможно, что изучение сил тяготения началось еще с того знаменательного времени, когда Ева вкусила яблоко в райском саду.

В своей количественной интерпретации закон всемирного тяготения записывается чрезвычайно просто:

(1)

гдеF – сила, с которой притягиваются две материальные точки, имеющие массыm₁,m₂ соответственно,r – расстояние между точками,f – гравитационная постоянная, равная 6,668 х 10^-8 см³/гхсек². Гравитационная постоянная численно равна величине силы, с которой притягиваются две материальные точки, имеющие массу 1 г каждая и расположенные на расстоянии 1 см.

Пользуясь этой формулой, вычислить силу притяжения двух тел конечных размеров, казалось бы, очень просто. Для этого достаточно каждое тело разделить на отдельные точки, затем найти силы притяжения каждой точкой одного тела и каждой точкой другого тела и после этого определить равнодействующую всех элементарных сил. Такой путь очевиден, но не так-то прост. Действительно, формула (1) в своем непосредственном представлении имеет смысл только для масс, сосредоточенных в точке. Но точка, по математическому определению, не имеет размеров. Значит, как бы мы ни делили данное тело на сколь угодно малые части, все равно не удастся получить точку, и поэтому мы не вправе применять для вычисления-силы притяжения такую простую формулу. Однако математики нашли выход из такого, на первый взгляд, безвыходного положения. Для того чтобы вычислить силу притяжения, они вначале разделяют все тело на отдельные элементарные части, например, кубики, и считают условно, что масса каждого из кубиков сосредоточена в его центре и из этого условия применяют формулу (1) для нахождения сил притяжения. После этого, написав формулу для равнодействующей всех элементарных сил, они пользуются предельным переходом, сводя объем каждого кубика к нулю (к точке), а число таких кубиков соответственно увеличивают безгранично (математики говорят – устремляют в бесконечность). В результате равнодействующая получается как сумма бесконечно малых сил, число которых бесконечно.

Отвлекаясь от рассматриваемой задачи, следует сказать, что описанный прием, состоящий в том, что какой-либо объем или протекающий процесс разбивается на бесконечно малые составляющие, которые в последующем суммируются, составляет существо большого раздела математики, называемого дифференциальным и интегральным исчислением. В настоящее время невозможно найти область науки и техники, где бы не применялся математический аппарат дифференциального и интегрального исчислений, и поэтому знание его и умение оперировать им так же уверенно, как мы оперируем сложением и вычитанием, умножением и делением, возведением в степень и извлечением корня, является неотъемлемой частью знаний всякого специалиста. Этот математический аппарат позволил существенным образом упростить и облегчить процесс вычисления сил притяжения и получить ряд практически важных выводов. Вот некоторые из них, которые широко используются в небесной механике и космической баллистике:

1. Сферическое тело (шар), плотность которого является постоянной по всему объему, притягивает всякое другое расположенное вне его тело так, как если бы вся его масса была сосредоточена в центре сферы. Это, в частности, означает, что для вычисления силы притяжения двух шариков уже нет необходимости разделять их на элементарные объемы, как это было описано выше, а можно просто воспользоваться формулой (1), в которойm₁,m₂ есть массы этих шариков, аr – расстояние между их центрами. Далее, если принять, что наша Земля есть шар (хотя в действительности это не совсем так), то для вычисления силы притяжения ею всякого другого тела можно положить (без всяких допущений!), что вся ее масса сосредоточена в центре. В этом случае баллистики говорят, что гравитационное поле являетсяцентральным, т. е. сила притяжения всегда направлена к центру Земли.

2. Если плотность тела имеет центральную сферическую симметрию, то оно (тело) притягивает всякое иное тело так, как будто вся масса его сосредоточена в точке симметрии. Отсюда следует, что пустотелый шар (наподобие детского мяча) или вложенные друг в друга различные шары (как куклы-матрешки) с совпадающими центрами притягивают другие внешние тела, как материальная точка, имеющая массу шара (или шаров), расположенная в центре его.

Необходимо отметить одно любопытное следствие, вытекающее из свойств притяжения пустотелого шара. Оказывается, что если какое-либо тело поместить внутрь шара – в центр или на внутреннюю оболочку или же где-то в промежуточном положении, то сумма всех сил притяжения, действующих на него со стороны оболочки, всегда будет равна нулю. Иными словами, это тело будет находиться в состоянии невесомости и, если вы окажетесь рядом с ним, вы уподобитесь космонавту, только для этого уже не надо лететь с космическими скоростями. Если вы оттолкнетесь от оболочки, то совершенно свободно долетите до ее противоположной стороны точно с такой же скоростью, с какой вы оттолкнулись.

И еще одно замечание. При опускании в глубь Земли (например, в шахту) ваш вес будет уменьшаться. Действительно, если вы опуститесь на некоторую глубину внутрь Земли, то тот шаровой слой Земли, который расположен выше вас, не будет, участвовать в создании веса, а вес образуется лишь той частью Земли, которая расположена ниже вас. Но это ведь уже только часть Земли и, значит, ее притяжение, т. е. ваш вес, станет меньше. Если представить, что вы достигли центра Земли, то здесь вы уже окажетесь в состоянии невесомости.

Значит, если у вас возникает желание ощутить невесомость, то для этой цели не обязательно лететь в космос. Попробуйте “всего-навсего” забраться в центр нашей Земли. Расчеты показывают, что при опускании в шахту на каждые 100 м вы будете “терять в весе” около 4 г.

Незнание законов притяжения или их неправильное истолкование может привести к курьезам. Вы, конечно, читали очень занимательную научно-фантастическую повесть В. А. Обручева “Плутония”. В ней описывается, что некая экспедиция где-то в акватории Северного Ледовитого океана случайно обнаружила вход во внутреннюю часть Земли. Оказалось, что Земля внутри пуста и представляет собой нечто вроде футбольного мяча. Внутри Земли экспедиция обнаружила доисторический мир, первобытную природу, животных и даже людей. Там тоже были реки, озера, моря, горы, пустыни – словом, все, что есть на наружной поверхности Земли. Только жизнь протекала с некоторым сдвигом назад во времени.

Прочитав только что написанное о свойствах притяжения шарового слоя, вы сразу же воскликнете: как же там могли ходить люди, животные, течь реки, если все они находились в состоянии невесомости? Попытаясь шагнуть, оттолкнувшись от Земли, человек неминуемо должен взлететь, после чего, уподобляясь птице, начнет свободно плавать внутри Земли!

Мало того, в этой же книге пишется, что внутри Земли было тоже какое-то светило, подобное Солнцу, которое плавало где-то в районе центра Земли (кстати, что его удерживало там?). Это светило притягивало к себе и оболочку Земли, и все-все предметы, расположенные на ее внутренней поверхности. И так как все предметы, лежащие на этой поверхности, люди, звери, вода не были как-то прикреплены к Земле, то они под влиянием сил притяжения внутреннего “солнца” должны были обязательно полететь к центру Земли. Вот вам и путешествие! Правда, если закрыть глаза на это досадное недоразумение, то книга читается с несомненным интересом. И мы ни в коей мере не упрекаем уважаемого Владимира Афанасьевича в незнании законов тяготения.

Сделаем одну оговорку. Все происходило бы именно так, как описано в книге, но только в том случае, если бы Земля не вращалась. За счет вращения Земли и с нею всех предметов возникают центробежные силы, стремящиеся разорвать Землю на части, оторвать от нее все предметы и выбросить их в космос. Значит люди, находящиеся внутри Земли, центробежной силой прижимаются к ее поверхности.

Центробежная сила действует в направлении, перпендикулярном оси вращения Земли. Если человек находится на экваторе (рис. 2, положение а), то эта сила будет действовать в точности через голову к ногам и он будет ощущать ее как увеличение веса. Когда же юн займет другое положение (б), то указанная сила будет стремиться свалить человека набок и “утащить” к экватору. Наконец, при нахождении в полюсах (положение в) центробежная сила будет отсутствовать и здесь будет наблюдаться состояние невесомости. За счет этих сил реки должны потечь от полюсов к экватору и в районе экватора широкой лентой образуется океан, опоясывающий всю внутреннюю часть Земли.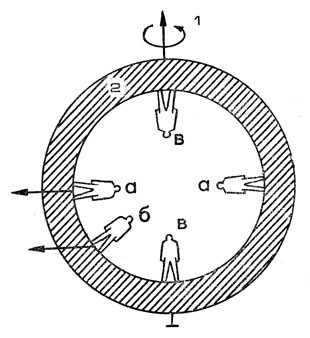

Рис. 2. Схема действия центробежных сил на человека, стоящего внутри Земли: 1 – ось вращения Земли; 2 – поперечный разрез Земли

Эти же эффекты должны наблюдаться при рассмотрении течения рек и на внешней поверхности Земли. Однако нам известно, что реки на Земле текут во все стороны света – и в направлении к северу, и к югу, и на запад, и на восток. Выходит, что центробежная сила не влияет? Но ведь она существует! Тогда в чем дело? Ответить на этот вопрос не просто и поэтому его рассмотрим несколько позже.

Возвращаясь же к экспедиции из “Плутонии”, укажем лишь, что она вошла во внутреннюю часть Земли в районе Северного полюса, т. е. в том районе, где центробежные силы чрезвычайно малы. Поэтому отважные путешественники едва ли могли бы сделать и один шаг, как оторвались от Земли. В этом состоит одно из недоразумений “Плутонии”.

Но вернемся из недр Земли в космос. В практических расчетах полетов космических аппаратов баллистикам часто бывает значительно удобнее оперировать не с величинами сил притяжения, а с ускорениями, создаваемыми этими силами. Действительно, второй закон Ньютона гласит, что сила притяжения измеряется произведением массыm на сообщенное ей ускорениеg, т. е.

Если под величиной т понимать массу космического аппарата, а подm3 – массу Земли, то, используя формулу (1), определим

гдеr – расстояние от центра Земли до космического аппарата. Полученная формула выглядит несколько проще, чем формула 1, поскольку здесь исчезла одна из масс, а именно масса космического аппарата. Значит, этой формулой можно пользоваться для вычисления величины ускорения, воздействующего на космический аппарат и направленного к центру Земли, совершенно забывая и даже не зная действительной массы космического аппарата. Произведение двух известных величинfm3 носит название гравитационного параметра Земли (или какой-либо другой планеты) и часто обозначается буквойb₀. Численные значения этого параметра для планет Солнечной системы и Луны, а также радиусы планет и ускорения силы тяжести на их поверхности даны в табл. 1.

Таким образом, формула для определения ускорения силы тяжести принимает следующий простой вид:

(2)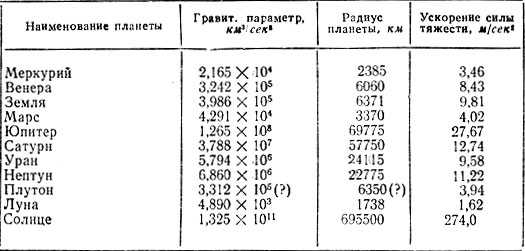

Таблица 1. Некоторые характеристики планет и Луны

Если бы космический аппарат летел непосредственно у поверхности Земли, то его ускорение составляло бы 9,81м/сек². По мере увеличения высоты полета (т. е. величиныr) в соответствии с полученной формулой величина ускорения будет уменьшаться. Так, если радиус орбиты увеличится в два раза по сравнению с радиусом поверхности Земли, то ускорение силы тяжести уменьшится уже в четыре раза и составит около 2,5м/сек². На расстоянии до Луны (r = 400 000 км) земное ускорение будет равно лишь 1,36мм/сек².

psmi.narod.ru

Гравитационная сила формула. Ссылки и примечания. Весомость как фундаментальное понятие механики

Гравитационное взаимодействие

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух точечных или сферических тел в пустом пространстве. Эта задача в рамках классической механики решается аналитически в замкнутой форме; результат её решения часто формулируют в виде трёх законов Кеплера .

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе эта неустойчивость не позволяет предсказать точно движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: Солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы , аттракторы , хаотичность и т. д. Наглядный пример таких явлений – сложная структура колец Сатурна.

Несмотря на попытки точно описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса .

Сильные гравитационные поля

В сильных гравитационных полях, а также при движении в гравитационном поле с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности (ОТО):

изменение геометрии пространства-времени;
- как следствие, отклонение закона тяготения от ньютоновского;
- и в экстремальных случаях – возникновение чёрных дыр ;
запаздывание потенциалов, связанное с конечной скоростью распространения гравитационных возмущений ;
- как следствие, появление гравитационных волн;
эффекты нелинейности: гравитация имеет свойство взаимодействовать сама с собой, поэтому принцип суперпозиции в сильных полях уже не выполняется.

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение , наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако существуют весомые косвенные свидетельства в пользу его существования, а именно: потери энергии в тесных двойных системах, содержащих компактные гравитирующие объекты (такие как нейтронные звезды или чёрные дыры), в частности, в знаменитой системе PSR B1913+16 (пульсаре Халса – Тейлора) – хорошо согласуются с моделью ОТО, в которой эта энергия уносится именно гравитационным излучением.

Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами , этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного n -польного источника пропорциональна , если мультиполь имеет электрический тип, и – если мультиполь магнитного типа , где v – характерная скорость движения источников в излучающей системе, а c – скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:

где – тензор квадрупольного момента распределения масс излучающей системы. Константа (1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ. )), предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (LIGO , VIRGO , TAMA (англ. ), GEO 600), а также проект космического гравитационного детектора LISA (Laser Interferometer Space Antenna – лазерно-интерферометрическая космическая антенна). Наземный детектор в России разрабатывается в Научном Центре Гравитационно-Волновых Исследований «Дулкын» республики Татарстан .

Тонкие эффекты гравитации

Измерение кривизны пространства на орбите Земли (рисунок художника)

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле . В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли. Обработка полученных данных велась до мая 2011 года и подтвердила существование и величину эффектов геодезической прецессии и увлечения инерциальных систем отсчёта, хотя и с точностью, несколько меньшей изначально предполагавшейся.

После интенсивной работы по анализу и извлечению помех измерений, окончательные итоги миссии были объявлены на пресс-конференции по NASA-TV 4 мая 2011 года и опубликованы в Physical Review Letters . Измеренная величина геодезической прецессии составила −6601,8±18,3 миллисекунды дуги в год, а эффекта увлечения – −37,2±7,2 миллисекунды дуги в год (ср. с теоретическими значениями −6606,1 mas/год и −39,2 mas/год ).

Классические теории гравитации

См. также: Теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая классическая теория гравитации – общая теория относительности , и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой. Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии . Гравитационное поле (обобщение ньютоновского гравитационного потенциала), иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем – метрикой четырёхмерного пространства-времени, а напряжённость гравитационного поля – с аффинной связностью пространства-времени, определяемой метрикой.

Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих геометрические свойства пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырёхмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием её формулировки, считается, что гра

dosaaf-khab.ru

понятие и особенности применения формулы для их расчета

определение, формула, роль в природе и космосе

Что такое сила тяжести или гравитациия?

Сэр Исаак Ньютон и всемирное тяготение

Эффекты, обусловленные существованием гравитации

понятие и особенности применения формулы для их расчета

Гравитационные силы. Закон всемирного тяготения. Вес тела

Гравитационные силы. Закон всемирного тяготения. Вес тела

понятие и особенности применения формулы для их расчета

Гравитационные силы

Гравитационные силы

Гравитационная сила формула. Ссылки и примечания. Весомость как фундаментальное понятие механики

Гравитационное взаимодействие

Сильные гравитационные поля

Гравитационное излучение

Тонкие эффекты гравитации

Классические теории гравитации

Общая теория относительности

Оставить комментарий Отменить ответ