Сила притяжения между телами формула – Классическая теория тяготения Ньютона — Википедия

Закон всемирного тяготения — урок. Физика, 9 класс.

Одна из важнейших в природе сил — сила гравитации или сила тяготения. Она действует на все тела во Вселенной.

 

Впервые к выводу о существовании сил всемирного тяготения пришёл Ньютон, когда изучал движение Луны вокруг Земли и планет Солнечной системы вокруг Солнца. Он открыл закон всемирного тяготения, т.е. формулу для расчёта силы гравитационного взаимодействия.

 

Закон всемирного тяготения гласит:

Два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.

 

 F=Gm1m2R2.

 

 G=6,67⋅10−11Н⋅мкг2 — гравитационная постоянная.          

 

                    

Обрати внимание!

    R — это расстояние между центрами тел.

 

Условия применимости закона всемирного тяготения:

1. Если размеры тел пренебрежимо малы по сравнению с расстоянием между ними.
2. Если оба тела однородны и имеют шарообразную форму.
3. Если одно из тел — шар, размеры и масса которого значительно больше, чем у второго тела (любой формы), находящегося на поверхности этого шара или вблизи неё.

 

 

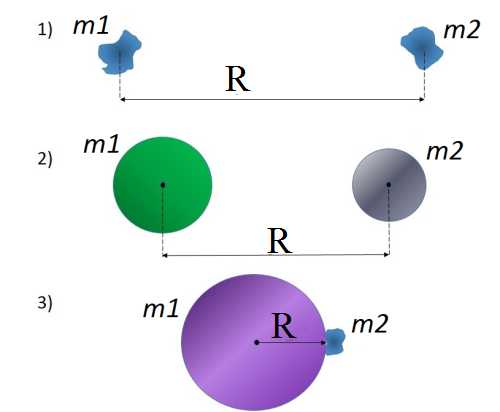
Третий из этих случаев помогает рассчитать силу тяжести, действующую на тела, которые находятся вблизи поверхности Земли. При этом расстояние между телами считается равным радиусу Земли (\(6370\) км), так как размеры тел, находящихся вблизи Земли, пренебрежимо малы по сравнению с земным радиусом.

 

 

 

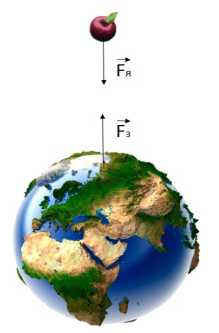
По третьему закону Ньютона, яблоко, висящее на ветке или падающее с неё с ускорением свободного падения, притягивает к себе Землю с такой же по модулю силой, с какой его притягивает Земля. Но ускорение Земли, вызванное силой её притяжения к яблоку, близко к нулю, поскольку масса Земли несоизмеримо больше массы яблока.

www.yaklass.ru

Закон всемирного тяготения Ньютона • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Между всеми телами во Вселенной действует сила взаимного притяжения.

На склоне своих дней Исаак Ньютон рассказал, как это произошло: он гулял по яблоневому саду в поместье своих родителей и вдруг увидел луну в дневном небе. И тут же на его глазах с ветки оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое время работал над законами движения (

см. Законы механики Ньютона), он уже знал, что яблоко упало под воздействием гравитационного поля Земли. Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.

Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории. Когда великие предшественники Ньютона, в частности Галилей, изучали равноускоренное движение тел, падающих на поверхность Земли, они были уверены, что наблюдают явление чисто земной природы — существующее только недалеко от поверхности нашей планеты. Когда другие ученые, например Иоганн Кеплер (см. Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.

Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.

Результаты ньютоновских расчетов теперь называют

законом всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы двух тел, а D — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:

F = GMm/D²

где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67 × 10^–11.

Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на все без исключения физические материальные тела во Вселенной. В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.

Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на вас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и вы ее реально ощущаете как свой

вес. Если вы что-нибудь уроните, оно под действием всё той же силы равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой g.

Для Галилея g было просто экспериментально измеряемой константой. По Ньютону же ускорение свободного падения можно вычислить, подставив в формулу закона всемирного тяготения массу Земли

M и радиус Земли D, помня при этом, что, согласно второму закону механики Ньютона, сила, действующая на тело, равняется его массе, умноженной на ускорение. Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.

Наконец, закон всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер — ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону законы Кеплера становятся прямым следствием универсальных законов механики и закона всемирного тяготения. То есть мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.

Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением

g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит — и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра падают всё дальше и дальше от подножия скалы.

Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет и продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим

искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.

Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.

Я допускаю, что кого-то из историков от моей версии хватит удар, но на самом деле меня этот вопрос мало беспокоит. Как бы то ни было, яблоко Ньютона остается красивой притчей и блестящей метафорой, описывающей непредсказуемость и таинство творческого познания природы человеком. А является ли этот рассказ исторически достоверным — это уже вопрос вторичный.

См. также:

elementy.ru

Referat. Всемирное тяготение — PhysBook

Введение

Почему выпущенный из рук камень падает на Землю? Потому что его притягивает Земля, скажет каждый из вас. В самом деле, камень падает на Землю с ускорением свободного падения. Следовательно, на камень со сто-роны Земли действует сила, направленная к Земле. Согласно третьему закону Ньютона и камень действует на Землю с такой же по модулю силой, направленной к камню. Иными словами, между Землей и камнем действуют силы взаимного притяжения.

Ньютон был первым, кто сначала догадался, а потом и строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила тяготения, действующая между любыми телами Вселенной. Вот ход его рассуждений, приведенных в главном труде Ньютона «Математические начала натуральной философии»:

«Брошенный горизонтально камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадет наконец на Землю. Если его бросить с большей скоростью, то он упадет дальше» (рис. 1).

Рис. 1

Продолжая эти рассуждения, Ньютон приходит к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определенной скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался вокруг нее «подобно тому, как планеты описывают в небесном пространстве свои орбиты».

Сейчас нам стало настолько привычным движение спутников вокруг Земли, что разъяснять мысль Ньютона подробнее нет необходимости.

Итак, по мнению Ньютона, движение Луны вокруг Земли или планет вокруг Солнца – это тоже свободное падение, но только падение, которое длится, не прекращаясь, миллиарды лет. Причиной такого «падения» (идет ли речь действительно о падении обычного камня на Землю или о движении планет по их орбитам) является сила всемирного тяготения. От чего же эта сила зависит?

Зависимость силы тяготения от массы тел

Галилей доказал, что при свободном падении Земля сообщает всем телам в данном месте одно и то же ускорение независимо от их массы. Но ускорение по второму закону Ньютона обратно пропорционально массе\[a = \frac {F}{m}\]. Как же объяснить, что ускорение, сообщаемое телу силой притяжения Земли, одинаково для всех тел? Это возможно лишь в том случае, если сила притяжения к Земле прямо пропорциональна массе тела. В этом случае увеличение массы т, например, вдвое приведет к увеличению модуля силы F тоже вдвое, а ускорение, которое равно \(a = \frac {F}{m}\), останется неизменным. Обобщая этот вывод для сил тяготения между любыми телами, заключаем, что сила всемирного тяготения прямо пропорциональна массе тела, на которое эта сила действует.

Но во взаимном притяжении участвуют по меньшей мере два тела. На каждое из них, согласно третьему закону Ньютона, действуют одинаковые по модулю силы тяготения. Поэтому каждая из этих сил должна быть пропорциональна как массе одного тела, так и массе другого тела. Поэтому сила всемирного тяготения между двумя телами прямо пропорциональна произведению их масс:

\(F \sim m_1 \cdot m_2\)

Зависимость силы тяготения от расстояния между телами

Из опыта хорошо известно, что ускорение свободного падения равно 9,8 м/с² и оно одинаково для тел, падающих с высоты 1, 10 и 100 м, т. е. не зависит от расстояния между телом и Землей. Это как будто бы означает, что и сила от расстояния не зависит. Но Ньютон считал, что отсчитывать расстояния надо не от поверхности, а от центра Земли. Но радиус Земли 6400 км. Понятно, что несколько десятков, сотен или даже тысяч метров над поверхностью Земли не могут заметно изменить значение ускорения свободного падения.

Чтобы выяснить, как влияет расстояние между телами на силу их вза-имного притяжения, нужно было бы узнать, каково ускорение тел, удаленных от Земли на достаточно большие расстояния. Однако наблюдать и изучать свободное падение тела с высоты в тысячи километров над Землей трудно. Но сама природа пришла здесь на помощь и дала возможность определить ускорение тела, движущегося по окружности вокруг Земли и обладающего поэтому центростремительным ускорением, вызванным, разумеется, той же силой притяжения к Земле. Таким телом является естественный спутник Земли – Луна. Если бы сила притяжения между Землей и Луной не зависела от расстояния между ними, то центростремительное ускорение Луны было бы таким же, как ускорение тела, свободно падающего близ поверхности Земли. В действительности же центростремительное ускорение Луны равно 0,0027 м/с².

Докажем это. Обращение Луны вокруг Земли происходит под действием силы тяготения между ними. Приближенно орбиту Луны можно считать окружностью. Следовательно, Земля сообщает Луне центростремительное ускорение. Оно вычисляется по формуле \(a = \frac {4 \pi^2 \cdot R}{T^2}\), где R – радиус лунной орбиты, равный примерно 60 радиусам Земли, Т ≈ 27 сут 7 ч 43 мин ≈ 2,4∙10⁶ с – период обращения Луны вокруг Земли. Учитывая, что радиус Земли R_з ≈ 6,4∙10⁶ м, получим, что центростремительное ускорение Луны равно:

\(a = \frac {4 \pi^2 \cdot 60 \cdot 6,4 \cdot 10^6}{(2,4 \cdot 10^6)^2} \approx 0,0027\) м/с².

Найденное значение ускорения меньше ускорения свободного падения тел у поверхности Земли (9,8 м/с²) приблизительно в 3600 = 60² раз.

Таким образом, увеличение расстояния между телом и Землей в 60 раз привело к уменьшению ускорения, сообщаемого земным притяжением, а следовательно, и самой силы притяжения в 60² раз.

Отсюда вытекает важный вывод: ускорение, которое сообщает телам сила притяжения к Земле, убывает обратно пропорционально квадрату расстояния до центра Земли

\(F \sim \frac {1}{R^2}\).

Закон всемирного тяготения

В 1667 г. Ньютон окончательно сформулировал закон всемирного тяготения:

\(F = G \cdot \frac {m_1 \cdot m_2}{R^2}.\quad (1)\)

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.

Коэффициент пропорциональности G называется гравитационной постоянной.

Закон всемирного тяготения справедлив только для таких тел, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. Иначе говоря, он справедлив только для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 2). Подобного рода силы называются центральными.

Рис. 2

Для нахождения силы тяготения, действующей на данное тело со сто-роны другого, в случае, когда размерами тел пренебречь нельзя, поступают следующим образом. Оба тела мысленно разделяют на столь малые элементы, чтобы каждый из них можно было считать точечным. Складывая силы тяготения, действующие на каждый элемент данного тела со стороны всех элементов другого тела, получают силу, действующую на этот элемент (рис. 3). Проделав такую операцию для каждого элемента данного тела и сложив полученные силы, находят полную силу тяготения, действующую на это тело. Задача эта сложная.

Рис. 3

Есть, однако, один практически важный случай, когда формула (1) применима к протяженным телам. Можно доказать, что сферические тела, плотность которых зависит только от расстояний до их центров, при расстояниях между ними, больших суммы их радиусов, притягиваются с силами, модули которых определяются формулой (1). В этом случае R – это расстояние между центрами шаров.

И наконец, так как размеры падающих на Землю тел много меньше размеров Земли, то эти тела можно рассматривать как точечные. Тогда под R в формуле (1) следует понимать расстояние от данного тела до центра Земли.

Между всеми телами действуют силы взаимного притяжения, зависящие от самих тел (их масс) и от расстояния между ними.

Физический смысл гравитационной постоянной

Из формулы (1) находим

\(G = F \cdot \frac {R^2}{m_1 \cdot m_2}\).

Отсюда следует, что если расстояние между телами численно равно единице (R = 1 м) и массы взаимодействующих тел тоже равны единице (m₁ = m₂ = 1 кг), то гравитационная постоянная численно равна модулю силы F. Таким образом (физический смысл),

гравитационная постоянная численно равна модулю силы тяготения, действующей на тело массой 1 кг со стороны другого тела такой же массы при расстоянии между телами, равном 1 м.

В СИ гравитационная постоянная выражается в

.

Опыт Кавендиша

Значение гравитационной постоянной G может быть найдено только опытным путем. Для этого надо измерить модуль силы тяготения F, действующей на тело массой m₁ со стороны тела массой m₂ при известном расстоянии R между телами.

Первые измерения гравитационной постоянной были осуществлены в середине XVIII в. Оценить, правда весьма грубо, значение G в то время удалось в результате рассмотрения притяжения маятника к горе, масса которой была определена геологическими методами.

Точные измерения гравитационной постоянной впервые были проведены в 1798 г. английским физиком Г. Кавендишем с помощью прибора, называемого крутильными весами. Схематично крутильные весы показаны на рисунке 4.

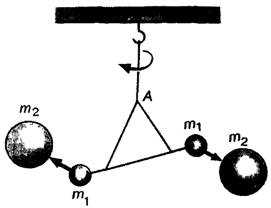
Рис. 4

Кавендиш закрепил два маленьких свинцовых шара (диаметром 5 см и массой m₁ = 775 г каждый) на противоположных концах двухметрового стержня. Стержень был подвешен на тонкой проволоке. Для этой проволоки предварительно определялись силы упругости, возникающие в ней при закручивании на различные углы. Два больших свинцовых шара (диаметром 20 см и массой m₂ = 49,5 кг) можно было близко подводить к маленьким шарам. Силы притяжения со стороны больших шаров заставляли маленькие шары перемещаться к ним, при этом натянутая проволока немного закручивалась. Степень закручивания была мерой силы, действующей между шарами. Угол закручивания проволоки (или поворота стержня с малыми шарами) оказался столь малым, что его пришлось измерять с помощью оптической трубы. Результат, полученный Кавендишем, только на 1% отличается от значения гравитационной постоянной, принятого сегодня:

G ≈ 6,67∙10^-11 (Н∙м²)/кг²

Таким образом, силы притяжения двух тел массой по 1 кг каждое, находящихся на расстоянии 1 м друг от друга, по модулям равны всего лишь 6,67∙10^-11 Н. Это очень малая сила. Только в том случае, когда взаимодействуют тела огромной массы (или по крайней мере масса одного из тел велика), сила тяготения становится большой. Например, Земля притягивает Луну с силой F ≈ 2∙10²⁰ Н.

Гравитационные силы – самые «слабые» из всех сил природы. Это связано с тем, что гравитационная постоянная мала. Но при больших массах космических тел силы всемирного тяготения становятся очень большими. Эти силы удерживают все планеты возле Солнца.

Значение закона всемирного тяготения

Закон всемирного тяготения лежит в основе небесной механики – науки о движении планет. С помощью этого закона с огромной точностью определяются положения небесных тел на небесном своде на многие десятки лет вперед и вычисляются их траектории. Закон всемирного тяготения применяется также в расчетах движения искусственных спутников Земли и межпланетных автоматических аппаратов.

Возмущения в движении планет. Планеты не движутся строго по законам Кеплера. Законы Кеплера точно соблюдались бы для движения данной планеты лишь в том случае, когда вокруг Солнца обращалась бы одна эта планета. Но в Солнечной системе планет много, все они притягиваются как Солнцем, так и друг другом. Поэтому возникают возмущения движения планет. В Солнечной системе возмущения невелики, потому что притяжение планеты Солнцем гораздо сильнее притяжения другими планетами. При вычислении видимого положения планет приходится учитывать возмущения. При запуске искусственных небесных тел и при расчете их траекторий пользуются приближенной теорией движения небесных тел – теорией возмущений.

Открытие Нептуна. Одним из ярких примеров триумфа закона все-мирного тяготения является открытие планеты Нептун. В 1781 г. английский астроном Вильям Гершель открыл планету Уран. Была вычислена ее орбита и составлена таблица положений этой планеты на много лет вперед. Однако проверка этой таблицы, проведенная в 1840 г., показала, что данные ее расходятся с действительностью.

Ученые предположили, что отклонение в движении Урана вызвано притяжением неизвестной планеты, находящейся от Солнца еще дальше, чем Уран. Зная отклонения от расчетной траектории (возмущения движения Урана), англичанин Адаме и француз Леверрье, пользуясь законом всемирного тяготения, вычислили положение этой планеты на небе. Адаме раньше закончил вычисления, но наблюдатели, которым он сообщил свои результаты, не торопились с проверкой. Тем временем Леверрье, закончив вычисления, указал немецкому астроному Галле место, где надо искать неизвестную планету. В первый же вечер, 28 сентября 1846 г., Галле, направив телескоп на указанное место, обнаружил новую планету. Ее назвали Нептуном.

Таким же образом 14 марта 1930 г. была открыта планета Плутон. Оба открытия, как говорят, были сделаны «на кончике пера».

При помощи закона всемирного тяготения можно вычислить массу планет и их спутников; объяснить такие явления, как приливы и отливы воды в океанах, и многое другое.

Силы всемирного тяготения – самые универсальные из всех сил природы. Они действуют между любыми телами, обладающими массой, а массу имеют все тела. Для сил тяготения не существует никаких преград. Они действуют сквозь любые тела.

Литература

1. Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Просвещение, 1992. – 191 с.
2. Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.

www.physbook.ru

Сила притяжения – Silamedia

 В продолжение разговора об энергии движения, рассмотрим взаимодействие тел в пространстве. Ещё Ньютон доказал, что все мы притягиваемся друг к другу:   

Закон всемирного тяготения гласит: «Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними» 
  

В этой формуле, как и в энергетической, одним из ключевых понятий является масса. Нас тянет к людям с большей массой, мы стараемся приблизиться к ним, повращаться вокруг. У большемассных есть свои центры притяжения, их, в свою очередь, тянет туда.   

Прислушайтесь к словам: мы испытываем тягу друг к другу, живём в привычном темпе, вращаемся в привычном кругу. Сильно напоминает взаимоотношения Солнца и планет, Земли и Луны, не правда ли? 

Для того чтобы начать вращаться, нам нужно придать первоначальное ускорение, вывести нас на орбиту. В жизни эту работу выполняют семья, иногда школа, практически всегда – сила наших амбиций. Но чтобы двигаться дальше, нужен собственный движок. Радует, что он может развиваться и совершенствоваться по ходу жизни. Можно наращивать собственную массу и менять траектории, но есть и те, кто вращается всю жизнь на одной орбите. 

Когда тело движется вокруг другого, на него действуют центростремительная и центробежная силы. Работая над собой, увеличивая свою массу и скорость, вы вполне можете дойти до точки, когда сила притяжения (например, вашего места работы) уже не сможет удержать вас. Такое случается часто, если масса одного тела (вашего) растёт стремительнее, чем масса другого (вашей компании). И вот вы отрываетесь от привычной орбиты и направляетесь к более массивному центру, способного какое-то время вас удержать. 

(Зависимость работает и в том случае, если масса компании растёт, а сотрудник своим развитием не занимается.) 

Понимая физику этого процесса, менеджеры вполне могут разработать «гравитационные методы работы с персоналом». Движением по орбитам можно управлять. Но «внешний лоск» здесь мало помогает. Наращивание массы компании не может быть «косметическим». 

Закон работает и в личных отношениях. Увеличение расстояния в знаменателе уменьшает силу притяжения. Эта зависимость прекрасно сформулирована в народной мудрости: «С глаз долой – из сердца вон». 

Ещё один вывод из формулы: два человека, сохраняющие стабильное расстояние между собой и занимающиеся наращиванием общей массы, увеличивают силу притяжения. Иными словами, живите рядом и развивайтесь. 

Техника безопасности: нужно держать дистанцию. Между телами не должно быть нулевого расстояния, нельзя «растворяться» в другом человеке. Ибо тогда придётся делить на ноль. В квадрате. 

Работая над изменением своей кинетической энергии, вы неизменно столкнётесь с изменениями вашей личной «планетарной системы». А, проанализировав, куда и как вас «потянуло», можно вполне достоверно предположить, какую внутреннюю работу вы проделали. 

(Особая благодарность автору учебника «Физика. 10 класс» Мякишеву Г.Я., хотя хрен продерёшься сквозь этот сухой, скучный, занудный текст).

sila-ksu.livejournal.com

Закон всемирного тяготения. Сила тяжести – FIZI4KA

1. Силы, с которыми все тела притягиваются друг к другу, называют силами всемирного тяготения или гравитационными силами.

Закон всемирного тяготения был установлен Ньютоном, и он утверждает, что тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними.

​\( F=G\frac{m_1m_2}{r^2} \)​

где ​\( m_1 \)​ и ​\( m_2 \)​ — массы тел, ​\( r \)​ — расстояние между телами, ​\( G \)​ — постоянная всемирного тяготения или гравитационная постоянная.

Значение гравитационной постоянной установлено опытным путём, оно равно ​\( G \)​ = 6,67·10^-11 Нм²/кг². Смысл её заключается в следующем: два тела, каждое массой 1 кг, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 6,67·10^-11 Н.

Значение гравитационной постоянной свидетельствует о том, что силы тяготения между телами малы. Они становятся заметными при больших значениях масс взаимодействующих тел. Например, притяжение шарика к Земле можно наблюдать без специальных приборов, а притяжение Земли к такому же шарику мы не можем наблюдать непосредственно.

Закон всемирного тяготения справедлив для тел, размерами которых можно пренебречь по сравнению с расстоянием между ними (для материальных точек). Закон применим также к шарам, в этом случае расстоянием между телами является расстояние между центрами шаров.

2. Все тела притягиваются к Земле. Силу притяжения тела к Земле называют силой тяжести ​\( (F_т) \)​.

По второму закону Ньютона сила равна произведению массы тела и ускорения, с которым оно движется под действием этой силы. Ускорение, с которым движется тело под действием силы тяжести, называется ускорением свободного падения и обозначается буквой ​\( g \)​. Ускорение свободного падения не зависит от массы тела. Соответственно, сила тяжести рассчитывается но формуле: ​\( F_т=mg \)​.

3. Закон всемирного тяготения позволяет получить формулу для вычисления значения ускорения свободного падения. С одной стороны, сила тяжести равна \( F_т=mg \), с другой стороны, сила притяжения тела к Земле может быть вычислена, исходя из закона всемирного тяготения: ​\( F_т=G\frac{M_Зm}{R^2} \)​, где ​\( M_З \)​ — масса Земли, ​\( m \)​ — масса тела, ​\( r \)​ — радиус Земли. Приравнивая правые части записанных равенств, получим: \( mg=G\frac{M_Зm}{R^2} \) или \( g=G\frac{M_З}{R^2} \).

Полученная формула позволяет вычислить ускорение свободного падения тела, находящегося на поверхности Земли. Она наглядно показывает, что значение ускорения свободного падения зависит от расстояния тела до центра Земли. Именно поэтому оно на экваторе больше, чем на полюсах.

По этой формуле можно вычислить ускорение свободного падения на любой планете, подставив вместо массы Земли массу соответствующей планеты, а вместо радиуса
Земли радиус планеты.

4. Если тело находится на высоте ​\( h \)​ относительно поверхности Земли, то ускорение свободного падения определяется равенством ​\( g=G\frac{M_З}{(R_З+h)^2} \)​. Из приведенного равенства понятно, что чем дальше тело находится от центра Земли, тем меньше ускорение свободного падения. Например, на высоте 18 км, на которой летают современные истребители, оно равно 9,72 м/с².

5. Пользуясь законом всемирного тяготения, можно вычислить скорость, которую необходимо сообщить телу для того, чтобы оно стало спутником Земли. Эта скорость
называется первой космической скоростью.

Центростремительное ускорение ​\( a \)​ спутнику массой ​\( m \)​ обеспечивает сила тяготения ​\( F_т \)​, которая по второму закону Ньютона равна ​\( F_т=ma \)​. Сила тяготения ​\( F_т=G\frac{M_Зm}{R^2} \)​, центростремительное ускорение равно ​\( a=\frac{v^2}{R} \)​, где ​\( v \)​ — линейная скорость спутника, ​\( R \)​ — радиус Земли. Откуда следует: ​\( G\frac{M_Зm}{R^2}=m\cdot\frac{v^2}{R} \)​ или ​\( g=\frac{v^2}{R} \)​. Отсюда ​\( v=\sqrt{gR} \)​, т.е. первая космическая скорость равна 7,9 км/с. Первый в мире искусственный спутник Земли был запущен в СССР в 1957 г.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Сила тяготения между двумя телами уменьшится в 2 раза, если массу каждого тела

1) увеличить в √2 раз
2) уменьшить в √2 раз
3) увеличить в 2 раза
4) уменьшить в 2 раза

2. Массу каждого из двух однородных шаров увеличили в 4 раза. Расстояние между ними тоже увеличили в 4 раза. Сила тяготения между ними

1) увеличилась в 64 раза
2) увеличилась в 16 раз
3) увеличилась в 4 раза
4) не изменилась

3. В вершинах прямоугольника расположены тела одинаковой массы. Со стороны какого тела на тело 1 действует наибольшая сила?

1) со стороны тела 2
2) со стороны тела 3
3) со стороны тела 4
4) со стороны всех тел одинаковая

4. Закон всемирного тяготения справедлив

A. Для всех тел
Б. Для однородных шаров
B. Для материальных точек

Правильный ответ

1) А
2) только Б
3) только В
4) и А, и Б

5. На ящик массой 5 кг, лежащий на полу лифта, движущегося с ускорением ​\( a \)​ вертикально вниз, действует сила тяжести

1) равная 50 Н
2) большая 50 Н
3) меньшая 50 Н
4) равная 5 Н

6. Сравните значения силы тяжести ​\( F_э \)​, действующей на груз на экваторе, с силой тяжести \( F_м \), действующей на этот же груз на широте Москвы, если груз находится на одной и той же высоте относительно поверхности Земли.

1) ​\( F_э=F_м \)​
2) \( F_э>F_м \)​
3) \( F_э<F_м \)​
4) ответ может быть любым в зависимости от массы тел

7. Сила тяжести, действующая на космонавта на поверхности Луны,

1) больше силы тяжести, действующей на него на поверхности Земли
2) меньше силы тяжести, действующей на него на поверхности Земли
3) равна силе тяжести, действующей на него на поверхности Земли
4) больше силы тяжести, действующей на него на поверхности Земли на экваторе, и меньше силы тяжести, действующей на него, на поверхности Земли на полюсе

8. Сила тяжести, действующая на тело, зависит от

А. Географической широты местности
Б. Скорости падения тела на поверхность Земли

Правильный ответ

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

9. Какое(-ие) из утверждений верно(-ы)?

Сила тяжести, действующая на тело у поверхности некоторой планеты, зависит от

А. Массы планеты.
Б. Массы тела.

1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б

10. Первая космическая скорость зависит

A. От радиуса планеты
Б. От массы планеты
B. От массы спутника

Правильный ответ

1) только А
2) только Б
3) только А и Б
4) А, Б, В

11. Установите соответствие между физической величиной (левый столбец) и формулой, выражающей её взаимосвязь с другими величинами (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Сила тяжести
Б. Ускорение свободного падения на поверхности Земли
B. Закон всемирного тяготения

ФОРМУЛА
1) ​\( F=G\frac{m_1m_2}{r^2} \)​
2) ​\( F_т=mg \)​
3) ​\( g=G\frac{M_З}{(R_З+h)^2} \)​
4) ​\( g=G\frac{M_З}{R^2} \)​

12. Среди приведённых утверждений выберите два правильных и запишите их номера в таблицу

1) Гравитационная постоянная показывает, с какой силой притягиваются друг к другу два тела массой 1 кг.
2) Значение силы тяжести, действующей на тело, зависит от скорости его движения.
3) Ускорение свободного падения зависит от массы и радиуса планеты.
4) При увеличении расстояния между телами в 3 раза сила тяготения между ними уменьшается в 9 раз.
5) Изменение массы одного из взаимодействующих тел не влияет на значение силы тяготения.

Часть 2

13. Человек на Земле притягивается к ней с силой 700 Н. С какой силой он притягивался бы к Марсу, находясь на его поверхности, если радиус Марса в 2 раза меньше радиуса Земли, а масса в 10 раз меньше, чем масса Земли?

Ответы

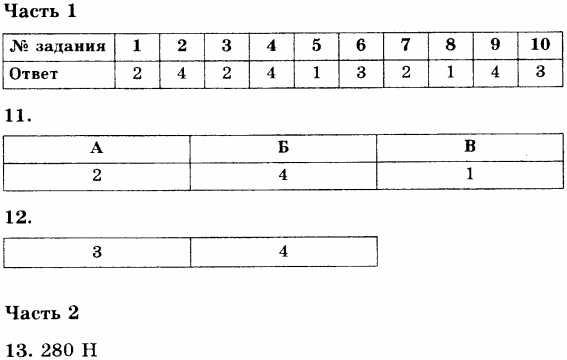
Закон всемирного тяготения. Сила тяжести

Оценка

fizi4ka.ru