Силы и законы ньютона – Сила. Первый закон Ньютона | Объединение учителей Санкт-Петербурга - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Сила. Три закона Ньютона | LAMPA

Три закона Ньютона

Три закона Ньютона определяют “правила жизни” в механике. Обычно в школе их излагают в прямой последовательности — от первого закона к третьему. Мы поступим по-другому. Мы изложим их в обратном порядке. Нам кажется, что так будет понятнее. Приступим.

Третий закон Ньютона. Попробуйте надавить рукой на стол. При этом ладонью своей руки вы почувствуете поверхность стола. И вы также почувствуете некоторое сопротивление со стороны стола. Будто и сам стол давит на вас. При этом, если бы вы не давили на стол, а держали руку неподвижно, а поверхность стола приближалась бы к вашей руке и сама давила на вашу руку, то ощущения были бы точно такими же.

Можно предположить, что когда тело А воздействует на другое тело — тело B (например, вы действуете на стол), — то и тело B действует на тело А.

Рассмотрим другой пример. Девочка А и девочка B стоят на коньках на льду. Девочка А начинает толкать девочку B. Наш жизненный опыт подсказывает нам, что девочка B будет двигаться в ту сторону, куда ее толкает девочка А. Но! Жизненный опыт нам подсказывает, что и девочка А начнет двигаться так, будто ее толкнула девочка B.

Это подтверждает нашу догадку, что когда тело А действует с некоторой силой на тело B, то и тело B действует на тело А.

Оказывается, что наше предположение — верное. Более того, силы, с которыми тела действуют друг на друга, одинаковые (!).

Итак, третий закон Ньютона звучит следующим образом:

Силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению: F⃗1→2=−F⃗2→1.\vec{F}_{1\to 2}=-\vec{F}_{2\to 1}{.}F⃗1→2=−F⃗2→1.

Второй закон Ньютона. Представьте себе ситуацию: на столе неподвижно стоит мячик. Мы толкаем его, то есть мы действуем силой. При этом мячик начинает двигаться. Значит, у него появилась скорость.

Итак, сначала мячик покоился и у него была нулевая скорость: V1=0V_1=0V1=0. А затем мячик двигался, и его скорость была уже не нулевой: V2≠0V_2\neq 0V2≠0. То есть скорость изменилась (!). У нас есть изменение скорости. А это значит, что есть ускорение.

Итак, можно сделать вывод, что сила придает телу ускорение, она “создает” ускорение тела. Логично будет предположить, что бОльшая сила даст мячику бОльшее ускорение: ускорение тела тем больше, чем больше сила. Но это еще не все.

Возьмем два мячика: легкий шарик для пинг-понга и тяжелый железный шарик из подшипника. Подействуем на них одинаковой силой. Оба они получат ускорение. Но ускорение будет разное. Это подсказывает нам жизненный опыт.

Более тяжелый (массивный, с большей массой) стальной шарик получит небольшую скорость; его ускорение будет небольшим.

Легкий (с меньшей массой) шарик для пинг-понга получит большую скорость; ускорение у него будет большим.

Само собой у нас получилось ввести некоторую величину — массу mmm. Получается, что масса показывает, насколько неохотно тело изменяет свою скорость. Если масса тела велика, то ускорение тела — мало. То есть, если величина силы неизменна (сила зафиксирована по величине), то чем больше масса — тем меньше ускорение, которое получает тело.

lampa.io

Законы механики Ньютона

1) Первый закон Ньютона: Существуют такие системы отсчета, называемые инерциальными, относительно которых свободные тела движется равномерно и прямолинейно.

Первый закон механики, или закон инерции, как его часто называют, бал, по существу, установлен еще Галилеем, но общую формулировку ему дал Ньютон.

Свободным телом – называют тело, на которое не действуют какие – либо другие тела или поля. При решении некоторых задач тело можно считать свободным, если внешние воздействия уравновешены.

Системы отсчета, в которых свободная материальная точка покоится или движется прямолинейно и равномерно, называются

инерциальными системами отсчета. Прямолинейное и равномерное движение свободной материальной точки в инерциальной системе отсчета называется движением по инерции. При таком движении вектор скорости материальной точки остается постоянным (= const ). Покой точки является частным случаем движения по инерции (=0).

В инерциальных системах отсчета покой или равномерное движение представляет собой естественное состояние, а динамика должна объяснить изменение этого состояния (т.е. появление ускорения тела под действием сил). Свободных тел, не подверженных воздействию со стороны других тел не существует. Однако, благодаря убыванию всех: известных взаимодействий с увеличением расстояния, такое тело можно реализовать с любой требуемой, точностью.

Системы отсчета, в которых свободное тело не сохраняет скорость движения неизменной, называются неинерциальными. Неинерциальной является система отсчета, движущаяся с ускорением относительно любой инерциальной системы отсчета. В неинерциальной системе отсчета даже свободное тело может двигаться с ускорением.

Равномерное и прямолинейное движение системы отсчета не влияет на ход механических явлений, протекающих в ней. Никакие механические опыты не позволяют отличить покой инерциальной системы отсчета от ее равномерного прямолинейного движения. Для любых механических явлений все инициальные системы отсчета оказываются равноправными. Эти утверждения выражают механический принцип относительности (принцип относительности Галилея)

. Принцип относительности является одним из наиболее общих законов природы, в специальной теории относительности он распространяется на электромагнитные и оптические явления.

2) Масса, плотность, сила.

Свойство тела сохранять свою скорость при отсутствии взаимодействия с другими телами называется инертностью. Физическая величина, являющаяся мерой инертности тела в поступательном движении, называется инертной массой

. Масса тела измеряется в килограммах: . Масса характеризует также способность тела взаимодействовать с другими телами в соответствии с законом всемирного тяготения. В этих случаях масса выступает как мера гравитации и ее называют гравитационной массой.

В современной физике с высокой степенью точности доказана тождественность значений инертной и гравитационной масс данного тела. Поэтому говорят просто о массе тела (m ).

В механике Ньютона считается, что

а) масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит;

б) для данной совокупности тел выполняется закон сохранения массы: при любых процессах, происходящих в системе тел, ее масса остается неизменной.

Плотность однородного тела равна . Единица плотности 1 кг/м³.

Силой называется векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей. Сила полностью определена, если заданы ее модуль, направление и точка приложения. Прямая, вдоль которой направлена сила, называется

линией действия силы.

В результате действия силы тело изменяет скорость движения (приобретает ускорение) или деформируется. На основании этих опытных фактов производится измерение сил.

Сила является причиной возникновения не скорости, а ускорения тела. С направлением силы совпадает во всех случаях направление ускорения, но не скорости.

В задачах механики учитываются гравитационные силы (силы тяготения) и две разновидности электромагнитных сил – силы упругости и силы трения.

3) Второй закон Ньютона

Второй закон Ньютона описывает движение частицы, вызванное влиянием окружающих тел, и устанавливает связь между ускорением частицы, ее массой и силой, с которой на нее действуют эти тела:

Если на частицу с массой т окружающие тела действуют с силой , то эта частица приобретает такое ускорение , что произведение ее массы на ускорение будет равно действующей силе.

Математически второй закон Ньютона записывается в виде:

На основе этого закона устанавливается единица силы — 1 Н (ньютон). 1 Н — это сила, с которой нужно действовать на тело массой 1 кг, чтобы сообщить ему ускорение 1 м/с

Если сила , с которой тела действуют на данную частицу, известна, то записанное для этой частицы уравнение второго закона Ньютона называют ее уравнением движения.

Второй закон Ньютона часто называют основным законом динамики, так как именно в нем находит наиболее полное математическое выражение принцип причинности и именно он, наконец, позволяет решить основную задачу механики. Для этого нужно выяснить, какие из окружающих частицу тел оказывают на нее существенное действие, и, выразив каждое из этих действий в виде соответствующей силы, следует составить уравнение движения данной частицы. Из уравнения движения (при известной массе) находится ускорение частицы. Зная

же ускорение можно определить ее скорость, а после скорости — и положение данной частицы в любой момент времени.

Практика показывает, что решение основной задачи механики с помощью второго закона Ньютона всегда приводит к правильным результатам. Это и является экспериментальным подтверждением справедливости второго закона Ньютона.

4) Третий закон Ньютона.

Третий закон Ньютона: Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.

Это означает, что если на тело А со стороны тела В действует сила , то одновременно на тело В со стороны тела А будет действовать сила ,

причем = –.

Используя второй закон Ньютона, можно записать:

Отсюда следует, что

т. е. отношение модулей ускорений и взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Более массивное тело получает меньшее ускорение, а легкое – большее.

Важно понимать, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому они не могут уравновешивать друг друга.

5) Следствия из законов Ньютона

Законы Ньютона представляют собой систему взаимосвязанных законов, которые позволяют глубже понять сущность понятий силы и массы. Следствия из законов:

1. Сила является мерой воздействия, оказываемого на данную частицу со стороны других тел, и с увеличением расстояния до них убывает, стремясь к нулю.

То, что сила является мерой воздействия со стороны окружающих частику тел, следует из того, что она зависит от состояния этих тел и при этом определяет ускорение данной частицы: . Убывания действующей силы до нуля при неограниченном удалении от частицы окружающих ее тел является следствием первого и второго законов Ньютона. Так как, согласно первому закону Ньютона, бесконечно удаленная от всех тел

частица имеет нулевое ускорение . Согласно второму закону Ньютона Поэтому при и сила .

2. Сила, с которой сразу несколько тел действует на данную частицу, равна сумме сил, с которыми эти тела действуют на нее по отдельности:

Это утверждение называется принципом независимости взаимодействий. С учетом этого принципа второй закон Ньютона записывается в виде:

Сумму сил, стоящую в правой части этого закона, называют равнодействующей силой.

Принцип независимости взаимодействий иначе называют принципом суперпозиции сил.

3. Сумма всех внутренних сил, действующих в любой системе, всегда равна нулю.

Под внутренними понимают те силы, которые действуют между телами самой рассматриваемой системы.

Внутренние силы не способны привести в движение систему тел как целое. Действительно, для этого нужно было бы сообщить ускорение, а ускорение, как это следует из второго закона Ньютона, могут сообщить системе лишь те силы, сумма которых отлична от нуля.

4. Отношение модулей ускорений, полученных двумя телами в результате взаимодействия друг с другом, равно обратному отношению их масс:

sfiz.ru

Законы Ньютона — Википедия

Зако́ны Нью́то́на — три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)^[1]^[2]. В ньютоновском изложении механики, широко используемом и в настоящее время, эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов.

Первый закон Ньютона

Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как закон инерции. Инерция (она же инертность) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[3]:

Историческая формулировка

Ньютон сформулировал первый закон механики так:

Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.

Видео по теме

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[4]^[5]^[6]^[7].

Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}

где a→{\displaystyle {\vec {a}}} — ускорение материальной точки;
F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к материальной точке;
m{\displaystyle m} — масса материальной точки.

Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил.

dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},}

где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени^[8]^[9]^[10].

Иногда предпринимаются попытки распространить сферу применения уравнения dp→dt=F→{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}} и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[11]^[12].

Замечания

Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:

ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}}

или

dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}

Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.

Следует учитывать, что нельзя рассматривать частный случай (при F→=0{\displaystyle {\vec {F}}=0}) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}}, а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}}. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}} равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}}.

Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.}

Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно^[13].

Историческая формулировка

Ньютон дал следующую формулировку закона^[1]:

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[14].

Следствия законов Ньютона

Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.

Уравнения движения

Уравнение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Закон сохранения импульса

Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю^[15].

Закон сохранения механической энергии

Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной^[16].

Законы Ньютона и силы инерции

Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.

Обычно речь идёт о силах инерции двух различных типов^[13]^[17]. Сила первого типа (даламберова сила инерции^[18]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции^[18]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой^[13]^[17]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются^[19]^[13], их называют фиктивными^[20], кажущимися^[21] или псевдосилами^[22].

Законы Ньютона в логике курса механики

Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.

Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Исторический очерк

Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем^[23].

Страница «Начал» Ньютона с аксиомами механики

Основные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»^[1]:

Оригинальный текст (лат.)
   LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.
   LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.
   LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.

Русский перевод этих формулировок законов см. в предыдущих разделах.

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)^[24]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта^[24]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).

В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).

Примечания

↑ ¹ ² ³ Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
↑ ¹ ² ³ ⁴ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
↑ ¹ ² Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494-495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ ¹ ² Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3-8.
↑ «”Силы инерции” — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186-197;
↑ ¹ ² Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;

Литература

Ссылки

wiki2.red

Законы Ньютона – это… Что такое Законы Ньютона?

Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год).

Первый закон Ньютона

Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[1]:

Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).

Историческая формулировка

Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:

Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях.

Второй закон Ньютона

Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где — ускорение материальной точки;
— сила, приложенная к материальной точке;
— масса материальной точки.

Или в более известном виде:

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.

где — импульс точки,

где — скорость точки;

— время;
— производная импульса по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

или

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка

Исходная формулировка Ньютона:

Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Современная формулировка

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Историческая формулировка

Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга равны и направлены в противоположные стороны.

Выводы

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел , то возникает закон сохранения суммарной механической энергии взаимодействующих тел:

Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.

Комментарии к законам Ньютона

Сила инерции

Законы Ньютона справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона: , где – это ускорение, наблюдаемое в рассматриваемой системе отсчёта, и – ускорение данной точки этой неинерциальной системы отсчёта относительно любой инерциальной системы отсчёта. Однако часто, для упрощения рассмотрения, вводят фиктивную «силу инерции» , и тогда эти уравнения движения переписываются в виде, идентичном второму закону Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального воздействия на тело. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличается движение в инерциальной и неинерциальной системах отсчета.

Законы Ньютона и Лагранжева механика

Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами). Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Решение уравнений движения

Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию(перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Исторический очерк

Страница «Начал» Ньютона с аксиомами механики

Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде.

   1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
   2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.
   3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.
Оригинальный текст (лат.)
   LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.
   LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.
   LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
— «Начала», страница 12

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес).

Завершили математизацию механики Эйлер и Лагранж.

См. также

Примечания

Ссылки

Литература

dik.academic.ru

Законы Ньютона. Второй закон Ньютона. Законы Ньютона

Изучение явлений природы на основании эксперимента возможно только при условии соблюдения всех этапов: наблюдение, гипотеза, эксперимент, теория. Наблюдение позволит выявить и сопоставить факты, гипотеза дает возможность дать им подробное научное пояснение, требующее экспериментального подтверждения. Проведение наблюдения за движением тел привело к интересному выводу: изменение скорости тела возможно только под действием другого тела.

К примеру, если быстро бежать по лестнице, то на повороте просто необходимо ухватиться за перила (изменение направления движения), либо приостановиться (изменением величины скорости), чтобы не столкнуться с противоположной стеной.

Наблюдения за аналогичными явлениями привело к созданию раздела физики, изучающего причины изменения скорости тел или их деформации.

Основы динамики

Ответить на сакраментальный вопрос о том, почему физическое тело движется тем или иным образом или покоится, призвана динамика.

Рассмотрим состояние покоя. Исходя из понятия относительности движения, можно сделать вывод: нет и не может быть абсолютно неподвижных тел. Любой предмет, будучи неподвижным по отношению к одному телу отсчета, движется относительно другого. К примеру, книга, лежащая на столе, неподвижна относительно стола, но если рассмотреть ее положение по отношению к проходящему человеку, то делаем естественный вывод: книга движется.

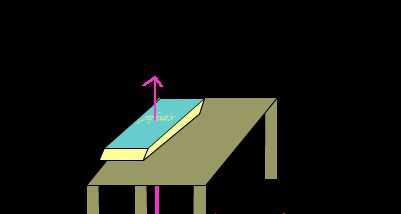
Поэтому законы движения тел рассматриваются в инерциальных системах отсчета. Что это такое?

Инерциальной называется система отсчета, в которой тело покоится или выполняет равномерное и прямолинейное движение при условии отсутствия воздействия на него иных предметов или объектов.

В приведенном выше примере система отсчета, связанная со столом, может быть названа инерциальной. Человек, движущийся равномерно и прямолинейно, может служить телом отсчета ИСО. Если его движение будет ускоренным, то связать с ним инерциальную СО нельзя.

По сути, такую систему можно соотнести с телами, жестко закрепленными на поверхности Земли. Однако сама планета не может служить телом отсчета для ИСО, так как равномерно вращается вокруг собственной оси. Тела на поверхности имеют центростремительное ускорение.

Что такое инерция?

Явление инерции напрямую связано с ИСО. Вспомните, что происходит, если движущийся автомобиль резко останавливается? Пассажиры подвергаются опасности, поскольку продолжают свое движение. Остановить его может кресло впереди либо ремни безопасности. Поясняют этот процесс инерцией пассажира. Так ли это?

Инерция – явление, предполагающее сохранение постоянной скорости тела при отсутствии воздействия на него других тел. Пассажир находится под действием ремней или кресел. Явление инерции здесь не наблюдается.

Объяснение кроется в свойстве тела, и, согласно ему, мгновенно изменить скорость того или иного предмета невозможно. Это – инертность. К примеру, инертность ртути в термометре позволяет опустить столбик, если мы встряхнем градусник.

Мерой инертности называют массу тела. При взаимодействии скорость быстрее меняется у тел с меньшей массой. Столкновение автомобиля с бетонной стеной для последней протекает практически бесследно. Автомобиль чаще всего претерпевает необратимые изменения: меняется скорость, происходит значительная деформация. Получается, что инертность бетонной стены значительно превышает инертность автомобиля.

Возможно ли в природе встретиться с явлением инерции? Условие, при котором тело находится без взаимосвязи с другими телами – глубокий космос, в котором движется космический корабль с выключенными двигателями. Но даже в этом случае гравитационный момент присутствует.

Основные величины

Изучение динамики на экспериментальном уровне предполагает проведение опыта с измерениями физических величин. Наиболее интересны:

ускорение как мера быстроты изменения скорости тел; обозначают ее буквой а, измеряют в м/с²;
масса как мера инертности; обозначена литерой m, измеряется в кг;
сила как мера взаимного действия тел; обозначается чаще всего буквой F, измеряется в Н (ньютонах).

Взаимосвязь этих величин изложена в трех закономерностях, выведенных величайшим английским физиком. Законы Ньютона призваны объяснить сложности взаимодействия различных тел. А также процессы, ими управляющие. Именно понятия “ускорение”, “сила”, “масса” законы Ньютона связывают математическими соотношениями. Попробуем разобраться, что же это значит.

Действие только одной силы – явление исключительное. К примеру, искусственный спутник, движущийся по орбите вокруг Земли, находится под действием только силы притяжения.

Равнодействующая

Действие нескольких сил можно заменить одной силой.

Геометрическая сумма сил, воздействующих на тело, именуется равнодействующей.

Речь идет именно о геометрической сумме, поскольку сила – векторная величина, которая зависит не только от точки приложения, но и от направления действия.

К примеру, если необходимо передвинуть достаточно массивный шкаф, то можно пригласить друзей. Совместными усилиями достигается желаемый результат. Но можно пригласить только одного, очень сильного человека. Его усилие равно действию всех друзей. Сила, приложенная богатырем, может быть названа равнодействующей.

Законы движения Ньютона формулируются на основании понятия «равнодействующая».

Закон инерции

Начинают изучать законы Ньютона с наиболее часто встречающегося явления. Первый закон обычно называют законом инерции, поскольку он устанавливает причины равномерного прямолинейного движения или состояния покоя тел.

Тело перемещается равномерно и прямолинейно или покоится, если на него не осуществляют действия силы, либо это действие скомпенсировано.

Можно утверждать, что равнодействующая в этом случае равна нулю. В таком состоянии находится, к примеру, движущийся с постоянной скоростью автомобиль на прямолинейном участке дороги. Действие силы притяжения скомпенсировано силой реакции опоры, а сила тяги двигателя по модулю равна силе сопротивления движению.

Люстра на потолке покоится, так как сила тяжести скомпенсирована силой натяжения ее креплений.

Скомпенсированными могут быть только те силы, которые приложены к одному телу.

Второй закон Ньютона

Идем далее. Причины, вызывающие изменение скорости тел, рассматривает второй закон Ньютона. О чем он говорит?

Равнодействующая сил, воздействующих на тело, определяется как произведение массы тела на приобретаемое под действием сил ускорение.

2 закон Ньютона (формула: F=ma), к сожалению, не устанавливает причинно-следственных связей между основными понятиями кинематики и динамики. Он не может с точностью указать, что является причиной появления ускорения тел.

Сформулируем иначе: ускорение, получаемое телом, прямо пропорционально равнодействующей сил и обратно пропорционально массе тела.

Так, можно установить, что изменение скорости происходит только в зависимости от силы, приложенной к нему, и массы тела.

2 закон Ньютона, формула которого может быть и такой: a = F/m, в векторном виде считают основополагающим, поскольку он дает возможность установить связь между разделами физики. Здесь, a – вектор ускорения тела, F – равнодействующая сил, m – масса тела.

Ускоренное движение автомобиля возможно, если сила тяги двигателей превышает силу сопротивления движению. С увеличением силы тяги возрастает и ускорение. Грузовые автомобили снабжаются двигателями большой мощности, ведь их масса значительно превышает массу легкового авто.

Болиды, созданные для скоростных гонок, облегчаются таким образом, что на них закрепляется минимум необходимых деталей, а мощность двигателей увеличивается до возможных пределов. Одной из важнейших характеристик спортивных авто является время разгона до 100 км/ч. Чем меньшее этот интервал времени, тем лучше скоростные свойства болида.

Закон взаимодействия

Законы Ньютона, основанные на силах природы, утверждают, что любое взаимодействие сопровождается появлением пары сил. Если шар висит на нити, то испытывает ее действие. При этом нить также растягивается под действием шара.

Завершает законы Ньютона формулировка третьей закономерности. Вкратце это звучит так: действие равно противодействию. Что это значит?

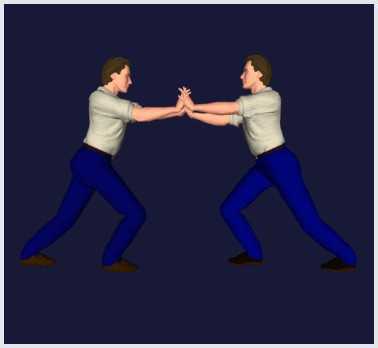
Силы, с которыми тела воздействуют друг на друга, равны по величине, противоположны по направлению и направлены вдоль линии, соединяющей центры тел. Интересно, что скомпенсированными их назвать нельзя, ведь действуют они на разные тела.

Применение законов

Знаменитая задача «Конь и телега» может поставить в тупик. Конь, запряженный в упомянутую повозку, сдвигает ее с места. В соответствии с третьим законом Ньютона, эти два объекта действуют друг на друга с равными по модулю силами, но на практике лошадь может сдвинуть телегу, что не укладывается в основы закономерности.

Решение найдется, если учесть, что эта система тел не замкнута. Дорога оказывает свое действие на оба тела. Сила трения покоя, действующая на копыта коня, превышает по значению силу трения качения колес телеги. Ведь момент движения начинается с попытки сдвинуть повозку. Если положение изменится, то конь ни при каких условиях не сдвинет её с места. Его копыта будут проскальзывать по дороге, и движения не будет.

В детстве, катая друг друга на санках, каждый мог столкнуться с таким примером. Если на санки сядут два-три ребенка, то усилий одного явно недостаточно, чтобы сдвинуть их с места.

Падение тел на поверхность земли, объясняемое Аристотелем («Каждое тело знает свое место») можно опровергнуть на основании вышеизложенного. Предмет движется к земле под действием такой же силы, что и Земля к нему. Сравнив их параметры (масса Земли намного больше массы тела), в соответствии со вторым законом Ньютона, утверждаем, что ускорение предмета во столько же раз больше ускорения Земли. Мы наблюдаем именно изменение скорости тела, Земля не смещается с орбиты.

Границы применимости

Современная физика законы Ньютона не отрицает, а лишь устанавливает границы их применимости. До начала XX века физики не сомневались в том, что эти законы объясняют все явления природы.

1, 2, 3 закон Ньютона полностью выявляет причины поведения макроскопических тел. Движение объектов с незначительными скоростями полностью описывается этими постулатами.

Попытка пояснить на их основании движение тел со скоростями, близкими к скорости света, обречена на провал. Полное изменение свойств пространства и времени при этих скоростях не позволяет использовать динамику Ньютона. Кроме того, законы меняют свой вид в неинерциальных СО. Для их применения вводится понятие силы инерции.

Пояснить движение астрономических тел, правила их расположения и взаимодействия могут законы Ньютона. Закон всемирного тяготения вводится с этой целью. Увидеть же результат притяжения малых тел невозможно, ведь сила мизерна.

Взаимное притяжение

Известна легенда, согласно которой господина Ньютона, сидевшего в саду и наблюдавшего падение яблок, посетила гениальная идея: объяснить движение предметов вблизи поверхности Земли и движение космических тел на основании взаимного притяжения. Это не так далеко от истины. Наблюдения и точный расчет касались не только падения яблок, но и перемещения Луны. Закономерности этого движения приводят к выводам, что сила притяжения возрастает с увеличением масс взаимодействующих тел и уменьшается с увеличением расстояния между ними.

Опираясь на второй и третий законы Ньютона, закон всемирного тяготения формулируют следующим образом: все тела во вселенной притягиваются друг к другу с силой, направленной вдоль линии, соединяющей центры тел, пропорциональной массам тел и обратно пропорциональной квадрату расстояния между центрами тел.

Математическая запись: F = GMm/r², где F – сила притяжения, M, m – массы взаимодействующих тел, r – расстояние между ними. Коэффициент пропорциональности (G = 6.62 х 10^-11 Нм²/кг²) получил название гравитационной постоянной.

Физический смысл: эта постоянная равна силе притяжения между двумя телами массами по 1 кг на расстоянии 1 м. Понятно, что для тел небольших масс сила столь незначительна, что ею можно пренебречь. Для планет, звезд, галактик сила притяжения настолько огромна, что полностью определяет их движение.

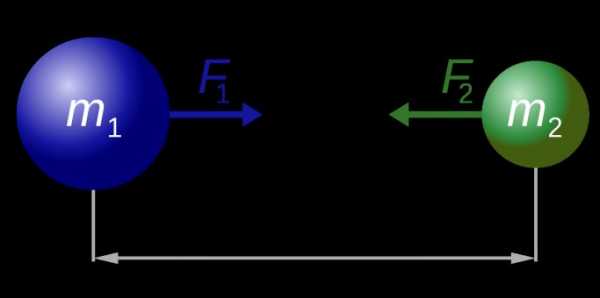
Именно закон притяжения Ньютона утверждает, что для запуска ракет необходимо топливо, способное создать такую реактивную тягу, чтобы преодолеть влияние Земли. Скорость, необходимая для этого – первая космическая скорость, равная 8 км/с.

Современная технология изготовления ракет позволяет запускать беспилотные станции как искусственные спутники Солнца к другим планетам, чтобы их исследовать. Скорость, развиваемая таким аппаратом, – вторая космическая скорость, равная 11 км/с.

Алгоритм применения законов

Решение задач динамики подчиняется определенной последовательности действий:

Провести анализ задачи, выявить данные, вид движения.
Выполнить рисунок с указанием всех сил, действующих на тело, и направления ускорения (при его наличии). Выбрать систему координат.
Записать первый или второй законы, в зависимости от наличия ускорения тела, в векторной форме. Учесть все силы (равнодействующая сила, законы Ньютона: первый, если скорость тела не меняется, второй, если есть ускорение).
Уравнение переписать в проекциях на выбранные оси координат.
Если полученной системы уравнений недостаточно, то записать иные: определения сил, уравнения кинематики и т. п.
Решить систему уравнений относительно искомой величины.
Выполнить проверку размерностей, чтобы определиться с правильностью полученной формулы.
Вычислить.

Обычно этих действий вполне достаточно для решения любой стандартной задачи.

fb.ru

Законы Ньютона Википедия

Первый закон Ньютона

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[3]:

Историческая формулировка

Ньютон сформулировал первый закон механики так:

Второй закон Ньютона

Современная формулировка

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}

Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:

dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},}

Замечания

ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}}

или

dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}

Историческая формулировка

Исходная формулировка Ньютона:

Третий закон Ньютона

Современная формулировка

F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.}

Историческая формулировка

Ньютон дал следующую формулировку закона^[1]:

Следствия законов Ньютона

Уравнения движения

Закон сохранения импульса

Закон сохранения механической энергии

Законы Ньютона и силы инерции

Законы Ньютона в логике курса механики

Исторический очерк

Страница «Начал» Ньютона с аксиомами механики

Оригинальный текст (лат.)
   LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.
   LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.
   LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.

Русский перевод этих формулировок законов см. в предыдущих разделах.

Примечания

↑ ¹ ² ³ Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
↑ ¹ ² ³ ⁴ Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
↑ ¹ ² Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494-495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ ¹ ² Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3-8.
↑ «”Силы инерции” — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186-197;
↑ ¹ ² Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;

Литература

Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
Спасский Б. И.. История физики. М., «Высшая школа», 1977.
Том 1. Часть 1-я; Часть 2-я
Том 2. Часть 1-я; Часть 2-я
Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
Feynman, R. P. The Feynman Lectures on Physics / R. P. Feynman, Leighton, Sands. — 2nd. — Pearson/Addison-Wesley, 2005. — Vol. Vol. 1. — ISBN 0-8053-9049-9.
Fowles, G. R. Analytical Mechanics / G. R. Fowles, Cassiday. — 6th. — Saunders College Publishing, 1999. — ISBN 0-03-022317-2.
Likins, Peter W. Elements of Engineering Mechanics. — McGraw-Hill Book Company, 1973. — ISBN 0-07-037852-5.
Marion, Jerry. Classical Dynamics of Particles and Systems / Jerry Marion, Thornton. — Harcourt College Publishers, 1995. — ISBN 0-03-097302-3.
NMJ Woodhouse. Special Relativity. — London/Berlin : Springer, 2003. — P. 6. — ISBN 1-85233-426-6.
Newton, Isaac, “Mathematical Principles of Natural Philosophy”, 1729 English translation based on 3rd Latin edition (1726), volume 1, containing Book 1, especially at the section Axioms or Laws of Motion, starting page 19.
Newton, Isaac, “Mathematical Principles of Natural Philosophy”, 1729 English translation based on 3rd Latin edition (1726), volume 2, containing Books 2 & 3.
Thomson, W (Lord Kelvin), and Tait, P G, (1867), Treatise on natural philosophy, volume 1, especially at Section 242, Newton’s laws of motion.

Ссылки

wikiredia.ru

Законы Ньютона | Virtual Laboratory Wiki

Зако́ны Нью́тона — законы классической механики, позволяющие записать уравнения движения для любой механической системы.

Первый закон Ньютона Править

Существуют такие системы отсчета, относительно которых тела сохраняют свою скорость постоянной, если на них не действуют другие тела и поля (или их действие взаимно скомпенсировано).

По сути, этот закон постулирует инерцию тел, то есть их свойство сопротивляться изменению их т

го состояния.

Второй закон Ньютона Править

Второй закон Ньютона— дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как мерило проявления инерции материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Второй закон Ньютона утверждает:

В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально приложенной к ней силе и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

где $ \vec a $ — ускорение материальной точки;
$ \vec {F} $ — сила, приложенная к материальной точке;
$ m $ — масса материальной точки.

Или в более известном виде:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна действующей на неё силе.

где $ \vec p $ — импульс точки,

где $ \vec v $ — скорость точки;

$ t $ — время;
$ \frac{d \vec p}{dt} $ — производная импульса по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:

или

Нельзя рассматривать частный случай (при $ \vec {F} = 0 $) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Третий закон Ньютона Править

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой $ \vec{F}_{1 \to 2} $, а второе — на первое с силой $ \vec{F}_{2 \to 1} $. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Сам закон: Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел $ U(|{r}_1 – {r}_2|) $. Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:

Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.

Например массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес).

Завершили математизацию механики Эйлер и Лагранж.

Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
Спасский Б. И.. История физики. М., «Высшая школа», 1977.
Кудрявцев П. С. Курс истории физики. Уч. пособие для физ.-мат. факультетов пед. институтов. М., «Просвещение», 1974.

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Законы Ньютона. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

ru.vlab.wikia.com