Метод Крамера . Применение для систем линейных уравнений
Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами – числа
Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй – при котором из неизвестным он находится.
Если определитель матрицы не равен нулю
то система линейных алгебраических уравнений имеет единственное решение.
Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.
Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной
Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае – несовместимой.
Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.
Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Эквивалентные преобразования СЛАУ
1) перестановка местами уравнений;
2) умножение (или деление) уравнений на отличное от нуля число;
3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.
Решение СЛАУ можно найти разными способами.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:
– определители, образованные с заменой -го столбца, столбцом из свободных членов.
Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
—————————————————————
Задача 1.
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера
Решение.
Найдем определитель матрицы коэффициентов при неизвестных
Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:
По формулам Крамера находим неизвестные
Итак единственное решение системы.
Задача 2.
Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.
Решение.
Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.
Найдем составляющие определителя:
Подставим найденные значения в определитель
Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:
Разложим каждый из определителей по столбцу в котором есть больше нулей.
По формулам Крамера находим
Решение системы
Данный пример можно решить математическим калькулятором YukhymCALC . Фрагмент программы и результаты вычислений наведены ниже.

—————————–
МЕТОД К Р А М Е Р А
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Посмотреть материалы:
{jcomments on}
yukhym.com
Метод Крамера
Пусть дана система трех линейных уравнений:
 (1)
(1)
Для
решения системы линейных уравнений
методом Крамера из коэффициентов при
неизвестных составляется главный
определитель
системы .
Для системы (1) главный определитель
имеет вид  .
.
Далее
составляются определители по переменным  ,
, ,
, .
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть
.
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть
 ,
,  ,
, .
.
Тогда решение системы находится по формулам Крамера
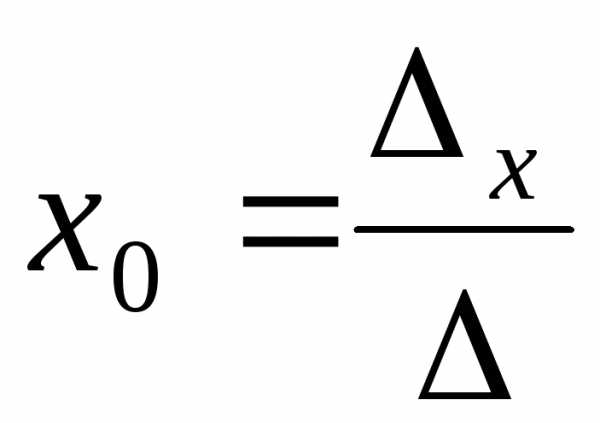 ,
,  ,
, 
Следует отметить, что система имеет единственное решение , если главный определитель
 .Если же
.Если же 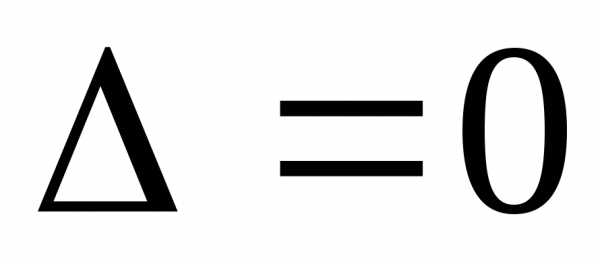 и
и  =
0,
=
0, =
0,
=
0, =
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же
=
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же  и
и 
 0,
или
0,
или
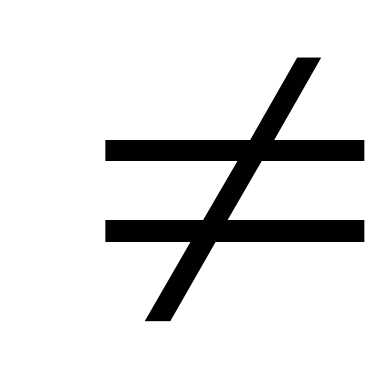 0,или
0,или
 0,
то система уравнений несовместна, то
есть решений не имеет.
0,
то система уравнений несовместна, то
есть решений не имеет.Пример
Решить
систему уравнений методом Крамера: 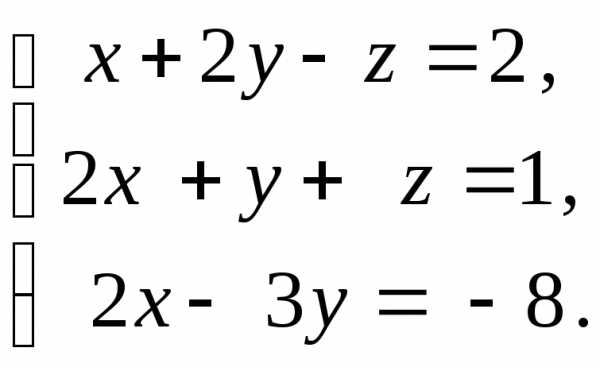
Решение:
1) Составим и вычислим главный определитель системы, состоящий из коэффициентов при неизвестных.
.
Следовательно, система имеет единственное решение.
2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в столбцом из свободных членов.
По формулам Крамера находим неизвестные:
, 
 .
.Сделаем проверку, чтобы убедиться в правильности решения
,
т.е. 
 .
.
,
т.е. 
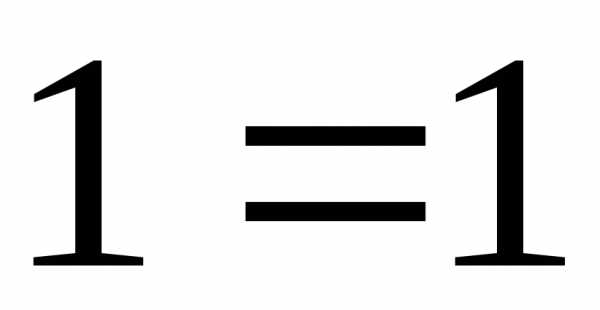
,
т.е. 
Ответ:
Пример
Решить систему уравнений методом Крамера:

Решение:
1) Составим и вычислим главный определитель системы из коэффициентов при неизвестных:
.
Следовательно, система не имеет единственного решения.
2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в столбцом из свободных членов:
.

 ,
следовательно, система несовместна.
,
следовательно, система несовместна.Ответ: система несовместна.
Метод Гаусса
Метод Гаусса состоит из двух этапов. Первый этап заключается в последовательном исключении переменных из уравнений системы при помощи действий, не нарушающих равносильности системы. Например, рассмотрим два первых уравнения системы (1).
 (1)
(1)
Необходимо
путем сложения этих двух уравнений
получить уравнение, в котором отсутствует
переменная 
 ,
а второе на (
,
а второе на ( )
и сложим полученные уравнения
)
и сложим полученные уравнения+
Заменим
коэффициент перед y, z и свободный член на  ,
, и
и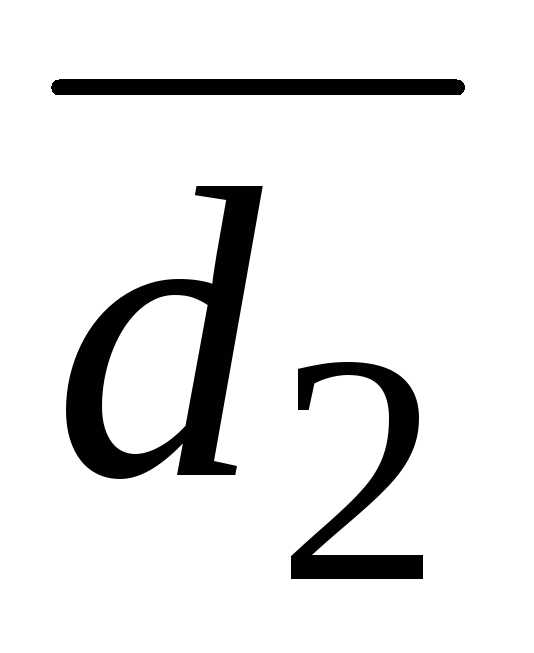

Заметим, что во втором уравнении отсутствует переменная x.
Проведя аналогичные действия над первым и третьим уравнениями системы (1), а затем над полученными в результате сложения вторым и третьим уравнениями, преобразуем систему (1) к виду

 (2)
(2)
Такой результат возможен, если система имеет единственное решение. В этом случае решение находится при помощи обратного хода метода Гаусса (второй этап). Из последнего уравнения системы (2) находим неизвестную переменную
Иногда в результате сложения двух уравнений суммарное уравнение может принять один из видов:
А)
,
где .
Это означает, что решаемая система
несовместна.
.
Это означает, что решаемая система
несовместна.
Б)
,
то есть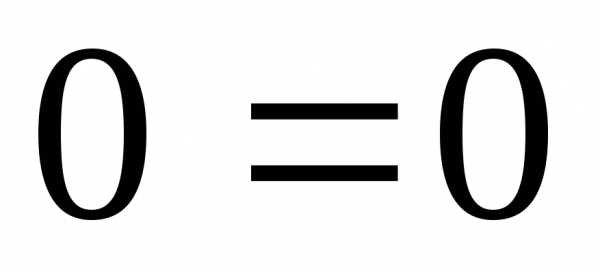 .
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
.
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
Пример
Решить
систему методом Гаусса: 
Решение:
Рассмотрим следующий способ осуществления первого этапа решения методом Гаусса. Запишем три строки коэффициентов при неизвестных и свободных членов, соответствующих трем уравнениям системы. Свободные члены отделим от коэффициентов вертикальной линией, а под третьей строкой проведем горизонтальную прямую.
Первую
строку, которая соответствует первому
уравнению системы, обведем – коэффициенты
в этом уравнении останутся неизменными.
Вместо второй строки (уравнения) надо
получить строку (уравнение), где
коэффициент при  равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент при
равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент при равен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.
равен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.
Все описанные действия изображены в таблице 1 при помощи арифметических знаков и стрелок. Обведенные в таблице строки запишем снова в виде уравнений (3) и, применив обратный ход метода Гаусса, найдем значения переменных x, y и z.
Таблица 1
1 | 1 | -2 | 6 | *(-2) | *(-5) |
2 | 3 | -7 | 16 | ||
5 | 2 | 1 | 16 | ||
0 | 1 | -3 | 4 | *( 3) | |
0 | -3 | 11 | -14 | ||
0 | 0 | 2 | -2 |
Восстанавливаем систему уравнений, полученную в результате наших преобразований:
 (3)
(3)
Обратный ход метода Гаусса
Из третьего уравнения находим.
Во
второе уравнение системы
подставим найденное значение ,
получимили
,
получимили .
.
Из
первого уравнения
,
подставляя уже найденные значения
переменных, получаем,
то есть .
.
Чтобы убедиться в правильности решения, проверку необходимо сделать во всех трех уравнениях системы.
Проверка:
,
получим 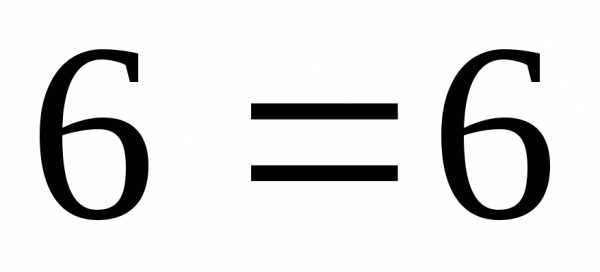
,
получим 
,
получим 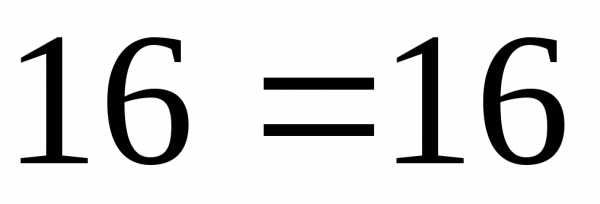
значит, система решена верно.
Ответ: 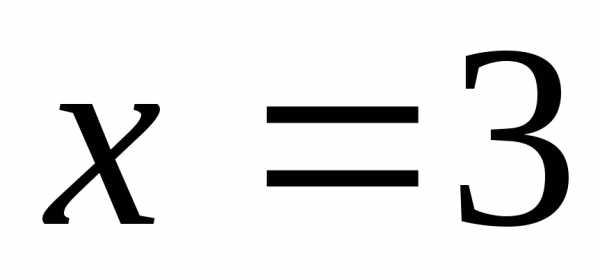 ,
, ,
, .
.
Пример
Решить
систему методом Гаусса: 
Решение:
Порядок действий в этом примере аналогичен порядку в предыдущем примере, а конкретные действия указаны в таблице 2.
Таблица2
2 | 2 | 1 | 1 | *(-3) | *(-5) |
3 | 5 | -2 | 0 | *2 | |
5 | 3 | 6 | -2 | *2 | |
0 | 4 | -7 | -3 | ||
0 | -4 | 7 | -9 | ||
0 | 0 | 0 | -12 |
В результате преобразований получим уравнение вида , следовательно, заданная система несовместна.
Ответ: система несовместна.
Пример
Решить
систему методом Гаусса: 
Решение:
Таблица 3
1 | 2 | -1 | 0 | *(-2) | *(-4) |
2 | -1 | 3 | 1 | ||
4 | 3 | 1 | 1 | ||
0 | -5 | 5 | 1 | *(-1) | |
0 | -5 | 5 | 1 | ||
0 | 0 | 0 | 0 |
В результате преобразований получим уравнение вида , которое исключается из рассмотрения. Таким образом, имеем систему уравнений, в которой число неизвестных 3, а число уравнений 2.

Система имеет бесчисленное множество решений. Чтобы отыскать эти решения, введем одну свободную переменную. (Число свободных переменных всегда равно разности между числом неизвестных и числом уравнений, оставшихся после преобразования системы. В нашем случае 3 – 2 = 1).
Пусть  – свободная переменная.
– свободная переменная.
Тогда
из второго уравнения найдем
,
откуда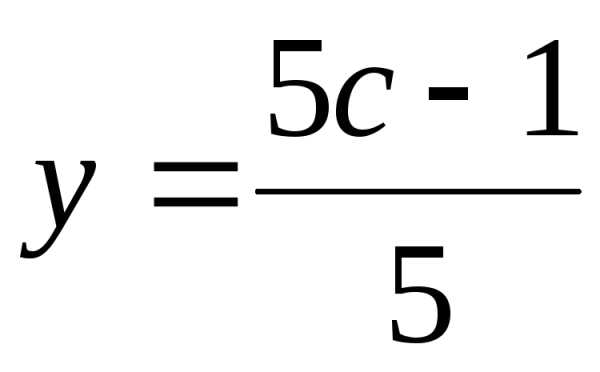 ,
а затем найдемx из первого уравнения
или.
,
а затем найдемx из первого уравнения
или.
Таким
образом,  ;
; ;
; .
.
Сделаем
проверку в уравнениях, которые не
участвовали в нахождении  и
и ,
то есть во втором и в третьем уравнениях
первоначальной системы.
,
то есть во втором и в третьем уравнениях
первоначальной системы.
Проверка:
или
,
получаем .
.
или
,
получаем .
.
Система
решена верно. Давая произвольной
постоянной  различные значения, будем получать
различные значенияx, y и z.
различные значения, будем получать
различные значенияx, y и z.
Ответ: 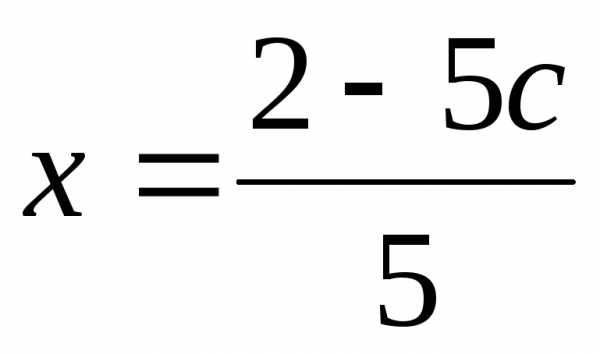 ;
; ;
; .
.
21
studfiles.net
Лекция 3 СЛУ Метод Крамера
6
Лекция 3. Системы линейных уравнений.
метод Крамера
Содержание
Основные определения.
Метод Крамера (определителей) решения систем линейных уравнений.
1. Основные определения
Системой
 линейных уравнений с
линейных уравнений с неизвестными называется совокупность уравнений, в
каждом из которых неизвестные присутствуют
в первой степени:
неизвестными называется совокупность уравнений, в
каждом из которых неизвестные присутствуют
в первой степени:
где
числа
– коэффициенты при неизвестных,-
номер уравнения,-
номер неизвестной, –
свободные члены.
–
свободные члены.
,
который при подстановке в каждое уравнение системы вместо неизвестных соответственно обращает их в верные равенства.
Решить СЛУ – это значит указать все решения системы, то есть такие наборы значений неизвестных, которые обращают уравнения системы в тождества.
Система линейных уравнений называется:
а) совместной, если она имеет хотя бы одно решение;
б) несовместной, если она не имеет решений;
в) определенной, если она имеет единственное решение;
г) неопределенной, если она имеет бесконечное множество решений;
д) однородной, если все свободные члены равны нулю ;
е) неоднородной,
если есть  .
.
2. Метод Крамера (определителей) решения систем линейных уравнений
Правило (метод) Крамера применяется к системам, у которых число уравнений равно числу неизвестных. Этот метод использует определители.
2.1. Число уравнений и неизвестных равно 2
Рассмотрим систему линейных уравнений

Вычисляются определители:
 ,
,  ,
,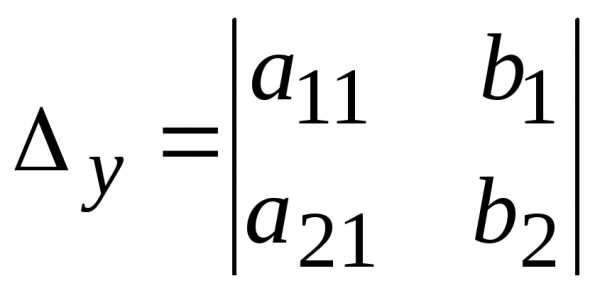 .
.
Здесь
 –
определитель системы, составленный из
коэффициентов при неизвестных;
–
определитель системы, составленный из
коэффициентов при неизвестных;
 –
это определитель, полученный из
определителя
–
это определитель, полученный из
определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при на столбец свободных членов;
на столбец свободных членов;
 –
это определитель, полученный из
определителя
–
это определитель, полученный из
определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при на столбец свободных членов.
на столбец свободных членов.
1. Если  ,
тосистема совместная
и определенная,
то есть имеет единственное
решение, которое находится по формулам
Крамера:
,
тосистема совместная
и определенная,
то есть имеет единственное
решение, которое находится по формулам
Крамера:

 .
.
2. Если  ,
а хотя бы один из определителей
,
а хотя бы один из определителей ,
, отличен от нуля, тосистема
не имеет решений (несовместная).
отличен от нуля, тосистема
не имеет решений (несовместная).
3. Если , тосистема имеет бесконечно много решений (совместная и неопределенная).
Пример 1. Решить с помощью метода Крамера систему уравнений

Решение
, поэтому СЛУ имеет единственное решение.
, .
Тогда  ;.
;.
Ответ: система уравнений совместна и определенна, ее единственное решение .
Пример 2. Решить с помощью метода Крамера систему уравнений
 .
.
Решение
Определитель системы равен нулю: , однако один из вспомогательных определителей не равен нулю:, значит, СЛУ не имеет решений, то есть СЛУнесовместная.
Пример 3. Решить с помощью метода Крамера систему уравнений

Решение
 ,
,  ,
, .
.
Поэтому система имеет бесконечно много решений.
Разделив
коэффициенты 2-го уравнения на 3, получим:  Оставим только одно из этих уравнений:.
Оставим только одно из этих уравнений:.
Выразим  через
через :
: ,
значение
,
значение – любое действительное число. Это и есть
выражение дляобщего
решения СЛУ.
Ответ можно записать так:
– любое действительное число. Это и есть
выражение дляобщего
решения СЛУ.
Ответ можно записать так:  ,
где
,
где .
.
Придавая  различные значения, будем получать
бесконечное множествочастных
решений.
Например, при
различные значения, будем получать
бесконечное множествочастных
решений.
Например, при  получим
получим и первое частное решение
и первое частное решение .
При
.
При получим
получим и второе частное решение
и второе частное решение ,
и так далее.
,
и так далее.
2.2. Число уравнений и неизвестных равно 3
Рассмотрим СЛУ
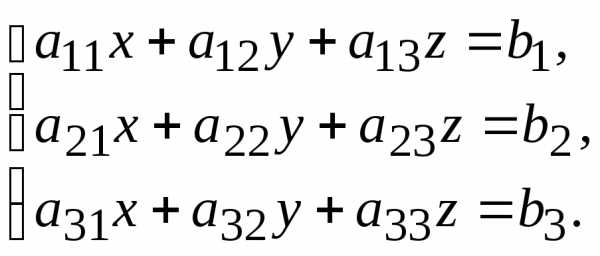
Вычисляются определители:
 ,
,  ,
,
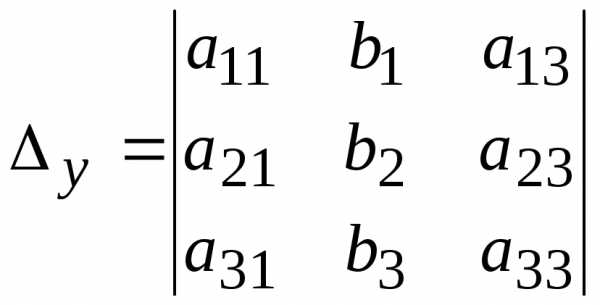 ,
.
,
.
1. Если  ,
то системаимеет единственное
решение, которое находится по формулам
Крамера:
,
то системаимеет единственное
решение, которое находится по формулам
Крамера:
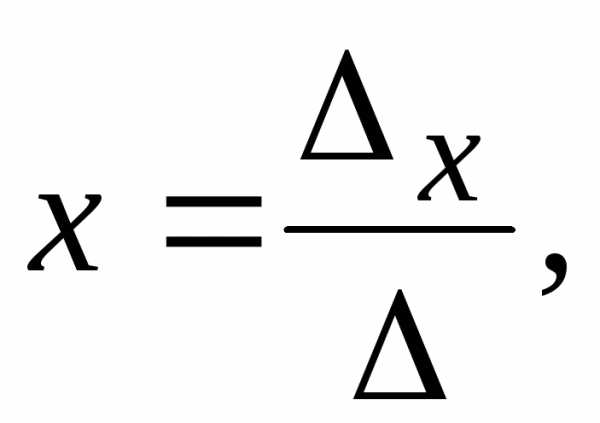
 ,
,  .
.
2. Если  ,
а хотя бы один из определителей
,
а хотя бы один из определителей ,
, ,
, отличен от нуля, тосистема
не имеет решений.
отличен от нуля, тосистема
не имеет решений.
3.Если , то системаимеет бесконечно много решений.
Пример
4. Решить
систему линейных уравнений  .
.
Составим определитель из коэффициентов при неизвестных и вычислим его: ,
значит, СЛУ имеет единственное решение.
Найдем вспомогательные определители и значения неизвестных.

Ответ: Система совместная и определенная, единственное решение .
Рассмотрим пример, в котором СЛУ имеет бесконечное множество решений, и они будут найдены с применением формул Крамера.
Пример 5. Решить СЛУ
Решение
Вычислим определитель системы:
Заметим, что третье уравнение системы равно сумме первых двух уравнений, т.е. зависит от первых двух уравнений.
Отбросив
третье уравнение, получим равносильную
систему двух уравнений с тремя
неизвестными: 
Оставим в левой части системы те неизвестные, коэффициенты при которых образуют определитель, не равный нулю.
Например,
коэффициенты при 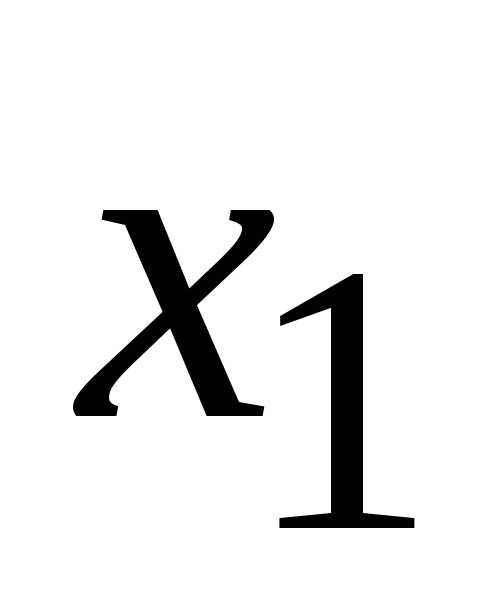 и
и образуют определитель.
Поэтому оставим в левой части уравнений
слагаемые с
образуют определитель.
Поэтому оставим в левой части уравнений
слагаемые с и
и ,
а слагаемые с
,
а слагаемые с перенесем в правую часть с противоположным
знаком.
перенесем в правую часть с противоположным
знаком.
Неизвестное назовем свободным, а неизвестные и– базисными неизвестными.
Запишем
систему в виде  и применим
к ней правило Крамера:
и применим
к ней правило Крамера:
;
Выражение
–
общее
решение неопределенной
СЛУ, где  – любое действительное число.
– любое действительное число.
Из общего решения можно получить частные решения, если придать свободной неизвестной какое-то конкретное значение.
Например, пусть , тогда; тогда частное решение. И так далее.
Контрольные вопросы
Запишите общий вид системы 2 линейных уравнений с тремя неизвестными.
Что называется решением СЛУ?
Что значит «решить систему линейных уравнений»?
Какие системы линейных уравнений называются совместными и несовместными?
При каком условии система линейных уравнений снеизвестными имеет единственное решение?
Напишите формулы Крамера для решения системы линейных уравнений. В каком случае они применимы?
Как, зная общее решение, записать частное решение неопределенной системы?
studfiles.net
1.3. Системы линейных уравнений. Метод Крамера
Рассмотрим систему 3-х уравнений с тремя неизвестными
 (1.3)
(1.3)
Используя определители 3-го порядка, решение такой системы можно записать в таком виде:
(1.4)
если 0. Здесь
 (1.5)
(1.5)
Это есть формулы Крамерарешения системы трех линейных уравнений с тремя неизвестными.
Пример 1.6.Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель основной матрицы системы:

Поскольку 0, то для нахождения решения системы можно применить метод Крамера. Вычислим остальные определители:
Тогда
Проверка:

Следовательно, решение найдено правильно.
Теорема Крамера.Квадратная система линейных неоднородных уравнений n-го порядка с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение, и это решение вычисляется по формулам:

где – определитель основной матрицы, i – определитель матрицы, полученной из основной, заменой i-го столбца столбцом свободных членов.
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо вообще не имеет решений, либо имеет бесконечное множество решений.
1.4. Матричный метод. Обратная матрица
Матрица А–1называетсяобратнойматрицей по отношению к матрицеА, если выполняется равенствоAA–1=A–1A=E. Только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрицаАимела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля:detA0.
Пример 1.7.Решить систему линейных уравнений матричным методом (при помощи обратной матрицы).

Решение. Запишем исходную систему уравнений в матричном виде:
 .
.
Тогда решение можно формально записать в виде:
 .
.
Таким образом, чтобы найти решение системы, нужно вычислить обратную матрицу
 .
.
Найдем ее
1) Вычисляем
определитель исходной матрицы:  .
.
2) Транспонируем
матрицу  .
.
3) Находим все алгебраические дополнения транспонированной матрицы:
4) Составляем присоединенную матрицу, для этого вместо элементов транспонированной матрицы ставим найденные алгебраические дополнения:
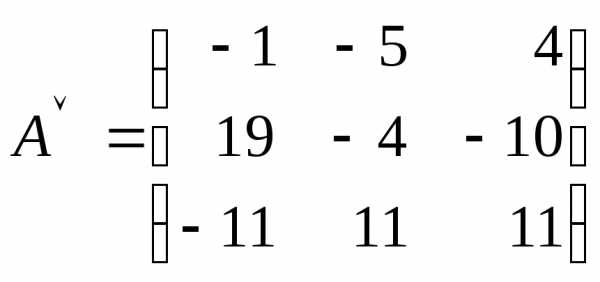
5) Записываем обратную матрицу, для этого все элементы присоединенной матрицы делим на определитель исходной матрицы:
.
6) Сделаем проверку:
.
Следовательно, обратная матрица найдена правильно.
Теперь, используя найденную обратную матрицу можно найти решение исходной системы:
.
1.5. Метод Гаусса
Рассмотрим произвольную систему линейных уравнений
 (1.5)
(1.5)
В общем случае nm.
Задача теории систем линейных уравнений состоит в том, чтобы найти все решения системы. При этом возможны три случая. 1) Система вообще не имеет решений. Системы линейных уравнений, не имеющие ни одного решения, называются несовместными. 2) Система имеет хотя бы одно решение. такие системы называютсясовместными. 3) Система имеет только одно решение. Такие системы называютсяопределёнными.
Метод Гаусса (метод последовательного исключения неизвестных)заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Рассмотрим метод Гаусса на конкретных примерах.
Пример 1.8. Решить систему линейных уравнений методом Гаусса.

Решение.Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее к треугольному виду:
 .
.
Теперь выписываем соответствующую укороченную систему уравнений. Из последнего уравнения находим значение z и подставляем его во второе уравнение. После этого из второго уравнения находим y. Найденные значения y и z подставляем в первое уравнение, из которого затем находим значение x:

Эта тройка чисел будет являться единственным решением системы.
Пример 1.9.Решить систему методом Гаусса:

Решение. Выписываем и преобразуем расширенную матрицу системы
Записываем упрощенную систему уравнений:

Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна.
Пример 1.10. Найти общее решение методом Гаусса
Решение. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее трапециевидной форме:
-1
4
3
3
:15
.Теперь выписываем соответствующую укороченную систему уравнений:
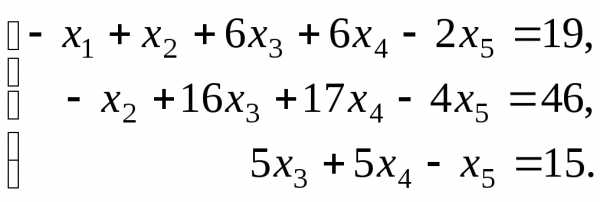
Пусть переменные x4 и x5 будут свободными, тогда переменные x1, x2 и x3 будут основными (или базисными). Их мы оставим в левой части:

Разрешая эту систему относительно x1, x2 и x3 получим

Это есть общее решение системы. Запишем это решение в параметрическом виде. Пусть x4=a и x5=5b. Тогда общее решение системы запишется в виде:

Давая числам a и b различные значения, будем получать частные решения. Например, если a=0, b=1, то x1=–7, x2=–2, x3=4, x4=0, x5=5.
studfiles.net
Примеры решения систем линейных алгебраических уравнений методом Крамера
Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .
Решение.
Основная матрица системы имеет вид . Вычислим ее определитель по формуле :
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .
Вычисляем эти определители:
Находим неизвестные переменные x1 и x2 по формулам :
Выполним проверку. Подставим полученные значения x1 и x2 в исходную систему уравнений:
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера .
Решение.
Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле
Имеем
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :
Таким образом,
Ответ:
.
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x1, x2, …, xn. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместоx1, x2 и x3). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:
Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:
Осталось найти неизвестные переменные по формулам :
Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите раздел операции над матрицами):
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3.
Пример.
Решите методом Крамера систему линейных уравнений , гдеa и b – некоторые действительные числа.
Решение.
Вычислим определитель основной матрицы системы:
Определитель отличен от нуля, следовательно, можно применить метод Крамера.
Находим неизвестные переменные
Рекомендуем проверить полученные результаты.
Ответ:
.
Пример.
Найдите решение системы уравнений методом Крамера, – некоторое действительное число.
Решение.
Вычислим определитель основной матрицы системы: . Область значений выражения есть интервал , поэтому при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем и :
Таким образом, .
Выполним проверку:
Уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
Пример.
Решите систему линейных алгебраических уравнений методом Крамера .
Решение.
Вычислим определитель основной матрицы системы уравнений:
Определитель основной матрицы равен нулю, следовательно, метод Крамера не подходит для решения такой системы уравнений.
Пример.
Методом Крамера найдите решение СЛАУ .
Решение.
Эта система однородная, так как все свободные члены равны нулю. Определитель основной матрицы отличен от нуля , поэтому ее единственным решением является x1 = 0, x2 = 0. О таких СЛАУ мы уже упоминали вышев замечании.
Ответ:
x1 = 0, x2 = 0.
Пример.
Найдите решение системы четырех линейных алгебраических уравнений содержащую четыре неизвестных переменных.
Решение.
Сразу скажем, что не будем подробно описывать вычисление определителей матриц, так как это выходит за рамки данной статьи.
Вычислим определитель основной матрицы системы, разложив его по элементам второй строки:
Определитель основной матрицы системы отличен от нуля, поэтому можно воспользоваться методом Крамера для решения системы.
Найдем :
аналогично вычисляются
Таким образом,
Ответ:
.
К началу страницы
Подведем итог.
Метод Крамера позволяет находить решение систем линейных алгебраических уравнений, если определитель основной матрицы отличен от нуля. По сути метод сводится к вычислению определителей матриц порядка n на n и применению соответствующих формул для нахождения неизвестных переменных.
megaobuchalka.ru
Метод Крамера — Циклопедия
Видеоурок “Метод определителей (Крамера)” // Математика от alwebra.com.ua [4:20]Метод Крамера — это способ решения системы линейных уравнений, при котором неизвестные вычисляются в виде отношений определителей.
[править] Описание метода
Суть метода Крамера состоит в расчёте определителей и применении формул Крамера, по которым решение xi равно отношению i-го вспомогательного определителя Δi к главному Δ.
Для решения методом Крамера системы линейных уравнений вида Ax=b (где A – квадратная матрица nxn коэффициентов системы, а b – вектор свободных членов системы), сначала найдём главный определитель системы Δ. Метод Крамера применим, если главный определитель системы Δ≠0.
[править] Решение системы двух уравнений с двумя неизвестными
[править] Решение системы трёх уравнений с тремя неизвестными
[править] Решение системы четырёх уравнений с четырьмя неизвестными
[править] Методы решения систем уравнений:
[править] Численные методы:
- Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.
- Участник:Logic-samara
cyclowiki.org
Метод Крамера и его применение
Метод Крамера – это один из точных методов решения систем линейных алгебраических уравнений (СЛАУ). Точность его обусловлена использованием определителей матрицы системы, а также некоторыми ограничениями, накладываемыми в ходе доказательства теоремы.
Системой линейных алгебраических уравнений с коэффициентами, принадлежащими, например, множеству R – действительных чисел, от неизвестных x1, x2 ,…, xn называют набор выражений вида
ai2 x1+ai2 x2 +… ain xn =bi при i=1, 2, … ,m, (1)
где aij, bi – действительные числа. Каждое из этих выражений называется линейным уравнением, aij – коэффициентами при неизвестных, bi – свободными коэффициентами уравнений.
Решением системы (1) называют n-мерный вектор x° = (x1°, x2°,…, xn°), при подстановке которого в систему вместо неизвестных x1, x2 ,…, xn каждая из строк в системе становится верным равенством.
Система называется совместной, если у нее есть хотя бы одно решение, и несовместной, если ее множество решений совпадает с пустым множеством.
Необходимо помнить, что для того, чтобы найти решение систем линейных алгебраических уравнений, используя метод Крамера, матрицы систем должны быть квадратными, что по сути означает одинаковое количество неизвестных и уравнений в системе.
Итак, чтобы использовать метод Крамера, необходимо как минимум знать, что такое матрица систем линейных алгебраических уравнений и как она выписывается. А во-вторых, понимать, что называют определителем матрицы и владеть навыками его вычисления.
Предположим, что этими знаниями вы владеете. Замечательно! Тогда вам остается всего лишь запомнить формулы, определяющие метод Крамера. Для упрощения запоминания воспользуемся следующими обозначениями:
Det – главный определитель матрицы системы;
deti – это определитель матрицы, полученной из основной матрицы системы, если заменить i-й столбец матрицы на вектор-столбец, элементами которого являются правые части систем линейных алгебраических уравнений;
n – количество неизвестных и уравнений в системе.
Тогда правило Крамера вычисления i-й компоненты xi (i=1,..n) n-мерного вектора x можно записать в виде
xi = deti/ Det, (2).
При этом Det строго отличен от нуля.
Единственность решения системы при ее совместности обеспечивает условие неравенства нулю главного определителя системы. В противном случае, если сумма (xi), возведенных в квадрат, строго положительна, то СЛАУ с квадратной матрицей будет несовместной. Это может произойти, в частности, когда, по крайней мере, один из deti отличен от нуля.
Пример 1. Решить трехмерную систему ЛАУ, используя формулы Крамера.
x1 + 2 x2 + 4 x3 = 31,
5 x1 + x2 + 2 x3 = 29,
3 x1 – x2 + x3 =10.
Решение. Выпишем матрицу системы построчно, где Ai – это i -я строка матрицы.
A1=(1 2 4), A2=(5 1 2), A3=(3 –1 1).
Столбец свободных коэффициентов b=(31 29 10).
Главный определитель Det системы равен
Det= a11 a22 a33 + a12 a23 a31 + a31 a21 a32 – a13 a22 a31 – a11 a32 a23 – a33 a21 a12 = 1 – 20 + 12 – 12 + 2 – 10 = –27.
Для вычисления det1 используем подстановку a11= b1, a21 = b2, a31 = b3. Тогда
det1= b1 a22 a33 + a12 a23 b3 + a31 b2 a32 – a13 a22 b3 – b1 a32 a23 – a33 b2 a12 =…= –81.
Аналогично, для вычисления det2 используем подстановку a12= b1, a22 = b2, a32 = b3 и, соответственно, для вычисления det3 – a13= b1, a23 = b2, a33 = b3.
Тогда можете проверить, что det2 = –108, а det3 = – 135.
Согласно формулам Крамера находим x1 = -81/(-27) = 3, x2 = -108/(-27) = 4, x3 = -135/(-27) = 5.
Ответ: x°=(3,4,5).
Опираясь на условия применимости данного правила, метод Крамера решения систем линейных уравнений можно использовать опосредованно, например, с целью исследовать систему на возможное число решений в зависимости от величины некоторого параметра k.
Пример 2. Определить, при каких значениях параметра k неравенство |kx – y – 4|+|x + ky + 4|<=0 имеет ровно одно решение.
Решение.
Данное неравенство в силу определения модуля функции может быть выполнено, только если оба выражения одновременно равны нулю. Поэтому эта задача сводится к нахождению решения линейной системы алгебраических уравнений
kx – y = 4,
x + ky = –4.
Решение данной системы единственное, если ее главный определитель
Det = k^{2} + 1 отличен от нуля. Очевидно, что это условие выполняется для всех действительных значений параметра k.
Ответ: для всех действительных значений параметра k.
К задачам данного вида также могут быть сведены многие практические задачи из области математики, физики или химии.
fb.ru
