Репетитор-онлайн — подготовка к ЦТ
Пример 9. Уравнение движения материальной точки имеет вид x(t) = (9,0 − 6,0t + 2,0t2) м, где координата задана в метрах, время — в секундах. Определить среднюю путевую скорость и величину средней скорости перемещения материальной точки за первые три секунды движения.
Решение. Для определения средней скорости перемещения необходимо рассчитать перемещение материальной точки. Модуль перемещения материальной точки в интервале времени от t1 = 0 с до t2 = 3,0 с вычислим как разность координат:
|Δr→|=|x(t2)−x(t1)|,
где
x(t1)=9,0−6,0t1+2,0t12=9,0−6,0⋅0+2,0⋅02=9,0 м;
x(t2)=9,0−6,0t2+2,0t22=9,0−6,0⋅3,0+2,0⋅(3,0)2=9,0 м.
Подстановка значений в формулу для вычисления модуля перемещения дает:
|Δr→|=|x(t2)−x(t1)|=9,0−9,0=0 м.
Таким образом, перемещение материальной точки равно нулю. Следовательно, модуль средней скорости перемещения также равен нулю:
|v→r|=|Δr→|t2−t1=03,0−0=0 м/с.
Для определения средней путевой скорости нужно рассчитать путь, пройденный материальной точкой за интервал времени от t1 = 0 с до t2 = 3,0 с. Движение точки является равнозамедленным, поэтому необходимо выяснить, попадает ли точка остановки в указанный интервал.
Для этого запишем закон изменения скорости материальной точки с течением времени в виде:
vx=v0x+axt=−6,0+4,0t,
где v0x = −6,0 м/с — проекция начальной скорости на ось Ox; ax = = 4,0 м/с2 — проекция ускорения на указанную ось.
Найдем точку остановки из условия
v(τост) = 0,
т.е.
τост=v0a=6,04,0=1,5 с.
Точка остановки попадает во временной интервал от t
S = S1 + S2,
где S1=|x(τост)−x(t1)| — путь, пройденный материальной точкой до остановки, т.е. за время от t1 = 0 с до τост = 1,5 с; S2=|x(t2)−x(τост)| — путь, пройденный материальной точкой после остановки, т.е. за время от τост = 1,5 с до t1 = 3,0 с.
Рассчитаем значения координат в указанные моменты времени:
x(t1)=9,0−6,0t1+2,0t12=9,0−6,0⋅0+2,0⋅02=9,0 м;
x(τост)=9,0−6,0τост+2,0τост2=9,0−6,0⋅1,5+2,0⋅(1,5)2=4,5 м;
x(t2)=9,0−6,0t2+2,0t22=9,0−6,0⋅3,0+2,0⋅(3,0)2=9,0 м.
Значения координат позволяют вычислить пути S1 и S2:
S1=|x(τост)−x(t1)|=|4,5−9,0|=4,5 м;
S2=|x(t2)−x(τост)|=|9,0−4,5|=4,5 м,
а также суммарный пройденный путь:
S=S1+S2=4,5+4,5=9,0 м.
Следовательно, искомое значение средней путевой скорости материальной точки равно
vs=St2−t1=9,03,0−0=3,0 м/с.
vedy.by
1.1.3 Скорость материальной точки. Сложение скоростей
Видеоурок 1: Перемещение и скорость материальной точки
Видеоурок 2: Сложение скоростей
Лекция: Скорость материальной точки. Сложение скоростейСкорость материальной точки
Все процессы вокруг нас характеризуются тем, насколько быстро они протекают – насколько быстро двигается тело, насколько быстро протекает ток по проводам, насколько быстро изменяется магнитный поток.
При рассмотрении кинематических законов скорость характеризует быстроту изменения положения тела.
Скорость – это векторная ФВ, которая характеризует, насколько быстро изменяется положение тела, а также направление этого изменения. Основной единицей измерения является 1 м/с.
Мгновенная скорость определяется пределом изменения положения тела в пространстве к бесконечно малому интервалу времени.
На рисунке скорость можно показать, как вектор, направленный по касательной к траектории движения.
Сложение скоростейСуществуют основные правила, позволяющие складывать скорости тел для удобства во время решения задач.
1. Если тела двигаются в одном направлении, то можно воспользоваться следующей формулой:
2. Если тела двигаются в разных направлениях вдоль одной прямой, то суммарная скорость будет равна:
3. Если перемещения тел направлены под углом друг к другу, то принято пользоваться правилом треугольника, где неизвестный суммарный вектор скорости представляется в виде неизвестной стороны треугольника, которая определяется по теореме косинусов:
4. Если тела двигаются по перпендикулярным перемещениям, то суммарная скорость равна:
Средняя скоростьЕсли за равные промежутки времени тело изменяет свою скорость, то можно воспользоваться следующей формулой:
Например, каждые 15 минут велосипедист изменял свою скорость:
Первые 15 минут его скорость была 3 м/с, вторые 15 минут – 4 м/с, а третьи – 5 м/с, то средняя скорость равна:
<v> = (3+4+5) : 3 = 4м/с.
Однако, если же тело меняло скорости не за равные промежутки времени, то следует пользоваться другой формулой:
cknow.ru
Средняя скорость Википедия
Сре́дняя ско́рость — в кинематике, некоторая усреднённая характеристика скорости, движущегося тела (или материальной точки). Самый простой метод вычисления это Vsr=(V1t1+V2t2)/(t1+t2). Различают два основных определения средней скорости, соответствующие рассмотрению скорости как скалярной либо векторной величины: средняя путевая скорость (скалярная величина) и средняя скорость по перемещению (векторная величина). При отсутствии дополнительных уточнений, под средней скоростью обычно понимают среднюю путевую скорость.
Средняя путевая скорость
Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:
- vcp=ΣsΣt.{\displaystyle v_{cp}={\frac {\Sigma s}{\Sigma t}}.}
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени. (В случае, если тело двигалось с разными скоростями неодинаковые промежутки времени, среднюю скорость можно вычислить как взвешенное среднее арифметическое этих скоростей с весами, равными соответствующим промежуткам времени.)
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути. Если участки пути, по которому двигалось тело с разными скоростями, не равны между собой, то средняя скорость будет равна взвешенному среднему гармоническому всех скоростей с весами — длинами соответствующих этим скоростям участков пути.
Средняя скорость по перемещению
Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:
- v→cp=s→Δt.{\displaystyle {\vec {v}}_{cp}={\frac {\vec {s}}{\Delta t}}.}
Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).
Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.
wikiredia.ru
[Физика билет 1] Система отсчета. Траектория, путь и перемещение. Материальная точка. Средняя скорость. Относительность движения. Закон сложения скоростей в классической механике. Прямолинейное равномерное движение. Уравнения движения и графики x(t), vx(t), s(t) для равномерного прямолинейного движения.
Система отсчета.Траектория, путь и перемещение.
Вектор перемещения – вектор начальная точка которого совпадает с начальным положением движущейся точки и конец вектора с ее конечным положением.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве (прямолинейная или криволинейная).
Путь точки – сумма длин всех участков траектории, пройденных точкой за рассматриваемый участок времени.
Материальная точка.
Материа́льная то́чка — тело, обладающее массой и скоростью, но размеры и формы которого в условиях данной задачи существенного значения не имеют.
Средняя скорость.
Сре́дняя ско́рость движущейся точки за промежуток времени t – векторная величина, равная отношению вектора перемещения к промежутку времени за которое это перемещение произошло.
Средняя (путевая) скорость
Средняя скорость по перемещению (средневекторная)Относительность движения.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Закон сложения скоростей в классической механике.
Vабс= Vотн + Vпер
Абсолютная скорость материальной точки равна векторной сумме переносной и относительной скорости.
Прямолинейное равномерное движение.
Прямолинейное равномерное движение — движения с постоянной по модулю и направлению скоростью.
Уравнения движения и графики x(t), vx(t), s(t) для равномерного прямолинейного движения.
уравнение равномерного прямолинейного движения материальной точки:
Формулы равномерного прямолинейного движения
Графики зависимости скорости, проекции скорости,пути и координаты от времени для равномерного прямолинейного движения
График скорости v = v(t)
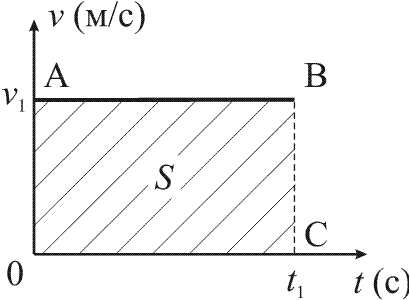
Рис. 22
= constГрафик скорости равномерного движения – прямая линия, параллельная оси абсцисс (оси t).
По графику v = v(t) можно найти пройденный путь за интервал времени t: он численно равен площади фигуры ОАВС (прямоугольника):
q (площадь прямоугольника OABC) = OA • OC v1 • t1 S
График пути S = S(t)

Рис. 23
S = v • t, где v = constГрафик пути равномерного движения – прямая линия, которая образует угол с осью времени.
На этом графике , но v ~ tg (скорость равномерного движения пропорциональна тангенсу угла , который график пути составляет с осью времени).
График зависимости координаты точки от времени: x = x(t)
Уравнение x = x0 + vx (t – t0) – линейная функция, поэтому график x = x(t) – прямая линия, которая образует угол с осью времени.

Рис. 24

Рис. 25
На графике x = x(t): , где v ~ tg.fizmatinf.blogspot.com
Кинематика материальной точки. Системы отсчета. Траектория, перемещение, путь, скорость, ускорение. Равномерное и равнопеременное прямолинейные движения.
54
Криволинейное движение. Нормальное и тангенциальное ускорения.
Механическим движением называется процесс изменения взаимного расположения тел или их частей в пространстве с течением времени.
Два способа задания положения точки:
, 
базис.
базис.
Материальная точка (МТ) это тело, формой и размерами которого в условиях данной задачи можно пренебречь.
Абсолютно твердое тело это тело, деформацией которого в условиях данной задачи можно пренебречь.
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Кинематические характеристики движения МТ:
Траектория, путь, перемещение, линейная скорость, линейное ускорение.
Траекторией МТ называют линию, описываемую ею в пространстве при движении.
Уравнение траектории
x = f1(t), y = f2(t), z = f3(t). (1)
Путь s скалярная величина, равная полной длине отрезка траектории, пройденной МТ за время движения.
Уравнение пути
s = s(t) . (2)
Перемещение  вектор, проведенный из начального
положения (точка А)
в конечное (точка В), ,
вектор, проведенный из начального
положения (точка А)
в конечное (точка В), ,
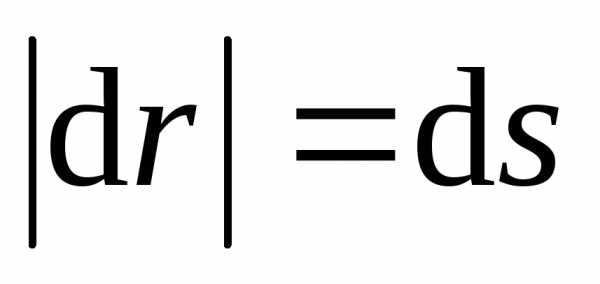 . (3)
. (3)
Средняя скорость
. (4)
Мгновенная скорость
, (5)
, (6)
. (7)
 единичный
вектор, касательный к траектории.
единичный
вектор, касательный к траектории.
Координатная форма
(8)
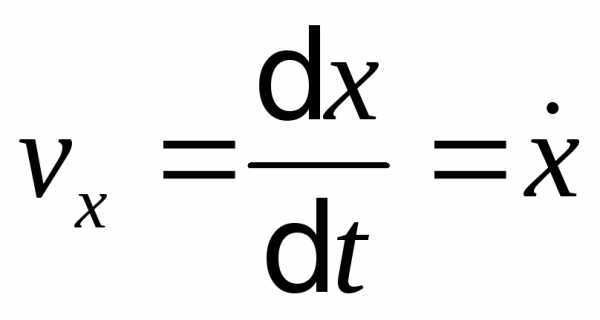 ,
,  ,
, 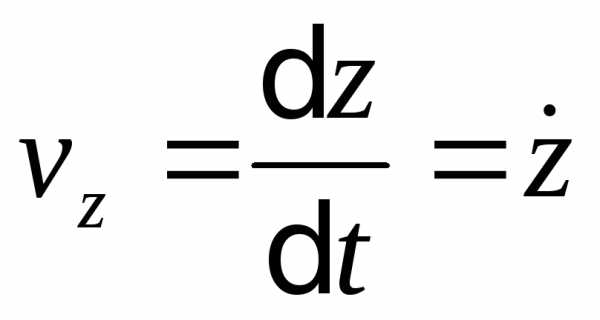 .
.
Модуль скорости
. (9)
Кинематические соотношения



 при vx = const
при vx = constУскорение вектор, характеризующий быстроту изменения скорости как по модулю, так и по направлению.
Среднее ускорение
. (10)
Мгновенное ускорение
. (11)
Тангенциальное
(касательное) ускорение 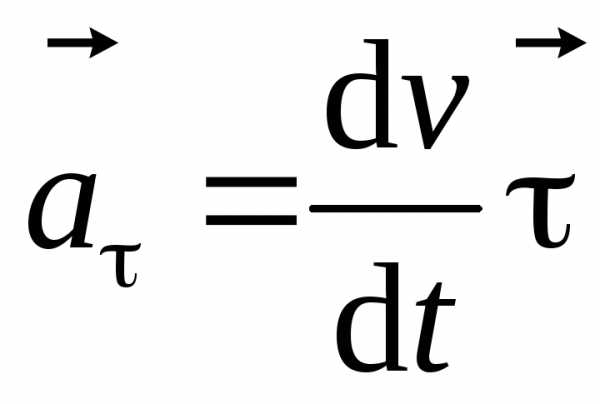 , м/c2 . (12)
, м/c2 . (12)
Нормальное
ускорение 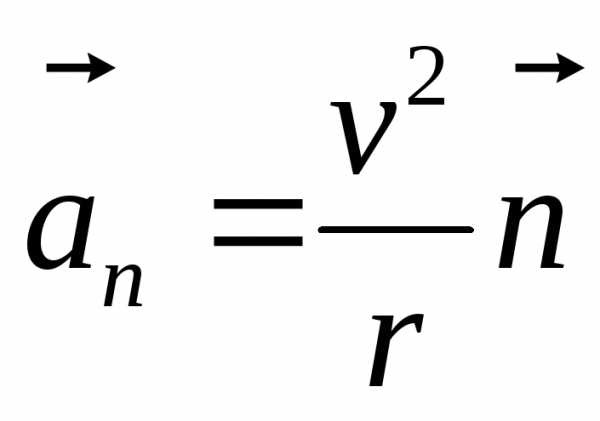 ,
м/c2 . (13)
,
м/c2 . (13)
(14)
Кинематические соотношения


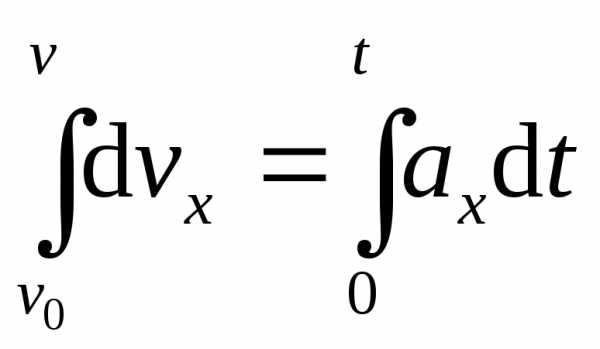
 при ax = a = const ,
при ax = a = const ,
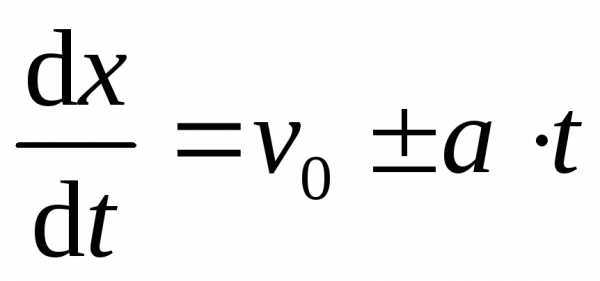



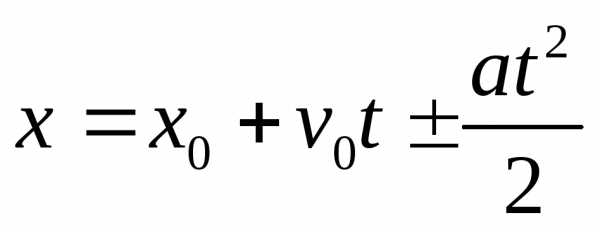 .
.
Частные случаи движения

 движение равномерное
и прямолинейное;
движение равномерное
и прямолинейное;
=
0, то v = const, движение равномерное; 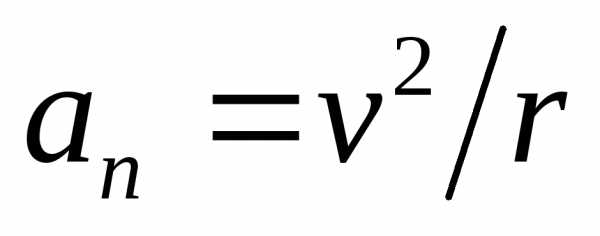 = 0, так как v
= 0, так как v 0,
то r
0,
то r ,
траектория
прямая линия.
,
траектория
прямая линия.
,

движение равнопеременное
и прямолинейное;
движение равнопеременное
и прямолинейное;
=
const, движение равнопеременное; 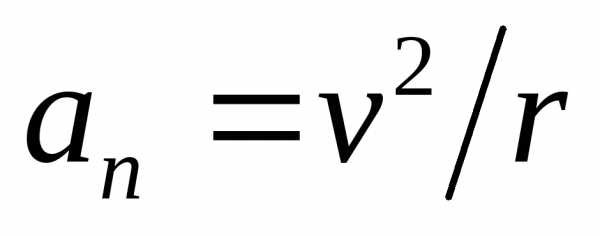 =
0, траектория
прямая линия.
=
0, траектория
прямая линия.
 ,
равномерное
движение по окружности;
,
равномерное
движение по окружности;
=
0, v = const, движение равномерное;  =
const , r = const траектория движения
окружность.
=
const , r = const траектория движения
окружность.
 ,
, 
движение равномерное
криволинейное;
движение равномерное
криволинейное;
=
0, v = const, движение равномерное;  ,
движение криволинейное.
,
движение криволинейное.
 ,
, неравномерное
криволинейное движение.
неравномерное
криволинейное движение.
studfiles.net
1.Кинематика материальной точки. Системы отсчета. Траектория, перемещение, путь, средняя путевая и средняя скорость по перемещению.
Кинема́тика точки— раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.
Основная задача механики– определить положение тела в любой момент времени.
Механическое движение– это изменение положения тела в пространстве с течением времени относительно других тел.
Материальная точка– тело, размерами которого в условиях данной задачи можно пренебречь.
Система отсчета– тело отсчета, система координат, связанная с ним, и прибор для измерения времени.
Перемещение– направленный отрезок (вектор) между начальным и конечным положением тела.
Траектория (l)– линия, вдоль которой движется тело.
Путь (S)– длина траектории.
Скорость (V)– величина, показывающая какой путь проходит тело за единицу времени.
Скорость движения
Средняя путевая скорость
Мгновенная скорость/ скорость движения
За единицу скоростипринимают скорость такого равномерного прямолинейного движения, при котором тело за одну секунду перемещается на один метр.
Ускорение– это величина, показывающая, как изменяется скорость за одну секунду.
При движении материальной точки М ее координаты и радиус-векторизменяются с течением времени t.
Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
(1.2) |
либо зависимость от времени радиус-вектора этой точки
(1.3) |
Три скалярных уравнения (1.2) или эквивалентное им одно векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки.
2. Мгновенная скорость. Путь, как интеграл.
Мгновенная скорость или скорость в данный момент времени. Если в выраженииперейти к пределу, устремляяк нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.
(1.6) |
В процессе уменьшения величины точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектори скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можно разложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.
(1.7) |
где – проекции вектора скорости на оси координат х, у, z.
Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:
(1.8) |
Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:
(1.9) |
Поэтому численное значение скорости:
(1.10) |
Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.
Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.
studfiles.net
Перемещение, путь, средняя скорость Примеры решения задач
1.Материальная точка прошла
половину окружности. Найти отношение
средней путевой скорости <v> к модулю
средней векторной скорости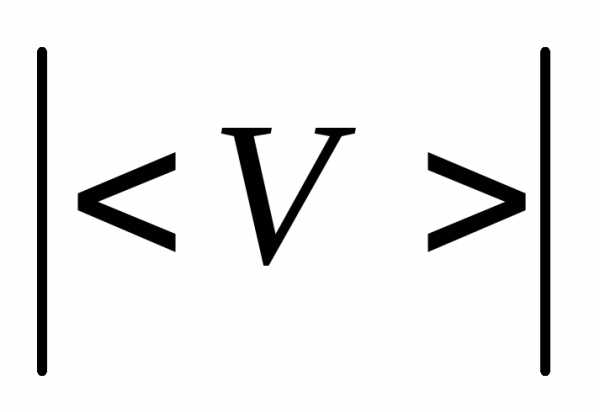 .
.
Решение. Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой за время движенияt, равенR, а величина перемещения 2R, гдеR– радиус окружности, получим:
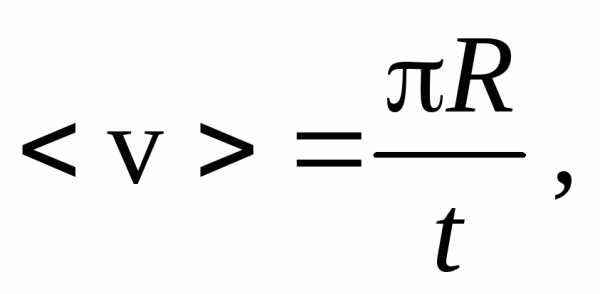


2.Автомобиль проехал первую треть пути со скоростью v1= 30 км/ч, а оставшуюся часть пути – со скоростью v2= 40 км/ч. Найти среднюю скорость <v> на всем пройденном пути.
Решение. По определению <v> = гдеS– путь, пройденный за времяt.
Очевидно, что
гдеS– путь, пройденный за времяt.
Очевидно, что Поэтому искомая средняя скорость равна
Поэтому искомая средняя скорость равна
3.Студент проехал половину пути на велосипеде со скоростьюv1= 12 км/ч. Далее половину оставшегося времени он ехал со скоростьюv2= 10 км/ч, а оставшуюся часть пути шел пешком со скоростьюv3= 6 км/ч. Определить среднюю скорость движения студента <v> на всем пути.
Решение. По определению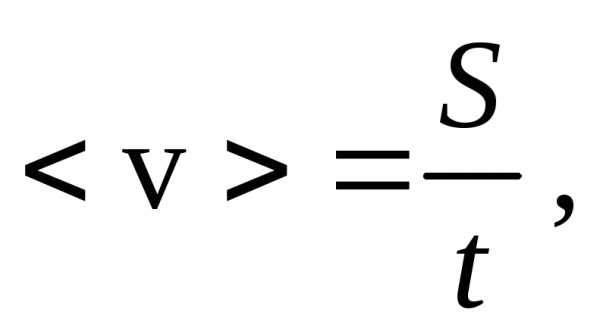 гдеS –путь, аt– время движения.
Ясно, чтоt=t1+t2+t3.
Здесь
гдеS –путь, аt– время движения.
Ясно, чтоt=t1+t2+t3.
Здесь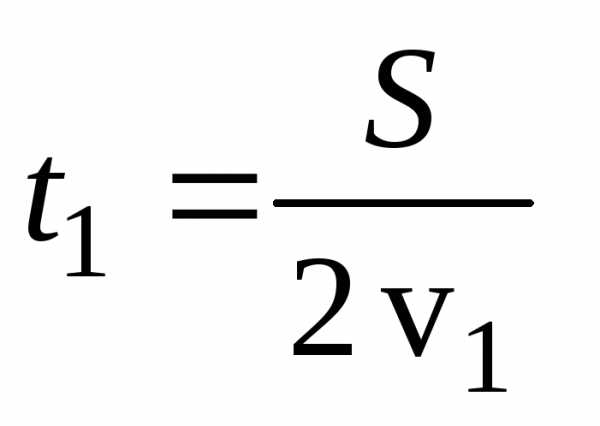 –
время движения на первой половине пути,t2– время движения на втором
участке пути иt3– на третьем.
По условию задачиt2=t3.
Кроме того,S/2 =v2t2+ v3t3= (v2+v3)t2.
Отсюда следует:
–
время движения на первой половине пути,t2– время движения на втором
участке пути иt3– на третьем.
По условию задачиt2=t3.
Кроме того,S/2 =v2t2+ v3t3= (v2+v3)t2.
Отсюда следует:

Подставив t1 и t2+t3 = 2t2 в выражение для средней скорости, получим:
4.Расстояние между двумя станциями поезд прошел за времяt1= 30 мин. Разгон и торможение длилисьt2= 8 мин, а остальное время поезд двигался равномерно со скоростью v = 90 км/ч. Определить среднюю скорость поезда <v>, считая, что при разгоне скорость увеличивалась с течением времени по линейному закону, а при торможении уменьшалась тоже по линейному закону.
Р
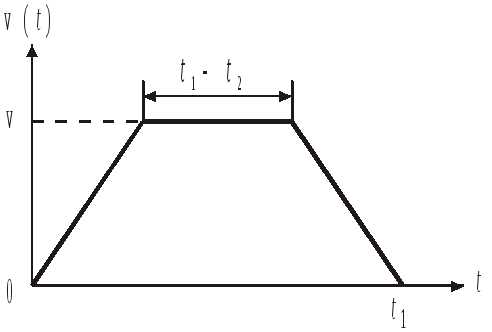
Задачи и упражнения
1.1.Мяч упал с высотыh1 = 4 м,
отскочил от пола и был пойман на
высотеh2= 1 м. Чему равен путьSи величина перемещения ?
?
1.2.Материальная точка переместилась на плоскости из точки с координатамиx1= 1 см иy1= 4cм в точку с координатамиx2= 5 см иy2= 1 см. Построить вектор перемещения и с помощью линейки определить модуль вектора перемещения и проекции вектора перемещения на осиxиy. Найти эти же величины аналитически и сравнить результаты.
1.3.Первую половину пути поезд шел со скоростью вn= 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути <v> = 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути ?
1.4.Первую половину времени своего движения велосипедист проехал со скоростью v1= 18 км/ч, а вторую половину времени – со скоростью v2= 12 км/ч. Определить среднюю скорость движения велосипедиста.
1.5. Движение двух автомобилей
описывается уравнениямии,
где все величины измеряются в системе
СИ. Запишите закон изменения расстояния между автомобилями от времени и найдитечерез время
между автомобилями от времени и найдитечерез время с.
после начала движения.
с.
после начала движения.
studfiles.net

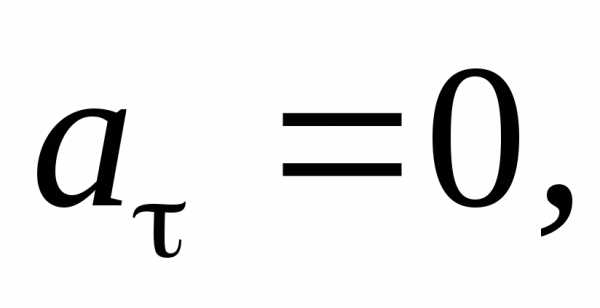
 движение равномерное
и прямолинейное;
движение равномерное
и прямолинейное;
движение равнопеременное
и прямолинейное;
движение равнопеременное
и прямолинейное; ,
равномерное
движение по окружности;
,
равномерное
движение по окружности;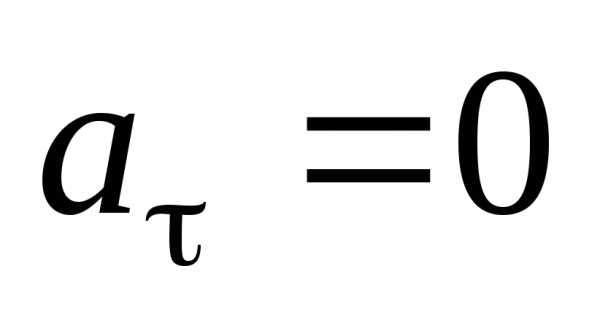 ,
, 
движение равномерное
криволинейное;
движение равномерное
криволинейное; ,
,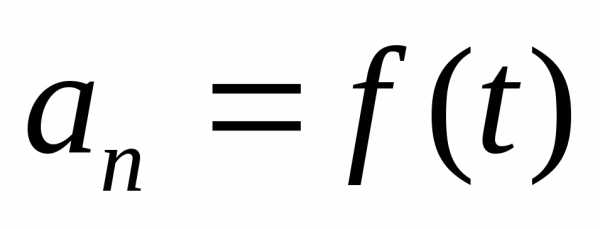 неравномерное
криволинейное движение.
неравномерное
криволинейное движение.