Скорость при равноускоренном движении мгновенная скорость – Кинематика. Основные понятия. Равномерное прямолинейное движение. Равноускоренное движение. Равномерное движение по окружности. Система отсчёта. Траектория, перемещение, путь, уравнение движения, скорость, ускорение, связь линейной и угловой скорости. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Скорость. Ускорение. Равноускоренное прямолинейное движение – FIZI4KA

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.

При неравномерном движении координату тола уже нельзя определить но формуле $ x=x_0+v_xt $, так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.

Средней скоростью $ \vec{v}_{ср} $ неравномерного движения называют физическую величину, равную отношению перемещении $ \vec{s} $ тела ко времени $ t $, за которое оно произошло: $ \vec{v}_{ср}=\frac{s}{t} $.

Записанная формула определяет среднюю скорость как векторную величину. В практических целях этой формулой можно воспользоваться для определения модуля средней скорости лишь в том случае, когда тело движется вдоль прямой в одну сторону. Если же нужно определить среднюю скорость движения автомобиля от Москвы до Санкт-Петербурга и обратно, чтобы рассчитать расход бензина, то эту формулу применить нельзя, поскольку перемещение в этом случае равно нулю и средняя скорость тоже равна нулю. Поэтому на практике при определении средней скорости пользуются величиной, равной отношению пути $ l $ ко времени $ t $, за которое этот путь пройден: $ v_{ср}=\frac{l}{t} $. Эта скорость обычно называется средней путевой скоростью.

2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.

3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.

Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.

Предположим, некоторое тело совершает неравномерное прямолинейное движение (рис. 17), его скорость в точке О можно определить следующим образом: выделим на траектории участок AB, внутри которого находится точка О. Перемещение тела на этом участке — $ \vec{s}_1 $ совершено за время $ t_1 $. Средняя скорость движения на этом участке – $ \vec{v}_{ср.1}=\frac{s_1}{t_1} $. Уменьшим перемещение тела. Пусть оно равно $ \vec{s}_2 $, а время движения — $ t_2 $. Тогда средняя скорость за это время: $ \vec{v}_{ср.2}=\frac{s_2}{t_2} $. Еще уменьшим перемещение, средняя скорость на этом участке: $ \vec{v}_{ср.3}=\frac{s_3}{t_3} $.

При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.

Таким образом, мгновенной скоростью называют векторную физическую величину, равную отношению малого перемещения ($ \Delta{\vec{s}} $) к малому промежутку времени $ \Delta{t} $, за которое это перемещение произошло: $ \vec{v}=\frac{\Delta{s}}{\Delta{t}} $.

4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.

Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.

5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.

Пусть в начальный момент времени $ t_0=0 $ скорость тела равна $ \vec{v}_0 $. В некоторый момент времени $ t $ она стала равной $ \vec{v} $. Изменение скорости за промежуток времени $ t-t_0=t $ равно $ \vec{v}-\vec{v}_0 $ (рис.18). Изменение скорости за единицу времени равно: $ \frac{\vec{v}-\vec{v}_0}{t} $. Эта величина и есть ускорение тела, она характеризует быстроту изменения скорости $ \vec{a}=\frac{\vec{v}-\vec{v}_0}{t} $.

Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

Единица ускорения $ [a]=[v]/[t] $; $ [a] $ = 1 м/с/1 с = 1 м/с². 1 м/с² — это такое ускорение, при котором скорость тела изменяется за 1 с на 1 м/с.

Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.

6. Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: $ \vec{v}=\vec{v}_0+\vec{a}t $. Если начальная скорость тела $ v_0=0 $, то $ \vec{v} = \vec{a}t $.

Чтобы определить значение скорости равноускоренного движения в любой момент времени, следует записать уравнение для проекции скорости на ось ОХ. Оно имеет вид: $ v_x = v_{0x} + a_xt $; если$ v_{0x}=0 $, то $ v_x = a_xt $.

7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.

График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью $ v_{02} $ и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью $ v_{03} $ и с ускорением, направленным в сторону, противоположную направлению скорости.

8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).

График 1 соответствует движению без начальной скорости с ускорением, направленным вдоль положительного направления оси X; график 2 — движению с начальной скоростью $ v_{02} $, с ускорением и скоростью, направленными вдоль положительного направления оси X; график 3 — движению с начальной скоростью $ v_{03} $ : до момента времени $ t_0 $ направление скорости совпадает с положительным направлением оси X, ускорение направлено в противоположную сторону. В момент времени $ t_0 $ скорость равна нулю, а затем и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.

9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.

График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.

10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).

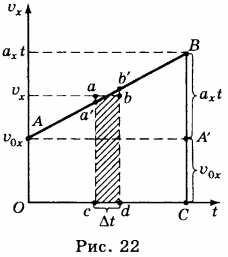
Выделим на графике малый участок $ ab $ и опустим перпендикуляры из точек $ a $ и $ b $ на ось абсцисс. Если промежуток времени $ \Delta{t} $, соответствующий участку $ cd $ на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура $ cabd $ мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку $ cd $.

На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время $ t $ численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: $ S_x= \frac{1}{2}(OA+BC)OC $.

Как видно из рисунка, $ OA=v_{0x},BC=v_x,OC=t $. Отсюда следует, что проекция перемещения выражается формулой $ S_x= \frac{1}{2}(v_{0x}+v_x)t $. Так как $ v_x = v_{0x} + a_{xt} $, то $ S_x= \frac{1}{2}(2v_{0x} + a_xt)t $, отсюда $ S_x=v_{0x}t+ \frac{a_xt^2}{2} $. Если начальная скорость равна нулю, то формула имеет вид $ S_x=\frac{at^2}{2} $. Проекция перемещения равна разности координат $ S_x=x-x_0 $, поэтому: $ x-x_0=v_{0x}t+\frac{at^2}{2} $, или $ x=x_{0x}+v_{0x}t+\frac{at^2}{2} $.

Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.

11. На практике часто используют формулу или $ v^2_x-v^2_{0x}=2a_xs_x $, или $ v^2-v^2_{0}=2as $.

Если начальная скорость тела равна нулю, то: $ v^2_x=2a_xs_x $.

Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с²
2) 20 м/с²
3) 2 м/с²
4) 0,5 м/с²

3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси $ Оx $. У какого из тел в момент времени $ t_1 $ скорость движения равна нулю?

4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси $ Оx $.

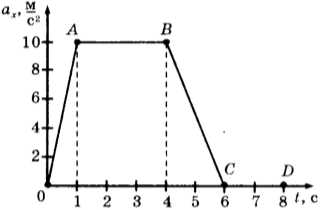
Равноускоренному движению соответствует участок

1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м
2) 4,5 м
3) 5 м
4) 9 м

6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1
2) только 2
3) только 4
4) 3 и 4

7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

1) 1 м/с²
2) -1 м/с²
3) 2 м/с²
4) -2 м/с²

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с

9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?

1) 1
2) 2
3) 3
4) 4

10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с

11. Два тела движутся по оси $ Оx $. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

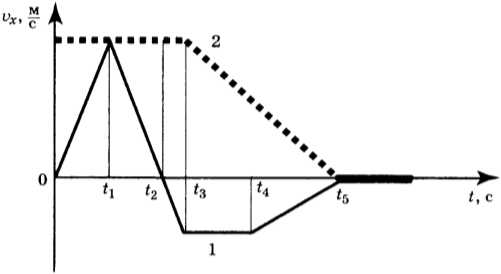
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени $ t_3-t_5 $ тело 2 движется равноускоренно.
2) К моменту времени $ t_2 $ от начала движения тела прошли одинаковые пути.
3) В промежутке времени $ 0-t_3 $ тело 2 находится в покое.
4) В момент времени $ t_5 $ тело 1 останавливается.
5) В промежутке времени $ t_3-t_4 $ ускорение $ a_x $ тела 1 отрицательно.

12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени $ t_1 $ тело имело максимальное по модулю ускорение.
4) Момент времени $ t_3 $ соответствует остановке тела.
5) В момент времени $ t_2 $ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением $ x=12t-t^2 $. В какой момент времени скорость движения равна нулю?

Ответы

Скорость. Ускорение. Равноускоренное прямолинейное движение

5 (100%) 1 vote

fizi4ka.ru

Скорость, ускорение, равномерное и равноускоренное прямолинейное движение

Основные понятия и законы кинематики

Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.

По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.

Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение – это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь – это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид:

x = x₀ + V_xt, где x₀ — начальная координата тела, V_x — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с², не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:

Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название

угловой скорости ω:

Угловая скорость связана с линейной скоростью соотношением

где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения —

Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется

инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.

Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело A (см. рис.).

Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.

Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде

где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения.

Сила трения скольжения подсчитывается по формуле

где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения

Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.

Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.

Сила тяжести — это сила, с которой все тела притягиваются к Земле:

При неподвижной опоре вес тела равен по модулю силе тяжести:

Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес

Видно, что вес тела больше веса покоящегося тела.

При движении тела с ускорением, направленным вниз, его вес

В этом случае вес тела меньше веса покоящегося тела.

Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.

где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна

1.3. Основные понятия и законы статики и гидростатики

Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).

Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.

Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.

Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:

Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей

где ρ — плотность жидкости, h — глубина проникновения в жидкость.

Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае

Высоты столбов жидкости обратно пропорциональны плотностям:

Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то

Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:

где ρ_жидк — плотность жидкости, в которую погружено тело; V_погр — объём погружённой части тела.

Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.

1.4. Законы сохранения

Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:

Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:

Мощность — это работа, совершённая в единицу времени:

Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле

Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле

где h — высота подъёма

Энергия сжатой пружины:

где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.

Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.

1.5. Механические колебания и волны

Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.

Величина A, равная наибольшему абсолютному значению колеблющейся физической величины x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:

Частота измеряется в с^-1. Эта единица называется герц (Гц).

Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.

Период колебаний математического маятника определяется по формуле

где l — длина маятника.

Период колебаний груза на пружине определяется по формуле

где k — жёсткость пружины, m — масса груза.

Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:

где v — скорость распространения волны.

Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.

examer.ru

1.Поступательное движение материальной точки. Скорость, ускорение (среднее, мгновенное). Уравнение движения при равноускоренном прямолинейном движении.

Механика – это область физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение взаимного расположения тел или их частей в пространстве с течением времени.

При этом выделяют следующие разделы:

1. кинематику, которая изучает движение тел, не рассматривая причины, вызывающие это движение;

2. динамику, которая изучает законы движения тел и причины, вызывающие или изменяющие это движение.

Материальная точка (частица) – это тело, размерами которого в условиях данной задачи можно пренебречь. Одно и то же тело в различных условиях или может считаться материальной точкой, или нет. Абсолютно твердое тело – это тело, деформацией которого под действием приложенных сил в условиях данной задачи можно пренебречь. При этом расстояние между любыми двумя точками этого тела в процессе движения не меняется. Траектория – линия, которую описывает МТ при движении. Путь – длина траектории (∆S). [∆S] = 1м. Перемещение(∆)– вектор, показывающий в каком направлении и на какое расстояние переместилась МТ по отношению к первоначальному положению.

Поступательным – называется движение, при котором прямая, соединяющая 2 любые точки тела, перемещается параллельно самой себе. При этом все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорение(колесо обозрения).

Скорость: средняя путевая скорость – пройденное телом расстояние, деленное на время, затраченное на прохождение этого расстояния.

Средняя скорость по перемещению – равна перемещению, деленное на потраченное время.

Мгновенная скорость. Нужно выбрать мгновение и определить пройденный во время этого движения путь.

Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Таким образом, модуль мгновенной скорости равен первой производной пути по времени:

Ускорение: Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.

Среднее ускорение за время, в течении которого скорость изменяется на , определяется как

Мгновенное ускорение

Равноускоренное прямолинейное движение – движение, когда скорость постоянна, а движение проходит по прямой линии

, ,

-уравнение движения,

+c,t=0,c=;

2. Вращательное движение (равномерное, неравномерное) материальной точки. Угловая скорость и ускорение. Связь между линейными и угловыми характеристиками движения.

= +, где– нормальное ускорение;

– тангенциальное ускорение

, – орты,=;

= =

R = ОА – радиус кривизны вращения точки А,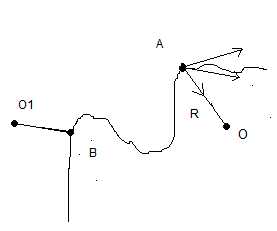

– нормальное ускорение

– скорость в точке А

– тангенциальное ускорение

Частные случаи движения:

Прямолинейное равномерное движение
Равномерное движение по окружности

=0, =

Прямолинейное равномерное движение

R==a=const,=0

Равномерное движение по окружности:

= =

= +– направление к центру траектории.

Неравномерное

= > 0

= A

a =

Связь между линейными и угловыми характеристикамими движения:

Равномерное движение:
Поступательное		Вращательное
S = vt v = constа= 0		= –const= 0
Равнопеременное
S = v₀t + at²/2 V = v₀ + at, а= const	= + = t +,= const

studfiles.net

Равноускоренное движение | ЭТО ФИЗИКА

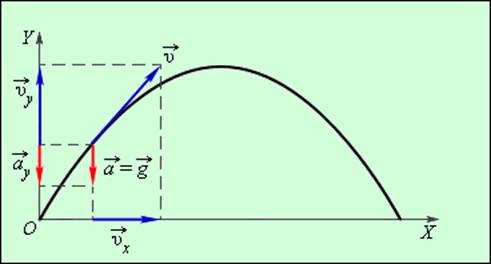
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).

Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.

Рисунок 1.4.1.

Проекции векторов скорости и ускорения на координатные оси. ax = 0, ay = –g

При равноускоренном прямолинейном движении скорость тела определяется формулой

(*)

В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).

Рисунок 1.4.2.

Графики скорости равноускоренного движения

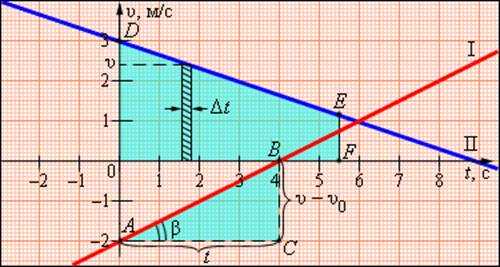
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ₀ = –2 м/с, a = 1/2 м/с².

Для графика II: υ₀ = 3 м/с, a = –1/3 м/с²

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

(**)

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t:

(***)

Это выражение называют законом равноускоренного движения.

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ₀, ускорение a и перемещение s:

Если начальная скорость υ₀ равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ₀, υ, s, a, y₀ являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

www.its-physics.org

Тема. Равноускоренное движение. Ускорение. Скорость тела и пройденный путь при равноускоренном прямолинейном движении. Графики движения

Занятие № 4

Тема. Равноускоренное движение. Ускорение. Скорость тела и пройденный путь при равноускоренном прямолинейном движении. Графики движения.

Цель: формирование знаний о равноускоренном прямолинейном движении, знакомство с его характеристиками: ускорением, средней и мгновенной скоростями, математическим описанием; рассмотрение графиков зависимости скорости, координат прямолинейного равноускоренного движения от времени.

Тип занятия: комбинированный урок, урок усвоения новых знаний

Организационный этап (2 мин)

Актуализация опорных знаний (5 мин)

Фронтальный опрос.

Что называется механическим движением?
Какое движение называется прямолинейным?
Какое движение называется равномерным?
Какие основные характеристики равномерного прямолинейного движения?
Что вы можете сказать про скорость неравномерного движения?

Сообщение темы, цели и заданий урока (2 мин)

План изучения темы

Равномерное прямолинейное движение.
Скорость равномерного прямолинейного движения как физическая величина.
Закон добавления скоростей.
Перемещение прямолинейного равномерного движения. Решение основной задачи механики для прямолинейного равномерного движения.
Графики движения.

Мотивация учебной деятельности

На предыдущих уроках мы рассматривали прямолинейное равномерное движение, при котором тело движется с постоянной скоростью. Но человеку в повседневной жизни чаще всего приходится сталкиваться с неравномерным прямолинейным движением. Так, поезд, отходя от станции, постепенно набирает скорость, а при подходе к следующей станции его скорость уменьшается; ракета, взлетая, увеличивает свою скорость сначала медленно, а затем летит все быстрее и быстрее. Если рассматривать падение тел, то они тоже движутся по прямой с возрастающей скоростью, если среда падения не сильно препятствует этому движению. Следовательно, изучение неравномерного прямолинейного движения является важным вопросом механики.

Средняя и мгновенная скорости.

Одно и то же перемещение материальная точка может совершать за различное время. Если за равные промежутки времени тело совершает равные по величине перемещения, то такое движение называется равномерным, если нет – неравномерным. Быстрота изменения положения материальной точки в пространстве характеризуется скоростью движения. При равномерном движении величина скорости остается все время постоянной, при неравномерном – меняется в процессе движения.

Отношение перемещения ко времени движения t материальной точки в случае неравномерного движения называется средней скоростью движения .

С практической точки зрения большее значение имеет средняя путевая скорость. ^ равна отношению пройденного телом пути ко времени его прохождения:

V_ср= S/t

и является скалярной величиной.

Именно эту физическую величину имеют ввиду, когда говорят, например, что спортсмен пробежал дистанцию со средней скоростью 6,5 м/с.

Для описания неравномерного движения можно определить среднюю скорость движения на нескольких участках пути. Однако это даст лишь приближенное понятие о характере движения. Дело в том, что, определяя средние скорости, мы заменяем неравномерное движение в течение каждого промежутка времени равномерным движением и считаем, что скорость меняется скачком от одного промежутка времени к другому.

Для более точного описания движения потребуется определять средние скорости за все меньшие и меньшие промежутки времени. По мере уменьшения промежутков времени фактическое движение в пределах каждого отдельного промежутка будет все менее отличаться от равномерного и, наконец, отличие перестанет улавливаться приборами, при помощи которых мы измеряем среднюю скорость. Этим ставится естественный предел уточнению описания движения при данной степени точности измерений длины и времени.

Зависимость пройденного пути от времени при определении средней скорости за различные промежутки времени.

Мгновенная скорость – средняя скорость за бесконечно малый интервал времени.

Если речь идёт ещё и о направлении, то определение мгновенной скорости будет таким:

Мгновенная скорость – векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, за который это перемещение произошло:

Направление скорости совпадает с направлением перемещения .

Мгновенная скорость тела направлена по касательной к траектории в сторону его движения.

Если рассмотреть проекции вектора скорости на координатные оси, то

Равноускоренное прямолинейное движение — это такое движение, при котором скорость тела за любые равные промежутки времени изменяется на одинаковую величину, а траектория движения является прямой линией.

Е
сли при таком движении скорость тела увеличивается, то его называют равноускоренным, а если уменьшается — равнозамедленным.

Одной из главных характеристик равноускоренного движения является ускорение.

Характеристика ускорения как физической величины

Ускорение характеризует скорость изменения скорости движения тела.
Ускорение — векторная физическая величина, которая определяется отношением изменения скорости тела ко времени, в течение которого это изменение состоялось.

5. Ускорение определяется методом непрямых измерений.

Ускорение равноускоренного движения — величина постоянная. В случае равноускоренного движения, когда начальная скорость меньше конечной, ускорение является положительной величиной (рис. 1, а), а в том случае, когда начальная скорость больше конечной, ускорение отрицательно (рис.1, б)

Обозначаем:

– вектор ускорения;

a_x, a_y – проекции вектора ускорения на координатные оси Ox, Oy;

а – модуль ускорения.

Вопрос к студентам:

Приведите примеры равноускоренного прямолинейного движения.
Как вы считаете, часто ли нам встречаются случаи равноускоренного прямолинейного движения?
Зачем изучать данный вид движения, уметь описывать его закономерности?

Перемещение. Уравнение движения для прямолинейного равноускоренного движения.

Уравнение движения для прямолинейного равноускоренного движения:

Модуль перемещения (путь) для прямолинейного равноускоренного движения определяется по формулам: ,

, т.к. за каждую единицу времени скорость тела изменяется на одинаковое значение, т.е. линейно.

Координата тела в данный момент времени для равноускоренного движения:

Это уравнение и есть решением основной задачи механики для равноускоренного движения, т.к. определяет положение тела в данный момент времени по известным начальным условиям.

Графики движения

Применение приобретённых знаний

Решение задач

На протяжении 10 с автомобиль двигался прямолинейно с ускорением 0,5 м/с² и достиг скорости 20 м/с. Определить начальную скорость автомобиля.
Первые 5 с тело двигалось равномерно со скоростью 4 м/с, а следующие 6 – с ускорением 2 м/с², направленным так же, как и скорость. Каким будет перемещение тела за всё время движения?

Что такое ускорение и для чего его нужно знать?
Во время любого неравномерного движения скорость меняется. Как характеризует это изменение ускорение?
Чем отличается замедленное прямолинейное движение от ускоренного?
Что такое равноускоренное движение?
Может ли тело двигаться с большой скоростью, но с малым ускорением?
Как направлен вектор ускорения в случае прямолинейного движения?
Скорость – векторная величина и может изменяться как модуль скорости, так и направление вектора скорости. Что именно изменяется при прямолинейном равноускоренном движении?
Может ли скорость движения тела быть равна нулю, когда его ускорение не равно нулю?
Как можно вывести формулы скорости и пути равнопеременного движения?
Что называют мгновенной скоростью переменного движения?

Подведение итогов урока и сообщение домашнего задания

Преподаватель подводит итоги урока, оценивает деятельность учеников.

Домашнее задание

Выучить теоретический материал по учебнику.
Решить задачи.

Тест

Найдите правильный ответ.

На рисунке точками обозначено положение тела через одинаковые интервалы времени. Выберите тело, которое двигается с возрастающей скоростью.

На рисунке выберите график проекции ускорения, который описывает равноускоренное прямолинейное движение.

Выберите строку, в которой приведены скорости в порядке возрастания модуля скорости (см. рисунок).

Ускорением называют векторную величину, которая определяется:

отношением скорости к интервалу времени;
произведением скорости и интервала времени, в течение которого тело двигалось;
отношением изменения скорости к интервалу времени, за который это изменение случилось;
отношением изменения пути к интервалу времени, за который это изменение случилось.

Выберите единицу ускорения в СИ.

А) м/с; Б) м∙с В) м/с²Г) м∙с²

Выберите определение прямолинейного равнопеременного движения.

Движение, при котором за любые равные интервалы времени осуществляются одинаковые перемещения
Движение, при котором за равные интервалы времени осуществляются одинаковые перемещения
Движение, которое происходит по прямолинейной траектории
Движение, при котором за любые равные интервалы времени скорость тела изменяется одинаково

Скорость движения тела изменяется по закону . Найдите модуль ускорения и определите характер движения тела.

а = 4 м/с²; в направлении оси ОХ; уменьшает скорость движения
а = 4 м/с²; в направлении оси ОХ; увеличивает скорость движения
а = 40 м/с²; в направлении, противоположном оси ОХ; увеличивает скорость движения
а =4 м/с²; в направлении, противоположном оси ОХ; увеличивает скорость движения

Пешеход за первые 200 с прошёл 240 м, за следующие 100 с – 180 м. Определите скорость движения пешехода на каждом участке и среднюю скорость.

1,2 м/с; 1,8 м/с; 1,5 м/с
1,4 м/с; 1,8 м/с; 1,6 м/с
1,2 м/с; 1,8 м/с; 1,4 м/с
2,4 м/с; 1,2 м/с; 1,8 м/с

Ответы к тесту

1	2	3	4	5	6	7	8
Б	В	Б	В	В	Г	А	В

sm.znaimo.com.ua

Ускорение. Равноускоренное движение | LAMPA

Что такое ускоренное движение

Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.

“Движение” — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.

“Ускоренное” — значит “убыстренное”, с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее… То есть скорость все время увеличивается.

Это может прозвучать странно, но случай, когда скорость уменьшается и уменьшается, а тело двигается все медленнее, медленнее и медленнее, – это тоже “ускоренное” движение. В это трудно поверить (и это трудно понять) прямо сейчас, но позже вам станет понятнее. Иногда такое движение с уменьшением скорости называют равнозамедленным движением.

Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 555 км/ч, потом 101010 км/ч, потом 151515 км/ч, 202020 км/ч, 252525 км/ч, 303030 км/ч и т.д. — насколько у него хватит сил.

Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 101010 км/ч, потом 555 км/ч, а потом 000 км/ч. То есть скорость все время уменьшается на 555 км/ч.

Следуя этой логике, через мгновение после скорости в 000 км/ч скорость должна вновь уменьшиться на 555 км/ч, и тогда скорость будет равна −5-5−5 км/ч, а потом еще уменьшиться на 555 км/ч и стать уже −10-10−10 км/ч, а потом и −15-15−15 км/ч и т.д. Ведь уменьшение скорости должно происходить и дальше. Кому-то отрицательная скорость может показаться странной. Тем, кому она кажется странной, хочу напомнить, что когда мы говорим о скорости не как о векторе (не как о “стрелочке”), то чаще всего мы имеем в виду проекцию скорости на некоторую ось. Если направление вектора совпадает с направлением этой оси, то проекция получается положительной. Если скорость противоположна направлению оси — то проекция получается отрицательной. Тем, кому приведенные объяснения кажутся непонятными, мы рекомендуем прочитать темы “Два вида физических величин: скалярные величины и векторные величины” и “Проектирование векторов на оси”. В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.

Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.

В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме “Равноускоренное движение”, а второй случай — с поворотом — в теме “Движение по окружности”, когда тело поворачивает, а значит — изменяет направление скорости.

lampa.io

Прямолинейное равноускоренное движение | Физика

1. Определение прямолинейного равноускоренного движения

Поставим опыт
Изучим, как скатывается шарик с наклонной плоскости. На рисунке 5.1 показаны последовательные положения шарика через равные промежутки времени.

Видно, что шарик движется неравномерно: пути, проходимые им за последовательные равные промежутки времени, увеличиваются. Следовательно, скорость шарика увеличивается.

Движение шарика, скатывающегося с наклонной плоскости, является примером прямолинейного равноускоренного движения. Такое движение вы уже изучали в курсе физики основной школы. Напомним его определение.

Прямолинейным равноускоренным движением называют прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется на одну и ту же величину.

Прямолинейно равноускоренно может двигаться, например, автомобиль во время разгона (рис. 5.2, а). Однако непривычным может показаться то, что при торможении (рис. 5.2, б) автомобиль тоже может двигаться прямолинейно равноускоренно! Ведь в определении прямолинейного равноускоренного движения речь идет не об увеличении скорости, а только об ее изменении.

Дело в том, что понятие ускорения в физике шире, чем в разговорном языке. В обыденной речи под ускорением понимают обычно только увеличение скорости. Мы же будем говорить, что тело движется с ускорением всегда, когда скорость тела изменяется со временем любым образом (увеличивается или уменьшается по модулю, изменяется по направлению и т. п.).

Может возникнуть вопрос: почему мы уделяем внимание именно прямолинейному равноускоренному движению? Забегая немного вперед, выдадим «секрет»: именно с таким движением мы будем очень часто иметь дело при изучении механики.

Напомним (об этом уже говорилось в курсе физики основной школы), что под действием постоянной силы тело движется прямолинейно равноускоренно. (Если начальная скорость тела равна нулю или направлена вдоль линии действия силы.) А во многих задачах по механике рассматривается именно такая ситуация. Ниже мы рассмотрим подробно ее различные варианты.

2. Ускорение

В определении прямолинейного равноускоренного движения речь идет об изменении скорости. Как определяют изменение скорости?

Обозначим ₀ скорость тела в начальный момент времени, а – скорость тела через промежуток времени t. Тогда изменение скорости за этот промежуток времени

Эту формулу можно переписать также в виде

На рисунке 5.3 показано, как найти вектор изменения скорости Δ в случае прямолинейного неравномерного движения.

? 1. Какому из рисунков 5.3 (а или б) соответствует увеличение скорости, а какому – уменьшение?

Введем теперь понятие ускорения.

Ускорением называют отношение изменения скорости Δ к промежутку времени Δt, за который произошло это изменение:

(Здесь в общем случае надо говорить о мгновенном ускорении, которое определяется с помощью достаточно малых промежутков времени – подобно тому, как мы определяли выше мгновенную скорость. При прямолинейном равноускоренном движении мгновенное ускорение постоянно.)

Как следует из этого определения, ускорение – векторная величина. Она характеризует скорость изменения скорости. Единицей ускорения в СИ является 1 м/с² (читают: «метр в секунду за секунду» или «метр делить на секунду в квадрате»). Если тело движется с таким по модулю ускорением в одном направлении, то его скорость каждую секунду увеличивается (или уменьшается!) на 1 м/с.

Когда тело падает, оно движется с ускорением, равным примерно 10 м/с² (если можно пренебречь сопротивлением воздуха).

Рассмотрим теперь, при каком условии скорость тела увеличивается, а при каком – уменьшается. Из определения (3) следует, что

На рисунке 5.4 мы заменили (по сравнению с рисунком 5.3) Δ на равное ему выражение Δt.

Мы видим теперь, что скорость тела увеличивается, если ускорение направлено так же, как начальная скорость (рис. 5.4, а). Если же ускорение направлено противоположно скорости (рис. 5.4, б), то скорость тела уменьшается.

? 2. На каком из рисунков 5.2 (а или б) ускорение автомобиля направлено влево?

Выберем начальный момент времени t₀ = 0, тогда Δt = t – t₀ = t – 0 = t. Поскольку Δ = – ₀, из формулы (4) получаем

Направим ось x вдоль траектории движения тела. Тогда

v_x = v_0x + a_xt. (6)

Здесь v_x – проекция скорости в момент времени t, v_0x – проекция начальной скорости, a_x – проекция ускорения.

В формуле (6) проекция начальной скорости v_0x и проекция ускорения a_x могут быть положительными и отрицательными. В зависимости от соотношения знаков v_0x и ax модуль скорости тела будет увеличиваться или уменьшаться со временем.

Рассмотрим примеры.

? 3. Четыре автомобиля движутся вдоль оси x. В течение некоторого времени зависимость vx(t) выражается для них (в единицах СИ) формулами:
1) v_x = 8 + 2t; 2) v_x = 20 – 4t; 3) v_x = –10 + t; 4) v_x = –15 – 3t.
а) Чему равны проекции начальной скорости и ускорения каждого автомобиля?
б) Какие автомобили разгоняются, а какие – тормозят?
в) Скорость какого автомобиля наибольшая по модулю в момент времени t = 2 с? наименьшая?

Выполнив это задание, вы заметите, что скорость тела увеличивается по модулю, если проекция начальной скорости и проекция ускорения имеют одинаковые знаки (обе положительные или обе отрицательные).

Если же проекции начальной скорости и ускорения имеют разные знаки, то скорость тела сначала уменьшается по модулю. В некоторый момент скорость тела станет равной нулю, после чего (если ускорение останется прежним) направление скорости изменится на противоположное и модуль скорости тела начнет увеличиваться. Далее мы рассмотрим это на примере тела, брошенного вертикально вверх.

3. График зависимости скорости от времени

Из формулы (6) следует, что при прямолинейном равноускоренном движении проекция скорости vx линейно зависит от времени t. Поэтому график зависимости v_x(t) – отрезок прямой.

На рисунке 5.5 изображены графики зависимости проекции скорости от времени для синего и красного автомобилей, движущихся вдоль оси x.
а) Какой из автомобилей тормозит? Чему равен модуль его ускорения?
б) У какого автомобиля модуль ускорения меньше? Чему он равен?
в) Запишите зависимость vx(t) для каждого автомобиля.
г) Используя эту запись, найдите момент времени, когда скорости автомобилей станут равными. Проверьте полученный ответ по приведенным графикам.

? 5. На рисунке 5.6 изображены графики зависимости проекции скорости от времени для тел, движущихся вдоль оси x.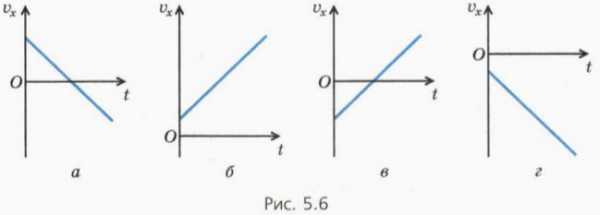

а) Какие графики описывают движение тела, скорость которого все время увеличивается по модулю?
б) На каких графиках v0x и ax имеют разные знаки?
в) Какие графики описывают случаи, когда направление скорости тела изменяется на противоположное?
г) Начертите для всех изображенных случаев графики зависимости модуля скорости от времени.

? 6. Зависимость проекции скорости от времени для первого тела выражается в единицах СИ формулой v₁₂ = 6 – Зt, а для второго – формулой v_2x = 2 + t.
а) Изобразите графики vx(t) для каждого тела.
б) В какой момент скорости тел равны (по модулю и по направлению)?
в) В какие моменты скорости тел равны по модулю?

Дополнительные вопросы и задания

7. От платформы отправляется поезд на восток. В это же время у соседней платформы тормозит поезд, идущий на запад. Сделайте схематический рисунок, на котором покажите направления скорости и ускорения каждого поезда.

8. Как направлено ускорение лифта, когда он:
а) начинает двигаться с первого этажа?
б) тормозит на верхнем этаже?
в) тормозит на третьем этаже, двигаясь вниз?
г) начинает движение на третьем этаже, двигаясь вверх?
Движение лифта при разгоне и торможении считайте равноускоренным.

9. Автомобиль трогается с места в направлении на север и набирает скорость 72 км/ч за 40 с. Движение автомобиля считайте прямолинейным равноускоренным.
а) Как направлено ускорение автомобиля?
б) Чему равно ускорение автомобиля по модулю?
в) Начертите график зависимости проекции скорости автомобиля от времени.
г) Какой была скорость автомобиля через 10 с после начала движения?

phscs.ru