Скорость при прямолинейном равноускоренном движении тела
Цели урока:
обучающая: повторить понятия равноускоренного движения, ускорения; научить учащихся определять проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, сформировать навыки построения графика скорости и его анализа.
развивающая: развитие умения наблюдать и анализировать конкретные ситуации; выделять определенные признаки; рассмотрение свойств объектов на основе анализа количественных и качественных характеристик.
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулирование активности учащихся.
Методы:
словесный — беседа;
наглядный — видеоурок, записи на доске;
контролирующий — тестирование или устный опрос, решение задач.
межпредметные: математика — линейная зависимость, график линейной функции;
внутрипредметные: равноускоренное движение, ускорение.
Ход урока:
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
На прошлом уроке, мы с вами рассмотрели такой вид движения, при котором тело, за любые равные промежутки времени совершает разные перемещения. Как мы назвали такое движение? {неравномерное}
Какое движение мы назвали ускоренным?
А замедленным? {когда скорость тела уменьшается с течением времени}.
Ответьте на вопрос, а что такое средняя скорость? {Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу времени}
А всегда ли мы можем пользоваться понятием средней скорости при решении задач? Приведите примеры.
Как мы с вами назвали скорость тела в данный момент времени или в данной точке траектории? {мгновенной скоростью}
Как направлена мгновенная скорость? {Она направлена по касательной к траектории в каждой её точке в сторону перемещения}
Что является основной характеристикой неравномерного движения?
{Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло}.
Откройте тетради и запишите число и тему нашего урока: Скорость тела при равноускоренном движении тела.
3. Объяснение нового материала.
Скачать видеоурок Скорость при прямолинейном равноускоренном движении тела
Нам известно, что при прямолинейном равноускоренном движении ускорение тела можно рассчитать по формуле;
Выразим из этой формулы скорость, которую могло бы иметь тело в конце промежутка времени Δt.
Получим
.
Или
Мы получили формулу, которая называется уравнением скорости при равноускоренном движении.
Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя.
Перепишем нашу формулу в проекции на ось х.
Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.
Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика.
Из курса математики вам известна линейная функция
у = kx + b,
где х — аргумент, k — постоянный коэффициент, b — свободный член. Графиком этой функции является прямая линия.
Функция
υx = υ0x + axΔt
тоже линейная с аргументом Δ

Рассмотрим, какой вид будет иметь график скорости в зависимости от знаков проекций ускорения и начальной скорости.
Если проекция вектора скорости тела и его ускорение направлены по оси Ох, то уравнение примет вид
В этом случае скорость тела с течением времени возрастает. При этом график скорости образует с положительным направлением оси
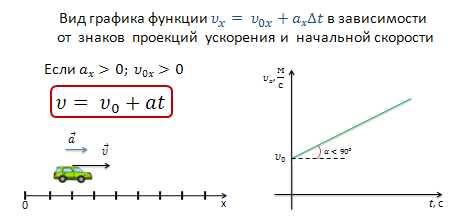
Если же проекция вектора скорости тела и его ускорение направлены против оси Ох, то уравнение примет вид
Скорость тела с течением времени возрастает, но тело, при этом, движется в отрицательном направлении. График скорости образует с положительным направлением оси t тупой угол.

В случае, если скорость тела направлена по оси О
Скорость тела убывает от некоторого значения до нуля. График скорости образует с положительным направлением оси t тупой угол.
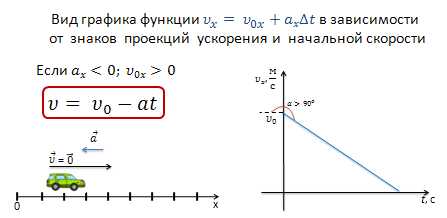
Когда ускорение направлено по оси х, а начальная скорость против оси х, то формула принимает вид:
скорость тела с течением времени возрастает. Но при этом график скорости образует с положительным направлением оси
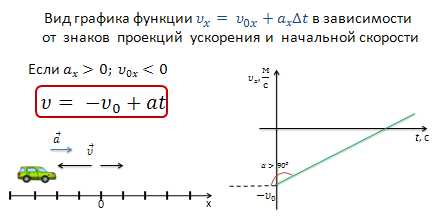
Если в начальный момент времени тело покоилось, то уравнение примет вид
если проекция вектора ускорения направлена по оси Ох, то скорость тела возрастает и график скорости, в этом случае, образует с положительным направлением оси t острый угол и начинается в точке (0;0).

Или
если проекция вектора ускорения направлена против оси х. Скорость тела возрастает, но при этом тело движется в отрицательном направлении, но так же начинается в точке (0;0).

И последнее, если проекции начальной скорости и ускорения равны нулю, то тело с течением времени не изменяет своего положения и графиком скорости является прямая, совпадающая с осью времени (тело покоится).
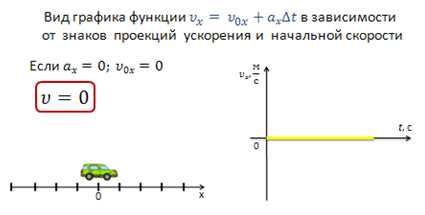
4. Этап обобщения и закрепления нового материала
Подведем основные итоги:
Ø Зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, по формуле:
Ø Зависимость проекции вектора скорости от времени при равноускоренном движении есть линейная функция, графиком которой является прямая линия.
Ø Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.
5. Рефлексия
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
Скорость при равноускоренном движении | Физика
 Теория равноускоренного движения была разработана знаменитым итальянским ученым Галилео Галилеем. В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению», вышедшей в 1638 г., Галилей впервые дал определение равноускоренного движения и доказал ряд теорем, в которых описывались его закономерности.
Теория равноускоренного движения была разработана знаменитым итальянским ученым Галилео Галилеем. В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к Механике и Местному движению», вышедшей в 1638 г., Галилей впервые дал определение равноускоренного движения и доказал ряд теорем, в которых описывались его закономерности.
Приступая к изучению равноускоренного прямолинейного движения, выясним сначала, как находится скорость тела, если известны ускорение этого тела и время движения.
Из формулы (2.1) следует, что при начальной скорости, равной нулю (v0 = 0),
Эта формула показывает, что для нахождения скорости тела через время t после начала движения надо ускорение тела умножить на время движения.
В противоположном случае, когда тело совершает замедленное движение и в конце концов останавливается (v = 0), формула ускорения (2.2) позволяет найти начальную скорость тела:
Наглядную картину того, как изменяется скорость тела в процессе равноускоренного движения, можно получить, построив график скорости.
Графики скорости впервые были введены в середине XIV в. францисканским ученым-монахом Джиованни ди Казалисом и архидьяконом Руанского собора Никола Оремом, ставшим впоследствии советником французского короля Карла V. По горизонтальной оси они предложили откладывать время, а по вертикальной оси — скорость. В такой системе координат графики скорости при равноускоренном движении имеют вид прямых линий, наклон которых показывает, как быстро изменяется скорость с течением времени.
Формуле (3.1), описывающей движение с возрастающей скоростью, соответствует, например, график скорости, изображенный на рисунке 5. График, изображенный на рисунке 6, соответствует движению с уменьшающейся скоростью.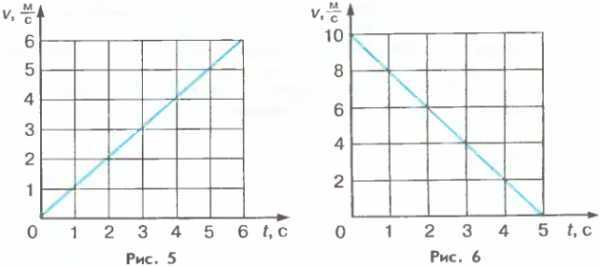
При равноускоренном движении скорость тела непрерывно изменяется. Графики скорости позволяют определить скорость тела в различные моменты времени. Но иногда бывает нужно знать не скорость в тот или иной конкретный момент времени (такую скорость называют мгновенной), а среднюю скорость движения на всем пути.
Задачу о нахождении средней скорости при равноускоренном движении впервые удалось решить Галилею. В своих исследованиях он использовал графический метод описания движения.
Согласно теории Галилея, если скорость тела при равноускоренном движении увеличивается от 0 до некоторого значения v, то средняя скорость движения будет равна половине достигнутой скорости:
Аналогичная формула справедлива и для движения с уменьшающейся скоростью. Если она уменьшается от некоторого начального значения v0 до 0, то средняя скорость такого движения оказывается равной
Полученные результаты можно проиллюстрировать с помощью графика скорости. Так, например, для нахождения средней скорости движения, которому соответствует график на рисунке 5, мы должны найти половину от 6 м/с. В результате получаем 3 м/с. Это и есть средняя скорость рассматриваемого движения.
1. Кто является автором первой теории равноускоренного движения? 2. Как находится скорость тела при равноускоренном движении из состояния покоя? 3. Используя график, изображенный на рисунке 5, определите скорость тела через 2 с после начала движения. 4. Используя график, изображенный на рисунке 6, определите среднюю скорость движения тела.
phscs.ru
Скорость при прямолинейном равноускоренном движении
При движении реального тела, например едущего из Москвы в Санкт-Петербург автомобиля, его ускорение может все время изменяться. При этом зависимость ускорения автомобиля от времени может быть достаточно сложной. Мы начнем изучение ускоренного движения с самого простого его вида – прямолинейного равноускоренного движения.
Прямолинейное движение тела называют равноускоренным, если в процессе движения значение ускорения остается постоянным, т. е. не изменяется с течением времени.
Если значение a ускорения движущегося тела постоянно, и мы знаем начальную скорость этого тела v0, то можно найти скорость тела vк в любой последующий момент времени t. Будем для упрощения дальнейших вычислений считать (так обычно и делают), что t0 = 0. Тогда Δt = t – t0 = t. Поскольку мы рассматриваем лишь случай прямолинейного движения тел вдоль оси X, то по определению значение ускорения вдоль этой оси
a = (vк – v0) / Δt = (vк – v0) / t.
Тогда vк – v0 = a · t, поэтому vк = v0 + a · t.
В полученном выражении vк – значение скорости вдоль оси X в момент времени t.
Это выражение называют зависимостью значения скорости от времени при прямолинейном равноускоренном движении. Обратим еще раз внимание на то, что начальный момент времени в этом выражении мы полагали равным нулю.
Зависимость значения скорости от времени при прямолинейном равноускоренном движении имеет вид:
v = v0 + a · t.
Если изобразить эту зависимость графически, то мы получим прямую линию (рис. 54). Из графика видно, что в момент t0 = 0 значение скорости равно v0. При увеличении времени на t значение скорости возрастает до величины v0 + a · t.
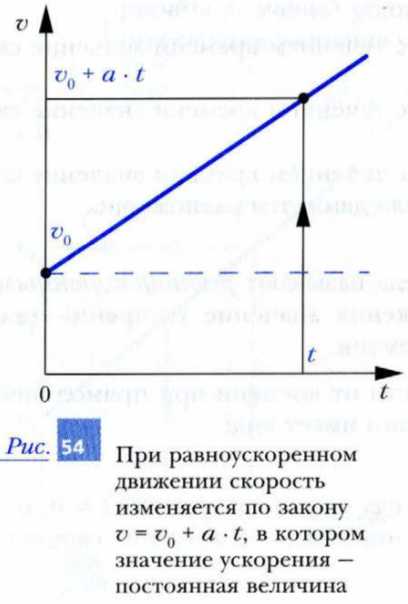
Рассмотрим пример равноускоренного движения.
Пусть водитель автомобиля, который движется в положительном направлении оси X со скоростью, имеющей значение v0 = 10 м/с в момент t = 0, нажимает на педаль газа. В результате автомобиль начинает разгоняться с постоянным ускорением, имеющим значение a = 2 м/с2. Опишем изменение скорости автомобиля аналитическим, табличным и графическим способами. Так как значение ускорения автомобиля a = 2 м/с2, то значение его скорости за каждую секунду будет увеличиваться на 2 м/с. Следовательно, в момент времени t = 1 с оно будет равно
v1 = 10 + 2 · 1 = 12 (м/с).
К моменту t = 2 с, т, е. через 2 секунды после начала равноускоренного движения,
v2 = 10 + 2 · 2 = 14 (м/с),
через 3 секунды –
v3 = 10 + 2 · 3 = 16 (м/с) и т. д.
Таким образом, через t секунд значение скорости будет равно
v = 10 + 2 · t = v0 + a · t.
Полученные результаты приведены в таблице и на рис. 55.

В заключение отметим, что:
1) если значение ускорения a > 0, то с течением времени значение скорости тела увеличивается;
2) если значение ускорения a < 0, то с течением времени значение скорости тела уменьшается;
3) если значение ускорения a = 0, то с течением времени значение скорости тела остается неизменным, т. е. тело движется равномерно.
Итоги
Прямолинейное движение тела называют равноускоренным, если в процессе этого движения значение ускорения тела не изменяется с течением времени. Зависимость значения скорости от времени при прямолинейном равноускоренном движении имеет вид:
v = v0 + a · t,
где v0 – значение скорости тела в момент времени t = 0, a – значение постоянного ускорения тела, v – значение скорости тела в момент времени t.
Вопросы
- Какое прямолинейное движение тела называют равноускоренным?
- Выведите зависимость значения скорости от времени при прямолинейном равноускоренном движении.
- Как изменяется значение скорости во времени при равноускоренном движении, если: а) a > 0; б) a < 0; в) a = 0?
Упражнения
1. Значение ускорения автомобиля при прямолинейном равноускоренном движении было равно a = 2 м/с2 в течение промежутка времени Δt = 4 с. В конце этого промежутка времени автомобиль двигался в положительном направлении оси X со скоростью, значение которой стало равным vк = 10 м/с. Найдите значение скорости этого автомобиля в момент времени, соответствующий началу данного промежутка времени. Предварительно ответьте на вопрос разгонялся или тормозил автомобиль в течение этого промежутка времени?
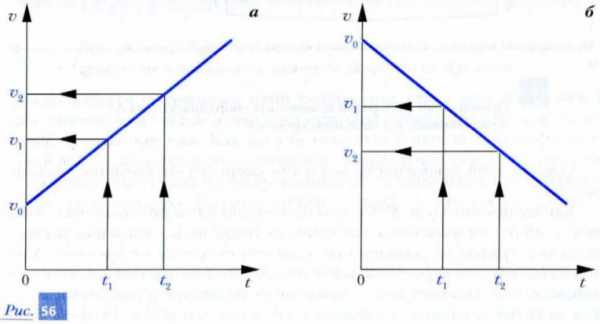
2. На рис. 56 изображены графики зависимости значения скорости от времени для двух точечных тел. Напишите выражения для расчета значений ускорений этих тел. В каком из представленных случаев значение ускорения положительно?
phscs.ru
Равноускоренное движение
Равноускоренным называют движение с постоянным ускорением. Простейшим примером такого движения является свободное падение тел, изучением которых занимался ещё Галилео Галилей. Скорость движения при этом не остаётся постоянной: в общем случае она меняется и по модулю, и по направлению. Описание данного движения значительно сложнее по сравнению с равномерным прямолинейном. Действия с числами здесь заменяют на действия с векторами, так как векторы содержат в себе информацию о направлений величин, характеризующих движение (о скорости, ускорений, перемещений).
Ускорение при равноускоренном движений показывает, на сколько изменяется скорость тела за каждую секунду движения:
(1)
Где V0 – начальная скорость тела, а V скорость того же тела спустя некоторое время t.
Ускорение показывает изменение скорости за единицу времени.
Из определения ускорения следует, что мгновенная скорость тела при равноускоренном движении изменяется с течением времени по линейному закону:
(2)
Эта формула позволяет по начальной скорости и ускорению тела вычислить его скорость в любой момент времени t. Между тем основная задача механики заключается в определении того, где будет находиться тело спустя заданное время. Для её решения необходимо знать перемещение, совершённое телом за это время. Перемещение можно найти, умножив среднюю скорость на время движения:
s=vcpt
При равноускоренном движении средняя скорость равна полусумме начальной и конечной скоростей движения:
Поэтому:
Подставляя сюда выражения (2), получаем:
s=v0t +at2/2(3)
Именно это уравнение является обобщением формулы:s=vt на случай движения с постоянным ускорением.
Уравнения (1),(2),(3) – векторные. Действия с векторами отличаются от действий с числами, поэтому никакие числовые значения перемещения, скорости и ускорения в такие уравнения подставлять нельзя. Между тем любые расчёты требуют проведений операций именно с числами. Чтобы это стало возможным, необходимо от векторного способа описания движения перейти к координатному. При координатном описаний движения вместо векторов используют проекций на оси координат. Поскольку любой вектор характеризуется тремя проекциями на оси X,Y и Z, следовательно каждому вектору уравнению в общем случае будут соответствовать три уравнения в координатной форме. Для плоского (двухмерного) движения таких уравнений только два. Если же движение является прямолинейным, то для его описания достаточно одного уравнения в проекций на ось X(при условии, что эта ось направлена параллельно вектору скорости частицы). Тогда уравнения (2) и (3).например, можно записать следующим образом:
vx=v0x+axt
sx=v0xt+axt2/2(4)
При координатном описаний движения, координота тела будет равна:x=x0+v0xt+axt2/2(5)
w-site.narod.ru
Скорость при прямолинейном равноускоренном движении
Известно, что при прямолинейном равноускоренном движении ускорение тела можно рассчитать по формуле:
Выразим из этой формулы скорость, которую могло бы иметь тело в конце промежутка времени Δt. Получим
Или
Таки образом получена формула, которая называется уравнением скорости при равноускоренном движении.
Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя. Перепишем эту формулу в проекции на ось х.
Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.
Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика.
Из курса математики известно, что линейная функция имеет вид
у = kx + b,
где х — аргумент, k — постоянный коэффициент, b— свободный член. Графиком этой функции является прямая линия.
Функция
υx = υ0x + axΔt
тоже линейная с аргументом Δt, постоянным коэффициентом ах и свободным членом υ0х. Значит, графиком этой функции тоже должна быть прямая линия.
Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.
Рассмотрим, какой вид будет иметь график скорости в зависимостиот знаков проекций ускорения и начальной скорости.
Если проекция вектора скорости тела и его ускорение направлены по оси Ох, то уравнение примет вид
В этом случае скорость тела с течением времени возрастает. При этом график скорости образует с положительным направлением оси t острый угол.
Если же проекция вектора скорости тела и его ускорение направлены против оси Ох, то уравнение примет вид
Скорость тела с течением времени возрастает, но тело, при этом, движется в отрицательном направлении. График скорости образует с положительным направлением оси t тупой угол.
В случае, если скорость тела направлена по оси Ох, а ускорение — против оси Ох, то формула принимает вид
Скорость тела убывает от некоторого значения до нуля. График скорости образует с положительным направлением оси t тупой угол.
Когда ускорение направлено по оси Ох, а начальная скорость против оси Ох, то формула принимает вид:
скорость тела с течением времени возрастает. Но при этом график скорости образует с положительным направлением оси t тупой угол.
Если в начальный момент времени тело покоилось, то уравнение примет вид
,
если проекция вектора ускорения направлена по оси Ох, то скорость тела возрастает и график скорости, в этом случае, образует с положительным направлением оси t острый угол и начинается в точке (0;0).
Если проекция вектора ускорения направлена против оси х.
Скорость тела возрастает, но при этом тело движется в отрицательном направлении, но так же начинается в точке (0;0).
Если проекции начальной скорости и ускорения равны нулю, то тело с течением времени не изменяет своего положения и графиком скорости является прямая, совпадающая с осью времени (тело покоится).
Основные выводы:
– Зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени, по формуле:
.
– Зависимость проекции вектора скорости от времени при равноускоренном движении есть линейная функция, графиком которой является прямая линия.
– Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.
videouroki.net
| Занятие № 4 Тема. Равноускоренное движение. Ускорение. Скорость тела и пройденный путь при равноускоренном прямолинейном движении. Графики движения. Цель: формирование знаний о равноускоренном прямолинейном движении, знакомство с его характеристиками: ускорением, средней и мгновенной скоростями, математическим описанием; рассмотрение графиков зависимости скорости, координат прямолинейного равноускоренного движения от времени. Тип занятия: комбинированный урок, урок усвоения новых знаний
Фронтальный опрос.
План изучения темы
На предыдущих уроках мы рассматривали прямолинейное равномерное движение, при котором тело движется с постоянной скоростью. Но человеку в повседневной жизни чаще всего приходится сталкиваться с неравномерным прямолинейным движением. Так, поезд, отходя от станции, постепенно набирает скорость, а при подходе к следующей станции его скорость уменьшается; ракета, взлетая, увеличивает свою скорость сначала медленно, а затем летит все быстрее и быстрее. Если рассматривать падение тел, то они тоже движутся по прямой с возрастающей скоростью, если среда падения не сильно препятствует этому движению. Следовательно, изучение неравномерного прямолинейного движения является важным вопросом механики.
Одно и то же перемещение материальная точка может совершать за различное время. Если за равные промежутки времени тело совершает равные по величине перемещения, то такое движение называется равномерным, если нет – неравномерным. Быстрота изменения положения материальной точки в пространстве характеризуется скоростью движения. При равномерном движении величина скорости остается все время постоянной, при неравномерном – меняется в процессе движения. Отношение перемещения ко времени движения t материальной точки в случае неравномерного движения называется средней скоростью движения . С практической точки зрения большее значение имеет средняя путевая скорость. ^ равна отношению пройденного телом пути ко времени его прохождения: Vср= S/t и является скалярной величиной. Именно эту физическую величину имеют ввиду, когда говорят, например, что спортсмен пробежал дистанцию со средней скоростью 6,5 м/с. Для описания неравномерного движения можно определить среднюю скорость движения на нескольких участках пути. Однако это даст лишь приближенное понятие о характере движения. Дело в том, что, определяя средние скорости, мы заменяем неравномерное движение в течение каждого промежутка времени равномерным движением и считаем, что скорость меняется скачком от одного промежутка времени к другому. Для более точного описания движения потребуется определять средние скорости за все меньшие и меньшие промежутки времени. По мере уменьшения промежутков времени фактическое движение в пределах каждого отдельного промежутка будет все менее отличаться от равномерного и, наконец, отличие перестанет улавливаться приборами, при помощи которых мы измеряем среднюю скорость. Этим ставится естественный предел уточнению описания движения при данной степени точности измерений длины и времени. Зависимость пройденного пути от времени при определении средней скорости за различные промежутки времени. Мгновенная скорость – средняя скорость за бесконечно малый интервал времени. Если речь идёт ещё и о направлении, то определение мгновенной скорости будет таким: Мгновенная скорость – векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, за который это перемещение произошло: Направление скорости совпадает с направлением перемещения . Мгновенная скорость тела направлена по касательной к траектории в сторону его движения. Если рассмотреть проекции вектора скорости на координатные оси, то
Равноускоренное прямолинейное движение — это такое движение, при котором скорость тела за любые равные промежутки времени изменяется на одинаковую величину, а траектория движения является прямой линией. Е Одной из главных характеристик равноускоренного движения является ускорение. Характеристика ускорения как физической величины
5. Ускорение определяется методом непрямых измерений. Ускорение равноускоренного движения — величина постоянная. В случае равноускоренного движения, когда начальная скорость меньше конечной, ускорение является положительной величиной (рис. 1, а), а в том случае, когда начальная скорость больше конечной, ускорение отрицательно (рис.1, б) Обозначаем: – вектор ускорения; ax, ay – проекции вектора ускорения на координатные оси Ox, Oy; а – модуль ускорения. Вопрос к студентам:
Уравнение движения для прямолинейного равноускоренного движения: Модуль перемещения (путь) для прямолинейного равноускоренного движения определяется по формулам: , , т.к. за каждую единицу времени скорость тела изменяется на одинаковое значение, т.е. линейно. Координата тела в данный момент времени для равноускоренного движения: Это уравнение и есть решением основной задачи механики для равноускоренного движения, т.к. определяет положение тела в данный момент времени по известным начальным условиям.
Решение задач
Преподаватель подводит итоги урока, оценивает деятельность учеников. Домашнее задание
Тест Найдите правильный ответ.
А) м/с; Б) м∙с В) м/с2 Г) м∙с2
Ответы к тесту
|
zavantag.com
Средняя скорость при равноускоренном движении
Чтобы определить среднюю путевую скорость, нужно разделить весь путь на все время. Это справедливо и для равноускоренного движения. Модуль средней скорости по перемещению определяется как модуль перемещения, деленный на все время движения. Также перемещение – векторная величина, и имеет направление, следовательно, можно определить и угол, под которым средняя скорость будет направлена к горизонту.
Задача 1. Тело падает без начальной скорости с высоты м. Найти среднюю скорость падения на второй половине пути.
Чтобы определить среднюю скорость, нужно разделить путь, пройденный телом, на время его движения.
Длина первой половины пути – .
Тогда можно записать, что , где – время прохождения телом первой половины пути, его можно найти:
Полное время падения тоже легко определить:
Тогда определим время, за которое тело прошло вторую половину пути:
Определим среднюю скорость:
Ответ: средняя скорость на второй половине пути равна 25,6 м/c.
Задача 2. Тело брошено со скоростью м/с вертикально вверх с высоты м над поверхностью земли. Определить среднюю скорость и среднюю путевую скорость за время полета.
Так как найти надо среднюю путевую и среднюю скорость по перемещению, то необходимо знать как путь, так и перемещение тела. Очевидно, что точку старта и точку финиша тела разделяет высота , с которой тело было сброшено, так как в конце оно окажется на земле. Итак, – это перемещение тела.
Чтобы определить путь, потребуется найти высоту, до которой тело смогло подняться. Путь тела тогда будет равен
Максимальная высота подъема тела равна , следовательно,
Также для определения средней скорости надо знать время движения тела. Это время будет складываться из времени взлета и времени падения .
Время взлета найдем из условия равенства нулю скорости тела:
Время падения тоже легко определить, зная, что тело падало с высоты :
Теперь, зная время взлета и время падения, можем определить общее время движения тела:
Осталось разделить путь на это время – и получим среднюю путевую скорость:
Средняя скорость по перемещению равна (или модуль средней скорости):
Задача 3. Мячик брошен с высоты м над поверхностью земли с начальной скоростью м/с под углом к горизонту. Найти модуль и направление его средней скорости за все время полета.
В этой задаче необходимо, по сути, определить вектор средней скорости тела по перемещению: его длину (модуль) и направление. Очевидно, для этого потребуется знать, как далеко тело улетело и сколько на это понадобилось времени. Мы помним, что проекция скорости тела на горизонтальную ось остается неизменной во времени и равной . Если удастся найти время полета тела – то мы узнаем, как далеко оно шлепнулось о землю.
Давайте запишем закон движения тела по оси :
Так как в итоге ордината тела оказалась равной 0, то приравняем и решим полученное квадратное уравнение:
Один из корней – отрицательный – отбросим, как неудовлетворяющий смыслу задачи.
Тело улетит от точки старта по горизонтали на расстояние:
Теперь определим перемещение тела по теореме Пифагора:
Разделив перемещение тела на время, получим среднюю скорость по перемещению:
Определим численно, чтобы потом проще было при подсчетах:
Теперь рассчитаем среднюю скрость:
Найдем, под каким углом к горизонту был направлен вектор средней скорости:
Ответ: модуль средней скорости равен 17,3 м/с, она направлена под углом к горизонту.
easy-physic.ru
