Скорость точки движения – , –

Кинематика

Кинематика– это раздел теоретической механики, в котором изучается движение тел без учета действия сил, вызывающих или поддерживающих это движение.

Основные определения

Движением тела называется изменение его положения в пространстве по отношению к заданной системе отсчета.

Системой отсчета называется любое тело, по отношению к которому изучается движение.

Время в механике считается независимой переменной, одинаковой для всех наблюдателей.

В отдельных случаях при изучении движения некоторых тел, их можно принять за геометрические точки, пренебрегая размерами, например, когда расстояние, проходимое телом, значительно больше его размеров. Это позволяет значительно упростить изучение характеристик движения.

Кинематика точки

Для изучения движения тела это движение нужно каким-либо образом задать, т.е. задать положение тела (точки) относительно данной системы отсчета в любой момент времени.

Способы задания движения

1. Естественный способ задания движения

Этим способом удобно пользоваться, когда известна траектория движения точки.

Т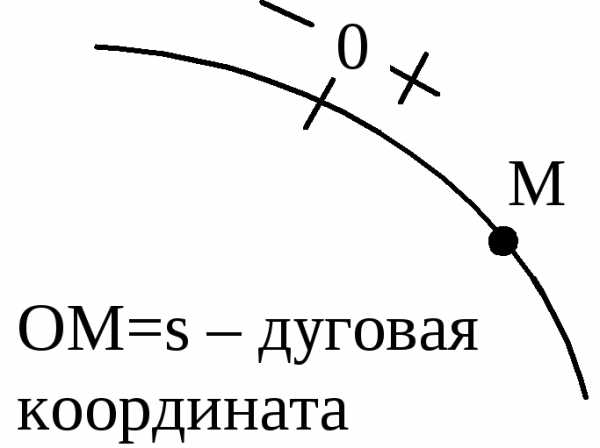раекториейназывается линия, которую описывает материальная точка при ее движении в пространстве.

При естественном способе задания движения должны быть заданы:

1. Траектория движения точки

2. Начало отсчета дуговой координаты

3. Направление отсчета

4. Закон движения точки по траектории в виде

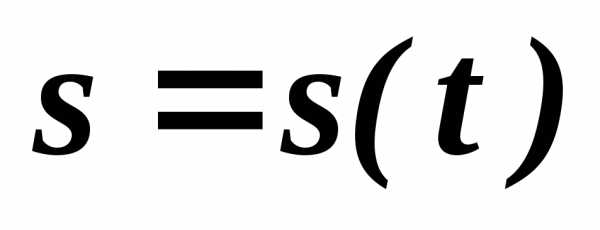(1)

2. Векторный способ задания движения

В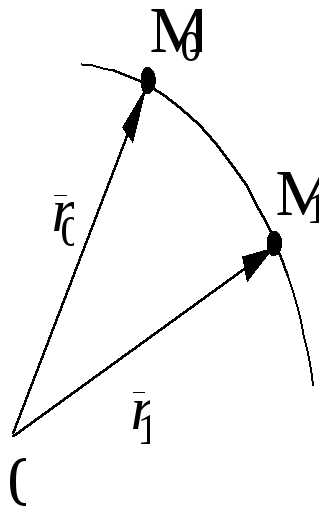этом случае для определения положения материальной точки в пространстве в любой момент времени нужно задать начало отсчета (точка О) и зависимость радиус-вектора от времени

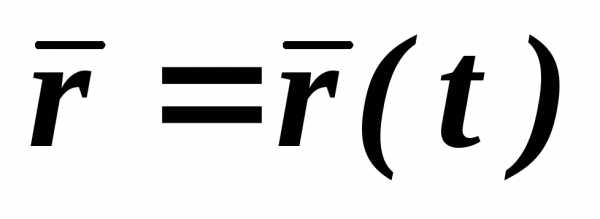(2)

(2) – уравнение движения точки в векторной форме

Геометрическое место концов вектора (годограф вектора) определяет траекторию движения точки.

3. Координатный способ задания движения

В этом случае, в отличие от естественного способа, траектория заранее не известна.

Задается система отсчета Oxyz и координаты материальной точки как функции времени

(3)

(3) – уравнения движения материальной точки в координатной форме.

Уравнение траектории можно получить в явном виде. Для этого надо исключить из уравнений (3) время.

4. Взаимосвязь между некоторыми характеристиками различных способов задания движения.

Связь между координатным и векторным способами задания движения.

– радиус-вектор,

– проекции радиус-вектора равны координатам точки,

– единичные векторы (орты),

тогда , или

. (4)

Уравнение (4) выражает связь между координатным и естественным способами движения. Положение радиус-вектора по отношению к координатным осям определяется по направляющим косинусам

.

Переход от координатного способа к естественному.

Для этого нужно найти из (3) уравнение траектории в явном виде и закон движения вдоль траектории на основе выражения для дифференциала дуги

. (5)

Скорость точки

Скоростью точки называется векторная величина, характеризующая быстроту изменения положения материальной точки в пространстве с течением времени.

Определение скорости при векторном способе задания движения.

– приращение времени,

– приращение радиус-вектора,

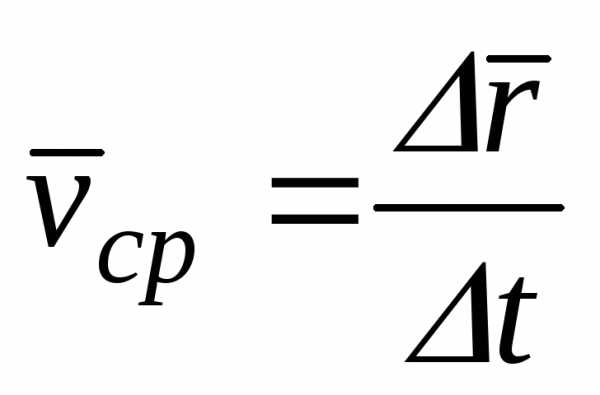. (6)

Средняя скорость точки равна отношению приращения радиус-вектора к соответствующему приращению времени.

Значение скорости в заданный момент времени найдем как предел

,

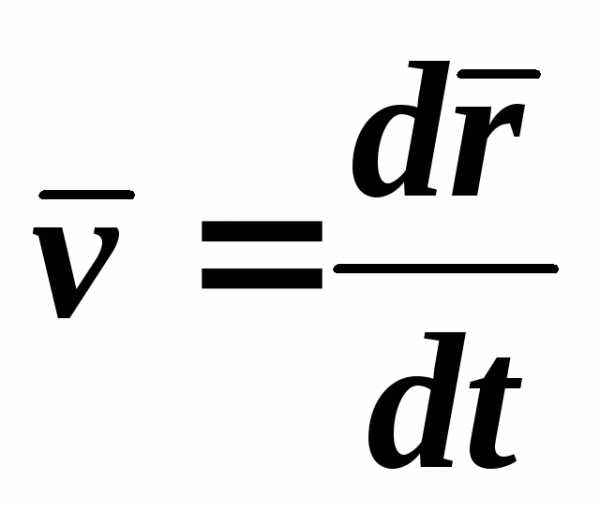. (7)

Вектор скорости материальной точки в данный момент времени равен первой производной от радиус-вектора точки по времени.

Вектор скорости всегда направлен по касательной к траектории точки в заданный момент времени.

studfiles.net

Скорость движения точки по прямой. Мгновенная скорость. Нахождение координаты по известной зависимости скорости по времени.

Б 1

Скорость движения точки по прямой. Мгновенная скорость. Нахождение координаты по известной зависимости скорости по времени.

Скорость движения-движения точки по прямой или данной кривой линии приходится говорить как о длине пути, пройденного точкою в течение какого-либо промежутка времени, так и о перемещении ее в течение того же промежутка; эти величины могут и не быть одинаковы, если движение происходило то в одну, то в другую сторону по пути

МГНОВЕННАЯ СКОРОСТЬ ( )

– векторная физическая величина, равная отношению перемещения Δ , совершенного частицей за очень малый промежуток времени Δt, к этому промежутку времени.

Под очень малым (или, как говорят, физически бесконечно малым) промежутком времени здесь понимается такой, на протяжении которого движение с достаточной точностью можно считать равномерным и прямолинейным.

В каждый момент времени мгновенная скорость направлена по касательной к траектории, по которой движется частица.

Ее единицей в СИ является метр в секунду (м/с).

Б 2

Векторный и координатный способы движения точки. Скорость и ускорение.

Положение точки в пространстве можно задать двумя способами:

1) с помощью координат,

2) с помощью радиус-вектора.
В первом случае положение точки определяется на осях декартовой системы координат ОХ, OY, OZ, связанных с телом отсчета (рис. 3). Для этого из точки А необходимо опустить перпендикуляры на плоскость YZ (координата х), XZ (координата / у), XY (координата г) соответственно. Итак, положение точки можно определить записи А (х, у, г), а для случая, изображенного на рис. С (х = 6, у = 10, z – 4,5), точка А обозначается следующим образом: А (6, 10, 4,5).

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения точки необходимо отложить значения координат на соответствующие оси и па трех взаимно перпендикулярных отрезках построить параллелепипед. Его вершина, противоположная началу координат О и размещена на диагонали параллелепипеда, и является точкой А.
Если точка движется в рамках какой-либо плоскости, то через выбранные па теле отсчет * в точке достаточно провести две координатные оси ОХ и OY.

Скорость- векторная величина, равная отношению перемещения тела ко времени, за которое это перемещение произошло. При неравномерном движении скорость тела изменяется с течением времени. При таком движении скорость определяется мгновенной скоростью тела. Мгновенная скорость- скорость тела в данный момент времени или в данной точке траектории.

Ускорение.При неравномерном движении скорость изменяется и по модулю и по направлению. Ускорение- это скорость изменения скорости. Оно равно отношению изменения скорости тела к промежутку времени, за которое это перемещение произошло.

Б 3

Баллистическое движение. Равномерное движение материальной точки по окружности . Криволинейное движение точки в пространстве

.

Равномерное движение по окружности.

Движение тела по окружности- криволинейное, при нем изменяется две координаты и направление движения. Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Движение по любой криволинейной траектории можно представить как движение по дугам некоторых окружностей. Равномерное движение по окружности- движение с ускорением, хотя по модулю скорость не изменяется. Равномерное движение по окружности- периодическое движение.

Криволинейное баллистическое движение тела можно рассматривать как результат сложения двух прямолинейных движений: равномерного движения по оси

х и равнопеременного движения по оси у.

Б 6

Кинетическая энергия системы материальных точек, её связь с работой сил. Теорема Кенига.

Изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.

Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

,

где — полная кинетическая энергия, — энергия движения центра масс, — относительная кинетическая энергия.

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы во вращательном движении относительно центра масс.

Б 4

Б 5

Б 7

Потенциальная энергия в поле центральных сил.

Центральным называют такое силовое поле, в котором потенциальная энергия частицы является функцией только от расстояния r до определенной точки- центра поля: U=U(r). Сила, действующая на частицу в таком поле, тоже зависит лишь от расстояния r и направлена в каждой точке пространства вдоль радиуса, проведенного в эту точку из центра поля.

Б 8

Понятие момента сил и момента импульса, связь между ними. Закон сохранения момента импульса. Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где — сила, действующая на частицу, и r — радиус-вектор частицы.

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса частицы относительно некоторого начала отсчета определяется векторным произведением ее радиус-вектора и импульса:

где — радиус-вектор частицы относительно выбранного начала отсчета, — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:

.

В рамках закона сохранения момента импульса консервативной величиной является угловой момент вращения массы — он не изменяется в отсутствие приложенного момента силы или крутящего момента — проекции вектора силы на плоскость вращения, перпендикулярно радиусу вращения, помноженной на рычаг (расстояние до оси вращения). Самый расхожий пример закона сохранения момента импульса — фигуристка, выполняющая фигуру вращения с ускорением. Спортсменка входит во вращение достаточно медленно, широко раскинув руки и ноги, а затем, по мере того, как она собирает массу своего тела всё ближе к оси вращения, прижимая конечности всё ближе к туловищу, скорость вращения многократно возрастает вследствие уменьшения момента инерции при сохранении момента вращения. Тут мы и убеждаемся наглядно, что чем меньше момент инерции, тем выше угловая скорость и, как следствие, короче период вращения, обратно пропорциональный ей.

Закон сохранения момента импульса: Момент импульса системы тел сохраняется, если результирующий момент внешних сил, действующих на систему, равен нулю:

.

Если результирующий момент внешних сил не равен нулю, но рана нулю проекция этого момента на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.

Б 9

Б 10

Момент инерции. Теорема Гюйгенса-Штейнера. Момент инерции и кинетическая энергия вращения твердого тела вокруг неподвижной оси.

^ Момент инерции точки– величина, равная произведению массы m точки на квадрат ее кратчайшего расстояния r до оси (центра) вращения: J_z = m r², J = m r², кг ^. м².

Теорема Штейнера:Моментом инерции твердого тела относительно любой оси равен сумме момента инерции относительно оси проходящей через центр масс и произведению массы этого тела на квадрат расстояния между осями. I=I₀+md² .Величина I, равная сумме произведений элементарных масс на квадраты их расстояния от некоторой оси, наз. моментом инерции тела относительно данной оси. I=m_iR_i² Суммирование производиться по всем элементарным массам на которые можно разбить тело.

Перейти к: навигация, поиск

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость ( ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия

где I_z — момент инерции тела относительно оси вращения.

Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I₁, I₂ и I₃. Вращательная энергия такой молекулы задана выражением

где ω₁, ω₂, и ω₃ — главные компоненты угловой скорости.

В общем случае, энергия при вращении с угловой скоростью находится по формуле:

, где — тензор инерции

 

Б 11

Инвариантность законов динамики в ИСО. Система отсчета движется поступательно и ускоренно. Система отсчета равномерно вращается. (Материальная точка покоится в НИСО, материальная точка движется в НИСО.). Теорема Кориолиса.

Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые её описавшего. Ускорение Кориолиса было получено Кориолисом в 1833 году, Гауссом в 1803 году и Эйлером в 1765 году.

Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.

Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной , где — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.

Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.

 

Б 12

ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР

– система, совершающая гармонические колебания

Колебания, обычно,связаны с попеременным превращением энергии одной формы (вида) в энергию другой формы (другого вида). В механическом маятнике энергия превращается из кинетической в потенциальную. В электрических LC контурах(то есть индуктивно-емкостных контурах)энергия превращается из электрической энергии ёмкости (энергии электрического поля конденсатора) в магнитную энергию катушки индуктивности (энергию магнитного поля соленоида)

 

Б 13

Примеры гармонических осцилляторов (физический маятник, математический маятник, крутильный маятник)

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения^[

Крути́льный ма́ятник (также торсио́нный ма́ятник, враща́тельный ма́ятник) — механическая система, представляющая собой тело, подвешенное в поле тяжести на тонкой нити и обладающее лишь одной степенью свободы: вращением вокруг оси, задаваемой неподвижной нитью

Б 14

Б 15

Области применения

Капиллярный эффект используется в неразрушающем контроле (капиллярный контроль или контроль проникающими веществами) для выявления дефектов, имеющих выход на поверхность контролируемого изделия. Позволяет выявлять трещины с раскрытием от 1 мкм, которые не видны невооруженным глазом.

Когезия (от лат. cohaesus — связанный, сцепленный), сцепление молекул (ионов) физического тела под действием сил притяжения. Это силы межмолекулярного взаимодействия, водородной связи и (или) иной химической связи. Они определяют совокупность физических и физико-химических свойств вещества: агрегатное состояние, летучесть, растворимость, механические свойства и т. д. Интенсивность межмолекулярного и межатомного взаимодействия (а, следовательно, силы когезии) резко убывает с расстоянием. Наиболее сильна когезия в твердых телах и жидкостях, то есть в конденсированных фазах, где расстояние между молекулами (ионами) малы — порядка нескольких размеров молекул. В газах средние расстояния между молекулами велики по сравнению с их размерами, и поэтому когезия в них незначительна. Мерой интенсивности межмолекулярного взаимодействия служит плотность энергии когезии. Она эквивалентна работе удаления взаимно притягивающихся молекул на бесконечно большое расстояние друг от друга, что практически соответствует испарению или сублимации вещества

Адгезия (от лат. adhaesio — прилипание) в физике — сцепление поверхностей разнородных твёрдых и/или жидких тел. Адгезия обусловлена межмолекулярным взаимодействием (вандерваальсовым, полярным, иногда — образованием химических связей или взаимной диффузией) в поверхностном слое и характеризуется удельной работой, необходимой для разделения поверхностей. В некоторых случаях адгезия может оказаться сильнее, чем когезия, то есть сцепление внутри однородного материала, в таких случаях при приложении разрывающего усилия происходит когезионный разрыв, то есть разрыв в объёме менее прочного из соприкасающихся материалов.

Б 16

Понятие потока жидкости (газа) и уравнение непрерывности. Вывод уравнения Бернулли.

В гидравлике потоком считают такое движение массы, когда эта масса ограничена:

1) твердыми поверхностями;

2) поверхностями, которые разделяют разные жидкости;

3) свободными поверхностями.

В зависимости от того, какого рода поверхностями или их сочетаниями ограничена движущаяся жидкость, различают следующие виды потоков:

1) безнапорные, когда поток ограничен сочетанием твердой и свободной поверхностей, например, река, канал, труба с неполным сечением;

2) напорные, например, труба с полным сечением;

3) гидравлические струи, которые ограничены жидкой (как мы увидим позже, такие струйки называют затопленными) или газовой средой.

Живое сечение и гидравлический радиус потока. Уравнение неразрывности в гидравлической форме

Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ωx, ωy,ωz угловой скорости w.

Условием того, что движение является установившимся, является отсутствие ускорения, то есть условие равенства нулю частных производных от всех компонентов скорости:

Если теперь сложить

то получим

Если проецировать перемещение на бесконечно малую величину dl на координатные оси, то получим:

dx = Uxdt; dy = Uy dt; dz = Uzdt. (3)

Теперь помножим каждое уравнение (3) соответственно на dx, dy, dz, и сложим их:

Предположив, что правая часть равна нулю, а это возможно, если вторая или третья строки равны нулю, получим:

Нами получено уравнение Бернулли

Анализ уравнения Бернулли

это уравнение есть не что иное, как уравнение линии тока при установившемся движении.

Отсюда следуют выводы:

1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.

2) пропорциональны строки 1 и 2, т. е.

Уравнение (2) является уравнением вихревой линии. Выводы из (2) аналогичны выводам из (1), только линии тока заменяют вихревые линии. Одним словом, в этом случае условие (2) выполняется для вихревых линий;

3) пропорциональны соответствующие члены строк 2 и 3, т. е.

где а – некоторая постоянная величина; если подставить (3) в (2), то получим уравнение линий тока (1), поскольку из (3) следует:

ω_x= aUx; ω_y= aUy; ω_z= aUz. (4)

Здесь следует интересный вывод о том, что векторы линейной скорости и угловой скорости сонаправлены, то есть параллельны.

В более широком понимании надо представить себе следующее: так как рассматриваемое движение установившееся, то получается, что частицы жидкости движутся по спирали и их траектории по спирали образуют линии тока. Следовательно, линии тока и траектории частиц – одно и то же. Движение такого рода называют винтовым.

4) вторая строка определителя (точнее, члены второй строки) равна нулю, т. е.

ω_x= ω_y= ω_z= 0. (5)

Но отсутствие угловой скорости равносильно отсутствию вихревости движения.

5) пусть строка 3 равна нулю, т. е.

Ux = Uy = Uz = 0.

Но это, как нам уже известно, условие равновесия жидкости.

Анализ уравнения Бернулли завершен.

 

Б 17

Б 18

Преобразование Галилея. Механический принцип относительности. Постулаты специальной (частной теории) относительности. Преобразование Лоренца и следствия из них.

Основным принципом, на котором базируется классическая механика является принцип относительности, сформулированный на основе эмпирических наблюдений Г. Галилеем. Согласно этому принципу существует бесконечно много систем отсчёта, в которых свободное тело покоится или движется с постоянной по модулю и направлению скоростью. Эти системы отсчёта называются инерциальными и движутся друг относительно друга равномерно и прямолинейно. Во всех инерциальных системах отсчёта свойства пространства и времени одинаковы, и все процессы в механических системах подчиняются одинаковым законам. Этот принцип можно также сформулировать как отсутствие абсолютных систем отсчёта, то есть систем отсчёта, каким-либо образом выделенных относительно других

При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями

Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов.

Преобразования Лоренца псевдоевклидова пространства сигнатуры находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространства выступает четырёхмерный пространственно-временной континуум (пространство Минковского

 

Б 19

Б 20

Б 21

Б 22

Б 23

Явление переноса.

В газе, находящемся в неравновесном состоянии, возникают необратимые процессы, называемые явлениями переноса. В ходе этих процессов происходит пространственный перенос вещества (диффузия), энергии (теплопроводность), импульса направленного движения (вязкое трение). Если течение процесса не изменяется со временем, то такой процесс называется стационарным. В противном случае это нестационарный процесс. Стационарные процессы возможны только в стационарных внешних условиях. В термодинамически изолированной системе могут возникать только нестационарные явления переноса, направленные на установление равновесного состояния

Б 24

Предмет и метод термодинамики. Основные понятия. Первый закон термодинамики.

Принцип построения термодинамики довольно прост. В ее основу положены три экспериментальных закона и уравнение состояния: первый закон (первое начало термодинамики) — закон сохранения и превращения энергии; второй закон (второе начало термодинамики) указывает направление, по кото­рому протекают естественные явления в природе; третий закон (третье начало термодинамики) утверждает, что абсолютный нуль температуры недо­стижимТермодинамика, в отличие от статистической физики, не рассматривает конкретные молекулярные картины. На основании опытных данных формулируются основные законы (принципы или начала). Эти законы и их следствия применяются к конкретным физическим явлениям, связанным с превращением энергии макроскопическим путем (без учета атомно-молекулярного строения), изучают свойства тел конкретных размеров. Термодинамический метод используется в физике, химии, ряде технических наук.

Термодинамика – учение о связи и взаимопревращениях различных видов энергии, теплоты и работы.

Понятие термодинамики произошло от греческих слов «термос» – теплота, жар; «динамикос» – сила, силовой.

Под телом в термодинамике понимают некоторую часть пространства, заполненную веществом. Форма тела, его цвет и другие свойства для термодинамики несущественны, следовательно, термодинамическое понятие тела отличается от геометрического.

Важную роль в термодинамике играет внутренняя энергия U.

U – сумма всех видов энергии, заключённых в изолированной системе (энергия теплового движения всех микрочастиц системы, энергия взаимодействия частиц, энергия электрических оболочек атомов и ионов, внутриядерная энергия и т.д.).

Внутренняя энергия является однозначной функцией состояния системы: её изменения DU при переходе системы из состояния 1 в 2 не зависит от вида процесса и равно ∆U = U₁ – U₂. Если система совершает круговой процесс, то:

Полное изменение её внутренней энергии равно 0.

Внутренняя энергия U системы определяется её состоянием, т. е. U системы есть функция параметров состояния:

U = f(p,V,T) (1)

При не слишком высоких температурах, внутреннюю энергию идеального газа можно считать равной сумме молекулярно-кинетических энергий теплового движения его молекул. Внутренняя энергия гомогенной, а в первом приближении и гетерогенной систем является аддитивной величиной – равной сумме внутренних энергий всех её макроскопических частей (или фаз системы).

 

Б 25

Б 26

Б 27

Адиабатный процесс. Уравнение Пуассона, адиабата. Политропный процесс, уравнение политропы.

Адиабатическим называется процесс, при котором отсутствует теплообмен

Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством . Серьёзное исследование адиабатических процессов началось в XVIII веке^[1].

Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна^[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы^[3].

Адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

• электростатическое поле,
• стационарное поле температуры,
• поле давления,
• поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид:

где — оператор Лапласа или лапласиан, а — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид:

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

Так же такие процессы получили ряд применений в технике.

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермический процесс ( ) и адиабатный процесс ( ).

В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными ^?

Уравнение политропы. Рассмотренные выше изохорический, изобарический, изотермический и адиабатический процессы обладают одним общим свойством – имеют постоянную теплоемкость.

Б 28

Идеальная тепловая машина и цикл Карно. К.П.Д. идеальной тепловой машины. Содержание второго закона К.П.Д. реальной тепловой машины.

Цикл Карно является идеальным термодинамическим циклом. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно^[8][29].

Максимальное КПД достигается при обратимом цикле^[8]. Для того, чтобы цикл был обратимым, из него должна быть исключена передача тепла при наличии разности температур. Чтобы доказать этот факт, предположим, что передача тепла при разности температур имеет место. Данная передача происходит от более горячего тела к более холодному. Если предположить процесс обратимым, то это означало бы возможность передачи тепла обратно от более холодного тела к более нагретому, что невозможно, следовательно процесс необратим^[25]. Соответственно, преобразование тепла в работу может происходить только изотермически^{[Комм 4]}. При этом обратный переход двигателя в начальную точку только путём изотермического процесса невозможен, так как в этом случае вся полученная работа будет затрачена на восстановление исходного положения. Так как выше было показано, что адиабатический процесс может быть обратимым — то этот вид адиабатического процесса подходит для использования в цикле Карно.

Всего при цикле Карно происходят два адиабатических процесса^[29]:

1. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс 2→3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

2. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс 4→1). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

Б 33

Б 38

Граничные условия Еn и Еt.

В проводящем теле, находящемся в электростатическом поле, все точки тела имеют одинаковый потенциал, поверхность проводящего тела является эквипотенциальной поверхностью и линии напряженности поля в диэлектрике нормальны к ней. Обозначив через Е_n и Е_t нормальную и касательную к поверхности проводника, составляющие вектора напряженности поля в диэлектрике около поверхности проводника, указанные условия можно записать в виде:

Е_t = 0; Е = Е_n = -¶U/¶n; D = -e*¶U/¶n = s,

где s – поверхностная плотность электрического заряда на поверхности проводника.

Таким образом, на границе раздела проводящего тела и диэлектрика отсутствует касательная к поверхности (тангенциальная) составляющая напряженности электрического поля, а вектор электрического смещения в любой точке, непосредственно примыкающей к поверхности проводящего тела численно равен плотности электрического заряда s на поверхности проводника

Б 29

Теорема Клаузиуса, неравенство Клаузиуса. Энтропия, её физический смысл. Изменение энтропии при необратимых процессов. Основное уравнение термодинамики.

сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса.

Рассматривая процессы превращения тепла в работу, Р. Клаузиус сформулировал термодинамическое неравенство, носящее его имя.

«Приведенное количество тепла, полученное системой в ходе произвольного кругового процесса, не может быть больше нуля»

где dQ – количество тепла, полученного системой при температуре Т, dQ₁ – количество тепла, получаемое системой от участков окружающей среды с температурой Т₁, dQ^¢₂ – количество тепла, отдаваемое системой участкам окружающей среды при температуре Т₂. Неравенство Клаузиуса позволяет установить верхний предел термического К.П.Д. при переменных температурах нагревателя и холодильника.

Из выражения для обратимого цикла Карно следует, что или , т.е. для обратимого цикла неравенство Клаузиуса переходит в равенство. Это означает, что приведенное количество тепла, полученного системой в ходе обратимого процесса, не зависит от вида процесса, а определяется только начальным и конечным состояниями системы. Поэтому приведенное количество тепла, полученное системой в ходе обратимого процесса, служит мерой изменения функции состояния системы, называемой энтропией.

Энтропия системы – функция ее состояния, определенная с точностью до произвольной постоянной. Приращение энтропии равно приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из начального состояния в конечное по любому обратимому процессу.

, .

Важной особенностью энтропии является ее возрастание в изолированных с

cyberpedia.su

Скорость и ускорение точки при различных способах задания движения

 

6.2.1. Скорость и ускорение точки при векторном способе задания движения

 

Скорость точки в данный момент времени равна первой производной от радиуса-вектора точки по времени:

. (6.8)

Вектор скорости точки в данный момент направлен по касательной к траектории точки в сторону движения (рис. 6.6).

Ускорение точки в данный момент времени равно первой производной от вектора скорости или второй производной от радиуса-вектора по времени:

. (6.9)

При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка. При криволинейном движении вектор ускорения направлен в сторону вогнутости траектории (рис. 6.6).

 

 

6.2.2. Скорость и ускорение точки при координатном способе задания движения

 

Вектор скорости точки можно представить равенством

, (6.10)

где – орты осей х, у, z. Проекции скорости на неподвижные оси декартовых координат равны:

, , . (6.11)

Модуль скорости равен

. (6.12)

Направление скорости определяется направляющими косинусами:

, , . (6.13)

Скорость точки направлена по касательной к траектории.

Ускорение точки можно представить равенством

.

Проекции ускорения на неподвижные декартовы оси координат равны:

, , . (6.14)

Модуль ускорения

. (6.15)

Направление ускорения определяется направляющими косинусами:

, , . (6.16)

 

6.2.3. Скорость и ускорение точки при естественном способе задания движения

 

В этом случае значения векторов и определяют по их проекциям на подвижные оси , имеющие начало в точке М и движущиеся вместе с точкой М (рис. 6.7). Эти оси, называемые осями естественного трехгранника, направлены следующим образом: ось направлена по касательной к траектории в сторону положительного отсчета расстояния S и называется касательной осью; ось Mn направлена по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории, и называется главной нормалью; ось Mb направлена перпендикулярно первым двум так, чтобы она образовала с ними правую тройку, и называется бинормалью.

Скорость точки, направленная по касательной к траектории, равна

, (6.17)

где -орт касательной, -проекция скорости на касательную, причем

. (6.18)

Ускорение точки лежит в соприкасающейся плоскости и определяется векторной суммой касательного и нормального ускорения точки:

. (6.19)

Проекция ускорения на касательную равна

. (6.20)

Модуль нормального ускорения определяется формулой

. (6.21)

где ρ-радиус кривизны траектории.

---

Дата добавления: 2018-03-20; просмотров: 266;

---

znatock.org

Скорость точки при сложном движении — КиберПедия

 

Докажем теорему о сложении скоростей для сложного движения точки, состоящегоиз относительного движения по отношению к под­вижной системе отсчета Охуz и переносного движения вместе с этой системой в случае, когда подвижная система отсчета связана с твер­дым телом, совершающим произвольное движение в пространстве (рис. 13.4).

Это произвольное движение в механике принято называть общим случаем движения, которое можно разложить на поступательное движение вместе с некоторым полюсом и вращательное движение вокруг этого полюса. В процессе вращения неподвижной остается только одна точка, поэтому такое вращение называется сферическим, а ось вращения, в отличие от обычного вращательного движения, мгновенной, т.к. ее положение в пространстве изменяется со временем.

Таким образом, само переносное движение является сложным, представляющим собой совокупность поступательного движения под­вижной системы вместе с точкой О (полюсом) и сферического движе­ния вокруг этого полюса. Это сферическое движение в каждый момент можно рассматривать как вращение подвижной системы с угловой скоростью вокруг мгновенной оси Ώ, проходящей через полюс О.

Во все время движения точки радиусы-векторы связаны зависимостью

. (13.1)

 

Вектор абсолютной скорости точки

.

 

Дифференцируя выражение (13.1) и учитывая, что орты подвижной системы Oxyz, оставаясь неизменными по модулю, вра­щаются вокруг мгновенной оси с угловой скоростью , получаем

 

(13.2)

 

Производная от каждого орта по времени представляет собой линейную скорость точки, для которой этот орт является радиусом-вектором (рис. 13.4):

.

 

 

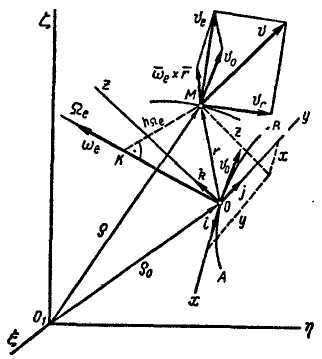
Рис. 13.4 Рис. 13.5

 

Но каждый орт вращается вокруг мгновенной оси, и враща­тельная скорость его конца определяется векторным произведением:

 

Следовательно,

Таким образом

 

(13.3)

 

Подставляем (13.3) в (13.2):

 

Здесь – скорость полюса О;

– относительная скорость точки М.

Поэтому

(13.4)

Переносная скорость точки, как указывалось ранее, представляет собой скорость точки, связанной с подвижной системой отсчета и совпа­дающей в данный момент с движущейся точкой М. В рассматриваемом случае такой точкой является точка М свободного твердого тела. Ско­рость этой точки состоит из скорости полюса О и вращательной скорости точки вокруг мгновенной осиΏ, т. е.

 

(13.5)

На этом основании формула (4) принимает вид

 

(13.6)

Это равенство выражает теорему о сложении скоростей, которая формулируется так: абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей.

Эту теорему называют правилом параллелограммаили треуголь­ника скоростей.

Как видно, в рассматриваемом случае сложного переносного дви­жения переносная скорость точки , сама определяется как диагональ параллелограмма, построенного на скорости полюса и вращательной скорости точки вокруг мгновенной оси Ώ_e, (рис. 13.4).

В случае поступательного переносного движения скорости всех точек, неизменно связанных с подвижной системой отсчета, в каждый момент геометрически равны. Поэтому переносная скорость точки М равна скорости полюса и формула (13.5) принимает вид

 

Очевидно, что в этом случае абсолютная скорость точки М также определяется по формуле (13.6).

Так как абсолютная скорость точки определяется диагональю параллелограмма, построенного на переносной скорости , и относи­тельной скорости , то ее модуль можно вычислить по формуле

 

(13.7)

 

cyberpedia.su

Закон движения, траектория, скорость и ускорения точки

Термин по теоретической механике

1. 
   Кинематика.
   
   1. 
      Закон движения, траектория, скорость и ускорения точки.
      

Скорость и ускорение точки в декартовой, цилиндрической и сферической системах координат (стр. 176-182). Проекции ускорения на оси естественного трехгранника (стр. 78-80).

Пусть – независимые координаты, однозначно связанные с компонентами законом преобразования .

Величины называются криволинейными координатами точки, таким образом, закон движения однозначно задается функциями

Цилиндрические координаты:

Сферические координаты:

Ускорение:

Ускорение точки:

Запишем скорость точки через , где – единичный вектор касательной к траектории, s – длина дуги траектории, тогда ускорение можно записать следующим образом: .

Пусть где – единичный вектор, называемый главной нормалью к траектории, – радиус кривизны в данной точке траектории. Плоскость векторов и называется соприкасающейся,

, – естественные оси

Тогда запишем ускорение через , , где – проекции ускорения на естественные оси, но , тогда

Модуль ускорения –

Закон движения твердого тела:

Для определения закона движения твердого тела достаточно задать законы движения трех его точек, не лежащих на одной прямой

Закон произвольного движения твердого тела есть аффинное линейное преобразование вида , где – постоянный вектор, – ортогональный линейный оператор, зависящий от времени, – радиус-вектор фиксированного в теле полюса.

2. 
   Способы задания движения твердого тела.
   

Группа SO(3).

Движение конкретной твердой точки –

Рассмотрим свойства первого преобразования: – оно состоит в применении ортогонального оператора А к векторному пространству . Множество таких операторов образуют относительно их композиции группу O(3).

OS(3) – подгруппа ортогональных операторов в O(3) с определителем равным 1.

Теорема Эйлера о конечном повороте. Угловые координаты (углы Эйлера, углы Брайнта),

Пусть в пространстве выбран ОНБ (правоориентированный). Рассмотрим движение твердого тела, определенное оператором . Таким образом оператор А осуществляет преобразование от базиса пространства к базису, связанному с твердым телом.

Предположим, что оператор А представляет композицию операторов.

Пусть , где матрицы соотв. операторов имеют вид: , где

– угол прецессии, – угол нутации, – угол собственного вращения, а матрица описывает поворот вокруг вектора , – , – . Углы , , называются углами Эйлера

Теорема Эйлера

Существуют углы Эйлера, задающие произвольное положение твердого тела относительно начального базиса

Если матрицы соотв. операторов имею вид:

, где

матрица описывает поворот вокруг вектора , – , – . Углы , , называются кардановыми углами (углами Брайнта)

Теорема

Существуют кардановы углы, задающие произвольное положение твердого тела относительно начального базиса

Параметры Эйлера

Пусть радиус-векторы x и r имеют начало координат в неподвижной точке О. Построим преобразование

Теорема

Преобразование вращения абсолютно твердого тела вокруг оси с направляющим вектором на угол выражается формулой , где скаляр и вектор

Разложим вектор по базисным векторам неподвижного репера :

Скалярные величины называются параметрами Эйлера

Очевидно, что параметры Эйлера удовлетворяют условию: , они существуют для любого оператора
Кватернионы. Изоморфизм характеристик углового движения твердого тела (стр. 81-112).

Множество кватернионов – пространство Н линейных комбинаций вида , где – действительные числа, а – некоторые ЛНЗ символы. В пространстве Н вводится билинейное умножение:

Кватернионы, у которых , коммутируют со всеми остальными кватернионами.

Каждому кватерниону h сопоставляется унитарная матрица , где i – мнимая единица.

Также выполняется свойство: , где – кватернионы

Сопряженный кватернион (к кватерниону h) –

Для кватернионов справедливы следующие равенства:

Норма кватерниона –

Для кватернионов справедливы следующие равенства: . Если , то ,

Пусть – множество кватернионов с нормой, равной 1, если , то . Очевидно, что – группа по умножению. изоморфна на .
Пусть – трехмерное пространство кватернионов x, для которых . Метрика в этом пространстве задается формулой: . – изоморфно евклидовому пространству

Теорема: Если , то преобразование , задаваемое формулой , есть вращение трехмерного евклидова пространства.

Коэффициенты кватерниона из , задающего преобразование , называются параметрами Родрига – Гамильтона

Формулы Эйлера для поля скоростей (стр. 120-125) и Ривальса для поля ускорений (стр. 130-141).

Пусть S – ортонормированный репер с началом в точке , который движется как твердое тело относительно репера S₀ ортонормированных векторов с началом в полюсе . Рассмотрим движение некоторой точки М.

Движение точки М по отношению к реперу S₀ называется абсолютным движением (траектория в этом репере – абсолютная траектория).

Движение точки М по отношению к реперу S называется относительным движением (траектория в этом репере – относительная траектория).

Движение репера S – переносное движение.

Скорость движения точки по абсолютной траектории – абсолютная скорость.

Скорость движения точки по отношению к неподвижному реперу S – относительная скорость.

В каждый конкретный момент времени t точка М совпадает с некоторой точкой пространства, жестко связанного с репером S.

Скорость точки – переносная скорость точки М.

Теорема (о сложении скоростей): Абсолютная скорость точки равна векторной сумме ее переносной и относительной скоростей: , где – вектор абсолютной скорости, – вектор переносной скорости, – вектор относительной скорости.

Теорема (случай нескольких реперов): Допустим, что точка М совершает движение в репере S₁, который движется относительно репера S₂. Репер S₂ движется в репере S₃ и т.д. Наконец репер S_k совершает движение относительно репера S₀. Тогда абсолютная скорость точки М выражается формулой , где – скорость М относительно репера S, а – скорость относительно S_i+1 той точки репера S_i, которая в данный момент совпадает с точкой М.
Поле скоростей твердого тела:

При поступательном движении векторы скоростей всех точек тела равны между собой. За скорость поступательного движения принимают скорость любой точки тела.

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором две точки тела неподвижно закреплены на этой оси.

Величина скорости точки М при движении по окружности есть , где выражение – угловая скорость тела, R – расстояние от точки до оси вращения.

Введем скользящий вектор:

Выберем в пространстве опорную точку , некоторую точку А. Зададим действительное число (параметр) и сопоставим ему точки (точки лежат на одной прямой). Тогда . Когда принимает произвольные действительные значения, получается множество векторов , которые принадлежат одному классу эквивалентности и называются скользящим вектором. Прямая, определенная уравнением называется основанием.

Формула Эйлера:

Пусть – скользящий вектор, основание которого совпадает с осью вращения. Полюс расположим на оси вращения, пусть – радиус-вектор некоторой точки твердого тела. Тогда скорость твердого тела может быть вычислена по формуле:

Поле скоростей:

Поле скоростей называется поступательным, если векторы скоростей всех точек тела совпадают.

Поле скоростей называется вращательным, если существует скользящий вектор (вектор угловой скорости) такой, что скорость любой точки тела дается по формуле , где – радиус-вектор рассматриваемой точки, имеющей начало на основании вектора , одинакового для всех точек тела.
Теорема Эйлера о поле скоростей твердого тела: В любой момент времени произвольного движения твердого тела его поле скоростей может быть представлено как сумма поступательного и вращательного поля скоростей: , где – скорость, одинаковая во всех точках тела, – радиус-вектор точки тела, имеющий начало в полюсе репера , связанного с телом, – скользящий вектор с основанием, проходящим через точку

Следствие: Проекции скоростей концов отрезка твердого тела на направление самого отрезка совпадают.

Теорема: Тройка элементов угловой скорости образует скользящий псевдовектор ( изменяет направление при изменении ориентированного базиса)
Дифференциал оператора и дифференциал вращения:

Любой закон движения твердого тела – , где – постоянный вектор, , – радиус-вектор фиксированного в теле полюса.

Движение, при котором все точки твердого тела получают одинаковое смещение в пространстве, называется поступательным.

Теорема: Поступательное движение реализуется тогда и только тогда, когда A – порожденный оператор.

Следствие: Произвольное движение твердого тела есть композиция вращения вокруг некоторой оси и поступательного движения.

Теорема: Всякое перемещение твердого тела можно представить либо как результат поступательного движения, либо как результат виннового движения, т.е. такого, при котором поступательный сдвиг осуществляется вдоль оси вращения, определенной оператором A. Если проекция точки на ось вращения отсутствует, то найдется точка твердого тела такая, что движение сводится к повороту вокруг оси, проходящей через эту точку.

Пусть – дифференцируемая функция некоторого скалярного параметра , причем – тождественному оператору. Изменяя , получим различные повороты вокруг различных в общем случае с.в. оператора , зависящих от параметра . Выделим линейную часть матрицы оператора A:

Матрица определяет линейный оператор, который называется дифференциалом оператора A.

Теорема: Дифференциалу оператора отвечает кососимметричная матрица.

Теорема: Дифференциал композиции операторов выражается суммой дифференциалов составляющих операторов: .

Следствие:

Когда величина , задающая дифференциалы мала, то с точностью до членов второго порядка малости действие операторов – можно представить с помощью векторных умножений:

Векторы – дифференциалы вращений.

Справедливо равенство: – это означает, что дифференциалы вращений образуют линейное пространство относительно композиции преобразований

Величина смещения: , где – угол между и .
Псевдовекторы и псевдоскаляр:

Любой закон движения твердого тела – , , в репере с началом в полюсе . Выберем другой ортонормированный репер с тем же началом и с постоянной матрицей направляющих косинусов : В базисе матрица угловой скорости примет вид ,

Если:

1) . Тогда зеркальные отображения осей координат отсутствуют и, если исходный базис был правоориентированным, то и базис окажется правоориетированным. В новом базисе компоненты матрицы угловой скорости получаются путем проектирования на новые базисные векторы.

1) .Тогда имеется зеркальное отображение одной из осей координат.

При переходе от правоориентированного базиса к левоориентированному помимо применения правила преобразования векторов требуется еще поменять ее знак на противоположный.

Объекты, обладающие таким свойством, называются псевдовекторами.

Скалярное произведение псевдовектора на вектор – псевдоскаляр.

Поле скоростей:

Движение называется плоскопараллельным, если скорости всех точек твердого тела в любой момент времени параллельны некоторой неподвижной оси.

Теорема: Поле плоскопараллельного движения может быть поступательным, либо вращательным с осью, перпендикулярной плоскости движения

Теорема: Плоскопараллельное поступательное поле скоростей есть предельный случай вращательного поля, когда угловая скорость стремится к нулю, а ось вращения уходит в бесконечность.

P.S. Плоскопараллельное поле скоростей всегда можно привести к вращательному полю.
Аксоид:

Множество положений, которые последовательно занимает винтовая ось в неподвижном пространстве, связанного с неподвижным репером, называется неподвижным аксоидом.

Множество положений, которые последовательно занимает винтовая ось в движущемся теле, называется подвижным аксоидом.
Аксоиды в плоскопараллельном движении представляют собой цилиндрические поверхности, образующие которых перпендикулярны плоскости движения. Аксоиды пересекаются с плоскостью движения по двум кривым, называемыми подвижной и неподвижной центроидами.

Тока пересечения основания угловой скорости вращательного поля скоростей с плоскостью движения называется мгновенным центром скоростей (мгновенным центром вращения).

Поле скоростей тела с одной неподвижной точкой

3. 
   Поле скоростей свободного твердого тела.
   

Аксоиды. Мгновенный центр скоростей и центроиды (стр. 128-133).

4. 
   Сложное движение.
   

Теоремы сложения скоростей (стр. 118-120) и ускорений (стр. 139-140). Ускорение точки в системе координат, связанной с вращающейся Землей (стр. 141-145). Сложное движение твердого тела. Сложение произвольной системы угловых скоростей (стр. 25-44, 125-128). Кинематические уравнения (уравнения Пуассона, уравнения Эйлера, кинематические уравнения для кватернионов) (стр. 133-139).

2. 
   Динамика системы.
   
   1. 
      Теория связей.
      

Классификация связей (стр. 305-307). Понятие первого интеграла системы уравнения движения. Критерий первого интеграла (стр. 174-176).

2. 
   Локальные вариационные принципы механики.
   

Реакции связей и виртуальные перемещения для систем с произвольными связями (стр. 332-338). Условия схода с неудерживающей связи. Идеальные связи (стр. 338-343). Принцип Даламбера-Лагранжа (стр. 378-380). Принцип Гаусса (стр. 418-420). Квазикоординаты. Уравнения Аппеля (стр. 421-428). Уравнения Лагранжа второго рода. Разрешимость уравнений Лагранжа относительно старших производных. Обобщенный интеграл энергии Якоби. Гироскопические и диссипативные силы. Циклические координаты и циклические интегралы. Метод Рауса игнорирования цилиндрических координат (стр. 523-525, 539-559, 564-566). Приведение позиционной линейной системы к главным координатам (стр. 572-576).

3. 
   Общие теоремы механики системы.
   
   1. 
      Статика.
      

Принцип виртуальных перемещений (стр. 343-345). Условия равновесия для систем с потенциальными силами. Принцип Торричелли (стр. 345-346). Основные теоремы статики (стр. 349-350). Условия равновесия голономных систем (стр. 350-352). Условия равновесия твердого тела. Эквивалентность систем сил, действующих на твердое тело. Принцип отвердевания (стр. 352-355). Приведение системы сил к точке. Приведение сил тяжести к центру масс тела. Уравнения геометрической статики (стр. 25-44). Уравнение равновесия нити. Аналогия формы равновесия нити и траектории движения материальной точки (стр. 364-373).

2. 
   Динамика.
   

Понятие о внутренних и внешних силах. Теоремы об изменении количества движения. Интегралы количества движения. Теоремы об изменении кинетического момента. Интегралы кинетического момента. Теорема об изменении кинетической энергии. Интеграл энергии (стр. 381-392). Теоремы Кенинга о вычислении кинетического момента, кинетической энергии и энергии ускорений системы материальных точек (стр. 397-400). Теоремы об изменении количества движения и кинетического момента систем переменного состава. Уравнение Мещерского (стр. 404-414). Общее уравнение теории удара. Удар о связь. Теоремы об изменении количества движения и кинетического момента при ударе (стр. 432-436).

4. 
   Динамика твердого тела.
   

Количество движения, кинетический момент и кинетическая энергия твёрдого тела (стр. 443-448). Тензор и эллипсоид инерции. Главные оси инерции (стр. 45-50). Уравнения движения свободного твердого тела. Вращение твердого тела вокруг неподвижной оси, определение реакций, условия отсутствия реакций при нулевых активных силах. Физический маятник, приведенная длина центра качания, зависимость периода малых колебаний от расстояния между точкой подвеса и центром масс маятника (стр. 448-462). Твердое тело с неподвижной точкой: уравнения Эйлера-Пуассона и их первые интегралы. Волчок Эйлера: геометрическая интерпретация Пуансо, картина полодий, устойчивость вращения относительно главных осей инерции, регулярная прецессия. Волчок Лагранжа: качественное исследование движения, регулярная прецессия, спящий волчок, псевдорегулярная прецессия (стр. 464-489).

Пусть – скользящий псевдовектор. Основание проходит через точку, определенную радиус-вектором и любая точка прямой , где – произвольный скаляр

dereksiz.org

Сложное движение точки Пример решения задачи

Теория, применяемая для решения приведенной ниже задачи, излагается на странице “Сложное движение точки, теорема Кориолиса”.

Условие задачи

Рисунок к условию задачи

Прямоугольная пластина вращается вокруг неподвижной оси по закону   φ = 6t ² – 3t³ . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO ₁ лежит в плоскости пластины (пластина вращается в пространстве).

По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость   s = AM = 40(t – 2t ³) – 40   (s – в сантиметрах, t – в секундах). Расстояние b = 20 см. На рисунке точка M показана в положении, при котором   s = AM > 0 (при   s < 0 точка M находится по другую сторону от точки A).

Найти абсолютную скорость и абсолютное ускорение точки M в момент времени   t ₁ = 1 с.

Указания. Эта задача – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений (теорема Кориолиса). Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени   t ₁ = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунке к задаче).

Решение задачи

Дано: b = 20 см, φ = 6t ² – 3t³, s = |AM| = 40(t – 2t³) – 40, t₁ = 1 c.

Найти: v_абс, a_абс

Определение положения точки

Определяем положение точки в момент времени t = t₁ = 1 c.
s = 40(t₁ – 2t₁³) – 40 = 40(1 – 2·1³) – 40 = –80 см.
Поскольку s < 0, то точка M ближе к точке B, чем к D.
|AM| = |–80| = 80 см.
Делаем рисунок.

Относительная, переносная и абсолютная скорость точки M

Определение абсолютной скорости точки

Согласно теореме о сложении скоростей, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.

Определение относительной скорости точки

Определяем относительную скорость   . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD. Дифференцируя s по времени t, находим проекцию скорости на направление BD:
.
В момент времени t = t₁ = 1 с,
см/с.
Поскольку   , то вектор     направлен в направлении, противоположном BD. То есть от точки M к точке B. Модуль относительной скорости
v_от = 200 см/с.
Изображаем вектор     на рисунке.

Определение переносной скорости точки

Определяем переносную скорость   . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO₁. Дифференцируя φ по времени t, находим угловую скорость вращения пластины:
.
В момент времени t = t₁ = 1 с,
.
Поскольку   , то вектор угловой скорости     направлен в сторону положительного угла поворота φ, то есть от точки O к точке O₁. Модуль угловой скорости:
ω = 3 с^-1.
Изображаем вектор угловой скорости пластины     на рисунке.

Из точки M опустим перпендикуляр HM на ось OO₁.
При переносном движении точка M движется по окружности радиуса |HM| с центром в точке H.
|HM| = |HK| + |KM| = 3b + |AM| sin 30° = 60 + 80·0,5 = 100 см;
Переносная скорость:
v_пер = ω|HM| = 3·100 = 300 см/с.

Вектор     направлен по касательной к окружности в сторону вращения.

Определение абсолютной скорости точки

Определяем абсолютную скорость   . Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Проводим оси неподвижной системы координат Oxyz . Ось z направим вдоль оси вращения пластины. Пусть в рассматриваемый момент времени ось x перпендикулярна пластине, ось y лежит в плоскости пластины. Тогда вектор относительной скорости     лежит в плоскости yz . Вектор переносной скорости     направлен противоположно оси x . Поскольку вектор     перпендикулярен вектору   , то по теореме Пифагора, модуль абсолютной скорости:
.

Определение абсолютного ускорения точки

Согласно теореме о сложении ускорений (теорема Кориолиса), абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.

Относительное, переносное, кориолисово и абсолютное ускорение точки M

Определение относительного ускорения

Определяем относительное ускорение   . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD. Дважды дифференцируя s по времени t, находим проекцию ускорения на направление BD:
.
В момент времени t = t₁ = 1 с,
см/с².
Поскольку   , то вектор     направлен в направлении, противоположном BD. То есть от точки M к точке B. Модуль относительного ускорения
a_от = 480 см/с².
Изображаем вектор     на рисунке.

Определение переносного ускорения

Определяем переносное ускорение   . При переносном движении точка M жестко связана с пластиной, то есть движется по окружности радиуса |HM| с центром в точке H. Разложим переносное ускорение на касательное к окружности     и нормальное     ускорения:
.
Дважды дифференцируя φ по времени t, находим проекцию углового ускорения пластины на ось OO₁:
.
В момент времени t = t₁ = 1 с,
с ^–2.
Поскольку   , то вектор углового ускорения     направлен в сторону, противоположную положительного угла поворота φ, то есть от точки O₁ к точке O. Модуль углового ускорения:
ε = 6 с^-2.
Изображаем вектор углового ускорения пластины     на рисунке.

Переносное касательное ускорение:
a^τ_пер = ε |HM| = 6·100 = 600 см/с².
Вектор     направлен по касательной к окружности. Поскольку вектор углового ускорения     направлен в сторону, противоположную положительного угла поворота φ, то     направлен в сторону, противоположную положительному направлению поворота φ . То есть направлен в сторону оси x .

Переносное нормальное ускорение:
aⁿ_пер = ω² |HM| = 3²·100 = 900 см/с².
Вектор     направлен к центру окружности. То есть в сторону, противоположную оси y .

Определение кориолисова ускорения

Кориолисово (поворотное) ускорение:
.
Вектор угловой скорости     направлен вдоль оси z . Вектор относительной скорости     направлен вдоль прямой |DB|. Угол между этими векторами равен 150° . По свойству векторного произведения,
.
Направление вектора     определяется по правилу буравчика. Если ручку буравчика повернуть из положения     в положение   , то винт буравчика переместится в направлении, противоположном оси x .

Определение абсолютного ускорения

Абсолютное ускорение:
.
Спроектируем это векторное уравнение на оси xyz системы координат.

;

;

.
Модуль абсолютного ускорения:

.

Ответ

Абсолютная скорость   ;
абсолютное ускорение   .

Автор: Олег Одинцов.     Опубликовано: 10-01-2016

1cov-edu.ru

тело отсчета, система отсчета. Понятие о траектории движения точки — Мегаобучалка

Кинематика – раздел механики, посвященный изучению геометрических свойств движений без учета их масс и действующих на них сил. Движение в кинематике рассматривают как изменение положения тела в пространстве с течением времени по отношению к выбранной системе отсчета. Тело отсчёта определяется как тело, относительно которого рассматривается движение. Система координат, тело отсчёта, выбранный способ измерения образуют систему отсчета. Траектория – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным. Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной. Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте. Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

2.Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный.

Векторный способ. Положение движущейся точки М в любой момент времени можно определить с помощью ее радиус-вектора, проведенного из центра О, связанного с телом отсчета, в точку М (рис. 1.1). Чтобы задать движение векторным способом, необходимо определить векторную функцию времени в виде:

(1.1)

Зависимость (1.1) называют уравнением движения точки в векторной форме. Начало радиус-вектора движущейся точки находится в точке О, а конец его перемещается по траектории вместе с точкой М. Геометрическое место концов радиус-вектора, т.е. годограф этого вектора, определяет траекторию движущейся точки.

Координатный способ. С телом отсчета связывают прямоугольную систему декартовых координат, при этом положение точки определяют ее координатами, которые являются скалярными функциями времени (рис. 1.2):

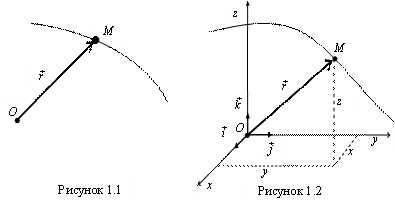Уравнения (1.2) называют уравнениями движения точки в координатной форме. Они являются параметрическими уравнениями траектории точки. Исключив из этих уравнений параметр – время, можно получить уравнение траектории.

 

Между способами задания движения точки имеется связь. Так, если начало декартовой системы координат совпадает с центром, из которого проводится радиус-вектор точки при векторном способе изучения ее движения (см. рис. 1.2), то координаты точки равны проекциям на соответствующие оси радиус-вектора точки

,

где – единичные орты координатных осей.

Естественный способ. Этот способ используют в тех случаях, когда заранее известна траектория точки. На траектории выбирают неподвижную точку О (начало отсчета), а также положительное и отрицательное направления отсчета расстояний точки от начала отсчета (рис. 1.3). Тогда положение точки М на траектории будет однозначно определяться зависимостью криволинейной координаты S = ОМ от времени

(1.3)

 

Связь между координатным и естественным способами определяется выражением

где – первые производные от координат точки по времени; С – постоянная интегрирования, зависящая от начальных условий.

3. Определение скорости точки при различных способах задания ее движения.

Одной из основных кинематических характеристик движения точки является скорость точки. Скорость точки – это векторная величина, характеризующая интенсивность и направление движения точки в пространстве в рассматриваемый момент времени.

В случае векторного способа задания движения вектор скорости точки равен первой производной по времени от ее радиус-вектора

 

(1.4)

где точка над функцией в теоретической механике означает первую производную по времени, а две точки – вторую производную по времени. Производные по другим переменным записывают обычным образом. Вектор скорости точки приложен в самой точке и направлен по касательной к траектории в сторону движения точки. Единица измерения скорости в системе СИ – 1 м/с.

При координатном способе задания движения точки ее скорость определяют через проекции вектора скорости на оси выбранной системы координат, которые равны первым производным от соответствующих координат по времени:

(1.5)

Если известны проекции скорости на оси координат, то модуль вектора скорости и его направляющие косинусы находят по формулам:

(1.6)

где – углы между вектором скорости и осями координат. При естественном способе задания движения точки вектор ее скорости определяют по формуле

(1.7)

Где – единичный вектор касательной к траектории в данной точке, направленный всегда в сторону положительного отсчета криволинейной координаты S. Скалярную величину , являющуюся проекцией вектора скорости на касательную к траектории, называют алгебраической скоростью точки (рис. 1.4). Знак алгебраической скорости определяет направление движения точки: если > 0, то вектор скорости совпадает по направлению с вектором ; в противном случае он направлен в противоположную сторону. На рисунке точка О1 означает центр кривизны траектории, а – радиус кривизны в точке М.

4. Определение ускорения точки при различных способах задания ее движения.

При координатном способе задания движения точки вектор ускорения определяют через его проекции на оси координат, которые равны вторым производным от соответствующих координат по времени:

, , . (1.9)

Если известны проекции ускорения на оси координат, то модуль вектора ускорения и его направляющие косинусы находят по формулам:

, (1.10)

где – углы между вектором ускорения и осями координат.

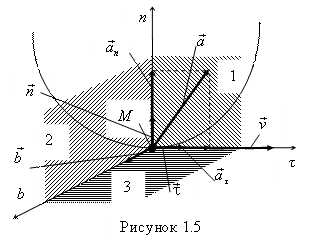При естественном способе задания движения с движущейся точкой связывают естественную систему координат (рис. 1.5). Естественный трехгранник составляется из трех пересекающихся взаимно перпендикулярных плоскостей: 1 – соприкасающейся, 2 – нормальной и 3 – спрямляющей. Линии пересечения плоскостей образуют правую систему естественных осей координат: τ, n и b, определяемых единичными векторами , которые называют единичными векторами касательной, главной нормали и бинормали соответственно.

Вектор ускорения точки в естественной системе определяют по формулам:

(1.11)

 

Здесь – касательное или тангенциальное ускорение точки, которое направлено по касательной к траектории в сторону движения, если движение ускоренное (алгебраическая скорость точки возрастает), и в противоположную сторону, если движение замедленное (алгебраическая скорость точки убывает). Нормальное ускорение всегда направлено по нормали к траектории в сторону вогнутости. Поскольку вектор ускорения точки лежит в соприкасающейся плоскости, то его проекция на бинормаль равна нулю. Касательное ускорение характеризует изменения скорости точки по модулю, а нормальное – по направлению.

Касательное ускорение точки по величине и направлению можно определить по известным проекциям векторов скорости и ускорения на координатные оси по формуле

.

 

(1.12)

 

5. Что называется ускорением? Определение ускорения точки при естественном способе задания ее движения. Ускорение точки является векторной мерой изменения ее скорости, как по величине, так и по направлению. Направление вектора ускорения совпадает с направлением изменения скорости При векторном способе задания движения вектор ускорения точки равен первой производной по времени от вектора ее скорости или второй производной по времени от ее радиус-вектора:

(1.8)

Вектор ускорения приложен к движущейся точке, лежит в соприкасающейся плоскости к траектории в данной точке и направлен в общем случае в сторону вогнутости траектории. Единица измерения ускорения в системе СИ – 1 .

При естественном способе задания движения с движущейся точкой связывают естественную систему координат (рис. 1.5). Естественный трехгранник составляется из трех пересекающихся взаимно перпендикулярных плоскостей: 1 – соприкасающейся, 2 – нормальной и 3 – спрямляющей. Линии пересечения плоскостей образуют правую систему естественных осей координат: τ, n и b, определяемых единичными векторами , которые называют единичными векторами касательной, главной нормали и бинормали соответственно.

 

Вектор ускорения точки в естественной системе определяют по формулам:

(1.11)

 

Здесь – касательное или тангенциальное ускорение точки, которое направлено по касательной к траектории в сторону движения, если движение ускоренное (алгебраическая скорость точки возрастает), и в противоположную сторону, если движение замедленное (алгебраическая скорость точки убывает). Нормальное ускорение всегда направлено по нормали к траектории в сторону вогнутости. Поскольку вектор ускорения точки лежит в соприкасающейся плоскости, то его проекция на бинормаль равна нулю. Касательное ускорение характеризует изменения скорости точки по модулю, а нормальное – по направлению.

Касательное ускорение точки по величине и направлению можно определить по известным проекциям векторов скорости и ускорения на координатные оси по формуле

. (1.12)

6. Касательное и нормальное ускорения точки. Их физический смысл. Направление векторов. Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела. Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории. Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю. Нормальное ускорение указывает,насколько быстро скорость тела изменяется по направлению.

7. Равномерное движение. Законы изменения дуговой координаты и скорости.

Равномерное движение– это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0). Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия. Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: v_cp = v.Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t: = / t. Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени. Перемещение при равномерном прямолинейном движении определяется формулой: = • t. Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

vx = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x0

где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени) .Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x0 + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x0 – vt криво

прямо

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение. Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

v = s1 / t1 = tg α где α – угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

tg α1 > tg α2

следовательно, скорость тела 1 выше скорости тела 2 (v1 > v2).

tg α3 = v3 < 0 Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0

megaobuchalka.ru