Собственный момент инерции это – Центробежный момент инерции – это… Что такое Центробежный момент инерции?

Момент инерции формула (сопромат)

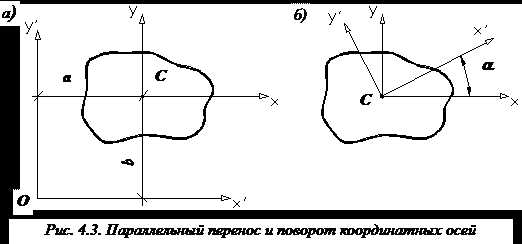
Пусть две взаимно перпендикулярные оси x и y проходят через центр тяжести C поперечного сечения стержня. Проведем другие оси координат и , параллельные осям x и y. Обозначим a и b координаты центра тяжести С в новых осях и (рис. 4.3, а).

Тогда формулы осевых и центробежных моментов инерции фигуры относительно параллельных осей и :

Первые слагаемые в формулах осевых и центробежных моментов инерции фигуры относительно параллельных осей названы собственными моментами инерции. Вторые (подчеркнутые) слагаемые называются переносными моментами инерции.

Отметим, что координаты a и b необходимо подставлять в формулы моментов инерции фигуры относительно параллельных осей с учетом их знаков, что является крайне важным для третьей из приведенных формул.

sopromato.ru

Осевой, полярный, центробежный Момент инерции (сопромат)

Осевой момент инерции фигуры – это интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:

Полярный момент инерции фигуры относительно данной точки (полюса) – это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:

Если через полюс проведена система взаимно перпендикулярных осей x и y, то , и формула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y:

Из формул осевых и полярного моментов инерции видно: значения осевых и полярного моментов инерции всегда положительны, так как координаты и расстояние возведены в квадрат.

Центробежный момент инерции фигуры – это интеграл произведений элементарных площадей на их расстояния до осей x и y:

Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см4).

Понятие момента инерции поперечного сечения ввел в 1834 г. французский ученый Н. Перси.

sopromato.ru

Главные моменты инерции (сопромат)

При повороте центральных осей и приближении их к главным центральным осям, больший из собственных осевых моментов инерции становится еще больше, стремясь максимальному значению (), а меньший – меньше, приближаясь к минимальному значению ().

Главные центральные моменты инерции – моменты инерции фигуры относительно главных центральных осей и . Формулы главных центральных моментов инерции, вытекающих из формул моментов инерции при повороте осей координат:

Если в частном случае , то осевые моменты инерции при повороте координатных осей вообще не изменяются, и тогда любые две взаимно перпендикулярные оси, проходящие через центр тяжести поперечного сечения, являются главными центральными осями.

sopromato.ru

8.Главные оси инерции и главный момент инерции.

Главные оси инерции и главные моменты инерции.

При изменении угла величины Ix1, Iy1 и Ix1y1 изменяются. Найдем значение угла, при котором Ix1 и Iy1имеют экстремальные значения; для этого возьмем от Ix1 или Iy1 первую производную по и преравняем ее нулю:илиоткуда(1.28)

Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой – минемален.

Такие оси называют главными. Моменты инерции относительно главных осей называются главными моментами инерции.

Значения главных моментов инерции найдем из формул (1.23) и (1.24), подставив в них из формулы (1.28), при этом используем известные формулы тригонометрии для функций двойных углов.

После преобразований получим следующую формулу для определения главных моментов инерции:  (1.29)

Исследуя вторую производную можно установить, что для данного случая (Ix < Iy) максимальный момент инерции Imax имеет место относительно главной оси, повернутой на угол по отношению к оси х, а минимальный момент инерции – относительно другой, перпендикулярной оси. В большинстве случаев в этом исследовании нет надобности, так как по конфигурации сечений видно, какая из главных осей соответствует максимуму момента инерции.

Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.

Во многих случаях удается сразу определить положение главных центральных осей. Если фигура имеет ось симметрии, то она является одной из главных центральных осей, вторая проходит через центр тяжести сечения перпендикулярно первой. Сказанное следует из того обстоятельства, что относительно оси симметрии и любой оси, ей перпендикулярной, центробежный момент инерции равен нулю.

В случае если два главных центральных момента инерции сечения равны между собой, то у этого сечения любая центральная ось является главной, и все главные центральные моменты инерции одинаковы (круг, квадрат, шестиугольник, равносторонний шестиугольник).

9.Основные геометрические характеристики сечений

Здесь: C – центр тяжести плоских сечений;

A – площадь сечения;

I

x , I_y – осевые моменты инерции сечения относительно главных осей;

I_xI , I_yI – осевые моменты инерции относительно вспомогательных осей;

I_p – полярный момент инерции сечения;

W_x , W_y – осевые моменты сопротивления;

W_p – полярный момент сопротивления

Прямоугольное сечение

Сечение равнобедренный треугольник

10.Основные виды сил, действующие на тело. Момент силы относительно центра. Свойства момента сил.

При рас­смот­ре­нии ме­ха­ни­че­ских задач боль­шин­ство сил, дей­ству­ю­щих на тела, можно от­не­сти к трем ос­нов­ным раз­но­вид­но­стям:

– сила все­мир­но­го тя­го­те­ния;

– сила тре­ния;

– сила упру­го­сти.

Все окру­жа­ю­щие нас тела при­тя­ги­ва­ют­ся к Земле, это обу­слов­ле­но дей­стви­ем сил все­мир­но­го тя­го­те­ния. Если мы будем пре­не­бре­гать со­про­тив­ле­ни­ем воз­ду­ха, то мы уже знаем, что все тела па­да­ют на Землю с оди­на­ко­вым уско­ре­ни­ем – уско­ре­ни­ем сво­бод­но­го па­де­ния.

Как и вся­кий пред­мет, тело, под­ве­шен­ное на пру­жине, стре­мит­ся упасть вниз из-за при­тя­же­ния Земли, но, когда пру­жи­на рас­тя­нет­ся до неко­то­рой длины, тело оста­нав­ли­ва­ет­ся, то есть при­хо­дит в со­сто­я­ние ме­ха­ни­че­ско­го рав­но­ве­сия. Мы уже знаем, что ме­ха­ни­че­ское рав­но­ве­сие на­сту­па­ет, когда сумма сил, дей­ству­ю­щих на тело, равна нулю. Это озна­ча­ет, что сила тя­же­сти, дей­ству­ю­щая на груз, долж­на урав­но­ве­сить­ся с неко­то­рой силой, дей­ству­ю­щей со сто­ро­ны пру­жи­ны. Эта сила, на­прав­лен­ная про­тив силы тя­же­сти и дей­ству­ю­щая со сто­ро­ны пру­жи­ны, на­зы­ва­ет­ся силой упру­го­сти.

Прой­дя неко­то­рое рас­сто­я­ние, тело оста­нав­ли­ва­ет­ся, ско­рость тела умень­ша­ет­ся от на­чаль­но­го зна­че­ния до нуля, то есть уско­ре­ние тела – ве­ли­чи­на от­ри­ца­тель­ная. Сле­до­ва­тель­но, на тело со сто­ро­ны по­верх­но­сти дей­ству­ет сила, ко­то­рая стре­мит­ся оста­но­вить это тело, то есть дей­ству­ет про­тив его ско­ро­сти. Эта сила на­зы­ва­ет­ся силой тре­ния.  

Момент силы относительно центра (точки).

    Моментом силы F относительно центра (точки) О называется вектор m_o(F) равный векторному произведению радиуса вектора r,  проведенного из центра О в точку А приложения силы, на вектор силы F:

    Вектор m_o(F) приложен в точке О и направлен  плоскости, проходящей через центр О и силу F, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода

 часовой стрелки.

    Модуль m_o(F) равен произведению модуля силы F на плечо h:

где плечо h  перпендикуляр, опущенный из центра О на линию действия силы F.

    Момент m_o(F) характеризует вращательный эффект силы F относительно центра (точки) О.

    Свойства момента силы:

    1. Момент силы относительно центра не изменяется при переносе силы вдоль линии ее действия в любую точку;

    2. Если линия действия силы проходит через центр О (h = 0), то момент силы относительно центра О равен нулю.

studfiles.net

МОМЕНТ ИНЕРЦИИ ТЕЛА

⇐ ПредыдущаяСтр 6 из 15Следующая ⇒

 

МОМЕНТ ИНЕРЦИИ ТОЧКИ относительно выбранной оси – это произведение массы точки на квадрат ее расстояния до выбранной оси.

МОМЕНТ ИНЕРЦИИ ТЕЛА относительно выбранной оси – это сумма моментов инерции всех точек тела относительно той же оси

(48)

СОБСТВЕННЫЙ МОМЕНТ ИНЕРЦИИ ТЕЛА – это момент инерции относительно оси, проходящей через центр масс данного тела.

В справочной литературе всегда приводятся ТОЛЬКО СОБСТВЕННЫЕ моменты инерции.

 

Моменты инерции некоторых тел

Для наиболее распространенных форм материальных тел собственные моменты инерции определены в более удобном виде, чем формула (48). Приведем некоторые из них. На рисунках показано плоское изображение тел, поэтому ось Z всегда направлена перпендикулярно рисунку.

 

1. Термин:КОЛЬЦО, ОБРУЧ, ПОЛЫЙ ЦИЛИНДР.

Примечание. Масса тела распределена по окружности.

Изображение:

* – кроме цилиндра.

2. Термин: ДИСК, КРУГЛАЯ ПЛАСТИНА, СПЛОШНОЙ ЦИЛИНДР.

Изображение:

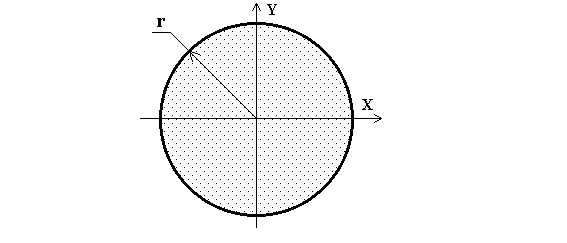
Примечание: Масса тела распределена по всей поверхности.

* – кроме цилиндра.

 

3. Термин: СТЕРЖЕНЬ, ТЯГА.

Примечание:Любая деталь, у которой один размер больше двух других.

Изображение:

 

4. Термин: ПРЯМОУГОЛЬНАЯ ПЛАСТИНА ИЛИ ЛИСТ.

Примечание: Масса тела распределена по всей поверхности.

Изображение:

 

РАДИУС ИНЕРЦИИ – это радиус такого кольца, которое имеет такую же массу и такой же собственный момент инерции, что и данное тело.

Если в задаче задан радиус инерции тела, то вычислять момент инерции следует обязательно по формуле

.

ТЕОРЕМА Д9 (Штейнера-Гюйгенса). Момент инерции относительно произвольной оси равен сумме собственного момента инерции относительно оси, параллельной данной, и произведения массы тела на квадрат расстояния от центра масс тела до оси.

Доказательство. Рассмотрим тело с центром масс в точке М(рис. 5). Требуется определить его момент инерции относительно оси х-х. Проведем ось y-y, параллельную оси х-х и отстоящую от нее на расстоянии L. Пусть расстояние от произвольной i-й точки тела до оси х-х – , a от той же точки до оси y-y – ( может быть и положительным, и отрицательным в зависимости от положения i–й точки относительно оси y-y). Тогда и, следовательно,

Вынеся из-под знака суммирования постоянные величины и учитывая, что

получим

ч.т.д. (49)

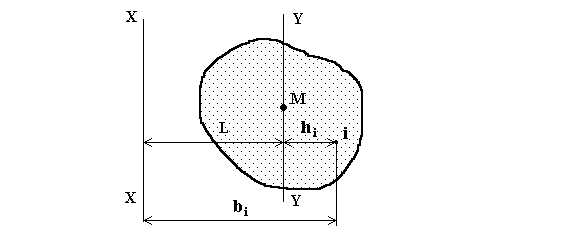
Рис. 5.

 

Основываясь на полученном результате, можем сделать вывод, что, поскольку величина всегда положительна, то СОБСТВЕННЫЙ МОМЕНТ ИНЕРЦИИ ЯВЛЯЕТСЯ МИНИМАЛЬНО ВОЗМОЖНЫМ МОМЕНТОМ ИНЕРЦИИ ДАННОГО ТЕЛА ПРИ СОХРАНЕНИИ НАПРАВЛЕНИЯ ОСИ ВРАЩЕНИЯ.

Кроме того, поскольку мы рассматриваем только абсолютно жесткие тела, то ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ.

 

mykonspekts.ru

Момент инерции Википедия

Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции[ | ]

Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси^[1]:

Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

Ja=∫

ru-wiki.ru

6.6. Главные оси инерции и главные моменты инерции

6.6. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

При изменении угла α значения Iz1, Iy1, Iz1y1 (6.13) изменяются, и при некотором значении угла α0 они принимают экстремальные значения. Взяв первую производную по углу α от формул (6.13) и приравняв ее нулю, получим: Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции. Их вычисляют следующим образом: Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны; для симметричных сечений оси симметрии являются главными. Главные оси, проходящие через центр тяжести фигуры, называют главными центральными осями инерции. Пример 6.4. Определить, каким образом изменяется момент инерции квадратного сечения при его повороте. Решение. Момент инерции относительно повернутой оси: Поскольку оси z, y квадрата являются осями симметрии, то есть главными, то центробежный момент инерции относительно них Izy = 0: Выводы. 1. Моменты инерции квадратного сечения с изменением положения центральных осей остаются постоянными. 2. В квадрате и других правильных многоугольниках (треугольниках, пятиугольниках) любая центральная ось является и главной. Такие фигуры называют фигурами равного сопротивления. Пример 6.5. Для фигуры, представленной в примере 6.1, определить главные центральные моменты инерции. Решение. Расстояния между центральной осью составной фигуры и собственными центральными осями элементов Моменты инерции относительно центральных осей, параллельных основанию и высоте a1= y1 – yC = 5 – 3,5 = 1,5 см; a2= y2 – yC = 1 – 3,5 = –2,5 см; b1= z1 – zC = 1 – 2,5 = –1,5 см; b2= z2 – zC = 5 – 2,5 = 2,5 см. Центробежный момент инерции Направления главных осей инерции Угол α0 (положительный) откладываем против хода часовой стрелки от оси с большим моментом инерции, то есть zC . Величины главных центральных моментов инерции

dx-dy.ru