Что такое средняя путевая скорость — Науколандия
В физике существует два понятия средней скорости. Одно — средняя путевая скорость. Второе — средняя скорость по перемещению. В чем же их сходство и различие?
Вообще понятие средней скорости вводится, когда движение тела является неравномерным, т. е. за равные промежутки времени тело двигается с разной скоростью. Например, за первую секунду тело двигалось со скоростью 10 км/ч, а за вторую — со скоростью 6 км/ч. Тогда средняя скорость тела за 2 секунды по-идее должна быть равна 8 км/ч, т. к. (10 + 6) / 2 = 8.
Однако, как известно, скорость можно вычислять по формуле 1) v = s/t или 2) v = Δx/t.
В первом случае s — это прошедший телом путь, или расстояние. Данная величина не может быть отрицательной, она не является вектором. И в таком случае vср будет скалярной величиной. Например, тело в течение одного часа двигалось из точки A в точку B по прямой линии 10 км, затем развернулось назад и за следующий час проехало еще 14 км, оказавшись в точке C на той же прямой линии. В данном случае средняя путевая скорость будет равна 12 км/ч, так как (14 км + 10 км) / 2 ч = 12 км/ч. Общее расстояние, покрытое движущимся телом, будет равно 24 км. Можно сказать, что в случае средней путевой скорости направление движения тела нас не интересует вообще. Нас интересуют лишь покрытые телом расстояния.
Во втором случае Δx (Δx = x2 – x1) — это разница между конечной и начальной координатами тела. Эта величина может быть как положительной, так и отрицательной (если конечная координата x2 меньше начальной x1). Таким образом, Δx является векторной величиной, а следовательно и скорость по перемещению будет векторной величиной. В примере, рассмотренном выше, Δx будет равно -4 км (0 + 10 – 14). Тогда v
Однако часто при прямолинейном движении модули обеих средних скоростей совпадают. Если бы тело из примера двигалось только до точки B, то средние скорости как путевая, так и по перемещению были бы равны 10 км/ч.
Итак, что такое средняя путевая скорость? Это скалярная физическая величина, равная отношению пройденного телом пути к длительности промежутка времени, за который тело прошло этот путь.
Средняя скорость по перемещению — это
scienceland.info
Как найти среднюю скорость

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:
Научимся ее находить на примере следующей задачи:
| Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела. |
- Переведем все величины в Международную систему единиц СИ. В этой системе единицей измерения времени является секунда. Следовательно, тело двигалось на первом участке пути в течение с, а на втором участке пути в течение с.
- Найдем теперь полный путь, пройденный телом. На первом участке тело прошло м пути. На втором участке пути тело прошло м пути. Следовательно, общий пройденный телом путь составляет м.
- Общее время движения составляет с. Следовательно, средняя скорость движения тела составляет:
м/с.
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скорос
Средняя скорость движения
Рассмотрим одну из самых простейших задач, которые можно встретить в школьной программе. Итак немного теории
Средняя скорость движения это отношение полного пути пройденного объектом на общее время затраченное на это путешествие
Естественно предположить, что если объект часть общего пути прошел за одно время, другую часть за другое время, а третью за третье время, то средняя скорость будет являтся отношением всех частей пути на все затраченное время.
А если известно например части пути и скорость объекта на каждом пути ? Не среднее арифметическое же брать от всех скоростей… хотя очень часто именно так и поступают впервые большинство учеников.
На самом деле, при известных частях пути и скоростей на участке формула будет следующая
наверняка догадались как она получилась из предыдущей формулы.
Если в задании пути буду обозначаться как часть от общего ( например первая половина пути, 2/3 пути и т.п.) то учитывая что сумма таких частей будет равна всему пути ( равной единице)
то средняя скорость будет определятся как
Пример:
Автомобиль проехал первую треть дороги со скоростью 60 км/ч, вторую треть дороги со скоростью 120 км/ч, третью треть дороги со скоростью 40 км/ч. найдите среднюю скорость.
Решение:
Ответ: 60 км/час
И последний вариант формулы на среднюю скорость это когда известно время и скорость на каждом из участков.
Правда есть еще четвертый вариант, но он практически никогда не встречается в задачах. Это когда встречаются комбинированные данные, например: Пешеход, преодолевает путь из точки А в точку Б. Первую половину пути пешеход прошел со скоростью 5 км/час а вторую половину пути за 1 час. Какое расстояние между А и Б, если средняя скорость пешехода, со всеми остановками и перекурами, была 3 км/час
Смотрим вот на эту формулу и думаем
Части пути нам известны, то есть общее расстояние нам известно и принимается за единицу ( половина пути+половина пути равна единице пути)
Теперь со временем
На первом участке время легко вычислить ( половину пути разделить на 5 км/ч). Получаем одну десятую пути. Не пугайтесь что получилось “время равно одной десятой пути”. Оно потом понадобится..
Время на втором участке известно и равно 1 час
Напишем нашу формулу по полученным данным
Выразим расстояние от точки А до точки Б через среднюю скорость и получим
Поставим значение средней скорости получим что общее расстояние которое преодолел пешеход равно 4 километра и почти 286 метров
Сложновато? Зато интересно и увлекательно.
Из последней формулы вытекает “парадоксальный” вывод: При средней скорости приближающейся к 10 км/час расстояние между точками А и Б становится неприлично большим и уходит в бесконечность, а при 11 км/час расстояние вообще становится отрицательным.
Взяв предыдущую формулу – мы бы увидели что при средней скорости в 10 км/ч , расстояние просто будет неопределено. То есть при заданных условиях средняя скорость никак не может быть больше 10 км/час.
- Упругое и неупругое столкновение >>
www.abakbot.ru
Конспект “Неравномерное движение. Средняя скорость”
«Неравномерное движение.
Средняя скорость»
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.

Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения , совершённого телом, к длительности этого промежутка времени.
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?

Ответ: 70 км/ч
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»

Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
Неравномерное движение. Средняя скорость
5 (100%) 1 voteuchitel.pro
Средняя скорость-Скоростьв физике
Средняя скорость
Средняя скорость – не
самое сложное понятие в кинематике. Однако для многих учащихся простота этого
понятия оказывается обманчивой.
Известно, что средняя скорость – это величина, равная отношению
пути, пройденного телом, ко времени, за которое пройден этот путь: Краткость
и простота определения скрывают от некоторых учеников важные для решения задач
вопросы и ответы на них.
1. Какое время следует учитывать при расчете средней
скорости, если тело в пути делало остановки?
В определении указано: “…ко времени, за которое пройден
этот путь”, то есть ко всему промежутку времени с момента, когда тело
тронулось в этот путь (представьте, что Вы включили секундомер), до момента,
когда тело преодолело этот путь (только в этот момент Вы останавливаете
секундомер!). О том, что время на остановки не следует учитывать, в определении
ничего не сказано (поэтому секундомер на промежуточных остановках не
выключайте!). Таким образом, при расчете средней скорости следует учитывать всё
время, которое ушло на преодоление пути (в том числе и время, потраченное на
остановки).
2. Как правильно
рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило
его в пункте В, но по дороге из А в В поворачивало назад (может быть ни
один раз!), а затем вновь продолжало движение к пункту В?
В определении указано “…равная отношению пути, пройденного
телом…”, значит, при расчете средней скорости определяющим является не
расстояние между точками (пунктами) начала и окончания движения, а реальный
путь, которое прошло тело.
Пример 1. Найти среднюю скорость человека на пути от дома до станции, расстояние между которыми l =800 м, если, пройдя четверть пути, он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через мин продолжил путь на станцию. Скорость движения человека постоянна и равна v =4 км/ч.
Решение. Началом движения человека, конечно, следует считать момент времени, когда он первый раз вышел из дома. Четверть пути составляет расстояние l1/4 =l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l1/4 =400 м. После этого он вышел из дома второй раз и дошел до станции. Путь, пройденный человеком с начала движения, составит:
S = 2l1/4 + l =400 + 800 =1200 м =1,2 км.
Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна (v =4 км/ч) и проделанный путь известен, то время движения составляет:
1,2 км : 4
км/ч =0,3 ч =18 мин.
Тогда все время, затраченное человеком, составляет:
t =+ T = 2 + 18 =20 мин =1/3 ч.
Найдем среднюю скорость:
1,2 км : ч =3,6 км/ч.
Ответ: vср =3,6 км/ч.
Среднюю скорость движения человек оценивает довольно часто, но судит о ней, глядя на часы. Торопящийся человек соотносит расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это, после чего делает вывод (хотя числовое значение средней скорости вряд ли при этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще поднажать, иначе не успею”.
Вернемся к рассмотренному примеру. Будем считать, что скорость v0 =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t0 =12 мин =0,2 ч:
= 0,8 км : 0,2 ч =4 км/ч.
По существу, это – средняя скорость, поскольку доподлинно неизвестно, с какой скоростью человек идет в каждый момент времени. Двигаясь с такой скоростью и затрачивая время t0, человек ежедневно успевает на станцию вовремя. Если приходится возвращаться домой (увеличивать путь, который надо преодолеть и на это требуется дополнительное время) или останавливаться (увеличивая время, необходимое на преодоление пути), выбранная скорость движения v0 не подходит: можно опоздать на станцию. Значит, надо увеличивать скорость движения. Но как это сделать без напрасных затрат сил?
Пример 2. Человек обычно доходит из дома до станции за время t0 =12 мин, проходя расстояние l =800 м. Однажды, пройдя четверть пути, он вспоминает, что не выключил электроприборы, и возвращается домой, выключает электроприборы, затрачивая время= 2 мин, и снова идет на станцию. С какой наименьшей скоростью надо двигаться человеку, после того как он повернул домой, чтобы успеть на станцию в обычное время (и не опоздать на электричку).
Решение.
1. Обычно человек двигается со скоростью
м/мин =4 км/ч.
2. Пройдя с такой скоростью четверть пути, он затратил время : 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время Т2 =t0 – T1 =12 – 3 =9 мин.
3. За время Т2 человек должен
преодолеть путь до дома, а затем снова до станции:
м =1 км и, кроме того, часть времени (= 2 мин)
потратить дома. Поэтому путь S человеку придется преодолевать за время
ч,
то есть со скоростью, не меньшей, чем
1 км : ч =км/ч =км/ч » 8,6 км/ч.
Проверьте, что добежав до дома со скоростью км/ч, а
затем шагая со скоростью v2 =2v0 =8 км/ч,
человек придет на станцию вовремя.
Ответ: человеку необходимо двигаться со скоростью, не меньшей, чем км/ч.
Обратите внимание, что средняя скорость за время (t =12 минут) от начала
движения до его окончания составляет
м/мин =100 м/мин =6 км/ч.
Найденное значение vср в полтора раза выше, чем v0, и показывает, с какой начальной скоростью следует выходить человеку из дома, если он забывчив.
На рис.1 показан график зависимости скорости человека от времени для примера 2 в случае, если человек бежит домой со скоростью v1 =3v0 ==12 км/ч, а затем идет до станции очень быстрым шагом со скоростью v2 =2v0 =8 км/ч. Штрихпунктирной линией указан график движения со скоростью v0, а тонкой линией – со скоростью vср =6 км/ч.
Подсчитаем среднее арифметическое для значений скорости v0, v1, v2:
км/ч.
Это значение не равно значению средней скорости vср. Убедитесь в этом и не совершайте в дальнейшем распространенную ошибку: не пытайтесь искать среднюю скорость как среднее арифметическое значение (оно не имеет физического смысла!).
Пример 3. Автомобиль проезжает первую треть пути равномерно со
скоростью v1 =108 км/ч, а остальные две трети пути – со
скоростью v2 =72 км/ч. Найти среднюю скорость автомобиля.
Решение. Неверно считать, что средняя скорость совпадает со средним
арифметическим значением v1 и v2, которое
составляет
км/ч.
1. Найдем время t1 движения
со скоростью v1, полагая, что весь путь равен L [км].
Из условия ясно, что
2. Время t2 движения на оставшемся участке пути составляет
3. Итак, время на продолжение пути L составляет
4. По определению средней скорости
км/ч.
Ответ: средняя скорость vср =81 км/ч.
Значение средней скорости совпадает со средним арифметическим значением скорости только в одном частном случае, когда тело двигается с различными скоростями так, что между последовательными моментами изменения (переключения) скорости проходит одинаковое время Т. Таким образом, тело двигается со скоростью v1 в течение времени t1=T, со скоростью v2 в течение времени t2=T, со скоростью v3 в течение времени t3=T и т.д. Если на протяжении пути скорость изменялась n раз, то пройденный путь
S =v1t1 + v2t2 + v3t3 + … +vntn =T(v1 + v2 + v3 + … +vn).
Время t, за которое пройден путь, составляет
t =t1 + t2 + t3 + … + tn =T*n.
По определению:
.
Не запрещено для этого частного случая двигаться со скоростью v0=0, т.е. делать остановки. Но время остановки должно составлять t0 =T.
Пример 4. Вертолет пролетает без остановок равномерно и прямолинейно над пунктами А, В, С (в указанном порядке) и возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Расстояние между А и В составляет LAB =150 км, между В и С LBC =200 км, между С и А LCA =100 км. Время, за которое вертолет пролетает от одного пункта до другого, составляет полчаса. Найти среднюю скорость движения вертолета на маршруте АВСА. Изменится ли средняя скорость, если LCA =200 км и всё расстояние вертолет преодолеет за 1 ч?
Решение. 1. Находим скорость движения вертолета на каждом участке:
км/ч;
км/ч;
км/ч.
2. Поскольку t =0,5 ч одинаково для всех участков движения, то
км/ч.
3. Если расстояние LСА =200 км и tCA=1ч, то не меняется vCA=200 км/ч. Но в этом случае нельзя подсчитывать (для простоты) среднюю скорость как среднее арифметическое, так как tCА ? tAB ==tBC.
км/ч.
Ответ: 1) vcp1 =300 км/ч; 2) vcp2 =275 км/ч.
Контрольные задания на эту тему
gym1517.narod.ru
Прямолинейное неравномерное движение. Средняя скорость
Как вы понимаете, в жизни практически невозможно встретить тело, движущееся точно равномерно. Поэтому мы с вами переходим к изучению более сложных видов движения. Рассмотрим простой пример. Пусть автомобиль, который едет из Москвы в Санкт-Петербург по прямой, за 10 ч проезжает 600 км (рис. 50). Будем считать автомобиль точечным телом, так как его размеры по сравнению с пройденным расстоянием пренебрежимо малы. Понятно, что за время своего движения автомобиль многократно разгонялся и тормозил и даже стоял перед светофорами. В результате движение автомобиля было неравномерным. Поэтому определение скорости равномерного прямолинейного движения здесь применять нельзя.

Для таких случаев вводят понятие «средняя путевая скорость». В рассмотренном примере за время t = 10 ч автомобиль проехал путь s = 600 км. Средняя путевая скорость автомобиля при этом равна
vср.п = s/t = 600 км / 10 ч = 60 км/ч.
Средней путевой скоростью тела называют физическую величину, равную отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
vср.п = s/t
Обратим внимание на то, что путь s не имеет направления и является скалярной неотрицательной величиной. Поэтому и средняя путевая скорость vср.п всегда является скалярной неотрицательной величиной. Она не имеет направления, а следовательно, не является вектором.
Средняя путевая скорость vср.п – скалярная неотрицательная величина.
Теперь рассмотрим определение еще одной физической величины, которая связана не с путем, пройденным телом, а с его перемещением за рассматриваемый промежуток времени.
Введем систему отсчета так, как показано на рис. 50. В результате мы найдем, что за время t = 10 ч автомобиль совершил перемещение Δx в положительном направлении оси X, модуль которого |Δx| = 600 км.
Средней скоростью тела за промежуток времени t называют физическую величину, равную отношению перемещения Δx, совершенного телом, к длительности этого промежутка времени.
vср = Δx/t
Поскольку перемещение Δx является вектором, то средняя скорость – тоже вектор. Направление средней скорости vср совпадает с направлением перемещения Δx.
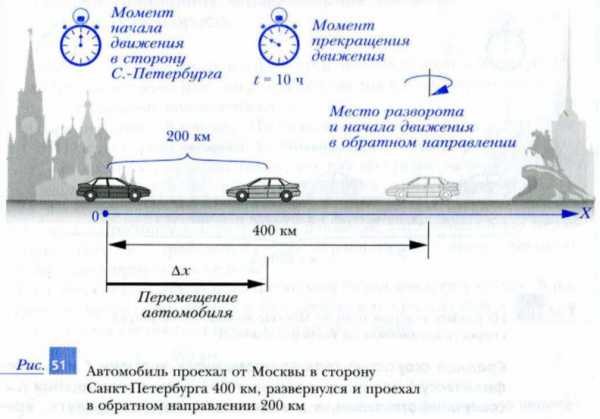
Чтобы лучше понять, чем отличаются друг от друга средняя скорость и средняя путевая скорость, обратимся к рис. 51. Пусть автомобиль, выехавший из Москвы в Санкт-Петербург, находился в пути 10 ч. При этом, проехав 400 км в сторону Санкт-Петербурга, он повернул обратно и проехал 200 км в сторону Москвы. Ясно, что путь, пройденный автомобилем за 10 ч, равен (400 + 200) км = 600 км. Значение перемещения автомобиля за то же время равно (400 – 200) км = 200 км. Используя данные определения, найдем среднюю путевую скорость и значение средней скорости автомобиля за 10 ч движения:
vср.п = s/t = 600 км / 10 ч = 60 км/ч;
vср = Δx/t = 200 км / 10 ч = 20 км/ч.
Итоги
Средняя путевая скорость – это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
vср.п = s/t
Средняя путевая скорость – скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t – это физическая величина, равная отношению перемещения Δx, совершенного телом, к длительности этого промежутка времени.
vср = Δx/t
Средняя скорость – вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело все время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Вопросы
- Дайте определение средней скорости и средней путевой скорости. Какая из этих величин является векторной? Почему средняя путевая скорость не может быть отрицательной?
- Чему равно значение средней скорости за промежуток времени, в течение которого перемещение тела было равно нулю? Всегда ли будет равна нулю средняя путевая скорость за этот же промежуток времени? Приведите примеры.
Упражнения
1. Пусть автомобиль проехал за первый час 90 км в положительном направлении оси X, а за второй час – 70 км в противоположном направлении.
Определите среднюю путевую скорость автомобиля и значение его средней скорости: а) за первый час; б) за второй час; в) за первые два часа движения.
Объясните, почему эти скорости отличаются друг от друга.
2.Представьте себе, что вы выехали на автомобиле со стоянки, находящейся рядом с вашим домом, в 8 часов утра. В 17 часов вечера вы вернули автомобиль на прежнее место. За день вы проехали путь s = 380 км, при этом в течение промежутка времени от 10 до 12 часов дня вы ехали по прямолинейной трассе строго на север с постоянной скоростью 60 км/ч. Ответьте на вопросы:
а) чему была равна ваша средняя путевая скорость за время с 8 часов утра до 17 часов вечера?
б) какова была ваша средняя скорость за интервалы времени: с 8 до 17 часов; с 10 до 12 часов?
3. Определите значение средней скорости и среднюю путевую скорость за промежуток времени от момента времени t0 = 0 до момента времени t2 = 7 с для тела, график движения которого приведен на рис. 47.
4. А) Измерьте шагами свой путь от дома до школы и время движения. Переведите это расстояние в метры, а время в секунды. Считайте, что длина одного шага приблизительно равна 0,6 м. Вычислите свою среднюю путевую скорость. Проделайте тот же путь на велосипеде и по результатам измерений найдите среднюю путевую скорость.
Б) Используя карту местности, найдите расстояние по прямой от дома до школы, чтобы затем рассчитать среднюю скорость при движении пешком и на велосипеде.
phscs.ru
Скорость
Скорость – физическая величина, что соответствует отношению перемещения тела к промежутку времени, за который это перемещение произошло. Скорость – величина векторная, то она должна абсолютную величину и направление.
Скорость основном обозначается буквой (От лат. Velocitas – Скорость).
В системе СИ скорость (точнее ее абсолютная величина) измеряется в метрах за секунду – м / с. В системе СГС единицей измерения скорости является сантиметр в секунду – см / с. В повседневной жизни самой практичной единицей измерения скорости является километр за час – км / час. В некоторых областях человеческой деятельности используются специфические единицы скорости, как, например, узел.
В науке используется также скорость в широком Смысл, как скорость изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другого (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о угловую скорость, скорость изменения температуры, скорость химической реакции, групповую скорость, скорости соединения и т.д.. Математически скорость характеризуется производной функции.
1. Мгновенная скорость
Скорость тела легче определить, когда оно совершает равномерное прямолинейное движение, т.е. преодолевает одинаковые расстояния за равные промежутки времени. В таком случае скорость определяется как отношение расстояния до времени:
- ,
где – Расстояние, пройденное телом за промежуток времени .
Радиус-векторы (черные стрелки). Векторы средней и мгновенных скоростей (зеленые стрелки). Траектория (красная линия)
Механика обобщает это естественное определение для произвольного движения, используя математический аппарат анализа. В общем случае тела движутся неравномерно и могут изменять направление движения. Для описания такого движения вводится понятие мгновенной скорости, механика дальнейшем и называет просто скоростью. Траектория движения тела разбивается на маленькие участки, на которых движение можно считать равномерным и прямолинейным, и определяется скорость на этих участках. Таким образом, сначала вводится вспомогательное определение:
Средняя скорость произвольного движения за интервал времени – Это векторная величина [1] [2]
- ,
где – перемещение тела за время
После применения предельного перехода вводится определение мгновенной скорости.
Мгновенная скорость неравномерного движения – это вектор в точке, которая является пределом средних скоростей, когда интервал времени стремится к нулю. Раскрывая определение, скорость – это отношение перемещения материальной точки за интервал времени, когда этот интервал стремится к нулю, т.е. производная :
- .
Вектор скорости направлен по касательной к траектории движения.
В свою очередь, производная от скорости дает мгновенное ускорение тела в момент времени t.
1.1. Среднее значение абсолютной величины скорости
В механике можно рассмотреть также понятие среднего значения абсолютной величины скорости тела за время t прошло путь s. Оно рассчитывается по простой формуле:
и совпадает с бытовым представлением о скорости.
Определенное таким образом среднее значение абсолютной величины скорости – скалярная величина и не связана с перемещением тела. Например, автомобиль, который проехал с Коломыи до Львова, а затем вернулся обратно, совершил нулевое перемещения, однако он двигался с определенной средней скоростью, скажем 50 км / час.
2. Прямолинейный равноускоренное движение
Конечная скорость v f объекта с начальной скоростью v i и постоянным во времени ускорением a в период времени t определяется как:
Средняя скорость объекта с постоянным ускорением составляет (v i + v f) / 2. Тогда для вычисления расстояния s перемещение тела за промежуток времени t получим формулу:
Если известна только начальная скорость, можно применять формулу:
Из этих базовых уравнений выводится формула, не зависит от параметра времени t:
Приведенные уравнения справедливы как для классической механики, так и для специальной теории относительности. Отличие ситуации заключается, в частности, в том, что в классической механике для всех наблюдателей в инерциальных системах отсчета ускорение тела, движущегося будет одинаковым. Для специальной теории относительности это не так.
3. Обобщенная скорость
В механике Лагранжа аналогичным образом вводится обобщенная скорость
где – обобщенная координата, т.е. одна из величин, определяющих мгновенное положение механической системы.
Например, при вращении твердого тела, обобщенная координата: угол поворота . Обобщенная скорость – это угловая скорость :
3.1. Скорость при вращении по кругу
При вращении материальной точки по кругу с радиусом R ее скорость определяется формулой
- .
В общем, если рассматривать движение материальной точки в плоскости в полярной системе координат, то скорость можно разложить на две составляющие: радиальную и тангенциальную. Радиальная составляющая скорости направлена вдоль радиус-вектора точки и описывает удаления или приближения точки до начала системы координат. Тангенциальная составляющая направлена перпендикулярно радиус-вектора, и описывает вращение точки вокруг начала отсчета системы координат.
4. Теория относительности
Основной постулат теории относительности устанавливает максимальную скорость, с которой может передаваться информация, а, следовательно, и двигаться тело. Это максимальная скорость – скорость света – есть универсальной физической постоянной.
Для описания движения тел в теории относительности вводится 4-вектор скорости, или 4-скорость
- ,
где ds – пространственно-временной интервал.
- ,
где – Обычная трехмерная скорость, а c – скорость света в вакууме.
4-скорость – безразмерная величина. Для 4-вектора скорости всегда справедливо уравнение
5. Относительная скорость
Значение скорости тела зависит от системы отсчета наблюдателя. В классической механике, которая использует принцип Галилея, скорость тела в новой системе отсчета является векторной разностью его скорости в старой системе и скорости новой системы отсчета относительно старой.
- ,
где – Скорость тела в новой системе отсчета, – Скорость тела в старой системе отсчета, – Скорость новой системы отсчета виносно старой.
В системе отсчета, движущейся с той же скоростью, что и тело, оно незыблемо.
В теории относительности приведена формула не является справедливой, поскольку ни одно тело не может двигаться со скоростью, которая превышала бы скорость света. Например, в случае, когда направление скорости новой системы отсчета совпадает с направлением движения тела, скорость в новой системе равно
- .
При малых скоростях или эта формула совпадает с формулой преобразований Галилея.
6. Связь с другими физическими величинами
Тело, которое движется с определенной скоростью, имеет импульс и энергию. Импульс материальной точки массой , Движущегося со скоростью , Равна
- .
Кинетическая энергия такой материальной точки в классической механике равна
- .
Благодаря кинетической энергии физическое тело, которое имеет отличную от нуля скорость, может осуществлять работу.
Уравнения движения механики задают связь между ускорением тел и силами, которые действуют на эти тела. Таким образом, они дифференциальными уравнениями относительно скоростей. Для описания временной эволюции механической системы нужно задать не только положение тел, но и их скорости в начальный момент времени. Так, например, высота, на которую взлетит подброшенный вверх мяч и время его полета зависит от того, какую начальную скорость ему предоставили.
7. Скорость процесса
В украинском языке термин скорость употребляется также не в механическом смысле для определения временных характеристик произвольных процессов : например, скорость химической реакции, скорость нагрева, скорость замерзания, скорость испарения. Если определенный процесс характеризуется зависимой от времени величиной , То мгновенная скорость этого процесса определяется производной . Соответственно, средняя скорость за промежуток времени определяется как .
8. Сноски
- Б.М.Яворский А.А.Пинский. Основы физики – том 1. М. Наука, 1981. с.22
- Н.Г.Четаев. Теоретическая механика. М. Наука 1987. с.27
См.. также
Источники
- Федорченко А.М. Теоретическая механика. – М.: Высшая школа, 1975., 516 с.
nado.znate.ru
