Предел функции на бесконечности
Продолжаем разбирать готовые ответы по теории пределов и сегодня остановимся только на случае, когда переменная в функции или номер в последовательности стремится к бесконечности. Инструкция по вычислению предела при переменной стремящейся к бесконечности приведена ранее, здесь только остановимся на отдельных случаях, которые не являются всем очевидными и простыми.
Пример 35. Имеем последовательность в виде дроби, где в числителе и знаменателе находятся корневые функции.
Нужно найти предел при номере стремящемся к бесконечности.
Здесь раскрывать иррациональности в числителе не нужно, а только внимательно проанализировать корни и найти где содержится более высокая степень номера.
В первом корни числителя имеем множителем n^4, то есть n^2 можем вынести за скобки.
Тоже самое проделаем со знаменателем.
Далее оцениваем значение подкоренных выражений при предельном переходе.
Получили деления на ноль, что является неправильно в школьном курсе, но в предельном переходе это допустимо.
Только с поправкой, “чтобы оценить куда стремится функция”.
Поэтому приведенную запись не все преподаватели могут трактовать правильной, хотя и понимают, что результирующий преде от этого не изменится.
Давайте рассмотрим ответ, составленный по требованиям преподавателей согласно теорией.
Для упрощения оценим только главные доданки под корнем
Далее в числителе степень равен 2, в знаменателе 2/3, следовательно числитель быстрее растет, а значит предел стремится к бесконечности.
Его знак зависит от множителей при n^2, n^(2/3), поэтому он положительный.
Пример 36.Рассмотрим пример предела на деление показательных функций. Таких примеров на практических рассматривается мало, поэтому не все студенты с легкостью видят, как раскрывать неопределенности, что возникают.
Максимальный множитель для числителя и знаменателя равен 8^n, на него и упрощаем
Далее оцениваем вклад каждого слагаемого
Слагаемые 3/8 стремятся к нулю при переменной направляюейся к бесконечности, поскольку 3/8<1 (свойство степенно-показательной функции).
Пример 37.Предел последовательности с факториалами раскрывается розписанням факториала к наибольшему общему множителю для числителя и знаменателя.
Далее на него сокращаем и оцениваем лимит по значению показателей номера в числителе и знаменателе.
В нашем примере знаменатель быстрее растет, поэтому предел равен нулю.
Здесь использована следующее
свойство факториала.
Пример 38.Не применяя правила Лопиталя сравниваем максимальные показатели переменной в числителе и знаменателе дроби.
Так как знаменатель содержит старший показатель переменной 4>2 то и растет он быстрее.
Отсюда делаем вывод, что предел функции стремится к нулю.
Пример 39.Раскрываем особенность вида бесконечность разделить на бесконечность методом вынесения x^4 с числителя и знаменателя дроби.
В результате предельного перехода получим бесконечность.
Пример 40. Имеем деление полиномов, нужно определить предел при переменной стремящейся к бесконечности.
Старший степень переменной в числителе и знаменателе равен 3, это значит что граница существует и равна сталой.
Вынесем x^3 и выполним предельный переход
Пример 41.Имеем особенность типа единица в степени бесконечность.
А это значит, что выражение в скобках и сам показатель надо свести под вторую важную границу.
Распишем числитель, чтобы выделить в нем выражение идентичное знаменателе.
Далее переходим к выражению, содержащем единицу плюс слагаемое.
В степени нужно выделить множителем 1/(слагаемое).
Таким образом получим экспоненту в степени предела дробной функции.
Для раскрития особенности использовали второй предел:
Пример 42.Имеем особенность типа единица в степени бесконечность.
Для ее раскрытия следует свести функцию под второй замечатеьный предел.
Как это сделать подробно показано в приведенной далее формуле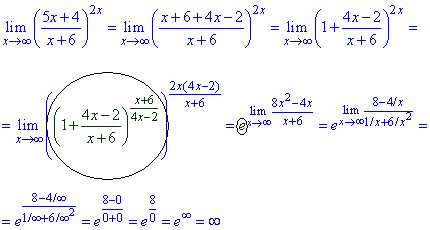
Подобных задач Вы можете найти очень много. Их суть в том, чтобы в показателе получить нужный степень, а он равен обратному значению слагаемого в скобках при единицы.
Таким методом получаем экспоненту. Дальнейшее вычисление сводится к вичислению предела степени экспоненты.
Здесь экспоненциальная функция стремится к бесконечности , поскольку значение больше единицы e=2.72>1.
Пример 43 В знаменателе дроби имеем неопределенность типа бесконечность минус бесконечность, фактически равное делению на ноль.
Чтобы избавиться корня домножим на сопряженное выражение, а дальше по формуле разности квадратов перепишем знаменатель.
Получим неопределенность бесконечность разделить на бесконечность, поэтому выносим переменную в наибольшей степени и сокращаем на нее.
Далее оцениваем вклад каждого слагаемого и находим предел функции на бесконечности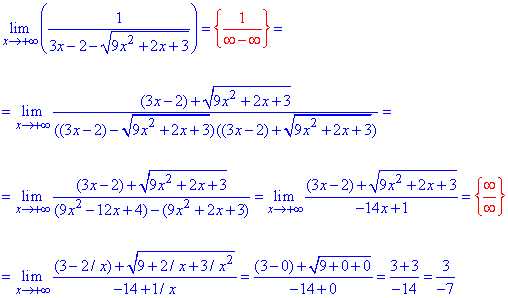
Пример 44.Найти повторные границы
Решение: Вычисляем предел функции двух переменных сначала по y, а дальше – x)
a)
б)
Пример 45. Вычислить повторные границы
Решение: Методика вычисления повторных границ не сложна:
сначала находим границу по одной переменной, считая вторую переменную постоянной.
Далее остается функция от одной переменной, а таких пределов мы разобрали очень много.
а)
б)
В этом задании предел по первой переменной равен нулю, поэтому повторные записываем только для формальности.
Предел в данном случае от порядка нахождения не зависит.
Однако, если взглянуть ответ из предыдущего примера то такое утверждение не всегда выполняется.
Ищите эффективные схемы вычисления пределов на страницах сайта, если возникают проблемы с пределами на экзаменах и модулях – обращайтесь за помощью!
yukhym.com
Предел функции на бесконечности
Определение предела функции на бесконечности
Геометрическое толкование предела функции на бесконечности изображено на рисунке 1.
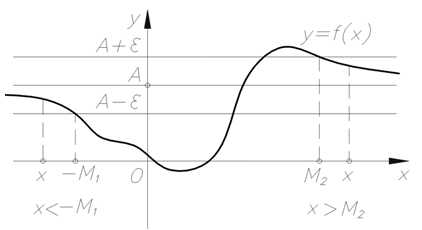
Рис. 1
Число называется пределом функции при , если для любого числа существует число такое, что для всех значений аргумента, больших этого числа, значения функции отличаются по величине от указанного числа меньше, чем на :
Геометрический смысл предела функции на бесконечности
Геометрический смысл предела функции при . Преобразуем неравенство в определении предела функции на плюс бесконечности следующим образом:
или
Полученное неравенство означает, что график рассматриваемой функции для всех будет лежать в полосе, которая ограничена прямыми (рис. 2).
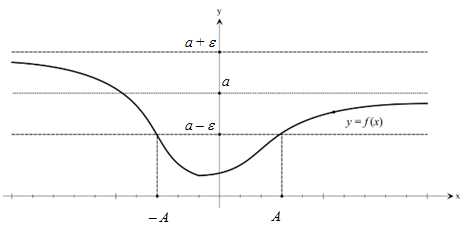
Рис. 2
Число называется пределом функции
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ – это… Что такое СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ?
- СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ
- СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ
(tend to infinity) Рост за пределы любого конечного размера, каким бы большим он ни был. То, что переменная х стремится к бесконечности, записывается как х; она становится бесконечно большой. Точно так же если х, она становится меньше, чем любое отрицательное число, однако по абсолютной величине оно может быть очень велико.
Экономика. Толковый словарь. — М.: “ИНФРА-М”, Издательство “Весь Мир”. Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М.. 2000.
Экономический словарь. 2000.
- СТРАХОВАЯ КОМПАНИЯ
- СТРЕМЛЕНИЕ К ПОЛУЧЕНИЮ РЕНТНЫХ ДОХОДОВ
Смотреть что такое “СТРЕМЛЕНИЕ К БЕСКОНЕЧНОСТИ” в других словарях:
СМЫСЛ ЖИЗНИ ЧЕЛОВЕКА — эйдос индивида, умопостигаемая целостность всех проявлений его души. Стихия С.Ж. не материя и не энергия, а информация. Догадка о чьем либо С. ж. (в т. ч. о собственном) есть попытка понять скрытую форму правления души в теле, заключить о… … Современный философский словарь
ВЁБЕР — (Weber) Альфред (1868 1958) нем. философ, социолог и теоретик культуры, экономист и политолог. Начав свою научную карьеру как экономист, исследователь проблем размещения нем. промышленности, В. переходит к проблемам философии и социологии… … Философская энциклопедия
ВЕБЕР — ВЁБЕР (Weber) Альфред (1868 1958) нем. философ, социолог и теоретик культуры, экономист и политолог. Начав свою научную карьеру как экономист, исследователь проблем размещения нем. промышленности, В. переходит к проблемам философии и социологии… … Философская энциклопедия
Соотношения Эренфеста
Неевклидовы геометрии — в буквальном понимании все геометрические системы, отличные от геометрии Евклида; однако обычно термин «Н. г.» применяется лишь к геометрическим системам (отличным от геометрии Евклида), в которых определено движение фигур, причём с той… … Большая советская энциклопедия
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — в буквальном понимании все геометрич. системы, отличные от геометрии Евклида; однако обычно термин Н. г. применяется лишь к геометрич. системам (отличным от геометрии Евклида), в к рых определено движение фигур, причем с той же степенью свободы,… … Математическая энциклопедия
ИОАНН ДУНС СКОТ — [лат. Ioannes (Johannes) Duns Scotus] († 8.11.1308, Кёльн), средневек. философ и богослов, католич. священник, член монашеского ордена францисканцев; в католич. Церкви прославлен в лике блаженных (пам. зап. 8 нояб.). Жизнь. Иоанн Дунс Скот. 1473… … Православная энциклопедия
ВЫШЕСЛАВЦЕВ — Борис Петрович (1877 1954) специалист по философии права, социальной философии, истории философии, этике, религии. Его творчество занимает видное место в рус. культурном ренессансе 20 в. В 1899 окончил юрид. ф т Моск. ун та. В 1902 В.… … Энциклопедия культурологии
КОГЕН — (Cohen) Герман (1842 1918) немецкий философ, основатель и виднейший представитель марбургской школы неокантианства. Основные работы: ‘Теория опыта Канта’ (1885), ‘Обоснование Кантом этики’ (1877), ‘Обоснование Кантом эстетики’ (1889), ‘Логика… … История Философии: Энциклопедия
БУДДИЙСКАЯ МИФОЛОГИЯ — комплекс мифологических образов, персонажей, символики, связанный с религиозно философской системой буддизма, возникшей в 6 5 вв. до н. э. в Индии, в период централизованного государства, и широко распространившейся в Южной, Юго Восточной и… … Энциклопедия мифологии
dic.academic.ru
стремиться к бесконечности – Русский-Английский Словарь
ru В этом случае, SQRT (е / т) при т стремится к нулю, э / м стремится к бесконечности, а SQRT (бесконечность) = бесконечности.
Common crawlen In this case, sqrt (e / m) when m tends to zero, e / m tends to infinity, and sqrt (infinity) = infinity.ru Мы доказываем, что и упругое и неупругое полные поперечные сечения стремятся к ненулевым пределам, когда энергия стремится к бесконечности.
springeren We prove that, consequently, both the elastic and inelastic total cross-sections approach nonzero limits as the energy goes to infinity.ru В частности, мы исследуем проблему бесконечного увеличения времени жизни, когда частота процессов измерения стремится к бесконечности, т.е. эффект, носящий название парадокса Зено в квантовой механике.
springeren In particular we investigate the problem of the indefinite increase of the lifetime when the frequency of the measurement processes tends to infinity, an effect referred to as Zeno’s paradox in quantum mechanics.ru Кроме того, асимптотическая свобода приводит к медленному уменьщению дифференциального поперечного сечения, когдаs Иt стремятся к бесконечности.
springeren Furthermore, the asymptotic freedom leads to a slow decrease of the differential cross-section ass andt tend to infinity.ru В соответствии со вторым свойством, амплитуда для любого экранированного кулоновского потенциала сходится, когда радиус экранирования стремится к бесконечности.
springeren The second property, the proof of which uses the first, is that the amplitude for any screened Coulomb potential converges as a distribution to the Coulomb amplitude (times an overall phase factor) when the screening radius tends to infinity.ru Решение, которое описывает критическое поведение, оказывается лишь асимптотически справедливым, если « эффективная константа связи », связанная с этой моделью, достигает нетривиальной « фиксированной точки », когда корреляционная длина стремится к бесконечности.
springeren The solution which describes the critical behaviour is only asymptotically valid if an « effective coupling constant », associated with the model, reaches a nontrivial « fixed point » as the correlation length goes to infinity.ru Этот метод основывается на том факте, что рассматриваемое основное Поведение долзно Проистекатя иэ сингулярности каздого феинмановского интеграла При бесконечнои Энергии, Причем, Эта сингулярностя воэникает иэ сузения эамкнутых имПулясных контуров интегрирования иэ-эа Полусов Подинтеграляного выразения, когда Энергия стремится к бесконечности.
springeren This method is based on the observation that such leading behaviour must come from the singularity of each Feynman integral at infinite energy, this singularity arising from a pinch of the loop-momentum contours of integration by the poles of the integrand when the energy becomes infinite.ru Показывается, что функуия η определяется только при условии, если нормальная скорость ударных волн не превышает скорости света в вакууме, в соответствии с требованиями теории относительности. Более того, скачок энтропии стремится к бесконечности, когда скорость волны приближается к скорости света и γ меньше двух, тогда как для γ=2 светоподобная унарная волна обращается в нуль.
springeren It is shown that the function η is defined only if the normal velocity of the shock waves does not exceed the speed of light in vacuo, consistently with the claims of relativity; moreover, the entropy jump goes to infinity as soon as the shock speed approaches the speed of light and γ is lower than 2, while, for γ=2, the lightlike shock vanishes.ru Получается, что перекрестная матрица сушест-венно упрошается в пределе, когда знергия в соответствуюшем канале стремится к бесконечности, тогда как переданные импульсы остаются фиксированными.
springeren It is found that the crossing matrix simplifies drastically in the limit when an appropriate channel energy tends to infinity, while the momentum transfers are kept fixed.ru Мы исследуем воэможность того, что, когда δ стремится к бесконечности, отнощения амплитуд рассеяния к амплитудам рассеяния вперед имеют следуюшее свойство: при фиксированном tg(δ). гдеg(s) иэвестная функция, сушествуют нетривиальные пределы для зтих отнощений.
springeren We study the possibility that ass approaches infinity the ratios of the scattering amplitudes to the forward ones have the following property: at fixedtg(s), whereg(s) is well defined, there exist nontrivial limits for these ratios.ru В противоположность реэультатам Гросса и Вилчека, покаэывается, что точный скейлинг Бьёркена вплоть до логарифмических членов имеет место не только в асимптотически свободных теориях поля, но также и в других теориях поля, где инвариантная константа свяэи стремится к бесконечности вполне определенным обраэом.
springeren In contrast with Gross and Wilczek, it is shown that exact Bjorken scaling is possible and that Bjorken scaling, up to logarithmic terms, takes place not only in asymptotically free field theories, but also in other field theories, where the invariant coupling constant goes to infinity in a well-defined manner.ru Это представление дает некоторое понимание различных эффектов, которые влияют на поведениеDm(n), когда порядокn приближения стремится к бесконечности.
springeren This representation gives some insight into the various effects that influence the behaviour ofDm(n) when the ordern of the approximants tends to infinity.ru Во втором варианте этот диапазон стремится к бесконечности, т.е. частота вращения выходного вала начинается от нуля.
patents-wipoen In the second variant, this range tends to infinity, i.e. the rotation frequency of the output shaft starts from zero.ru Во втором варианте этот диапазон стремится к бесконечности, т.е. частота вращения выходного вала (35) начинается от нуля.
patents-wipoen In the second embodiment, this range tends to infinity, i.e. the rotation frequency of the output shaft (35) starts from zero.ru И если N стремится к бесконечности ошибки сходят к нулю.
OpenSubtitles2018.v3en And as N goes to infinity… The error goes to zero.ru Мы покаэываем, что зти сингулярности привильно описывают первые два члена в асимптотическом раэложении верщинной функции в импульсном пространстве, в пределе подобия и в пределе, в котором одна иэ токовых масс стремится к бесконечности, тогда как вторая остается конечной.
springeren We demonstrate that these singularities correctly describe the first two terms in the asymptotic expansion of the momentum space vertex function, both in the scaling limit and in the limit in which one of the current masses goes to infinity while the second is held finite.ru Они не стремятся к обладанию бесконечными материальными благами.
LDSen They are not concerned about having endless material possessions.ru В частности, предполагая, что вещественная (в остальном произвольная) функцияf(y) стремится к положительной бесконечности, когдаy→+∞, изменяет, по крайней мере, один раз знак и является конечной для положительныхy, обнаруживаются явления конденсации (с соответствующим насыщением) и коллапса, которые соответствуют положительной или отрицательной величнинам «константы связи»g.
springeren In particular, if one assumes the (otherwise arbitrary) real functionf(y) to diverge to positive infinity asy→+∞, to change sign at least once and to be finite valued for positivey, the phenomena of condensation (with proper saturation) and of collapse are displayed, corresponding respectively to positive or negative values of the “coupling constant”g.ru Обнаружено, что волновая функция не стремится к пределу при бесконечных временах.
springeren It is found that the wave function does not tend to a limit at infinite times.ru Предсказывается, что отношениеσl:σt стремится к нукю на бесконечности.
springeren It is predicted that the ratioσl:σt tends to zero at infinity.ru Гравитационные потенциалы стремятся к потенциалам Шварцшильда на бесконечности, тогда как скалярное поле обладает асимптотическим поведением типа Укавы.
springeren The gravitational potentials tend to the Schwarzschild ones at infinity, while the scalar field presents Yukawa-type asymptotic behaviour.ru Любое конечное число, поделенное на бесконечность, стремится к нулю так быстро, что результат просто невозможно заметить, так что в среднем население населенной планеты в этой Вселенной, можно сказать, равно нулю
opensubtitles2en We picked them up in Sector ZZ# Plural Z Alpha.- Yeah!- Does that mean anything to you?ru Смысл в том, чтобы показать, что в потоке Риччи положительная кривизна стремится к растяжению наружу, пока в бесконечности времени многообразие не достигнет постоянной кривизны.
OpenSubtitles2018.v3en The idea is to show that, under the Ricy flow, positive curvature tends to spread outwards, until at infinite time the manifold will achieve constant curvature.ru В рамках формализмаS-матрицы в статистической механике иссдедуется связь между свойствами адронной системы и асимптотическим поведением полных поперечных сечений. Получается, что адронная система имеет конечную температуру, эсли полное поперечное сечение уменьщается или стремится к постоянной величине сверху, тогда как бесконечный рост полного поперечного сечения или приближение к пределу снизу означает, что адронная система допускает неограниченное нагревание.
springeren Within the framework ofS-matrix formulation of statistical mechanics the connection between the properties of the hadronic system and the asymptotic behaviour of total cross-sections is studied; it is found that the hadronic system has an ultimate temperature if the total crosssection decreases, or it tends to a constant value from above, while the indefinite growth of the total cross-section or its approach to a limit from below means that the hadronic system allows an unlimited heating.ru.glosbe.com
Пределы. Понятие пределов. Вычисление пределов.
Понятие пределов рассмотрим на показательных примерах.
Пусть х – числовая переменная величина, Х – область ее изменения. Если каждому числу х, принадлежащему Х, поставлено в соответствие некоторое число у, то говорят, что на множестве Х определена функция, и записывают у = f(x).
Множество Х в данном случае – плоскость, состоящая из двух координатных осей – 0X и 0Y. Для примера изобразим функцию у = х2. Оси 0X и 0Y образуют Х – область ее изменения. На рисунке прекрасно видно, как ведет себя функция. В таком случае говорят, что на множестве Х определена функция у = х
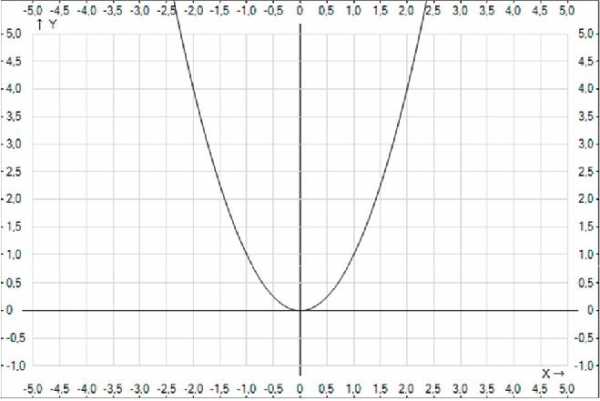
Совокупность Y всех частных значений функции называется множеством значений f(x). Другими словами, множество значений – это промежуток по оси 0Y, где определена функция. Изображенная парабола явно показывает, что f(x) > 0 , т.к. x2 > 0. Поэтому область значений будет [0; +]. Множество значений смотрим по 0Y.
Совокупность всех х называется областью определения f(x). Множество определений смотрим по 0X и в нашем случае областью допустимых значений является [-; +].
Точка а (а принадлежит или Х) называется предельной точкой множества Х, если в любой окрестности точки а имеются точки множества Х, отличные от а.
Пришла пора понять – что же такое предел функции?
Чисто b, к которому стремится функция при стремлении х к числу а, называется пределом функции. Записывается это следующим образом:
Например, f(x) = х2. Нам надо узнать, к чему стремится (не равна) функция при х 2. Сначала запишем предел:
Посмотрим на график.
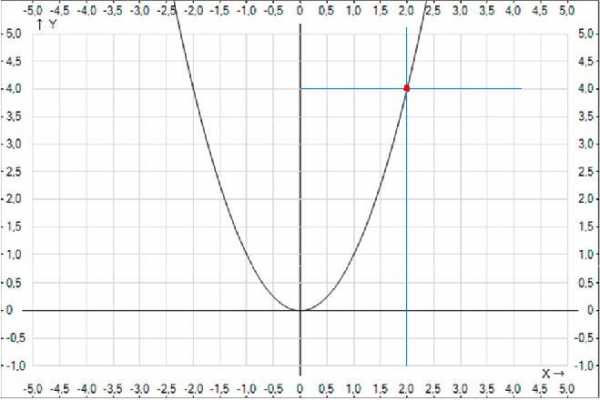
Проведем параллельно оси 0Y линию через точку 2 на оси 0X. Она пересечет наш график в точке (2;4). Опустим из этой точки на ось 0Y перпендикуляр – и попадем в точку 4. Вот к чему стремится наша функция при х 2. Если теперь подставить в функцию f(x) значение 2, то ответ будет таким же.
Теперь прежде чем перейти к вычислению пределов, введем базовые определения.
Понятие пределов введено французским математиком Огюстеном Луи Коши в XIX веке.
Допустим, функция f(x) определена на некотором интервале, в котором содержится точка x = A, однако совсем не обязательно, чтобы значение f(А) было определено.
Тогда, согласно определению Коши, пределом функции f(x) будет некое число B при x, стремящимся к А, если для каждого C > 0 найдется число D > 0, при котором
Т.е. если функция f(x) при x А ограничена пределом В, это записывается в виде
.
Пределом последовательности называется некое число А, если для любого сколь угодно малого положительного числа В > 0 найдется такое число N, при котором все значения в случае n > N удовлетворяют неравенству
Такой предел имеет вид .
Последовательность, у которой есть предел, будем называть сходящейся, если нет – расходящейся.
Как Вы уже заметили, пределы обозначаются значком lim, под которым записывается некоторое условие для переменной, и далее уже записывается сама функция. Такой набор будет читаться, как «предел функции при условии…». Например:
– предел функции при х, стремящимся к 1.
Выражение «стремящимся к 1» означает, что х последовательно принимает такие значения, которые бесконечно близко приближаются к 1.
Теперь становится ясно, что для вычисления данного предела достаточно подставить вместо х значение 1:
Ответ: -3.
Кроме конкретного числового значения х может стремиться и к бесконечности. Например:
Выражение х означает, что х постоянно возрастает и неограниченно близко приближается к бесконечности. Поэтому подставив вместо х бесконечность станет очевидно, что функция 1- х будет стремиться к , но с обратным знаком:
Таким образом, вычисление пределов сводится к нахождению его конкретного значения либо определенной области, в которую попадает функция, ограниченная пределом.
Исходя из вышеизложенного следует, что при вычислении пределов важно пользоваться несколькими правилами:
- Сперва попытаемся подставить в функцию число. Результат вычисление и будет ответом.
- Если х стремиться не к числу, например в пределах вида или , то такие пределы решаются сразу, т.к число деленное на бесконечность всегда дает ноль, а деленное на 0 всегда бесконечность. Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ.
- Есть еще одна интересная группа пределов, где мы и в числите и в знаменателе при подстановке получаем или 0 или бесконечность. Так называемые пределы с неопределенностью, часть из которых замечательные. Их мы рассматриваем отдельно в статьях “Вычисление пределов. Пределы с неопределенностью” и “Замечательные пределы: Первый и второй замечательный предел”.
Понимая сущность предела и основные правила вычисления пределов, вы получите ключевое представление о том, как их решать. Если какой предел будет вызывать у вас затруднения, то пишите в комментарии и мы обязательно вам поможем.
Заметка: Юриспруденция – наука о законах, помогающее в конфлитных и других жизненных трудностях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Функция, стремящаяся к бесконечности
Определение предела последовательности
Определение. Перенумерованное множество чисел называется последовательностью.
Последовательность можно задать так называемой формулой -го члена Здесь подразумевается, что
Определение. Последовательность стремится к b при , если для любого существует такое , что для всех справедливо неравенство Коротко это можно записать так: , если
Значок читается «для любого». Значок читается «существует». Значок : читается «такое, что при».
Пример 1.1. Докажем, что
Способ 1. Для заданного возьмем . Тогда из неравенства следует . Отсюда Ч.т.д.
Способ 2. В предыдущем способе не понятно, как мы догадались, что в качестве нужно взять . Это следует из цепочки формул: = .
Способ 3. Нестрогое, но наглядное доказательство следует из таблицы:
| 1,1 | 1,001 | 1,000001 | 1,00000000001 |
Определение предела функции
Определение. Пусть имеем два множества А и B. Предположим, что каждой точке сопоставлена точка . В этом случае говорят, что задана функция у от х.
Такую функцию обозначают или и так далее.
Примеры: .
Функции можно задать аналитически, графически, таблично.
Частным случаем функции является последовательность
Определение. Число b называется пределом функции при х, стремящемся к а,(обозначается ) если для любого положительного числа существует такое положительное число , что для всех х, не совпадающих с а и удовлетворяющих неравенству выполняется неравенство . Коротко это определение можно записать так: , если .
Замечание. В определении предела мы неявно предполагаем существование такого , что функция определена при любом .
Пример 2.1. Докажем формулу:
Действительно: Рассмотрим цепочку формул: . Теперь ясно, что для заданного положительного нужно взять , ибо из неравенства последует . Ч.т.д.
Функция, стремящаяся к бесконечности
Определение. Функция стремится к бесконечности при х, стремящегося к а, если
.
Пример 3.1. Докажем
Для этого необходимо доказать Убедимся в следующей цепочке формул: . Поэтому для заданного возьмем . Тогда из неравенства последует . Ч.т.д.
Не строгое, но достаточно наглядное доказательство формулы следует из таблицы
| 0,1 | 0.001 | 0.00001 | ||
Пример 3.2. Рассмотрим графики трех функций :
Рис. 3.1 Рис. 3.2 Рис. 3.3
Из этих рисунков можно догадаться в справедливости формул:
.
Замечание 3.1. Знак означает, что х стремится к 0, оставаясь все время больше нуля. Аналогично, означает, что х стремится к 2, оставаясь все время больше двух.
Замечание 3.2. означает, что В этом можно убедиться из рис. 3.2.
Замечание 3.3. Мы часто будем говорить, что 1/0 не существует в том смысле, что оно равняется бесконечности.
Пример 3.3. Для построения графиков необходимо привлекать современные компьютеры. В этом пособии приведены графики, построенные в Еxcel. Например, график (рис. 3.1) в Еxcel можно построить следующим образом:
1) в ячейку А1 вводим число -2;
2) в ячейке А2 программируем формулу =А1+0,1;
3) содержимое ячейки А2 растягиваем вплоть до ячейки А41; в ячейке А41 появиться число 2;
4) в ячейке В1 программируем =1/А1;
5) содержимое ячейки В1 растягиваем вплоть до ячейки В41;
6) ЛК(левой кнопкой мыши) выделяем содержимое ячеек А1:В20;
7) ЛК по Вставка;
8) ЛК по Точечная;
9) ЛК по выбранному типу графика;
10) ПК (правой кнопкой мыши) по графику;
11) ЛК по Выбрать данные;
12) ЛК по Добавить;
13) ЛК по полю Значения Х:;
14) ЛК выделяешь содержимое ячеек А2:А41;
15) ЛК по полю Значения У: и стираешь содержимое этого поля;
16) ЛК выделяешь содержимое ячеек В22:В41;
17) ЛК по ОК;
18) ЛК по ОК.
Пример 3.4. Чтобы график из Еxcel перенести а Уорд, нужно:
1) ЛК по графику;
2) ЛК по знаку меню Копировать;
3) ПК в том месте листа Уорда, где предполагаете вставить график;
4) ЛК по Вставить.
studopedya.ru
7. Предел функции при стремлении аргумента к бесконечности.
Пусть
функция  определена на промежутке
определена на промежутке .
Число А называется пределом функции
.
Число А называется пределом функции при,
если для любого положительного
при,
если для любого положительного существует такое число,
что для всех
существует такое число,
что для всех ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ,
выполнится неравенство.
,
выполнится неравенство.
8. Основные теоремы о пределах.
1) Предел суммы (разности) двух функций равен сумме (разности) их пределов.
Пусть  ,
,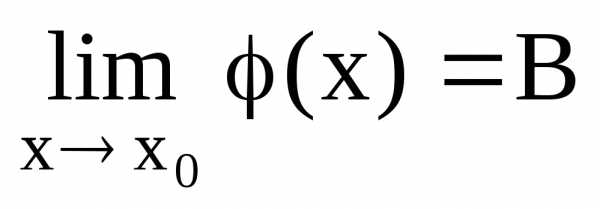 Тогда
по теореме о связи функции, ее предела
и б.м.ф. можно записатьи.
Следовательно,.
Здесь- б.м.ф., как сума б.м.ф. По теореме о связи
функции, ее предела и б.м.ф. можно записать,
т.е.
Тогда
по теореме о связи функции, ее предела
и б.м.ф. можно записатьи.
Следовательно,.
Здесь- б.м.ф., как сума б.м.ф. По теореме о связи
функции, ее предела и б.м.ф. можно записать,
т.е.
2) Функция имеет только
один предел при 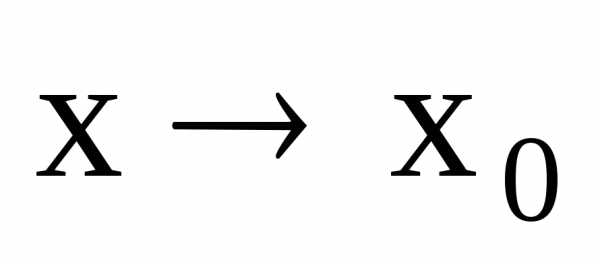
Пусть 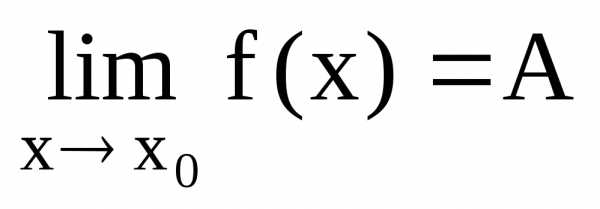 ,
, Тогда
по предыдущей теореме,
отсюда А = В.
Тогда
по предыдущей теореме,
отсюда А = В.
3) Предел произведения (частного) функций равен произведению (частному) их пределов.
Доказательство аналогичного 1.
4) Постоянный множитель можно выносить из под знака предела.
5) Предел степени с натуральным показателем равен той же степени предела.
9. Бесконечно малые функции.
Функция 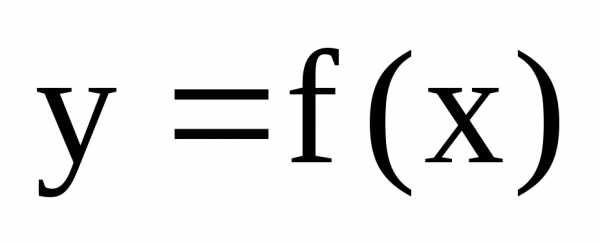 называетсябесконечно
малой при
называетсябесконечно
малой при 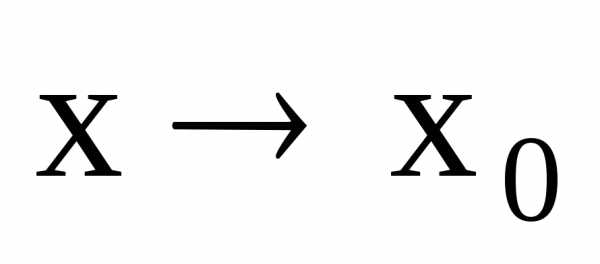 ,
если
,
если .
.
Б.м.ф.
часто называют бесконечно малыми
величинами или бесконечно малыми;
обозначают обычно греческими буквами 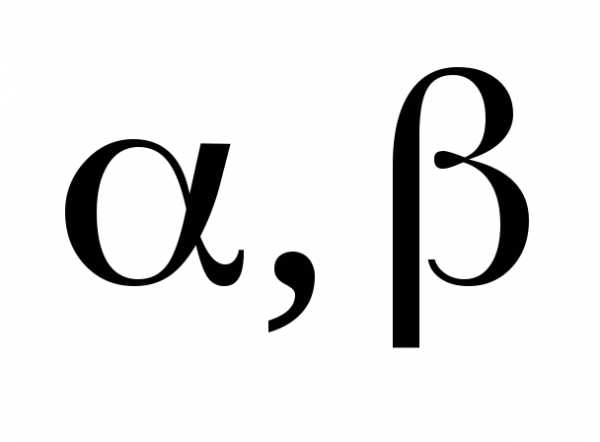 и т.п.
и т.п.
Алгебраическая сумма б.м.ф. есть б.м.ф.
Произведение ограниченной функции на б.м.ф. есть б.м.ф.
10. Свойства бесконечно малых функций.
Функция 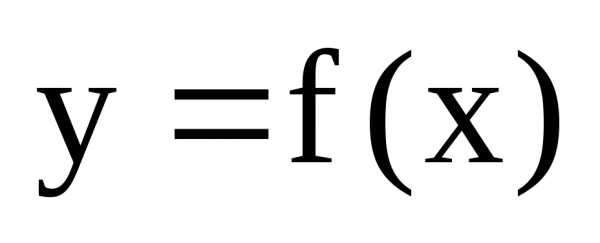 называетсябесконечно
малой при
называетсябесконечно
малой при  ,
если
,
если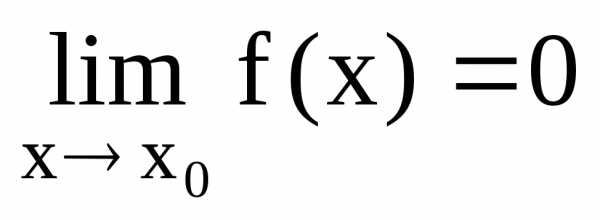 .
.
Алгебраическая сумма б.м.ф. есть б.м.ф.
Пусть  и
и – две б.м.ф. при
– две б.м.ф. при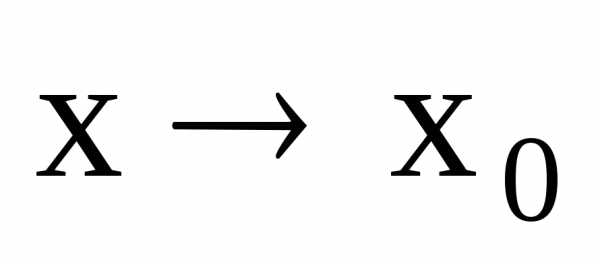 .
Это значит, что
.
Это значит, что ,
т.е. для любого
,
т.е. для любого ,
а значит, и
,
а значит, и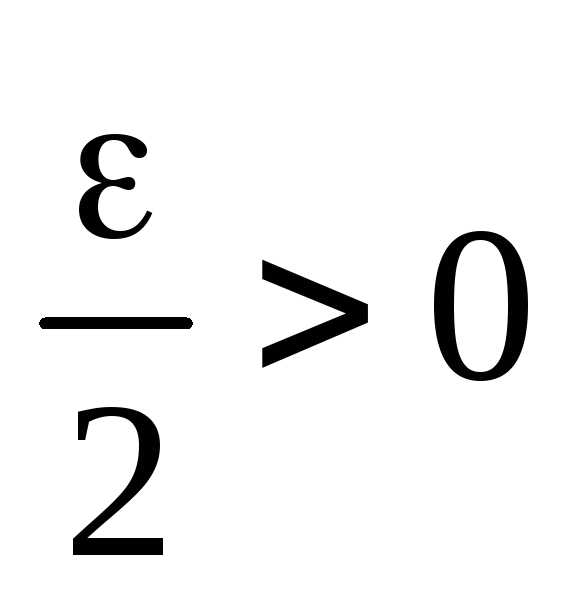 найдется число
найдется число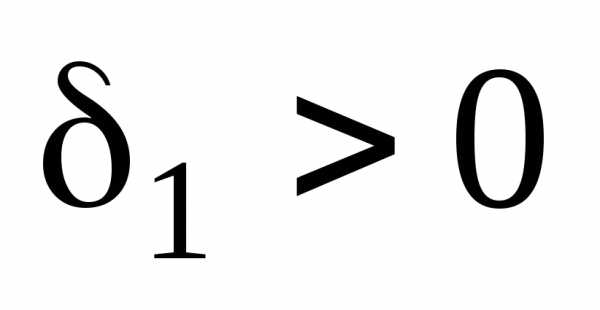 ,
такое, что для всех х, удовлетворяющих
неравенству,
выполняется неравенство
,
такое, что для всех х, удовлетворяющих
неравенству,
выполняется неравенство .
Тоже самое проделаем для
.
Тоже самое проделаем для (,
(,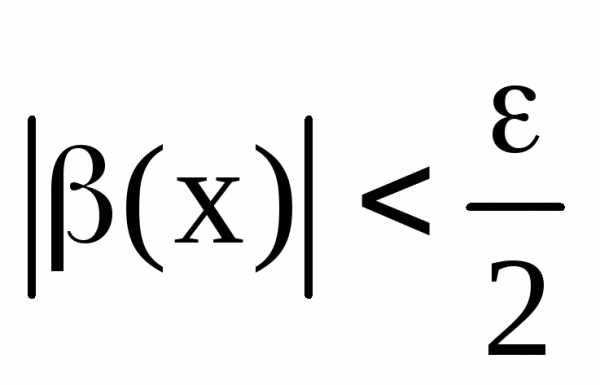 )
)
Пусть  – наименьшее из чисел
– наименьшее из чисел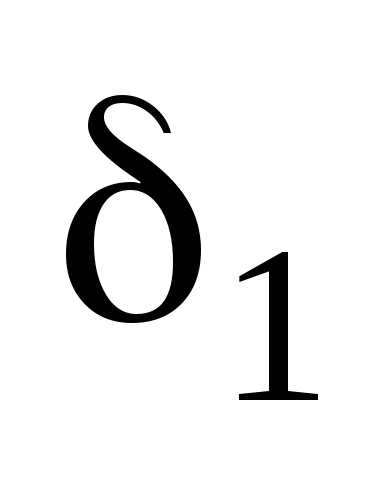 и
и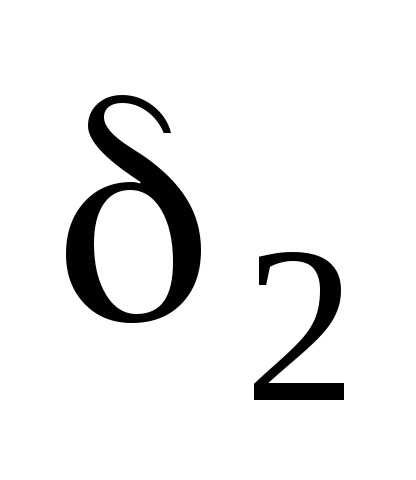 .
Тогда для всех х, удовлетворяющих
неравенству,
выполняются неравенства
.
Тогда для всех х, удовлетворяющих
неравенству,
выполняются неравенства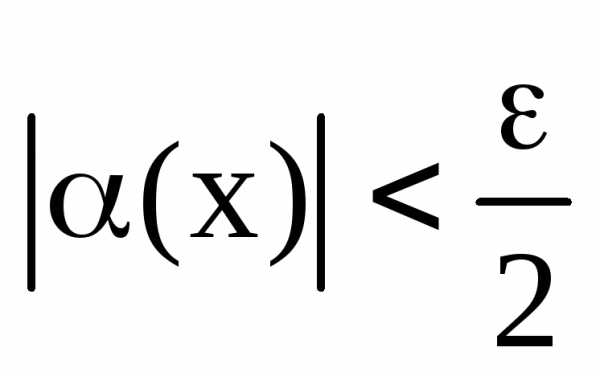 и
и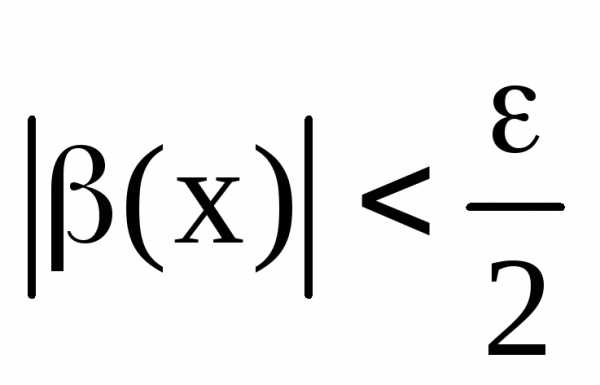 ,
следовательно имеет место соотношение,
таким образом,
т.е.- б.м.ф. при
,
следовательно имеет место соотношение,
таким образом,
т.е.- б.м.ф. при
Произведение ограниченной функции на б.м.ф. есть б.м.ф.
Пусть
функция  ограничена при
ограничена при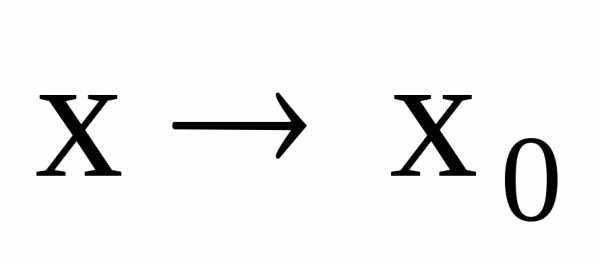 .
Тогда существует такое число
.
Тогда существует такое число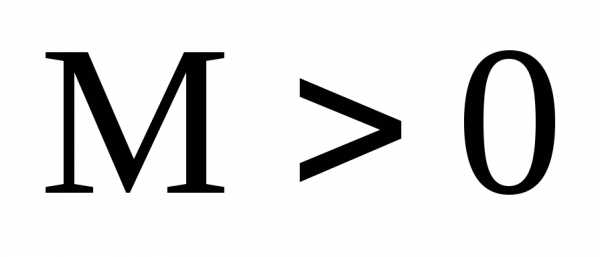 ,
что
,
что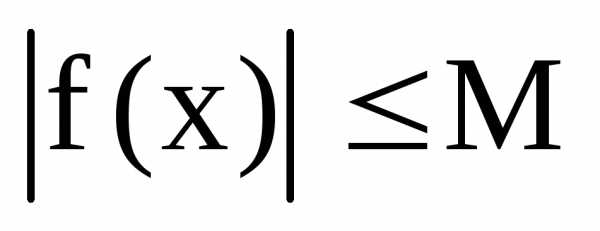 для всех х
для всех х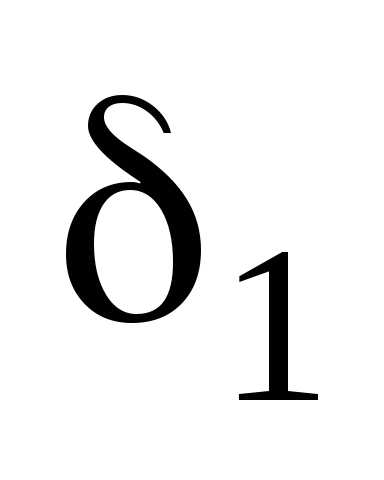 -окрестности
точки
-окрестности
точки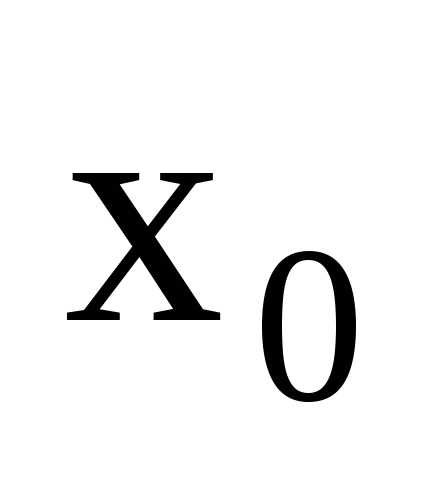 .
И пусть
.
И пусть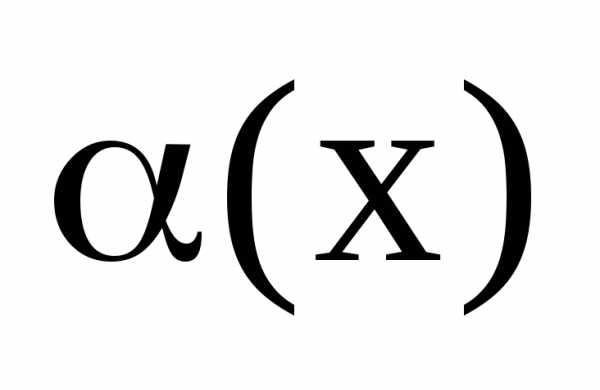 – б.м.ф. при
– б.м.ф. при .
Тогда для любого
.
Тогда для любого ,
а значит и
,
а значит и ,
найдется такое число
,
найдется такое число ,
что при всех х, удовлетворяющих неравенству,
выполняется неравенство
,
что при всех х, удовлетворяющих неравенству,
выполняется неравенство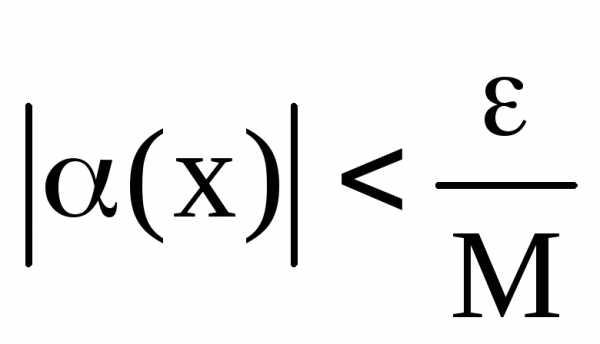
Пусть  – наименьшее из чисел
– наименьшее из чисел и
и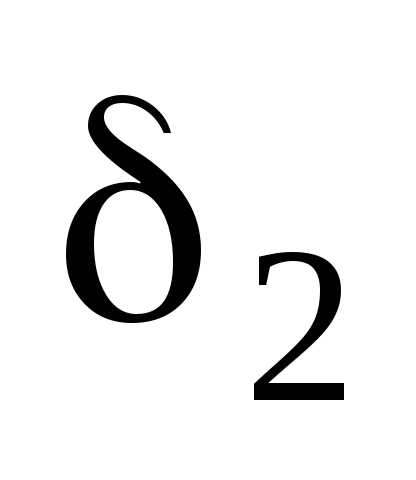 .
Тогда для всех х, удовлетворяющих
неравенству,
выполняются неравенства
.
Тогда для всех х, удовлетворяющих
неравенству,
выполняются неравенства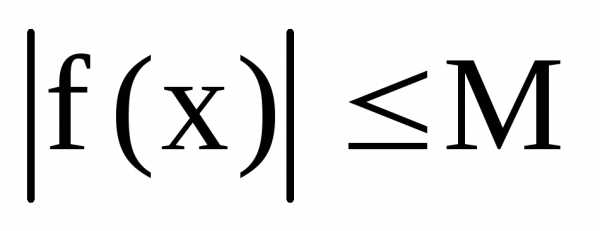 и
и ,
следовательно,.
А это означает, что- б.м.ф. при
,
следовательно,.
А это означает, что- б.м.ф. при
11. Бесконечно большие функции и их связь с бесконечно малыми.
Функция  называетсябесконечно
большой при
называетсябесконечно
большой при 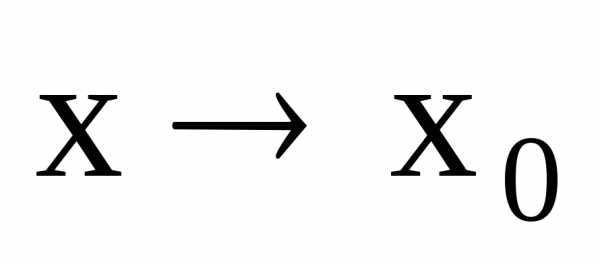 ,
если для любого числа
,
если для любого числа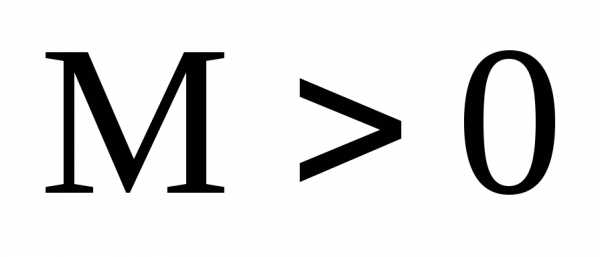 ,
существует число,
такое, что для всех х, удовлетворяющих
неравенству,
выполняется неравенство
,
существует число,
такое, что для всех х, удовлетворяющих
неравенству,
выполняется неравенство .
.
Если
функция 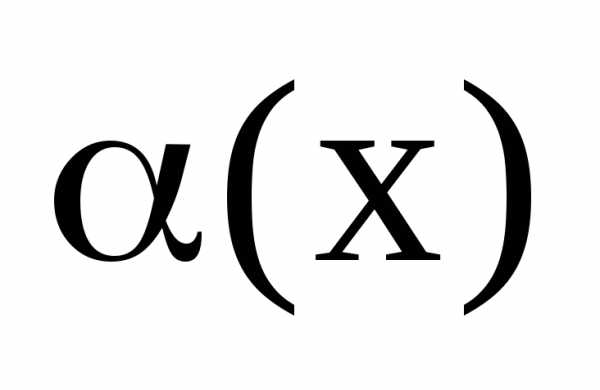 – бесконечно малая (
– бесконечно малая (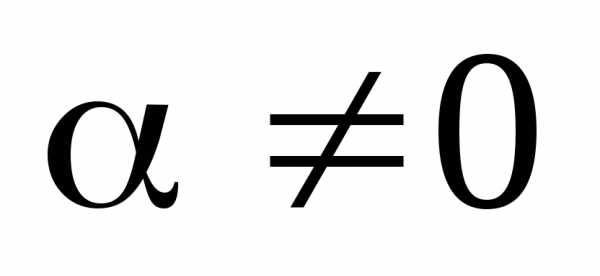 ),
то функция
),
то функция есть бесконечно большая функция (и
наоборот).
есть бесконечно большая функция (и
наоборот).
12. Сравнение бесконечно малых функций.
Две
б.м.ф сравниваются между собой с помощью
их отношения. Пусть  и
и есть б.м.ф. при
есть б.м.ф. при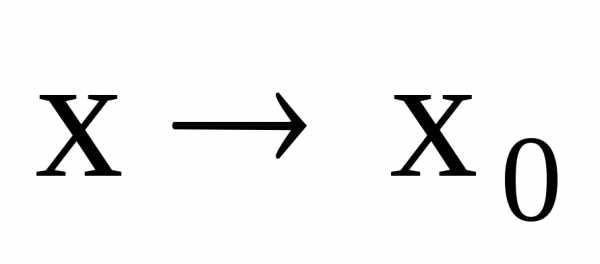 ,
т.е.
,
т.е. и
и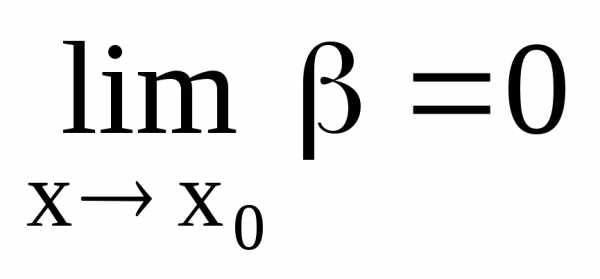 .
.
1)
Если 
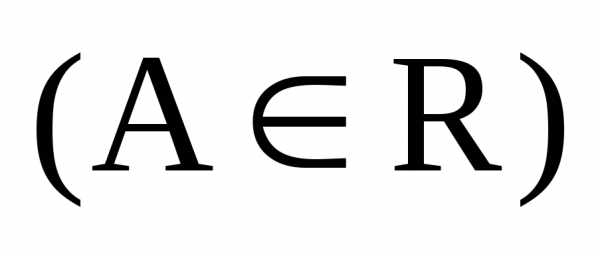 ,
то
,
то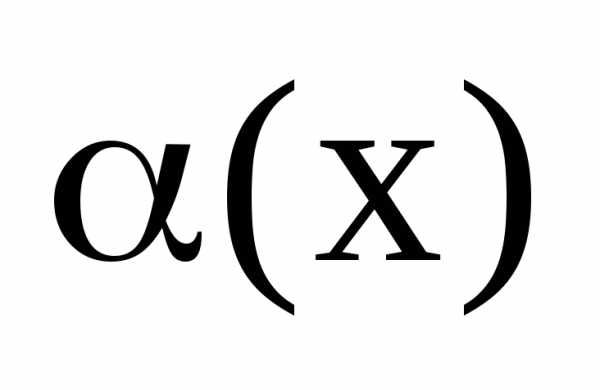 и
и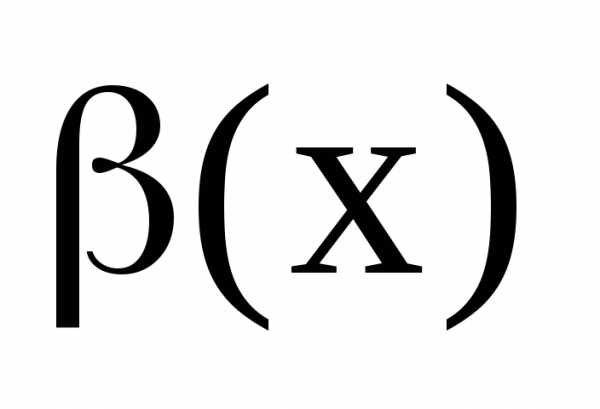 называютсябесконечно
малыми одного порядка.
называютсябесконечно
малыми одного порядка.
2)
Если 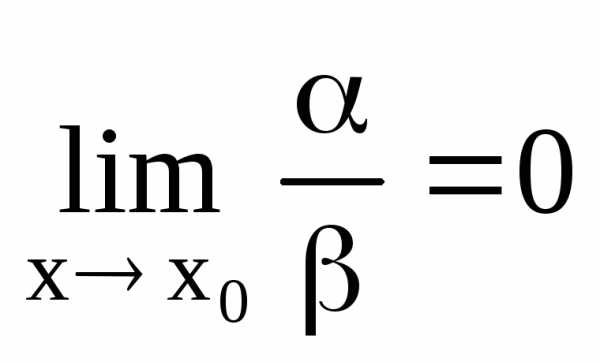 ,
то
,
то называетсябесконечно
малой более высокого порядка,
чем
называетсябесконечно
малой более высокого порядка,
чем  .
.
3)
Если 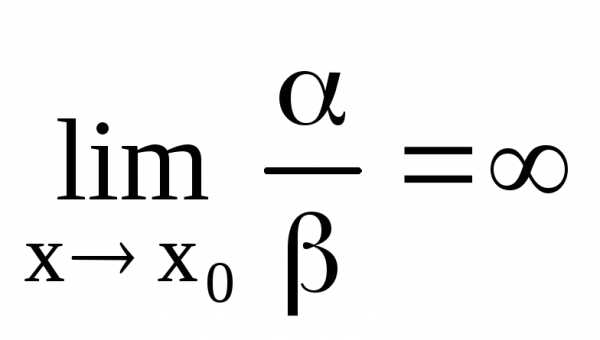 ,
то
,
то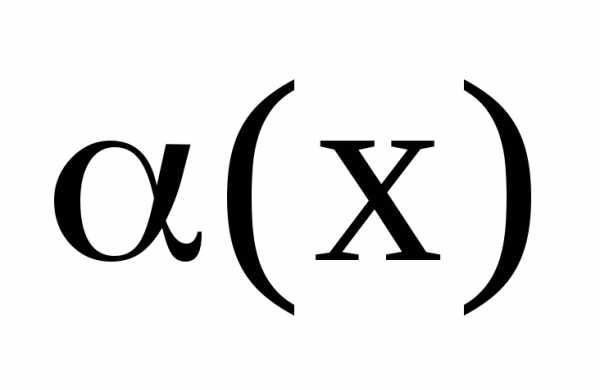 называетсябесконечно
малой более низкого порядка,
чем
называетсябесконечно
малой более низкого порядка,
чем 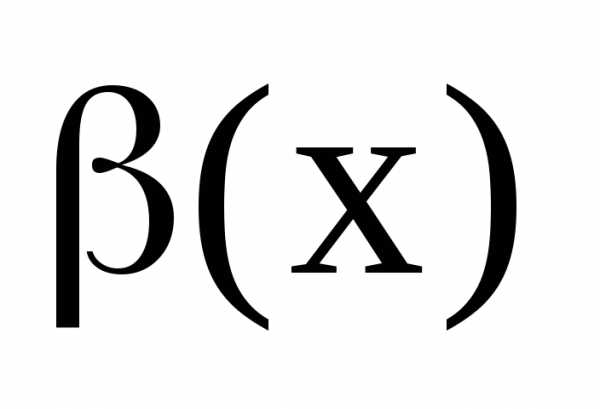 .
.
4)
Если 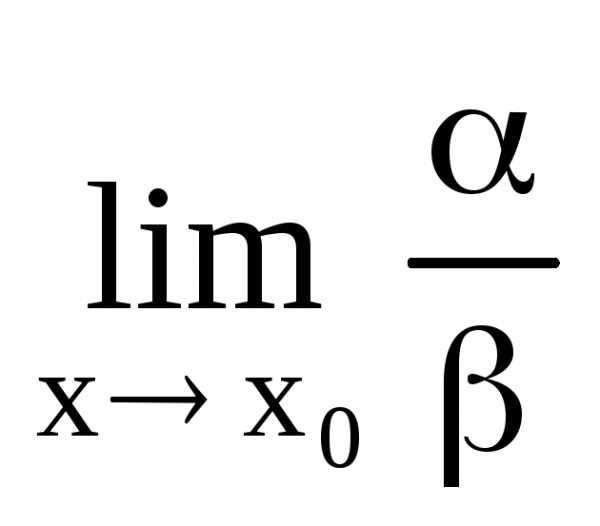 не существует, то
не существует, то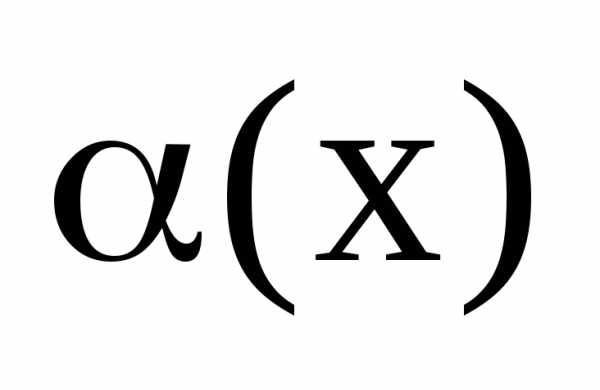 и
и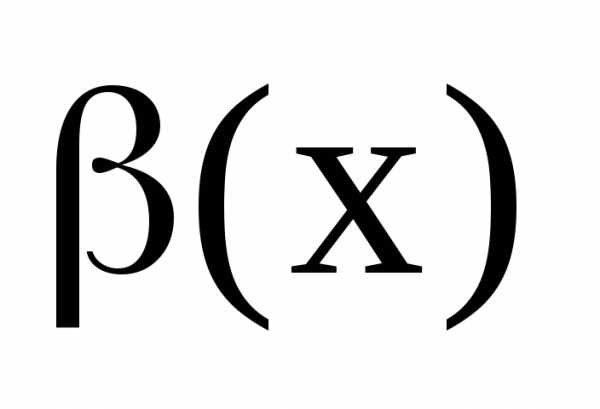 называютсянесравнимыми
бесконечно малыми.
называютсянесравнимыми
бесконечно малыми.
Такие же сравнения и для случаев, когда ,
13. Свойства эквивалентных бесконечно малых.
1) Предел отношения двух б.м.ф. не изменится, если каждую из них заменить эквивалентной бесконечно малой.
Пусть 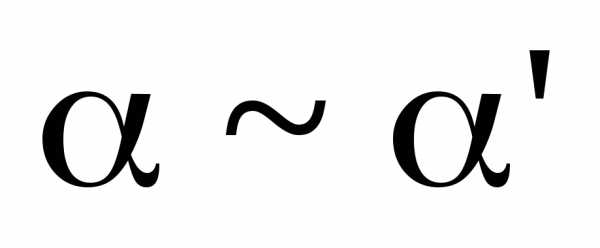 и
и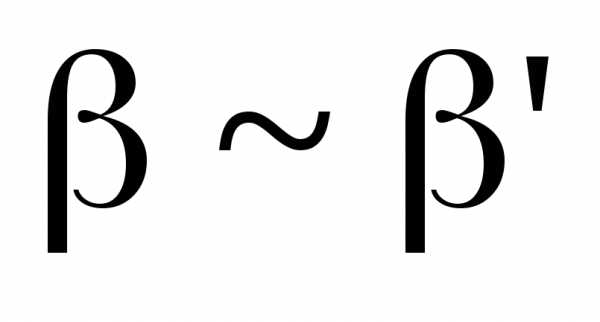 при
при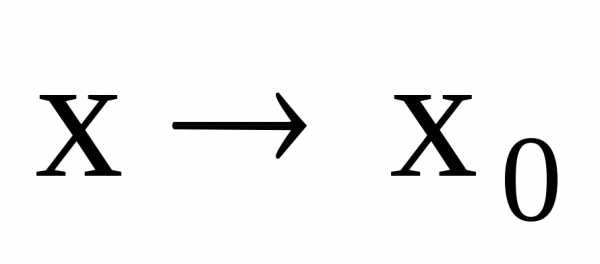 ,
тогда
,
тогда
2) Разность б.м.ф. есть б.м.ф. более высокого порядка, чем каждая из них.
Пусть  при
при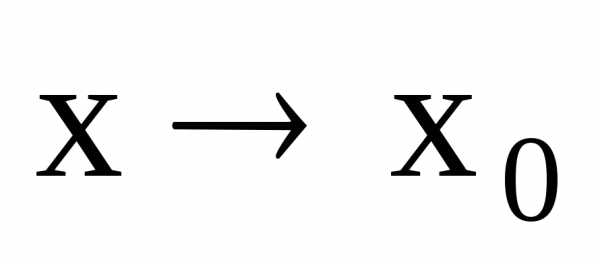 ,
тогда,
аналогично
,
тогда,
аналогично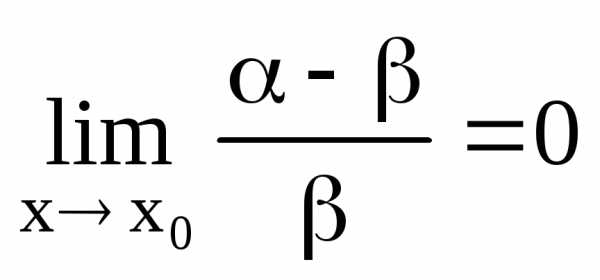
3) Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.
Пусть  и
и есть б.м.ф. при
есть б.м.ф. при ,
причём
,
причём – б.м.ф. высшего порядка, чем
– б.м.ф. высшего порядка, чем ,
т.е.
,
т.е.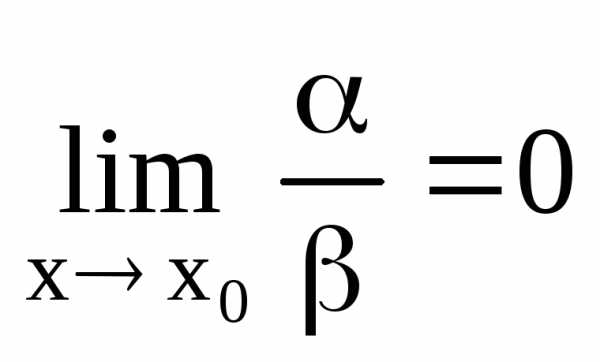 .
.
Тогда
,
следовательно,при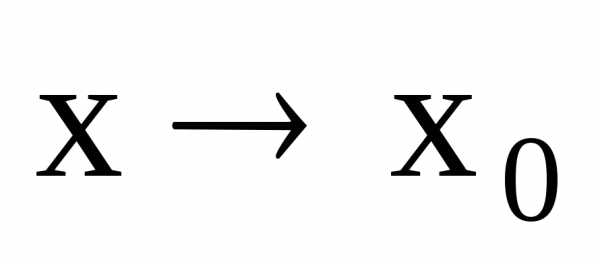 .
.
14. Первый замечательный предел.
 – первый
замечательный предел
– первый
замечательный предел
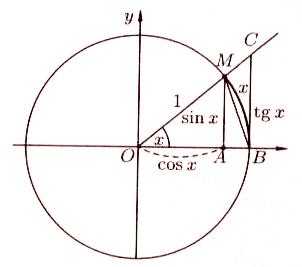
Возьмем
круг радиуса 1, обозначим радиальную
меру угла MOB
через х. Пусть 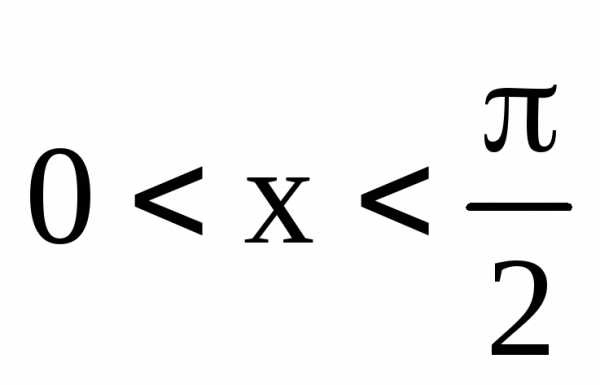 .
На рисунке,
дугаMB
численно равна центральному углу х,
.
На рисунке,
дугаMB
численно равна центральному углу х, 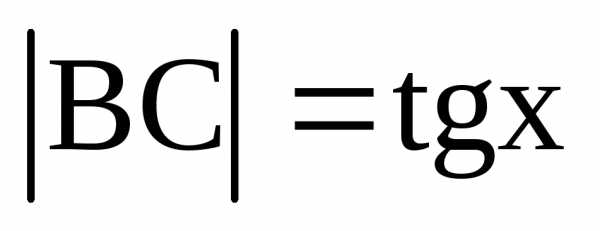 .
Очевидно имеем.На
основании соответствующих формул
геометрии получаем,
разделим неравенство на
.
Очевидно имеем.На
основании соответствующих формул
геометрии получаем,
разделим неравенство на ,
получим
,
получим или
или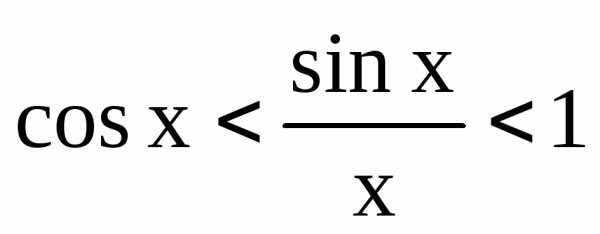 .
Так как
.
Так как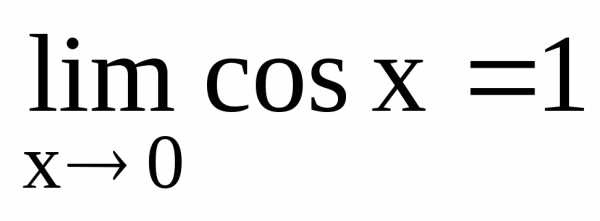 и
и ,
то по признаку о пределе промежуточной
функции
,
то по признаку о пределе промежуточной
функции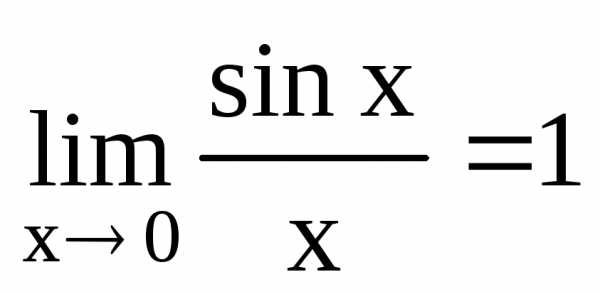
15. Второй замечательный предел.
 – второй
замечательный предел
– второй
замечательный предел
Мы
знаем, что числовая последовательность  имеет предел, равный е.
имеет предел, равный е.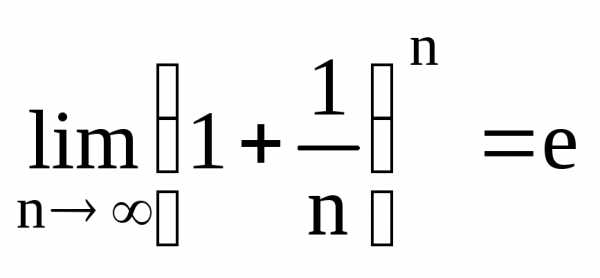
1.
Пусть
.
Каждое значение х заключено между двумя
целыми числами:,гдеn
= {x}
– целая часть х. Отсюда следует 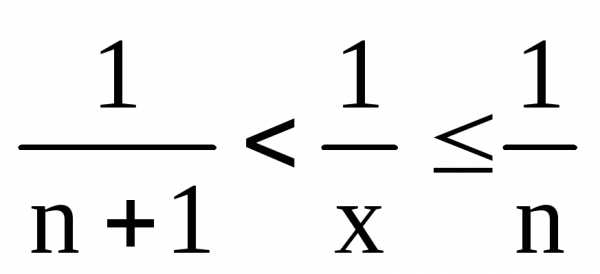 ,.
Поэтому
,.
Поэтому
Если , то, поэтому
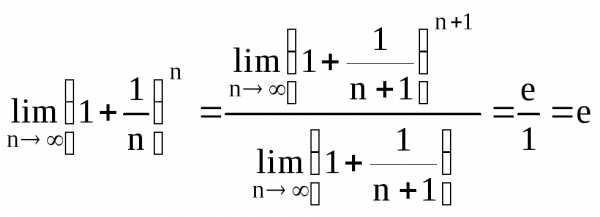 ,
,
По
признаку о пределе промежуточной
функции: 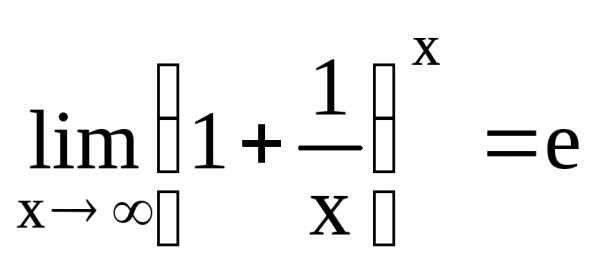
2.
Пусть
.
Сделаем подстановку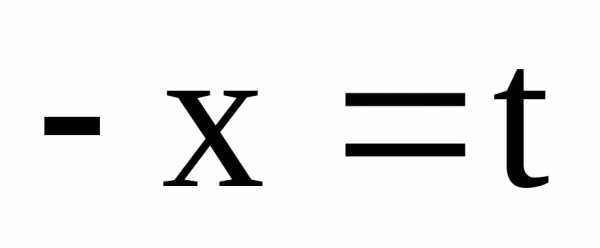 ,
тогда,
следовательно
,
тогда,
следовательно
16. Непрерывность функции в точке.
Пусть
функция
определена в точке и некоторой окрестности этой точки.
Функция
и некоторой окрестности этой точки.
Функция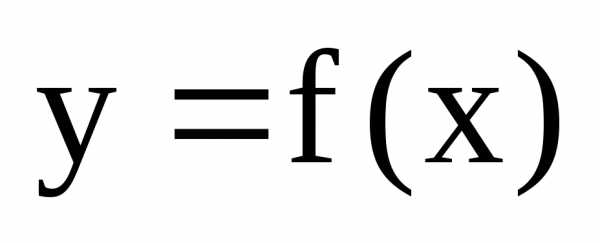 называетсянепрерывной
в точке
называетсянепрерывной
в точке  ,
если существует предел функции в этой
точке и он равен значению функции в
этой точке
,
если существует предел функции в этой
точке и он равен значению функции в
этой точке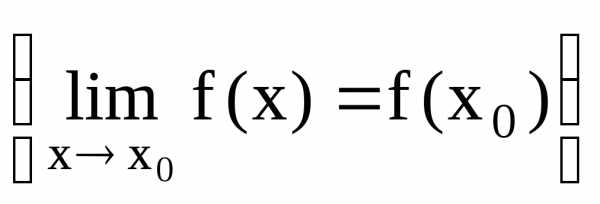
Функция непрерывна, если выполняются 3 условия:
функция
 определена в точке
определена в точке и в ее окрестности
и в ее окрестностифункция
 имеет предел при
имеет предел при
предел функции в точке
 равен значению функции в этой точке
равен значению функции в этой точке
Это
значит, что при нахождении предела
некоторой функции f(x)
можно перейти к пределу под знаком
функции, т.е. в функцию f(x)
вместо аргумента х подставить его
предельное значение 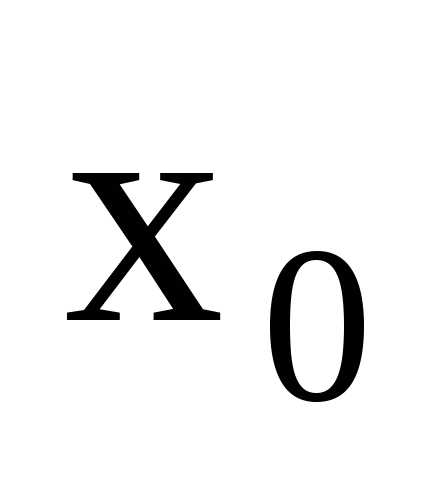 .
.
Пример.  .
.
studfiles.net

 определена в точке
определена в точке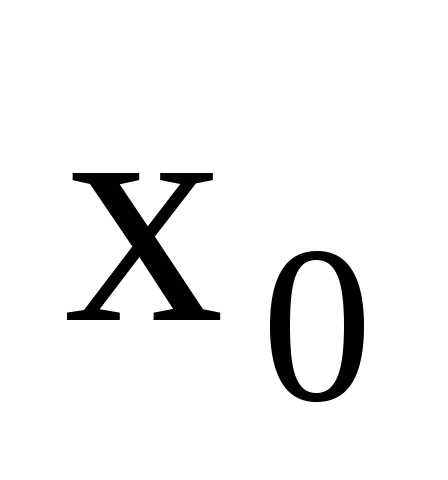 и в ее окрестности
и в ее окрестности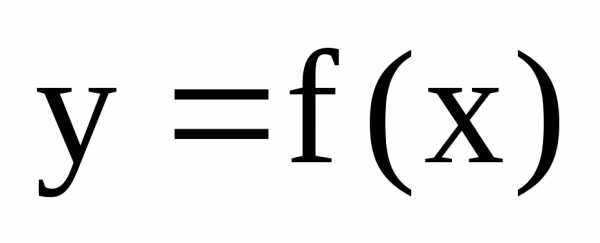 имеет предел при
имеет предел при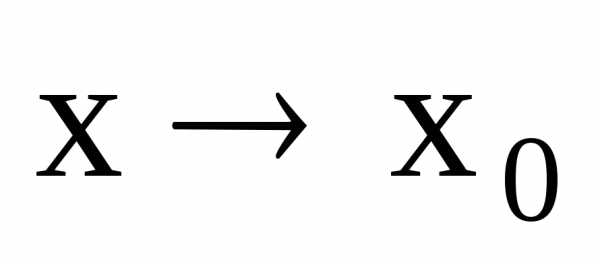
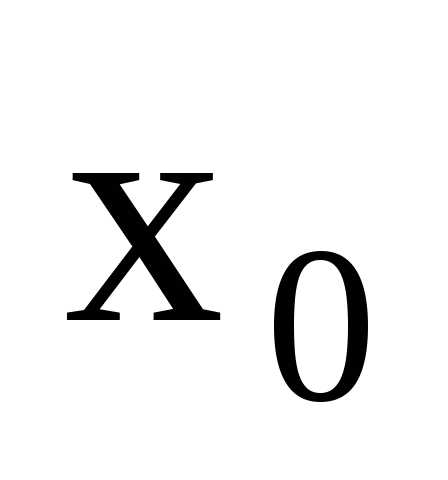 равен значению функции в этой точке
равен значению функции в этой точке