Таблица три закона ньютона – “3 ЗАКОНА НЬЮТОНА. Ньютон – величайший ученый не только своего времени, но и истории. Он изучал природу света, построил зеркальный телескоп, но самая главная.”. Скачать бесплатно и без регистрации.

3 закона Ньютона

3 закона ньютона

3 Закона ньютона

• Ньютон – величайший ученый не только своего времени, но и истории. Он изучал природу света, построил зеркальный телескоп, но самая главная заслуга Ньютона в том, что он вывел три закона механики, которые управляют движением тел во Вселенной.

• Итак, сегодня наш урок посвящен “Законам Ньютона”.

• Давайте вспомним, о чем говорят эти законы.

Первый Закон ньютона

Первый Закон ньютона

• Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными.

• Инерциальными системами отсчета называются такие системы, в которых свободные (т.е. не участвующие во взаимодействиях с другими телами) тела движутся без ускорения (т.е. равномерно и прямолинейно) или покоятся (состояние покоя, вообще говоря, следует рассматривать как частный случай равномерного движения с нулевой скоростью).

• Системы отсчета, в которых первый закон Ньютона не выполняется, называют неинерциальными .

Первый Закон ньютона

• Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы или векторная сумма всех действующих сил (то есть равнодействующая) равна нулю.

• Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью.

• Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.

Первый Закон ньютона

• Современная формулировка

• В современной физике первый закон Ньютона принято формулировать в следующем виде:
• Существуют такие системы отсчёта, называемые инерциальными, относительно которых свободная материальная точка сохраняет величину и направление своей скорости неограниченно долго.

Второй закон Ньютона

Второй закон Ньютона

• Современная формулировка
• В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
• Второй закон Ньютона утверждает, что ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела
• При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
• a⃗ =F⃗ m,
• где a⃗ — ускорение материальной точки;
• F⃗ — сила, приложенная к материальной точке;
• m — масса материальной точки.
• Или в более известном виде:
• F⃗ =ma⃗ .

Второй закон Ньютона

• В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
• В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.
• dp⃗/dt=F⃗ ,
• где p⃗ — импульс точки,
• p⃗ =mv⃗ ,
• где v⃗ — скорость точки;
• t — время;

Третий закон Ньютона

Третий закон Ньютона

Третий закон Ньютона

• Этот закон объясняет, что происходит с двумя взаимодействующими телами.

• Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F⃗ 1→2, а второе — на первое с силой F⃗ 2→1. Как соотносятся силы?

• Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются

Третий закон Ньютона

• Современная формулировка
• Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
• F⃗ 2→1=−F⃗ 1→2.

Особенности законов Ньютона.

1-й закон Ньютона

2-й закон Ньютона

• Справедлив для любых сил;
• Силы уравновешиваются, т.к. приложены к одному телу;
• Если результирующая равна 0, то ускорение тоже равно 0

3-й закон Ньютона

• Верен для любых сил;
• Сила – причина изменения скорости;
• Вектор ускорения сонаправлен с вектором силы;

• Силы возникают только парами и всегда при взаимодействии;
• Силы не уравновешивают друг друга;
• Силы одной природы;
• Верен для всех сил в природе.

Составление обобщающей таблицы

 

Первый закон Ньютона

Физическая система

Макроскопическое тело

Второй закон Ньютона

Модель

Третий закон Ньютона

Макроскопическое тело

Материальная точка

Описываемое явление

Состояние покоя или равномерного прямолинейного движения

Система двух тел

Материальная точка

Суть закона

Примеры проявления

Существование инерциальной СО

Система двух материальных точек

Движение с ускорением

Взаимодействие тел

Движение космического корабля вдали от поверхности Земли.

Взаимодействие определяет изменение скорости, т.е. ускорение

Силы действия и противодействия равны по модулю и противоположны по направлению.

Движение планет, падение тел; разгон и торможение автомобиля.

Взаимодействие тел: Солнца и планет; автомобиля по поверхности земли

Исторический очерк

• Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде.

1.Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

2.Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.

3.Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Подумай и ответь!

Назовите тела, действие которых компенсируется в следующих случаях:

Аэростат равномерно и прямолинейно поднимается вверх.

Аэростат удерживается у поверхности Земли канатами.

Парашютист спускается, двигаясь равномерно и прямолинейно.

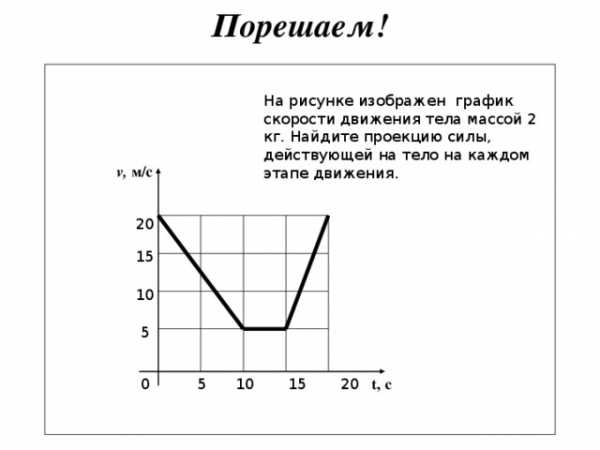
Порешаем!

На рисунке изображен график скорости движения тела массой 2 кг. Найдите проекцию силы, действующей на тело на каждом этапе движения.

v, м/с

20

15

10

5

0

t, с

5 10 15 20

Подумай и ответь!

Изменится ли положение космонавта при свободном полете космического корабля, если: а) он выпустит без толчка из рук массивный предмет? б) он бросит его?

Подумай и ответь!

В каких случаях речь идет о движении тела по инерции?

а) Книга лежит на поверхности стола.

б) Катер после выключения двигателя продолжает двигаться по поверхности воды.

videouroki.net

Законы Ньютона – FIZI4KA

1. В основе классической механики лежат три закона Ньютона, которые были сформулированы им при обобщении результатов наблюдений и опытов в конце XVII в.

Первый закон, включённый Ньютоном в систему законов, был открыт Галилеем и назван им законом инерции. Закон инерции формулируется следующим образом: если на тело не действуют другие тела, то оно либо находится в покое, либо движется равномерно прямолинейно.

2. В природе не существует отдельных изолированных тел. Любое тело взаимодействует с окружающими телами. Несмотря на это, взаимодействующие тела могут находиться в покое или двигаться равномерно и прямолинейно.

Например, лежащая на столе книга взаимодействует с Землёй, и на неё действует сила тяжести ​\( (\vec{F}_т) \)​, направленная вниз (рис. 33). Книга также взаимодействует со столом, и со стороны стола на неё действует сила, направленная вертикально вверх \( (\vec{F}) \). При этом книга находится в покое, следовательно, \( |\vec{F}_т|=|\vec{F}| \), т.е. действия Земли и стола на книгу компенсируют друг друга.

3. При компенсации действия на тело других тел оно может двигаться равномерно прямолинейно.

Например, если по прямой горизонтальной дороге движется автомобиль, то при компенсации действия на него силы тяги двигателя и силы трения со стороны поверхности дороги движение автомобиля будет равномерным.

Можно утверждать, что тело сохраняет состояние покоя, если действие на него других тел скомпенсировано.

Явление сохранения скорости тела постоянной (в том числе и равной нулю) называют явлением инерции.

4. Тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела или действие других тел скомпенсировано не во всех системах отсчёта, а только в инерциальных системах отсчёта.

Инерциальными системами отсчёта называются такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия других тел компенсируются. Инерциальной можно считать систему отсчёта, связанную с Землёй. Системы отсчёта, движущиеся относительно Земли равномерно и прямолинейно, также являются инерциальными.

Системы отсчёта, движущиеся с ускорением относительно инерциальной системы отсчёта, например относительно Земли, называют неинерциальными.

5. Значение первого закона Ньютона состоит в том, что он устанавливает существование инерциальных систем отсчёта (таких систем отсчёта, относительно которых тела движутся с постоянной скоростью при компенсации внешних воздействий). Именно для таких систем отсчёта справедливы все другие законы Ньютона.

6. Второй закон Ньютона устанавливает зависимость ускорения одного из взаимодействующих тел от его массы и действующей на него силы. Наблюдения и опыты свидетельствуют о том, что чем больше сила, действующая на тело, тем больше ускорение, которое оно приобретает. Так, чем сильнее водитель нажимает на педаль тормоза, тем
больше сила и тем быстрее автомобиль остановится. Значит, чем больше действующая на автомобиль сила сопротивления, тем больше его ускорение.

Ускорение, которое приобретают тела под действием одинаковой силы, зависит от массы тел. Например, грузовому автомобилю требуется большее время, чем легковому, для того, чтобы, имея некоторую одинаковую скорость, остановиться, выключив двигатель. Из этого примера следует, что чем больше масса тела, тем меньшее ускорение оно получает под действием некоторой постоянной силы.

7. Второй закон Ньютона формулируется следующим образом: ускорение, с которым движется тело прямо пропорционально действующей на тело силе и обратно пропорционально массе тела.

\[ \vec{a}=\frac{\vec{F}}{m} \]

Записанное равенство представляет собой второй закон Ньютона.

В механике Ньютона ускорение тел обусловлено только их взаимодействием. Следовательно, второй закон Ньютона справедлив в инерциальных системах отсчёта.

8. Действие тел друг на друга носит взаимный характер, т.е. в результате взаимодействия
каждое тело приобретает ускорение, и, следовательно, на каждое из взаимодействующих тел действует сила. Например, груз, висящий на нити, действует на нить с силой, направленной вертикально вниз \( (\vec{F}_1) \)​, и растягивает её (рис. 34). В свою очередь, нить действует на груз с силой, направленной вертикально вверх \( (\vec{F}_2) \)​.

9. Измерения показывают, что:

• при взаимодействии тел сила действует как на одно тело, так и на другое;
• модуль силы, действующей на одно тело, равен модулю силы, действующей на другое тело;
• силы, действующие на тела, направлены в противоположные стороны.

10. Из соотношения следует: ​\( m_1a_1=m_2a_2 \)​.

Поскольку ускорение — величина векторная и ускорения, которые получают тела, направлены в противоположные стороны, то ​\( m_1\vec{a}_1=-m_2\vec{a}_2 \)​.

Так как \( m_1\vec{a}_1=\vec{F}_1 \), а \( m_2\vec{a}_2=\vec{F}_2 \), то можно записать: ​\( \vec{F}_1=-\vec{F}_2 \)​.

Это равенство и выражает третий закон Ньютона.

Третий закон Ньютона формулируется следующим образом: тела действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны. Эти силы направлены вдоль прямой, соединяющей взаимодействующие тела (материальные точки).

Третий закон Ньютона говорит о том, что силы всегда проявляются парами.

Эти силы часто называют силами действия и противодействия. При этом безразлично, какую из двух сил назвать силой действия, а какую — силой противодействия.

Эти силы приложены к разным телам, и их нельзя складывать, т.е. нельзя сказать, что силы действия и противодействия уравновешивают друг друга.

Силы, с которыми взаимодействуют тела, всегда одной природы.

Третий закон Ньютона, так же как первый и второй законы, справедлив в инерциальных системах отсчёта.

10. При переходе от одной инерциальной системы отсчёта к другой не изменяются ни ускорение, ни масса тала, ни действующая на него сила. Следовательно, можно утверждать, что законы механики одинаковы для всех инерциальных систем отсчёта, или, что то же самое, все механические явления протекают одинаково во всех инерциальных системах отсчёта при одинаковых начальных условиях. Это утверждение называется принципом относительности Галилея.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Утверждение, что материальная точка покоится или движется равномерно прямолинейно, если на неё не действуют другие тела или действие на неё других тел взаимно уравновешено,

1) неверно ни для каких систем отсчёта
2) верно для инерциальных систем отсчёта
3) верно для неинерциальных систем отсчёта
4) верно при любых условиях

2. Система отсчёта, связанная с Землёй, может считаться инерциальной. Система отсчёта, связанная с автобусом, тоже будет инерциальной, если он

1) движется равномерно по извилистой дороге
2) тормозит у остановки
3) отъезжает от светофора
4) движется равномерно по прямолинейному участку пути

3. В каком из приведённых примеров тело движется по инерции:

1) равномерно движущийся по горизонтальной дороге автомобиль
2) автомобиль, движущийся по горизонтальной дороге с выключенным двигателем
3) автомобиль, поворачивающий направо
4) автомобиль, выезжающий со стоянки

4. Яблоко, лежащее неподвижно на столе вагона движущегося поезда покатился вправо, если смотреть по ходу поезда. Как изменилось движение поезда?

1) скорость поезда увеличилась
2) скорость поезда уменьшилась
3) поезд повернул влево
4) поезд повернул вправо

5. Можно ли считать инерциальной системой отсчёта движущийся автомобиль?

1) можно всегда
2) можно, только если он движется равномерно и прямолинейно
3) можно только во время разгона и торможения
4) нельзя ни при каких условиях

6. Массивный груз подвешен на тонкой нити 1. К грузу прикреплена такая же нить 2. Если
медленно тянуть за нить 2, то оборвётся

1) только нить 1
2) только нить 2
3) нить 1 и нить 2 одновременно
4) либо нить 1, либо нить 2, в зависимости от массы груза

7. Нить, привязанная одним концом к вбитому в стену гвоздю, разорвётся, если другой её конец тянуть с силой не менее 50 Н. Чему равно наименьшее значение сил, с которыми растягивают эту же нить за оба конца, при котором она рвётся?

1) 25 Н
2) 50 Н
3) 75 Н
4) 100 Н

8. Два ученика тянут динамометр в противоположные стороны с силой 60 Н каждый. Каково показание динамометра?

1) 0 Н
2) 30 Н
3) 60 Н
4) 120 Н

9. Земля притягивает яблоко с силой ​\( \vec{F}_1 \)​. Яблоко притягивает Землю с силой \( \vec{F}_2 \). При этом

1) ​\( F_2 = 0 \)​
2) ​\( F_1=F_2 \)​
3) \( F_1>F_2 \)
4) \( F_1<F_2 \)

10. Чему равна масса автомобиля, трогающегося с места с ускорением 0,6 м/с², если развиваемая им сила тяги равна 15 000 Н? Сила сопротивления, действующая на автомобиль, равна 6000 Н.

1) 1,5 т
2) 7,5 т
3) 15 т
4) 75 т

11. Из приведенных утверждений выберите два правильных и запишите их номера в таблицу.

1) законы Ньютона справедливы во всех системах отсчета
2) первый закон Ньютона утверждает существование инерциальных систем отсчета
3) равнодействующая сил действия и противодействия равна нулю
4) силы действия и противодействия имеют одинаковую природу
5) второй закон Ньютона говорит о том, что масса тела прямо пропорциональна действующей на тело силе

12. Два тела движутся по оси ​\( Ox \)​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

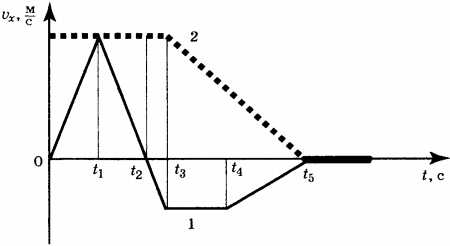
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​\( t_3-t_5 \)​ на тело 2 действует постоянная сила.
2) В промежутке времени ​\( 0-t_3 \)​ сила сообщает телу 1 положительное ускорение
3) В промежутке времени ​\( t_4-t_5 \)​ на тело 1 сила не действует
4) Модуль силы, действующей на тело 1 в промежутки времени ​\( 0-t_1 \)​, ​\( t_1-t_2 \)​ различен.
5) В промежутке времени ​\( t_1-t_2 \)​ сила сообщает телу 1 отрицательное ускорение

Часть 2

13. Тело массой 7 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 4 с груз был поднят на высоту 16 м?

Ответы

Законы Ньютона

5 (100%) 1 vote

fizi4ka.ru

Третий закон Ньютона, формула и примеры решений

Описание третьего закона Ньютона

Например, книга, лежащая на столе, действует на стол с силой, прямо пропорциональной своей массе и направленной вертикально вниз. Согласно третьему закону Ньютона стол в это же время действует на книгу с абсолютно такой же по величине силой, но направленной не вниз, а вверх.

Когда яблоко падает с дерева, это Земля действует на яблоко силой своего гравитационного притяжения (вследствие чего яблоко равноускоренно движется к поверхности Земли), но при этом и яблоко притягивает к себе Землю с такой же силой. А то, что нам кажется, что это именно яблоко падает на Землю, а не наоборот, является следствием второго закона Ньютона. Масса яблока по сравнению с массой Земли мала до несопоставимости, поэтому именно ускорение яблока заметно для глаз наблюдателя. Масса же Земли, по сравнению с массой яблока, огромна, поэтому ее ускорение практически незаметно.

Аналогично, если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не чувствуется. Однако если пнуть тяжелый железный мяч, ответное воздействие хорошо ощущается. Фактически, мы каждый день по многу раз «пинаем» очень и очень тяжелый мяч — нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе.

Таким образом, третий закон Ньютона утверждает, что силы как меры взаимодействия всегда возникают парами. Эти силы не уравновешиваются, так как всегда приложены к разным телам.

Третий закон Ньютона выполняется только в инерциальных системах отсчета и справедлив для сил любой природы.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Закона ньютона 3 Закона ньютона

3 закона ньютона 3 Закона ньютона Ньютон – величайший ученый не только своего времени, но и истории. Он изучал природу света, построил зеркальный телескоп, но самая главная заслуга Ньютона в том, что он вывел три закона механики, которые управляют движением тел во Вселенной. Итак, сегодня наш урок посвящен “Законам Ньютона”. Давайте вспомним, о чем говорят эти законы. Первый Закон ньютона Первый Закон ньютона Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Инерциальными системами отсчета называются такие системы, в которых свободные (т.е. не участвующие во взаимодействиях с другими телами) тела движутся без ускорения (т.е. равномерно и прямолинейно) или покоятся (состояние покоя, вообще говоря, следует рассматривать как частный случай равномерного движения с нулевой скоростью). Системы отсчета, в которых первый закон Ньютона не выполняется, называют неинерциальными. Первый Закон ньютона Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы или векторная сумма всех действующих сил (то есть равнодействующая) равна нулю. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела. Первый Закон ньютона Современная формулировка В современной физике первый закон Ньютона принято формулировать в следующем виде: Существуют такие системы отсчёта, называемые инерциальными, относительно которых свободная материальная точка сохраняет величину и направление своей скорости неограниченно долго. Второй закон Ньютона Второй закон Ньютона Современная формулировка В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. Второй закон Ньютона утверждает, что ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела При подходящем выборе единиц измерения, этот закон можно записать в виде формулы: a⃗ =F⃗ m, где a⃗ — ускорение материальной точки; F⃗ — сила, приложенная к материальной точке; m — масса материальной точки. Или в более известном виде: F⃗ =ma⃗ . Второй закон Ньютона В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс: В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. dp⃗/dt=F⃗ , где p⃗ — импульс точки, p⃗ =mv⃗ , где v⃗ — скорость точки; t — время; Третий закон Ньютона Третий закон Ньютона Третий закон Ньютона Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F⃗ 1→2, а второе — на первое с силой F⃗ 2→1. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются Третий закон Ньютона Современная формулировка Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F⃗ 2→1=−F⃗ 1→2. Особенности законов Ньютона. Составление обобщающей таблицы Исторический очерк Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде. 1.Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. 2.Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует. 3.Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

rpp.nashaucheba.ru

1.3. Законы Ньютона

1.3. Законы Ньютона

1.3. Законы Ньютона

 

Первый закон Ньютона (или закон инерции) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем.

Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению. Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инертностью. Поэтому первый закон Ньютона называют законом инерции. Масса тела – количественная мера инертности тела. В СИ масса тела измеряется в килограммах.

Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Системы отсчета, движущиеся относительно инерциальных с ускорением, называются неинерциальными. Сила – количественная мера взаимодействия тел. Сила – векторная величина. В СИ сила измеряется в ньютонах (Н). Если на тело действует несколько сил, то их векторная сумма называется равнодействующей этих сил.

Второй закон Ньютона. Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

Если два тела взаимодействуют друг с другом, то ускорения этих тел обратно пропорциональны их массам.

Рисунок 1.3.1. Взаимодействие двух тел.

Третий закон Ньютона. Силы, с которыми тела взаимодействуют друг с другом, равны по модулю и направлены вдоль одной прямой в противоположные стороны.

www.askskb.net

Законы Ньютона — WiKi

Первый закон Ньютона

Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как закон инерции. Инерция (она же инертность) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.

Современная формулировка

В современной физике первый закон Ньютона принято формулировать в следующем виде^[3]:

Историческая формулировка

Ньютон сформулировал первый закон механики так:

Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).

Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами^[4][5][6][7].

Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},} 

где a→{\displaystyle {\vec {a}}}  — ускорение материальной точки;
F→{\displaystyle {\vec {F}}}  — равнодействующая всех сил, приложенных к материальной точке;
m{\displaystyle m}  — масса материальной точки.

Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},}

где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}  — импульс точки, v→{\displaystyle {\vec {v}}}  — её скорость, а t{\displaystyle t}  — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени^[8][9][10].

Иногда предпринимаются попытки распространить сферу применения уравнения dp→dt=F→{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}}  и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[11][12].

Замечания

Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:

ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}} 

или

dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.} 

Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.

Следует учитывать, что нельзя рассматривать частный случай (при F→=0{\displaystyle {\vec {F}}=0} ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Историческая формулировка

Исходная формулировка Ньютона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.

Третий закон Ньютона

Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}} , а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}} . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}}  равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}} .

Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.}

Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно^[13].

Историческая формулировка

Ньютон дал следующую формулировку закона^[1]:

Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.

Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость^[14].

Следствия законов Ньютона

Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.

Уравнения движения

Уравнение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}  является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Закон сохранения импульса

Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю^[15].

Закон сохранения механической энергии

Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной^[16].

Законы Ньютона и силы инерции

Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.

Обычно речь идёт о силах инерции двух различных типов^[13][17]. Сила первого типа (даламберова сила инерции^[18]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции^[18]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой^[13][17]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются^[19][13], их называют фиктивными^[20], кажущимися^[21] или псевдосилами^[22].

Законы Ньютона в логике курса механики

Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.

Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.

Исторический очерк

Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем^[23].

  Страница «Начал» Ньютона с аксиомами механики

Основные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»^[1]:

Оригинальный текст (лат.)

   LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.

   LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.

   LEX III

Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.

Русский перевод этих формулировок законов см. в предыдущих разделах.

Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)^[24]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».

Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта^[24]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).

В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).

Примечания

1. ↑ ^{1 2 3} Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
2. ↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
3. ↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
4. ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
5. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
6. ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
7. ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
8. ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
9. ↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
10. ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
11. ↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
12. ↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
13. ↑ ^{1 2 3 4} Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
14. ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
15. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
16. ↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
17. ↑ ^{1 2} Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494-495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
18. ↑ ^{1 2} Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3-8.
19. ↑ «”Силы инерции” — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
20. ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
21. ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
22. ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
23. ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186-197;
24. ↑ ^{1 2} Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;

Литература

Ссылки

ru-wiki.org

определение, формула + рассуждения по теме

 

В первом законе Ньютона говорится о поведении тела, изолированного от воздействия других тел. Второй закон говорит о прямо противоположной ситуации. В нем рассматриваются случаи, когда тело или несколько тел воздействуют на данное.

Оба эти закона описывают поведение одного конкретного тела. Но во взаимодействии всегда участвуют минимум два тела. Что будет происходить с обоими этими телами? Как описать их взаимодействие? Анализом этой ситуации и занялся Ньютон после формулировки своих первых двух законов. Займемся и мы такими же изысканиями.

Взаимодействие двух тел

Мы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы. Такое может происходить среди по-разному воспитанных людей, но никак не в природе.

Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо.

Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие. Фактически, мы каждый день по многу раз пинаем очень и очень тяжелый мяч нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе.

Соотношение сил во взаимодействии между телами

Так что из этих рассуждений видно, что при взаимодействии двух тел, не только первое действует на второе с некоторой силой, но и второе в ответ действует на первое также с некоторой силой. Возникает вопрос: а как соотносятся эти силы? Какая из них больше, какая меньше?

Для этого необходимо проделать некоторые измерения. Потребуются два динамометра, но в домашних условиях их вполне могу заменить два безмена. Они измеряют вес, а вес это тоже сила, только выраженная в единицах массы в случае безмена. Поэтому, если у вас есть два безмена, то проделайте следующее.

Один из них оденьте колечком на что-то неподвижное, например, на гвоздь в стене, а второй соедините с первым крючками. И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен.

И хотя мы тянем только за один из них, окажется, что показания обоих, как на очной ставке, будут совпадать. Получается, что сила, с которой мы воздействуем вторым безменом на первый, равна силе, с которой первый безмен воздействует на второй.

Третий закон Ньютона: определение и формула

Сила действия равна силе противодействия. В этом и состоит суть третьего закона Ньютона. Определение его таково: силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. Третий закон Ньютона можно записать в виде формулы:

F_1  = – F_2,

Где F_1 и F_2 силы действия друг на друга соответственно первого и второго тела.

Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.

Нужна помощь в учебе?

Предыдущая тема: Второй закон Ньютона: формула и определение + маленький опыт
Следующая тема:&nbsp&nbsp&nbspСвободное падение тел: суть, ускорение свободного падения, формулы

Все неприличные комментарии будут удаляться.

www.nado5.ru