Лекции и примеры решения задач механики
Кинематика — это раздел теоретической механики, в котором изучается движение механических систем с геометрической точки зрения, без учета причин (сил), вызывающих это движение и изменение движения.
Положение тела, его движение в пространстве может быть определено относительно другого неизменяемого тела. С ним связывают выбранную систему отсчёта — систему координат, в которой и определяют параметры движения.
Установление способов, с помощью которых может быть задано движение точек или тел по отношению к выбранной системе отсчёта, позволит определить кинематические характеристики движения (траектории точек, их скорости, ускорения, угловые параметры тел.)
Движение любой механической системы относительно выбранной системы отсчёта будет известно, если известно движение каждой точки этой системы. Поэтому изучение раздела «Кинематика» начинается с темы «Кинематика точки», далее рассматривается тема «Кинематика твёрдого тела».
Данное учебно-методическое пособие поможет студентам при выполнении контрольных работ по разделу «Кинематика».
В пособии кратко изложена теория, даны основные формулы, приведены примеры решения типовых задач.
Краткость изложения теории предполагает предварительное изучение курса по учебникам, в которых даны подробные обоснования определений, выводы, доказательства теорем.
Методическое пособие может быть рекомендовано и на практических занятиях и при выполнении расчётно-графических работ.
Содержание
- Кинематика точки
- Способы задания закона движения точки
- Векторный
- Координатный
- Естественный
- Кинематика твердого тела
- Поступательное движение
- Вращательное движение твердого тела
- Вращение твердого тела вокруг неподвижной оси
- Угловая скорость и угловое ускорение
- Скорости и ускорения точек вращающегося твердого тела
- Передаточные механизмы
- Плоскопараллельное движение твердого тела
- Определение скоростей точек в плоскопараллельном движении
- Теорема о скоростях точек в ППД
- Следствие из теоремы о скоростях точек
- Мгновенный центр скоростей
- Определение МЦС
- Ускорение точки в плоскопараллельном движении
- Мгновенный центр ускорений
- Частные случаи МЦУ
- Сложное движение точки
- Определение скоростей и ускорений точек в сложном движении
- Ускорение Кориолиса
- Сферическое движение
- Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку
- Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки
- Скорости и ускорения точек при вращении тела вокруг неподвижной точки
Теоретическая механика
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Кубанский государственный технологический университет»
Конспект лекций
для бакалавров ЗиДО
технических направлений
часть II
КИНЕМАТИКА
Составители: д.т.н., проф. Смелягин А.И.
к.т.н., доц. Кегелес В.Л.
Краснодар 2011
СОДЕРЖАНИЕ
1 Кинематика. Общие понятия 2
2 Кинематика точки 2
3 Кинематика твердого тела 7
3.1 Поступательное движение твердого тела 7
3.2 Вращение твердого тела вокруг неподвижной оси 7
3.3 Плоскопараллельное (плоское) движение твердого тела 9
3.4 Сферическое движение 15
4 Сложное движение точки 17
1 Кинематика. Общие понятия
Кинематика – раздел теоретической механики, в котором изучается движение материальных тел без учета причин, вызывающих это движение.
В классической механике движение материальных тел рассматривается в трехмерном евклидовом пространстве, а время считается абсолютным, независящим от системы отсчета.
Система отсчета – система координат, неизменно связанная с телом, по отношению к которому рассматривается движение изучаемых объектов.
Если система отсчета находится в покое, то движение объекта относительно нее называют абсолютным. Движение объекта по отношению к подвижной системе отсчета называют относительным.
Методы кинематики дают возможность определить положение изучаемого объекта в рассматриваемой системе отсчета, а также найти его скорость и ускорение в любой момент времени.
Изучение раздела начинают с кинематики точки (изолированной, принадлежащей твердому телу или сплошной среде), затем переходят к рассмотрению движения твердых тел и их систем.
2 Кинематика точки
Характеристиками движения точки в любой момент времени являются ее положение, скорость и ускорение.
Геометрическое место последовательных положений точки называется траекторией.
Для определения характеристик движения и траектории точки обычно используют три способа задания ее движения – векторный, координатный, естественный.
Векторный способ задания движения
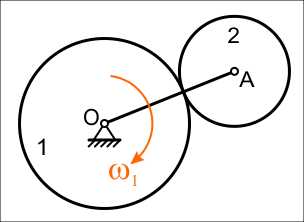
Положение точки в любой момент времени задается
радиус-вектором 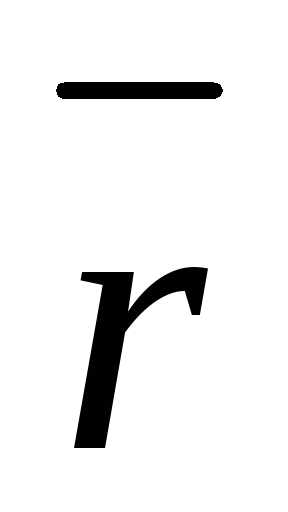
Уравнение
движения: 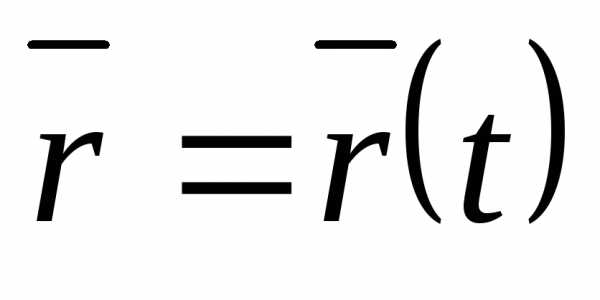 .
.
Траектория точки – это годограф вектора  .
.
Средняя скорость точки за время Δt
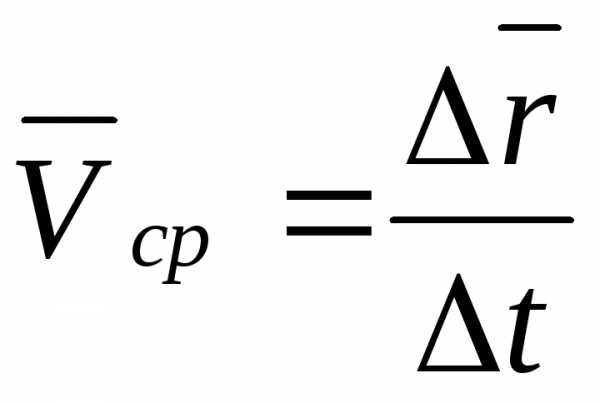 ,
где
.
,
где
.
Скорость точки в момент времени t
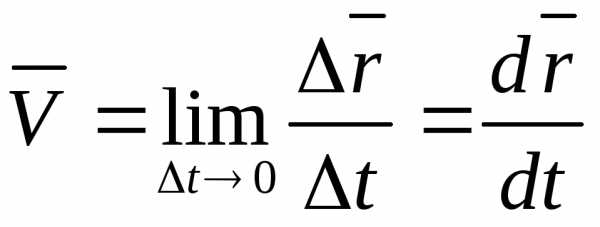 .
.
Вектор скорости направлен по касательной к траектории в данной точке.
Среднее ускорение точки за время Δt
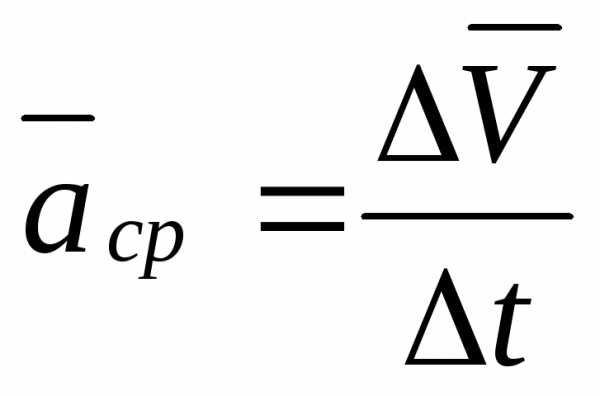
Ускорение точки в момент времени t
.
Этот способ используется, как правило, при теоретическом анализе закономерностей движения.
Итак, 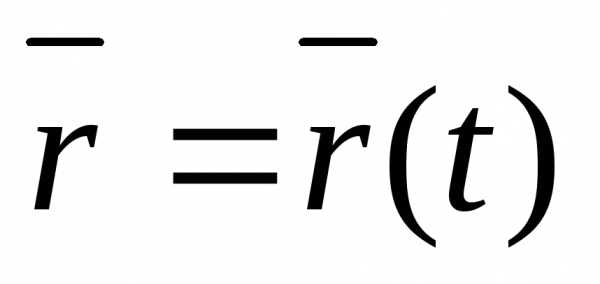 ;
;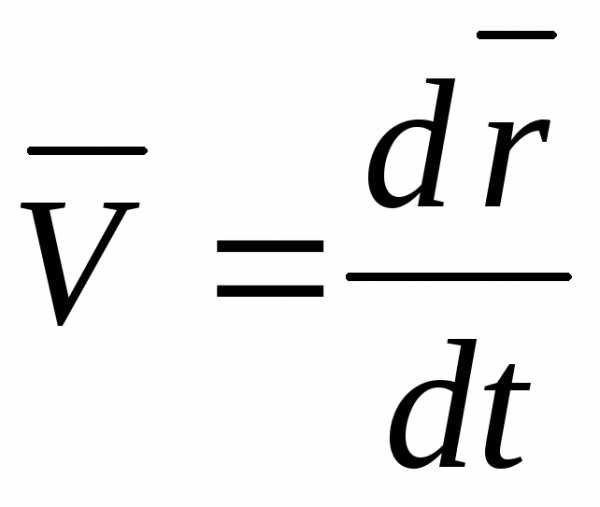 ;
;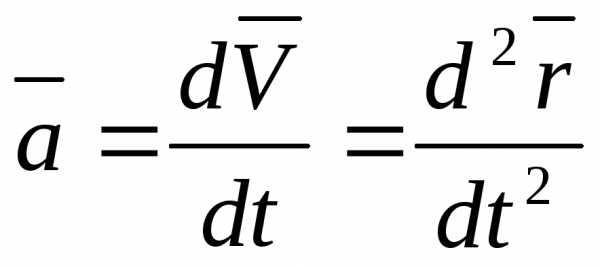 .
.
Координатный способ задания движения
Для описания движения точки используются системы координат: декартовая, полярная, цилиндрическая, сферическая и др.
Положение точки в декартовой системе координат в любой момент времени определяется ее координатами x, у, z.
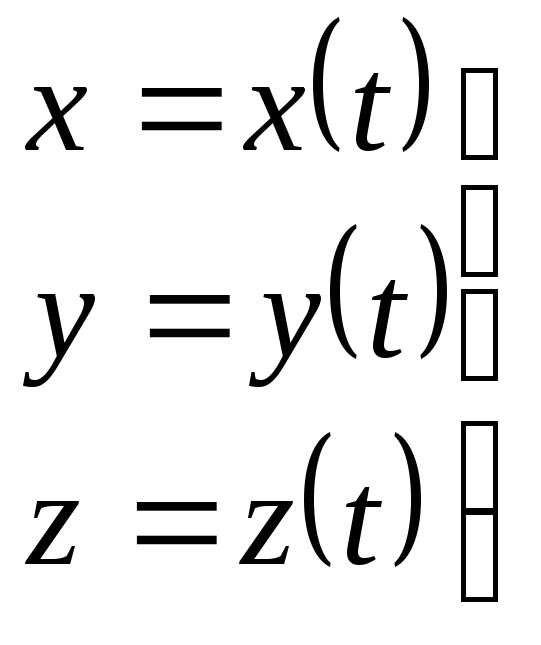
Эти уравнения определяют траекторию точки в параметрической форме.
Уравнения траектории точки в координатной форме можно получить,
исключая
параметр t
из уравнений движения, в виде системы
уравнений 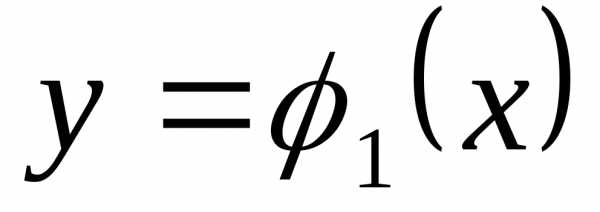 ,
,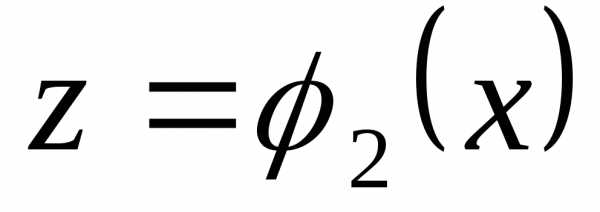 .
.
Скорость .
Таким
образом, 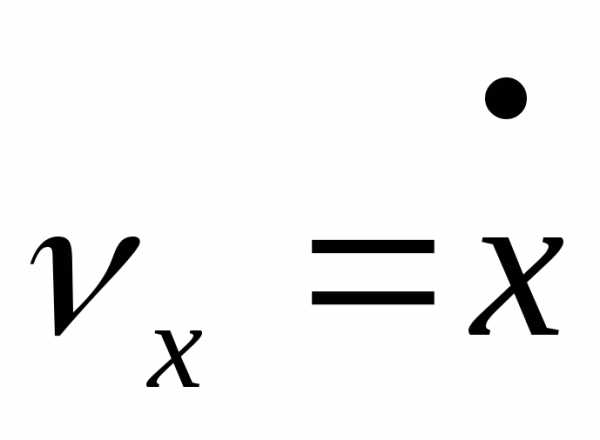 ,
,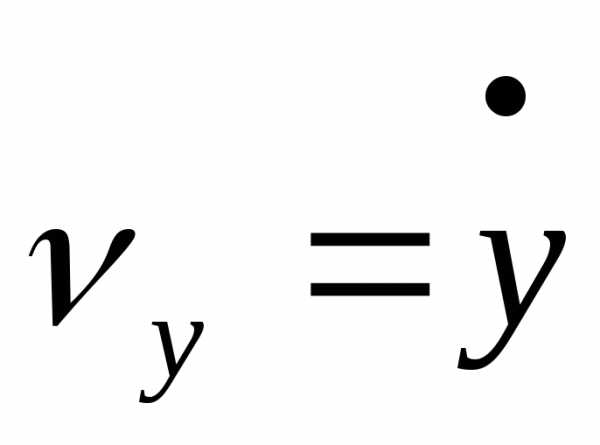 ,
,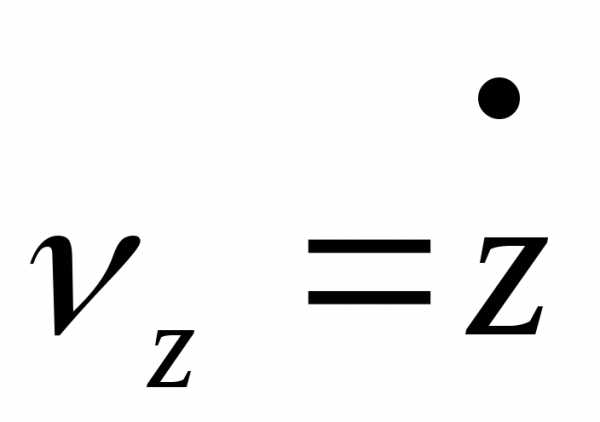 .
.
Модуль скорости .
Направляющие косинусы
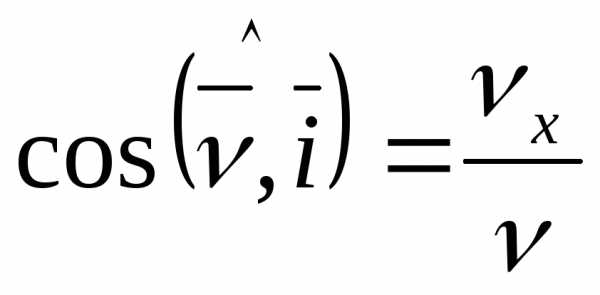 ;
; 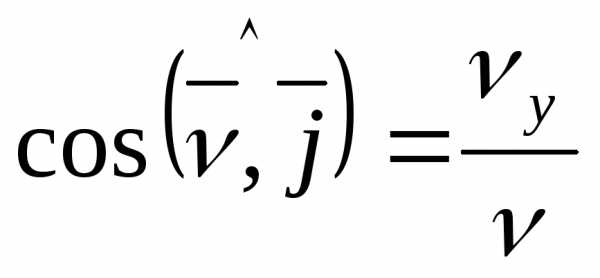 ;
; 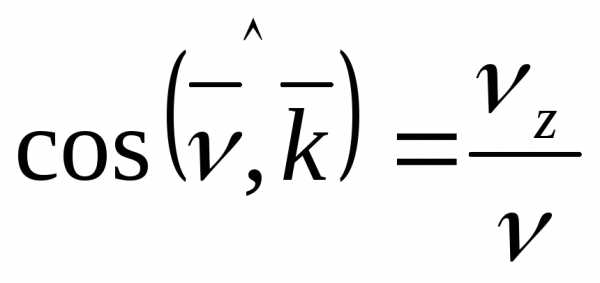 .
.
Ускорение ,
тогда 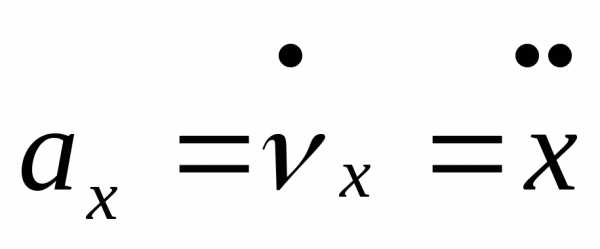 ,
, ,
,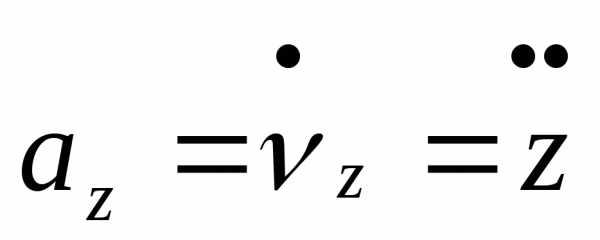 .
.
Модуль ускорения .
Направляющие
косинусы 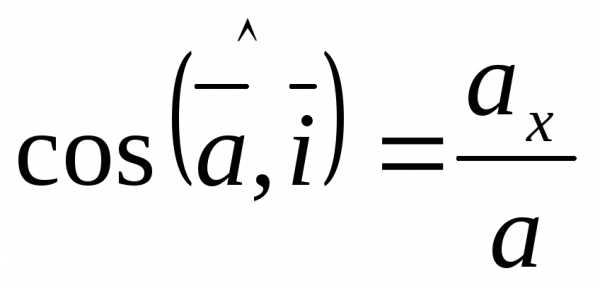 ;
; 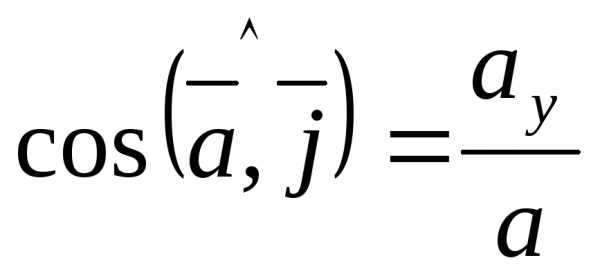 ;
;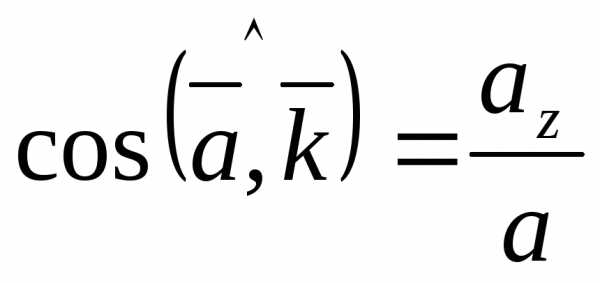
studfiles.net
Скорость точки | Лекции и примеры решения задач механики
Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета.
Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.
Вектор скорости направлен по касательной к траектории точки в сторону движения.
Рассмотрим перемещение точки за малый промежуток времени Δt:
тогда
средняя скорость точки за промежуток времени
Положение движущейся точки М относительно системы отсчета в момент времени t1 определяется радиус-вектором r.
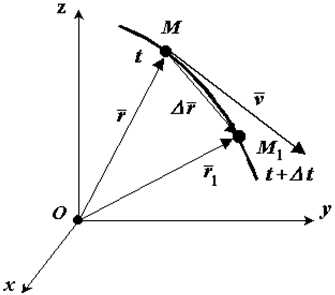
Рис. 1
В другой момент времени t1=t+Δt точка займет положение М1 с радиус-вектором r1.
За время Δt радиус-вектор движущейся точки изменится на
Средней скоростью vср называется отношение изменения радиус-вектора Δr к изменению времени Δt.
Скорость точки равна первой производной по времени от ее радиус-вектора.
Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим
После дифференцирования
Отсюда следует
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.
Модуль скорости и направляющие косинусы равны:

Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда
Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).
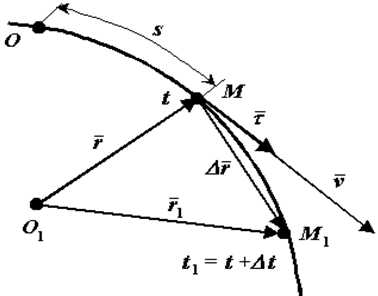
Рис. 2
Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O1
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.
При ds>0 направления векторов τ и dr совпадают.
Если точка движется в сторону убывающих расстояний, то ds и направления векторов τ и dr противоположны.
При
вектор скорости направлен по τ, т.е. в сторону возрастающих расстояний;
при
он имеет направление, противоположное τ, т.е. в сторону убывающих расстояний.
— алгебраическая скорость точки, проекция скорости v на положительное направление касательной к траектории.
Естественное задание движения точки полностью определяет скорость по величине и направлению.
Ускорение точки >
isopromat.ru
1.1 КИНЕМАТИКА – Всё для чайников
- Главная
- Видеотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Обществознание
- Обществознание – как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение
- Материаловедение
- Сварка
- Электротехника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
- Естествознание
- Библиотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Астрономия
- Обществознание
- Иностранные языки
- Технические науки
- Естествознание
forkettle.ru
Лекции по теоретической механике | Лекции и примеры решения задач механики
Выберите предметМеханикаТеоретическая механикаСопротивление материаловТеория машин и механизмовДетали машинВысшая математикаФизикаНачертательная геометрияИнформатикаАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАрхитектура и строительствоБазы данныхВысшая математикаГеометрияГидравликаДетали машинИздательское делоИнформатикаИнформационная безопасностьИнформационные технологииМатериаловедениеМашиностроениеМеталлургияМетрологияМеханикаМорская техникаНаноинженерияНачертательная геометрияПолиграфияПриборостроение и оптотехникаПрограммированиеПроцессы и аппаратыРабота на компьютереРадиофизикаСопротивление материаловТелевидениеТеоретическая механикаТеория вероятностейТеория машин и механизмовТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТранспортные средстваФизикаХолодильная техникаЧертежиЧерчениеЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЯдерная энергетика и теплофизикаЯдерные физика и технологииАнализ хозяйственной деятельностиАнтикризисное управлениеБанковское делоБизнес-планированиеБухгалтерский учет и аудитВнешнеэкономическая деятельностьГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиИнвестицииИнновационный менеджментКредитЛогистикаМаркетингМеждународные рынкиМенеджментМенеджмент организацииМикро-, макроэкономикаНалогиОрганизационное развитиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментСервисСтандартизацияСтатистикаСтратегический менеджментСтрахованиеТаможенное делоТеория управленияТовароведениеТорговое делоТуризмУправление персоналомФинансовый менеджментФинансыЦенообразование и оценка бизнесаЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализАрхеологияАстрономияБезопасность жизнедеятельностиБиологияБиотехнологияВетеринарияВоспроизводство и переработка лесных ресурсовГеографияГеодезияГеологияГидрометеорологияЕстествознаниеКартография и геоинформатикаМедицинаНефтегазовое делоПочвоведениеПриродообустройство и водопользованиеСельское и рыбное хозяйствоХимияХирургияЭкологияБиблиотечно-информационная деятельностьДизайнДокументоведение и архивоведениеЖурналистикаИскусствоИсторияКонфликтологияКриминалистикаКультурологияЛитератураЛогикаМеждународные отношенияМузыкаПедагогикаПолитологияПраво и юриспруденцияПсихологияРежиссураРеклама и PRРелигияСвязи с общественностьюСоциальная работаСоциологияСтрановедениеТеатроведениеФизическая культураФилософияЭтикаЯзыки (переводы)Языкознание и филология
Выберите вид работы…Решение задачКонтрольная работаКурсовая работаПомощь на экзаменеОтветы на вопросыОтчёт по практикеЧертёжДипломная работаРефератМонографияБизнес-планТворческая работаЭссеСочиненияРецензияДокладНабор текстаМагистерская диссертацияКандидатская диссертацияСтатьяЛабораторная работаПереводПрезентацииПовышение уникальности текстаДругое
isopromat.ru
