Термодинамика формула – Термодинамическая формула - Большая Энциклопедия Нефти и Газа, статья, страница 1 - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Формулы термодинамики

Определение и формулы термодинамики

При этом считается, что любое тело имеет внутреннюю энергию (U), которая зависит от его температуры:

где i – число степеней свободы молекулы; m – масса; – молярная масса; – универсальная газовая постоянная; T – температура по абсолютной шкале.

При теплообмене количество теплоты (Q) служит мерой изменения внутренней энергии. Количество теплоты, которое получает тело массы m при увеличении его температуры на величину равную , равно:

где – удельная теплоемкость вещества. В общем случае теплоемкость тела (C) определена как:

В соответствии с первым началом термодинамики, теплота, которую получает термодинамическая система (), расходуется ей на совершение работы (A) и изменение ее внутренней энергии ():

Для элементарного изменения состояния термодинамической системы первый закон термодинамики записывают как:

или:

где p – давление; – элементарное изменение объема.

Термодинамическим коэффициентом полезного действия (КПД) () называют отношение работы (A), которое совершает рабочее тело к количеству теплоты (), которое получает данное тело:

где — количество теплоты, отданное рабочим телом холодильнику.

Для цикла Карно, который состоит из двух изотерм и двух адиабат и проводится с идеальным газом КПД равно:

где – температура нагревателя; – температура холодильника.

Энтропия в термодинамике

Энтропией называют функцию состояния термодинамической системы, элемент которой в обратимом процессе равен:

В соответствии со вторым началом термодинамики в необратимом элементарном процессе изменение энтропии:

Для адиабатного процесса выражение (10) имеет вид:

где знак равно относится к обратимому процессу. Выражение (11) – математическая запись второго начала термодинамики (Следует помнить, что рассматривается замкнутая система).

Работа в термодинамике вычисляется как:

где – начальный объем системы; – конечный объем. Работа считается большей нуля, если работу выполняет система (газ) над внешними силами.

Примеры решения задач по теме «Термодинамика»

ru.solverbook.com

Основные формулы термодинамики

В термодинамике изучают самые общие законы и физические процессы преобразований внутренней энергии. При этом считается, что любое материальное тело имеет тепловую энергию $U$, которая зависит от его температур.

Перед тем, как рассмотреть основные термодинамические формулы необходимо дать определение термодинамике.

Определение 1

Термодинамика – это обширный раздел физики, который исследует и описывает процессы, происходящие в системах, а также их состояния.

Указанное научное направление опирается на обобщенные факты, которые были получены опытным путем. Происходящие в термодинамических концепциях явления описываются посредством использования макроскопических величин.

В их список входят такие параметры, как:

давление;
температура;
концентрация;
энергия;
объем.

К отдельным молекулам данные параметры неприменимы, а сводятся к детальному описанию системы в общем ее виде. Много решений, которые основаны на термодинамических законах, можно встретить в сфере электроэнергетики и тепловой техники. Что и свидетельствует о понимании фазовых переходов, химических процессов и явлений переноса. В некотором роде термодинамика тесно “сотрудничает” с квантовой динамикой.

Уравнение идеального газа в термодинамике

Рисунок 1. Работа в термодинамике. Автор24 — интернет-биржа студенческих работ

Определение 2

Идеальный газ – это некая идеализация, такая же, как и материальная точка.

Молекулы такого элемента являются материальными точками, а соударения частиц – абсолютно упругие и постоянные. В задачах по термодинамике реальные газы зачастую принимаются за идеальные. Так гораздо легче составлять формулы, и не нужно иметь дела с огромным количеством новых величин в уравнениях.

Итак, молекулы идеального газа движутся, а вот чтобы узнать с какой скоростью и массой, необходимо использовать уравнение состояния идеального газа, или формулу Клапейрона-Менделеева: $PV = \frac{m}{M}RT$. Здесь $m$ – масса исследуемого газа, $M$ – его изначальная молекулярная масса, $R$ – универсальная постоянная, равная 8,3144598 Дж/(моль*кг).

В этом аспекте массу идеального газа также можно вычислить, как произведение объема и плотности $m = pV$. Существует некая связь между средней кинетической энергией $E$ и давлением газа. Эта взаимосвязь называется в физике основным уравнением молекулярно-кинетической теории и имеет вид: $p = \frac{2}{3}nE$, где $n$ – концентрация движущихся молекул по отношению к общему объему, $E$ – коэффициент средней кинетической энергии.

Первое начало термодинамики. Формулы для изопроцессов

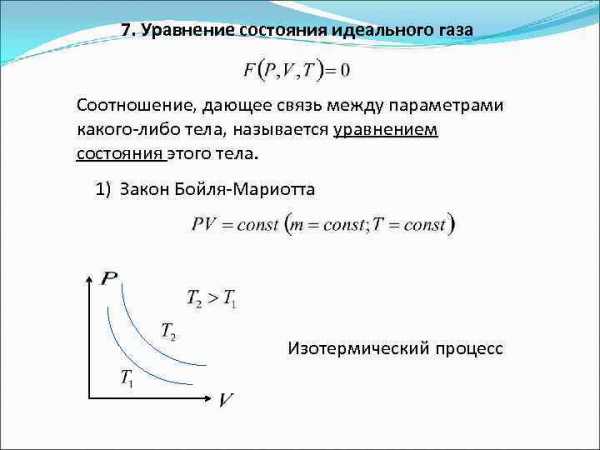
Рисунок 2. Уравнение состояния идеального газа. Автор24 — интернет-биржа студенческих работ

Первый термодинамический закон гласит: количество внутренней теплоты, переданное газу, идёт только на изменение общей энергии газа $U$ и на совершение веществом работы $A$. Формула первого начала термодинамики записывается так: $Q = ΔU + A$.

как известно, с газом в системе всегда что-то происходит, ведь его можно сжать или нагреть. В данном случае необходимо рассмотреть такие процессы, которые протекают при одном стабильном параметре. Первое начало термодинамики в изотермическом случае, который протекает при постоянной температуре, задействует закон Бойля-Мариотта.

В результате изотермического процесса давление газа обратно пропорционально его изначальному объёму: $Q = A.$

Изохорный – наблюдается при постоянном объеме. Для этого явление применим закон Шарля, согласно которому, давление прямо пропорционально общей температуре. В изохорном процессе все подведенное к газу тепло идет на изменение его внутренней энергии и записывается в таком виде: $Q = ΔA.$

Изобарный процесс – происходит при постоянном давлении. Закон Гей-Люссака предполагает, что при неизменном давлении идеального газа его начальный объём прямо пропорционален итоговой температуре. При изобарном процессе тепло идет на совершение газом работы и на изменение внутреннего энергетического потенциала: $Q = \Delta U+p\Delta V.$

Формула теплоемкости и главная формула КПД в термодинамике

Рисунок 3. Количество теплоты. Автор24 — интернет-биржа студенческих работ

Замечание 1

Удельная теплоемкость в термодинамической системе всегда равна количеству теплоты, которое выделяется для нагревания одного килограмма действующего вещества на один градус Цельсия.

Уравнение теплоемкости записывается таким образом: $c = \frac{Q}{m\Delta t}$. Помимо указанного параметра, существует и молярная теплоемкость, которая работает при постоянном объеме и давлении.

Ее действия видно в следующей формуле: $C_v = \frac {i}{2}R$ где $i$ – количество степеней свободы молекул газа.

Тепловая машина, в самом простейшем случае, состоит из холодильника, нагревателя и рабочего материального тела. Нагреватель изначально сообщает тепло физическому веществу и совершает определенную работу, а затем постепенно охлаждается холодильником, и все повторяется по кругу. Типичным примером тепловой машины выступает двигатель внутреннего сгорания.

Коэффициент полезного действия теплового устройства вычисляется по формуле: $n = \frac {Q_h-Q_x }{Q_h }.$

При изучении основ и уравнений термодинамики следует понять, что на сегодняшний день существует два метода описания физических процессов, происходящих в макроскопических материальных телах: статистический и термодинамический.

Методы термодинамики и ее формулы позволяет раскрыть и описать смысл экспериментальных закономерностей в виде закона Менделеева-Клапейрона. Важно понять, что в термодинамических концепциях, в отличие от систем молекулярной физики, не изучаются конкретные взаимодействия, происходящие с определенными молекулами или атомами, а рассматривается постоянные взаимопревращения и связь разнообразных видов теплоты, энергии и работы.

Уравнение состояния и его функции

Рисунок 4. Термодинамические уравнения состояния. Автор24 — интернет-биржа студенческих работ

При исследовании макросостояний применяются функции состояния, которые предполагают показатель, демонстрирующий определённые состояния термодинамического равновесия, независящий от предыстории концепции и метода её перехода в абсолютное состояние.

Основными функциями состояния при грамотном построении термодинамики являются:

внутренняя энергия;
энтропия;
температура;
термодинамические потенциалы.

Однако функции состояния в термодинамики не являются полностью независимыми, и для однородной системы любой термодинамический принцип может быть записан как выражение двух самостоятельных переменных. Такие функциональные взаимосвязи называются уравнениями общего состояния.

На сегодняшний день различают такие виды уравнений:

термическое уравнение состояние – определяющее связь между давлением, температурой и объёмом;
калорическое уравнение – выражающее внутренний энергетический потенциал, как функцию от объёма и температуры;
каноническое уравнение состояние – записываемое в качестве термодинамического потенциала в соответствующих переменных.

Знание уравнения состояния очень важно для использования на практике общих принципов термодинамики. Для каждой конкретной термодинамической концепции такие выражения определяются из опыта или способами статистической механики, и в пределах термодинамики оно считается заданным при изначальном определении системы.

spravochnick.ru

Конспект “Термодинамика. Теория, формулы, схемы” для ОГЭ

Термодинамика – раздел физики, изучающий тела, находящиеся в состоянии термодинамического равновесия и явления, сопровождающие переходы между этими состояниями.

Термодинамическое равновесие – состояние тел (или частей тела), при котором остаются постоянными все величины, характеризующие эти тела (или части тела): объёмы, давления, расположение масс и др.

Температура – единственная физическая величина, всегда одинаковая у всех тел (или частей тела), находящихся в состоянии термодинамического равновесия.

Термометр – прибор для измерения температуры. Единица температуры – 1 кельвин (1 К). Также используется 1 °С, равный 1 К.

Теплообмен – переход внутренней энергии одного тела во внутреннюю энергию другого тела без совершения механической работы.

Количество теплоты

– физическая величина, показывающая энергию, полученную (отданную) телом при теплообмене.

Калориметр – прибор для измерения количества теплоты. Единица количества теплоты – 1 джоуль (1 Дж).

Удельная теплоемкость вещества – физическая величина, показывающая количество теплоты, необходимое для изменения температуры 1 кг этого вещества на 1 °С. Единица удельной теплоёмкости – 1 Дж/(кг·°С).

Количество теплоты, полученное (отданное) телом при теплообмене, пропорционально массе тела и изменению его температуры. Коэффициент пропорциональности – удельная теплоёмкость вещества.

Превращение твёрдого тела в жидкость называют плавлением.Обратное явление называют отвердеванием. Если при этом получается кристаллическое тело, то отвердевание называют кристаллизацией.

Температура

Температурой плавления называют температуру, при которой нагреваемое кристаллическое тело тело начинает плавиться, и при этом одновременно существуют твёрдое и жидкое состояния его вещества.

Температурой кристаллизации называют температуру, при которой охлаждаемая жидкость начинает кристаллизоваться, и при этом одновременно существуют её твёрдое и жидкое состояния.

Как правило, температура кристаллизации вещества равна температуре его плавления. Температура плавления/кристаллизации вещества зависит от внешнего давления и других факторов.

Удельная теплота плавления – физическая величина, показывающая количество теплоты, необходимое для плавления или выделяющееся при кристаллизации 1 кг вещества, находящегося при температуре плавления/кристаллизации. Единица удельной теплоты плавления – 1 Дж/кг.

Количество теплоты, поглощаемое (выделяющееся) при плавлении (кристаллизации), пропорционально массе расплавившегося (кристаллизовавшегося) вещества. Коэффициент пропорциональности – удельная теплота плавления вещества.

Видами парообразования являются: испарение – парообразование, происходящее с поверхности жидкости; кипение – парообразование, происходящее по всему объёму жидкости вследствие возникновения и всплытия на поверхность пузырей пара; сублимация – парообразование, происходящее с поверхности твёрдого тела.

Температурой кипения называют температуру, при которой наблюдается кипение вещества (интенсивное парообразование по всему объёму этого вещества). Температура кипения зависит от внешнего давления и других факторов.

Удельная теплота парообразования – физическая величина, показывающая количество теплоты, необходимое для превращения в пар 1 кг вещества (как правило, при температуре кипения). Единица удельной теплоты парообразования – 1 Дж/кг.

Количество теплоты, поглощённое кипящей (или испаряющейся при постоянной температуре) жидкостью, прямо пропорционально массе образовавшегося пара. Коэффициент пропорциональности – удельная теплота парообразования вещества.

При охлаждении/кристаллизации/конденсации выделяется точно такое же количество теплоты, которое было затрачено для нагревания/плавления/парообразования вещества (если температуры и давления при прямом и обратном процессах соответствуют друг другу).Утверждение будет верным и наоборот.

Тепловые явления

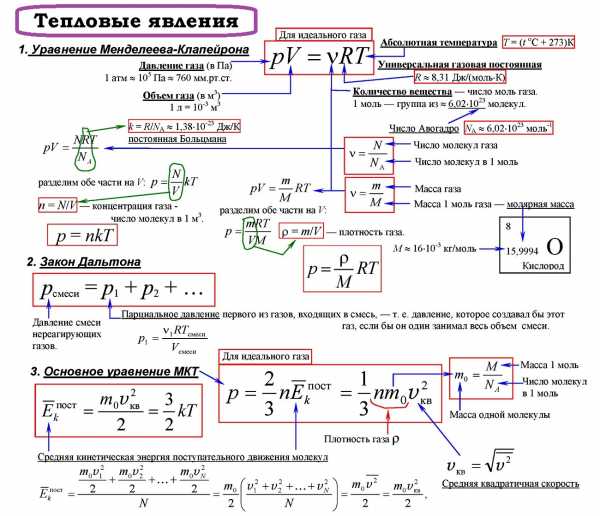
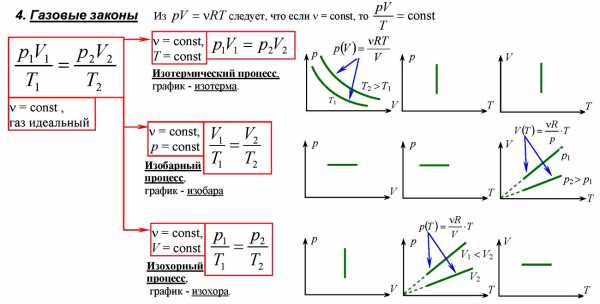
Законы термодинамика

Первый закон термодинамики устанавливает равенство между изменением внутренней энергии тела и суммой полученной телом теплоты и совершённой над ним работы.

Тепловой двигатель – периодически действующее устройство, служащее для превращения внутренней энергии рабочего тела (как правило, газа или пара) в механическую энергию.

Количество теплоты, выделяющееся при полном сгорании вещества (топлива), прямо пропорционально массе сгоревшего вещества (топлива). Коэффициент пропорциональности – удельная теплота сгорания топлива.

Известно три способа теплопередачи (теплообмена) – теплопроводность, конвекция и излучение. При теплопроводности теплота проникает через вещество без его перемещения (в случае отсутствия вещества теплопроводность является нулевой). При конвекции теплота перемещается неравномерно нагретым движущимся веществом (в условиях, когда возможно возникновение архимедовой силы). При излучении теплота передаётся через пространство или вещество в виде электромагнитных волн (для излучения наличие вещества не является обязательным, в отличие от первых двух способов теплопередачи).

Второй закон термодинамики гласит, что теплообмен самостоятельно протекает только в таком направлении, что температура менее нагретого тела возрастает, а более нагретого – уменьшается.

Дополнительные материалы по теме:

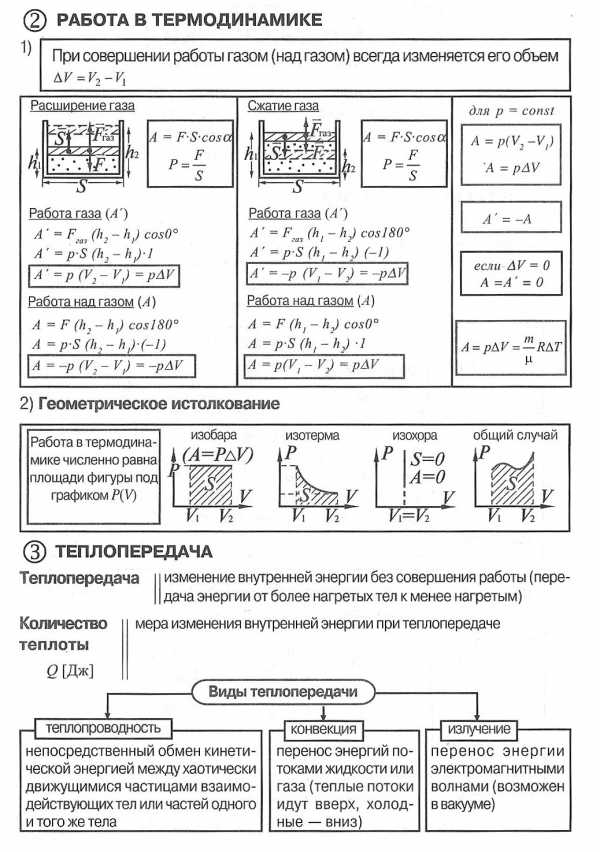
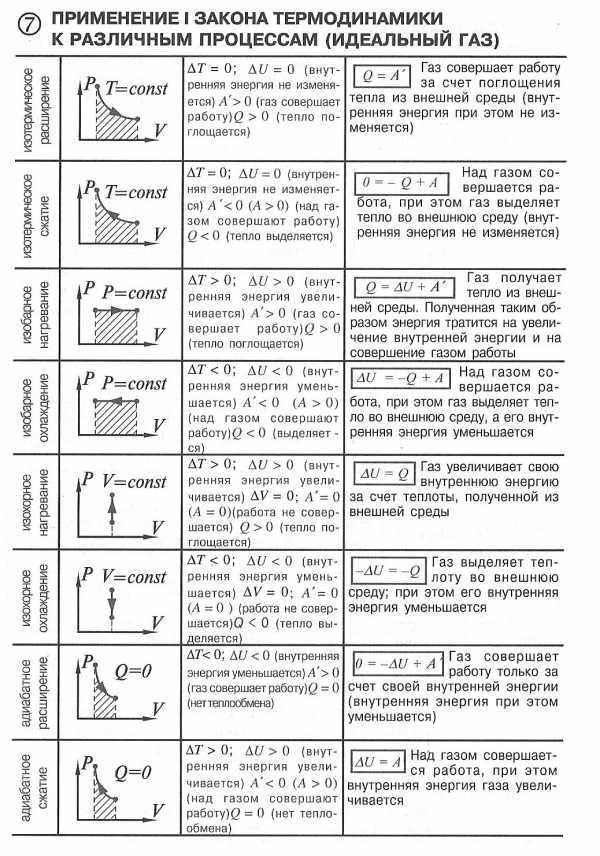
Конспект темы «Термодинамика. Теория, формулы, схемы»

Следующая тема «Электростатика. Теория, формулы, схемы для ОГЭ»

Термодинамика. Теория, формулы, схемы

5 (100%) 2 votes

uchitel.pro

Термодинамика – Физика – Теория, тесты, формулы и задачи

Основные теоретические сведения

Теплоемкость вещества

К оглавлению…

Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c. Тогда количество теплоты (энергии) необходимое для изменения температуры некоторого тела массой m можно рассчитать по формуле:

При этом в этой формуле абсолютно не важно в каких единицах подставлена температура, так как нам важно не ее абсолютное значение, а изменение. Единица измерения удельной теплоемкости вещества: Дж/(кг∙К).

Если t₂ > t₁, то Q > 0 – тело нагревается (получает тепло).
Если t₂ < t₁, то Q < 0 – тело охлаждается (отдает тепло).

Произведение массы тела на удельную теплоемкость вещества, из которого оно изготовлено называется теплоемкостью тела (т.е. просто теплоемкостью без слова «удельная»):

Если в условии задачи сказано про теплоемкость тела, то количество теплоты, отданное или полученное этим телом, можно рассчитать по формуле:

Итак, запомните:

Удельная теплоемкость обозначается маленькой буквой с, и является характеристикой вещества.
(Просто) Теплоемкость обозначается большой буквой С, и является характеристикой данного тела.

Напомним, что количество теплоты Q отданное каким–либо источником (нагревателем) рассчитывается по формуле: Q = Pt, где: P – мощность источника, t – время, в течение которого источник отдавал тепло. При решении задач не путайте время работа источника и температуру.

Фазовые превращения

К оглавлению…

Фазой вещества называется однородная система, например, твердое тело, физические свойства которой во всех точках одинаковые. Между различными фазами вещества при обычных условиях существует четко выраженная граница (поверхность) раздела. При изменении внешних условий (температуры, давления, электрических и магнитных полей) вещество может переходить из одной фазы в другую. Такие процессы называются фазовыми превращениями (переходами).

Процесс фазового перехода из жидкого состояния в газообразное (парообразование) или из твердого в жидкое (плавление) может происходить только при сообщении веществу некоторого количества теплоты. Обратные фазовые переходы (конденсация и кристаллизация, или отвердевание) сопровождаются выделением такого же количества теплоты.

Количество теплоты, поступающее в систему или выделяющееся из нее, изменяет ее внутреннюю энергию. Это означает, что внутренняя энергия пара при 100°С больше, чем жидкости при той же температуре. Указанные фазовые переходы идут при постоянных температурах, которые называются соответственно температурой кипения и температурой плавления. Количество теплоты, необходимое для превращения жидкости в пар или выделяемое паром при конденсации, называется теплотой парообразования:

где: r – удельная теплота парообразования. Единица измерения [r] = 1 Дж/кг. Физический смысл удельной теплоты парообразования: она равна количеству теплоты, необходимому для превращения в пар 1 кг жидкости, находящейся при температуре кипения. Превращение жидкости в пар не требует доведение жидкости до кипения. Вода может превратиться в пар и при комнатной температуре. Такой процесс называется испарением.

Количество теплоты, необходимое для плавления тела или выделяемое при кристаллизации (отвердевании), называется теплотой плавления:

где: λ – удельная теплота плавления. Единица измерения [λ] = 1 Дж/кг. Физический смысл удельной теплоты плавления: теплота, необходимая для плавления 1 кг вещества, находящегося при температуре плавления. Удельные теплоты парообразования и плавления называются также скрытыми теплотами, поскольку при фазовых переходах температура системы не меняется, несмотря на то, что теплота к ней подводится.

Обратите внимание: что во время фазовых переходов температура системы не изменяется. А также на то, что сами фазовые переходы начинаются только после достижения необходимой температуры.

Наиболее распространенным источником энергии для нужд человека является топливо – вещество, при сгорании которого выделяется некоторое количество теплоты. Количество теплоты, выделяемое при сгорании топлива массой m, называется теплотой сгорания топлива:

где: q – удельная теплота сгорания (теплотворная способность, калорийность) топлива. Единица измерения [q] = 1 Дж/кг. Физический смысл удельной теплоты сгорания топлива: величина, показывающая, какое количество теплоты выделяется при полном сгорании 1 кг топлива.

Уравнение теплового баланса

К оглавлению…

В соответствии с законом сохранения энергии для замкнутой системы тел, в которой не происходит никаких превращений энергии, кроме теплообмена, количество теплоты, отдаваемое более нагретыми телами, равно количеству теплоты, получаемому более холодными. Теплообмен прекращается в состоянии термодинамического равновесия, т.е. когда температура всех тел системы становится одинаковой. Сформулируем уравнение теплового баланса: в замкнутой системе тел алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующими в теплообмене, равна нулю:

При использовании такой формы записи уравнения теплового баланса, чтобы не сделать ошибку, запомните: когда Вы будете считать теплоту при нагревании или охлаждении тела, нужно из большей температуры вычитать меньшую, чтобы теплота всегда была положительной. Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то уравнение теплового баланса можно записать в виде:

При использовании такой формы записи, нужно всегда от конечной температуры отнимать начальную. При таком подходе знак их разности сам «покажет» отдаёт тело теплоту или получает.

Запомните, что тело поглощает теплоту если происходит:

Нагревание,
Плавление,
Парообразование.

Тело отдает теплоту если происходит:

Охлаждение,
Кристаллизация,
Конденсация,
Сгорание топлива.

Именно в этой теме, имеет смысл не решать задачи в общем виде, а сразу подставлять числа.

Взаимные превращения механической и внутренней энергии

При неупругих ударах механическая энергия частично или полностью переходит во внутреннюю энергию тел, то есть тела могут нагреваться и плавится. В общем случае изменение механической энергии равно выделяющемуся количеству теплоты.

Работа идеального газа

К оглавлению…

Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно–кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно–кинетические модели для иллюстрации своих выводов.

Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.

Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом. Если процесс протекает достаточно медленно (в пределе бесконечно медленно), то система в каждый момент времени оказывается близкой к равновесному состоянию. Процессы, состоящие из последовательности равновесных состояний, называются квазистатическими (или квазистационарными, еще одно название таких процессов – равновесные).

В изобарном процессе работу идеального газа можно рассчитывать по формулам:

Подчеркнем еще раз: работу газа по расширению можно считать по этим формулам только если давление постоянно. Согласно данной формуле, при расширении газ совершает положительную работу, а при сжатии – отрицательную (т.е. газ сопротивляется сжатию и над ним нужно совершать работу чтобы оно состоялось).

Если давление нельзя считать постоянным, то работу газа находят, как площадь фигуры под графиком в координатах (p, V). Очевидно, что в изохорном процессе работа газа равна нулю.

Ввиду того, что работа газа численно равна площади под графиком, становится понятно, что величина работы зависит от того, какой именно процесс происходил, ведь у каждого процесса свой график, а под ним своя площадь. Таким образом, работа зависит не только и не столько от начального и конечного состояний газа, сколько от процесса, с помощью которого конечное состояние было достигнуто.

Внутренняя энергия

К оглавлению…

Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно–кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема. Внутренняя энергия одноатомного идеального газа рассчитывается по формулам:

Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния. Это значит, что изменение внутренней энергии не зависит от того, как система была переведена из одного состояния в другое (а зависит лишь от характеристик первоначального и конечного состояний) и всегда, в любых процессах для одноатомного идеального газа определяется выражением:

Обратите внимание: эта формула верна только для одноатомного газа, зато она применима ко всем процессам (а не только к изобарному, как формула для работы). Как видно из формулы, если температура не изменялась, то внутренняя энергия остаётся постоянной.

Первый закон термодинамики

К оглавлению…

Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, то есть изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.

Первый закон (начало) термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом: Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами. Однако, соотношение, выражающее первый закон термодинамики, чаще записывают в немного другой форме:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами (такая формулировка более удобна и понятна, в таком виде совсем очевидно, что это просто закон сохранения энергии).

Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких–либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.

Адиабатным (адиабатическим) называют процесс, в ходе которого система не обменивается теплотой с окружающей средой. При адиабатном процессе Q = 0. Поэтому: ΔU + A = 0, то есть: A = – ΔU. Газ совершает работу за счет уменьшения собственной внутренней энергии.

Первое начало термодинамики и изопроцессы

К оглавлению…

Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплотаQ, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):

Изобарный процесс (p = const):

Изотермический процесс (T = const):

Адиабатный процесс (Q = 0):

Если в задаче явно не сказано, что газ одноатомный (или не назван один из инертных газов, например, гелий), то применять формулы из этого раздела нельзя.

Циклы. Тепловые машины

К оглавлению…

Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.

Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т.д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние.

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ > 0 и отдает холодильнику количество теплоты Q₂ < 0.

КПД тепловой машины может быть рассчитан по формуле:

где: Q₁ – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q₂ – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:

Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1).

Наибольший КПД при заданных температурах нагревателя T₁ и холодильника T₂, достигается если тепловая машина работает по циклу Карно. Цикл Карно состоит из двух изотерм и двух адиабат. КПД цикла Карно равен:

Второе начало (второй закон) термодинамики

К оглавлению…

Первый закон термодинамики не устанавливает направление протекания тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.

Обратимыми процессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.

Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из–за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т.д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.

Первый закон термодинамики не может отличить обратимые процессы от необратимых. Он просто требует от термодинамического процесса определенного энергетического баланса и ничего не говорит о том, возможен такой процесс или нет. Направление самопроизвольно протекающих процессов устанавливает второй закон термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов.

Английский физик У.Кельвин дал в 1851 году следующую формулировку второго закона: В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.

Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют «вечным двигателем второго рода». Как уже должно было стать понятно, второе начало термодинамики запрещает существование такого двигателя.

Немецкий физик Р.Клаузиус дал другую формулировку второго закона термодинамики: Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой. Следует отметить, что обе формулировки второго закона термодинамики эквивалентны.

Сложные задачи по термодинамике

К оглавлению…

При решении различных нестандартных задач по термодинамике необходимо учитывать следующие замечания:

Для нахождения работы идеального газа надо построить график процесса в координатах p(V) и найти площадь фигуры под графиком. Если дан график процесса в координатах p(T) или V(T), то его сначала перестраивают в координаты p(V). Если же в условии задаётся математическая зависимость между параметрами газа, то сначала находят зависимость между давлением и объёмом, а затем строят график p(V).
Для нахождения работы смеси газов используют закон Дальтона.
При объединении теплоизолированных сосудов не должна изменяться внутренняя энергия всей системы, т.е. на сколько джоулей увеличится внутренняя энергия газа в одном сосуде, на столько уменьшится в другом.
Вообще говоря, давление и температуру газа можно измерять только в состоянии термодинамического равновесия, когда давление и температура во всех точках сосуда одинаковы. Но бывают ситуации, когда давление одинаково во всех точках, а температура нет. Это может быть следствием разной концентрации молекул в разных частях сосуда (проанализируйте формулу: p = nkT).
Иногда приходится в задачах по термодинамике использовать знания из механики.

Расчет КПД циклов по графику

К оглавлению…

Задачи данной темы по праву считаются одними из самых сложных задач в термодинамике. Итак, для решения Вам придется, во-первых, перевести график процесса в p(V) – координаты. Во-вторых, надо рассчитать работу газа за цикл. Полезная работа равна площади фигуры внутри графика циклического процесса в координатах p(V). В-третьих, необходимо разобраться, где газ получает, а где отдает теплоту. Для этого вспомните первое начало термодинамики. Внутренняя энергия идеального газа зависит только от его температуры, а работа – от объема. Поэтому, газ получает теплоту, если:

Увеличиваются и его температура, и объем;
Увеличивается объем, а температура постоянна;
Увеличивается температура, а объем постоянен.

Газ отдает теплоту, если:

Уменьшаются и его температура, и объем;
Уменьшается объем, а температура постоянна;
Уменьшается температура, а объем постоянен.

Если один из параметров увеличивается, а другой уменьшается, для того, чтобы понять, отдает газ теплоту или получает ее, необходимо «в лоб» по первому началу термодинамики рассчитать теплоту и посмотреть на ее знак. Положительная теплота – газ ее получает. Отрицательная – отдает.

Первый тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ получает теплоту в изохорных и изобарных процессах. Применяйте формулу:

Обратите внимание, что в знаменателе стоит только теплота, полученная газом за один цикл, то есть теплота только в тех процессах, в которых газ получал ее.

Второй тип задач. В p(V) – координатах график цикла представляет собой фигуру с легко вычисляемой площадью, и газ отдает теплоту в изохорных и изобарных процессах. Применяйте формулу:

Обратите внимание, что в знаменателе стоит только теплота, отданная газом за один цикл, то есть теплота только в тех процессах, в которых газ отдавал ее.

Третий тип задач. Газ получает теплоту не в удобных для расчета изохорных или изобарных процессах, в цикле есть изотермы или адиабаты, или вообще «никакие» процессы. Применяйте формулу:

Свойства паров. Влажность

К оглавлению…

Любое вещество при определенных условиях может находиться в различных агрегатных состояниях – твердом, жидком и газообразном. Переход из одного состояния в другое называется фазовым переходом. Испарение и конденсация являются примерами фазовых переходов.

Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно–кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, то есть к охлаждению жидкости (если нет подвода энергии от окружающих тел).

Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость.

В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, т.е. число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, это значит, что скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.

Насыщенный пар имеет максимальные: давление, концентрацию, плотность при данной температуре. Они зависят только от температуры насыщенного пара, но не от его объема.

Это означает, что если бы мы сосуд закрыли не крышкой, а поршнем, и после того, как пар стал насыщенным, стали бы его сжимать, то давление, плотность и концентрация пара не изменились бы. Если быть более точным, то давление, плотность и концентрация на небольшое время увеличились бы, и пар стал бы перенасыщенным. Но сразу же часть пара превратилась бы в воду, и параметры пара стали бы прежними. Если поднять поршень, то пар перестанет быть насыщенным. Однако за счёт испарения через некоторое время снова станет насыщенным. Здесь следует учесть, что если воды на дне сосуда нет или её немного, то это испарение может оказаться недостаточным, чтобы пар снова стал насыщенным.

Фраза: «В закрытом сосуде с водой…» – означает, что над водой насыщенный пар.
Выпадение росы означает, что пар становится насыщенным.

Абсолютной влажностью ρ называют количество водяного пара, содержащегося в 1 м³ воздуха (т.е. просто плотность водяных паров; из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):

где: р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура. Единица измерения абсолютной влажности в СИ [ρ] = 1 кг/м³, хотя обычно используют 1 г/м³.

Относительной влажностью φ называется отношение абсолютной влажности ρ к тому количеству водяного пара ρ₀, которое необходимо для насыщения 1 м³ воздуха при данной температуре:

Относительную влажность можно также определить как отношение давления водяного пара р к давлению насыщенного пара р₀ при данной температуре:

Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (то есть давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.

В частности, при нормальном атмосферном давлении вода кипит при температуре 100°С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. Важно знать, что температура кипения жидкости зависит от давления. В герметически закрытом сосуде жидкость кипеть не может, т.к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром.

Поверхностное натяжение

К оглавлению…

Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может скачком переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах, и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей.

Вследствие плотной упаковки молекул сжимаемость жидкостей, то есть изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах.

Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (то есть увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔA_внеш, пропорциональную изменению ΔS площади поверхности.

Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия E_p поверхности жидкости пропорциональна ее площади:

Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости на единицу при постоянной температуре. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м²) или в ньютонах на метр (1 Н/м = 1 Дж/м²).

Из механики известно, что ра

educon.by

Основные формулы молекулярной физики и термодинамики

⇐ ПредыдущаяСтр 4 из 8Следующая ⇒

Уравнение состояния идеального газа:

p=nkT,

где p – давление;

V – объем;

M – молярная масса;

m – масса;

T – термодинамическая температура;

R =8,31 Дж/(моль·K) – универсальная газовая постоянная;

n – концентрация;

k =1,38 · 10^-23 Дж/К постоянная Больцмана.

Уравнение состояния ван-дер-ваальсовского газа (для одного моля):

где V_M – молярный объем, занимаемый при p и Т ;

a, b – постоянные Ван-дер-Ваальса, которые связаны с критической температурой T_k, критическим давлением p_k и критическим объемом V_k соотношениями:

, .

Закон Дальтона:

p=p₁+p₂+…+p_n,

где p – давление смеси идеальных газов;

p₁, p₂, …, p_n– парциальные давления входящих в смесь газов.

Средняя квадратичная скорость молекул:

где R – универсальная газовая постоянная;

T – термодинамическая температура;

M – молярная масса.

Энергия теплового движения молекул (внутренняя энергия) газа:

где R – универсальная газовая постоянная;

m – масса газа;

M – молярная масса газа;

T – термодинамическая температура;

i – число степеней свободы молекул:

для одноатомного газа i=3;

для двухатомного газа i=5;

для многоатомного газа i=6.

Уравнение адиабатного процесса (уравнение Пуассона):

pV^γ=const,

где γ=с_p/c_V – показатель адиабаты.

Уравнение политропного процесса (уравнение Пуассона):

pVⁿ=const,

где n – показатель политропы.

Связь между молярнойСи удельнойстеплоемкостями:

С=Mc,

где M – молярная масса.

Молярная теплоемкость при постоянном объеме:

С_V= R,

где i – число степеней свободы молекул;

R – универсальная газовая постоянная.

Молярная теплоемкость при постоянном давлении:

С_p=C_V+R.

Молярная теплоемкость газа при политропическом процессе (pVⁿ=const):

где n – показатель политропы;

γ – показатель адиабаты.

Закон распределения молекул по скоростям (закон Максвелла):

где ΔN – число молекул, относительные скорости которых лежат в интервале от u до Δu:

u=v/v_в – относительная скорость, v– данная скорость, v_в= – наиболее вероятная скорость молекул;

Δu – интервал относительных скоростей, малый по сравнению со скоростью u;

N – общее число молекул.

Распределение молекул по концентрациям:

где n – концентрация молекул на высоте h;

n₀ – концентрация молекул на высоте h=0;

U – потенциальная энергия молекулы в поле тяготения;

k – постоянная Больцмана;

T – термодинамическая температура.

Барометрическая формула:

где p₀ – давление на высоте h=0.

M – молярная масса воздуха;

h – высота;

R – универсальная газовая постоянная;

T – термодинамическая температура.

Средняя длина свободного пробега молекул газа:

где σ – эффективный диаметр молекулы;

n – число молекул в единице объема (концентрация молекул).

Первое начало термодинамики:

Q=ΔU+A,

где Q – количество теплоты;

ΔU – приращение внутренней энергии системы;

A – работа, совершаемая газом.

Внутренняя энергия идеального газа:

где m – масса газа;

M – молярная масса газа;

T – термодинамическая температура;

С_V– молярная теплоемкость при постоянном объеме.

Работа, совершаемая газом:

где V₁ – начальный объем;

V – конечный объем;

p – давление газа;

dV – изменение объема.

Коэффициент полезного действия тепловой машины:

где Q₁ – теплота, получаемая рабочим телом;

Q₂ – отдаваемая теплота.

Коэффициент полезного действия цикла Карно:

где T₁ – температура нагревателя;

T₂ – температура холодильника.

Энтропия системы:

S=klnW,

где k – постоянная Больцмана;

W – статистический вес (термодинамическая вероятность).

Приращение энтропии системы:

где δQ – элементарная теплота;

T – термодинамическая температура.

2.2. Понятия и определения молекулярной физики и термодинамики

? Перечислите основные положения МКТ.

1. Все тела состоят из мельчайших частиц.

2. Частицы-молекулы находятся в непрерывном тепловом движении.

3. Между молекулами существуют силы взаимодействия, природа сил – электромагнитная.

? Запишите основное уравнение МКТ. В чем заключается молекулярно-кинетический смысл температуры?
( – давление, n-концентрация, m₀ –масса молекулы, v– скорость молекулы). Температура – энергетическая характеристика.
? Что такое степень свободы молекулы? Сформулируйте закон равномерного распределения молекул по степеням свободы.
Количество независимых координат, полностью описывающих положение молекулы в пространстве называют степенями свободы молекулы. Для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится кинетическая энергия, равная ( -постоянная Больцмана, – температура).
? Поясните понятие «идеальный газ». Запишите уравнение состояния идеального газа. Что вы знаете о изопроцессах?
Идеальный газ – объем молекул пренебрежимо мал по сравнению с объемом сосуда, силы взаимодействия между молекулами отсутствуют, столкновения молекул между собой и со стенками сосуда носят абсолютно упругий характер. Уравнение: ( -давление, V-объем, m– масса газа, М – молярная масса, R-газовая постоянная, Т-температура). Изопроцесс – процесс, протекающий в системе с неизменной массой при постоянном значении одного из параметров (температуре, давлении, объеме)
? Какой процесс называют адиабатический процессом? Запишите уравнение Пуассона.
Процесс, при котором отсутствует теплообмен с окружающей средой. Уравнение: V^g = const ( – давление, V-объем, g-показатель адиабаты)
? Что такое теплоемкость тела? Удельная и молярная теплоемкость?
Теплоемкость тела – количество тепла, необходимое, чтобы нагреть тело на 1 градус К. Удельная теплоемкость – количество тепла, необходимое, чтобы нагреть 1 кг вещества на 1 градус К. Молярная теплоемкость – количество тепла, необходимое, чтобы нагреть 1 моль вещества на 1 градус К.
? Работа идеального газа. Внутренняя энергия тела. Внутренняя энергия идеального газа.
Работа в термодинамике: (А-работа, – давление, DV-изменение объема). Внутренняя энергия термодинамической системы – сумма кинетической энергии теплового движения молекул (атомов) и потенциальной энергии их взаимодействия. В идеальном газе потенциальная энергия взаимодействия равна 0, поэтому (для одного моля, U-внутренняя энергия, i-степени свободы, R-газовая постоянная, Т-температура).
? Сформулируйте первое начало термодинамики. Его применение к изопроцессам.
Количество теплоты, сообщенное системе, расходуется на изменение внутренней энергии системы и совершение системой работы.
Изотермический процесс: Q=A.
Изобарный процесс: Q=DU+A.
Изохорный процесс Q=DU.
Адиабатный процесс Q=0.
? Сформулируйте второе начало термодинамики.
Отражает односторонность тепловых процессов – теплота не может сама собой переходить от холодного тела к горячему без совершения работы.
? Идеальная тепловая машина. КПД идеальной тепловой машины.
Идеальный тепловой двигатель – двигатель, не имеющий потерь на механическое трение и работающий по особому круговому циклу – циклу Карно. КПД идеального теплового двигателя (Т₁– температура нагревателя, Т₂– холодильника).
? Энтропия в термодинамике. Свойства энтропии.
(S– энтропия системы, – ее изменение). В термодинамике: энтропия замкнутой системы не убывает. Обладает свойством аддитивности – энтропия системы равна сумме энтропий тел, входящих в систему).
? Сформулируйте третье начало термодинамики (теорема Нернста).
Энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина.
? Четыре основные термодинамические функции. Принцип минимума свободной энергии, термодинамического потенциала.
В термодинамике можно получать информацию о т. системе с помощью метода термодинамических функций, характеризующих термодинамические свойства тел. Их 4: внутренняя энергия – W, энтальпия – Н, свободная энергия –F, термодинамический потенциал –G. Принцип минимума свободной энергии – если в системе, находящейся в условиях постоянного объема и постоянной температуры, протекает самопроизвольный необратимый процесс, то свободная энергия системы убывает и при достижении равновесия принимает минимальное значение ( ). Принцип минимума термодинамического потенциала – если в системе, находящейся в условиях постоянного давления и постоянной температуры, протекает самопроизвольный необратимый процесс, то термодинамический потенциал системы убывает и при достижении равновесия принимает минимальное значение. ( ).
? Реальные газы. Изотермы Ван-дер-Ваальса.
Молекулы реальных газов в отличие от идеального, занимают некоторый объем. Между ними существует притяжение. Добавки, учитывающие эти факторы, включены в уравнение Ван-дер-Ваальса. Теоретические зависимости , соответствующие при разных температурах этому уравнению, называют изотермами Ван-дер-Ваальса.
? Фазы и фазовые превращения.
Фаза – термодинамически равновесное состояние вещества, отличающееся физическими свойствами от других возможных равновесных состояний того же вещества. Фазовый переход –связан с качественными изменениями состояния вещества. Фазовый переход 1 рода –сопровождается выделением или поглощением тепла, 2 рода – скачкообразно меняющейся теплоемкостью.
? Что вы знаете о явлениях переноса? (диффузия, вязкость, теплопроводность).
Процессы переноса возникают в термодинамически неравновесных системах, когда системе невозможно приписать определенные термодинамические параметры. Диффузия – перенос массы некоторого вещества под действием градиента (перепада) его концентрации. Вязкость (внутреннее трение) – перенос импульса (за счет градиента скорости). Теплопроводность – перенос энергии за счет перепада температуры.
? Что вы знаете о распределении молекул по скоростям (распределении Максвелла)?
Максвелл вывел с помощью теории вероятностей вывел закон распределения молекул идеального газа по скоростям, т.е. формулу, определяющую, какое относительное число молекул приходится на некоторый интервал скоростей для системы, состоящей из большого числа тождественных частиц. Температура системы не меняется, силовые поля не действуют.
? Запишите барометрическую формулу. Что из себя представляет распределение Больцмана?
. Здесь р₀ –давление на уровне моря, М – молярная масса, g-ускорение свободного падения, h– высота над уровнем моря, R-газовая постоянная, Т-температура, р – изменение давления с высотой. Больцман предполагал, что молекулы находятся в поле тяготения Земли, температура не меняется с высотой. Распределение Больцмана для внешнего потенциального поля: (n₀ –концентрация молекул на нулевой высоте, n– концентрация на высоте h, к – постоянная Больцмана, Т-температура, П– потенциальная энергия молекулы газа).
? Какие физические обьекты описываются статистикой Ферми – Дирака. Что такое энергия Ферми?
Идеальный газ из фермионов – ферми-газ – описывается квантовой статистикой Ферми – Дирака. Фермионы – частицы с полуцелым спином, числа заполнения могут принимать два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц системы. При высоких температурах «квантовый» газ ведет себя подобно идеальному. Поведение такого газа при низких температурах и больших плотностях отличается от идеального, поэтому он называется вырожденным. Температурой вырождения Т₀ называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц. Если Т>>Т₀, то поведение газа описывается классическими законами.
Энергия Ферми – максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле, при нуле К называется энергией Ферми.
? Какие физические обьекты описываются статистикой Бозе –Эйнштейна. Их особенности.
Идеальный газ из бозонов – бозе – газ – описывается квантовой статистикой Бозе – Эйнштейна. Бозоны – частицы с нулевым или целым спином, числа заполнения могут принимать любые целые значения: 0,1, 2, … При высоких температурах «квантовый» газ ведет себя подобно идеальному. Поведение такого газа при низких температурах и больших плотностях отличается от идеального, поэтому он называется вырожденным. Температурой вырождения Т₀ называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц. Если Т>>Т₀, то поведение газа описывается классическими законами.
Электродинамика

Рекомендуемые страницы:
lektsia.com
Основные формулы термодинамики Условные обозначения
Обозначение
Название величины
Размерность / Значение
Формула
Абсолютная температура
K
^[4]
Давление
Па
Объём
м³
Средняя энергия молекулы
Дж
Средняя кинетическая энергия молекулы
Дж
Масса
кг
^[5]
Молярная масса
кг/моль
Постоянная Авогадро
6.0221415(10)·10²³ моль^-1
Постоянная Больцмана
1.3806505(24)·10⁻²³ Дж/К
Газовая постоянная
8.314472(15) Дж/(К·моль)
Число степеней свободы молекулы
–
Количество вещества в -й компоненте -компонентной смеси
моль
вектор с координатами
моль
Химический потенциал -й компоненты -компонентной смеси
Дж/моль
Внутренняя энергия
Дж
Энтропия
Дж/К
Энтальпия
Дж
^[6]
Изохорно-изотермический потенциал (свободная энергия Гельмгольца)
Дж
Изобарно-изотермический потенциал (свободная энергия Гиббса, свободная энтальпия)
Дж
Работа, совершённая газом
Дж
Тепло, переданное газу
Дж
Молярная теплоёмкость газа при постоянном давлении
Дж/(К·моль)
Молярная теплоёмкость газа при постоянном объёме
Дж/(К·моль)
Удельная теплоёмкость
Дж/(К·кг)
Показатель адиабаты
–
Формулы термодинамики идеального газа
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Изменение внутренней энергии газа
Работа газа
Средняя энергия молекулы газа
Средняя кинетическая энергия молекулы газа:
Внутренняя энергия газа
Теплоёмкость газа при постоянном объёме
Теплоёмкость газа при постоянном давлении
Выражение основных величин через термодинамические потенциалы
Все термодинамические потенциалы имеют свои канонические наборы переменных и используются для анализа процессов при соответствующих условиях. Так, для изотермических изохорических процессов () удобно использовать , для изотермических изобарических () — , а для изолированных систем () — .
Термодинамический потенциал  (энтропия)— независимые переменные;
Термодинамический потенциал  (свободная энергия Гельмгольца) — независимые переменные;
Термодинамический потенциал  (энергия Гиббса) — независимые переменные;
Термодинамический потенциал  (внутренняя энергия)— независимые переменные;
Фундаментальное уравнение Гиббса, экстенсивность и уравнение Гиббса — Дюгема
Выражение для полного дифференциала внутренней энергии называется фундаментальным уравнением Гиббса или просто уравнением Гиббса:
Значимость этого уравнения (и его более общих вариантов) состоит в том, что оно представляет собой тот фундамент, на котором базируется весь математический аппарат современной феноменологической термодинамики, как равновесной, так и неравновесной. По большому счёту, рассмотренные выше законы (начала) термодинамики нужны были именно для обоснования этого соотношения. Всю аксиоматику равновесной термодинамики можно свести к постулированию самого этого уравнения и свойств входящих в него термодинамических переменных.
С использованием других термодинамических потенциалов уравнение Гиббса можно переписать в следующих эквивалентных формах:
Среди термодинамических величин выделяют экстенсивные (внутренняя энергия, энтропия, объём и др.) и интенсивные (давление, температура и др.) величины. Величина называется экстенсивной, если ее значение для системы, сложенной из нескольких частей, равно сумме значений этой величины для каждой части. Предположением об экстенсивности термодинамических величин, однако, можно пользоваться, если рассматриваемые системы достаточно большие и можно пренебречь различными краевыми эффектами при соединении нескольких систем, например, энергией поверхностного натяжения. Пусть U (экстенсивная величина) является однородной функцией первого порядка от своих экстенсивных аргументов (математическое выражение аксиомы экстенсивности): для любого
Для любой дифференцируемой однородной функции первого порядка  выполняется теорема Эйлера:
Для энергии  теорема Эйлера имеет вид:
Отсюда легко следует уравнение Гиббса — Дюгема:
Это уравнение показывает, что между интенсивными переменными существует одна связь, являющаяся следствием предположения об аддитивности свойств системы. В частности, непосредственным следствием соотношений Гиббса-Дюгема является выражение для термодинамического потенциала Гиббса через химические потенциалы  компонент смеси:
studfiles.net
Законы термодинамики, теория и примеры
Начала термодинамики
Свои выводы эта наука делает на общих принципах, началах (законах термодинамики). Эти начала получены эмпирически, обобщением экспериментальных данных.
Теоретическую основу термодинамики составляют три закона.
Формулировка первого закона термодинамики
Первое начало термодинамики — это специализированная формулировка закона сохранения энергии: Подводимая к термодинамической системе теплота (Q) идет на совершение данной системой работы (A) и увеличение ее внутренней энергии (). В виде формулы первое начало запишем как:

Выражение (1) интегральная форма первого начала термодинамики.
В дифференциальном виде первое начало термодинамики представлено как:

где — бесконечно малое количество теплоты, которое подводят к системе, — элементарная работа, совершаемая системой, — бесконечно малое приращение внутренней энергии термодинамической системы.
Первое начало термодинамики показывает, как (насколько) изменяются термодинамические параметры, которые характеризуют систему, но не предсказывает направление развития процесса.
Формулировка второго закона термодинамики
Второе начало термодинамики имеет несколько формулировок. Приведем четыре из них.
Формулировка, которую дал В. Томсон. Не существует кругового процесса, единственным результатом которого является осуществление работы за счет охлаждения резервуара тепла. Здесь тепловым резервуаром считают систему тел, находящуюся в состоянии теплового равновесия и имеющую запас внутренней энергии. При этом считают, что сам резервуар не производит работы, он лишь передает теплоту.
Формулировка М. Планка. Невозможно сделать периодически работающую машину, действие которой заключается только в том, что она поднимает груз за счет получения теплоты от теплового резервуара, который охлаждается. Формулировка Планка отличается от формулировки Томсона только формой.
Формулировка Клаузиуса. Теплота не способна к самопроизвольному переходу от менее нагретого тела к телу с большей температурой. Под теплотой здесь понимают внутреннюю энергию. При этом имеется в виду не только тепловой контакт, а передача тепла любым способом. Надо учитывать, что невозможным считается не просто передача теплоты от тела с меньшей температурой, но такая передача без каких-либо изменений во внешних телах.
Формулировка через энтропию. Если термодинамический процесс происходит в изолированной системе, то энтропия не убывает. В математической форме второе начало термодинамики записывается как:

где — энтропия для состояний (1) и (2). Рост энтропии обозначает то, что система приближается к состоянию термодинамического равновесия.
Второе начало термодинамики отображает направление процесса.
Формулировка третьего начала термодинамики
Иначе третье начало термодинамики называют теоремой Нернста (по имени ученого, который ее предложил). Эту теорему можно представить в виде двух утверждений:
Если температура системы стремится к абсолютному нулю, то ее энтропия стремится к определённому конечному пределу. Причем этот предел не зависит от того в каком равновесном состоянии находится рассматриваемая система.

При абсолютном нуле температур переходы системы из одного равновесного состояния в другое происходят без изменения энтропии.

Другой формулировкой третьего начала термодинамики (теоремы Нернста) считают следующую:
Если температура термодинамической системы стремится к абсолютному нулю, то энтропия также стремится к нулю.
Поведение вещества около абсолютного нуля показывает справедливость теоремы Нернста. Объяснение третье начало термодинамики находит в квантовой механике.
Третье начало термодинамики имеет ряд важных следствий:
Около абсолютного нуля температур теплоемкости всех веществ стремятся к нулю.

Вблизи абсолютного нуля стремятся к нулю коэффициенты теплового расширения и термический коэффициент давления.

Тело невозможно охладить до абсолютного нуля.

Примеры решения задач
ru.solverbook.com

Обозначение	Название величины	Размерность / Значение	Формула
	Абсолютная температура	K
^[4]	Давление	Па
	Объём	м³
	Средняя энергия молекулы	Дж
	Средняя кинетическая энергия молекулы	Дж
	Масса	кг
^[5]	Молярная масса	кг/моль
	Постоянная Авогадро	6.0221415(10)·10²³ моль^-1
	Постоянная Больцмана	1.3806505(24)·10⁻²³ Дж/К
	Газовая постоянная	8.314472(15) Дж/(К·моль)
	Число степеней свободы молекулы	–
	Количество вещества в -й компоненте -компонентной смеси	моль
	вектор с координатами	моль
	Химический потенциал -й компоненты -компонентной смеси	Дж/моль
	Внутренняя энергия	Дж
	Энтропия	Дж/К
	Энтальпия	Дж
^[6]	Изохорно-изотермический потенциал (свободная энергия Гельмгольца)	Дж
	Изобарно-изотермический потенциал (свободная энергия Гиббса, свободная энтальпия)	Дж
	Работа, совершённая газом	Дж
	Тепло, переданное газу	Дж
	Молярная теплоёмкость газа при постоянном давлении	Дж/(К·моль)
	Молярная теплоёмкость газа при постоянном объёме	Дж/(К·моль)
	Удельная теплоёмкость	Дж/(К·кг)
	Показатель адиабаты	–

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Изменение внутренней энергии газа
Работа газа
Средняя энергия молекулы газа
Средняя кинетическая энергия молекулы газа:
Внутренняя энергия газа
Теплоёмкость газа при постоянном объёме
Теплоёмкость газа при постоянном давлении

Формулы термодинамики

Определение и формулы термодинамики

Энтропия в термодинамике

Примеры решения задач по теме «Термодинамика»

Основные формулы термодинамики

Уравнение идеального газа в термодинамике

Первое начало термодинамики. Формулы для изопроцессов

Формула теплоемкости и главная формула КПД в термодинамике

Уравнение состояния и его функции

Конспект “Термодинамика. Теория, формулы, схемы” для ОГЭ

Температура

Тепловые явления

Законы термодинамика

Дополнительные материалы по теме:

Термодинамика – Физика – Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Теплоемкость вещества

Фазовые превращения

Уравнение теплового баланса

Взаимные превращения механической и внутренней энергии

Работа идеального газа

Внутренняя энергия

Первый закон термодинамики

Первое начало термодинамики и изопроцессы

Циклы. Тепловые машины

Второе начало (второй закон) термодинамики

Сложные задачи по термодинамике

Расчет КПД циклов по графику

Свойства паров. Влажность

Поверхностное натяжение

Основные формулы молекулярной физики и термодинамики

Основные формулы термодинамики Условные обозначения

Формулы термодинамики идеального газа

Законы термодинамики, теория и примеры

Начала термодинамики

Формулировка первого закона термодинамики

Формулировка второго закона термодинамики

Формулировка третьего начала термодинамики

Примеры решения задач

Оставить комментарий Отменить ответ