Тест дифференциальные уравнения – Тесты к экзамену по учебной дисциплине “Высшая математика” (дифференциальные уравнения)

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7	8	9	10	11	12
Правильный ответ	3	1	3	4	2	4	3	1	2	3	2	2

Номер теста	13	14	15	16	17	18
Правильный ответ	4	4	1	2	5	1

Дифференциальные уравнения второго порядка

1) Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами

p и q называется уравнение вида

(8)

Алгебраическое уравнение k² + pk + q = 0 называется характеристическим уравнением для данного дифференциального уравнения, а его корни – характеристическими числами (корнями).

Для нахождения общего решения уравнения (8):

1. Запишем соответствующее характеристическое уравнение

k² + pk + q = 0.

2. В соответствии со знаком дискриминанта возможны три случая:

а) D > 0. Тогда характеристическое уравнение имеет два действительных корня k₁  k₂, и общее решение уравнения (8) имеет вид

(9)

б) D = 0. Тогда k = k₁ = k₂ – действительный корень и общее решение уравнения (8) имеет вид

(10)

в) D < 0. Тогда корни k₁, k₂ – комплексно-сопряженные числа, т. е. k_{1, 2} =   i, где ,  – действительные числа, и общее решение уравнения (8) имеет вид

(11)

Отметим, что во всех перечисленных случаях С₁, С₂ – произвольные постоянные.

Пример 9. Найти общее решение дифференциальных уравнений:

1)

2)

3)

Решение

1. Запишем характеристическое уравнение k² + k – 2 = 0.

Найдем его корни

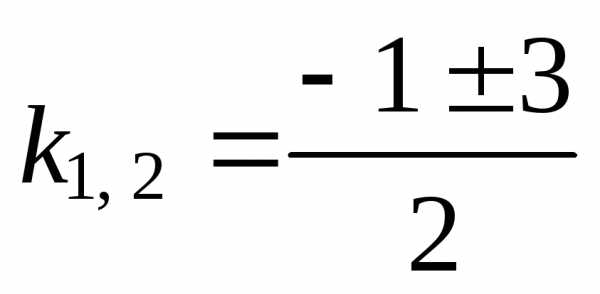; k₁ = –2; k₂ = 1.

Так как k₁ ¹ k₂ – действительные числа, то общее решение находим по формуле (9)

2. Запишем характеристическое уравнение k² + 2k + 1 = 0.

Найдем его корни

k₁ = k₂ = –1.

В этом случае общее решение находим по формуле (10)

3. Запишем характеристическое уравнение k² + 4k + 5 = 0.

Найдем его корни

Здесь

Общее решение находим по формуле (11)

Тест 19. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является уравнение вида:

1)

2)

3)

4)

5)

Тест 20. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является:

1)

2)

3)

4)

5)

Тест 21. При решении однородного дифференциального уравнения второго порядка с постоянными коэффициентами = 0:

1) вводится подстановка вида y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

2) вводится подстановка вида y = u × x, где u = u(x) – некоторая неизвестная функция;

3) составляется характеристическое уравнение k² + pk + q = 0.

Тест 22. Характеристическое уравнение k² + pk + q = 0 имеет два различных действительных корня k₁ и k₂. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид:

1) 

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3) 

4) 

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 23. Характеристическое уравнение k² + pk + q = 0 имеет комплексные корни Тогда общее решение однородного диф- ференциального уравнения второго порядка с постоянными коэффициентамиимеет вид:

1)

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3)

4)

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 24. Характеристическое уравнение k² + pk + q = 0 имеет равные корни k₁ = k₂. Тогда общее решение однородного дифферен- циального уравнения второго порядка с постоянными коэффициентами имеет вид:

1) 

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3) 

4) 

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 25. Характеристическое уравнение k² + pk + q = 0 имеет комплексные корни Тогда общее решение однородного диф- ференциального уравнения второго порядка с постоянными коэффициентамиимеет вид:

1)

2)  y = u ×

x, где u = u(x) – некоторая неизвестная функция;

3)

4)

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 26. Характеристическое уравнение k² + pk + q = 0 имеет D = 0. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид:

1)

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3)

4)

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 27. Характеристическое уравнение k² + pk + q = 0 имеет D < 0. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид:

1)

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3)

4)

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 28. Общее решение дифференциального уравнения у + 2у + у = 0 находим по формуле:

1)

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3)

4)

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 29. Общее решение дифференциального уравнения y + 4y + 5y = 0 находим по формуле:

1)

2)  y = u × x, где u = u(x) – некоторая неизвестная функция;

3)

4)

5)  y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции.

Тест 30. Общим решением дифференциального уравнения может являться функция:

1)

2)

3)

4)

5)

studfiles.net

Тест по математике на тему “Дифференциальные уравнения”

ТЕСТ по теме: «Дифференциальные уравнения» (ДУ)

ЧАСТЬ 1(теория)

1. Вставить пропущенное слово

Дифференциальным уравнением (ДУ) называется уравнение, связывающее между собой независимую переменную x, искомую функции y и её … или дифференциалы.

а) интеграл б) производные в) значения функции

2. ДУ первого порядка называется уравнение вида

а) б) в) aх+b=0

3. Уравнение вида называется

а) линейное уравнение б) ДУ с разделяющими переменными

в) ДУ второго порядка с постоянными коэффициентами

4. Характеристическое уравнение ДУ имеет вид

а) а²х+с=0 б) в)

5. Решение вида: имеет ДУ, если

а) б) в)

ЧАСТЬ 2 (практика)

1. Решить уравнение y’ = 6x

ОТВЕТ:______________________

2. Решением ДУ: является

а) б) в)

3. Решением ДУ: является

а)

4. Решить уравнение

ОТВЕТ__________________________

5. Решить уравнение

а) y’ = 3x²+5

б)

( полное решение)

Теорема (вставить формулы)

1. Пусть характеристическое уравнение имеет действительные корни , причем . Тогда общее решение уравнения

имеет вид…

2. Если характеристическое уравнение имеет один корень λ (кратности 2, т.е. λ₁= λ₂), то общее решение уравнения

имеет вид…

3. Если характеристическое уравнение не имеет действительных корней, то общее решение уравнения

имеет вид…

infourok.ru

Онлайн-тесты на oltest.ru: Математический анализ

Онлайн-тестыТестыМатематика и статистикаМатематический анализвопросы

---

91. Дифференциальное уравнение = x³ln t — (t²+1) является:
• уравнением Бернулли

92. Дифференциальное уравнение является:
• однородным уравнением первого порядка

93. Дифференциальное уравнение является:
• уравнением с разделяющимися переменными

94. Дифференциальное уравнение является:
• однородным уравнением первого порядка

95. Дифференциальное уравнение является:
• однородным уравнением первого порядка

96. Дифференциальное уравнение является:
• однородным уравнением первого порядка

97. Дифференциальное уравнение является:
• уравнением Бернулли

98. Дифференциальное уравнение является:
• уравнением с полным дифференциалом

99. Дифференциальное уравнение является:
• однородным уравнением первого порядка

100. Дифференциальное уравнение является:
• однородным уравнением первого порядка

101. Дифференциальное уравнение является:
• однородным уравнением первого порядка

102. Дифференциальное уравнение является:
• уравнением Бернулли

103. Дифференциальное уравнение = 0 является:
• уравнением с полным дифференциалом

104. Дифференциальное уравнение является:
• однородным уравнением первого порядка

105. Дифференциальное уравнение является:
• уравнением Бернулли

---

oltest.ru

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7
Правильный ответ	1	4	3	2	2	4	1

2.11. Обыкновенные дифференциальные уравнения Основные понятия

Обыкновенным дифференциальным уравнением п-го порядка называется уравнение вида

(1)

связывающее независимую переменную х, искомую функцию у = у(х) и ее производные

Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Пример 1. Примерами дифференциальных уравнений первого порядка являются: xy + sin x  y = 0, yy + (x² + y²)y = e^x; дифференциальных уравнений второго порядка являются: y + ysin x + y = 1, y + y – 2 = cos x; дифференциальных уравнений третьего порядка являются: и т. д.

Решением дифференциального уравнения (1) называется такая дифференцируемая функция y = (x), которая вместе со своими производными при подстановке в уравнение (1) обращает его в тождество. График этой функции называетсяинтегральной кривой. Процесс отыскания решений называется интегрированием дифференциального уравнения.

Общим решением дифференциального уравнения 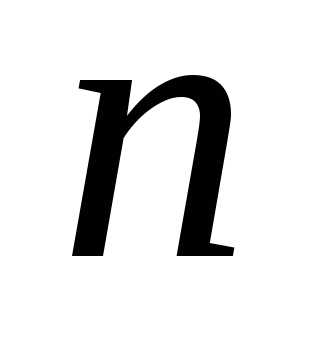-го порядка называется функция y = (x; C₁; C₂; ; C_n), которая зависит от переменной x и n независимых произвольных постоянных C₁, C₂, , C_n и вместе со своими производными обращает уравнение (1) в тождество.

Если решение задано в неявном виде (х; у) = 0, то оно называется интегралом уравнения (1).

Общее решение, заданное в неявном виде F(x; y; C₁; C₂; ; C_n) = 0, называется общим интегралом уравнения. Частным решением уравнения (1) называется решение, которое получается из общего решения, если придавать постоянным C₁, C₂, , C_n определенные числовые значения.

Задача Коши для дифференциального уравнения n-го порядка формулируется следующим образом: найти частное решение y = y(x) дифференциального уравнения (1), удовлетворяющее начальным условиям

Пример 2. Проверить, является ли функция y = Cx³ решением дифференциального уравнения 3y – xy = 0.

Решение

По условию: y = Cx³. Дифференцируя по переменной x, получаем y = (Cx³) = 3Cx². Подставляя выражения y и y в данное дифференциальное уравнение, получаем тождество 3Cx³ – x  3Cx² = 0. Следовательно, функция y = Cx³ является общим решением дифференциального уравнения 3y – xy = 0.

Пример 3. По общему решению y = Cx³ некоторого дифференциального уравнения найти частное решение, удовлетворяющее начальным условиям y(1) = 3.

Решение

Подставим y = 3 и x = 1 в общее решение и найдем значение C : 3 = = C  1³, C = 3.При подстановке C = 3 в общее решение, получаем частное решение y = 3x³.

Пример 4. Из общего интеграла x² + y² = C некоторого дифференциального уравнения найти частный интеграл, удовлетворяющий начальным условиям y(4) = –3.

Решение

Подставим y = –3 и x = 4 в общий интеграл и найдем значение C : 4² + (–3)² = C, 25 = C. Из общего интеграла при C = 25 получаем частный интеграл x² + y² = 25.

Тест 1. Дифференциальным уравнением является уравнение:

1) x + 4 = 7;

2)

3)

4)

5)

Тест 2. Дифференциальным уравнением первого порядка является уравнение:

1)

2)

3)

4)

5)

Тест 3. Дифференциальным уравнением второго порядка является:

1)

2)

3)

4)

5)

Тест 4. Дифференциальным уравнением третьего порядка является:

1)

2)

3)

4)

5)

Тест 5. Решением дифференциального уравнения является функция:

1)

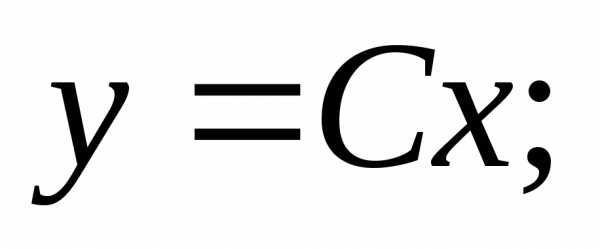
2)

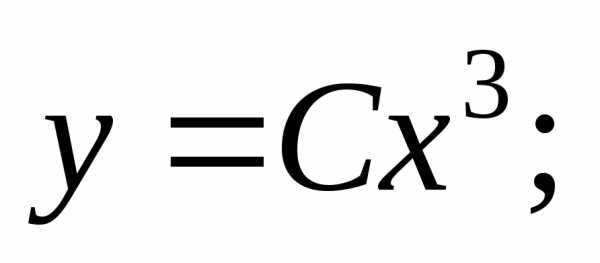
3)

4)

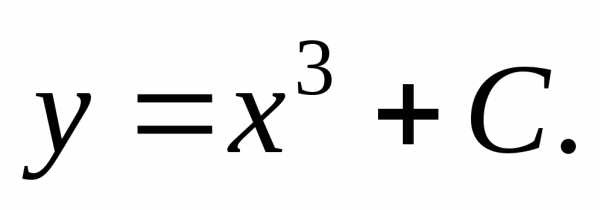
Тест 6. Общим решением некоторого дифференциального уравнения является функция y = Cx³, тогда частным решением этого дифференциального уравнения, удовлетворяющим начальным условиям y(1) = 3, является:

1)

2)

3)

4)

5)

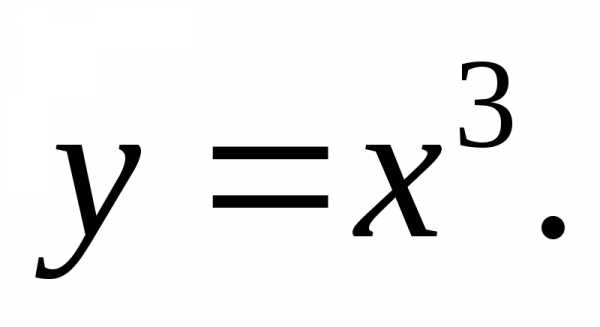
Тест 7. Общий интеграл некоторого дифференциального уравнения имеет вид x² + y² = C, тогда частным интегралом этого дифференциального уравнения, удовлетворяющим начальным условиям y(4) = –3, является:

1)

2)

3)

4)

5)

studfiles.net

Тест 5. Дифференциальные уравнения

Часть V. Тесты

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

Тест 5

Численное решение обыкновенных дифференциальных уравнений

Начало теста.

1.Неявным методом Эйлера для уравнения ′( ) = ( , ( )) является разностное уравнение

+1 = − (+1, )	+1 = + ( ,+1)
+1 = + (+1,+1)	+1 = + ( , )

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

2.Явным методом Эйлера для уравнения ′( ) = ( , ( )) является разностное уравнение

+1 = − (+1, )	+1 = + ( ,+1)
+1 = + (+1,+1)	+1 = + ( , )

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню			Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
3. Порядок точности метода+1 = +			(3 − −1) равен
		2
1	2	3	4

Часть V. Тесты

Тест 5. Дифференциальные уравнения

	Меню				Вверх Назад Вперёд Пред. След. Указатель Помощь Экран
	4. Порядок точности метода+1		= +		( + +1) равен
				2
	1	2		3	4

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

5.Интервал устойчивости явного метода Эйлера, определённый на модельном уравнении ′( ) = ( ), < 0, равен

(−1, 0)	(−∞, 0) (2, +∞)
(−2, 0)	(0, 2)

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

6.Интервал устойчивости неявного метода Эйлера, определённый на модельном уравнении ′( ) = ( ), < 0, равен

(−1, 0)	(−∞, 0) (2, +∞)
(−2, 0)	(0, 2)

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

7.Отметьте правильную замену 2-йпроизводной в случае равноотстоящих узлов:

′′( ) =

′′( ) =

′′( ) =

′′( ) =

( −1) − 2 ( ) + (+1)+ ( 2)

2

( −1) + 2 ( ) + (+1)+ ( 2)

2

( −1) − 2 ( ) + (+1)+ ( 2) 2

( −1) + 2 ( ) + (+1)+ ( 2) 2

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

8.Найденное методом Галёркина приближенное решение 1 граничной задачи

′′ = 1, (0) = (1) = 0

свыбором в качестве базисной функции 1( ) = (1 − ) имеет вид

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

9. Погрешность аппроксимации разностной схемы

¯ + = 0,

(0) = (1) = 0,

вычисленная на решении задачи

′′ +′ = 0,

(0) = (1) = 0

Часть V. Тесты

Тест 5. Дифференциальные уравнения

Меню	Вверх Назад Вперёд Пред. След. Указатель Помощь Экран

10. Метод разностной прогонки предназначен для решения СЛАУ общего вида

СЛАУ с 5-диагональнойматрицей

СЛАУ с 3-диагональнойматрицей

систем нелинейных уравнений

studfiles.net

1-61 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Вопрос 098 Решите уравнение: Ответ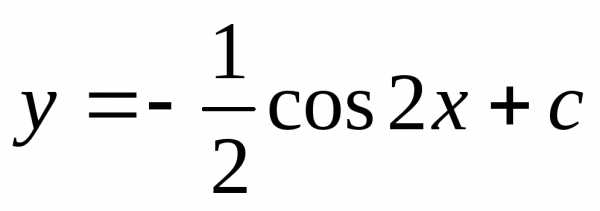

Вопрос 108 Решите уравнение: Ответ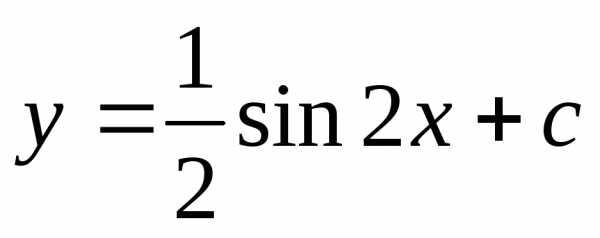

Вопрос 109 Решите уравнение: Ответ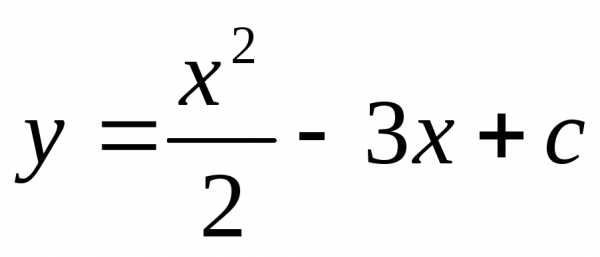

Вопрос 110 Решите уравнение: Ответ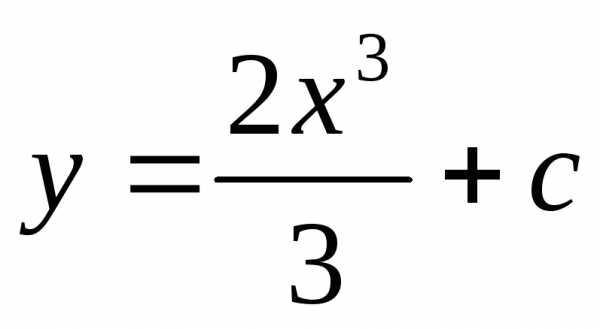

Вопрос 111 Решите уравнение: Ответ

Вопрос 116 Решите уравнение: Ответ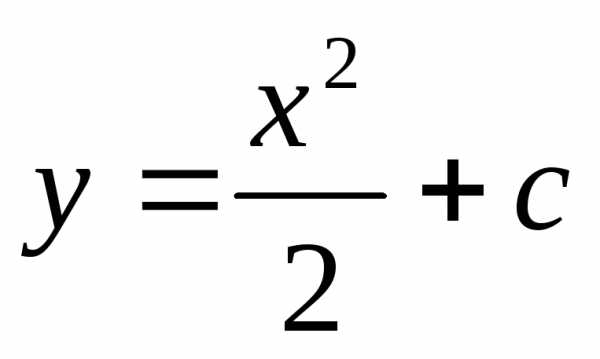

Вопрос 117 Решите уравнение: Ответ

Вопрос 118 Решите уравнение: Ответ

Вопрос 119 Решите уравнение: Ответ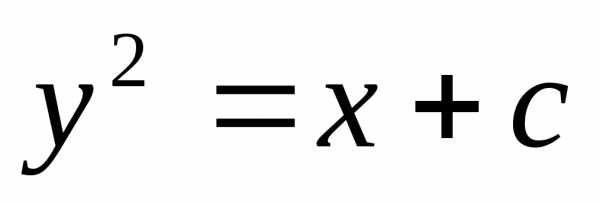

Вопрос 120 Решите уравнение: Ответ

Вопрос 121 Решите уравнение: Ответ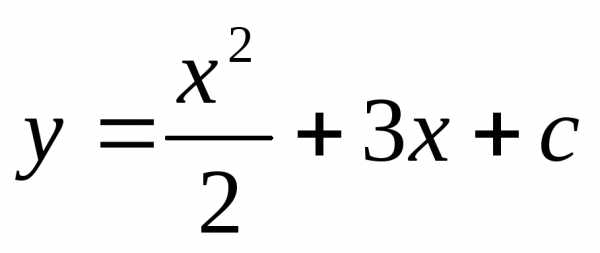

Вопрос 122 Решите уравнение: Ответ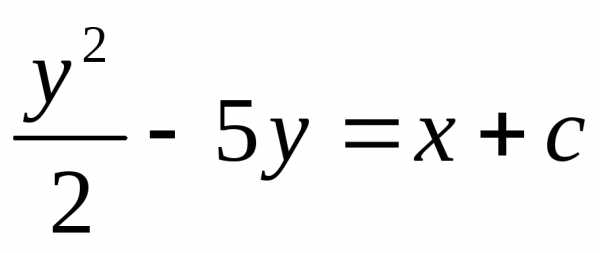

Вопрос 123 Решите уравнение: Ответ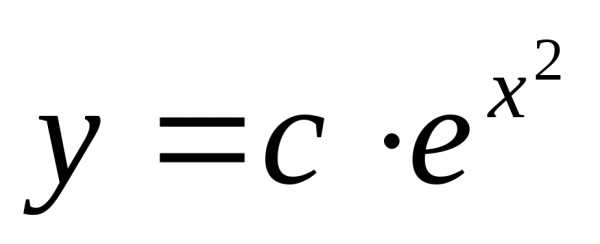

Вопрос 124 Решите уравнение: Ответ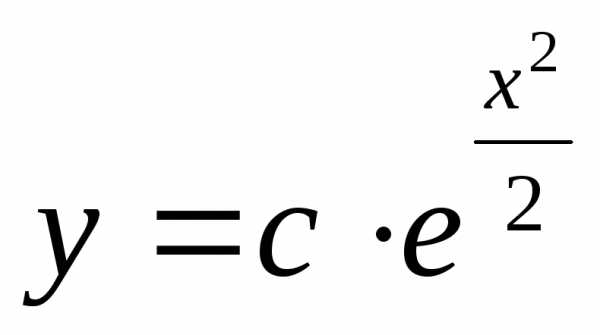

Вопрос 127 Найти общее решение дифференциального уравнения Ответ

Вопрос 128 Найти общее решение дифференциального уравнения 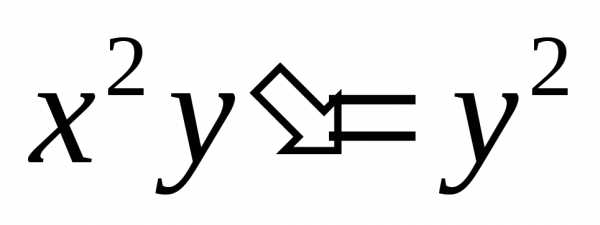Ответ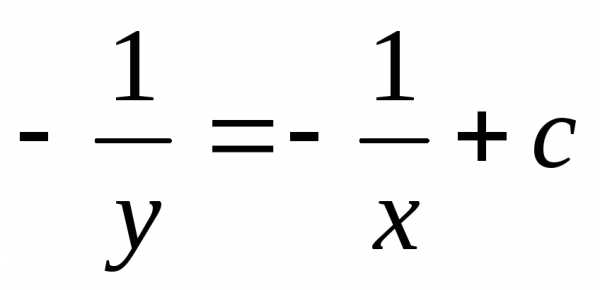

Вопрос 129 Найти общее решение дифференциального уравнения Ответ

Вопрос 130 Найти общее решение дифференциального уравнения 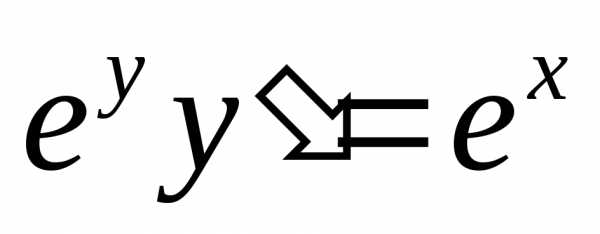Ответ

Вопрос 131 Найти общее решение дифференциального уравнения Ответ

Вопрос 132Найти общее решение дифференциального уравнения Ответ

Вопрос 133 Найти общее решение дифференциального уравнения Ответ

Вопрос 239. Общий интеграл или общее решение дифференциального уравнения 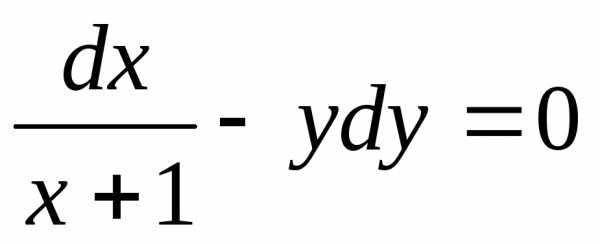есть функция: Ответ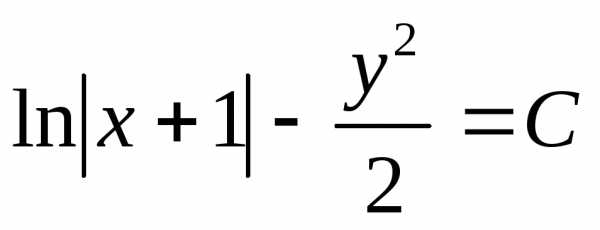

Вопрос 247 Найти общее решение дифференциального уравнения Ответ

Вопрос 134Найти общее решение дифференциального уравнения Ответ

Вопрос 135Найти общее решение дифференциального уравнения Ответ

Вопрос 097 Решите уравнение: Ответ

Вопрос 099 Решите уравнение: Ответ

Вопрос 100 Решите уравнение: , еслиОтвет

Вопрос 101 Решите уравнение: , если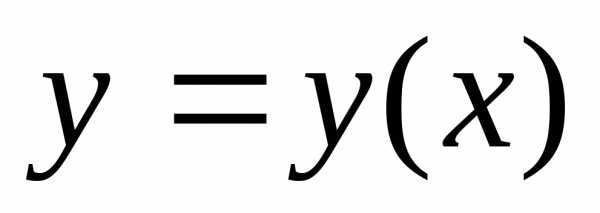Ответ

Вопрос 112 Решите уравнение: , еслиОтвет

Вопрос 113 Решите уравнение: , если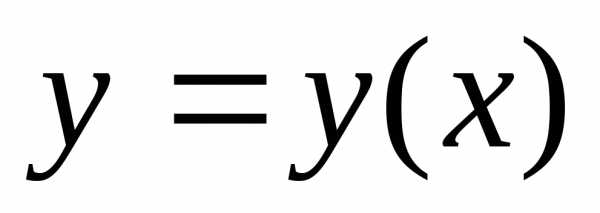Ответ у=

Вопрос 114 Решите уравнение: , если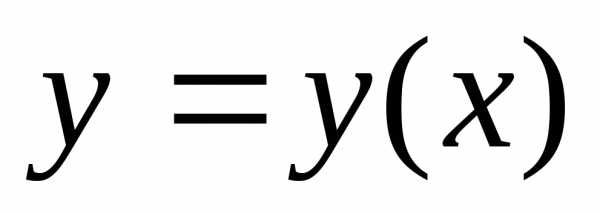Ответ

Вопрос 115 Решите уравнение: , еслиОтвет

Вопрос 273 Решите уравнение: , если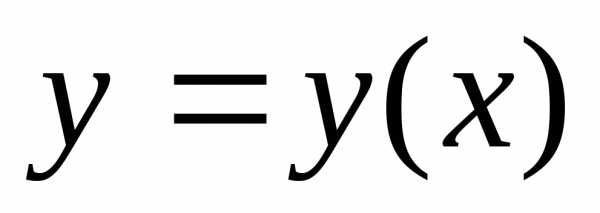Ответ

Вопрос 303 Решить уравнение Ответ

Вопрос 304 Решить уравнение Ответ

Вопрос 305 Решить уравнение Ответ

Вопрос 306 Решить уравнение Ответ

Вопрос 307 Решить уравнение Ответ

Вопрос 145 Решить уравнение Ответ

Вопрос 236. Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами имеет вид Ответ

Вопрос 240. Найти решение дифференциального уравнения y´´-2y´+2y=0 Ответ

Вопрос 105 Если дифференциальное уравнение первого порядка, то функция называется его …. Ответ решением

Вопрос 106 В дифференциальном уравнении, кривая заданная уравнением определяет … кривую

Ответ интегральную

Вопрос 107 Дифференциальное уравнение удовлетворяющее начальным условиям, называется …. решением

Ответ частным

Вопрос 136 Найти общее решение дифференциального уравнения Ответ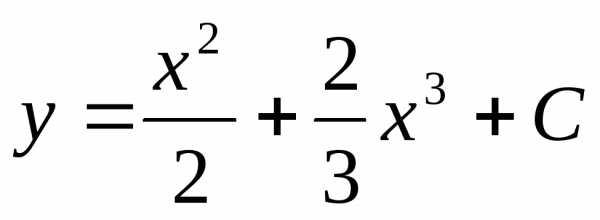

Вопрос 137 Найти общее решение дифференциального уравнения Ответ

Вопрос 238. Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами имеет вид: Ответ

Вопрос 138 Найти общее решение дифференциального уравнения Ответ

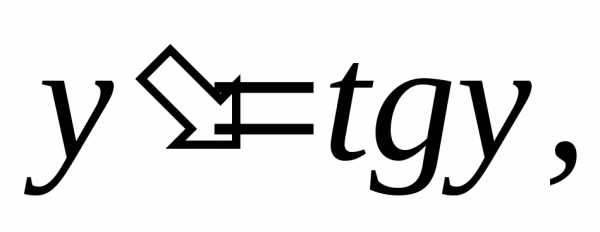
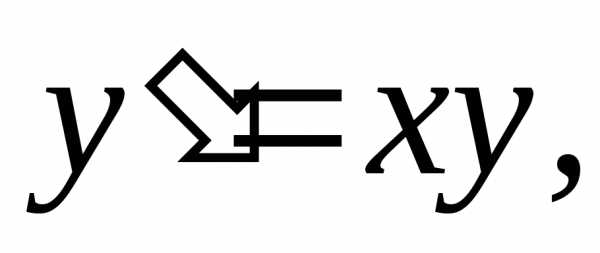
Вопрос 200 Какие из следующих дифференциальных уравнений первого порядка являются линейными: 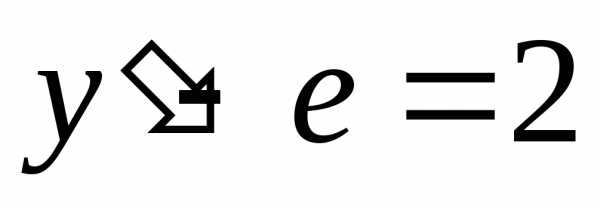.Ответ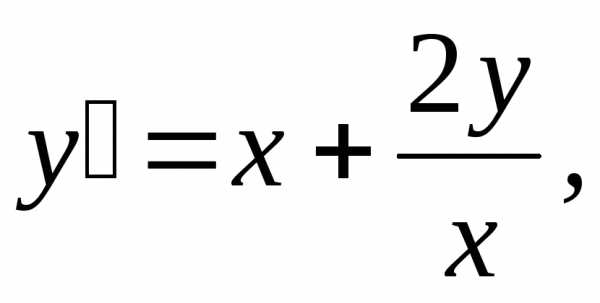

Вопрос 201 Уравнение Бернули, это уравнение вида: Ответ

Вопрос 202 Какие из следующих дифференциальных уравнений первого порядка являются уравнениями с разделяющими переменными: ,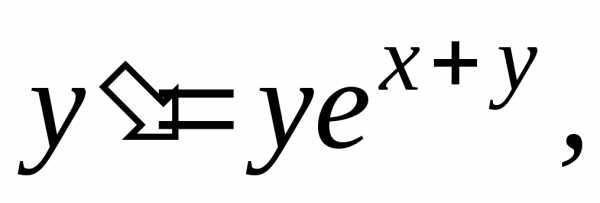.Ответ

Вопрос 215 Укажите дифференциальное уравнение n–го порядка: Ответ

Вопрос 237. Уравнение является дифференциальным уравнением:

Ответ в полных дифференциалах.

Вопрос 245. Дифференциальным уравнением 1-го порядка называется … Ответ уравнение связывающие независимую переменную, искомую функцию и производную

Вопрос 246 Дифференциальное уравнение называется однородным, если функция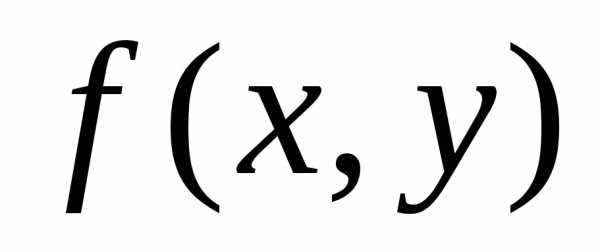есть

Ответ однородная функция нулевого порядка

Вопрос 248. Дифференциальным уравнением п-го порядка называется уравнение … Ответ связывающие независимую переменную, искомую функцию и производную п-го порядка

Вопрос 250 Дифференциальное уравнение называется уравнением в полных дифференциалах, есл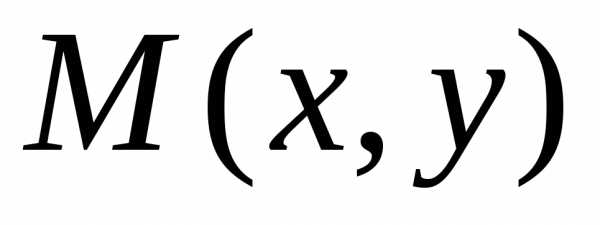иинепрерывные функции, имеющие непрерывные частные производные 1-го порядка и удовлетворяющие условиюОтвет

Вопрос 251 Пусть и– решения дифференциального уравнения, в каком из следующих случаев они являются линейно независимыми:

Ответ

Вопрос 253 Линейные неоднородные дифференциальные уравнения, это уравнения Ответ содержащие искомую функцию, производные и правую часть специального вида.

Вопрос 268 Какие из следующих формул могут определять общее решение некоторого линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами: Ответ .

studfiles.net

Тест по математике на тему «Дифференциальные уравнения» — iitu

ТЕСТ по теме: «Дифференциальные уравнения» (ДУ)

ЧАСТЬ 1(теория)

1. Вставить пропущенное слово

Дифференциальным уравнением (ДУ) называется уравнение, связывающее между собой независимую переменную x, искомую функции y и её … или дифференциалы.

а) интеграл б) производные в) значения функции

2. ДУ первого порядка называется уравнение вида

а) б) в) aх+b=0

3. Уравнение вида называется

а) линейное уравнение б) ДУ с разделяющими переменными

в) ДУ второго порядка с постоянными коэффициентами

4. Характеристическое уравнение ДУ имеет вид

а) а²х+с=0 б) в)

5. Решение вида: имеет ДУ, если

а) б) в)

ЧАСТЬ 2 (практика)

1. Решить уравнение y’ = 6x

ОТВЕТ:______________________

2. Решением ДУ: является

а) б) в)

3. Решением ДУ: является

а)

4. Решить уравнение

ОТВЕТ__________________________

5. Решить уравнение

а) y‘ = 3x²+5

б)

( полное решение)

Теорема (вставить формулы)

1. Пусть характеристическое уравнение имеет действительные корни , причем . Тогда общее решение уравнения

имеет вид…

2. Если характеристическое уравнение имеет один корень λ (кратности 2, т.е. λ₁= λ₂), то общее решение уравнения

имеет вид…

3. Если характеристическое уравнение не имеет действительных корней, то общее решение уравнения

имеет вид…

---

Внимание, только СЕГОДНЯ!

iitu.ru