Примеры решения задач по теоретической механике.
Решение задач по технической механике
Примеры решения задач по теоретической механике
Принципы и способы решения задач теоретической механики рассмотрены на простейших примерах, где необходимо определить какие-либо силовые факторы, действующие на тело, скорость, ускорение, работу, мощность и другие физические величины. На основе результатов расчетов с использованием приемов теоретической механики приступают к решению задач методами сопротивления материалов, а затем переходят к расширенным практическим вопросам, которые ставит раздел “Детали машин”.
Решение задачи с использованием метода кинетостатики
Определить силу натяжения в канате крановой установки, поднимающей груз G с ускорением а.
Исходные данные:
Масса груза m = 5 тонн;
Ускорение груза а = 2 м/сек2;
Ускорение свободного падения принять равным g = 10
Силой сопротивления воздуха пренебречь.
Решение:
Для решения задачи используем метод кинетостатики (принцип Д’Аламбера), который основывается на введении понятия силы инерции и приведении подвижной системы к состоянию условного равновесия. Это позволяет использовать для решения задач Кинематики способы и методы Статики.
Чтобы понять сущность этого принципа, представьте себе просмотр киносюжета, кадры которого сняты при малой скоростью съемки, и движение тел на экране словно состоит из отдельных прерывистых фрагментов (или – как передвигается робот – урывками). Т. е. движение тела рассматривается состоящим из отдельных крохотных моментов, и в каждый такой микромомент тело находится в состоянии равновесия под действием движущей силы и силы инерции, сопротивляющейся движению.
Итак, для решения этой задачи следует рассмотреть условие равновесия груза, который поднимается с ускорением а под действием некоторой системы сил. Реально к грузу приложены две силы – сила натяжения каната, и сила тяжести груза. Очевидно, что эти силы не равны по величине, поскольку груз поднимается с ускорением, значит, сила натяжения в канате больше силы тяжести.
Введем в систему упомянутую выше силу инерции, которая условно уравнивает разницу между силой натяжения в канате и силой тяжести, тогда груз будет находиться в условном равновесии.
Составим уравнение этого равновесия: Fк – G – Fин = 0,
где: Fк – сила натяжения каната (тяга крановой установки), G – вес груза, Fин – сила инерции.
Очевидно, что условие равновесия будет соблюдаться, если искомая сила Fк будет равна сумме сил тяжести и инерции.
Силу тяжести G и силу инерции Fин можно вычислить, используя второй закон Ньютона, как произведение массы тела на ускорение, вызываемое этими силами:
Fин = ma, тогда:
Fк = G + Fин = mg + ma = m(g + a) = 5000 × (10 + 2) = 60 000 Н = 60 кН.
Задача решена.
***
Решение задачи на на трение
Определить силу F, необходимую для равномерного перемещения бруса по горизонтальной шероховатой поверхности.
Исходные данные:
Коэффициент трения между брусом и поверхностью f = 0,6;
Масса бруса m = 12 кг;
Ускорение свободного падения g принять равным 10 м/сек
Решение:
Эта задача решается с использованием законов движения тел под действием сил трения скольжения.
Для того, чтобы тело равномерно перемещалось по поверхности без ускорения, сила трения должна быть равна силе тяги (т. е. искомой силе F): F = Fтр.
Поскольку поверхность горизонтальная, сила трения равна весу тела, умноженному на коэффициент трения:
Fтр = fG, где: G = mg – вес тела.
Тогда:
F = Fтр = fG = 0,6×12×10 = 72 Н.
Задача решена.
***
Решение задачи из раздела Статика
Найти силу натяжения упругой нити, удерживающей груз в состоянии равновесия на идеально гладкой наклонной плоскости.
Исходные данные:
Вес груза G = 100 Н,
угол наклона поверхности указан на рисунке.
Решение:
Поскольку груз находится в равновесии, решение задачи возможно с применением методов Статики, т. е. с на основе анализа причин, по которым тело находится в неподвижном состоянии (в равновесии).
Итак, сначала необходимо определить – под влиянием каких сил груз находится в состоянии равновесия.
Кроме силы тяжести G, на груз наложены две связи, ограничивающие его перемещение: гибкая связь (упругая нить) и наклонная плоскость. Реакция гибкой связи Rн
Задача может быть решена двумя методами.
Определив направление реакций, можно решить эту задачу графическим методом, построив силовой треугольник, который будет замкнутым, поскольку векторная сумма сил равна нулю (равновесие груза).
Для построения векторной цепочки (в нашем случае – треугольник) откладываем силу тяжести груза G в определенном масштабе (поскольку нам известны и направление, и величина этой силы).
Для реакций мы знаем лишь их направление (величина сил неизвестна). От концов вектора силы G откладываем отрезки прямых, параллельные реакциям, и точка пересечения этих прямых позволит нам получить искомый треугольник сил. Теперь можно определить величину любой из реакций, измерив ее длину на чертеже линейкой и умножив на масштаб чертежа, который задает сила G. Порядок построений показан на
Аналитическим методом эта задача решается с помощью уравнений равновесия, исходя из условия, что сумма проекций всех сил на любую координатную ось равна нулю. Разумеется, необходимо выбрать удобную систему координат, тогда для решения задачи потребуется минимальное количество уравнений.
Поскольку нам необходимо найти силу натяжения нити (реакция Rн), то расположим координатную ось y так, чтобы реакция плоскости (Rп) была ей перпендикулярна (рис. в). Тогда реактивная сила Rп проецируется в точку, т. е. в ноль, и для решения задачи потребуется лишь сумма проекций сил G и Rн на ось y:
ΣFy = 0 => Rн – G cos60˚ = 0, откуда найдем искомую реакцию Rн:
Задача решена двумя методами.
***
Пример решения задачи из раздела Динамика
Какую работу W необходимо совершить, чтобы повалить кубический предмет на боковую грань?
Исходные данные:
Длина грани кубического предмета (ящика) a = 1 м;
Масса кубического предмета m = 100 кг;
Центр тяжести кубического предмета расположен в точке пересечения диагоналей;
Ускорение свободного падения принять равным g = 10 м/сек2
Решение:
Как известно, работа любой силы равна произведению модуля этой силы на величину перемещения тела, вызванного действием этой силы.
Длину диагонали грани можно найти по теореме Пифагора, или с применением тригонометрических зависимостей.
Тогда:
W = mgΔh = mgа(√2 – 1)/2 = 100×10×1×(1,414 – 1)/2 ≈ 207 Дж
***
Пример решения задачи из раздела кинематика
Автомобиль движется между городами Барнаул и Камень-на-Оби с постоянной скоростью v = 60 км/час.
Определить частоту вращения n колес автомобиля и сколько оборотов n
Расстояние между городами принять равным l = 180 км.
Решение:
Для определения числа оборотов каждого колеса по пути следования, надо всю длину маршрута (180 км = 180 000 м) разделить на длину окружности колеса (lк = πd), тогда:
nl = 180 000/πd ≈ 95541 оборотов.
Для определения частоты вращения колеса можно определить время в пути автомобиля между городами
(t = S/v = 3 часа, т. е. 180 минут) и, разделив количество оборотов n
Получим:
n = 95541/180 ≈ 530 об/мин.
Задача решена.
***
Пример решения задачи из Статики
Балка висит на гибких связях горизонтально, нагружена собственным весом G, силой F и находится в состоянии равновесия.
Определить реакцию гибкой связи RА.
Исходные данные:
Вес балки G = 1200 Н;
Сила F = 600 Н;
Расположение гибких связей и силовых факторов приведено на схеме.
Решение:
Из условия равновесия балки: сумма моментов всех приложенных к ней сил относительно любой точки балки равна нулю.
Поскольку по условию задания нас интересует лишь реакция RA, то уравнение моментов составляем относительно точки В (момент неизвестной силы RВ относительно этой точки равен нулю), при этом силы, стремящиеся повернуть балку вокруг точки В по часовой стрелке, мы считаем положительными, против часовой стрелки – отрицательными.
Тогда:
4RA – 2G – F = 0, откуда: RA = (2G + F)/4 = 750 Н.
Задача решена.
***
Решение задачи из раздела Динамика
Для изображенной на схеме передачи определить вращающий момент Т2 на ведомом валу.
Исходные данные:
Мощность на ведущем валу Р1 = 8 кВт;
Угловая скорость ведущего вала ω1 = 40 рад/сек;
Коэффициент полезного действия передачи η = 0,97;
Передаточное число передачи u = 4.
Решение:
Сначала определим мощность Р2 на ведомом валу редуктора, с учетом потерь (исходя из величины КПД):
Р2 = ηР1 = 0,97×8000 = 7760 Вт
Для определения мощности ведомого вала необходимо знать его угловую скорость ω2, которая определяется из соотношения u = ω1/ω2, где u = 4 – передаточное число передачи. Получаем: ω2 = ω1/u = 10 рад/сек.
Вращающий момент равен отношению мощности ведомого вала к его угловой скорости:
Т2 = Р2/ω2 = 7760/10 = 776 Нм
Задача решена.
***
Задача из раздела динамика
Лебедка состоит из цилиндрической передачи и барабана, к которому посредством троса прикреплен груз G. Определить требуемую мощность Рм электродвигателя лебедки, если скорость подъема груза должна составлять v = 4 м/сек.
Исходные данные:
Вес груза G = 1000 Н;
Скорость подъема груза v = 4 м/сек;
КПД барабана лебедки ηб = 0,9;
КПД цилиндрической передачи ηц = 0,98;
Элементы конструкции приведены на схеме.
Решение:
Определим мощность на выходе из привода, необходимую для подъема груза с данной скоростью:
Р2 = Gv = 1000×4 = 4000 Вт.
Чтобы найти требуемую мощность электродвигателя для лебедки необходимо определить КПД всей передачи:
ηп = ηб×ηц = 0,9×0,98 = 0,882.
Требуемая мощность электродвигателя:
Рм = Р2 / ηп= 4000/0,882 ≈ 4535 Вт.
Задача решена.
***
Пример расчета пространственной конструкции или рамы
Правильные ответы на вопросы тестов:
Тест №1 2-4-1-3-4
Тест №2 1-3-4-4-1
Тест №3 3-1-1-2-2
Тест №4 4-2-2-3-3
Тест №5 2-1-1-1-4
Тест №6 3-2-4-2-3
Тест №7 2-2-1-1-3
Тест №8 1-4-1-2-2
Тест №9 3-2-4-4-1
Тест №10 1-1-4-2-3
k-a-t.ru
Краткая теория по теоретической механике
Напишите или выберитеМеханикаТеоретическая механикаСопротивление материаловТеория машин и механизмовДетали машинВысшая математикаФизикаНачертательная геометрияИнформатикаАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАрхитектура и строительствоБазы данныхВысшая математикаГеометрияГидравликаДетали машинИздательское делоИнформатикаИнформационная безопасностьИнформационные технологииМатериаловедениеМашиностроениеМеталлургияМетрологияМеханикаМорская техникаНаноинженерияНачертательная геометрияПолиграфияПриборостроение и оптотехникаПрограммированиеПроцессы и аппаратыРабота на компьютереРадиофизикаСопротивление материаловТелевидениеТеоретическая механикаТеория вероятностейТеория машин и механизмовТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТранспортные средстваФизикаХолодильная техникаЧертежиЧерчениеЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЯдерная энергетика и теплофизикаЯдерные физика и технологииАнализ хозяйственной деятельностиАнтикризисное управлениеБанковское делоБизнес-планированиеБухгалтерский учет и аудитВнешнеэкономическая деятельностьГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиИнвестицииИнновационный менеджментКредитЛогистикаМаркетингМеждународные рынкиМенеджментМенеджмент организацииМикро-, макроэкономикаНалогиОрганизационное развитиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментСервисСтандартизацияСтатистикаСтратегический менеджментСтрахованиеТаможенное делоТеория управленияТовароведениеТорговое делоТуризмУправление персоналомФинансовый менеджментФинансыЦенообразование и оценка бизнесаЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализАрхеологияАстрономияБезопасность жизнедеятельностиБиологияБиотехнологияВетеринарияВоспроизводство и переработка лесных ресурсовГеографияГеодезияГеологияГидрометеорологияЕстествознаниеКартография и геоинформатикаМедицинаНефтегазовое делоПочвоведениеПриродообустройство и водопользованиеСельское и рыбное хозяйствоХимияХирургияЭкологияБиблиотечно-информационная деятельностьДизайнДокументоведение и архивоведениеЖурналистикаИскусствоИсторияКонфликтологияКриминалистикаКультурологияЛитератураЛогикаМеждународные отношенияМузыкаПедагогикаПолитологияПраво и юриспруденцияПсихологияРежиссураРеклама и PRРелигияСвязи с общественностьюСоциальная работаСоциологияСтрановедениеТеатроведениеФизическая культураФилософияЭтикаЯзыки (переводы)Языкознание и филология
Выберите вид работы…Решение задачКонтрольная работаКурсовая работаПомощь на экзаменеОтветы на вопросыОтчёт по практикеЧертёжДипломная работаРефератМонографияБизнес-планТворческая работаЭссеСочиненияРецензияДокладНабор текстаМагистерская диссертацияКандидатская диссертацияСтатьяЛабораторная работаПереводПрезентацииПовышение уникальности текстаДругое
isopromat.ru
Примеры решения задач по сопротивлению материалов
В этом разделе рассмотрены примеры решения задач по сопромату, с необходимыми пояснениями и графическими иллюстрациями.
- Определение опорных реакций
- Расчеты на прочность
- Построение эпюр
- Расчет балки
- Расчет напряжений
- Проверка на прочность
- Расчет деформаций и перемещений
- Расчеты на жесткость
- Растяжение-сжатие
- Кручение
- Изгиб
- Другие примеры
- Олимпиадные задачи
Задачи по условию
Определение опорных реакций
Примеры определения опорных реакций при растяжении-сжатии и плоском поперечном изгибе, определение неизвестного крутящего момента для вала.
Расчеты на прочность
Примеры решения задач по расчету стержней, балок и валов на прочность.
Подбор сечений, проверка на прочность и определение грузоподъемности.
Построение эпюр
Примеры построения эпюр внутренних усилий, напряжений и перемещений при растяжении-сжатии, кручении, изгибе и других видах деформации.
Расчет напряжений
Примеры расчетов нормальных, касательных и главных напряжений при различных видах деформации. Рассмотрены аналитические и графический способ (круг Мора) определения напряжений.
Расчет деформаций и перемещений
Примеры расчетов деформации бруса при различных видах нагружения.
Задачи по видам нагружения
Растяжение-сжатие
Примеры решения задач и расчетно-графических работ по теме растяжение-сжатие стержней и стержневых систем.
Кручение
Примеры решения задач и РГР на тему кручение валов.
Изгиб
Примеры решения задач и РГР по теме плоский поперечный изгиб балок.
Расчет балки
Примеры расчетов двухопорных и консольных балок.
Примеры решения задач для олимпиад по сопротивлению материалов.
Другие задачи
- Определение положение центра тяжести сложного сечения
- Определение положения центра тяжести составной фигуры, расчет главных центральных моментов и радиусов инерции, построение эллипса инерции
- Определение реакций в опорах рамы
- Построение эпюр N, Q и M для рамы
- Проверка построенных эпюр в рамах
- Перемещение точки нити перекинутой через блок
isopromat.ru
Примеры решения задач. Статика | Лекции и примеры решения задач механики
Напишите или выберитеМеханикаТеоретическая механикаСопротивление материаловТеория машин и механизмовДетали машинВысшая математикаФизикаНачертательная геометрияИнформатикаАвиационная и ракетно-космическая техникаАвтоматизация технологических процессовАвтоматика и управлениеАрхитектура и строительствоБазы данныхВысшая математикаГеометрияГидравликаДетали машинИздательское делоИнформатикаИнформационная безопасностьИнформационные технологииМатериаловедениеМашиностроениеМеталлургияМетрологияМеханикаМорская техникаНаноинженерияНачертательная геометрияПолиграфияПриборостроение и оптотехникаПрограммированиеПроцессы и аппаратыРабота на компьютереРадиофизикаСопротивление материаловТелевидениеТеоретическая механикаТеория вероятностейТеория машин и механизмовТеплоэнергетика и теплотехникаТехнологические машины и оборудованиеТехнология продовольственных продуктов и товаровТранспортные средстваФизикаХолодильная техникаЧертежиЧерчениеЭлектроника, электротехника, радиотехникаЭнергетическое машиностроениеЯдерная энергетика и теплофизикаЯдерные физика и технологииАнализ хозяйственной деятельностиАнтикризисное управлениеБанковское делоБизнес-планированиеБухгалтерский учет и аудитВнешнеэкономическая деятельностьГостиничное делоГосударственное и муниципальное управлениеДеловой этикетДеньгиИнвестицииИнновационный менеджментКредитЛогистикаМаркетингМеждународные рынкиМенеджментМенеджмент организацииМикро-, макроэкономикаНалогиОрганизационное развитиеПроизводственный маркетинг и менеджментПромышленный маркетинг и менеджментСервисСтандартизацияСтатистикаСтратегический менеджментСтрахованиеТаможенное делоТеория управленияТовароведениеТорговое делоТуризмУправление персоналомФинансовый менеджментФинансыЦенообразование и оценка бизнесаЭконометрикаЭкономикаЭкономика предприятияЭкономика трудаЭкономическая теорияЭкономический анализАрхеологияАстрономияБезопасность жизнедеятельностиБиологияБиотехнологияВетеринарияВоспроизводство и переработка лесных ресурсовГеографияГеодезияГеологияГидрометеорологияЕстествознаниеКартография и геоинформатикаМедицинаНефтегазовое делоПочвоведениеПриродообустройство и водопользованиеСельское и рыбное хозяйствоХимияХирургияЭкологияБиблиотечно-информационная деятельностьДизайнДокументоведение и архивоведениеЖурналистикаИскусствоИсторияКонфликтологияКриминалистикаКультурологияЛитератураЛогикаМеждународные отношенияМузыкаПедагогикаПолитологияПраво и юриспруденцияПсихологияРежиссураРеклама и PRРелигияСвязи с общественностьюСоциальная работаСоциологияСтрановедениеТеатроведениеФизическая культураФилософияЭтикаЯзыки (переводы)Языкознание и филология
Выберите вид работы…Решение задачКонтрольная работаКурсовая работаПомощь на экзаменеОтветы на вопросыОтчёт по практикеЧертёжДипломная работаРефератМонографияБизнес-планТворческая работаЭссеСочиненияРецензияДокладНабор текстаМагистерская диссертацияКандидатская диссертацияСтатьяЛабораторная работаПереводПрезентацииПовышение уникальности текстаДругое
isopromat.ru
Теоретическая механика | Лекции и примеры решения задач механики
Теоретическая механика – наука об общих законах механических взаимодействий между материальными телами, а также об общих законах движения тел по отношению друг к другу.
Механическое взаимодействие между материальными телами является простейшим и одновременно самым распространенным видом взаимодействия между физическими объектами. Механическое движение, будучи самым простым видом движения, является фундаментальным свойством материи.
Основные разделы
Теоретическая механика, преподаваемая в техническом вузе, содержит три раздела: кинематику, статику и динамику.
- Кинематика – часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.
- Статика – это учение о равновесии совокупности тел некоторой системы отсчета.
- Динамика – часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.
Объекты и цель изучения
Целью изучения дисциплины «Теоретическая механика» является формирование необходимой базы знаний для изучения других технических дисциплин по профилю будущей профессиональной деятельности, таких как сопротивление материалов и теория механизмов и машин.
В разделах теоретической механики изучаются общие законы движения и равновесия материальных систем; исследуются простейшие логические модели, на которые могут быть разложены объекты техники и природы, дается научный метод познания законов механического движения систем.
Задачи курса
Задачами курса теоретической механики являются:
- выработка практических навыков решения задач механики путем изучения методов и алгоритмов построения математических моделей движения или состояния рассматриваемых механических систем, а также методов исследования этих математических моделей;
- воспитание естественнонаучного мировоззрения на базе изучения основных законов природы и механики.
Учебные материалы по теормеху
На нашем сайте Вы можете просмотреть и использовать для изучения курса теоретической механики следующие учебные материалы:
Другие разделы механики:
isopromat.ru
Решение задач по теоретической механике
Здесь собраны избранные разделы теоретической механики и примеры решения задач.
Избранные разделы по теоретической механике
Статика > > > Кинематика > > >Примеры решения задач по теоретической механике
Статика
Условия задач
 Найти реакции опор для того способа закрепления, при котором момент MA в опоре A имеет наименьшее значение.
Найти реакции опор для того способа закрепления, при котором момент MA в опоре A имеет наименьшее значение.Решение >>>
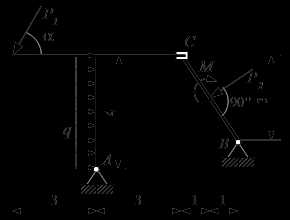 Найти реакции опор составной конструкции.
Найти реакции опор составной конструкции.Решение >>>
 Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве.
Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве.Решение >>>
Кинематика
Кинематика материальной точки
Условие задачи
Определение скорости и ускорения точки по заданным уравнениям ее движения.
По заданным уравнениям движения точки установить вид ее траектории и для момента времени t = 1 с найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Уравнения движения точки:
x = 12 sin(πt/6), см;
y = 6 cos2(πt/6), см.
Решение задачи >>>
Кинематический анализ плоского механизма
Условие задачи
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна E. Стержни между собой, с ползунами и неподвижными опорами соединены с помощью цилиндрических шарниров. Точка D расположена в середине стержня AB. Длины стержней равны, соответственно
l1 = 0,4 м; l2 = 1,2 м; l3 = 1,6 м; l4 = 0,6 м.
Взаимное расположение элементов механизма в конкретном варианте задачи определяется углами α, β, γ, φ, ϑ. Стержень 1 (стержень O1A) вращается вокруг неподвижной точки O1 против хода часовой стрелки с постоянной угловой скоростью ω1.
Для заданного положения механизма необходимо определить:
- линейные скорости VA, VB, VD и VE точек A, B, D, E;
- угловые скорости ω2, ω3 и ω4 звеньев 2, 3 и 4;
- линейное ускорение aB точки B;
- угловое ускорение εAB звена AB;
- положения мгновенных центров скоростей C2 и C3 звеньев 2 и 3 механизма.
Скачать решение задачи >>>
Определение абсолютной скорости и абсолютного ускорения точки
Условие задачи
В приведенной ниже схеме рассматривается движение точки M в желобе вращающегося тела. По заданным уравнениям переносного движения φ = φ(t) и относительного движения OM = OM(t) определить абсолютную скорость и абсолютное ускорение точки в заданный момент времени. 
Скачать решение задачи >>>
См. также:
Сложное движение точки, теорема Кориолиса >>>
Сложное движение точки. Пример решения задачи >>>
Динамика
Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Условие задачи
Груз D массой m, получив в точке A начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV2, вектор R направлен противоположно скорости V груза).
Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция Fx которой на ось x задана.
Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
Скачать решение задачи >>>
Теорема об изменении кинетической энергии механической системы
Условие задачи
Механическая система состоит из грузов 1 и 2, цилиндрического катка 3, двухступенчатых шкивов 4 и 5. Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Каток (сплошной однородный цилиндр) катится по опорной плоскости без скольжения. Радиусы ступеней шкивов 4 и 5 равны соответственно R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м. Массу каждого шкива считать равномерно распределенной по его внешнему ободу. Опорные плоскости грузов 1 и 2 шероховатые, коэффициент трения скольжения для каждого груза f = 0.1.
Под действием силы F, модуль которой изменяется по закону F = F(s), где s – перемещение точки ее приложения, система приходит в движение из состояния покоя. При движении системы на шкив 5 действуют силы сопротивления, момент которых относительно оси вращения постоянный и равен M5.
Определить значение угловой скорости шкива 4 в тот момент времени, когда перемещение s точки приложения силы F станет равным s1 = 1,2 м.
Скачать решение задачи >>>
См. также: Теорема об изменении кинетической энергии. Пример решения задачи >>>
Применение общего уравнения динамики к исследованию движения механической системы
Условие задачи
Для механической системы определить линейное ускорение a1. Считать, что у блоков и катков массы распределены по наружному радиусу. Тросы и ремни считать невесомыми и нерастяжимыми; проскальзывание отсутствует. Трением качения и трением скольжения пренебречь.
Скачать решение задачи >>>
См. также: Общее уравнение динамики. Пример решения задачи >>>
Применение принципа Даламбера к определению реакций опор вращающегося тела
Условие задачи
Вертикальный вал AK, вращающийся равномерно с угловой скоростью ω = 10 с-1, закреплен подпятником в точке A и цилиндрическим подшипником в точке D.
К валу жестко прикреплены невесомый стержень 1 длиной l1 = 0,3 м, на свободном конце которого расположен груз массой m1 = 4 кг, и однородный стержень 2 длиной l2 = 0,6 м, имеющий массу m2 = 8 кг. Оба стержня лежат в одной вертикальной плоскости. Точки прикрепления стержней к валу, а также углы α и β указаны в таблице. Размеры AB=BD=DE=EK=b, где b = 0,4 м. Груз принять за материальную точку.
Пренебрегая массой вала, определить реакции подпятника и подшипника.
Скачать решение задачи >>>
1cov-edu.ru
Теоретическая механика. Теория, задания и примеры решения задач (Б.Е.Ермаков)
80
Стержни 3, 7, 11 – называются стойками. Стержни 1, 4, 9, 12 – называются раскосами.
Стержни, образующие замкнутый треугольник, называют панелью фермы.
Рис. 56
Ферма на рис. 56 имеет 6 панелей.
При расчете фермы принимают следующие допущения.
1.Все стержни фермы прямолинейные и невесомые.
2.Узлы фермы — идеальные шарниры.
3.Внешние силы приложены к узлам фермы.
4.Стержни фермы воспринимают только продольные усилия: сжатие или растяжение.
Расчет фермы состоит в определении опорных реакций и внутренних усилий в стержнях фермы.
При расчете опорных реакций ферма рассматривается как твердое тело, на которое действует плоская система сил. Расчет заключается в составлении расчетной схемы, составлении уравнений равновесия и определении неизвестных реакций.
Усилия в стержнях фермы определяются:
1.Методом вырезания узлов.
2.Методом сечений (методом Риттера).
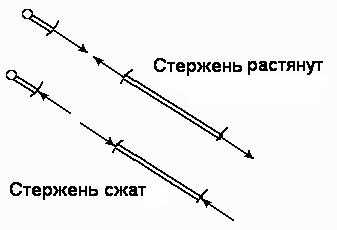
При составлении расчетных схем следует иметь в виду, что если стержень растянут, то сила, с которой он действует на узел, направлена от узла к стержню. Если же стержень сжат, то усилие направлено к узлу от стержня (рис. 57).
81
Рис. 57
Метод вырезания узлов
Метод вырезания узлов состоит в последовательном вырезании узлов фермы и рассмотрении их равновесия. Так как на узел действует плоская сходящаяся система сил, для которой можно записать только два уравнения равновесия, то вырезать узлы надо так, чтобы неизвестных сил было не больше двух. При составлении расчетной схемы будем считать, что все стержни растянуты, т.е. все внутренние усилия направим от узла к стержню. Для каждого узла составляются уравнения равновесия
n
∑Fkx = 0, k=1
n
∑Fky = 0. k=1
Если усилия в стержнях, найденные по этим формулам, имеют знак « + », то формально это указывает на то, что стержень растянут, если же знак усилия « – », то стержень сжат.
Метод сечений
Метод сечений (метод Риттера) заключается в том, что ферма рассекается на две части. Одна часть фермы отбрасывается, а ее действие отображается усилиями в стержнях оставшейся части, которые попали в сечение. Усилия в стержнях направляются вдоль
82
стержней к отброшенной части фермы, т.е. опять предполагаем, что все стержни растянуты. Рассматриваемая часть фермы, на которую действуют активные (заданные) силы, опорные реакции и усилия в стержнях, находится в равновесии. При этом получается произвольная плоская (не сходящаяся) система сил, для которой можно записать три уравнения равновесия. Поэтому неизвестных сил в сечении не должно быть больше трех.
Как известно, существуют три формы уравнений равновесия для плоской системы:
n
∑Fkx = 0;
k=1
n
∑Fky = 0;
k=1
n
∑Mo(Fk ) = 0.
k=1
1-яформа
n
∑Fkx = 0;
k=1
n
∑MA (Fk ) = 0.
k=1
n
∑MB(Fk ) = 0.
k=1
2-яформа
n
∑MA (Fk ) = 0.
k=1
n
∑MB(Fk ) = 0.
k=1
n
∑MC(Fk ) = 0.
k=1
3-яформа
При составлении уравнений равновесия выбирается та форма, которая позволяет получить наиболее простые уравнения. Например, если в сечении две неизвестные силы параллельны, то удобно применить 2-юформу уравнений. Если все силы в сечении попарно пересекаются, то3-юформу. В этом случае точки пересечения сил выбираются в качестве моментных точек. Полученное таким образом каждое уравнение равновесия будет содержать одну неизвестную. По сравнению с методом вырезания узлов это значительно ускоряет расчет и увеличивает точность вычислений.
Если в сечении оказывается больше трех неизвестных усилий, то приходится проводить дополнительные сечения.
83
Пример решения задачи
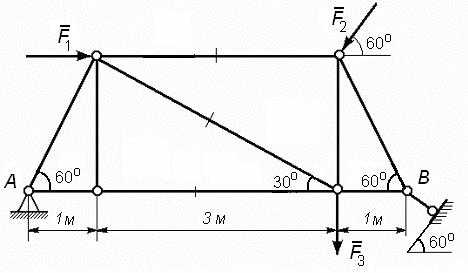
На ферму, показанную на рис. 58, действуют силы F1 = 1 кН, F2 = 2 кН и F3 = 3 кН.
Рис. 58
Определить реакции опор, усилия в стержнях фермы методом вырезания узлов. Для отмеченных стержней проверить усилия методом сечений.
Решение
Обозначим все узлы буквами, а стержни цифрами. Отбросим все опоры и заменим их действие опорными реакциями N1, N2 и NB.
Покажем координатные оси. Полученная расчетная схема представлена на рис. 59.
Проверим ферму на статическую определимость. Ферма имеет 6 узлов и 9 стержней, т.е. У = 6, С = 9. Подставив эти значения в формулу С = 2У – 3, получаем тождество 9 = 2•6 – 3 = 9. Ферма статически определимая.
Для определения опорных реакций воспользуемся первой формой уравнения равновесия для плоской системы сил.
∑Fkx =N1 +F1 −F2 cos600 −NB cos300 = 0;

84
∑Fky =N2 −F2 sin60o −F3 −NB sin30o = 0;
∑MA(Fk ) = −F1 1tg60o +F2 cos60o 1tg60o −F2 sin60o 4 − −F3 4 −NB sin30o 5 = 0.
|
|
| Рис. 59 |
|
Из последнего уравнения находим |
| |||
N = |
| 1 | (F 1tg60o −F cos60o 1tg60o + | |
|
| |||
B | 5 | sin300 | 1 | 2 |
|
|
| ||
+F3 4) = 0,4 (1,732 −1,732 + 6,928 +12) =
=0,4 18,928 =7,571 кН.
Подставив это значение в первые два уравнения, находим
N1 = −F1 +F2 cos60o +NB cos30o = −1+ 2 0,5 + 7,571 0,866 = = −1+1+ 6,557 = 6,557кН,
85
N2 = +F2 sin60o +F3 −NB sin30o = 2 0,866 + 3 − 7,571 0,5 = =1,732 + 3 − 3,785 = 0,947кН.
Итак, N1 = 6, 557кН, N2 = 0,947кН, NB = 7,571кН.
Теперь определим усилия в стержнях фермы методом вырезания узлов. Начинать вырезание можно с узла A или узла B, так как в них неизвестны усилия только в двух стержнях. Начнем с узла A. Вырежем узел A и рассмотрим его равновесие. На узел действует сходящаяся система сил: реакции опорN1 иN2, а также усилия в стержне 1 –S1 и в стержне 2 -S2 . Усилия в стержнях направляем от узла в сторону соответствующих стержней, т.е. мы предполагаем, что эти стержни растянуты. В точке A поместим начало прямоугольной координатной системыAxy. Расчетная схема для узла A показана на рис. 60.
Узел A
Рис. 60
Вэтом случае уравнения равновесия имеют вид
∑Fkx =N1 +S1 cos60о +S2 = 0;
∑Fky =N2 +S1 sin60о = 0.
Из второго уравнения находим

86
S1 = −sinN602 O = − 0,9470,866 = −1,093кН .
Из первого уравнения находим
S2 = −N1 −S1 cos60O = −6,557 −(−1,093) 0,5 = −6,01кН.
Знак « – » формально указывает, что оба стержня сжаты.
Так как усилие в стержне 2 найдено, то можно переходить к узлу C. В этом случае неизвестны усилия в стержнях 3, 4 – S3, S4.
Вырежем узел C и составим для него расчетную схему также, как это было сделано для узла A (рис. 61).
Узел C
Рис. 61
Уравнения равновесия имеют вид
∑Fkx = −S2′ +S4 = 0,
∑Fky =S3 = 0.
Так как S2\ = S2 = –6,01кН,то из уравнений находим
S4 =S2′ = −6,01кН,S3 = 0.
Следовательно, стержень 4 сжат, а в стержне 3 усилия нет. Вырежем узел D. Расчетная схема для него показана на рис. 62.
Неизвестными здесь являются усилия в стержнях 5 и 6 – S5 ,S6.

87
Узел D
Рис. 62
Уравнения равновесия имеют вид
∑Fkx =F1 −S1′cos600 +S5 cos300 +S6 = 0,
∑Fky = −S1′sin600 −S3′ −S5 sin300 = 0.
Так как S1\ = S1 = –1,093кН,S3\ = S3 = 0, то из уравнений находим
S5 =sin301 0 (−S1′sin600 −S3′)=0,51 −(−1,093) 0,866 − 0 =1,893кН,S6 = −F1 +S1′cos600 −S5 cos300 =
=−1+(−1,093) 0,5 −1,893 0,866 = −3,186кН.
Стержень 5 растянут, стержень6 сжат.
Так как усилия в стержнях 4, 5 и 6 найдены, то можно переходить
кузлу E или H.
Вырежем узел E. Расчетная схема для него показана на рис. 63. Неизвестными здесь являются усилия в стержнях 7 и 9 – S7,S9.
Узел E
88
Уравнения равновесия имеют вид
∑Fkx = −S4′ −S5′ cos300 +S9 = 0,
∑Fky =S5′ sin300 +S7 −F3 = 0.
Так как S’4 = S4 =–6,01кНи S’5 = S5 = 1,893 кН, то из уравнений находим
S9 =S4′ +S5′ cos300 = 6,01+1,893 0,866 = −4,371кН,S7 =F3 −S5′ sin300 = 3 −1,893 0,5 = 2,054кН.
Стержень 7 растянут, а стержень9 сжат.
Вырежем узел H. Расчетная схема для него показана на рис.64. Неизвестным здесь является усилие в стержнях 8 – S8.
Узел H
Рис. 64
Уравнения равновесия для этого узла имеют вид
∑Fkx = −S6′ −F2 cos600 +S8 cos600 = 0,
∑Fky = −S7′ −S8 sin600 −F2 sin600 = 0.
Так как S’6 = S6 = -3,186 кН, то из первого уравнения находим
S | = F | + | S6′ | = 2 + −3,186 = −4,372кН. |
| ||||
8 | 2 | cos600 | 0,5 | |
|
|
| ||
Стержень 8 сжат. Второе уравнение используем для проверки уже найденного усилия S7
S7′ = −S8 sin600 −F2 sin600 = −(−4,372) 0,866 − 2 0,866 = = 2,054кН.
89
Усилия в стержне 7, найденные при вырезании узлов E и H, совпали.
Узел B можно использовать для проверки выполненного расчета. Вырежем узел B и рассмотрим его равновесие. Усилия в стержнях 8 и 9 будем считать неизвестными. Из уравнений равновесия для узла B определим эти усилия. Если они совпадут с соответствующими усилиями, найденными выше, то расчет верен, если нет – то следует искать ошибки в предыдущих вычислениях. Расчетная схема для узла B показана на рис. 65.
Узел B
Рис. 65
Уравнения равновесия для узла B имеют вид
∑Fkx = −S9′ −S8′ cos600 −NB cos300 = 0,
∑Fky =S8′ sin600 +NB sin300 = 0.
Решая эту систему уравнений, находим
sin300 |
| 0,5 |
|
S8′ = −NB sin600 | = −7,571 |
| = −4,371кН, |
0,866 | |||
S9′ = −S8′ cos600 | − NB cos300 = −(−4,371) 0,5 − 7,571 0,866 = | ||
= −4,371кН. |
|
|
|
Так как значения усилий в стержнях 8 и 9 совпали, то выполненные вычисления верны.
studfiles.net
