Эффективные способы быстрого счета в уме
Многие спрашивают, как научиться быстро считать в уме, чтобы это выглядело незаметно и неглупо. Ведь современные технологии позволяют меньше пользоваться своей памятью и умственными способностями. Но иногда нет под рукой данных технологий и порой легче и быстрее посчитать что-то в уме. Многие люди начали считать на калькуляторе или телефоне даже элементарные вещи, что также не очень хорошо. Умение считать в уме остается полезным навыком и для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него. Возможность обходиться без специальных девайсов и в нужный момент оперативно решить поставленную арифметическую задачу – это не единственное применение данного навыка. Помимо утилитарного назначения, приемы устного счета позволят научиться организовывать себя в различных жизненных ситуациях. Кроме того, умение считать в уме, несомненно, положительно скажется на имидже ваших интеллектуальных способностей и выделит вас среди окружающих «гуманитариев».
Способы быстрого счета
Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:
Вычитание 7, 8, 9
Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.
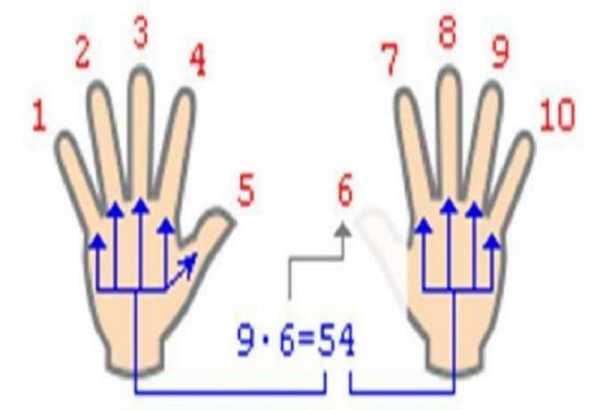
Умножение на 9
Быстро умножить любое число на 9 можно при помощи пальцев рук.
Деление и умножение на 4 и 8
Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.
Например, 46*4=46*2*2 =92*2= 184.
Умножение на 5
Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.
Умножение на 25
Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.
Умножение на однозначные числа
Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.
Например, умножим 83*7.
Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.
Возьмем более сложный пример: 236*3.
Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.
Определение диапазонов
Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).
Раскладка на десятки и единицы
Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Например:
63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355
Проще такие примеры решаются в 3 действия:
1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.
Схематично это можно описать так:
— Первое действие: 60*80 = 4800 — запоминаем
— Второе действие: 60*5+3*80 = 540 – запоминаем
— Третье действие: (4800+540)+3*5= 5355 – ответ
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Мысленная визуализация умножения в столбик
56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.
Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752
Частные методики умножения двузначных чисел до 30
Преимуществом трех способов умножения двузначных для устного счета состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
Умножение на 11
Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры.
Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.
Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10.
Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа.
Например: 324 * 11=3(3+2)(2+4)4=3564
Квадрат суммы, квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
23²= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529
69² = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5.Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
25² = (2*(2+1)) 25 = 625
85² = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
155² = (15*(15+1)) 25 = (15*16)25 = 24 025
Методика умножения чисел до 20 очень проста:
16*18 = (16+8)*10+6*8 = 288
Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода. По сути, этот метод является частным способом использования опорных чисел . В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100…
Опорное число
Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8.
Для того, чтобы узнать их произведение, нужно совершить следующие операции:
15*18
1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.
Опорное число при умножении чисел до 100.Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа
Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.
Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа. Тут возможны три случая. Покажем, все 3 методики на примерах.
Оба числа меньше опорного (под опорным). Допустим, мы хотим умножить 48 на 47.
Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:
47*48
1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или
из 48 вычесть 3 – это всегда одно и то же)
2. Дальше 45 умножаем на 50 = 2250
3. Затем прибавляем 2*3 к этому результату – 2 256
50 (опорное число)
47 48
3(50-47) 2(50-48)
(47-2)*50+2*3=2250+6=2256
Если числа меньше опорного, то из первого множителя вычитаем разность между опорным числом и вторым множителем. Если числа больше опорного, то к первому множителю прибавляем разность опорного числа и второго множителя .
50(опорное число)
51 63
1 13
(51+13)*50+(13*1)=3200+13=3213
Одно число под опорным, а другое над.Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие. Меньший множитель увеличиваем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей. Или больший множитель уменьшаем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей.
50(опорное число)
45 52
5(50-45) 2(52-50)
(52-5)*50-5*2=47*50-10=2340 или (45+2)*50-5*2=47*50-10=2340
При умножении двузначных чисел из разных десятков в качестве опорного числа удобнее
брать круглое число , которое больше большего множителя.
27*89
90(опорное число)
27 89
63 (90-27) 1 (90-89)
(89-63)*90+63*1=2340+63=2403
Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел. Описанные выше методики можно разделить на универсальные (подходящие для любых чисел) и частные (удобные для конкретных случаев).
В крайнем случае, можно воспользоваться «крестьянским» счетом. Чтобы умножить одно число на другое, допустим 21*75, нам нужно записать числа в две колонки. Первое число левой колонки 21, первое число правого столбика 75. Затем числа стоящие в левой колонке делить на 2 и отбрасывать остаток, пока не получим единицу, а числа в правой колонке умножаем на 2. Все строчки, имеющие четные числа в левой колонке вычеркиваем, а оставшиеся числа в правой колонке складываем, у нас получается точный результат.
21*75
21 75
10 150
5 300
2 600
1 1200
Чтобы научиться быстро считать в уме, нужна практика, нет волшебных методик, чтобы с первого раза начать быстро считать в голове, необходимо постоянно тренировать свой мозг и заставлять его быстро работать и считать.
Заключение
Как и все способы вычислений, данные методы быстрого счета имеют свои достоинства и недостатки:
ПЛЮСЫ:
1.С помощью различных методов быстрых вычислений даже самый малообразованный человек может считать.
2. Способы быстрого счета могут помочь избавиться от сложного действия, путем замены его на несколько более простых.
3.Способы быстрого счета полезны в ситуациях, когда нельзя воспользоваться умножением в столбик.
4.Способы быстрого счета позволяют сократить время вычислений.
5.Устный счет развивает умственную деятельность, что помогает быстрее ориентироваться в сложных жизненных ситуациях.
6. Техника устного счета делает процесс вычислений более увлекательным и интересным.
МИНУСЫ:
1.Зачастую, решать пример, пользуясь способами быстрого счета, оказывается дольше, чем просто перемножать в столбик, так как приходится выполнять большее количество действий, каждое из которых проще первоначального.
2.Бывают ситуации, когда человек от волнения или еще чего-то забывает способы быстрого счета или вовсе — путается в них; в таких случаях ответ получается неправильным, а способы являются фактически бесполезными.
3.Не для всех случаев разработаны способы быстрого счета .
4.Вычисляя с использованием техники быстрого счета, нужно держать множество ответов в голове, в чем можно запутаться и прийти к ошибочному результату.
Несомненно, практика играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые способны считать в уме сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать арифметические операции, которые не каждый человек и в столбик сможет посчитать. Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме.
Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:
1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.
2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.
3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете удивить даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.
1001sposob.ru
Быстрый счет. Тридцать простых приемов устного счета
БЫСТРЫЙ СЧЕТ
Тридцать простых приемов устного счета
title: Купить книгу “Быстрый счет. Тридцать простых приемов устного счета”: feed_id: 5296 pattern_id: 2266 book_author: Перельман Яков book_name: Быстрый счет. Тридцать простых приемов устного счетаЛенинград.
От составителя
В настоящее время в продаже нет руководств, содержащих наставления к быстрому выполнению счетных операций в уме. Мы сочли поэтому полезным собрать в краткой брошюре наиболее простые и легко усваиваемые приемы быстрого устного счета, Они рассчитаны на средние способности имеют в виду не публичные выступления на эстраде, а потребности повседневной жизни. Пользующиеся книжечкой должны помнить, что успешное овладение ее указаниями предполагает не механическое, а вполне сознательное распоряжение приемами и, кроме того, более или менее продолжительную тренировку. Зато, усвоив рекомендуемые приемы, можно выполнять быстрые расчеты в уме с безошибочностью письменных вычислений.
Умножение на однозначное число
§ 1.
Чтобы устно умножить число на однозначный множитель (например, 27 X 8) выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20X8 = 160), затем единицы (7*8 =56) и оба результата складывают.
Еще примеры:
34*7=30*7+4*7=210+28=238
17*6=40*6+7*6=240+42=282
§ 2.
Полезно знать на память таблицу умножения до 19*9:
| 2 | 3 | 4 | 6 | 7 | 8 | 9 | ||
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 |
| 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 |
| 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 |
| 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 |
| 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 |
| 16 | 33 | 48 | 64 | 80 | 96 | 112 | 128 | 144 |
| 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 |
| 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 |
| 19 | 39 | 57 | 76 | 95 | 114 | 133 | 152 | 171 |
Зная эту таблицу, можно умножение например, 147*8 выполнить в уме так: 147*8-140*8+7*8= 1120 + 56= 1176
§ 3.
Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350
Умножение на двузначное число
§ 4
Умножение на двузначное число стараются облегчить для устного выполнения, приводя это действие к более привычному умножению на однозначное число.
Когда множимое однозначное, мысленно переставляют множители и выполняют действие, как указано в § 1. Например:
6*28=28*6=120+48=168
§ 5.
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
29*12=29*10+29*2=290+58= 348
41*16=41*10+41*6 = 410+246 =656
(или 41*16=16*41 = 16*40+16*1=640+16=656
Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.
§ 6.
Если множимое или множитель легко разложить в уме на однозначные числа (напр., 14 = 2*7), то пользуются этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз (ср. § 3). Например:
45*14 =90*7=630
Умножение на 4 и на 8
Чтобы устно умножить число на 4, его дважды удваивают. Например:
112*4 =224*2=448
335*4 = 670*2 =1340
§ 8.
Чтобы устно умножить число на 8, его трижды удваивают. Например:
217*8 = 434*4=868*2=1736
(Eще удобнее: 217*8=200*8 +17*8= 1600*13=1736.
Деление на 4 и на 8
§ 9.
Чтобы устно разделить число на 4, его дважды делят пополам. Например:
76:4 =38:2=19
236:4=118:2=59
§ 10.
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
464:8=232:4=116:2=58
516:8=258:4=129:2= 64 1/2
Умножение на 5 и на 25
§ 11.
Чтобы устно умножить число на 5 умножают его на 10/2, т. е. приписывают к числу ноль и делят пополам. Например:
74*5= 740:2= 370
243*5=2430:2=1215
При умножении на 5 числа четного удобнее сначала делить пополам и к полученному приписать ноль. Например:
74X5 = 74/2*10=370
§ 12.
Чтобы устно умножить число на 25, умножают его на 100/4 , т. е.—если число кратно 4-х —делят на 4 и к частному приписывают два ноля. Например:
72*25=72/4*100= 1800
Если же число при делении на 4 дает остаток, то прибавляют
при остатке: к частному
1 25
2 50
3 75
Основание приема ясно из того, что
100:4=25;
200:4=50;
300:4=75
Умножение на 11/2, на 1 1/4, на 21/2, на 3/4
§ 13.
Чтобы устно умножить число на 11/2 прибавляют к множимому его половину. Например:
34*11/2 = 34 + 17=51
23*11/2=23 + 111/2 = 341/2 (или 34,5)
§ 14.
Чтобы устно умножить число на 1
48*11/4 =48 +12=60
58*11/4 = 58+14 1/2=721/2 или 72,5
§ 15
Чтобы устно умножить число на 21/2. к удвоенному числу прибавляют половину множимого.
Например: 18*21/2.=36+9= 45;
39*21/2.= 78 + 19′1/2.= 971/2 (или 97,5)
Другой способ состоит в умножении на 5 и делении пополам:
18*21/2 = 90:2 = 45
§ 16.
Чтобы устно умножить число на 3/4 (т. е. чтобы найти 3/4 этого числа), умножают число на 11/2 и делит пополам. Например:
30 * 3/4 = (30+15)/2= 221/2 (или 22,5)
Видоизменение способа состоит в том, что от множимого отнимают его четверть или к половине множимого прибавляют половину этой половины.
Умножение на 15, на 125, на 75
§ 17
Умножение на 15 заменяют умножением на 10 и на 11/2, (потому что 10*11/2 =15) Например:
18*15=18*1
45*15=450+225=675
§ 18.
Умножение на 125 заменяют умножением на 100 и на 11/4 (потому что 100*11/4=125). Например:
26*125 = 26*100*11/4 = 2600 + 650 = 3250
47*125 = 47*100*11/4 = 4700+4700/4= 4700+1175 = 5875
§ 19.
Умножение на 75 заменяют умножением на 100 и на 3/4 (потому что 100*3/4=75). Например:
18*75= 18*100*3/4 =1800* 3/4 =(1800 + 900)/2=1350
Примечание. Некоторые из приведенных примеров удобно выполняются также приемом § 6
18*15 = 90*3 = 270
26*125 = 130*25 = 3250
Умножение на 9 и на 11
§ 20.
Чтобы устно умножить число на 9, приписывают к нему ноль и отнимают множимое. Например:
62*9=620-62=600—42=558
73*9=730-73=700—43=657
§ 21
Чтобы устно умножить число на 11, приписывают к нему ноль и прибавляют множимое. Например:
87*11=870+87=957
Деление на 5, на 11/2,на 15
§ 22
Чтобы устно разделить число на 5, отделяют запятой в удвоенном числ-последнюю цифру. Например:
68:5=136:10=13,6
237:5 =474:10=47,4
§ 23
Чтобы устно разделить число на 11/2 делят удвоенное число на 3. Например:
36:11/2=72:3=24
53:11/2=106:3=351/3
§ 24.
Чтобы устно разделить число на 15, делят удвоенное число на 30. Например
240:15=480:30=48:3=16
462:15=924:30=3024/30=304/5=30,8 (или 924:30 =308:10=30,8)
Возвышение в квадрат
$ 25.
Чтобы возвысить в квадрат число, оканчивающееся цифрой 5 (например 85), умножают число десятков (8) на него же плюс единица (8*9=72) и приписывают 25 (в нашем примере получается 7225). Еще примеры:
252; 2*3=6; 625
452; 4*5= 20; 2025
1452; 14*15 = 210; 21025
Прием этот вытекает из формулы (10х+5)2 = 100х2+100х+25=100х(х+1)+25
§ 26.
Сейчас указанный прием приложим и к десятичным дробям, оканчивающимся цифрой 5:
8,52 = 72,25
14,52=210,25
0,352 = 0,1225f и т. п.
§ 27.
Так как 0,5= ½, а 0,25 = ¼, то приемом § 25 можно пользоваться также и для возвышения в квадрат чисел, оканчивающихся дробью ½:
(8½ )2 =72 ¼
(14½)2 = 210 ¼ и т п.
§ 28.
При устном возвышении в квадрат часто удобно бывает пользоваться формулой (a +-b)2 = a2 +b2+- 2ab.
Например: 412=402 +1+2*40= 1601+80= 1681
692=702+1-2*70=4901-140=4761
362 =(35+1)2=1225+1+ 2*35=1296
Прием удобен для чисел, оканчивающихся на 1, 4, 6 и 9.
Вычисления по формуле
(а+b) (а-b) = а2 — b2
§ 29.
Пусть требуется выполнить устно умножение 52*48
Мысленно представляем эти множители в виде (50 + 2)*(50—2)
и применяем приведенную в заголовке формулу:
(50+2)*(50—2)=502-22= 2496
Подобным же образом поступают во всех вообще случаях, когда один множитель удобно представить в виде суммы двух чисел, другой — в виде разности тех же чисел:
69X71=(70—1)*(70+1)=4899
33X27=(30+3)*(30—3)=891
53X57=(55—2)*(55+2)=3021
84X86=(85-1)*(85+1)=7224
§ 30.
Указанным сейчас приемом удобно пользоваться и для вычислений следующего рода:
7 ½*6½=(7 + ½ )*(7 — ½)=48 ¾
11 3/4*12 1/4= (12 – 1/4)*(12 +1/4) =143 15/16
Полезно запомнить:
37*З =111
Запомнив это, легко выполнять устно умножение числа 37 на 6, 9, 12 и т. п.
37*6=37*3*2=222
37*9=37*3*3=333
37*12=37*3*4=444
37*15=37*3*5 =555 и т. д,
7*11*13=1001
Запомнив это, легко выполнять устно умножения следующего рода:
77*13=1001
77*26=2002
77*39=3003 и т. д.
91*11=1001
91*22=2002
91*33=3003 и т. д.
143*7=1001
143*14=2002
143*21=3003 и т. д.
В нашей книжечке указаны только простейшие, наиболее удобоприменимые способы устного выполнения действий умножения, деления и возвышения в квадрат. Практикуясь в сознательном пользовании ими, вдумчивый читатель выработает для себя ряд еще и других приемов, облегчающих вычислительную работу.
www.e-reading.club
Приемы быстрого счета
Автор: Еремина Ольга Андреевна
ВВЕДЕНИЕ
Вступление
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учёбе, в быту, в профессиональной деятельности. Кроме того, быстрый счёт – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях.
Я поставила перед собой проблему: найти и рассмотреть нестандартные приёмы устного быстрого счёта, не рассматриваемые непосредственно в школьном курсе математики.
Актуальность
Актуальность выбранной темы заключается в том, что нижеперечисленные способы быстрого счёта рассчитаны на ум «обычного» человека и не требуют уникальных способностей.
Практическая ценность
Приемы быстрого счета пригодятся для сдачи экзаменов, где запрещено пользоваться калькуляторами, облегчат и ускорят счет на уроках, помогут в будущей профессии. Главное – более или менее продолжительная тренировка. Кроме того, освоение этих навыков развивает логику и память учащегося.
Задачи
1) Узнать об упрощённых, нестандартных способах устных вычислений при умножении натуральных чисел.
2) Рассмотреть и показать на примерах применение нестандартных способов при умножении и делении чисел.
3) Провести опрос среди одноклассников.
4) Провести презентацию проекта и рассказать одноклассникам о приемах быстрого счета.
Цели
Целью является изучить методы и приёмы быстрого счёта и доказать необходимость умения быстрого счёта и эффективного использования этих приёмов.
ОСНОВНАЯ ЧАСТЬ
Опрос
Я решила провести опрос в своем классе, чтобы уяснить актуальность данной темы и узнать о ее распространении.
Результаты:
Вопрос | Ответ |
Нужно ли уметь выполнять арифметические действия с натуральными числами современному человеку? | Да – 18 Нет – 4 Не знаю – 1
|
Умеете ли вы умножать, складывать, вычитать числа столбиком, делить «уголком»? | Да – 20 Нет – 2 Не знаю – 1 |
Знаете ли вы другие способы выполнения арифметических действий? | Да – 10 Нет – 11 Не знаю – 2 |
А хотели бы узнать? | Да – 20 Нет – 1 Не знаю – 2 |
Теоретическая часть
В теоретической части я расскажу про способы быстрого счета без калькулятора.
Умножение на 11
Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:
53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583
59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649
Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.
85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225
45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025
Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6
Умножение двузначного числа на 101, 1001 и т.д.
Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено. Пример:
32 х 101 = 3232; 47 х 101 = 4747;
324 х 1001 = 324 324; 675 х 1001 = 675 675;
6478 х 10001 = 64786478;
846932 х 1000001 = 846932846932.
Умножение на 37
Прежде чем научиться устно умножать на 37,надо хорошо знать признак делимости и таблицу умножения на 3. Чтобы устно умножить число на 37, надо это число разделить на 3 и умножить на 111.
Примеры:
24 х 37 = (24 : 3) х 37 х 3 = 8 х 111 = 888;
18 х 37 = (18 : 3) х 111 = 6 х 111 = 666.
Умножение трехзначного числа на 999
Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9. Например:
385 * 999 = 384615
573 * 999 = 572427
943 * 999 = 942057
Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это.
Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
И, как следствие): чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину.
Например,
34*1,5 = 34+17=51
125*1,5= 125+62,5=187,5
Практическая часть
В практической части я предлагаю решить примеры с натуральными числами с применением полученных знаний.
35 х 37 =
36458 х 10001 =
567 х 999 =
495 : 5 =
65 х 65 =
32 х 11 =
120 х 0,15 =
ЗАКЛЮЧЕНИЕ
Как мы видим, быстрый счёт это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит её можно изучать, ей можно следовать, ею можно овладевать.
Все рассмотренные мною методы устного умножения говорят о многолетнем интересе ученых, и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.
СПИСОК ИСТОЧНИКОВ
1. «Устный счёт – гимнастика ума» Г.А.Филиппов
2. «Алгоритмы ускоренных вычислений» Л.В.Бикташева
3. «Устный счет». Э.Л.Струнников
4. «Математическая шкатулка» Ф.Ф.Нагибин, Е.С.Канин
5. «Мир чисел» Г.И. Зубелевич, В.И.Ефимов
6. «Задачи для математического кружка» Е.Г.Козлова
7. «Развитие вычислительной культуры учащихся» Н.Л. Мельникова
8. http://anisim.org/articles/priemy-bystrogo-scheta-bez-kalkulyatora
Прикрепленные файлы:
%d0%bf%d1%80%d0%be%d0%b5%d0%ba%d1%82-%d0%b5%d1%80%d0%b5%d0%bc%d0%b8%d0%bd%d0%b0 comments powered by HyperComments
solncesvet.ru
Некоторые способы быстрого счета

Быстрый счёт без калькулятора. Приемы быстрого счета.

Научиться быстро считать не так уж сложно, а хорошему математику просто необходимо владеть основными приемами быстрого счета.
Рассмотрим некоторые способы быстрого устного счета, которые рассчитаны на ум “обычного” человека и не требуют уникальных способностей.

РАЗЛИЧНЫЕ СПОСОБЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

СЛОЖЕНИЕ
Основное правило для выполнения сложения в уме звучит так:
Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1; чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т.д.
Например, 56+8=56+10-2=64;
65+9=65+10 -1=74.

СЛОЖЕНИЕ В УМЕ ДВУЗНАЧНЫХ ЧИСЕЛ
Если цифра единиц в прибавляемом числе больше5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы.
Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы.
Например, 34+48=34+50 – 2 = 82;
27+31=27+30+1 =58.

СЛОЖЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ
Складываем слева на право, то есть сначала сотни, потом десятки, а затем единицы.
Например, 359+523= 300+500+50+20+9+3=
=800 +70 +12 = 882;
456+298=400+200+50+90+6+8=600+140+14=754 .

ВЫЧИТАНИЕ
Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректируйте полученный ответ.
Например, 56 – 9 = 56 – 10 + 1 = 47;
436 – 87 = 436 – 100 + 13 = 349.

Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом:
Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
Например, 1000 – 648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

РАЗЛИЧНЫЕ СПОСОБЫ УМНОЖЕНИЯ И ДЕЛЕНИЯ

Умножение и деление на 4.
Чтобы умножить число на 4, его дважды удваивают.
Например, 527 · 4 = (527 · 2) · 2 = 1054 · 2 = 2108.
Чтобы число разделить на 4 , его дважды делят на 2.
Например, 2648 : 4 = (2648 : 2) : 2 = 1324 : 2 = 662.

Умножение и деление на 5.
Чтобы умножить число на 5, нужно его умножить на 10 и разделить на 2.
Например, 348 · 5= (348 · 10) : 2 = 3480 : 2 = 1740.
Чтобы число разделить на 5, нужно умножить его на 0,2, то есть в удвоенном исходном числе отделить запятой последнюю цифру.
Например, 51 : 5 = 51 · 0,2 = 10,2.

Умножение на число, оканчивающееся на 5.
Чтобы четное двузначное число умножить на число, оканчивающееся на 5, следует применить правило: если один из сомножителей увеличить в несколько раз, а другой – уменьшить во столько же раз, произведение не изменится.
Например,
44 · 5 = (44 : 2) · 5 · 2 = 22 · 10 = 220;
26 · 35 = (26 : 2) · 35 · 2 = 13 · 70 = 910;
36 · 45 = (36 : 2) · 45 · 2 = 18 · 90 = 1625;
18 · 65 = (18 : 2) · 65 · 2 = 9 · 130 = 1170;
12 · 75 = (12 : 2) · 75 · 2 = 6 · 150 = 900;
14 · 85 = (14 : 2) · 85 · 2 = 7 · 170 = 1190;
12 · 95 = (12 : 2) · 95 · 2 = 6 · 190 = 1140.
При умножении на 65, 75, 85, 95 числа следует брать небольшие, в пределах второго десятка. В противном случае вычисления усложнятся.

Умножение на 25 .
Чтобы умножить число на 25, нужно его умножить на 100/4, то есть умножить на 100 и разделить на 4.
Например, 348 · 25 = (348 · 100) : 4 = (34800 : 2) : 2 = 17400 : 2 = 8700.
Умножение на 1,5.
Чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину.
Например, 228 · 1,5 = 228 + 114 = 342.

Умножение на 9
Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки.
Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ: 27.

Умножение на 9.
Чтобы умножить число на 9, к нему приписывают 0 и отнимают исходное число.
Например, 847 · 9 = 8470 – 847 = 7623.

Умножение многозначных чисел на 9 .
1. Число десятков увеличим на 1 и вычтем из множимого.
2. К результату приписываем дополнение цифры единиц множимого до 10.
Например , 576 · 9
1. 576 – (57+1)=518
2. 10 – 6 =4
Ответ: 5184
379 · 9
1. 379 – (37 + 1) =341
2.10 – 9 = 1
Ответ: 3411

Умножение на 99
1. Из числа вычитаем число его сотен, увеличенное на 1.
2. Находим дополнение числа, образованного двумя последними цифрами до 100.
3. Приписываем дополнение к предшествующему результату.
Пример:
27 · 99 134 · 99
27 – 1 = 26 (сотен – 0+1) 134 – 2 = 132 (сотня – 1 + 1)
100 – 27 = 73 100 – 34 = 66
27 · 99 = 2673 134 · 99 = 13266

Умножение на 11 .
1 способ. Чтобы число умножить на 11, к нему приписывают 0 и прибавляют исходное число.
Например, 243 · 11 = 2430 + 243 = 2673.
2 способ. Если хочешь умножить число на 11, то поступай так: запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр.
Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа.
Например, 45 · 11 = 4 (4+5)7= 967.

Умножение на 12.
Чтобы умножить число на 12: нужно удваивать поочередно каждую цифру и прибавлять к ней поочередно ее «соседа».
Например, 63247 · 12
Необходимо записывать цифры множимого через интервал и каждую цифру результата писать точно под цифрой числа 63247, из которой она образовалась.
63247 · 12 дважды 7 будет = 14, переносим 1
4
63247 · 12 дважды 4 + 7 + 1 = 16, переносим 1
64
63247 · 12 дважды 2 + 4 + 1 = 9
964
Следующие шаги аналогичны.
Окончательный ответ : 63247 · 12= 758964.

Умножение на 22, 33, …, 99.
Чтобы двузначное число умножить на 22, 33, …, 99, надо этот множитель представить в виде произведения однозначного числа на 11, то есть 44 = 4 · 11; 55 = 5 · 11.
Затем произведение первых чисел умножить на 11:
Например, 24 · 22 = 24 · 2 · 11 = 48 · 11 = 528
23 · 66 =23 · 6 · 11=138 · 11=1518

Умножение трехзначного числа на 101 .
Чтобы умножить трехзначное на 101, увеличиваем первый множитель на число его сотен и приписываем к нему справа две последние цифры первого множителя.
Например, 125 · 101 = 126(125+1)25 =12625
Этот прием дети легко усваивают при записи вычисления в столбик.
х125
101
+ 125
125
12625

Возведение в квадрат числа, оканчивающегося цифрой 5 .
Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 65), умножают число его десятков (6) на число десятков, увеличенное на 1 (на 6+1 = 7), и к полученному числу приписывают 25
(6 · 7)25 = 4225
Например: 95 2 =(9 · 10)25= 9025; 125 2 = (12 · 13)25=15625
Возведение в квадрат числа, близкого к 50.
Если хочешь возвести в квадрат число, близкое к 50, но большее 50, то поступай так:
1) вычти из этого числа 25;
2) припиши к результату двумя цифрами квадрат избытка данного числа над 50.
Примеры:
1) 58 2 = 3364. Объяснение: 58 – 25 = 33, 58-50=8, 8 2 = 64, 58 2 = 3364.
2) 67 2 = 4489. Объяснение: 67 – 25 = 42, 67 – 50 = 17, 17 2 =289, 67 2 = 4200 + 289 = = 4489.
Если хочешь возвести в квадрат число, близкое к 50, но меньшее 50, то поступай так :
1) вычти из этого числа 25;
2) припиши к результату двумя цифрами квадрат недостатка данного числа до 50.
Примеры:
1) 48 2 = 2304. Объяснение: 48 – 25 = 23, 50 – 48 =2, 2 2 = 4, 48 2 = 2304.
2) 37 2 = 1369. Объяснение: 37 – 25 = 12,= 13, 13 2 =169, 37 2 = 1200 + 169 = 1369.

Умножение на 37.
Чтобы умножить число на 37, надо это число разделить на 3 и умножить на 111.
Например: 24 · 37 = (24 : 3) · 37 · 3 = 8 · 111 = 888;
27 · 37 = (27 : 3) · 111 = 999.
Деление на 37.
Чтобы число разделить на 37, надо это число разделить на 111 и умножить на 3.
Например: 999 : 37 = 999 :111 · 3 = 27;
888 : 37 = 888 :111 · 3 = 24.
Чтобы научиться устно умножать и делить на 37, надо хорошо знать таблицу умножения на три и признак делимости на три.

Умножение двух рядом стоящих чисел
При умножении двух рядом стоящих чисел надо сначала перемножить цифры десятков, затем цифру десятков умножить на сумму цифр единиц и, наконец, надо перемножить цифры единиц. Получим ответ.
Например: 12 ×13
Шаг1. 1 × 1 = 1
Шаг 2. 1 × (2+3) = 5
Шаг 3. 2 × 3 = 6
Ответ: 156

Умножение пары чисел, у которых цифры десятков одинаковые, а сумма цифр единиц составляет 10
Пример:
24 × 26 = (24 – 4) × (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.
Числа 24 и 26 округляем до десятков, чтобы получить число сотен, и к числу сотен прибавляем произведение единиц.
18 × 12 = 2 × 1 сот. + 8 × 2 = 200 + 16 = 216;
23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;
34 × 36 = 3 × 4 сот. + 4 × 6 = 1224;
71 × 79 = 7 × 8 сот. + 1 × 9 = 5609;
82 × 88 = 8 × 9 сот. + 2 × 8 = 7216.
Можно решать устно и более сложные примеры:
108 × 102 = 10 × 11 сот. + 8 × 2 = 11016;
204 × 206 = 20 × 21 сот. +4 × 6 = 42024;
802 × 808 = 80 × 81 сот. +2 × 8 = 648016.
Проверка:
× 802
808
6416
6416 __
648016

Умножение чисел, оканчивающихся на 1.
При умножении чисел, оканчивающихся на 1, надо сначала перемножить цифры десятков и правее полученного произведения записать под этим числом сумму цифр десятков, а затем перемножить 1 на 1 и записать еще правее.
Сложив столбиком, получим ответ.
1) 81 × 31 = ?
8 × 3 = 24
8 + 3 = 11
1 × 1 = 1
2511
81 × 31 = 2511
2) 21 × 31 = ?
2 × 3 = 6
2 +3 = 5
1 × 1 = 1
651
21 × 31 = 651
3) 91 × 71 = ?
9 × 7 = 63
9 + 7 = 16
1 × 1 = 1
6461
91 × 71 = 6461

Умножение двузначных чисел, у которых сумма цифр десятков равна 10, а цифры единиц одинаковые.
Правило. При умножении двузначных чисел. у которых сумма цифр десятков равна 10, а цифры единиц одинаковые, надо перемножить цифры десятков. и прибавить цифру единиц, получим число сотен и к числу сотен прибавим произведение единиц.
Примеры:
72 × 32 = (7 × 3 + 2)сот. + 2 × 2 = 2304;
64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;
53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;
18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;
24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;
63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;
35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.

Заключение.
Как мы видим, быстрый счет это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит ее можно изучать, ей можно следовать, ею можно овладеть.
Все рассмотренные нами методы устного счёта говорят о многолетнем интересе ученых и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.
multiurok.ru
маленькие секреты репетитора — Колпаков Александр Николаевич
Умеете ли Вы быстро считать? Этот вопрос можно задать не только школьникам и родителям, но и начинающим репетиторам по математике 5 — 9 классов. Как-то, прочитывая старую литературу по занимательной математике, я наткнулся на сообщение о том, что до революции, когда не было калькуляторов и компьютеров школьники, по крайней мере, в школе Рачинского, умели возводить в квадрат числа до 100 в уме. Не столбиком, а именно в уме. Как они это делали? Казалось бы, процесс достаточно трудоемкий, однако при ближайшем рассмотрении выясняется, что освоить возведение в квадрат может любой, даже не слишком продвинутый в математике ученик. Ну, например, сколько будет 96 в квадрате? Конечно, можно взять калькулятор, набрать нужные кнопки и получить ответ. Можно взять листок бумаги и подсчитать это столбиком. А можно и в уме. Вот о методах быстрого счета, с которым репетитор по математике ежедневно сталкивается в практике своей работе, я и расскажу в этой статье.
Какие вычисления производит репетитор по математике в уме?
За свою многолетнюю историю репетиторства я никогда и ни на одно занятие не брал и не беру с собой калькулятор, предпочитая пользоваться, главным образом, устным счетом.
Для начала возьмем пример попроще. Например, сколько будет 11232-9889 ? Конечно, можно подсчитать это столбиком, каждый раз занимая и ставя точки по этому поводу над каждой цифрой, но ведь можно сосчитать и в уме. Представим себе числовую ось. Репетитор по математике может сделать для нее схематический рисунок:
Сколько не хватает числу 9889 до 10000? – 111. А на сколько 11232 больше, чем 10000? На 1232. А теперь складываем 1232 и 111 и получаем результат: 1232+111=1343.
А теперь разберем пример посложнее – умножение. Сколько будет 64×15? Техника быстрого счета позволяет репетитору по математике дать молниеносный ответ. Это будет 960. Стоит только увидеть число 15 в каком-нибудь примере, как сразу возникает возможность быстрого счета. Как умножить число на полтора, т.е. на 1,5? Для этого надо взять само это число, прибавить к нему половинку от него самого и получить результат. Если в примере фигурирует на 1,5, а 15, или 150, то надо приписать еще справа определенное количество нулей. Ну, например, 64 плюс половинка от этого числа, то есть 32 и ноль приписываем. То есть 64+32=96 96×10=960.
Аналогичный пример, но в этом случае можно подсчитать разными способами. 84×25. Можно рассматривать 25 как 2,5×10. Иными словами взять 84 два раза и прибавить к полученному результату 42. 84+84+42=210. И приписываем ноль. Итого получаем 2100. А можно и по-другому. 84×0,25×100. То есть разбиваем 25 на 0,25 и 100. Зачем нам это надо? Дело в том, что 0,25 это ¼ (одна четвертая). Иными словами 84 делим на 4, получается 21, и приписываем два ноля. То есть получается те же 2100.
Подобные способы использования обыкновенных дробей достаточно многочисленны, и при должном желании репетитор по математике, хорошо знающий свой предмет, может придумать еще несколько таких. Вот, пример, из реального занятия. Ученику 5-го класса следовало подсчитать, сколько будет 375 умножить на 48. Правильно то, репетитор по математике запрещает пользоваться калькулятором. Но произвести вычисления столбиком в 5 классе — это значит потратить уйму времени. Тем не менее, такое произведение можно найди в уме. Что такое 375? – Это 125×3. Число 125 – это одна восьмая, умноженная на тысячу. Следовательно, превращаем 375 в три восьмых и умножаем на 1000, так как одна восьмая – это 125 тысячных – 0,125).
Далее 48 делим на восемь и умножаем на 3. Итого получается 48:8×3=18. И приписываем три ноля. Получается 18000. Казалось бы, подобные вычисление не менее сложны, чем подсчет столбиком. Однако при постоянной практике быстрого счета «сокращенные» вычисления репетитор по математике может довести до автоматизма.
Работа с формулами сокращенного умножения
Формулы сокращенного умножения, изучающиеся в 7-м классе, позволяют репетитору облегчить устный счет. В этой статье я не буду подробно рассматривать все приемы, думаю, что им легко обучиться самостоятельно. Например, ученик, знакомый с формулой разности квадратов без труда умножит в уме 43 на 37. Я же остановлюсь на правиле, позволяющем возводить в квадрат числа, оканчивающиеся на пятерку. Например, 25 в квадрате, 35 в квадрате, 45 в квадрате, 95 в квадрате. Правило такое. Для этого, количество десятков возводимого в квадрат числа (например, 95) умножить на число, которое на единицу больше (то есть на 10 в случае 95) и приписать 25. Получается 9025.
Почему так получается комментировать не буду, думаю, ученик, знакомый с формулами сокращенного умножения без труда поймет это. Более того, в некоторых школах, учителя знакомят учеников с таким методом. Однако на занятиях у репетитора по математике этому приему внимание практически не уделяется. Едва ли где говорится, что это знание в некоторых случаях помогает возводить в квадрат числа. Берем таблицу квадратов, имеющуюся в учебниках 7-го, 8-го, 9-го классов. Среди чисел, перечисленных в ней, есть т.н. «опорные» числа. Это, во-первых, 10, 20, 30, 40, ….90 и во-вторых, 15, 25, 35… 95. Это те числа, возвести которые в квадрат очень просто.
Теперь берем число 96 и возводим его в квадрат. Для этого репетитор по математике возводит в квадрат 95 и прибавляет 95+96. Число 95 в квадрате дает 9025. Прибавляем 200 и отнимаем (5+4 – числа, дополняющие 95 и 96 до ста). Пишем результат – 9216. Аналогичным способом при соответствующей тренировке можно возводить в квадрат любое число из таблицы квадратов, вплоть до того, чтобы показывать фокусы быстрого счета перед одноклассниками. Для тех, кто всё еще побаивается столь больших чисел, репетитор по математике упрощает объяснение принципа. Как это делается? Берем 4 в квадрате. Это будет 16. Берем 5 в квадрате. Это будет 25. Берем 6 в квадрате. Это будет 36. Зная 4 в квадрате, результат следующего числа в квадрате получается прибавлением к предыдущему суммы возводимых в квадрат чисел. Например, 5 в квадрате = 4 в квадрате + 5+4 (т.е. 16+9). Или 7 в квадрате = 36 (6×6) + (6+7) = 49.
Это далеко не все способы быстрого счета, которые встречаются в практике репетитора.
Аркуров А.А. Репетитор по математике, Москва
ankolpakov.ru
описание методики, результаты, отзывы. Ментальная арифметика :: BusinessMan.ru
Многие родители наверняка мечтают о том, чтобы их малыш вырос особенным и непременно стал таким, чтобы им можно было гордиться. Но если одни папы и мамы лишь хвастаются способностями своих детей, то другие ведут их в специальные школы, помогающие развивать данные природой задатки.
А можно ли вырастить из ребенка гения? Если в прежние времена ответ на такой вопрос был однозначен и требовал наличия таланта и удивительных способностей, то сегодня задача намного упростилась. Например, для того чтобы ребенок проявлял недюжинные познания в математике и считал так же быстро и правильно, как калькулятор, предлагается необычная программа, которая обучит малыша математике. А называется она «ментальная арифметика». Что это за программа и какими она обладает преимуществами?
Популярность методики
С 1993 г. ментальная арифметика используется для обучения детей в 52 странах мира, начиная с Канады и заканчивая Великобританией. В некоторых из них методику рекомендуют для включения в программу школ.
Наибольшее распространение ментальный счет получил в государствах Ближнего Востока, а также в Китае, Австралии, Таиланде, Австрии, США и Канаде. Начинают появляться специализированные организации в Казахстане, Киргизии и России.
Ментальный счет является одним из самых молодых и стремительно развивающихся способов, применяемых для детского образования. Благодаря этой методике можно без труда развить умственные способности ребенка, которые в первую очередь имеют математическую направленность. Благодаря освоению детьми техники ментального счета любая математическая задача превращается для них в простой и быстрый вычислительный процесс.
История возникновения
Методика ментального счета имеет древние корни. И это несмотря на то, что разработана она сравнительно недавно ученым из Турции Халитом Шеном. Что же он использовал для своей системы ментального счета? Абакус, который был создан в Китае еще 5 тыс. лет назад. Этот предмет представляет собой счеты, которые внесли огромный вклад в развитие всей мировой арифметики. После изобретения абакус начал свое постепенное распространение по всему миру. В 16-м веке из Китая он попал в Японию. На протяжении четырех сотен лет жители Страны восходящего солнца не только успешно использовали такие счеты, но и тщательно прорабатывали их, пытаясь усовершенствовать такой нужный для совершения арифметических действий предмет. И это им удалось. Японцы создали счеты соробан, которые и до сегодняшнего дня используются для обучения детей в начальной школе.
На протяжении всей истории развития человечества совершенствовалась математическая наука. И сегодня она может предложить нам огромное количество своих достижений. Но, несмотря на это, ученые считают, что использование абакуса приносит больше пользы в обучении детей точному счету.
Польза ментальной арифметики
Считается, что каждое из полушарий человеческого мозга отвечает за свои направления. Так, правое из них позволяет развить творчество, образное восприятие и мышление. Левое же в ответе за логическое мышление.

Деятельность полушарий активизируется в тот момент, когда человек начинает работать руками. Если активна правая из них, то начинает работать левое полушарие. И наоборот. Человек, работающий левой рукой, способствует активизации работы правого полушария.
Задача менара – заставить весь мозг принимать участие в образовательном процессе. Как же достигнуть таких результатов? Это возможно при выполнении математических операций на абакусе обеими руками. В конечном итоге менар способствует освоению быстрого счета, а также развитию и совершенствованию аналитических навыков.
Ученые сравнили калькулятор с абакусом и пришли к однозначному выводу, что первый из них расслабляет активность мозга. Абакус же, напротив, оттачивает и тренирует полушария.
Когда следует начать изучать ментальный счет? Отзывы приверженцев данной методики утверждают, что лучше всего осваивать этот способ в возрасте от четырех до двенадцати лет. И только в некоторых случаях период может быть продлен еще на четыре года. Это время, когда происходит бурное развитие мозга. И данный факт является замечательным посылом к тому, чтобы прививать ребенку базовые навыки, проводить изучение иностранных языков, развивать мышление, осваивать игру на музыкальных инструментах и боевые искусства.
Суть ментальной методики
Вся программа по освоению устного счета построена на последовательном прохождении двух этапов. На первом из них происходит ознакомление и овладение техникой выполнения арифметических действий с использованием косточек, во время которых задействованы одновременно две руки. Благодаря этому в процессе участвует как левое, так и правое полушарие. Это позволяет достигнуть максимально быстрого усвоения и выполнения арифметических действий. В своей работе ребенок использует абакус. Этот предмет позволяет ему совершенно свободно вычитать и умножать, складывать и делить, вычислять квадратный и кубический корень.
Во время прохождения второго этапа ученики обучаются ментальному счету, который производится в уме. Ребенок перестает постоянно привязываться к абакусу, что также стимулирует и его воображение. Левые полушария детей воспринимают цифры, а правые – образ костяшек. На этом и основана методика ментального счета. Мозг начинает работать с воображаемым абакусом, воспринимая при этом числа в форме картинок. Выполнение же математического счета ассоциируется с движением косточек.
Обучение ментальной арифметике быстрого счета является очень интересным и увлекательным процессом. Он по достоинству оценен сотнями тысяч людей и получил огромное количество положительных отзывов.
Абакус
Что же представляет собой эта загадочная и древняя счетная машинка? Абакус, или счеты для ментального счета, очень напоминают старые советские «костяшки». Весьма схожим является и принцип работы на этих двух приспособлениях. В чем же отличие этих счетов? Оно заключено в количестве костяшек, находящихся на спицах и в удобстве эксплуатации.
Стоит сказать о том, что для получения результата абакус потребует сделать большее количество движений руками. Как же устроен этот древний предмет, пришедший к нам из Китая? Он представляет собой рамку, в которую вставлены спицы. Причем их количество может быть разным. На спицах находится по пять штук нанизанных костяшек.

По длине каждую спицу пересекает разделительная планка. Над ней находится одна костяшка, а под ней, соответственно, четыре.
Методика ментального счета предусматривает определенное движение человека пальцами. Из них задействуются только указательный и большой. Все движения должны быть доведены до автоматизма, чему содействует их многократное повторение.
Интересно, что данный навык легко может быть утерян. Именно поэтому при освоении методики не стоит пропускать занятия.
Расположение чисел
Каковы азы счета в ментальной арифметике? Для того чтобы освоить данную методику, необходимо знать, как располагаются на абакусе числовые линейки. В его правой стороне находятся единицы. После этого идут десятки, затем сотни, после тысячи, десятки тысяч и так далее. Каждый из этих разрядов располагается на отдельной спице.
Костяшки, расположенные под разделительной планкой, это «1», а над ней – «5». Например, для того, чтобы на абакусе набрать число 3, понадобится отделить три костяшки, расположенные под разделительной планкой на спице, находящейся правее остальных. Рассмотрим пример с двойными числами, например, с 15. Для его набора на абакусе следует поднять вверх одну костяшку на спице десятков и опустить одну, находящуюся над верхней планкой на спице единиц.
Операции сложения
Как научиться ментальному счету? Для этого потребуется изучить, как проводятся на абакусе арифметические действия. Рассмотрим, например, сложение. Посмотрим, чему будет равна сумма чисел 22 и 13. Для начала понадобится отложить по две костяшки на спицах десятков и единиц, расположенные внизу разделительной планки. Далее к двум десяткам добавим еще один. Получится 30. Теперь приступим к сложению единичек. К двум прибавим еще три. Получится число «пять», которое обозначается костяшкой вверху разделительной планки. В итоге получается 35. Для освоения более сложных операций понадобится тщательным образом изучить специальную литературу. После освоения самых простых примеров рекомендуется потренироваться на абакусе. Таким образом, обучение становится максимально интересным.
Освоение второго этапа
После того как операции на абакусе не будут вызывать затруднений, можно приступить к устному счету ментальной арифметики. Это следующий уровень обучения. Он предполагает ментальный счет, то есть произведенный в уме. Для этого понадобится сделать для ребенка картинку абакуса. Самым простым вариантом является распечатка изображения этого предмета, которое затем должно быть наклеено на картон (можно взять его от коробки из-под обуви). По возможности картинка должна быть цветной. Это позволит ребенку легче представить ее в своем воображении.
Во избежание ошибок стоит помнить о том, что ментальный счет должен производиться слева направо. Что необходимо предпринять, чтобы отложить на абакусе двухзначное число? Для этого ребенку следует вначале левой рукой набрать костяшки, соответствующие десяткам, а после правой отделить на спице нужные единицы.

Так, для набора 6, 7, 8 и 9 следует использовать «Щепоточку». Этот процесс представляет собой сведение вместе указательного и большого пальца к разделительной планке и сбор костяшек, обозначающих цифру 5, и необходимого их числа на спице, которая расположена в нижней части абакуса. Вычитание чисел производится аналогичным образом. Той же «Щепоточкой» одновременно отбрасываются «пятерочки» и нужное количество косточек внизу.
Цели и результаты методики
Обучение ментальному счету позволяет ребенку добиться небывалых успехов в области математики. Детки, прошедшие специальный курс, с легкостью могут вычислить в уме десятизначные числа, умножить их и вычесть. Но стоит сказать о том, что и это не является главной целью подобного обучения. Счет представляет собой лишь способ, с помощью которого развиваются умственные способности человека.

Освоение ментальной арифметики способствует следующему:
- активизации зрительной и слуховой памяти;
- умению концентрации внимания;
- совершенствованию смекалки и интуиции;
- креативному мышлению;
- проявлению уверенности в себе и самостоятельности;
- быстрому освоению иностранных языков;
- реализации способностей в будущем.
В тех случаях, когда для освоения менара был использован профессиональный подход и специалисты достигли поставленных перед ними целей, ребенок без труда начинает решать в уме как простые, так и сложные задачи по математике. А арифметические действия на умножение и сложение он производит даже быстрее калькулятора.
Школы по обучению ментальной арифметике
Где же можно освоить эту уникальную методику? На сегодняшний день для изучения ментальной арифметики необходимо записаться в специализированный образовательный центр. В них специалисты занимаются с детьми на протяжении двух-трех лет. Помимо описанных выше этапов, с помощью которых можно освоить методику, существует еще десять ступеней. Причем каждую из них ученики проходят за 2-3 месяца.
Каждый из таких специализированных центров разрабатывает собственные программы обучения. Однако, несмотря на это, существуют и общие правила, которых придерживаются абсолютно все. Они состоят в том, что группы учеников формируются в зависимости от их возраста. Так, существует три базовых вида таких групп.

Это kinder, kids и junior. Занятия проводят опытные высококвалифицированные психологи и педагоги, которые прошли соответствующую подготовку и имеют необходимую аттестацию.
Помимо центров по обучению ментальному счету сегодня работают и специализированные школы, готовящие специалистов по соответствующему профилю. Как правило, преподаватели менара – это люди, имеющие не только психологическое и педагогическое образование, но и определенный опыт работы с детьми. И это очень важно. Ведь обучение ментальному счету представляет собой не только освоение навыков, позволяющих работать с древними счетами. В этом процессе непременно учитываются используемые в педагогической практике психологические особенности в развитии ребенка.
Отзывы о методике
Ментальная арифметика – это довольно новая программа, применяемая для обучения устному счету. Однако, несмотря на немногочисленные годы существования, она уже успела получить большую популярность и показала превосходные результаты. Отзывы многих родителей и детей подтверждают тот факт, что данная программа не только эффективна, но и максимально полезна. При этом стоит учесть, что менар вполне может быть успешно внедрен в школьное обучение, став для детей дополнительным инструментом в освоении математических навыков.
По отзывам родителей, отличные результаты у детей можно наблюдать уже по истечении двух-трех месяцев после начала занятий, которые проводятся всего по несколько часов в неделю. Многие родители подтверждают, что у их ребенка заметно улучшилась память, повысилась способность к сосредоточению, а мышление приняло креативный характер. При этом школьник начал радовать своих близких хорошими оценками, которые получает не только на уроках математики. Он повысил уровень своих знаний и по всем остальным предметам. Кроме того, ему с легкостью стал даваться иностранный язык.

Все это позволяет сделать однозначный вывод о том, что менар представляет собой не только новый способ освоения навыков вычисления. Отличные результаты методика дает и в сфере всестороннего развития личности. Кроме того, во время занятий ментальной арифметикой активизируется потенциал маленького человека. Это способствует формированию здоровой и успешной натуры, у которой имеется надежный и крепкий фундамент, позволяющий без особых усилий вступить во взрослую жизнь.
businessman.ru
Мастер-класс по математике: «Техника быстрого счета»
Мастер-класс по теме: «Техника быстрого счета».
Цель: научить приемам быстрого устного счета
Задачи:
– привить интерес к предмету математика.
Оборудование: меловая доска, мел, мультемедийный проектор.
Ход мастера – класса
Просмотр фрагмента мультфильма «В стране не выученных уроков»
Известно, что учащиеся, владеющие твердыми навыками устного счета, быстрее овладевают технику алгебраических преобразований, лучше справляются с различными заданиями, составной частью которых являются вычисления. В устных вычислениях развиваются память учащихся, быстрота их реакции, сосредоточенность.
Хорошо развитые навыки устного счета – одно из условий успешного обучения учащихся в средних классах и залог успешной сдачи ГИА. При этом возрастает роль устных вычислений и вычислений вообще, так как на экзамене не разрешается использовать калькулятор и таблицы. Заметим, что многие вычислительные операции, которые записываются в ходе подробного решения задачи, в рамках теста совершенно не требуют этого. Можно научить учащихся выполнять простейшие преобразования устно. Для этого требуется организованная отработка такого навыка до автоматизма. Решение устных упражнений – наиболее приемлемый способ для решения этой задачи.
Как показывает практика, темп работы учащихся является замедленным. Подсчет ведется медленно и неточно, причем использую вычислительную технику. Часто запланированные задания на урок выполняются не полностью. Приходится отводить дополнительное время на прохождение той или иной темы. Поэтому на уроках необходимо отрабатывать у учащихся навыки устного счета.
Начинать развивать эти навыки необходимо, когда учащиеся приходят из начальной школы. Именно в 5-6 классах закладываются основы обучения математики, поэтому если не научить считать в этот период, в дальнейшем появятся трудности в работе.
Как научиться быстро, считать в уме? Не так уж сложно, как многие думают. Для этого вовсе не надо быть математическим гением. Достаточно выучить несложные правила и методы счета в уме, чтобы значительно увеличить скорость вычислений.
Приведу несколько приемов устного счета, после которых дети увлекаются математикой.
1) Умножение двузначного числа на 11.
13 * 11 (найдите значение данного выражения)
Я расскажу вам как это сделать быстрее и проще:
раздвигаем число 13 (1 – первая цифра будущего ответа, а 3 последняя) Находим сумму цифр: 1 + 3 = 4. Вставляем 4 между 1 и 3. Получаем 143.
Если сумма цифр больше 9, то мы записывает число единиц, а число десятков прибавляет к первой цифре ответа. Например: 79*11 = 7 (7+9)9= = 7 (16) 9 = (7+1)69= 869
А теперь пробуйте вы. (Называю числа и ученики находят результат)
2) Умножение двузначного числа на 111.
13 * 111 (найдите значение данного выражения)
Я расскажу вам как это сделать быстрее и проще:
раздвигаем число 13 (1 – первая цифра будущего ответа, а 3 последняя) Находим сумму цифр: 1 + 3 = 4. Вставляем 4 между 1 и 3 два раза. Получаем 1443.
Если сумма цифр больше 9, то мы записывает число единиц, а число десятков прибавляет к первой цифре ответа. Например: 79*111 = 7 (7+9)(7+9)9= = 7 (16) (16)9 = 7(16+1)69= 7(17)69= (7+1)769= 8769
А теперь пробуйте вы. (Называю числа и ученики находят результат)
3) Возведение чисел оканчивающихся на 5 в квадрат.
252 (найдите значение данного выражения)
Как вычислить быстро? Так как в конце числа стоит цифра 5, то квадрат 5 есть 25, значит последние цифра нашего ответа будет 25.
Теперь найдем остальные числа. Для этого найдем произведение 2 и 3 (идет за двойкой) = 6. Отсюда следует, что квадрат 25 = 625.
А теперь попробуйте вы.
Умеете ли Вы быстро считать? Этот вопрос можно задать не только школьникам и родителям, но и начинающим репетиторам по математике 5 — 9 классов. Как-то, прочитывая старую литературу по занимательной математике, я наткнулся на сообщение о том, что до революции, когда не было калькуляторов и компьютеров школьники, по крайней мере, в школе Рачинского, умели возводить в квадрат числа до 100 в уме. Не столбиком, а именно в уме. Как они это делали? Казалось бы, процесс достаточно трудоемкий, однако при ближайшем рассмотрении выясняется, что освоить возведение в квадрат может любой, даже не слишком продвинутый в математике ученик. Ну, например, сколько будет 96 в квадрате? Конечно, можно взять калькулятор, набрать нужные кнопки и получить ответ. Можно взять листок бумаги и подсчитать это столбиком. А можно и в уме.
Для начала возьмем пример попроще. Например, таблица умножения. У многих
Встречаются трудности при умножении на 7,8,9. Здесь на помощь могут прийти пальцы. Поверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.
Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.
А теперь считаем пальцы: количество пальцев под соединенными — это десятки.
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.
Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
Ученик, поднаторевший в применении этих приемов быстрого устного счета вполне может придумать свои приемы, внимательно вглядываясь в числа и находить в них свои закономерности. Как показывает опыт, это стремление приучает его не ошибаться в счете, а поиск своих приемов прививает ему интерес к предмету, позволяет творчески подходить к его изучению и находить в нем что-то свое.
Рассмотрим алгоритм, который позволяет перемножить в уме два двузначных числа, близкие к 100.
Если спросить шестиклассника, какие двузначные числа труднее всего перемножить, то он, вероятно, скажет: “Числа, близкие к 100, например: 98·97”. На самом же деле такие двузначные числа очень легко умножить даже в уме. Назовите каких-либо 2 числа, близких к 100. Пусть назвали 94 и 97.
Пишем: 94·97= 9118 (девяносто один – восемнадцать).
6 3
Как мы произвели умножение? Узнаем, каков недостаток первого сомножителя (94) до 100. Это будет 6. Недостаток второго сомножителя (97) до 100 равен 3. Затем из одного сомножителя (94) вычитаем недостаток (3) второго сомножителя до 100; получаем 91. Приписываем к результату произведения 3·6, то есть 18.
Здесь мы пользуемся таким алгоритмом: если хочешь перемножить два двузначных числа, близких к 100, то поступай так:
найди недостатки сомножителей до сотни;
вычти из одного сомножителя недостаток второго до сотни;
к результату припиши двумя цифрами произведение недостатков сомножителей до сотни.
В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает удивление. Такие навыки помогут человеку в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет – настоящая гимнастика ума.
infourok.ru
