Геометрическая интерпретация уравнения Бернулли
Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.
Как и в гидростатике, величину Z называют нивелирной высотой.
Второе слагаемое –
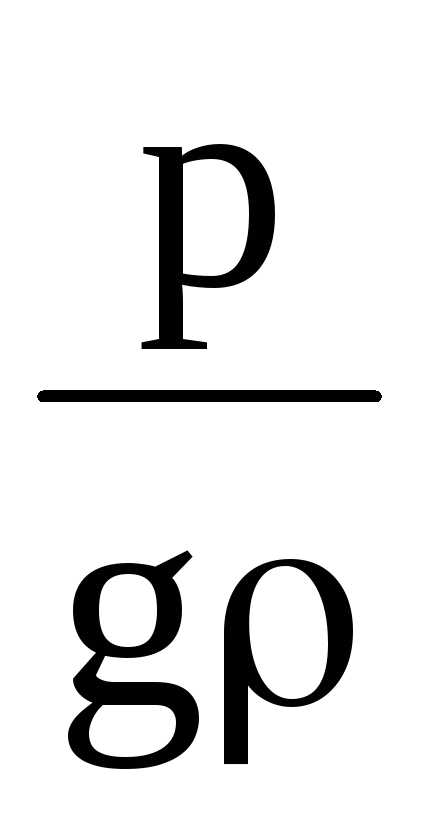 носит название пьезометрическая
высота.
Эта величина соответствует высоте, на
которую поднимется жидкость в пьезометре,
если его установить в рассматриваемом
сечении, под действием давления
носит название пьезометрическая
высота.
Эта величина соответствует высоте, на
которую поднимется жидкость в пьезометре,
если его установить в рассматриваемом
сечении, под действием давления Сумма первых двух членов уравнения
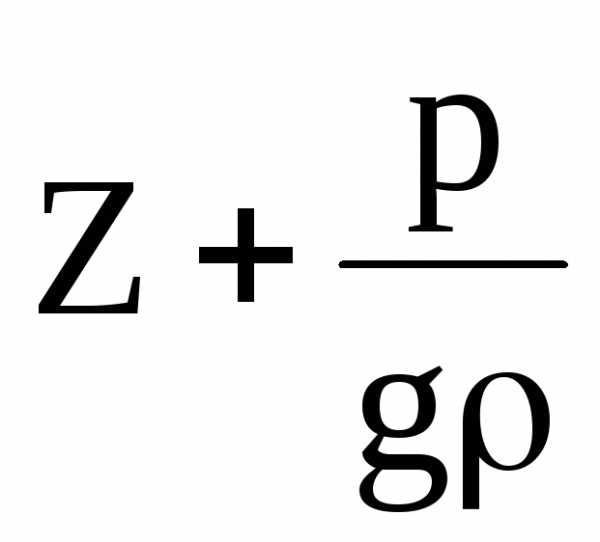 гидростатический
напор.
гидростатический
напор.Третье слагаемое в уравнения Бернулли
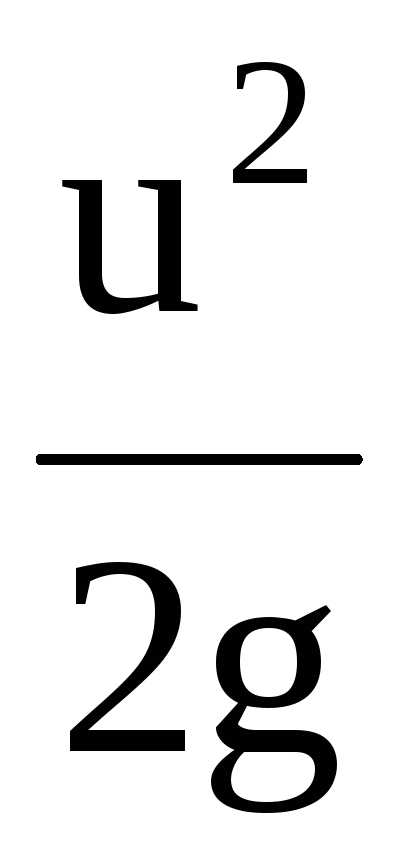 называется скоростной
высотой или скоростным
напором.
Данную величину можно представить как
высоту, на которую поднимется жидкость,
начавшая двигаться вертикально со
скорость u при отсутствии сопротивления движению.
называется скоростной
высотой или скоростным
напором.
Данную величину можно представить как
высоту, на которую поднимется жидкость,
начавшая двигаться вертикально со
скорость u при отсутствии сопротивления движению.Сумму всех трёх членов (высот) называют
В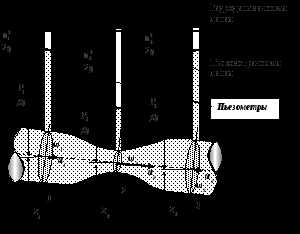 се
слагаемые уравнения Бернулли имеют
размерность длины и их можно изобразитьграфически.
се
слагаемые уравнения Бернулли имеют
размерность длины и их можно изобразитьграфически.
Значения 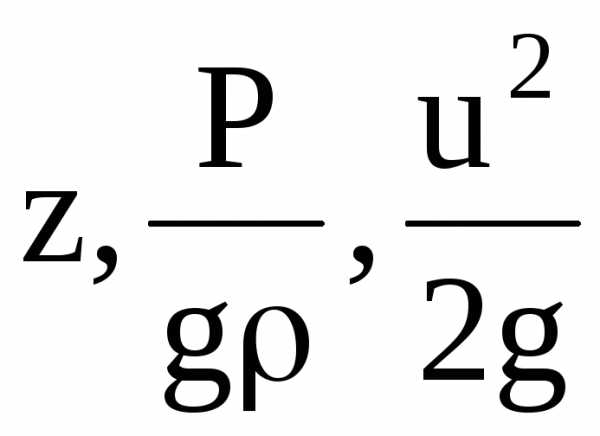 –нивелирную,
пьезометрическую и скоростную высоты можно определить для каждого сечения
элементарной струйки жидкости.
Геометрическое место точек, высоты
которых равны
–нивелирную,
пьезометрическую и скоростную высоты можно определить для каждого сечения
элементарной струйки жидкости.
Геометрическое место точек, высоты
которых равны 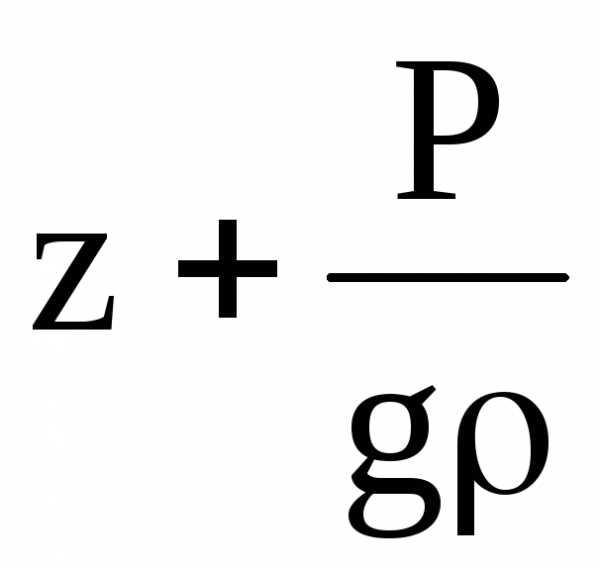
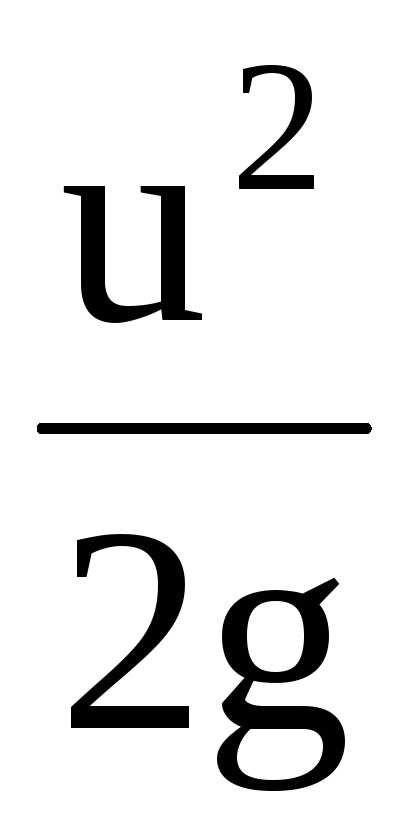 ,
то получится другая линия, которая
называетсягидродинамической или напорной
линией.
,
то получится другая линия, которая
называетсягидродинамической или напорной
линией.Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.
Энергетическая интерпретация уравнения Бернулли
Выше было получено
уравнение Бернулли с использованием
э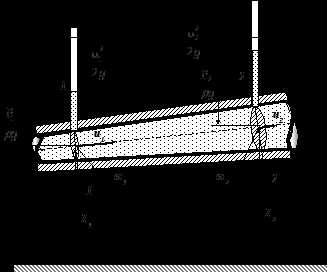 нергетических
характеристик жидкости. Суммарной
энергетической характеристикой жидкости
является её гидродинамическийнапор.
нергетических
характеристик жидкости. Суммарной
энергетической характеристикой жидкости
является её гидродинамическийнапор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.
Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удельная потенциальная энергия положения; Р/ — удельная потенциальная энергия давления;
Умножив все члены уравнения на удельный вес жидкости , получим
z – весовое давление, Па; P — гидродинамическое давление, Па; и2 /2 — динамическое давление Па; H — полное давление, Па
Уравнение Бернулли для потока идеальной жидкости
Поток
идеальной жидкости, как указывалось
ранее, можно представить совокупностью
элементарных струек жидкости. Скорости
по сечению потока неодинаковы, причём
в середине потока скорости наибольшие,
а к периферии они уменьшаются (струйная
модель потока). Это означает, что различные
струйки в одном сечении имеют различные
значения кинетической энергии. Отсюда
следует, что кинетическая энергия,
посчитанная с использованием скоростей
элементарных струек uS,
и кинетическая энергия, посчитанная с
использованием значения средней скорости
потока V,
будет иметь разные значения. Выясним,
какова эта разница. Кинетическая энергия
элементарной струйки 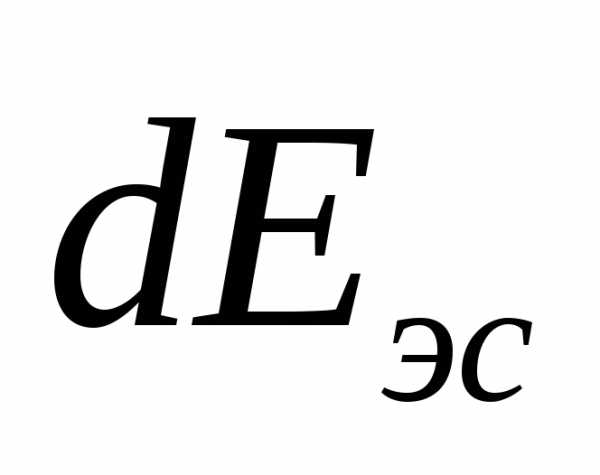

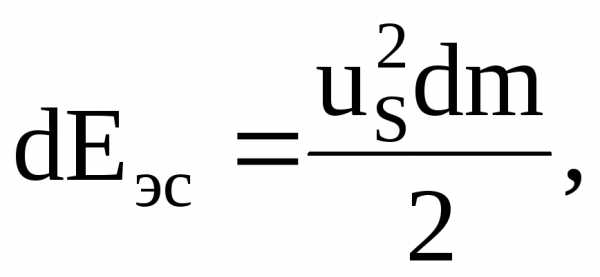
где 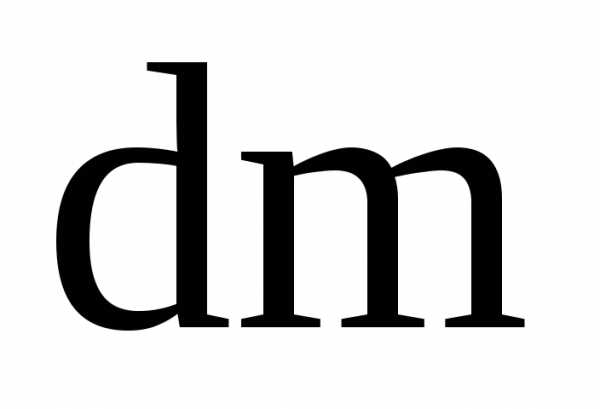 – масса жидкости плотностью
– масса жидкости плотностью ,
протекающей через живое сечение
элементарной струйки
,
протекающей через живое сечение
элементарной струйки со скоростью
со скоростью
.
Проинтегрировав
выражение для  ,
получим выражение для кинетической
энергии потока идеальной жидкости
,
получим выражение для кинетической
энергии потока идеальной жидкости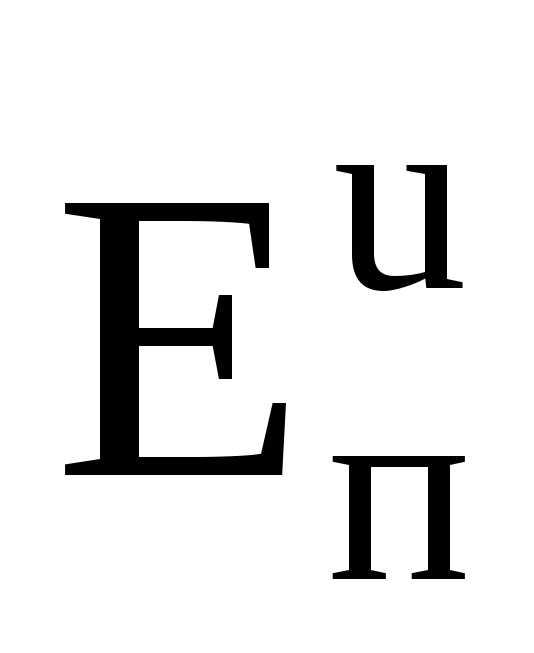 .
.
.
Если принять, что t=1, получим:
 .
.
Последняя формула определяет энергию потока с использованием скоростей элементарных струек
Если получить значение кинетической энергии потока с использованием значения средней скорости потока V , получим формулу:
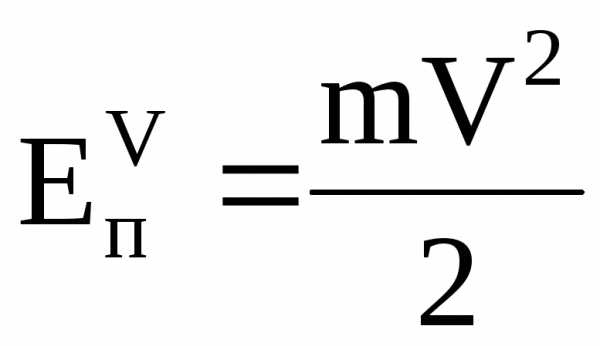 ,
,
где  – масса жидкости плотностью
– масса жидкости плотностью ,
протекающей через живое сечение потока
,
протекающей через живое сечение потока
 за времяt,
равная:
за времяt,
равная:.
После подстановки при t=1 окончательно получим:
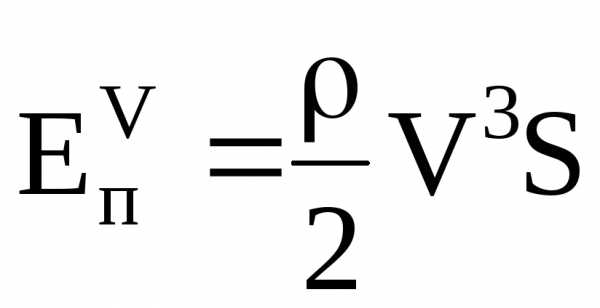 .
.
Отношение 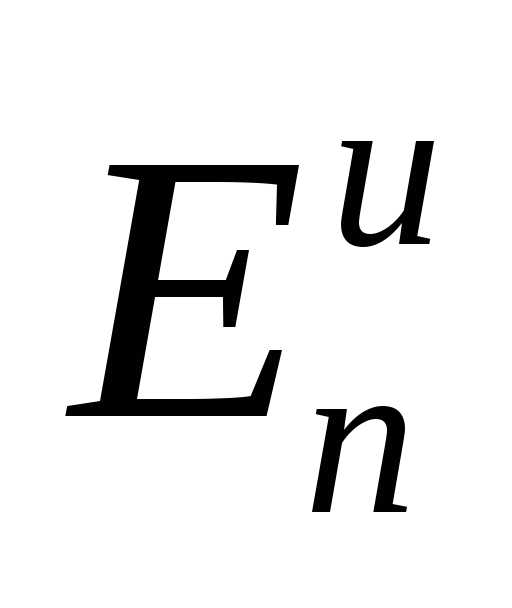 и
и ,
равное:
,
равное:
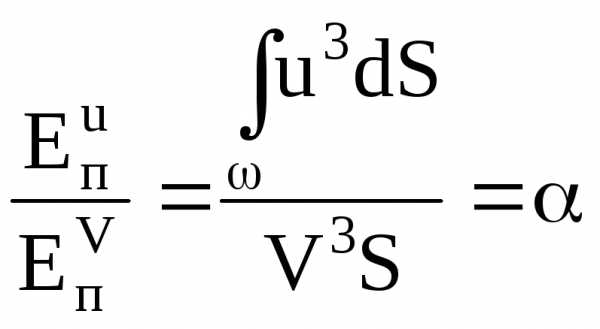
Полученная величина α носит наименование коэффициента кинетической энергии или коэффициента Кориолиса. Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.
Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:
Надо учесть, что в общем случае в разных сечениях потока коэффициент α будет иметь различные значения.
studfiles.net
Уравнение Бернулли для потока реальной жидкости
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока
,
где H1-1– напор в первом сечении потока жидкости,
H2-2 – напор во втором сечении потока,
∆h – потерянный напор – энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.
Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём
 .
.
Изменение энергии
по длине потока удобно проследить на
графиках. Из
уравнения Бернулли
для потока реальной жидкости (закона
сохранения энергии) видно, что
гидродинамическая линия для потока
реальной жидкости (с одним источником
энергии) всегда ниспадающая. То же
справедливо и для пьезометрической
линии, но только в случае равномерного
движения, когда скоростной напор 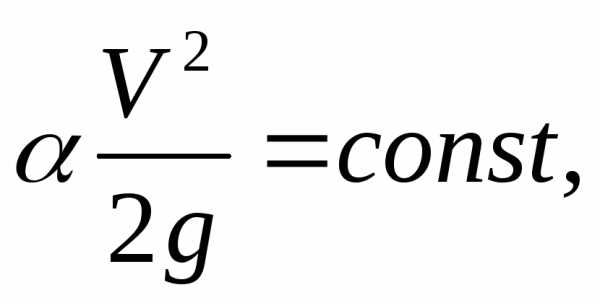 а уменьшение напора происходит только
за счёт изменения потенциальной энергии
потока, главным образом за счёт уменьшения
давления P.
а уменьшение напора происходит только
за счёт изменения потенциальной энергии
потока, главным образом за счёт уменьшения
давления P.
Пьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.

Если гидравлический уклон всегда положителен, то пьезометрический может быть и положительным, и отрицательным. При равномерном движении жидкости, когда скорость по длине потока не изменяется, скоростной напор вдоль потока v2 / (2g) = const. Следовательно, пьезометрическая линия параллельна энергетической, и пьезометрический уклон равен гидравлическому.
Изменение удельной потенциальной энергии положения вдоль потока жидкости, приходящееся на единицу длины, называют геометрическим уклоном i и определяют по формуле
где l — расстояние между сечениями потока.
Сформулируем два условия применимости к потоку жидкости уравнения Бернулли: 1) движение жидкости должно быть установившимся; 2) движение жидкости в сечениях 1—2, 2—2 и 3—3,cоединяемых уравнением Бернулли, должно быть параллельно струйным или плавноизменяющимся, в промежутке же между сечениями 1—1, 2—2 и 3—3 движение жидкости может быть и резко меняющимся.
Hа применении уравнения Бернулли основан принцип действия приборов для измерения скоростей и расходов жидкости. Одним из таких приборов является расходомер Вентури, состоящий из двух конических отрезков трубы, узкие концы которых соединены коротким цилиндрическим патрубком длиной менее 10 диаметров трубопровода (отношение диаметра конфузора и диффузора соответственно d/D=:0,3…0,7). Принцип работы расходомера Вентури базируется на уравнении Бернулли и уравнении неразрывности потока, а также на том, что перепад давлений на диафрагме, измеряемый пьезометром либо дифманометром пропорционален квадрату протекающего через нее расхода
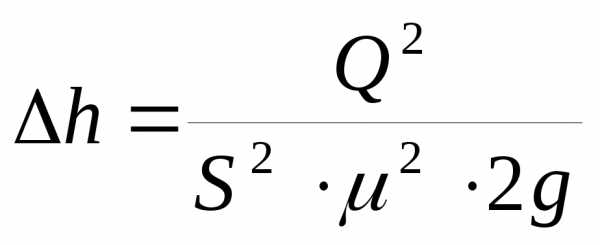
Для определения местных скоростей при плавноизменяющемся безнапорном движении применяют метод Пито. Трубку, нижний конец которой изогнут под прямым углом, опускают навстречу потоку, и жидкость в трубке начинает подниматься над свободной поверхностью, где давление равно атмосферному, на высоту .
При определении местных скоростей в напорном потоке используют систему из двух трубок, одна из которых представляет собой обычный пьезометр, показывающий напор Р/, а другая,только что описанная, измеряет величину напора
Разность уровней
в обеих трубках h представляет собой скоростной напор 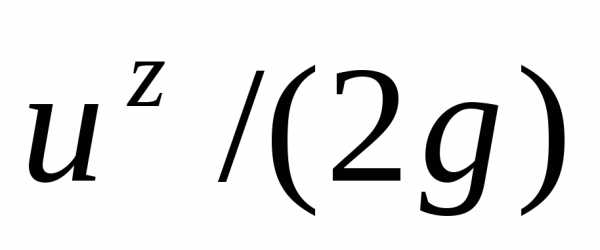
Местные скорости находят с помощью трубки Пито по формуле
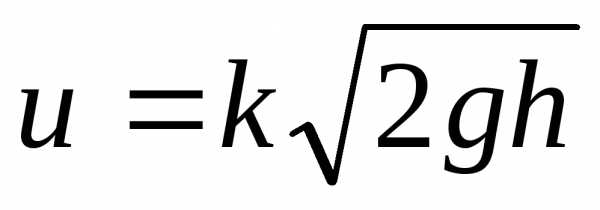
где k– поправочный коэффициент, определяемый для каждой трубки опытным путем
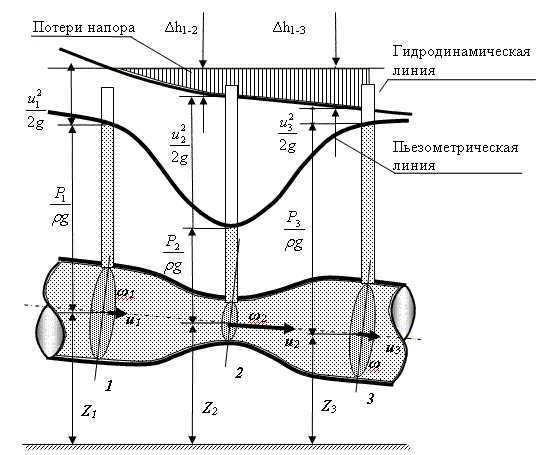
studfiles.net
1. Уравнение Бернулли для струйки идеальной жидкости
Лекция №6 Уравнение Бернулли
2. Геометрическая интерпретация уравнения Бернулли
3. Энергетическая интерпретация уравнения Бернулли
4. Уравнение Бернулли для потока идеальной жидкости
5. Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для струйки идеальной жидкости
Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и 2-2. Площади живых сечений потока обозначим dω1 и dω2.Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0 – 0 характеризуется величинами z1 и z2. Давления и скорости жидкости в этих сечениях имеют значения P1, P2 и u1, u2 соответственно.
Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.
З а
малый промежуток времениdt частицы жидкости
из 1-1 переместятся
в 1′-1′ на расстояние, равное u1dt,
а частицы из 2-2 в 2′ – 2′ на расстояние u2dt.
а
малый промежуток времениdt частицы жидкости
из 1-1 переместятся
в 1′-1′ на расстояние, равное u1dt,
а частицы из 2-2 в 2′ – 2′ на расстояние u2dt.
Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.
Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы p1dω1 на путь u1dt:
.
Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение
.
Полная работа, выполненная силами давления, примет вид:
.
Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса dG:
.
При перетекании от сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот (z1 – z2) и работа, произведённая силами тяжести, составит:
.
Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.
Приращение кинетической энергии выделенного объёма за dt равно разности его кинетических энергий в сечениях 1-1 и 2-2. Это приращение составит
.
Приравнивая приращение кинетической энергии сумме работ сил тяжести и сил давления, придём к виду:
.
Разделив обе части на вес dG, т.е. приведя уравнение к единичному весу, получим
.
После сокращения и преобразований придём к искомому виду
Если учесть, что
сечения 1-1 и 2-2 выбраны
произвольно, можно прийти к выводу, что
сумма приведённых выше величин 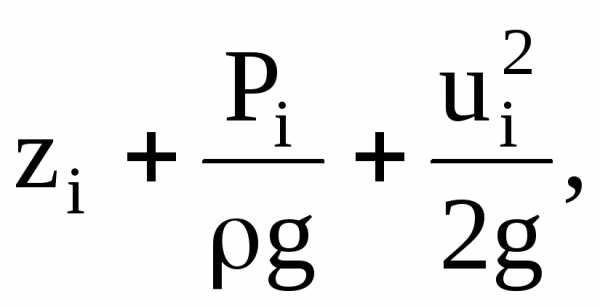 описывающих движение жидкости под
действием сил давления и сил тяжести
есть величина постоянная для элементарной
струйки, т.е.
описывающих движение жидкости под
действием сил давления и сил тяжести
есть величина постоянная для элементарной
струйки, т.е.
Таким образом, снова получено то же (ранее полученное интегрированием уравнений Эйлера) уравнение Бернулли для элементарной струйки невязкой жидкости при установившемся движении под действием сил тяжести.
studfiles.net
Уравнение Бернулли для реальной жидкости
При движении реальной жидкости, вследствие её вязкости, действуют гидравлические сопротивления, на преодоление которых затрачивается энергия. Эта энергия превращается в теплоту и рассеивается в дальнейшем движущей жидкостью.
Уравнение Бернулли для струйки реальной жидкости имеет вид
(3.8)
где  ─ потери напора на участке длиной
─ потери напора на участке длиной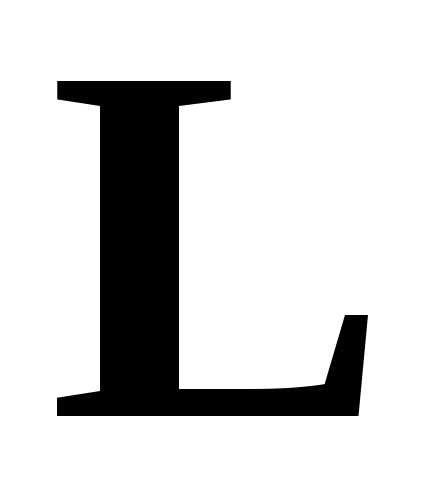 вдоль оси струйки между двумя сечениями.
вдоль оси струйки между двумя сечениями.
Уравнение Бернулли для потока реальной жидкости имеет вид:
(3.9)
где 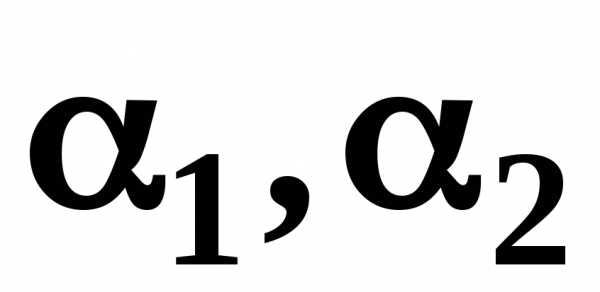 ─ коэффициенты Кориолиса, учитывающие
различие скоростей в разных точках
сечения потока реальной жидкости.
─ коэффициенты Кориолиса, учитывающие
различие скоростей в разных точках
сечения потока реальной жидкости.
На
практике
:
для ламинарного режима течения жидкости
в круглых трубах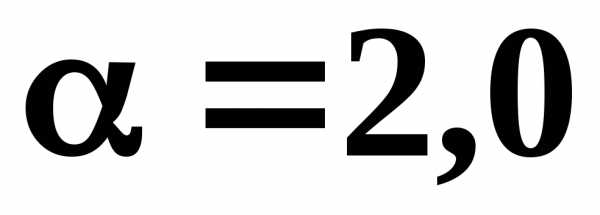 ;
для турбулентного режима.
;
для турбулентного режима.
С
помощью уравнения Бернулли решается
большинство задач практической
гидравлики. Для этого выбирают два
сечения по длине потока, таким образом,
чтобы для одного из них были известны
величины 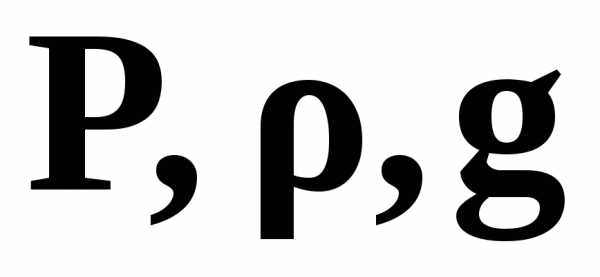 ,
а для другого сечения одна или величины
подлежали определению. При двух
неизвестных для второго сечения
используют уравнение постоянства
расхода жидкостиυ1ω 1 = υ2ω2.
,
а для другого сечения одна или величины
подлежали определению. При двух
неизвестных для второго сечения
используют уравнение постоянства
расхода жидкостиυ1ω 1 = υ2ω2.
Гидравлические сопротивления
Движущийся поток жидкости на своем пути преодолевает силы трения жидкости о стенки трубы или канала и различные местные сопротивления, вследствие чего возникают потери удельной энергии. Потери напора различают двух видов:
–
потери по длине потока  ;
;
–
потери на преодоление местных сопротивлений 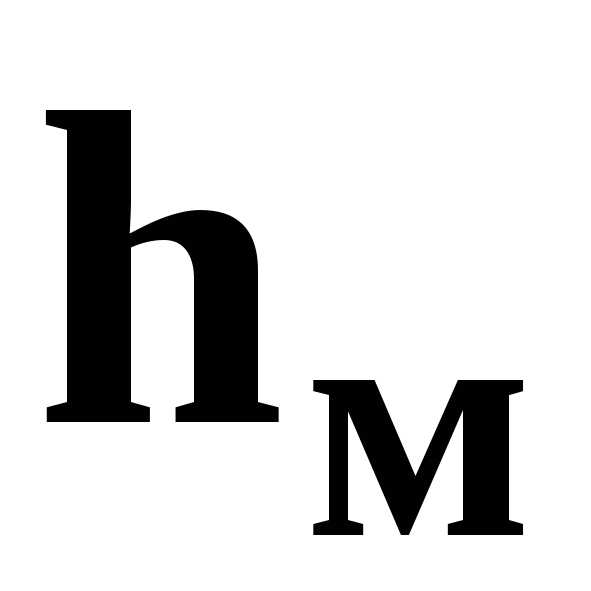 .
.
Полные потери напора равны сумме всех потерь
(3.10)
Потери напора по длине
При равномерном движении в трубах потери напора по длине, как при турбулентном, так и при ламинарном движении определяются для круглых труб по формуле Дарси
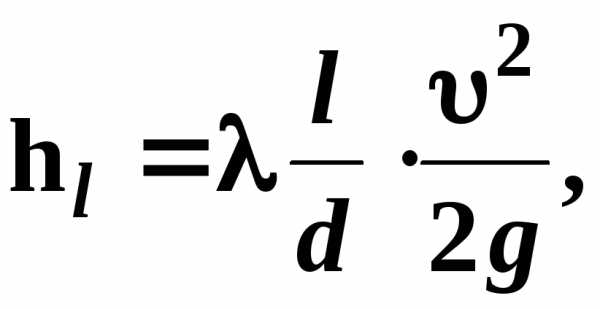 (3.11)
(3.11)
а для труб любой другой формы сечения по формуле
(3.12)
В некоторых случаях также используют формулу
 (3.13)
(3.13)
Потери
давления на трение по длине  ,
Па, определяются по формуле
,
Па, определяются по формуле
 (3.14)
(3.14)
где  ─ длина участка трубы или канала, м;
─ длина участка трубы или канала, м;
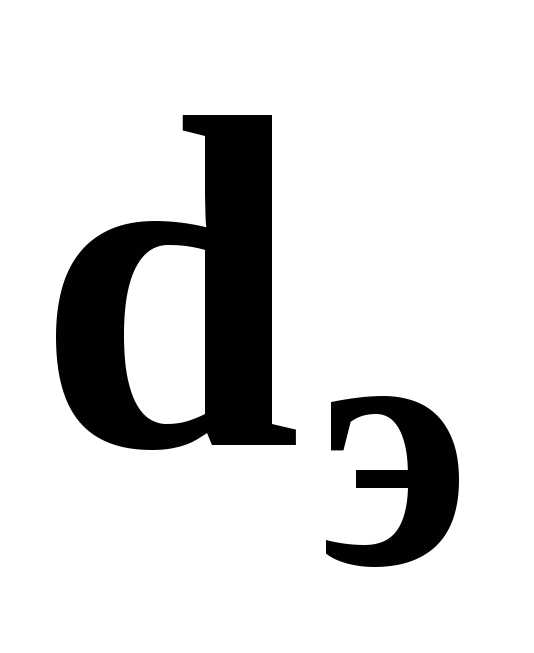 ─эквивалентный
диаметр, м;
─эквивалентный
диаметр, м;
 ─средняя
скорость течения, м/с;
─средняя
скорость течения, м/с;
 ─гидравлический
радиус трубы, м;
─гидравлический
радиус трубы, м;
 ─коэффициент
гидравлического трения;
─коэффициент
гидравлического трения;
 ─коэффициент
Шези, связанный с коэффициентом
гидравлического трения зависимостями
─коэффициент
Шези, связанный с коэффициентом
гидравлического трения зависимостями
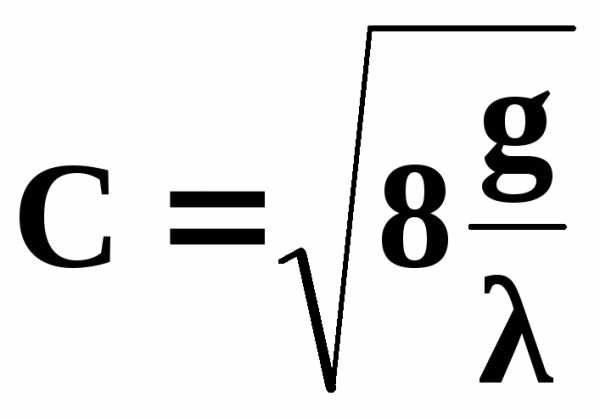 ;
; 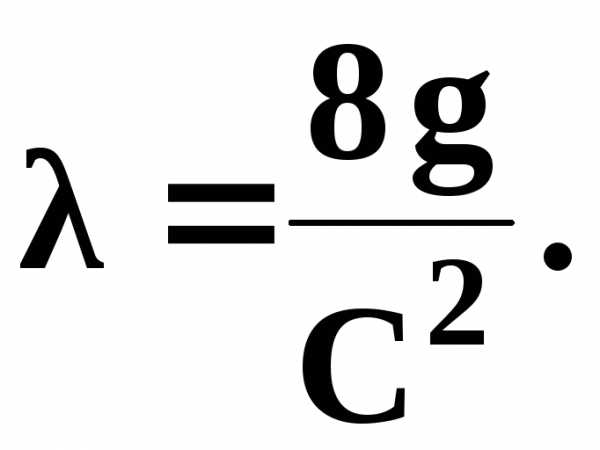
В зависимости от режима движения применяются различные формулы для определения коэффициента гидравлического трения.
При ламинарном движении по трубам круглого сечения коэффициент гидравлического трения определяется по формуле
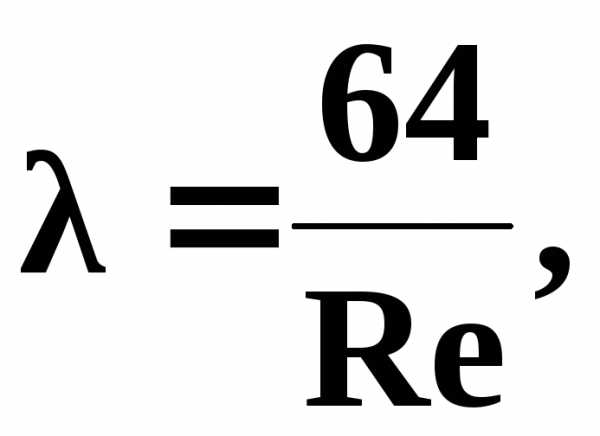 (3.15)
(3.15)
а для труб любой формы сечения
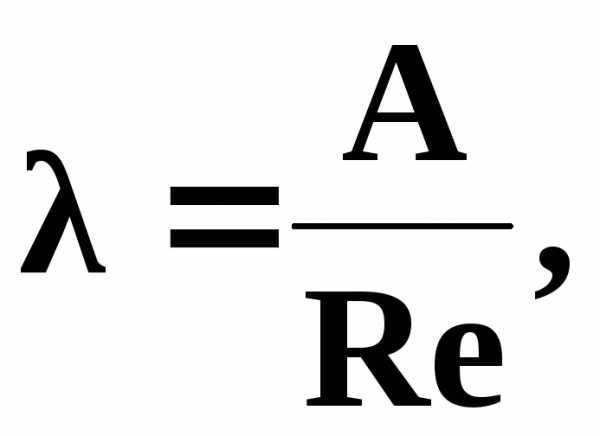 (3.16)
(3.16)
где А ─ коэффициент, численное значение которого зависит от формы поперечного сечения трубы.
Тогда формула для определения потерь напора по длине при ламинарном режиме принимает вид
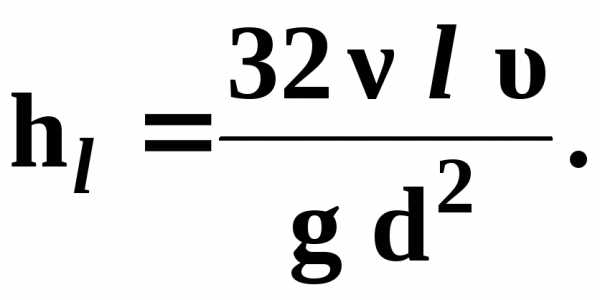 (3.17)
(3.17)
Впервые
наиболее исчерпывающие работы по
определению  были даны И.И. Никурадзе, который на
основе опытных данных построил график
зависимостиот
были даны И.И. Никурадзе, который на
основе опытных данных построил график
зависимостиот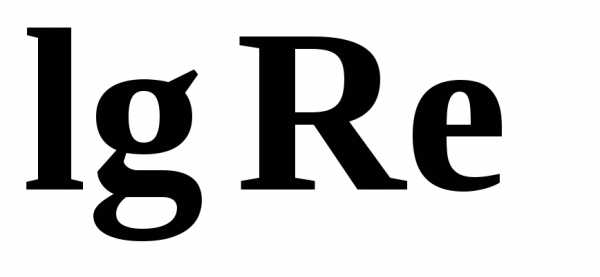 для ряда значений
для ряда значений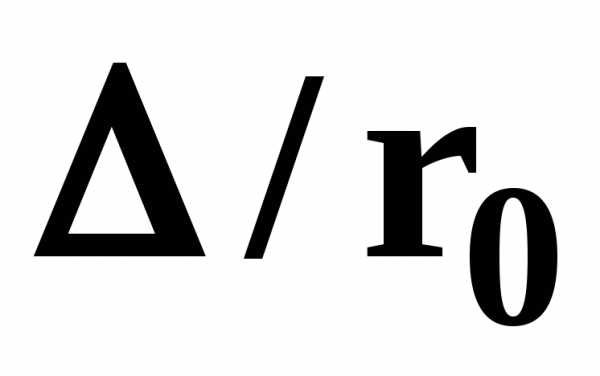 .
Опыты Никурадзе были проведены на трубах
с искусственно заданной шероховатостью,
полученной путем приклейки песчинок
определенного размера на внутренние
стенки трубопровода. Результаты этих
исследований представлены на рисунке
3.5, где построены зависимостиот
.
Опыты Никурадзе были проведены на трубах
с искусственно заданной шероховатостью,
полученной путем приклейки песчинок
определенного размера на внутренние
стенки трубопровода. Результаты этих
исследований представлены на рисунке
3.5, где построены зависимостиот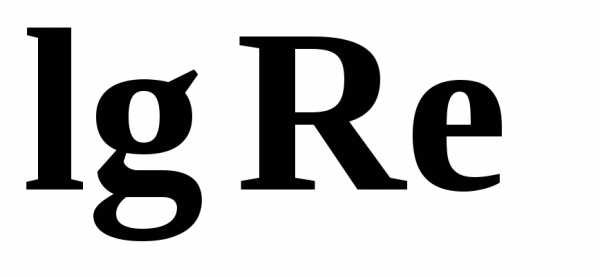 для ряда значений
для ряда значений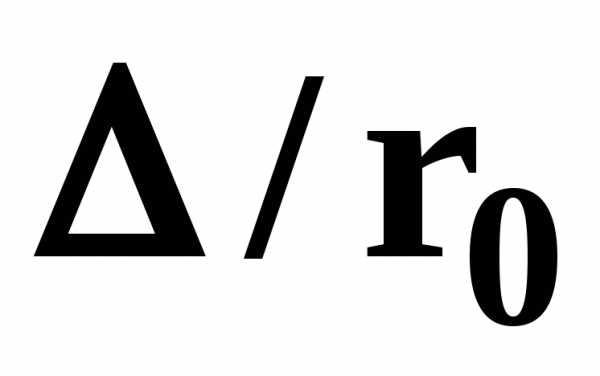 .
.
Прямая I соответствует ламинарному режиму движения жидкости в соответствии с выражением (3.15).
При турбулентном режиме различают три области гидравлических сопротивлений, установленных в результате опытов, проведенных Никурадзе (см. рисунок 3.5)
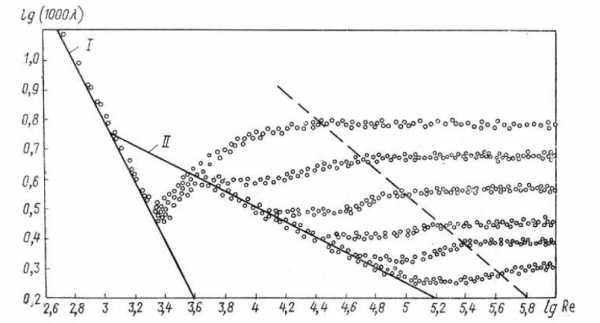
Рисунок 3.5 ─ График Никурадзе
Первая
область ─ область малых  и
и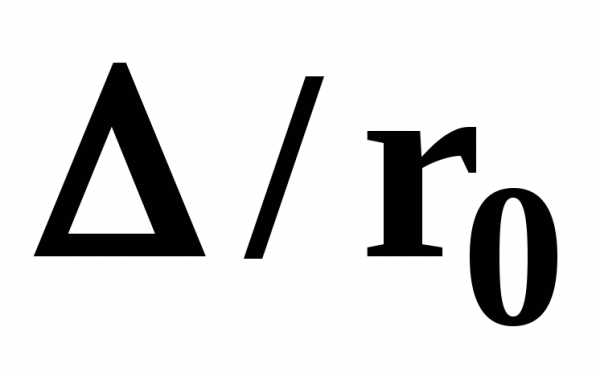 ,
где коэффициент
,
где коэффициент не зависит от шероховатости, а определяется
лишь числом
не зависит от шероховатости, а определяется
лишь числом (отмечена на рисунке 3.5 прямой II).
(отмечена на рисунке 3.5 прямой II).
Это область
гидравлически гладких труб.
Если число Рейнольдса лежит в диапазоне
коэффициент определяется по полуэмпирической
формуле Блазиуса
определяется по полуэмпирической
формуле Блазиуса
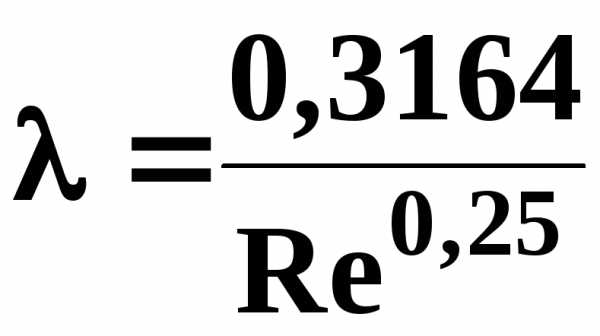 .
(3.18)
.
(3.18)
или по формуле П.Н. Конакова
(3.19)
Во
второй области, расположенной между
линий II и пунктирной линией справа,
коэффициент  зависит одновременно от двух параметров
─ числа
зависит одновременно от двух параметров
─ числа и относительной шероховатости,
которую можно заменить на
и относительной шероховатости,
которую можно заменить на .
Для определения в этой области может
служить универсальная формула А.Д.
Альтшуля
.
Для определения в этой области может
служить универсальная формула А.Д.
Альтшуля
. (3.20)
где  ─
эквивалентная абсолютная шероховатость.
─
эквивалентная абсолютная шероховатость.
Третья
область ─ область больших  и
и ,
где
,
где не зависит от числа
не зависит от числа ,
а определяется лишь относительной
шероховатостью (область расположена
справа от пунктирной линии). Этообласть
шероховатых труб,
в которой все линии с различными
шероховатостями параллельны между
собой. Эту область называют областью
автомодельности или режимом квадратичного
сопротивления, так как здесь гидравлические
потери пропорциональны квадрату
скорости.
,
а определяется лишь относительной
шероховатостью (область расположена
справа от пунктирной линии). Этообласть
шероховатых труб,
в которой все линии с различными
шероховатостями параллельны между
собой. Эту область называют областью
автомодельности или режимом квадратичного
сопротивления, так как здесь гидравлические
потери пропорциональны квадрату
скорости.
Определение  для этой области производят по упрощенной
формуле Альтшуля
для этой области производят по упрощенной
формуле Альтшуля
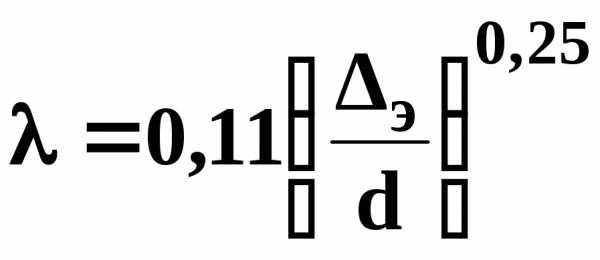 .
(3.21)
.
(3.21)
studfiles.net
А) Уравнение Бернулли для идеальной и реальной жидкостей.
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ ГРОДНЕНСКОГО ОБЛИСПОЛКОМА
УО «ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ ПРОФЕССИОНАЛЬНО-ТЕХНИЧЕСКИЙ КОЛЛЕДЖ КОММУНАЛЬНОГО ХОЗЯЙСТВА»
Контрольная работа №1
по учебной дисциплине «Основы гидравлики»
ВАРИАНТ №12
| Выполнил: ____________ подпись | Шмат А.А. |
| Специальность:СТОЗиС; Курс:1; Форма обучения:заочная; Группа: №5з-ТС | |
| Проверил: ____________ подпись | Косицкая Н.И. |
Гродно
Содержание
1.Теоретическая часть. 3
А) Уравнение Бернулли для идеальной и реальной жидкостей. 3
Б) Насосная установка, её характеристики. 9
В) Законы изменения состояния газов. Изотермический процесс. 13
2. Практическая часть. 15
Задача №1. 15
Задача №2. 16
Список использованных источников. 17
Теоретическая часть.
А) Уравнение Бернулли для идеальной и реальной жидкостей.
Основное уравнение равномерного движения.
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.1).
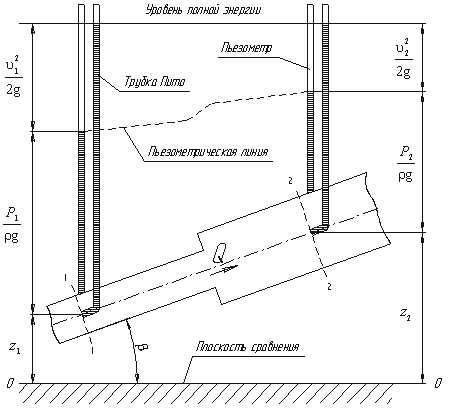
Рис.1 Схема к выводу уравнения Бернулли для идеальной жидкости
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для измерения давления жидкости применяют пьезометры – тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту . В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.1).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
и -удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
– удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
– удельные кинетические энергии в тех же сечениях.
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.1, можно заметить, что z1 и z2 – геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; – пьезометрические высоты; – скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для реальной жидкости
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.2).
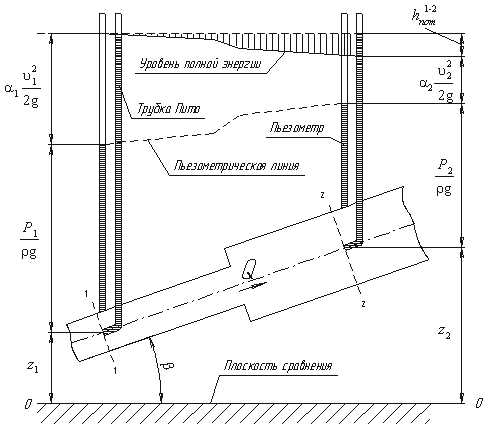
Рис.2. Схема к выводу уравнения Бернулли для идеальной жидкости
Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рис.2 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента
и , которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).
Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
= hлин + hмест
С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ1ω 1 = υ2ω2.
Для двух сечений потока 1—1 и 2—2 реальной жидкости (рисунок 1) при установившемся плавно изменяющемся движении уравнение Бернулли имеет вид:
где z — ордината, определяющая высоту положения центра выбранного сечения над произвольной горизонтальной плоскостью сравнения 0—0; p/γ — пьезометрическая высота; z + p/γ = Hп — гидростатический напор; αυ2/(2g) = hv — скоростная высота, или скоростной напор; α — коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в живом сечении потока.
Сумма трех членов:
z + p/γ + αυ2/(2g) = H
есть полный напор; Σhп — потеря напора между выбранными сечениями потока. Вместо выражения (1) можно написать:
h2 = h3 + Σhп
Все члены уравнения Бернулли в формуле (1) имеют линейную размерность и в энергетическом смысле представляют удельную энергию жидкости, т. е. энергию, отнесенную к единице веса жидкости.
Так, z и p/γ – удельная потенциальная энергия соответственно положения и давления;
z + p/γ – удельная потенциальная энергия жидкости;
αυ2/(2g) – удельная кинетическая энергия, выраженная через среднюю скорость потока в данном сечении. Сумма всех трех членов z + p/γ + αυ2/(2g) = H представляет полный запас удельной механической энергии жидкости в данном сечении потока;
Σhп – удельная механическая энергия, затрачиваемая на преодоление сопротивления движению жидкости между сечениями потока и переходящая в тепловую энергию, которая состоит из следующих слагаемых:
Σhп = Σhдл + Σhмест
где Σhдл — потери энергии (напора) на трение по длине; Σhмест — местные потери энергии (напора).
Если уравнение (1) умножить на γ, то получим:
Члены уравнения (2) имеют размерность давления и представляют энергию, отнесенную к единице объема.
Если уравнение (1) умножить на g, то получим
(3)
Члены уравнения (3) имеют размерность м2/с2 и представляют энергию, отнесенную к единице массы.
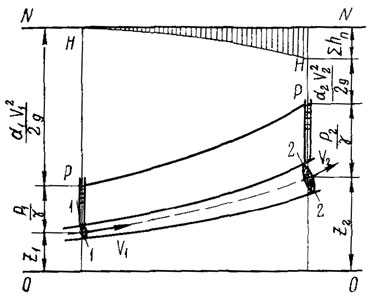
Рисунок 3
На рисунке 3 приведена диаграмма уравнения Бернулли для потока реальной жидкости. Здесь 0—0 — плоскость сравнения; N—N — плоскость начального напора; Н—Н — напорная линия, или линия полной удельной энергии. Падение ее на единицу длины представляет гидравлический уклон J; Р—Р — пьезометрическая линия, или линия удельной потенциальной энергии. Падение ее на единицу длины представляет пьезометрический уклон Jп.
Так как общий запас удельной энергии вдоль потока непрерывно уменьшается, линияН—Н всегда нисходящая, а гидравлический уклон всегда положительный (J>0). Пьезометрическая линия может быть и нисходящей, и восходящей (последнее имеет место на расширяющихся участках, когда средняя скорость потока уменьшается), поэтому пьезометрический уклон может быть и положительным (J>0), и отрицательным(J<0).
На участках с равномерным движением жидкости, где имеют место только потери напора на трение по длине, линии Н—Н и Р—Р представляют взаимно параллельные прямые, поэтому J = Jп =hдл/L. В этом случае потеря напора может быть определена по разности гидростатических напоров:
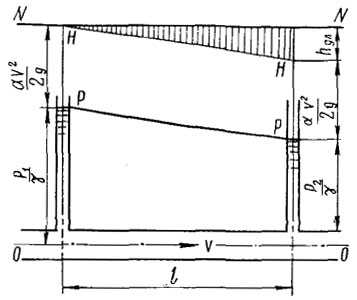
Рисунок 4
Для горизонтальных участков потоков ( ) или в случае, если плоскость сравнения0—0 проведена по оси потока ( =0) (рисунок 4), потеря напора на трение по длине может быть определена непосредственно по разности показаний пьезометров:
stydopedia.ru
Уравнение Бернулли для струйки идеальной жидкости
Для вывода уравнения Бернулли используется теорема об изменения кинетической энергии – изменение кинетической энергии равно работе внешних сил.
Рис.3.23 – силы действующие на элементарную струйку |
(3.0) |
dV – объём массы жидкостиdm.
Тогда изменение кинетической энергии dЭкинравно
. | (3.0) |
При движении от первого сечения ко второму на массу действует сила тяжести, поэтому изменение работы сил тяжести dAтяжравно:
. | (3.0) |
На поперечное сечение dсо стороны окружающей жидкости действует сила давленияdP = p d. За времяdtмасса частицы жидкости перемещается на расстояниеdS, тогда работа, совершаемая силами давления, равнаdAдав = dP dS = p d dS = p dV(d dS = dV– объем частицы жидкости). Поэтому работа сил давления равна
. | (3.0) |
В общем случае на боковой поверхности элементарной струйки действуют силы трения, которые противодействуют движению жидкости. В данном случае рассматривается идеальная жидкость, вязкость которой равна нулю, поэтому сил трения равны нулю и работы не совершают.
Используя теорему изменения кинетической энергии, запишем:
, | (3.0) |
или
. | (3.0) |
Разделим это выражение на вес частицы жидкости, которая проходит за время dtчерез сечение струйки,dG=gdm= ρgdV:
. | (3.0) |
Так, как сечения 1-1 и 2-2 были выбраны произвольно, то последнее уравнение можно переписать в виде:
. | (3.0) |
Уравнение (3.24) или (3.25) называется уравнением Бернулли. Уравнение Бернулли в таком виде можно записать только для установившегося движения несжимаемой идеальной жидкости. Уравнение Бернулли выражает закон сохранения энергии – для идеальной жидкости полная энергия вдоль элементарной струйки сохраняется. В уравнения (3.24) и (3.25) входит не сама энергия, а энергия отнесённая к весу частицы жидкости, которая называется удельнойэнергией, поэтому каждое слагаемое в уравнении Бернулли представляет собой удельную потенциальную энергию положения, удельную потенциальную энергию давления и удельную кинетическую энергию и в системе СИ измеряется в метрах. Сумма этих энергий называется полной удельной энергией.
Уравнение Бернулли для струйки и потока реальной жидкости
Если по элементарной струйке движется реальная жидкость, то возникают силы трения и часть полной механической энергии переходит в тепловую энергию, которая в уравнении (3.24) не учитывается. Поэтому полная механическая энергия в начале струйки будет больше, чем в конце. Потерей напораилипотерей полной удельной энергии h1-2– называется разность полных удельных энергий в начале и в конце элементарной струйки.
. | (3.0) |
Тогда уравнение для элементарной струйки реальной жидкости запишется:
. | (3.0) |
Рассмотрим поток жидкости. Поток жидкости состоит из элементарных струек, скользящих друг относительно друга с разными скоростями. Пусть за время dt = 1через поперечное сечение элементарной струйки проходит массаdm = u d. Осредним уравнение Бернулли для элементарной струйки реальной жидкости по поперечному сечению. Так, как в поперечном сечении давление распределяется по гидростатическому закону, сумма первых двух слагаемых постоянна и при осреднении не изменится. Усредняя третье слагаемое и выражая его через среднюю скорость, получим
. | (3.0) |
Тогда для потока реальной жидкости уравнение Бернулли запишется:
. | (3.0) |
z– расстояние от плоскости сравнения до любой точки поперечного сечения, м;
p– давление именно в этой точке, Па;
v– средняя скорость в данном поперечном сечении, м/с;
– имеет три названия: коэффициент неравномерности распределения скоростей, средняя коэффициент Кариолиса, коэффициент кинетической энергии.
Коэффициент неравномерности распределения скоростей определяется
| (3.0) |
Коэффициент неравномерности распределения скоростей определяется в зависимости от режимов движения жидкости
Ламинарный режим | Турбулентный режим | V |
=2 | =1,11,2 | =1 |
На практике обычно выбирают значение = 1.
При применении уравнения Бернулли следует придерживаться следующих правил:
Выбрать два поперечных сечения. Поперечные сечения выбираются по направлению движения жидкости в начале потока 1 – 1 в конце 2 – 2. Поперечные сечения выбираются там, где известны давления или где одно из давлений необходимо найти.
Выбирают плоскость сравнения 0 – 0. Плоскостью сравнения может служить любая горизонтальная поверхность. Обычно выбирают плоскость сравнения, проходящую через центр тяжести нижнего поперечного сечения.
Записывают значения zиpдля поперечных сечений. Для напорных потоков (движение жидкости в трубе) за характерную точку обычно принимают центр тяжести трубы. Для безнапорных потоков (движение жидкости в реке) за характерную точку обычно принимают точку на свободной поверхности жидкости. Давлениеpдолжно иметь один и тот же тип или абсолютное в обеих частях уравнения или манометрическое.
Расписывают скорости в поперечных сечениях. В уравнении Бернулли, как минимум, входят три скорости: v1– средняя скорость в первом сечении,v2– средняя скорость во втором сечении,v– средняя скорость в трубе, которая соединяет эти сечения (от этой скорости зависят потери напора h1-2). Если известен расход, то скорости находятся:
. | (3.0) |
Если расход неизвестен, то неизвестны и скорости. В этом случае удобно все скорости выразит через скорость в трубе:
. | (3.0) |
Полученные значения z, p, vподставляют в уравнение Бернулли и находят неизвестную величину.
studfiles.net
4.4. Уравнение Даниила Бернулли для потока реальной жидкости.
Энергетический баланс потока жидкости определяется уравнением Даниила Бернулли, впервые выведенным им в 1738 г. для элементарной струйки идеальной жидкости (т.е. не имеющейся вязкости) при установившемся движении.
В последующем на
основании работ как Д.Бернулли, так и
других ученых (Л. Эйлера, Г. Кориолиса,
Ж. Буссинеска и др.), это уравнение было
сформировано для целого потока реальной
жидкости, однако в истории науки оно
известно как уравнение Даниила Бернулли.
Для составления энергетического баланса
рассмотрим поток, проходящий по
трубопроводу переменного сечения от
живого сечения 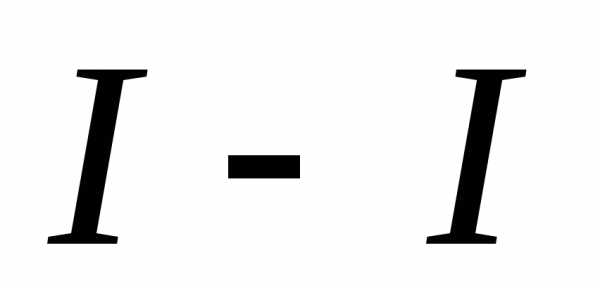 к живому сечению
к живому сечению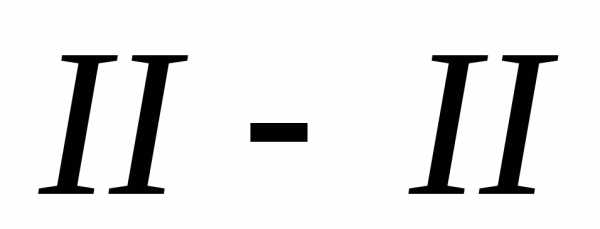 (рис. 25).
(рис. 25).
hw
Рис. 25. Графическое изображение уравнения Д. Бернулли для потока реальной жидкости при установившемся движении:
1 – поток; 2 – пьезометр; 3 – трубка Пито; 4 – линия полной энергии;
 –
плоскость сравнения.
–
плоскость сравнения.
Рассмотрим полную
удельную энергию в сечениях относительно
плоскости сравнения  с
учетом ранее полученного уравнения
(69):
с
учетом ранее полученного уравнения
(69):
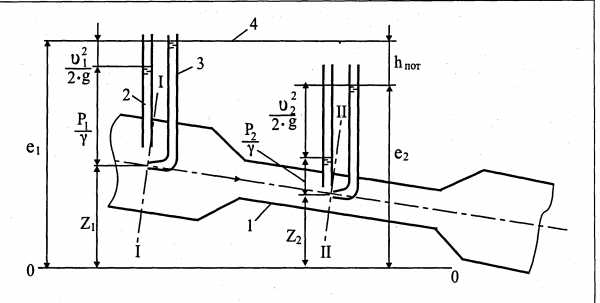
Полная удельная
энергия потока в сечении 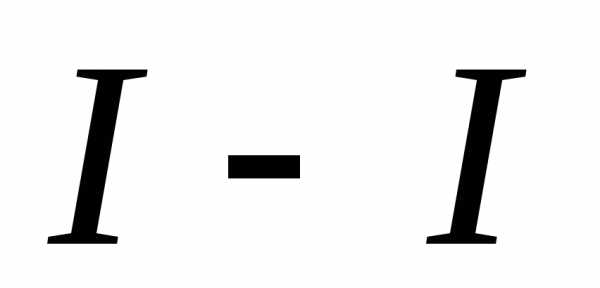 :
:
 (70)
(70)
Полная удельная
энергия потока в сечении  :
:
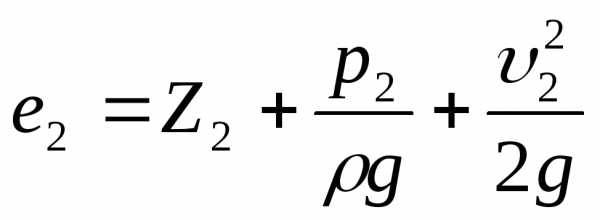 ,
(71)
,
(71)
Показания пьезометров
и скоростных трубок, установленных в
сечениях 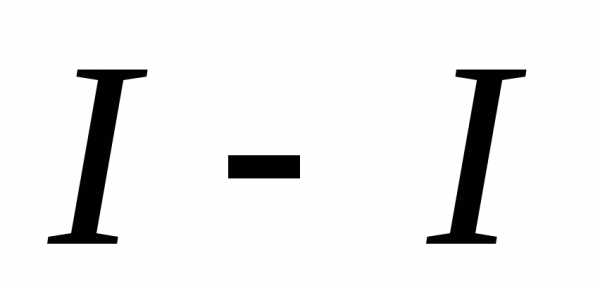 и
и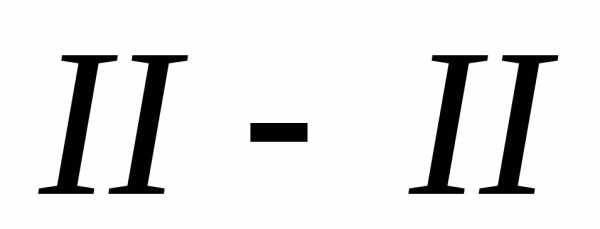 ,
демонстрируют, что
,
демонстрируют, что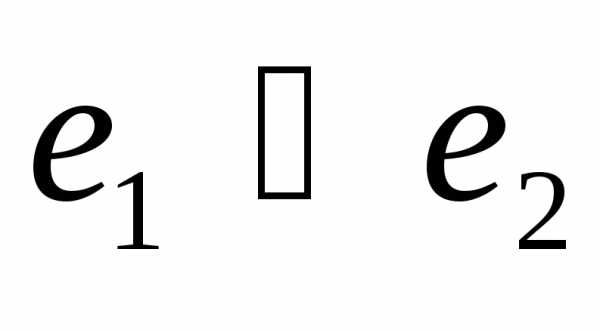 .
.
Это вызвано тем, что часть энергии потока расходуется на преодоление гидравлических сопротивлений при движении жидкости от одного сечения к другому.
Величина 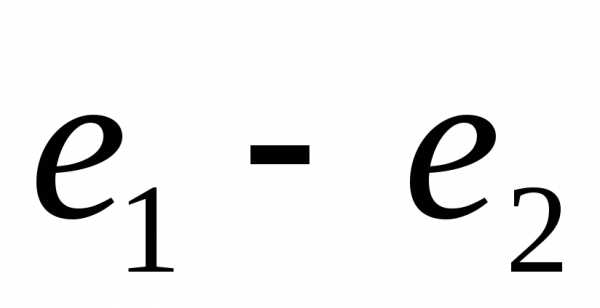 называется удельной потерей энергии
(или потерей напора) и обозначается
называется удельной потерей энергии
(или потерей напора) и обозначается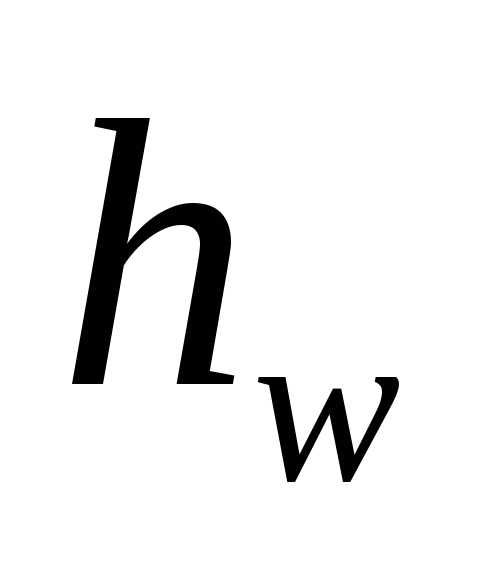 .
Отсюда на основании закона сохранения
энергии запишем следующее уравнение
.
Отсюда на основании закона сохранения
энергии запишем следующее уравнение
(72)
Полученное выражение и называется уравнением Бернулли для потока реальной жидкости.
Влияние вязкости жидкости приводит к неравномерному распределению скоростей в поперечном сечении потока (трубопровода). Поэтому уравнение (72) перепишется в следующем виде:
, (73)
где  –
коэффициент, характеризующий
неравномерность распределения скоростей
(коэффициент Кориолиса).
–
коэффициент, характеризующий
неравномерность распределения скоростей
(коэффициент Кориолиса).
При равномерном движении воды в трубах и каналах небольшого поперечного сечения коэффициент Кориолиса принимается равным 1,05….1,1. В большинстве случаев при практических расчетах полагают
Каждая составляющая уравнения Бернулли имеет геометрический и энергетический смысл.
Все члены уравнения (73) имеют линейную размерность, и каждый из них может называться высотой:

– геометрическая высота, или высота положения,

– пьезометрическая высота;
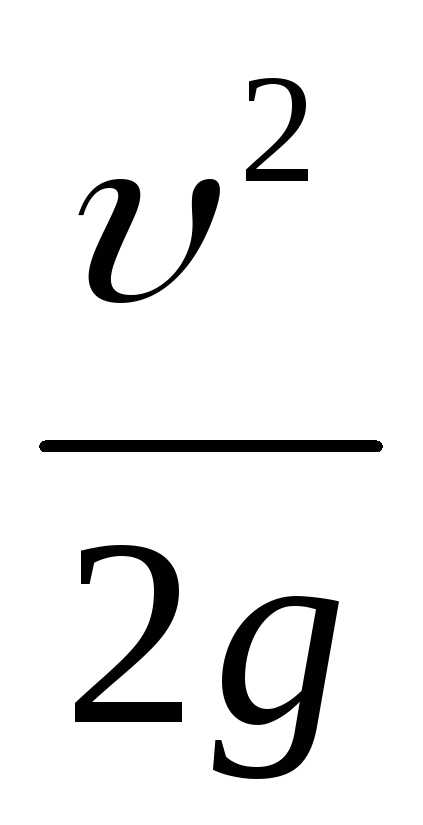
– высота скоростного напора;
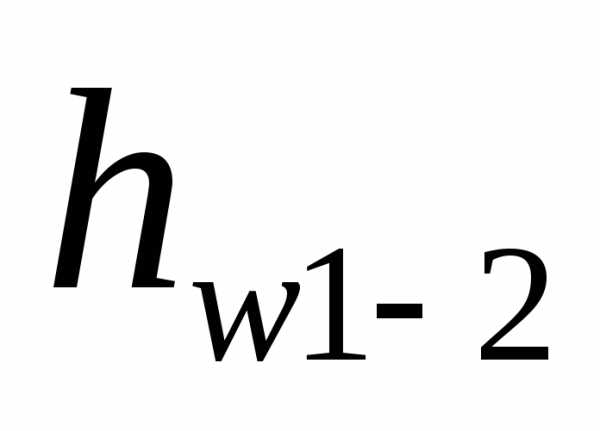
– высота потерь напора.
Сформулируем геометрический смысл уравнения Бернулли для потока реальной жидкости.
При установившемся потоке реальной жидкости сумма четырех высот (высота положения, пьезометрическая высота, высота скоростного напора и высота потерь напора) есть величина постоянная для любого сечения потока.
Энергетический смысл уравнения Бернулли заключается в следующем: при установившемся потоке реальной жидкости сумма четырех удельных энергий (энергии положения, энергии давления, кинетической энергии и энергии потерь) остается неизменной для любого сечения потока.
Уравнение Бернулли является основным уравнение гидродинамики, с помощью которого выводятся расчетные формулы для различных случаев движения жидкости, и решается большое количество практических задач равномерного движения жидкости в трубах и открытых руслах.
Для решения этих задач используют два основных уравнения гидродинамики:
уравнение Бернулли
, (74)
уравнение неразрывности потока
, (75)
При решении задач
обычно по длине потока выбирают два
характерных поперечных сечения ( и
и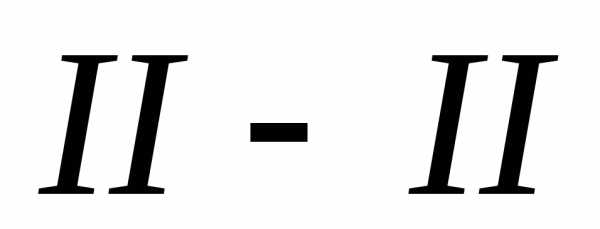 ).
Горизонтальная плоскость сравнения
).
Горизонтальная плоскость сравнения ,
как правило, выбирается по оси трубопровода.
При этом сечения выбираются с таким
расчетом, чтобы для одного из них были
известны величины
,
как правило, выбирается по оси трубопровода.
При этом сечения выбираются с таким
расчетом, чтобы для одного из них были
известны величины ,
,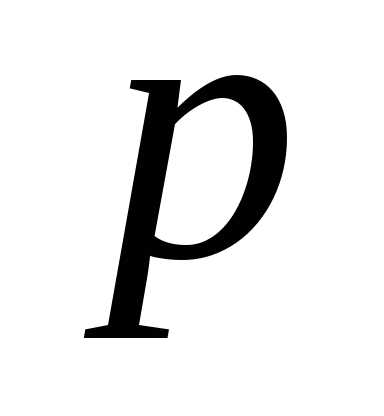 и
и ,
а для другого – одна или две из них были
неизвестны и подлежали определению.
,
а для другого – одна или две из них были
неизвестны и подлежали определению.
Взаимосвязь между тремя параметрами: скоростью, давлением и живым сечением послужила основой для конструирования различных гидравлических и пневматических машин, устройств и приспособлений, получивших широкое применение в технике.
studfiles.net

 .
.