Уравнения движения тела формула – Уравнение движения тела. Все виды уравнений движения

Уравнение движения тела. Все виды уравнений движения

Понятие «движение» определить не так уж просто, как это может показаться. С житейской точки зрения, это состояние является полной противоположностью покоя, но современная физика считает, что это не совсем так. В философии под движением подразумеваются любые изменения, происходящие с материей. Аристотель полагал, что данное явление равносильно самой жизни. А для математика любое перемещение тела выражается уравнением движения, записанным при помощи переменных и цифр.

Материальная точка

В физике перемещение различных тел в пространстве изучает раздел механики, именуемый кинематикой. Если размеры некоего объекта слишком малы в сравнении с расстоянием, которое ему приходится преодолевать вследствие его движения, то он рассматривается здесь как материальная точка. Примером тому может служить автомобиль, едущий по дороге из одного города в другой, птица, летящая в небе, а также многое другое. Подобная упрощенная модель удобна при написании уравнения движения точки, за которую принимается определённое тело.

Бывают и другие ситуации. Представим, что тот же автомобиль хозяин решил переместить с одного конца гаража в другой. Здесь изменение местоположения сравнимо с размерами объекта. Поэтому каждая из точек автомобиля будет иметь разные координаты, а сам он рассматривается как объёмное тело в пространстве.

Основные понятия

Следует учитывать, что для физика путь, пройденный определённым объектом, и перемещение – совсем не одно и то же, а эти слова не являются синонимами. Уяснить разницу между данными понятиями можно, рассмотрев движение самолёта в небе.

След, который он оставляет, наглядно показывает его траекторию, то есть линию. При этом путь представляет собой её длину и выражается в определённых единицах (к примеру, в метрах). А перемещение – это вектор, соединяющий лишь точки начала и конца движения.

Подобное можно увидеть на рисунке, приведённом ниже, который демонстрирует маршрут машины, едущей по извилистой дороге, и вертолёта, летящего по прямой. Векторы перемещения для этих объектов будут одинаковые, а пути и траектории – разными.

Равномерное движение по прямой

Теперь рассмотрим различные виды уравнений движения. И начнём с самого простого случая, когда некий объект перемещается по прямой с одинаковой скоростью. Это значит, что по истечении равных промежутков времени путь, который он проходит за данный период, не меняется по величине.

Что нам потребуется для описания данного движения тела, вернее, материальной точки, как уже было условлено его называть? Важно выбрать систему координат. Для простоты предположим, что перемещение происходит вдоль некоей оси 0Х.

Тогда уравнение движения: x = х₀ + v_хt. Оно и будет описывать процесс в общем виде.

Важным понятием при изменении местоположения тела является скорость. В физике она является векторной величиной, поэтому принимает положительное и отрицательное значение. Здесь всё зависит от направления, ведь тело может перемещаться по выбранной оси с возрастающей координатой и в противоположную сторону.

Относительность движения

Почему так важно выбрать систему координат, а также точку отсчёта для описания указанного процесса? Просто потому, что законы мироздания таковы, что без всего этого уравнение движения не будет иметь смысла. Это показано такими великими учёными, как Галилей, Ньютон и Эйнштейн. С начала жизни, находясь на Земле и интуитивно привыкнув выбирать её за систему отсчёта, человек ошибочно полагает, что существует покой, хотя для природы не бывает такого состояния. Тело может менять местоположение или оставаться статичным лишь относительно какого-либо объекта.

Мало того, тело может двигаться и находиться в покое одновременно. Примером тому может послужить чемодан пассажира поезда, который лежит на верхней полке купе. Он движется относительно деревни, мимо которой проезжает состав, и покоится по мнению своего хозяина, расположившегося на нижнем сидении у окна. Космическое тело, некогда получив начальную скорость, способно лететь в пространстве миллионы лет, пока не столкнётся с другим объектом. Движение его не будет прекращаться потому, что перемещается оно лишь относительно прочих тел, а в системе отсчёта, связанной с ним, космический путешественник находится в покое.

Пример составления уравнений

Итак, выберем за точку отсчёта некий пункт А, при этом координатной осью пусть будет для нас автомагистраль, находящаяся рядом. А направление её будет проходить с запада на восток. Предположим, что в эту же сторону в пункт В, расположенный за 300 км, пешком отправился путешественник со скоростью 4 км/ч.

Получается, что уравнение движения задаётся в виде: х = 4t, где t – время в пути. Согласно этой формуле, появляется возможность вычислить местонахождение пешехода в любой необходимый момент. Становится понятно, что через час он пройдёт 4 км, через два – 8 и достигнет пункта Б спустя 75 часов, так как его координата х = 300 окажется при t = 75.

Если скорость отрицательна

Предположим теперь, что из В в А едет автомобиль, имея скорость 80 км/час. Здесь уравнение движения имеет вид: х = 300 – 80t. Это действительно так, ведь х₀ = 300, а v = -80. Следует обратить внимание, что скорость в данном случае указывается со знаком “минус”, потому что объект перемещается в отрицательном направлении оси 0Х. Через какое время автомобиль достигнет пункта назначения? Это произойдёт, когда координата примет нулевое значение, то есть при х = 0.

Остаётся решить уравнение 0 = 300 – 80t. Получаем, что t = 3,75. Это означает, что автомобиль достигнет пункта В через 3 часа 45 минут.

Необходимо помнить, что координата тоже может быть отрицательной. В нашем случае это оказалось бы, если б существовал некий пункт С, находящийся в западном направлении от А.

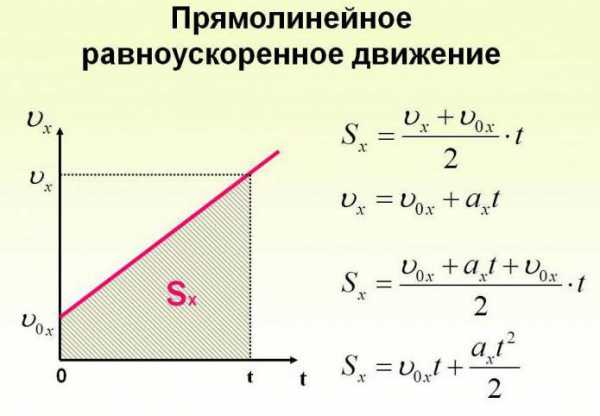
Движение с увеличением скорости

Перемещаться объект может не только с постоянной скоростью, но и менять её с течением времени. Движение тела может происходить по очень сложным законам. Но для простоты следует рассмотреть случай, когда ускорение увеличивается на определённое постоянное значение, а объект перемещается по прямой. В данном случае говорят, что это равноускоренное движение. Формулы, описывающие этот процесс, приведены ниже.

А теперь рассмотрим конкретные задачи. Допустим, что девочка, сев на санки на вершине горы, которую мы выберем за начало воображаемой системы координат с направлением оси по наклону вниз, начинает двигаться под действием силы тяжести с ускорением, равным 0,1 м/с².

Тогда уравнение движения тела имеет вид: s_{x= 0,05t².}

Понимая это, можно узнать расстояние, которое девочка проедет на санках, для любого из моментов перемещения. Через 10 секунд это будет 5 м, а через 20 секунд после начала движения под гору путь составит 20 м.

Как выразить скорость на языке формул? Поскольку v_{0x= 0 (ведь санки начали катиться с горы без начальной скорости только под действием силы притяжения), то запись не будет слишком сложной.}

Уравнение скорости движения примет вид: v_x= 0,1t. Из него мы сможет узнать, как изменяется этот параметр с течением времени.

К примеру, через десять секунд v_x= 1 м/с², а через 20 с примет значение 2 м/с².

Если ускорение отрицательно

Существует и другой вид перемещения, относящийся к тому же типу. Это движение называют равнозамедленным. В данном случае скорость тела тоже изменяется, но с течение времени не увеличивается, а уменьшается, и тоже на постоянную величину. Снова приведём конкретный пример. Поезд, ехавший до этого с постоянной скоростью 20 м/с, начал тормозить. При этом ускорение его составило 0,4 м/с². Для решения примем за начало отсчёта точку пути поезда, где он начал тормозить, а координатную ось направим по линии его перемещения.

Тогда становится понятно, что движение задано уравнением: s_{x= 20t – 0,2t².}

А скорость описывается выражением: v_{x= 20– 0,4t. Необходимо заметить, что перед ускорением ставится знак “минус”, так как поезд тормозит, и данная величина отрицательна. Из полученных уравнений возможно заключить, что состав остановится через 50 секунд, проехав при этом 500 м.}

Сложное движение

Для решения задач в физике обычно создаются упрощённые математические модели реальных ситуаций. Но многогранный мир и явления, происходящие в нём, далеко не всегда вписываются в подобные рамки. Как составить уравнение движения в сложных случаях? Проблема решаема, ведь любой запутанный процесс возможно описать поэтапно. Для пояснения снова приведём пример. Вообразим, что при запуске фейерверков одна из ракет, взлетевшая с земли с начальной скоростью 30 м/с, достигнув верхней точки своего полёта, разорвалась на две части. При этом соотношение масс получившихся осколков составило 2:1. Далее обе части ракеты продолжили двигаться отдельно одна от другой таким образом, что первая полетела вертикально вверх со скоростью 20 м/с, а вторая сразу упала вниз. Следует узнать: какова была скорость второй части в момент, когда она достигла земли?

Первым этапом данного процесса окажется полёт ракеты вертикально вверх с начальной скоростью. Перемещение будет равнозамедленным. При описании понятно, что уравнение движения тела имеет вид: s_x = 30t – 5t². Здесь мы полагаем, что ускорение свободного падения для удобства округляется до значения 10 м/с². Скорость при этом будет описываться следующим выражением: v = 30 – 10t. По этим данным уже возможно вычислить, что высота подъёма составит 45 м.

Вторым этапом движения (в данном случае уже второго осколка) окажется свободное падение этого тела с начальной скоростью, получаемой в момент распадения ракеты на части. При этом процесс будет равноускоренным. Для нахождения окончательного ответа сначала вычисляет v₀ из закона сохранения импульса. Массы тел относятся 2:1, а скорости находятся в обратной зависимости. Следовательно, второй осколок полетит вниз с v₀ = 10 м/c, а уравнение скорости примет вид: v = 10 + 10t.

Время падения мы узнаем из уравнения движения s_{x= 10t + 5t². Подставим уже полученное значение высоты подъёма. В результате выходит, что скорость второго осколка приблизительно равна 31,6 м/с².}

Таким образом, разделяя сложное движение на простые составные части, можно решать любые запутанные задачи и составлять уравнения движения всех видов.

fb.ru

Уравнение движения тела в физике

В том случае, если мы имеем дело с твердым телом, которое в общем случае имеет 6 степеней свободы, то общая система уравнений движения должна содержать шесть независимых уравнений. Их можно представить в виде производных по времени от двух векторов: импульса и момента импульса тела.

Общие законы и уравнения движения системы тел

Произвольную систему тел всегда можно свести к системе материальных точек. Это видно из того, что отдельное тело конечных размеров всегда мысленно можно разбить на столь малые части (частицы), что каждую часть можно рассматривать как материальную точку. Таким образом, выясняя общие законы движения системы тел, можно исходить из представления о системе материальных точек. Соответственно, имеем первое уравнение:

   

где — полный импульс тела, – результирующая внешних сил, действующих на тело.

В случае поступательного движения твердого тела его скорость скорости центра масс этого тела: . Соответственно, основное уравнение динамики поступательного движения твердого тела имеет вид:

   

или

   

где — масса тела, — его ускорение.

Второе уравнение движения записывается для тела вращающегося относительно неподвижной точки (полюса), и имеет вид:

   

где — момент импульса, — момент внешних сил, приложенных к телу.

Уравнение движения твердого тела

Уравнение динамики твердого тела, вращающегося вокруг неподвижной точки О, в жестко связанной с телом подвижной системе координат (x’,y’,z’), начало которой находится в точке О, имеет вид:

   

где — угловая скорость вращения тела, а — относительная производная по времени от вектора — орты подвижной системы.

Если оси подвижной системы координат совпадают с главными осями инерции тела в точке О, то уравнения движения тела в проекциях на эти оси имеют вид:

   

   

   

где – главные моменты инерции тела в точке О, – проекции вектора угловой скорости тела на главные оси инерции, – моменты внешних сил относительно тех же осей. Эти уравнения называют динамическими уравнениями Эйлера.

Уравнение движения тела, вращающегося вокруг неподвижной оси

Уравнение движения тела, вращающегося вокруг неподвижной оси (например, оси Оz):

   

или

   

где – момент инерции тела относительно оси Oz. Если тело не деформируется, то — постоянная, тогда уравнение движения:

   

где – угловое ускорение тела.

Свободное твердое тело в общем случае участвует одновременно в двух движениях- поступательном со скоростью центра масс и вращательном вокруг центра масс с угловой скоростью . Векторы и удовлетворяют двум дифференциальным уравнениям движения свободного тела (которые получают из 2 и 3), подстановкой соответствующих скоростей центра масс:

   

   

где m- масса тела, — скорость центра масс, — вектор результирующей внешней силы, — вектор результирующий моментов внешних сил относительно центра масс C, , где — радиус вектор и скорость малого элемента массой dm в поступательно движущейся системе координат с началом в точке C.

Примеры решения задач

ru.solverbook.com

Уравнение движения в физике

Как получить уравнение движения?

Допустим, в какой-то момент времени мы знаем все параметры, определяющие состояние системы – например, скорости и координаты, — а также их производные по времени. Тогда мы можем рассчитать эти параметры и для момента времени, отстоящего от начального на малый промежуток времени. Если мы выберем малый, но конечный промежуток времени , мы можем приближенно оценить состояние системы в любой момент времени. Для получения точного уравнения движения нужно определить функцию, описывающую процесс: если временной шаг выбран достаточно малым, то приближенно вычисленные характеристики системы будут лежать к этой функции очень близко.

Для каждой области физики существуют свои уравнения движения

В классической механике эту функцию, в первую очередь, выполняют законы Ньютона. Их дополняют закон тяготения и кинематические законы, связывающие перемещение, скорость и ускорение. Так, второй закон Ньютона – это уравнение движения материальной точки массой , связывающий силу , приложенную к точке, и ускорение , которое точка вследствие этого приобрела:

   

В то время как законы движения классической механики определяют движение макроскопических материальных тел, то движение микроскопических частичек (например, в газе) описывается с помощью статистических распределений. К примеру, уравнение движение Больцмана позволяет найти распределение плотности частичек в пространстве f:

   

В этом уравнении – пространственная координата, – импульс, – масса частичек, – время, – поле действующих сил, а слагаемая учитывает столкновения частиц.

Движение сплошной среды описывают с помощью системы уравнений Коши, частными случаями которой являются уравнения Эйлера и Навье-Стокса:

   

   

В квантовой механике также существуют уравнения, которые характеризуют движение волновой функции (а элементарные частицы одновременно являются и волнами). Однако можно ли их называть уравнениями движения – спорный вопрос. Ведь квантовые системы неопределенны по своей природе, а значит, нельзя получить точное решение уравнения движения.

Примеры решения задач

ru.solverbook.com

Уравнение движения — Википедия

Материал из Википедии — свободной энциклопедии

Уравне́ние движе́ния (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или динамической системы (например, поля) во времени и пространстве^[1].

Эволюция физической системы однозначно определяется уравнениями движения и начальными условиями.

В уравнении движения динамической системы входит полный набор переменных, определяющий состояние этой системы (например, все координаты и скорости, или все координаты и импульсы), а также их производные по времени, что позволяет, зная такой набор в некий момент времени, вычислить его для момента времени, отстоящего на малый (бесконечно малый) промежуток времени. В принципе, повторяя этот процесс вычисления последовательно большое (бесконечное) количество раз, можно вычислить значение всех этих переменных для момента времени, как угодно далеко

[2] отстоящего от начального. С помощью такого процесса можно (выбрав Δt{\displaystyle \Delta t} достаточно малым, но конечным) получить приближённое численное решение уравнений движения. Однако чтобы получить точное ^[3] решение, приходится применять другие математические методы.

В современной квантовой теории термин уравнение движения нередко используется для обозначения именно только классических уравнений движения, то есть как раз для различения классического и квантового случая. В таком употреблении, например, слова «решение уравнений движения» означают именно классическое (неквантовое) приближение, которое может затем так или иначе использоваться при получении квантового результата или для сравнения с ним. В этом смысле уравнения эволюции волновой функции не называют уравнениями движения, например упомянутые ниже уравнение Шредингера и уравнение Дирака нельзя назвать уравнением движения электрона. Определённую ясность тут вносит дополнение, указывающее на то, об уравнении движения чего идёт речь: так, хотя уравнение Дирака нельзя назвать уравнением движения электрона, его можно, даже в смысле, обсуждаемом в этом абзаце, назвать классическим уравнением движения спино

ru.wikipedia.org

Вращательное движение твердого тела: уравнение, формулы

В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.

Что такое вращение?

Каждый из нас интуитивно представляет, о каком движении пойдет речь. Вращение – это процесс, при котором тело или материальная точка движется по круговой траектории вокруг некоторой оси. С геометрической точки зрения ось вращения твердого тела – это прямая, расстояние до которой в процессе перемещения остается неизменным. Это расстояние называют радиусом вращения. Далее будем обозначать его буквой r. Если ось вращения проходит через центр масс тела, то ее называют собственной осью. Примером вращения вокруг собственной оси является соответствующее движение планет Солнечной системы.

Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.

Описывающие вращение физические величины

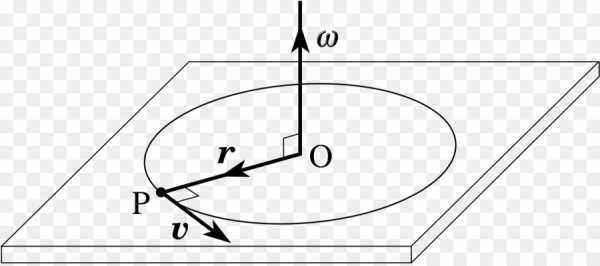
Во-первых, это динамические характеристики. К ним относятся:

• момент импульса L;
• момент инерции I;
• момент силы M.

Во-вторых, это кинематические характеристики. Перечислим их:

• угол поворота θ;
• скорость угловая ω;
• ускорение угловое α.

Кратко опишем каждую из названных величин.

Момент импульса определяется по формуле:

L = p*r = m*v*r

Где p – линейный импульс, m – масса материальной точки, v – ее линейная скорость.

Момент инерции материальной точки рассчитывается с помощью выражения:

I = m*r²

Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.

Момент силы M вычисляется так:

M = F*d

Здесь F – внешняя сила, d – расстояние от точки ее приложения до оси вращения.

Физический смысл всех величин, в названии которых присутствует слово “момент”, аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.

Кинематические характеристики математически определяются следующими формулами:

ω = dθ/dt;

α = dω/dt.

Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.

Динамика вращения

В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.

Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:

M = I*α

Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.

Закон сохранения величины L

Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:

M*dt = dL

Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:

L = m*v*r = m*ω*r² = I*ω.

Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.

Центростремительное ускорение

Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его a_c.

Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:

a_c = v²/r;

a_c = ω²*r.

Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).

Кинематика вращения

Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:

θ = ω*t => ω = const., α = 0;

θ = ω₀*t + α*t²/2 => ω = ω₀ + α*t, α = const.

В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.

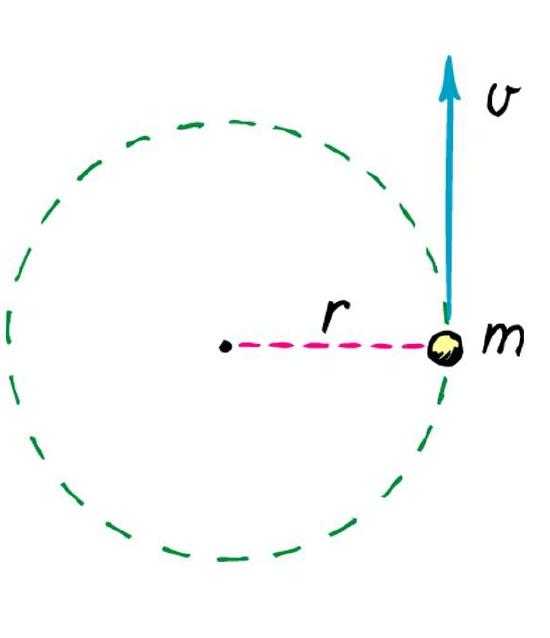
Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.

Пример решения задачи

На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м², необходимо определить угловую скорость, которую придал валу упомянутый момент силы.

Применяя основное уравнение вращения, вычислим ускорение вала:

M = I*α =>

α = M/I.

Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:

ω = ω₀ + α*t = M/I*t.

Здесь ω₀ = 0 (вал не вращался до действия момента сил M).

Подставляем в равенство численные значения величин, получаем:

ω = 1000/50*10 = 200 рад/с.

Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.

fb.ru

Закон движения тела: определение, формулы

Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни. Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.

О каких типах движения пойдет речь?

Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:

1. Равномерное по прямой линии.
2. Равноускоренное (равнозамедленное) по прямой линии.
3. Равномерное по окружности.
4. Равноускоренное по окружности.
5. Движение по эллиптической траектории.

Равномерное движение, или состояние покоя

Этим движением с научной точки зрения начал интересоваться впервые Галилей в конце XVI – начале XVII века. Изучая инерционные свойства тела, а также введя понятие о системе отсчета, он догадался, что состояние покоя и равномерного движения – это одно и то же (все зависит от выбора объекта, относительно которого рассчитывают скорость).

Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.

Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:

s = v * t

Где s – расстояние, которое преодолеет тело за время t, двигаясь со скоростью v. Это простое выражение также записывается в следующих формах (все зависит от величин, которые известны):

v = s / t; t = s / v

Перемещение по прямой с ускорением

Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:

a = v / t или v = a * t

Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).

Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:

s = a * t² / 2

Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с².

Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости

По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах. Представим простую ситуацию: автомобиль ехал с некоторой скоростью v₀, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:

v = v₀ – a * t

Здесь v₀ – начальная скорость (до торможения авто). Знак минус говорит о том, что внешняя сила (трения скольжения) направлена против скорости v₀.

Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:

s = v₀ * t – a * t² / 2

Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.

В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак “-” на “+”.

Движение по окружности

Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:

a_c = v² / r, r – радиус

В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае a_c будет быстро расти (квадратичная зависимость).

Центростремительное ускорение определяет силу, которую нужно прикладывать, чтобы удерживать тело на круговой орбите. Примером являются соревнования по метанию молота, когда спортсмены прикладывают значительные усилия, чтобы раскрутить снаряд до его метания.

Вращение вокруг оси с постоянной скоростью

Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:

L =I * ω

Здесь L и I – моменты импульса и инерции, соответственно, ω – угловая скорость, которая с линейной связана равенством:

v = ω * r

Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:

θ = ω * t

Примером этого типа движения является вращение маховика, находящегося на коленчатом вале в двигателе автомобиля. Маховик – это массивный диск, которому очень тяжело придать какое-либо ускорение. Благодаря этому он обеспечивает плавность изменения крутящего момента, который передается от двигателя к колесам.

Вращение вокруг оси с ускорением

Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:

F * d = I * dω / dt

Здесь F – внешняя сила, которая приложена к системе на расстоянии d от оси вращения. Произведение в левой части равенства носит название момента силы.

Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:

ω = α * t, где α = F * d / I – угловое ускорение

В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:

θ = α * t² / 2

Если же тело уже вращалось с некоторой скоростью ω₀, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:

ω = ω₀ + α * t;

θ = ω₀ * t + α * t² / 2

Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.

Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:

I * ω = const

Движение по эллиптической траектории на примере планет Солнечной системы

Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:

1. Планеты Солнечной системы движутся по эллиптическим орбитам, причем Солнце расположено в одном из фокусов эллипса.
2. Радиус-вектор, который соединяет Солнце и планету, за равные промежутки времени описывает одинаковые площади. Этот факт следует из сохранения момента импульса.
3. Если поделить квадрат периода обращения на куб большой полуоси эллиптической орбиты планеты, то получается некоторая константа, которая одинакова для всех планет нашей системы. Математически это записывается так:

T² / a³ = С = const

Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:

C = 4 * pi² / (G * M)

Где G – гравитационная универсальная константа, а M – масса Солнца.

Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.

fb.ru

Уравнения движения твердого тела | Политех в Сети

Для получения уравнений движения твердого тела запишем его функцию Лагранжа. В качестве обобщенных координат выбе­рем три координаты центра инерции твердого тела: X, Y, Z, зада­ющие его положение относительно неподвижной системы отсчета, и три угла Эйлера:

θ, φ, ψ, определяющие ориентацию подвижной системы координат относительно неподвижной системы координат. Начало подвижной системы координат поместим в центр инерции твердого тела, а оси подвижной системы координат направим по главным осям инерции твердого тела. Тогда функция Лагранжа твердого тела будет иметь вид

. (6.25)

При таком выборе подвижной системы координат в формуле для кинетической энергии твердого тела отделяются слагаемые, опи­сывающие кинетическую энергию поступательного движения тела и кинетическую энергию его вращения. Проекции угловой скоро­сти, согласно формулам , , (6.10) выражаются через углы Эйлера и не содержат координат центра инерции твердого тела.

Уравнения движения твердого тела разобьются на две группы уравнений. Первая группа получается при дифференцировании по координатам центра инерции. Она имеет вид уравнений второ­го закона Ньютона для материальной точки, масса которой равна массе твердого тела и координаты которой совпадают с координа­тами центра инерции твердого тела: , , . (6.26)

В левой части этих уравнений стоят проекции ускорения центра инерции, в правой — проекции силы, приложенной к центру инер­ции. Уравнения (6.26) совпадают с уравнениями движения мате­риальной точки, имеющей массу твердого тела и координаты, рав­ные координатам центра инерции твердого тела. Их решение дает закон движения центра инерции твердого тела. Центр инерции твердого тела движется как материальная точка, масса которой равна массе твердого тела.

Другая группа уравнений движения для твердого тела получа­ется при дифференцировании функции Лагранжа по углам Эйле­ра. Найдем производные по И . Используем для этого функцию Лагранжа (6.25) и формулы Эйлера (6.10). Вычисления дают , (6.27)

. (6.28) Смысл частной производной можно уяснить, если ее рассматри­вать как производную от сложной ф-ции, когда вначале берутся производные по координатам отдельных точек твердого тела: . (6.29)

Используя формулу (3.33) для производной радиуса-вектора по угловой координате, найдем , (6.30)

Где— проекция на подвижную ось Oz моменга действующих на твердое тело сил. В результате уравнение Лагранжа по координа­те ψ принимает вид

. (6.31)

Эго уравнение записано в проекции на ось Oz подвижной системы координат. Уравнения Лагранжа по координатам θ и φ дадут про­екции уравнений движения соответственно на ось узлов и ось OZ Неподвижной системы координат. Эти проекции обычно не исполь­зуются. Вместо них записывают уравнения в проекциях на оси Ох И Оу подвижной системы координат. Вследствие равноправности всех осей декартовой системы координат эти уравнения можно по­лучить из (6.31) циклической перестановкой индексов. Они имеют вид

, (6.32)

. (6.33)

Уравнения (6.31) — (6.33) называются Уравнениями движения твер­дого тела в форме Эйлера. Они записаны в подвижной, жестко связанной с твердым телом системе координат. Их решение дает угловую скорость вращения твердого тела.

www.webpoliteh.ru