примеры уравнений с разделяющимися переменными
Рассмотрим примеры решения дифференциальных уравнений с разделяющимися переменными.
1) Проинтегрировать дифференциальное уравнение: (1+x²)dy-2xydx=0.
Данное уравнение является уравнением с разделяющимися переменными, записанное в виде
Оставляем слагаемое с dy в левой части уравнения, с dx — переносим в правую часть:
(1+x²)dy = 2xydx
Разделяем переменные, то есть в левой части оставляем только dy и все, что содержит y, в правой dx и x. Для этого обе части уравнения делим на (1+x²) и на y. Получаем
Интегрируем обе части уравнения:
В левой части — табличный интеграл. Интеграл в правой части можно найти, например, сделав замену t=1+x², тогда
dt=(1+x²)’dx=2xdx.
В примерах, где есть возможность провести потенцирование, то есть убрать логарифмы, удобно брать не С, а lnC. Именно так мы и сделаем: ln│y│=ln│t│+ln│C│. Так как сумма логарифмов равна логарифму произведения, то ln│y│=ln│Сt│, откуда y=Ct. Делаем обратную замену,и получаем общее решение: y=C(1+x²).
Мы делили на 1+x² и на y при условии, что они не равны нулю. Но 1+x² не равно нулю при любых x. А y=0 при С=0, таким образом, потери корней не произошло.
Ответ: y=C(1+x²).
2) Найти общий интеграл уравнения
Переменные можно разделить.
Умножаем обе части уравнения на dx и делим на
Получаем:
Теперь интегрируем
В левой части — табличный интеграл. Справа — делаем замену 4-x²=t, тогда dt=(4-x²)’dx=-2xdx. Получаем
Если вместо С взять 1/2 ln│C│, можно ответ записать более компактно:
Умножим обе части на 2 и применим свойство логарифма:
Мы делили на
Они не равны нулю: y²+1 — так как сумма неотрицательных чисел не равна нулю, а подкоренное выражение не равно нулю по смыслу условия. Значит, потери корней не произошло.
Ответ:
3) a) Найти общий интеграл уравнения (xy²+y²)dx+(x²-x²y)dy=0.
б) Найти частный интеграл этого уравнения, удовлетворяющий начальному условию y(е)=1.
Решение.
а) Преобразуем левую часть уравнения: y²(x+1)dx+x²(1-y)dy=0, затем
y²(x+1)dx=-x²(1-y)dy. Делим обе части на x²y² при условии, что ни x, ни y не равны нулю. Получаем:
Интегрируем уравнение:
Отсюда
Так как разность логарифмов равна логарифму частного, имеем:
Это — общий интеграл уравнения. В процессе решения мы ставили условие, что произведение x²y² не равно нулю, откуда следует, что x и y не должны быть равными нулю. Подставив x=0 и y=0 в условие:(0.0²+0²)dx+(0²-0²0)dy=0 получаем верное равенство 0=0. Значит, x=0 и y=0 тоже являются решениями данного уравнения. Но в общий интеграл они не входят ни при каких С (нули не могут стоять под знаком логарифма и в знаменателе дроби), поэтому эти решения следует записать дополнительно к общему интегралу.
Ответ:
б) Так как y(е)=1, подставляем в полученное решение x=e, y=1 и находим С:
Ответ:
Примеры для самопроверки:
Показать решение
Ответ:
\
Ответ:
Ответ:
уравнения, приводимые с разделяющимися переменными
Рассмотрим, как решать уравнения вида y’=f(ax+by+c), где a,b,c — некоторые числа. Это — дифференциальные уравнения, приводимые к уравнениям с разделяющимися переменными.
Такие уравнения приводятся к уравнениям с разделяющимися переменными с помощью замены z=ax+by+c. Дифференцируем обе части этого равенства по иксу:
Поскольку x’=1, а так как y’=f(ax+by+c), то y’=f(z).
Соответственно, получаем, что
При условии a+bf(z)≠0 переменные можем разделить:
Интегрируем полученное уравнение
В полученном решении возвращаемся к исходным переменным z=ax+by+c.
Если a+bf(z)=0, то значит, и dz/dx=0, то ax+by+c=С.
Пример
Решить уравнение y’=(x+y+1)².
Решение: Замена z=x+y+1. Тогда dz/dx=1+dy/dx, а так как dy/dx=y’=(x+y+1)²=z², то dz/dx=1+z². Разделяем переменные, для этого обе части делим на 1+z² (это выражение не равно нулю при любом z) и умножаем на dx:
Интегрируем уравнение:
откуда
arctgz=x+C. Так как z=x+y+1, то общее решение arctg(x+y+1)=x+C, откуда arctg(x+y+1)-x=C.
www.matematika.uznateshe.ru
1.3. Уравнения с разделяющимися переменными
Дифференциальное уравнение называетсяуравнением с разделяющимися переменными, если его можно записать в виде:
.
Общее решение дифференциального уравнения с разделяющимися переменными получается после нахождения соответствующих интегралов, то есть .
Если уравнение с разделяющимися переменными имеет вид: , то путем почленного деления его наони сводится к уравнению.
Замечания.
При проведении почленного деления ДУ на могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнениеи установить те решения ДУ, которые не могут быть получены из общего решения, –
Уравнение также сводится к уравнению с разделенными переменными. Для этого достаточно положить
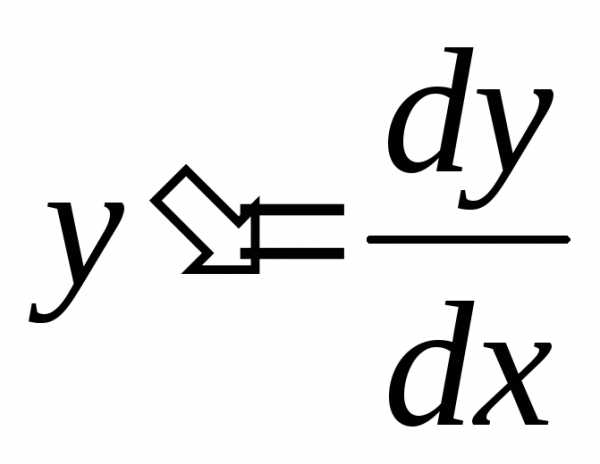 и разделить переменные:
и разделить переменные: .
.Уравнение , гдеa,b,c – числа, сводится к уравнению с разделенными переменными путем замены . Дифференцируяпо
Пример. Найти все решения уравнения .
Разделяем
переменные: 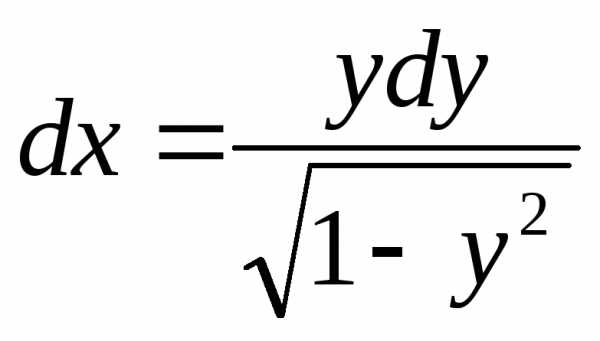 .Интегрируем:
.Интегрируем:  .
.
Получаем: или .
Вполученном выражении содержатся не все
решения данного уравнения. При делении
на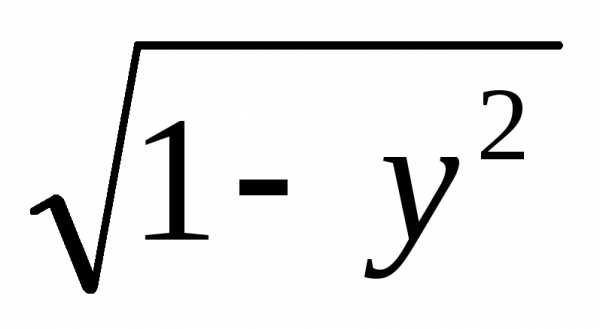
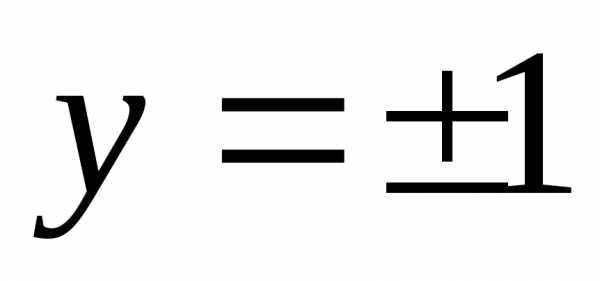 – это особые решения, которые невозможно
включить в решение. Множество интегральных
кривых данного уравнения состоит из
семейства окружностей радиусом 1 с
центром в точке (С; 0) и прямых
– это особые решения, которые невозможно
включить в решение. Множество интегральных
кривых данного уравнения состоит из
семейства окружностей радиусом 1 с
центром в точке (С; 0) и прямых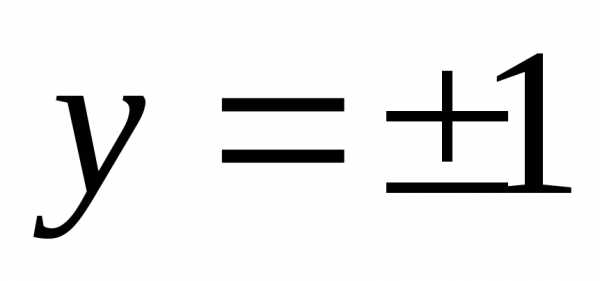 .
.Рис. 2
1.4. Однородные уравнения
Однородной
функцией f(x, y) нулевого измерения, или, просто, однородной
функцией, называется функция только от
отношения 
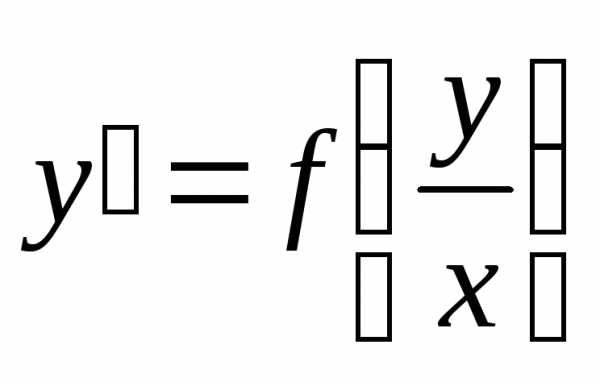 .
. При
решении однородных дифференциальных
уравнений сохраняя прежнюю независимую
переменную х, вводят вспомогательную неизвестную
функцию t по формуле:  .
Откуда.
Преобразуя уравнение
.
Откуда.
Преобразуя уравнение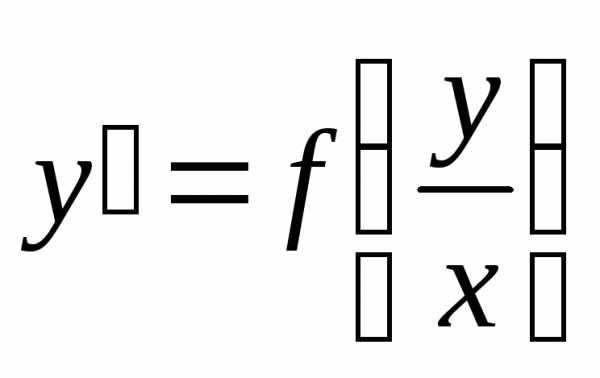 ,
получаем:
,
получаем:
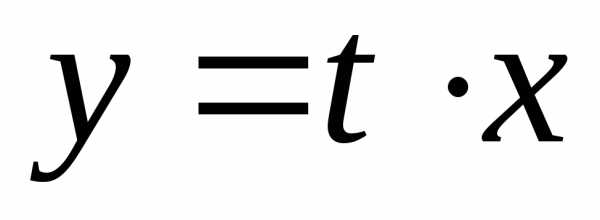 ,
получая при этом решение однородного
дифференциального уравнения.
,
получая при этом решение однородного
дифференциального уравнения. Замечание: Иногда
целесообразно вместо постановки 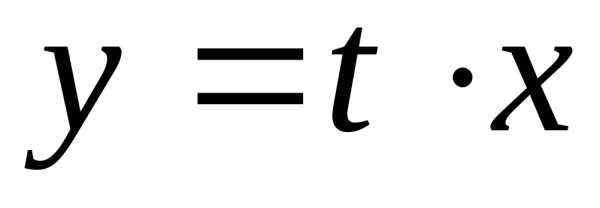 использовать подстановку
использовать подстановку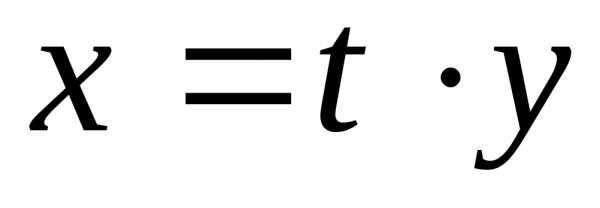 .
.
Пример. Решить уравнение 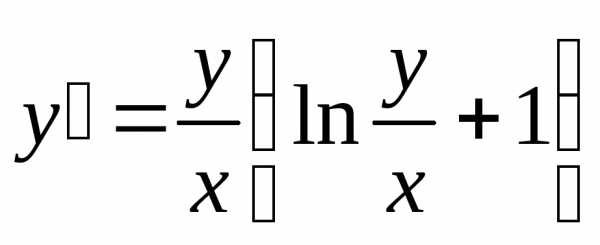
Делаем замену: .
Подставляем в исходное уравнение:
Разделяем
переменные:  .
.
Интегрируя:  ,
получаем:
,
получаем:
Переходя
от вспомогательной функции обратно к
функции у, получаем общее решение: 
1.5. Уравнения, приводящиеся к однородным
Дифференциальное
уравнение вида:  приводится к однородному дифференциальному
уравнению или к дифференциальному
уравнению с разделяющимися переменными.
приводится к однородному дифференциальному
уравнению или к дифференциальному
уравнению с разделяющимися переменными.
1 случай. Уравнение, приводящиеся к однородному дифференциальному уравнению.
Если
определитель 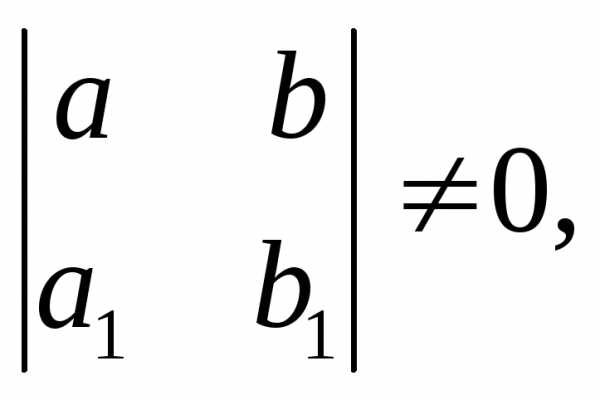 то совершается замена:где
и
– решения системы уравнений
то совершается замена:где
и
– решения системы уравнений 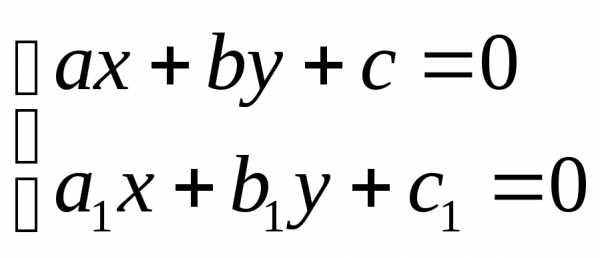 .
Подставляя замену, получим однородное
дифференциальное уравнение вида:
.
Подставляя замену, получим однородное
дифференциальное уравнение вида: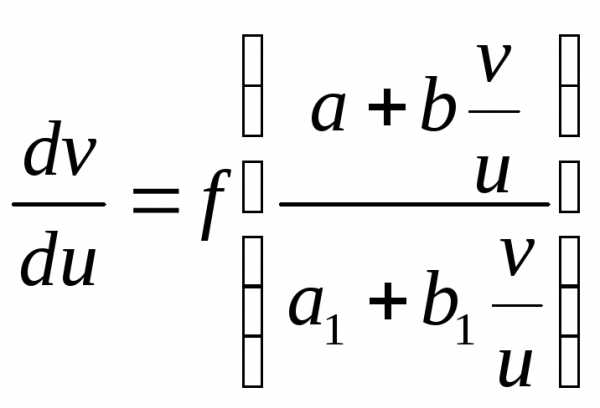 .
.
Пример. Решить уравнение
Получаем
Находим значение определителя .
Решаем систему уравнений
Применяем подстановку в исходное уравнение:
Получили
однородное уравнение и осуществляем
замену переменных
при подстановке в выражение имеем: 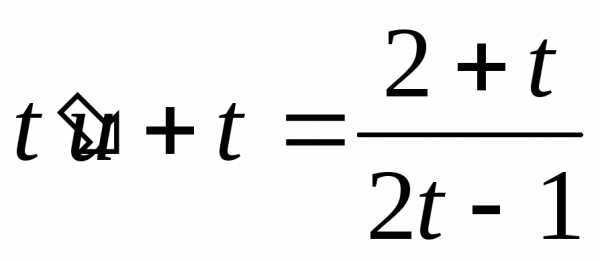 .
.
Разделяем переменные:
; ; .
Вернемся к первоначальной функции у и переменной х.
;
;
; .
Получаем выражение , которое является общим интегралом исходного дифференциального уравнения.
2 случай. Уравнение, приводящиеся к дифференциальному уравнению с разделяющимися переменными.
Если
определитель 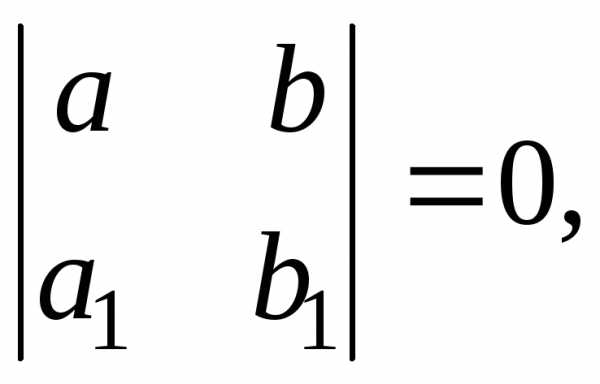 то совершается замена:,
где.
Отсюда,.
Подставляя замену, получим дифференциальное
уравнение вида:
то совершается замена:,
где.
Отсюда,.
Подставляя замену, получим дифференциальное
уравнение вида: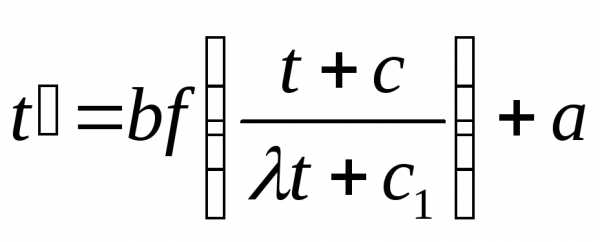 .
.
Пример. Решить уравнение
Получаем
Находим
значение определителя 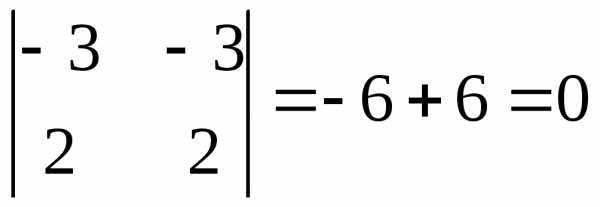 .
.
Применяем
подстановку
,
тогда  .
.
Подставляем это выражение в исходное уравнение:
.
Разделяем переменные:
.
Далее возвращаемся к первоначальной функции у и переменной х.
–получили общий интеграл исходного дифференциального уравнения.
studfiles.net
Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными
Копцова Александра Владимировича
Дифференциальные уравнения с разделяющимися переменными.
- Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых возможно переменные x и y разнести по разные стороны знака равенства. В уравнениях вида переменные уже разделены, а в ОДУ переменные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
Дифференциальные уравнения с разделенными переменными .
Дифференциальные уравнения называют уравнениями с разделенными переменными.
Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него.
Будем считать, что функции f(y) и g(x) непрерывны.
Общим интегралом уравнения с разделенными переменными является равенство . Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде.
Пример.
Найдите общее решение дифференциального уравнения с разделенными переменными .
Решение.
Проинтегрируем обе части равенства: . По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их, используя таблицу первообразных:
где С1 и С2 – произвольные постоянные.
Мы пришли к неявно заданной функции , которая является общим решением исходного дифференциального уравнения с разделенными переменными. Ответ можно оставить в таком виде. Но в нашем случае искомую функцию y можно выразить явно через аргумент x. Итак, , где . То есть, функция является общим решением исходного дифференциального уравнения.
Замечание.
Ответ можно записать в любом из трех видов или , или .
Дифференциальные уравнения с разделяющимися переменными
Прежде чем продолжить, напомним, что когда y является функцией аргумента x.
В дифференциальных уравнениях или переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как .
Пример.
Найти все решения дифференциального уравнения .
Решение.
Это уравнение с разделяющимися переменными, так как мы можем разделить x и y:
Для нулевой функции y исходное уравнение обращается в тождество , поэтому, y = 0 является решением дифференциального уравнения. Это решение мы могли упустить из виду.
Проинтегрируем дифференциальное уравнение с разделенными переменными :

В преобразованиях мы заменили C2 – C1 на С.
Мы получили решение ДУ в виде неявно заданной функции . На этом можно закончить. Однако в нашем случае функцию y можно выразить явно, проведя потенцирование полученного равенства:
Ответ: .
Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными , a ≠ 0, b ≠ 0
Обыкновенные дифференциальные уравнения первого порядка вида , a ≠ 0,
b ≠ 0 приводятся к уравнениям с разделяющимися переменными введением новой переменной z = ax + by, где z представляет собой функцию аргумента x.
В этом случае
После подстановки в исходное уравнение и небольших преобразований приходим к уравнению с разделенными переменными
Рассмотрим пример.
Пример.
Найдите общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию y(0) = e.
Решение.
Пусть z = 2x + y, тогда
Подставим полученные результаты в исходное уравнение и преобразуем его к дифференциальному уравнению с разделяющимися переменными:
Разделяем переменные и интегрируем обе части равенства . Интеграл в левой части найдем методом интегрирования по частям, а интеграл в правой части является табличным:
Следовательно, . Если принять C = C2 – C1 и сделать обратную замену z = 2x + y, то получим общее решение дифференциального уравнения в виде неявно заданной функции: .
Осталось найти частное решение, удовлетворяющее начальному условию y(0) = e. Для этого подставляем x = 0 и y(0) = e в общее решение дифференциального уравнения и находим значение константы С:
Следовательно, искомое частное решение, удовлетворяющее условию y(0) = e, имеет вид .
Замечание.
В условии задачи ничего не сказано об интервале, на котором требуется найти общее решение дифференциального уравнения. В таких случаях решение проводится для всех значений аргумента x, при которых исходное дифференциальное уравнение и его решения имеют смысл. Для данного примера дифференциальное уравнение имеет смысл при .
Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными или .
Дифференциальные уравнения вида или могут быть сведены к ОДУ с разделяющимися переменными, если произвести замену или , где z – функция аргумента x.
Если , то и по правилу дифференцирования дроби . В этом случае уравнения примут вид или .
Если принять , то y = x ⋅ z и по правилу производной произведения . В этому случае уравнения сведутся к или .
Пример.
Решите дифференциальное уравнение .
Решение.
Примем , тогда . Подставим в исходное уравнение:
Получили уравнение с разделенными переменными. Проинтегрируем его.
После обратной замены получаем общее решение исходного дифференциального уравнения в виде неявно заданной функции .
Следует остановиться на дифференциальных уравнениях вида
.
Делением числителя и знаменателя правой части на yn или xn такие дифференциальные уравнения приводятся к виду или .
Пример.
Найти общее решение дифференциального уравнения .
Решение.
В этом примере x и y отличны от нуля. Разделим и числитель и знаменатель правой части равенства наx2:
Введем новую переменную , тогда .
Подставляем в исходное уравнение
Получили дифференциальное уравнение с разделенными переменными. Решаем его
В этом примере можно получить решение и в явном виде. Для этого примем и воспользуемся свойствами логарифма:
Осталось сделать обратную замену y = x ⋅ z и записать ответ . Это общее решение дифференциального уравнения.
Замечание: это уравнение (как и другие подобного типа) можно решить и используя замену .
Опишем решение для этой замены.
Разделим и числитель и знаменатель на y2:
Пусть , тогда .
Подставляем все в исходное уравнение и получаем дифференциальное уравнение с разделяющимися переменными . После разделения переменных приходим к равенству . Интегрируем его
Возьмем сначала интеграл . После разложения на простейшие дроби подынтегральной функции интеграл примет вид . Теперь проведем интегрирование простейших дробей:
Теперь найдем интеграл :
В итоге имеем или , где .
После проведения обратной замены и некоторых преобразований придем к тому же результату .
Сделаем вывод. В этом примере при замене решение оказалось более трудоемким, чем при замене . Для себя можно отметить, что если решение дифференциального уравнения или оказывается сложным при выбранной замене , то можно попробовать ввести другую переменную, то есть .
Дифференциальные уравнения, сводящиеся к уравнениям с разделяющимися переменными .
Дифференциальные уравнения можно свести к уравнениям или , следовательно, к уравнениям с разделяющимися переменными. Для этого находится (x0 , y0) – решение системы двух линейных однородных уравнений и вводятся новые переменные . После такой замены уравнение примет вид .
Разберемся на примере.
Пример.
Найти общее решение дифференциального уравнения .
Решение.
Составляем и решаем систему линейных уравнений
Делаем замену переменных
После подстановки в исходное уравнение получаем . После деления на u числителя и знаменателя правой части имеем .
Вводим новую переменную , тогда
Возвращаемся к исходным переменным, производя обратную замену :
Это есть общее решение дифференциального уравнения.
megaobuchalka.ru
1. Уравнения с разделяющимися переменными
Дифференциальные уравнения вида:
(1)
называются уравнениями с разделяющимися переменными. Решая такие уравнения, необходимо преобразовать их так, чтобы одна часть уравнения содержала только переменную у, а другая – толькох, а затем проинтегрировать обе части (поуи похсоответственно).
Например, уравнение
(1) надо разделить на
,
тогда получим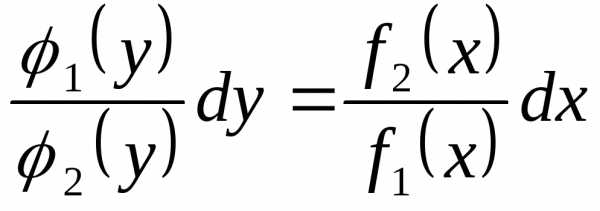 .
Проинтегрировав обе части, найдем общий
интеграл:
.
Проинтегрировав обе части, найдем общий
интеграл:
. (2)
Кроме найденного общего интеграла (2) уравнению (1) могут также удовлетворять решения, получаемые из уравнения . Если эти решения не входят в общий интеграл (2), то они будут особыми решениями уравнения (1).
Приведем примеры решения конкретного уравнения этого типа.
Задача №1. Найти общий интеграл дифференциального уравнения (ответ представить в виде (х, у)=с).
1.31 .
Решение. Уравнение представлено в дифференциальной форме. Для разделения переменных перенесем все слагаемые в одну часть уравнения и сгруппируем содержащие dxиdy:
Разделим обе части уравнения на , получим.
Почленно интегрируя, получим искомый общий интеграл:
.
В первообразных модули можно опустить, т.к. 1+х2и4+у2величины всегда неотрицательные.
Умножая обе части уравнения на 2 и учитывая свойства логарифма, получим
 .
.
В нашем примере уравнение представлено в дифференциальной форме. Возможны случаи, когда уравнение разрешено относительно производной, т.е. оно имеет вид и, когда не разрешено относительно производной —.
Например, для
первого случая 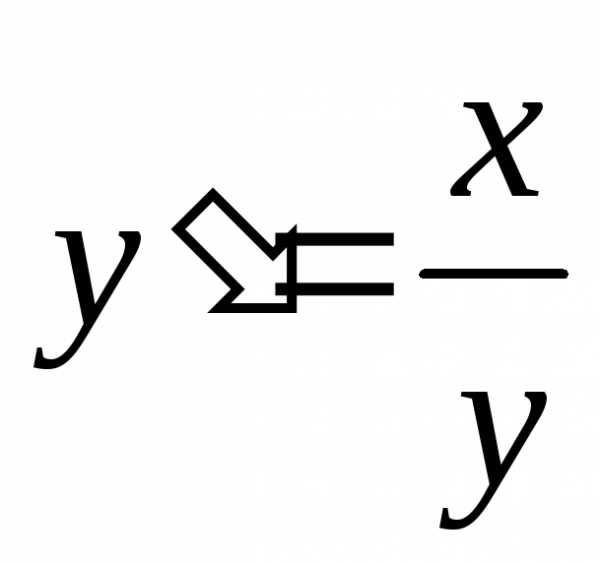 .
В таких задачах нужно учитывать, что
.
В таких задачах нужно учитывать, что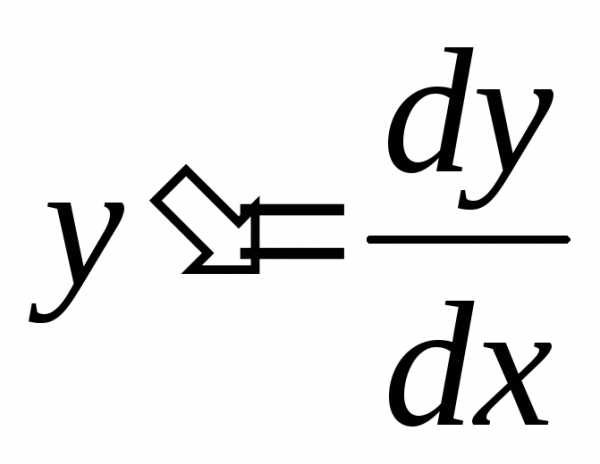 .
Тогда,.
.
Тогда,.
Пример ко второму случаю: . Уравнение можно разрешить относительно производной и, таким образом, придем к первому случаю.
2. Однородные уравнения первого порядка
Уравнение первого
порядка
называется однородным, еслиf(x,y)можно представить как функцию только
одного отношения переменных ,
т.е. уравнение вида
,
т.е. уравнение вида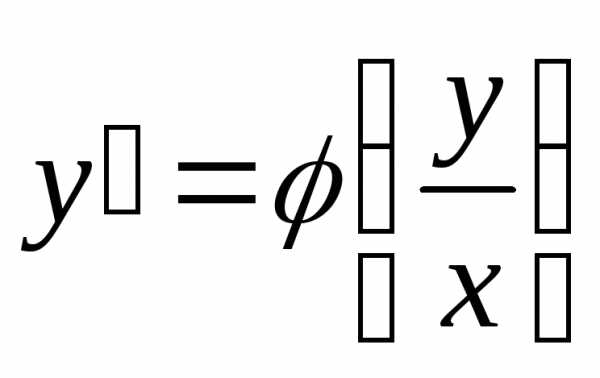 .
Однородное уравнение приводится к
уравнению с разделяющимися переменными
посредством замены функцииу(илих) новой функциейtпо формулеy=tx(x=ty),
причем.
.
Однородное уравнение приводится к
уравнению с разделяющимися переменными
посредством замены функцииу(илих) новой функциейtпо формулеy=tx(x=ty),
причем.
Дифференциальное уравнение типа:
приводится к однородному с помощью переноса начала координат в точку (х0,у0)пересечения прямых, т.е. замена переменныхХ=х-х0, У=у-у0.
Если эти прямые
не пересекаются, то
,
и рассматриваемое уравнение сводится
к виду,
которое приводится
к уравнению с разделяющимися переменными
заменой,
тогда
приводится
к уравнению с разделяющимися переменными
заменой,
тогда
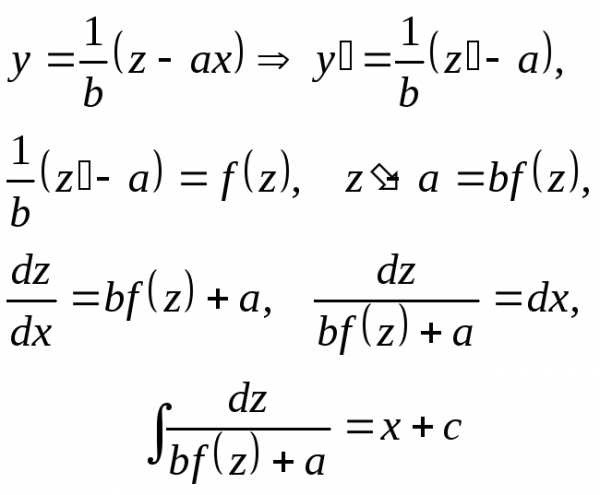
Задача №2. Найти общий интеграл дифференциального уравнения
2.31  .
.
Решение. Данное
уравнение первого порядка уже разрешено
относительно производной. Установим,
что она является функцией только
отношения переменных 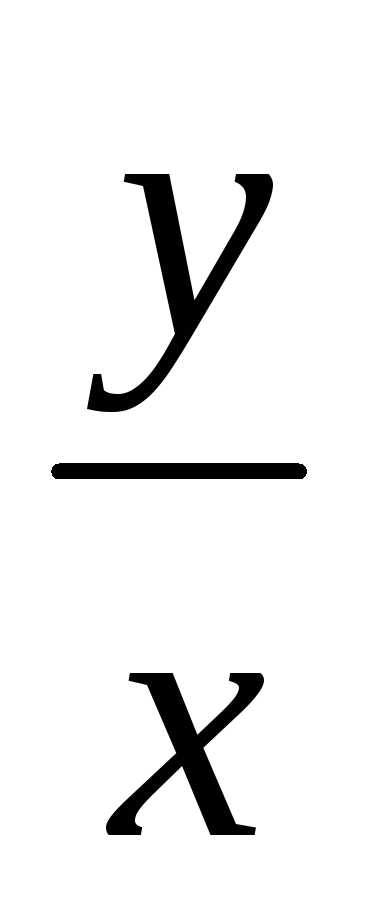 ,
т.е. установим, что данное уравнение
является однородным. Для этого числитель
и знаменатель дроби разделим наx2.
(Другими словами, сократим дробь наx2.)
,
т.е. установим, что данное уравнение
является однородным. Для этого числитель
и знаменатель дроби разделим наx2.
(Другими словами, сократим дробь наx2.)
 .
.
Далее вводим новую
функцию  .
Отсюда,
.
Отсюда, .
После подстановки данное уравнение
преобразуется в уравнение с разделяющимися
переменными.
Разделим переменные:
.
После подстановки данное уравнение
преобразуется в уравнение с разделяющимися
переменными.
Разделим переменные: и, интегрируя, найдем
и, интегрируя, найдем

Возвращаясь к старым переменным, получим

Ответ: 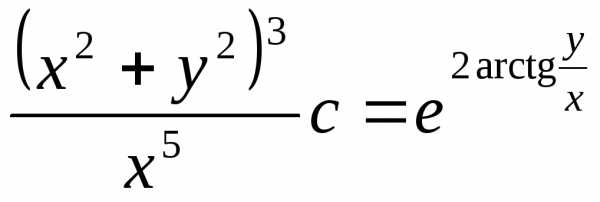
Задача №3. Найти общий интеграл дифференциального уравнения
3.31 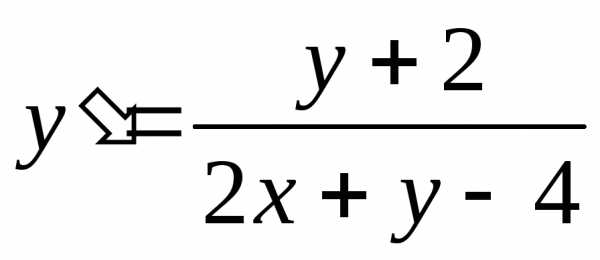
Решение. Также как и в задаче №2 это тоже однородное дифференциальное уравнение. Докажем это, найдя точку пересечения прямых, стоящих в числителе и знаменателе и сделав соответствующую замену переменных.
Из последней
системы легко видеть, что 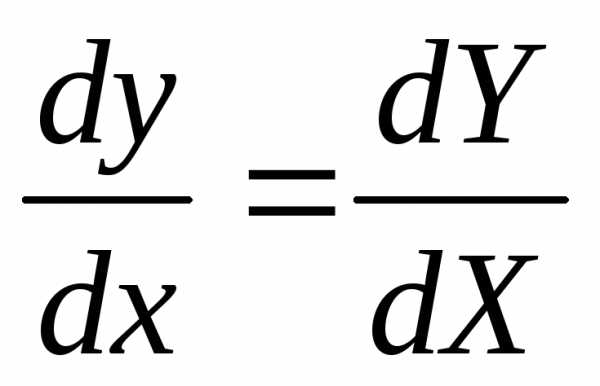 .
Подставим найденныехиув
исходное уравнение, получим
.
Подставим найденныехиув
исходное уравнение, получим
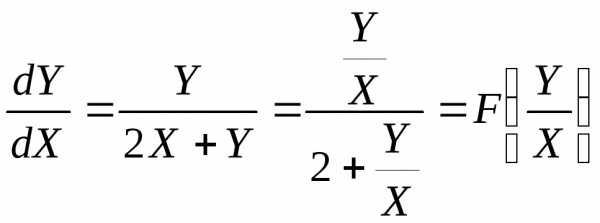 .
.
Далее решаем полученное однородное уравнение путем замены.
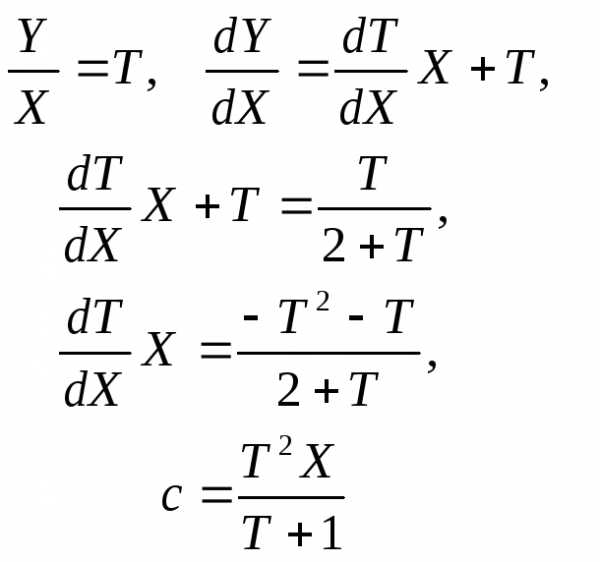
Возвращаясь к старым переменным, получим: , что и является ответом.
studfiles.net
Дифференциальные уравнения с разделенными переменными
Дифференциальные уравнения с разделенными переменными имеют вид f(y)dy=g(x)dx. К ним сводятся многие дифференциальные уравнения первого порядка. В общем случае решение такого уравнения — это интегрирование обеих частей:
Однако оставлять ответ в таком виде не принято. Нужно взять интегралы от обеих функций, если это возможно.
Замечание
Другая форма записи дифференциального уравнения с разделенными переменными:f(y)dy+g(x)dx=0. Его общее решение, заданное в неявном виде, выглядит так:
и называется общим интегралом уравнения.
Проиллюстрируем решение дифференциальных уравнений с разделенными переменными конкретными примерами.
Переносим слагаемое с x в левую часть и интегрируем:
Получаем
Переносим слагаемое с иксом в левую часть и интегрируем:
Замечаем, что (x²-5x+12)’=2x-5. Значит, выражение x²-5x+12 можно подвести под знак дифференциала: d(x²-5x+12)=(2x-5)dx,
В правой части — табличный интеграл. В левой — можно подвести косинус под знак интеграла. Но ради разнообразия сделаем замену:
cos x=t, отсюда dt = (cos x)’dx=-sinxdx. Отсюда
и можно записать решение в виде общего интеграла
либо выразить y через x:
Разделим обе части равенства на 2, затем возведём в квадрат:
Обозначим
Здесь удалось выразить ответ в виде функции в явном виде: y=f(x).
www.matematika.uznateshe.ru
Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение с разделенными переменными записывается в виде: (1).В этом уравнении одно слагаемое зависит только от x, а другое – от y. Проинтегрировав почленно это уравнение, получаем: – его общий интеграл.
Пример: найти общий интеграл уравнения: .
Решение: данное уравнение
– дифференциальное уравнение с
разделенными переменными. Поэтому
или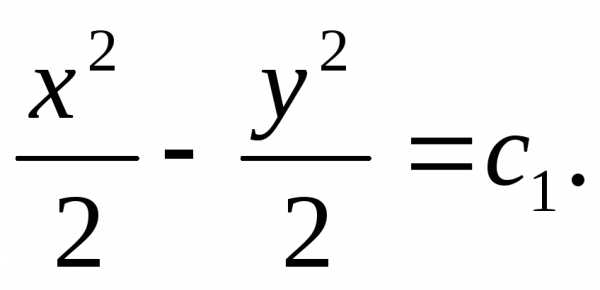 Обозначим
Обозначим .
Тогда–
общий интеграл дифференциального
уравнения.
.
Тогда–
общий интеграл дифференциального
уравнения.
Уравнение с разделяющимися переменными имеет вид (2).Уравнение (2) легко сводиться к уравнению (1) путем почленного деления его на . Получаем:– общий интеграл.
Пример: Решить уравнение .
Решение: преобразуем левую
часть уравнения:
.
Делим обе части уравнения на Решением является выражение:т.е.
Решением является выражение:т.е.
Однородные дифференциальные уравнения. Уравнения Бернулли. Линейные дифференциальные уравнения первого порядка.
Уравнение вида
называетсяоднородным,
если 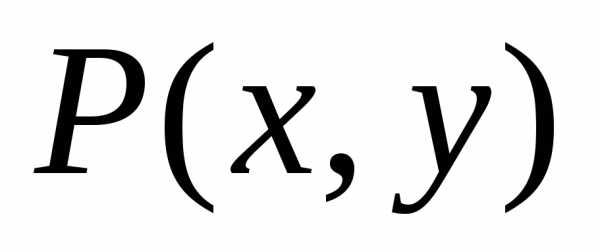 и
и –
однородные функции одного порядка
(измерения). Функция
–
однородные функции одного порядка
(измерения). Функция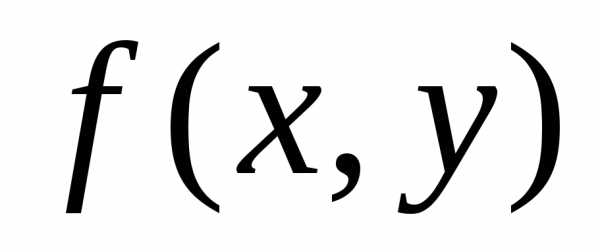 называется
однородной функцией первого порядка
(измерения), если при умножении каждого
ее аргумента на произвольный множитель
называется
однородной функцией первого порядка
(измерения), если при умножении каждого
ее аргумента на произвольный множитель вся функция умножиться на
вся функция умножиться на ,
т.е.=
,
т.е.= .
.
Однородное уравнение может быть приведено
к виду  .
С помощью подстановки
.
С помощью подстановки (
( )однородное
уравнение приводится к уравнению с
разделяющимися переменными по отношению
к новой функции
)однородное
уравнение приводится к уравнению с
разделяющимися переменными по отношению
к новой функции .
.
Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде.
Метод Бернулли
Решение уравнения ищется в виде произведения двух других функций, т.е. с помощью подстановки().
Пример: проинтегрировать уравнение .
Полагаем
.
Тогда
,
т.е.
.
Сначала решаем уравнение=0:

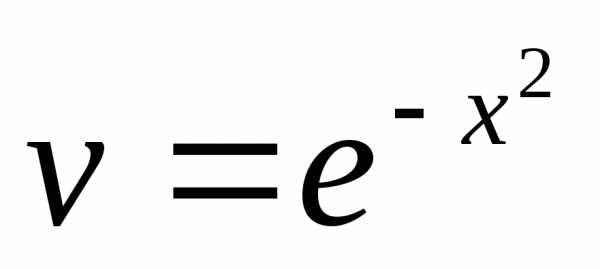 .
.
Теперь решаем уравнение
т.е.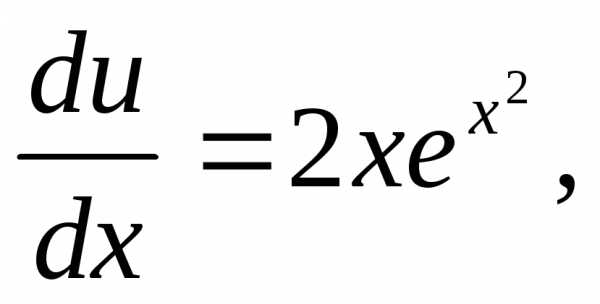 .
Итак, общее решение данного уравнения
естьт.е.
.
Итак, общее решение данного уравнения
естьт.е.
Уравнение Я. Бернулли
Уравнение вида , гденазываетсяуравнением Бернулли.Данное уравнение решается с помощью метода Бернулли.
Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Однородным линейным дифференциальным
уравнением второго порядка называется
уравнение вида (1), где и
и постоянны.
постоянны.
Частные решения уравнения (1) будем
искать в виде  ,
гдек – некоторое число. Дифференцируя
эту функцию два раза и подставляя
выражения для
,
гдек – некоторое число. Дифференцируя
эту функцию два раза и подставляя
выражения для в
уравнение (1), получимт.е.или(2)(
в
уравнение (1), получимт.е.или(2)(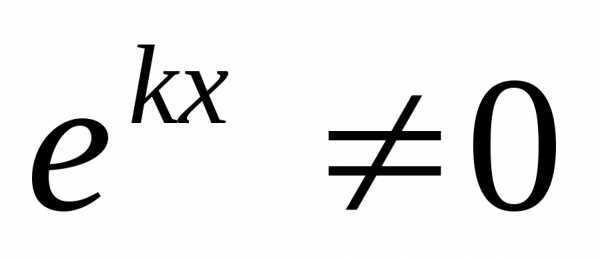 ).
).
Уравнение 2 называется характеристическим уравнением дифференциального уравнения.
При решении характеристического уравнения (2) возможны три случая.
Случай 1.Корни и
и уравнения (2) действительные и различные:
уравнения (2) действительные и различные: .
В этом случае частными решениями
уравнения (1) являются функции
.
В этом случае частными решениями
уравнения (1) являются функции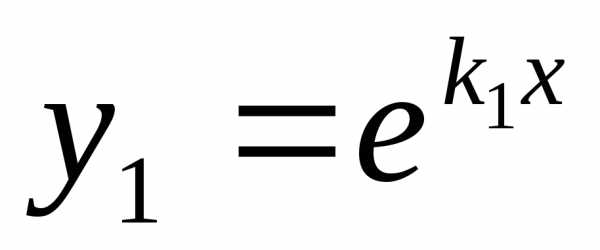 и
и .
Следовательно, общее решение уравнения
(1) имеет вид.
.
Следовательно, общее решение уравнения
(1) имеет вид.
Случай 2.Корни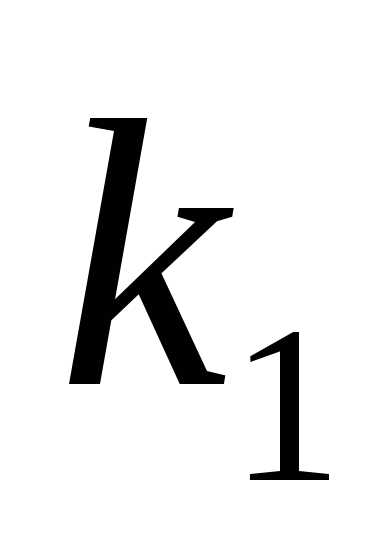 и
и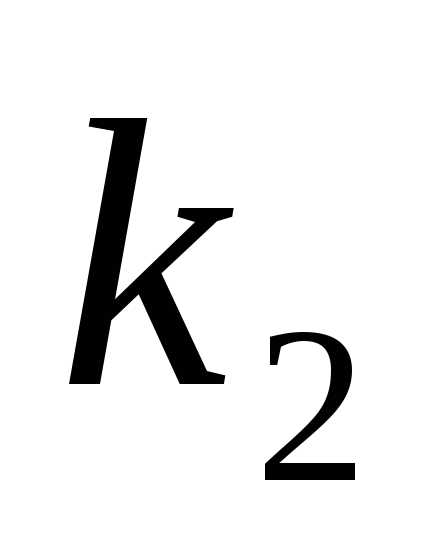 уравнения (2) действительные и равные:
уравнения (2) действительные и равные: .
В этом случае частными решениями
уравнения (1) являются функции
.
В этом случае частными решениями
уравнения (1) являются функции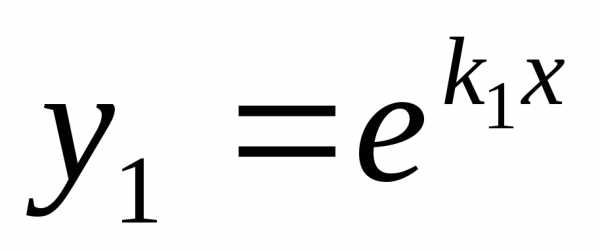 и
и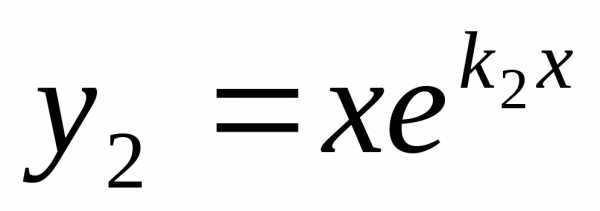 .
Следовательно, общее решение уравнения
(1) имеет вид.
.
Следовательно, общее решение уравнения
(1) имеет вид.
Случай 3.Корни и
и уравнения (2) комплексные:,.
В этом случае частными решениями
уравнения (1) являются функциии.
Следовательно, общее решение уравнения
(1) имеет вид
уравнения (2) комплексные:,.
В этом случае частными решениями
уравнения (1) являются функциии.
Следовательно, общее решение уравнения
(1) имеет вид
Пример. Решить уравнение .
Решение: составим характеристическое уравнение:. Тогда. Общее решение данного уравнения.
Экстремум функции нескольких переменных. Условный экстремум.
Экстремум функции нескольких переменных
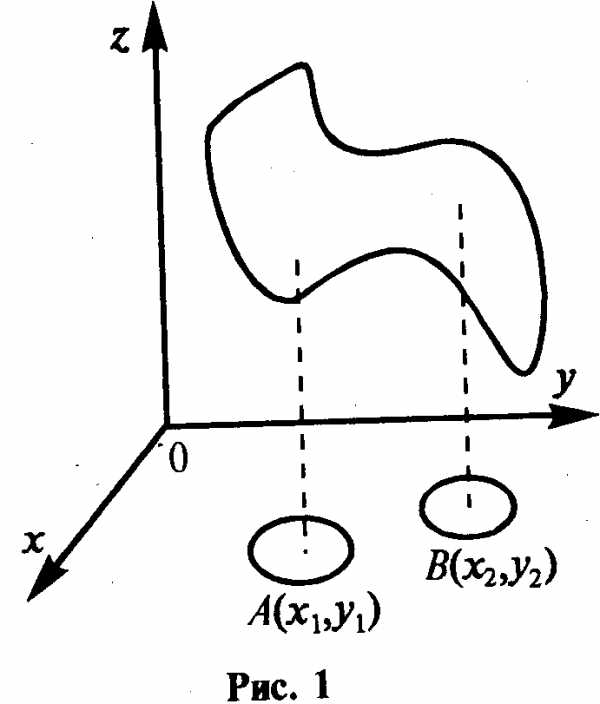
Определение. Точка М (хо,уо) называется точкой максимума (минимума) функции z=f(x, у), если существует окрестность точки М, такая, что для всех точек {х, у) из этой окрестности выполняется неравенство ()
На рис. 1 точка А —
есть точка минимума, а точка В
—
есть точка минимума, а точка В —точка максимума.
—точка максимума.
Необходимое условие экстремума — многомерный аналог теоремы Ферма.
Теорема. Пусть
точка 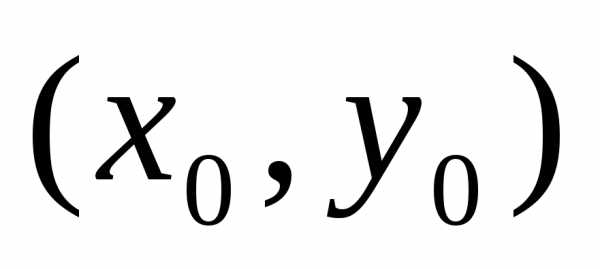 –
есть точка экстремума дифференцируемой
функцииz=f(x,
у). Тогда частные производные
–
есть точка экстремума дифференцируемой
функцииz=f(x,
у). Тогда частные производные  и
и  в этой точке равны нулю.
в этой точке равны нулю.
Точки, в которых выполнены необходимые условия экстремума функции z=f(x, у), т.е. частные производные z‘x и z‘y равны нулю, называются критическими или стационарными.
Равенство частных производных нулю выражает лишь необходимое, но недостаточное условие экстремума функции нескольких переменных.
На рис. изображена так
называемая седловая
точка М (хо,уо). Частные производные 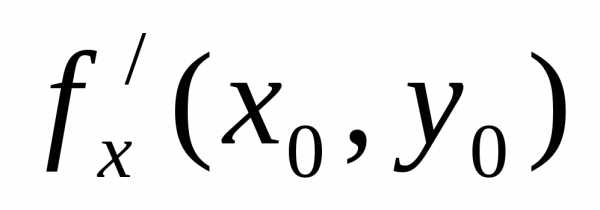 и
и  равны
нулю, но, очевидно, никакого экстремума
в точке М(хо,уо) нет.
равны
нулю, но, очевидно, никакого экстремума
в точке М(хо,уо) нет.
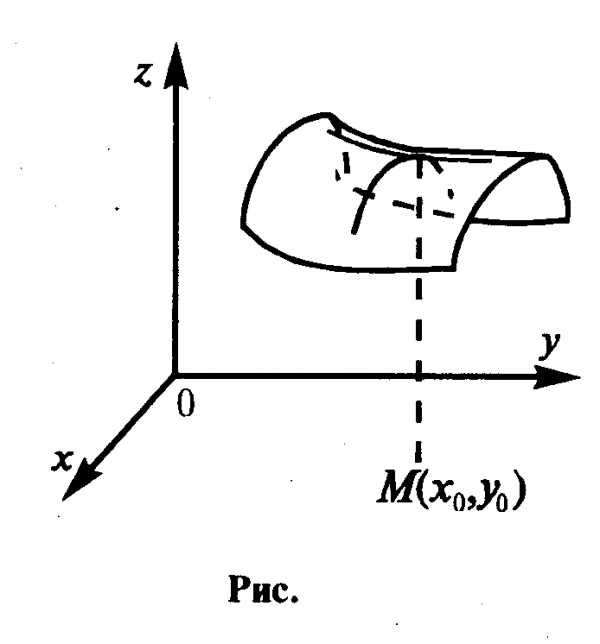
Такие седловые точки являются двумерными аналогами точек перегиба функций одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Иными словами, требуется знать достаточное условие экстремума.
Теорема (достаточное
условие экстремума функции двух
переменных). Пусть
функция z=f(x,
у): а) определена
в некоторой окрестности критической
точки (хо,уо),
в которой  =0
и
=0
и  =0;
=0;
б) имеет в этой точке непрерывные частные производные второго порядка;;Тогда, если ∆=АС— В2 >0, то в точке (хо,уо) функция z=f(x, у) имеет экстремум, причем если А<0 — максимум, если А>0 — минимум. В случае ∆=АС— В2<0, функция z=f(x, у) экстремума не имеет. Если ∆=АС— В2=0, то вопрос о наличии экстремума остается открытым.
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
Найти частные производные функции z‘x и z‘y.
Решить систему уравнений z‘x =0, z‘y =0 и найти критические точки функции.
Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
Найти экстремумы (экстремальные значения) функции.
Пример. Найти экстремумы функции
Решение. 1. Находим частные производные
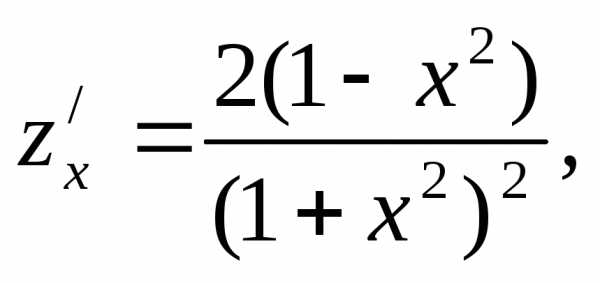
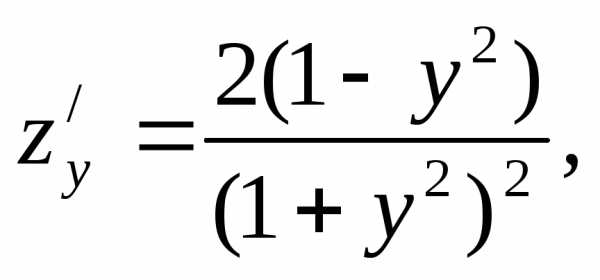
2. Критические точки функции находим из системы уравнений:
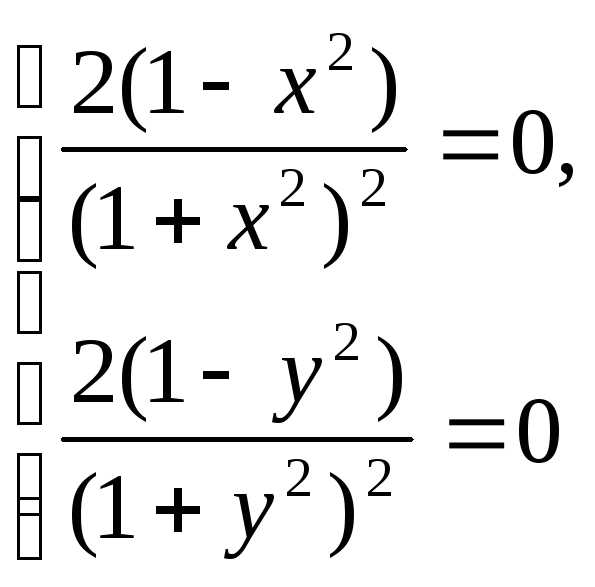
имеющей четыре решения (1; 1), (1; —1), (—1; 1) и (—1; -1).
3. Находим частные производные второго порядка:
 ;;,
вычисляем их значения в каждой критической
точке и проверяем в ней выполнение
достаточного условия экстремума.
;;,
вычисляем их значения в каждой критической
точке и проверяем в ней выполнение
достаточного условия экстремума.
Например, в точке (1; 1) A=z“(1; 1)= -1; В=0; С= -1. Так как ∆= АС— В2 = (-1)2-0=1 >0 и А=-1<0, то точка (1; 1) есть точка максимума.
Аналогично устанавливаем, что (-1; -1) — точка минимума, а в точках (1; —1) и (—1; 1), в которых ∆=АС— В2 <0, — экстремума нет. Эти точки являются седловыми.
4. Находим экстремумы функции zmax = z(l; 1) = 2, zmin = z(-l; -1) = -2,
Условный экстремум. Метод множителей Лагранжа.
Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть рассматривается функция z = f(x,y), аргументы х и у которой удовлетворяют условию g (х,у) = С, называемому уравнением связи.
Определение. Точка  называется точкойусловного
максимума (минимума), если
существует такая окрестность этой
точки, что для всех точек (х,у) из этой
окрестности удовлетворяющих условию g (x,y)
= С, выполняется неравенство
называется точкойусловного
максимума (минимума), если
существует такая окрестность этой
точки, что для всех точек (х,у) из этой
окрестности удовлетворяющих условию g (x,y)
= С, выполняется неравенство
().
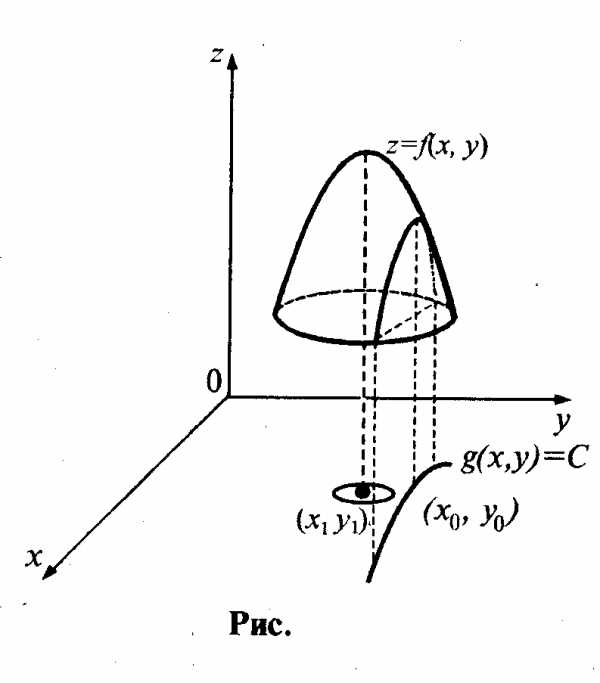
На рис. изображена точка
условного максимума  .Очевидно, что она не
является точкой безусловного экстремума
функции z
= f(x,y) (на рис. это точка
.Очевидно, что она не
является точкой безусловного экстремума
функции z
= f(x,y) (на рис. это точка  ).
).
Наиболее простым способом
нахождения условного экстремума
функции двух переменных является
сведение задачи к отысканию экстремума
функции одной переменной. Допустим
уравнение связи g (x,y) = С удалось разрешить
относительно одной из переменных,
например, выразить у через х: 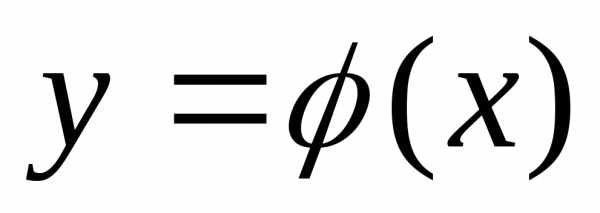 .Подставив полученное
выражение в функцию двух переменных,
получим z
= f(x,y) =, т.е. функцию одной
переменной. Ее экстремум и будет условным
экстремумом функции z = f(x,y).
.Подставив полученное
выражение в функцию двух переменных,
получим z
= f(x,y) =, т.е. функцию одной
переменной. Ее экстремум и будет условным
экстремумом функции z = f(x,y).
Пример. Найти точки максимума и минимума функции z = х2 + y2 при условии 3х +2у = 11.
Решение. Выразим из уравнения
3х +2у = 11
переменную y
через переменную x
и подставим полученное 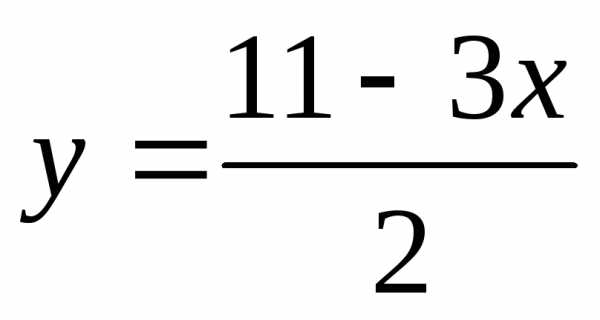 в функциюz.
Получим z=x2+2
в функциюz.
Получим z=x2+2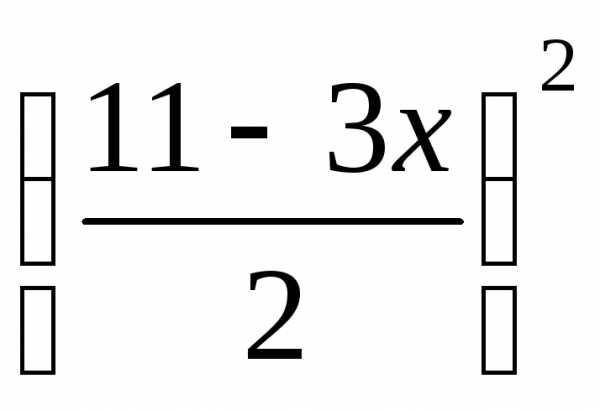 илиz =
илиz = .Эта функция имеет
единственный минимум при
.Эта функция имеет
единственный минимум при 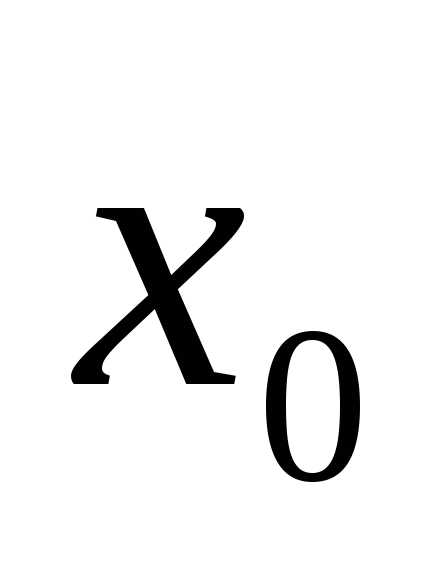 = 3. Соответствующее
значение функции
= 3. Соответствующее
значение функции  Таким образом, (3; 1) — точка условного
экстремума (минимума).
Таким образом, (3; 1) — точка условного
экстремума (минимума).
В рассмотренном примере уравнение связи g(x, у) = С оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.
Для отыскания условного экстремума в общем случае используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
Эта функция называется функцией Лагранжа, а  —
множителем Лагранжа. Верна
следующая теорема.
—
множителем Лагранжа. Верна
следующая теорема.
Теорема. Если
точка 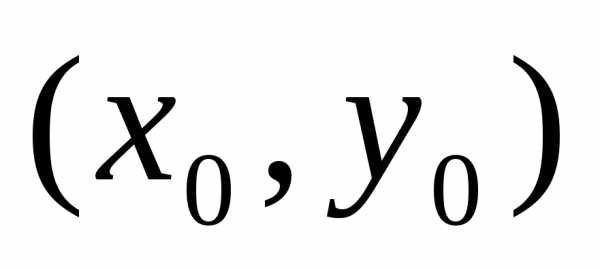 является
точкой условного экстремума функцииz = f(x,y)
при условии g (x,y)
= С, то существует значение
является
точкой условного экстремума функцииz = f(x,y)
при условии g (x,y)
= С, то существует значение 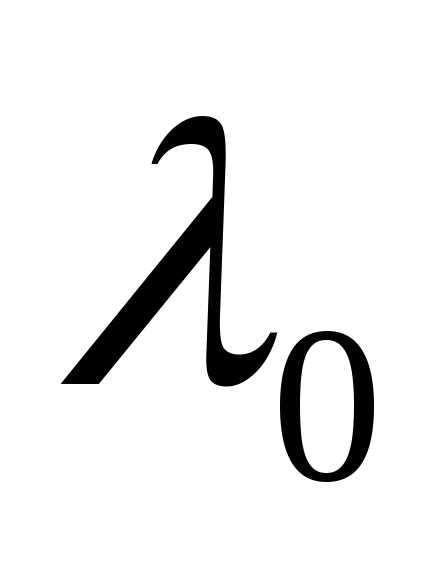 такое,
что точкаявляется
точкой экстремума функцииL{x,y,
такое,
что точкаявляется
точкой экстремума функцииL{x,y,  ).
).
Таким образом, для нахождения условного экстремума функции z = f(х,у) при условии g(x,y) = С требуется найти решение системы

На рис. показан геометрический смысл условий Лагранжа. Линия g (х,у) = С пунктирная, линия уровня g(x,y) = Q функции z = f(x,y) сплошные.
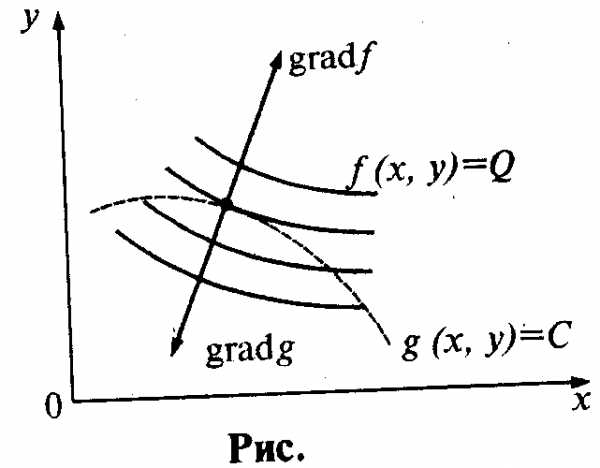
Из рис. следует, что в точке условного экстремума линия уровня функции z = f(x,y) касается линии g(x,y) = С.
Пример. Найти точки максимума и минимума функции z = х2 + y2 при условии 3х +2у = 11, используя метод множителей Лагранжа.
Решение. Составляем функцию Лагранжа L = х2 + 2у2 +
Приравнивая к нулю ее частные производные, получим систему уравнений

Ее единственное решение
(х=3, у=1,  =—2). Таким образом, точкой
условного экстремума может быть только
точка (3;1). Нетрудно убедиться в том,
что в этой точке функция z=f(x,y) имеет условный минимум.
=—2). Таким образом, точкой
условного экстремума может быть только
точка (3;1). Нетрудно убедиться в том,
что в этой точке функция z=f(x,y) имеет условный минимум.
studfiles.net
