Кинематика Что верно? 1. Физическая величина, равная отношению перемещения материальной точки к
Что верно?
1. Физическая величина, равная отношению перемещения материальной точки к физически малому промежутку времени, в течении которого произошло это перемещение, называется:
1) Средней скоростью неравномерного движения материальной точки
2) Мгновенной скоростью материальной точки
3) Скоростью равномерного движения материальной точки
2. Направление ускорения всегда совпадает с :
1) Направлением скорости
2) Направлением перемещения
3) Направлением вектора изменения скорости
3. Ускорение это:
1) Физическая величина, равная отношению изменения скорости к тому промежутку времени, за который это изменение произошло
2) Физическая величина, равная отношению изменения скорости к тому физически малому промежутку времени, за которое это изменение произошло
3) Физическая величина, равная отношению перемещения ко времени
4. Проекция ускорения на координатную ось может быть:
1) Только положительной
2) Только отрицательной
3) И положительной, и отрицательной, и равной нулю
5. В каком случае модуль ускорения больше?
1) Тело движется с большой постоянной скоростью
2) Тело быстро набирает или теряет скорость
3) Тело медленно набирает или теряет скорость
6. Два поезда движутся на встречу друг другу по прямолинейному участку пути. Один из них движется ускоренно, второй замедленно. Их ускорения направлены:
1) В одну сторону
2) В противоположные стороны
3) Однозначно об их направлениях нельзя сказать
7. Локомотив разгоняется до скорости 20 м/с, двигаясь по прямой с ускорением в 5 м/с2. Начальная скорость его равна нулю. Сколько времени длится разгон?
1) 0,25 с
2) 2 с
3) 100 с
4) 4 с
8. При подходе к станции поезд уменьшил скорость на 10 м/с в течении 20 с. С каким ускорением двигался поезд?
1) – 0,5 с2
2) 2 м / с2
3) 0,5 м / с2
4) – 2 м / с2
9. Автомобиль, трогаясь с места, движется с ускорением 3 м / с2. Через 4 с скорость автомобиля будет равна:
1) 12 м/с
2) 0,75 м/с
3) 48 м/с
4) 6 м/с
iotvet.com
Ускорение. Нормальная и тангенциальная составляющие ускорения
На этом уроке мы вспомним, что такое ускорение. Рассмотрим две его составляющие, тангенциальную и нормальную, и пример нахождения этих составляющих. А также решим две задачи из сборника для подготовки к Единому государственному экзамену на нахождение радиуса траектории в наивысшей точке.
Механическое движение по характеру подразделяется на поступательное, вращательное и колебательное; по виду траектории – прямолинейное и криволинейное. Также механическое движение можно подразделять по характеру изменения скорости.
Физическая величина, которая определяет быстроту изменения скорости, называется ускорением. Математически ускорение определяется отношением изменения скорости к промежутку времени, за которое оно произошло (производная от скорости по времени): , где – ускорение; – изменение скорости; – промежуток времени, за которое произошло изменение скорости; – производная скорости по времени.
Так как скорость – величина векторная, то она может меняться по модулю и направлению, поэтому ускорение имеет две естественные составляющие: тангенциальную (параллельную вектору скорости) и нормальную (перпендикулярную вектору скорости).
, где – полное ускорение; – тангенциальная составляющая ускорения; – нормальная составляющая ускорения (см. рис. 1).
Рис. 1. Тангенциальная и нормальная составляющие полного ускорения
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное (см. рис. 2).
Рис. 2. Тангенциальная составляющая ускорения сонаправлена со скоростью
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным (см. рис. 3).
Рис. 3. Тангенциальная составляющая ускорения противонаправлена скорости
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело (см. рис. 4).
Рис. 4. Направление нормального ускорения
Величина нормального ускорения связана с радиусом траектории и со скоростью движения следующим соотношением:
При прямолинейном движении тело имеет только тангенциальное ускорение. Нормальное ускорение отсутствует, так как скорость тела по направлению остаётся неизменной (см. рис. 5).
Рис. 5. Прямолинейное движение
При криволинейном движении, как правило, тело имеет тангенциальную и нормальную составляющую ускорения (см. рис. 6).
Рис. 6. Криволинейное движение
Рассмотрим движение тела, брошенного под углом к горизонту (см. рис. 7). Найдём составляющие ускорения в тот момент, когда скорость тела направлена под углом к горизонту.

Рис. 7. Траектория движения тела
Касательная к траектории в точке A – это направление скорости . Ускорение тела, брошенного под углом к горизонту, всегда равно ускорению свободного падения: .
Спроецируем данное ускорение на две взаимно перпендикулярные оси, одна из которых перпендикулярна скорости, другая направлена вдоль скорости.
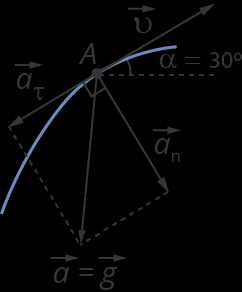
Рис. 8. Проекции ускорения
На рисунке видно, что тангенциальная составляющая ускорения направлена против скорости, то есть скорость тела в данный момент уменьшается (см. рис. 8). Нормальная составляющая ускорения направлена перпендикулярно скорости, следовательно, скорость в следующий момент наклонится в сторону .
Величины составляющих ускорения находим геометрически.
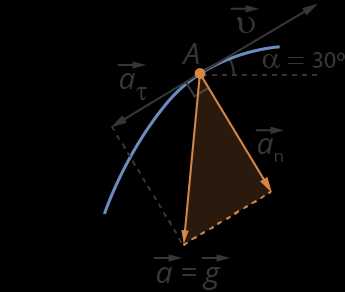
Рис. 9. Геометрическое определение величины составляющих ускорения
Угол A в треугольнике разложения на составляющие (треугольник выделен жёлтым на рисунке) имеет взаимно перпендикулярные стороны с углом (см. рис. 9), поэтому .
Следовательно, тангенциальная составляющая равна: .
Нормальная составляющая ускорения равна: .
Обод радиусом 1 метр катится по горизонтальной поверхности со скоростью 10 м/с. Найти радиус траектории точки поверхности обода при прохождении наивысшего положения.
Дано: ; .
Найти: .
Решение
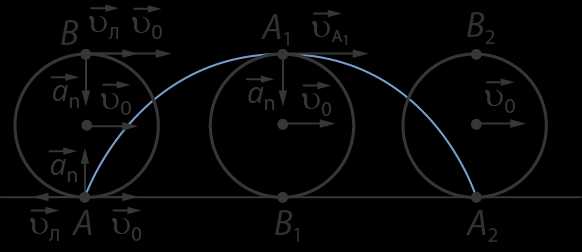
Рис. 10. Иллюстрация к задаче
На рисунке изображён обод, который катится по горизонтальной поверхности со скоростью (см. рис. 10). Точка A – точка касания обода горизонтальной поверхности, точкаB – наивысшая точка в начальный момент времени. Точка A будет перемещаться по траектории, которая обозначена жёлтым цветом, она называется циклоидой. Эта точка вновь коснётся поверхности, пройдя путь, равный длине траектории: .
Скорость точки A относительно горизонтальной поверхности при движении обода без проскальзывания равна нулю. Это объясняется тем, что она движется вместе с ободом по горизонтали со скоростью и относительно центра обода совершает движение по окружности со скоростью . В точке
Скорости точек в верхней части обода равны: . Эта скорость будет направлена по горизонтали в сторону движения обода.
С центром обода у всех точек, лежащих на её поверхности, связано нормальное ускорение, так как оно направлено перпендикулярно скорости движения точки по окружности в любой момент времени.
Ускорение остаётся неизменным для всех точек поверхности обода, так как при переходе к системе отсчёта, связанной с Землёй, центр обода движется равномерно:
Тогда для точки получается следующее соотношение: , где r – искомый радиус.
В этой задаче заданное значение начальной скорости было лишним. Избыточные данные часто включают в задания ЕГЭ по физике.
Ответ: .
После удара футбольный мяч за 2 с пролетел 40 м и упал на землю. Чему равен радиус траектории мяча в верхней точке траектории?
Дано: ; ; .
Найти: .
Решение
Рис. 11. Иллюстрация к задаче
На рисунке изображена траектория полёта мяча (см. рис. 11). Точка A – верхняя точка траектории, скорость мяча в которой . Ускорение g в верхней точке направлено вниз. Очевидно, что это нормальная составляющая ускорения, так как она направлена перпе
interneturok.ru
Механическое движение. Путь. Скорость. Ускорение
Механическим движением называют изменение положения тела (или его частей) относительно других тел. Положение тела задается координатой. Линию, вдоль которой движется материальная точка, называют траекторией. Длину траектории называют путем. Единица пути — метр. Путь = скорость* время. S=v*t. Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением. Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением (s). Перемещение — величина векторная. Единица перемещения — метр. Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка времени. Формула скорости имеет вид v = s/t. Единица скорости — м/с. На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с) . Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Формула для вычисления ускорения: a=(v-v0)/t; Единица ускорения – метр/(секунда в квадрате) .
Пора-бы Ньютона пересмотреть… Его формулы сдерживают расчёты… 1. s=att, а НЕ att/2=s 2.V=at. V-это СРЕДНЯЯ скорость. V ср. =at 3. S/t=at. Почему : at*t=2S ? 4. S/t=V=at. Средняя скорость НЕ зависит от графика движения. И “а”-тоже! 5. V cр. и at- это равномерное движение, нач. скорость = конечной. 6. Ускорение надо находить ТОЛЬКО из СРЕДНЕЙ скорости! 7. Нельзя отнимать “скорость от скорости” 8. Ускорение- это ЭНЕРГИЯ. Её надо находить из формулы F/m 9. При равномерном движении скорость постоянна, но “а” со временем убывает. Неизбежно наступает остановка движения, т. к. “движущая сила” иссякает. (почему звёзды не исчезают?) 10. Энергия ускорения не может быть бесконечной. У ДВС-это крутящий момент, у всего живого-мускульная сила…. Основная цель поиска ускорения-“увязать” S,t,F,m. S/tt и F/m. Зная 3 величины-просто найти 4-ю. Если ускорение левой половины уравнения равны правой-значит это конкретный движущийся объект-(предмет, машина, человек….) S/tt=F/m. Пример: t-5 сек., S-120 м., m-12 кг. F-? Решение: 120:25=F:12. F=57,6 кг. м/с Автомобиль проехал …150 м. за ..12,2 сек. Мощность двигателя… 90 л. с. m-? КПД бензинового ДВС 16%. Значит: двигало машину всего 14,4 л. с. -1080 кг. м Решение: 150:12,2:12,2=1080:m m=1073 кг. Ещё пример: бегун m-75 кг. пробежал 100 м за 10 секунд. Какую он развил мощность-(приложил силу). Решение: 100*75/100=75 кг. м. -ОДНУ л. с. !
2. Механика. Механическое движение. Понятие механики. Механика – это часть физики, в которой изучают движение тел, взаимодействие тел или, движение тел под каким-либо взаимодействием. Главная задача механики – это определение местоположения тела в любой момент времени. Разделы механики: кинематика и динамика. Кинематика – это раздел механики, изучающий геометрические свойства движений без учета их масс и действующих на них сил. Динамика – это раздел механики, изучающий движение тел под действием приложенных к ним сил. Движение. Характеристики движения. Движение – это изменение положения тела в пространстве с течением времени относительно других тел. Характеристики движения: пройденный путь, перемещение, скорость, ускорение. Механическое движение – это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени. Поступательное движение. Демонстрируется видеопоказом с объяснениями. Равномерное движение тела. Демонстрируется видеопоказом с объяснениями. Неравномерное механическое движение – это движение, при котором за равные промежутки времени тело совершает неравные перемещения. Относительность механического движения. Демонстрируется видеопоказом с объяснениями. Точка отсчёта и система отсчёта в механическом движении. Тело, относительно которого рассматривается движение, называется точкой отсчёта. Система отсчёта в механическом движении – это точка отсчёта и система координат и часами. Система отсчета. Характеристики механического движения. Система отсчета демонстрируется видеопоказом с объяснениями. Механическое движение имеет характеристики: Траектория; Путь; Скорость; Время. Траектория прямолинейного движения – это линия, вдоль которой движется тело. Криволинейное движение. Демонстрируется видеопоказом с объяснениями. Путь и понятие скалярной величины. Демонстрируется видеопоказом с объяснениями. Физические формулы и единицы измерения характеристик механического движения: Обозначение величины Единицы измерения величины Формула для определения величины Путь-s м, км S = vt Время- t с, час T = s/v Скорость -v м/с, км/ч V = s/t Понятие ускорения. Раскрывается демонстрацией видеопоказа, с объяснениями. Формула для определения величины ускорения: 3. Законы динамики Ньютона. Великий физик И. Ньютон. И. Ньютон развенчал античные представления, что законы движения земных и небесных тел совершенно различны. Вся Вселенная подчинена единым законам, допускающим математическую формулировку. Две фундаментальные задачи, решенные физикой И. Ньютона: 1. Создание для механики аксиоматической основы, которая перевела эту науку в разряд строгих математических теорий. 2. Создание динамики, связывающей поведение тела с характеристиками внешних воздействий на него (сил). Законы динамики И. Ньютона в его авторской редакции: 1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. 2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует. 3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Первый закон динамики И. Ньютона. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. Понятия инерции и инертности тела. Инерция – это явление, при котором тело стремится сохранить свое первоначальное состояние. Инертность – это свойство тела сохранять состояние движения. Свойство инертности характеризуется массой тела. Развитие Ньютоном теории механики Галил
touch.otvet.mail.ru
Кинематика [wiki.eduVdom.com]
Кинематика материальной точки
Материальная точка – тело, размерами которого в данной задаче можно пренебречь.
Перемещение – вектор, проведенный из начального положения материальной точки в конечное.
Путь – расстояние, пройденное телом вдоль траектории.
Путь (пройденный путь) – длина траектории, по которой движется тело в течение нeкoтoporo промежутка времени.
Траектория – линия, по которой движется (или может двиrаться) тело.
Скорость – величина, характеризующая быстроту изменения положения тела по отношению к другим телам с течением времени.
Средняя скорость – скорость неравномерного движения на данном участке пути или за данный промежуток времени.
Средняя путевая скорость – скалярная величина, равная отношению пути к промежутку времени, затраченному на его прохождение:
$$ V_{cp}= \frac{\Delta r}{\Delta t}$$
Скорость – векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, в течение которого это перемещение произошло:
$$ \vec{V}=\lim_{t\rightarrow 0} \frac{\Delta \vec{r}}{\Delta t} $$
Скорость тела направлена по касательной к траектории в сторону движения тела.
Равномерное движение – движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Ускорение – векторная физическая величина, равная пределу отношения изменения скорости тела к промежутку времени, в течение которого это изменение произошло:
$$\vec{a}=\lim_{\Delta t\rightarrow 0} \frac{\Delta \vec{v}}{\Delta t}$$
Основные виды движения:
Три важнейших типа прямолинейного движения:
wiki.eduvdom.com
1)Основные кинематические величины
Перемещение— векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:
.
Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.
Средняя скорость— векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:
.
Мгновенная скорость— векторная физическая величина, равная первойпроизводнойот радиус-вектора по времени:
.
Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:
.
Единица измерения скорости в системе СИ—м/с, в системеСГС— см/с. Мгновенная скорость всегда направлена по касательной к траектории.
Мгновенное ускорение— векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:
.
Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить посопутствующему базису: на вектор нормального и тангенциального ускорения:
.
Здесь — единичныйвектор нормали,— единичный вектор касательной. Величинаназываетсянормальным ускорениеми характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость ирадиус кривизнытраектории:
.
В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.
Величина называетсятангенциальным ускорениеми характеризует величину изменения модуля скорости:
.
2) Первый закон Ньютона
1-й закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет его из этого состояния.
– I закон Ньютона
Этот закон называют законом инерции. Инерция – способность тела сохранять скорость. Движение по инерции – движение с постоянной скоростью.
1-й закон Ньютона выполняется не во всех системах отсчета. Системы отсчета, в которых выполняется 1-й закон Ньютона, называются инерциальными. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.
Примером инерциальной системы отсчета может служить гелиоцентрическая система отсчета, т. е. система отсчета, связанная с Солнцем.
Любая система отсчета, движущаяся относительно гелиоцентрической равномерно и прямолинейно будет являться инерциальной.
Лабораторная система отсчета, оси координат которой жестко связаны с Землей, неинерциальная из-за суточного вращения Земли. Однако вращение Земли происходит очень медленно с а=0,034 м/с2, и поэтому в большинстве задач лабораторную систему отсчета можно приближенно считать инерциальной.
Содержание 1-го з. Н. сводится к двум утверждениям:
1) все тела обладают свойством инертности;
2) существуют инерциальные системы отсчета.
Инерциальные системы отсчета играют особую роль не только в механике, но и в других разделах физики, т. к. согласно принципу относительности Эйнштейна математическая запись любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчета.
3) Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.
Примером такого движения является движение тела, брошенного под углом к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением , направленным вертикально вниз.
При равноускоренном движении по прямой скорость тела определяется формулой:
Зная, что , найдём формулу для определения координаты x:
Примечание. Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора и противонаправлены). Равнозамедленное движение также является равноускоренным.
4) Свобо́дное падéние — равноускоренное движение под действием силы тяжести. На поверхности Земли, на уровне моря, ускорение свободного падения меняется от 9,81 м/с² на полюсах до 9,78 м/с² на экваторе.
В частности парашютист, в течение нескольких первых секунд прыжка, находится практически в свободном падении.
Свободное падение возможно на поверхность любого тела, обладающего достаточной массой (планеты и их спутники, звезды, и т. п.).
На объекте, находящемся в состоянии свободного падения, все физические процессы протекают так же, как и в состоянии невесомости. Это используется, например, при тренировке космонавтов: самолёт с космонавтами набирает большую высоту и пикирует, в течение нескольких минут находясь в состоянии свободного падения, при этом космонавты и экипаж испытывают состояние невесомости.
5) Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; — полная фаза колебаний, — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
(Любое нетривиальное[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )
6) 2-й закон Ньютона.
Ускорение, полученное телом в результате взаимодействия, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела:. Выражение справедливо для любых сил любой природы.
7) Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.
В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения[1]. Период малых собственных колебанийматематического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит[2] от амплитуды колебаний и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
8) 3-й закон Ньютона.
Силы, с которыми два тела действуют друг на друга, равны по величине, направлены в противоположные стороны F12 = – F21.
F12 – сила, действующая со стороны второго тела на первое, приложена к первому телу, F21 – сила, действующая на второе тело со стороны первого, приложена ко второму телу
9) Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообщераспределенной системы это может быть записано как где — импульс бесконечно малого точечного элемента системы).
В системе СИ момент импульса измеряется в единицах джоуль–секунда; Дж·с.
Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют всопротивлении материалов).
10) Динамика вращательного движения материальной точки. Рассмотрим частицу массы m, вращающуюся вокруг токи О по окружности радиуса R, под действием результирующей силы F (см. рис. 6.5). В инерциальной системе отсчета справедлив 2ой закон Ньютона. Запишем его применительно к произвольному моменту времени:
F = m·a.
Нормальная составляющая силы не способна вызвать вращения тела, поэтому рассмотрим только действие ее тангенциальной составляющей. В проекции на тангенциальное направление уравнение движения примет вид:
F= m·a.
Поскольку a = ·R, то
F= m··R(6.6)
Умножив левую и правую части уравнения скалярно на R, получим:
F·R= m··R2 (6.7) M = I· (6.8)
Уравнение (6.8) представляет собой 2ой закон Ньютона (уравнение динамики) для вращательного движения материальной точки. Ему можно придать векторный характер, учитывая, что наличие момента сил вызывает появление параллельного ему вектора углового ускорения, направленного вдоль оси вращения (см. рис. 6.5):
M = I· (6.9)
Основной закон динамики материальной точки при вращательном движении можно сформулировать следующим образом:
произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.
studfiles.net
Технические заведения,справочное пособие, физика, информатика
Справочное пособие.Кинематика.
Глава 4. Кинематика.
§1. Системы отсчета в механике.
Механика – это раздеп физики, изучающий движение тел.
Механическое движение – это изменение положения тела в пространстве с течением времени .
В дальнейшем мы будем опускать прилагательное «механическое» и говорить просто о «движении» тела.
При изучении движения тела необходимо уметь определять его положение в пространстве. Для этого достаточно указать положение всех его точек .
Для определения положения точки можно воспользоваться известными из геометрии системами координат . Но в отличие от геометрии, где любые точки, линии и фигуры никак не связаны с реальными предметами, физика имеет дело с физическими телами и любая рассматриваемая нами точка относится к какому?то определенному телу. Поэтому ее называют еще материальной точкой .
Помимо этого всегда необходимо указывать относительно каких тел мы рассматриваем движение нашего тела. По отношению к разным телам оно будет двигаться по?разному. Возьмем к примеру движущийся вагон поезда, в котором на полке лежит чемодан. Относительно вагона чемодан будет покоиться , а относительно Земли – двигаться вместе с вагоном. Поэтому говорят, что всякое движение (а также и покой ) тела относительны . В механике движение тел рассматривают относительно специально выбранного тела, которое называют телом отсчета . Система координат относительно тела отсчета всегда остается неподвижной .
Поскольку механика изучает изменение положения тел с течением времени , при проведении опытов обязательно потребуется еще прибор для измерения времени , которым могут быть и обыкновенные часы .
Совокупность тела отсчета , системы координат и прибора для измерения времени (часов) называется системой отсчета .
Имея в распоряжении систему отсчета , мы можем описывать любые движения тел.
Кинематика – это раздел механики, занимающийся описанием движения тел.
Причины , по которым движутся тела, в кинематике не рассматриваются .
§2. Движение материальной точки.
Для описания движения тела достаточно описать движение всех его точек , которые вообще-то могут двигаться по-разному, особенно, если мы рассматриваем жидкие или газообразные тела. Поэтому поговорим сначала о том, как в механике описывается движение одной точки . В этом разделе мы по-прежнему будем употреблять слово «тело», но понимать под ним будем только одну материальную точку .
Траектория движения – это линия , по которой движется материальная точка .
Движение точки может быть прямолинейным или криволинейным .
Прямолинейное движение – это движение по прямой линии .
Криволинейное движение – это движение по кривой линии .
Физические величины , используемые для описания движения материальной точки.
Перемещение.
Предположим, что тело, двигаясь по некоторой траектории, переместилось за промежуток времени D t из точки A в точку B . (Рис.) Говоря о точках A и B , мы имеем ввиду не материальные точки (которые мы называем здесь телами), а точки в пространстве .
Для того, чтобы определить в какую точку пространства переместилось тело за промежуток времени D t , нам совсем не обязательно знать всю траекторию. Достаточно указать, в каком направлении и на какое расстояние переместилось тело за это время. Поэтому в механике ввели специальную физическую величину – перемещение .
Перемещение – это физическая величина,
числовое значение которой равно расстоянию между начальной и конечной точками траектории,
а направление совпадает с направлением от начальной точки траектории к конечной .
Перемещение является векторной величиной.
Обозначение – S .
Единица измерения в системе СИ – м .
Перемещение изображается на рисунках в виде вектора.
Скорость.
Рассмотрим вначале частный случай прямолинейного равномерного движения.
Словосочетание «равномерное движение» означает, что тело за равные промежутки времени проходит равные расстояния. Иными словами, тело не ускоряет и не замедляет своего движения.
Скорость тела при прямолинейном равномерном движении – это физическая величина, равная отношению перемещения S к промежутку времени D t , за который это перемещение было совершено.
Обозначение – v .
Единица измерения в системе СИ – м/с .
В виде математической формулы это определение можно записать следующим образом: 
(1)
Скорость является векторной величиной.
Числовое значение скорости равно отношению модуля перемещения S к промежутку времени D t ,
а направление совпадает с направлением перемещения S .
Физический смысл скорости.
Скорость характеризует быстроту движения тела (как быстро тело перемещается).
При прямолинейном равномерном движении скорость – постоянная величина. Направление скорости не меняется, числовое значение также постоянно. Математически это записывается следующим образом: v = const .
В общем случае движение может быть криволинейным и неравномерным . Тогда скорость не будет постоянной величиной, ее числовое значение и направление будут меняться.
Рассмотрим какую-нибудь криволинейную траекторию.
Если мы рассмотрим очень маленький промежуток времени D t , то за это время тело не успеет сильно изменить направление своего движения и этот маленький участок траектории можно будет считать почти прямым .
При неравномерном движении может меняться не только направление, но и само числовое значение скорости. Но если мы рассмотрим очень маленький промежуток времени D t , то за это время значение скорости не успеет сильно измениться, поэтому движение в течение этого времени можно будет считать
почти равномерным .
Эти рассуждения приводят нас к выводу, что если выбирать промежуток времени D t очень маленьким , то движение тела в течение этого времени можно считать прямолинейным и равномерным . А значит, подходит определение скорости, которое мы давали ранее. Разделяя мысленно время движения тела на такие маленькие промежутки D t , мы сможем определить скорость тела в течение всего времени.
Таким образом, в общем случае определение скорости будет следующим.
Скорость тела – это физическая величина, равная отношению перемещения S к промежутку времени D t , за который это перемещение было совершено.
Промежуток времени D t выбирается настолько малым , чтобы движение в течение этого времени можно было считать прямолинейным и равномерным .
Для скорости остается также справедливой формула (1).
Ускорение.
Рассмотрим вначале частный случай равноускоренного движения.
Словосочетание «равноускоренное движение» означает, что за равные промежутки времени скорость тела меняется на одну и ту же величину .
Ускорение тела при равноускоренном движении – это физическая величина, равная отношению изменения скорости D v к промежутку времени D t , за который это изменение произошло.
Обозначение – a .
Единица измерения в системе СИ – м/с 2 .
В виде математической формулы это определение можно записать следующим образом:
(2)
Ускорение является векторной величиной, т. е. характеризуется как числовым значением , так и направлением .
Физический смысл ускорения.
Ускорение характеризует быстроту изменения скорости .
При равноускоренном движении ускорение – постоянная величина. Направление и числовое значение ускорения не меняются ( a = const ).
В общем случае движение может быть неравноускоренным . Тогда ускорение не будет постоянной величиной, его числовое значение и направление будут меняться.
Но если мы рассмотрим очень маленький промежуток времени D t , то за это время ускорение тела не успеет сильно измениться, поэтому движение в течение этого промежутка времени можно считать почти равноускоренным .
А значит, подходит определение ускорения, которое мы давали ранее. Разделяя мысленно время движения тела на такие маленькие промежутки D t , мы сможем определить ускорение тела в течение всего времени движения.
Таким образом, в общем случае определение ускорения будет следующим.
Ускорение тела – это физическая величина, равная отношению изменения скорости D v к промежутку времени D t , за который это изменение произошло.
Промежуток времени D t выбирается настолько малым , чтобы движение в течение этого времени можно было считать равноускоренным .
Для ускорения остается также справедливой формула (2).
§3. Поступательное и вращательное движение твердого тела.
До сих пор мы говорили только о движении одной материальной точки . Теперь же рассмотрим движение всего тела в целом.
В нашем рассмотрении мы ограничимся только твердыми телами . Отличительным свойством любого твердого тела является то, что оно всегда имеет определенную форму и объем . Движение твердого тела может быть довольно своеобразным и сложным. Но существует два простых типа движения, которые играют в механике важную роль, – поступательное и вращательное .
Любое сколь угодно сложное движение твердого тела можно представить как сочетание поступательного и вращательного движений. Поэтому, если мы умеем описывать поступательное и вращательное движения, мы сможем описать и любое другое движение твердого тела.
Поступательное движение – это движение, при котором все точки тела движутся одинаково .
Примеры поступательного движения
Пунктиром обозначены траектории точек тела. Обратите внимание, что траектории всех точек тела одинаковы .
При поступательном движении все точки тела движутся одинаково, поэтому описание движения сводится к описанию движения одной произвольной точки тела. В этом случае мы можем говорить о скорости и ускорении всего тела целиком , поскольку эти величины будут одинаковы для всех его точек.
Вращательное движение – это движение, при котором все точки тела движутся по окружностям , центры которых лежат на одной прямой .
Эту прямую называют осью вращения .
Плоскости окружностей перпендикулярны оси вращения .
Примеры вращательного движения.
Траектории всех точек являются окружностями с разными радиусами.
Ось вращения направлена перпендикулярно плоскости рисунка
Траектории всех точек являются окружностями с разными радиусами.
MN – ось вращения .
При вращательном движении все точки тела движутся по-разному – с разной скоростью, с разным ускорением, и говорить о скорости и ускорении тела как единого целого мы уже не можем . Поэтому для описания вращательного движения используются свои физические величины – угловая скорость и угловое ускорение . Мы коснемся только первой из них.
Угловая скорость – это физическая величина, равная отношению угла a поворота тела при вращательном движении к промежутку времени D t , за который это поворот был совершен.
Промежуток времени D t выбирается настолько малым , чтобы вращательное движение в течение этого времени можно было считать равномерным .
Обозначение – w .
Единица измерения в системе СИ – радиан / с .
В виде математической формулы это определение можно записать следующим образом:
(3)
Вверх–На главную–Ввернуться к списку
||Учебный комбинат||О лаборатории||Выбор профессии||Высшее образование||Среднее специальное||Справочное пособие||Новости||Карта сайта||Контакты||Web-мастеру||
www.techmind.narod.ru
| Равнопеременное движение. Ускорение. | |
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением. | |
Обозначим: – вектор начальной скорости, – изменение скорости, а Δt – промежуток времени. Пусть Δt1= Δt2=Δt3=…, тогда по определению | |
Следовательно,
Т.о., это характеристика движения. | |
Если t0=0, то | |
УСКОРЕНИЕ – физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло. | |
Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ – м/с2. | Например, ускорение равно 5 м/с2 – это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения. |
В случае не равнопеременного движения: тогда мгновенное ускорение | |
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает. | Условие р.у.д. –. |
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается. | Условие р.з.д. – . |
Графики равнопеременного движения. | |
или – в проекциях; или – через модули. | |
Линейная функция. График – прямая. | |
Движения, совпадающие с направлением координатной оси:
| |
Перемещение при равнопеременном движении. | |
Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению. | |
Решение основной задачи механики для р.у.д. : | |
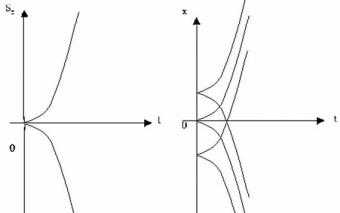
Графики перемещения и координаты. | |
Функции и – квадратичные. График – парабола! | |
 | |
www.eduspb.com
