Векторная величина в физике. Примеры векторных величин
Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Как отличить скалярную величину от векторной?
Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.
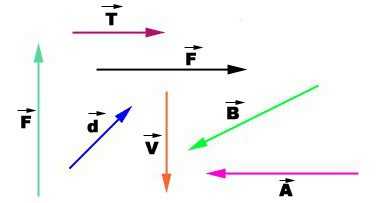
Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.
При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.
Какие действия чаще всего выполняются с векторами?
Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.
Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.
Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Какие векторы изучают в физике?
Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.
| Обозначение в формуле | Наименование |
| v | скорость |
| r | перемещение |
| а | ускорение |
| F | сила |
| р | импульс |
| Е | напряженность электрического поля |
| В | магнитная индукция |
| М | момент силы |
Теперь немного подробнее о некоторых из этих величин.
Первая величина — скорость
С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.
Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.
Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.
Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.
Вторая величина — сила
Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.
| Сила | Точка приложения | Направление |
| тяжести | центр тела | к центру Земли |
| всемирного тяготения | центр тела | к центру другого тела |
| упругости | место соприкосновения взаимодействующих тел | против внешнего воздействия |
| трения | между соприкасающимися поверхностями | в сторону, противоположную движению |
Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.
Третья величина — перемещение
Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.
Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Четвертая величина — ускорение
Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.
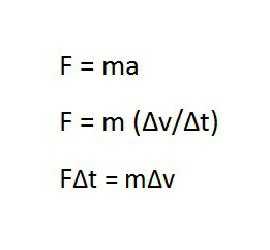
Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.
В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.
Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.
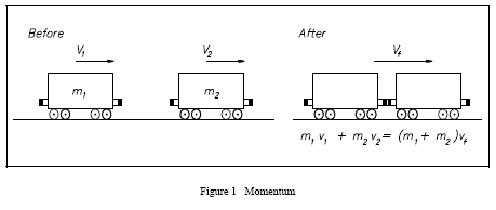
Задача о неупругом ударе
Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона – 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы “вагон-платформа” после удара.
Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. По условию задачи необходимо узнать значение скорости v.
Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.
В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.
Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.
Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.
Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.
Ответ. Скорость вагона с платформой равна 0,75 м/с.
Задача с разделением тела на части
Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?
Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2.
Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.
В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.
Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м/с.
Ответ. Скорость маленького осколка равна 25 м/с.
Задача про выстрел под углом
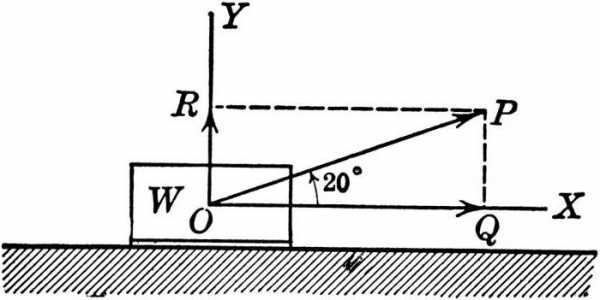
Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.
Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.
За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.
Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.
Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = – Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.
Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.
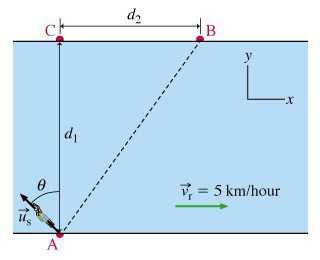
Задача о переправе через реку
Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.
Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2).
2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
v = √(v22 – v12), тогда t = l / (√(v22 – v12)).
Ответ. 1). s = l * (v1 / v2), 2). sin α = v1 / v2, t = l / (√(v22 – v12)).
fb.ru
Вопрос 1
Система отсчёта— это совокупность тел отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.
Путь– длина траектории.
Радиус-вектор— вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Перемещение— изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ).
Скорость— векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
Ускорение— производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки при её движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Ускорение2– это векторная физическая величина, характеризующая быстроту изменения скорости по величине и направлению.
Вопрос 2
Угловое перемещение — векторная величина, характеризующая изменение угловой координаты в процессе её движения.
Угловая скорость— векторная величина, характеризующая быстроту вращения материальной точки. Вектор направлен вдоль оси вращения таким образом, чтобы, смотря с его конца, вращение казалось происходящим против часовой стрелки.
Угловое ускорение— псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
Вектор углового ускорения направлен вдоль оси вращения (в сторону W(омега) при ускоренном вращении и противоположноW(омега)— при замедленном).
При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости по времени.
Существует связь между тангенциальным и угловым ускорениями:
где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/с2 .
Связь между линейными и угловыми величинами, характеризующими движение:
Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют
свое направление и зависят от угловой скорости ω и расстояния r соответствующей точки до оси вращения.
Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ. Поделим обе части равенства на
Переходя к пределам при , получим или .
Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. По определению
ускорения, или
что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси
вращения. Формула устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны
друг к другу.
Ускорение при криволинейном движении:
При криволинейном движении точки направление ее скорости все время изменяется, а модуль скорости может как изменяться, так и оставаться постоянным. Но даже если модуль скорости не изменяется, ее все равно нельзя считать постоянной. Ведь скорость – величина векторная, а для векторных величин модуль и направление одинаково важны. Поэтому криволинейное движение всегда движение ускоренное.
С изменением скорости по модулю мы уже знакомы. Ведь при равноускоренном прямолинейном движении изменяется именно модуль скорости. И мы знаем, что в этом случае вектор ускорения направлен вдоль вектора скорости или против него, а модуль ускорении определяется изменением модуля скорости в единицу времени. Так как нам это уже известно, то в дальнейшем мы будем рассматривать только такое криволинейное движение, при котором модуль скорости остается все время постоянным, так что ускорение будет связано только с изменением направления вектора скорости. Как направлено и чему равно это ускорение?
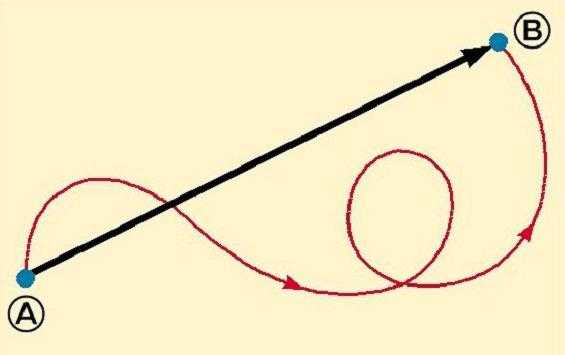
И модуль, и направление ускорения должны, очевидно, зависеть от формы криволинейной траектории. Но нам не придется рассматривать каждую из бесчисленных форм криволинейных траекторий. На рисунке 1 показана сложная траектория, по которой движется тело. Из рисунка видно, что отдельные участки криволинейной траектории представляют собой приблизительно дуги окружностей, изображенных тонкими линиями. Например, участки KL или ВМ – это дуги окружностей малых радиусов, участок EF – это дуга окружности большого радиуса.
Таким образом, движение по любой криволинейной траектории можно представить как движение по дугам некоторых окружностей. Поэтому задача нахождения ускорения при криволинейном движении сводится к отысканию ускорения при равномерном движении тела по окружности.
studfiles.net
Векторная величина в физике. Примеры векторных величин

Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Как отличить скалярную величину от векторной?
Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.
Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.
При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.
Какие действия чаще всего выполняются с векторами?
Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.
Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.
Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Какие векторы изучают в физике?
Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.
Теперь немного подробнее о некоторых из этих величин.
Первая величина — скорость
С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.
Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.
Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.
Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.
Вторая величина — сила
Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.
Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.
Третья величина — перемещение
Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.
Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Четвертая величина — ускорение
Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.
Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.
В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.
Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.
Задача о неупругом ударе
Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара.
Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. По условию задачи необходимо узнать значение скорости v.
Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.
В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.
Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.
Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.
Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.
Ответ. Скорость вагона с платформой равна 0,75 м/с.
Задача с разделением тела на части
Условие. С
teora-holding.ru
Скорость – векторная величина — Науколандия
Скорость тела можно определить как расстояние, которое это самое тело проходит за единицу времени. В системе СИ измеряется в м/с (метрах в секунду). Однако в физике скорость рассматривают как расстояние, которое тело проходит
Также нередко в физике понятие «скорость» заменяют на «вектор скорости». Однако часто в русском языке под просто «скоростью» понимают как раз векторную величину. В английском есть два понятия скорости: velocity — скорость как векторная величина, speed – скорость как скалярная величина, обозначающая быстроту перемещения.
Чтобы указать перемещение тела за единицу времени (т. е. его скорость), надо показать 1) насколько переместилось тело за единицу времени и 2) в каком направлении.
На графиках зависимости координаты тела от времени отражается не только скорость тела, но и направление скорости тела. Так, если координата с течением времени увеличивается, то тело движется в положительном направлении. Если координата с течением времени уменьшается, то тело движется в отрицательном направлении. В первом случае скорость будет положительной величиной, во втором отрицательной. Таким образом и отсюда следует, что скорость — векторная величина.
Для прямолинейного равномерного движения координата (x) тела в момент времени t определяется по формуле x = x0 + vt. Здесь x0
Ниже в системе координат изображены графики движения трех тел. По графикам видно, как с течением времени менялись координаты тел. Тело, чей график изображен зеленым цветом, двигалось в положительном направлении оси X (которая изображена вертикально), так как чем больше секунд проходило, тем координата x тела становилась больше. То же самое можно сказать о движении тела, чей график синий. Оранжевый график показывает, что тело двигалось в отрицательном направлении оси X (по вертикали вниз), так как с каждой последующей секундой движения его координата уменьшалась.
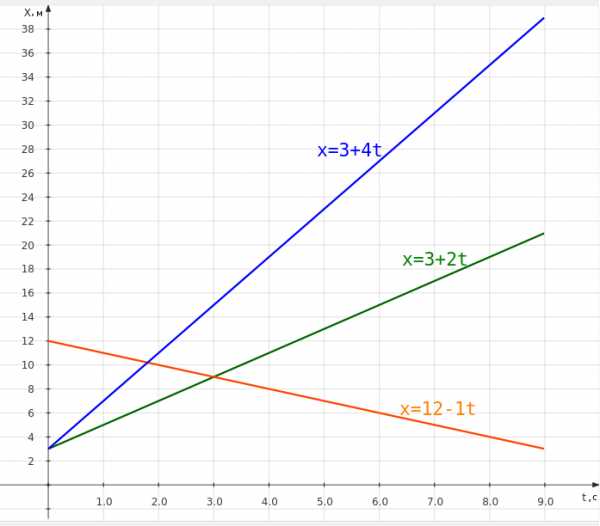
«Синее» тело двигалось быстрее «зеленого», так как его график имеет более крутой подъем, т. е. координата с каждой секундой менялась сильнее. Это можно увидеть и по формулам. У одного тела v = 2 м/с, у другого v = 4 м/с. Векторная скорость «оранжевого» тела равна -1 м/с. Минус говорит, что оно двигалось в противоположном положительному направлению. Модуль же скорости равен 1 м/с.
Минус перед численным значением скорости вовсе не значит, что тело двигается медленнее, чем то, у которого плюс. Так тело, имеющее вектор скорости -10 м/с, движется быстрее, чем тело, у которого скорость равна 9 м/с. Минус отражает лишь то, что тело движется в обратном направлении.
То, что скорость в физике принимают за векторную величину, есть в том числе следствие того, что в зависимости от направления движения изменение координаты тела на графике может быть как положительной, так и отрицательной величиной. Изменение координаты находится как разность между последующим и предыдущим моментом времени. Если, например, тело в момент времени через 5 с от начала измерения было в точке с координатой 12 м, а через 6 с — в точке с координатой 16 м, то изменение равно 16 – 12 = 4 м (величина положительная). Если же тело сначала было в точке 12 м, а потом 8 м, то 8 – 12 = -4 м (величина отрицательная).
scienceland.info
Векторная физическая величина Википедия
Ве́кторная величина́ — физическая величина, являющаяся вектором (тензором ранга 1). Противопоставляется с одной стороны скалярным (тензорам ранга 0), с другой — тензорным величинам (строго говоря — тензорам ранга 2 и более). Также может противопоставляться тем или иным объектам совершенно другой математической природы.
В большинстве случаев термин вектор употребляется в физике для обозначения вектора в так называемом «физическом пространстве», то есть в обычном трёхмерном пространстве классической физики или в четырёхмерном[1] пространстве-времени в современной физике (в последнем случае понятие вектора и векторной величины совпадают с понятием 4-вектора и 4-векторной величины).
Употребление словосочетания «векторная величина» практически исчерпывается этим. Что же касается употребления термина «вектор», то оно, несмотря на тяготение по умолчанию к этому же полю применимости, в большом количестве случаев всё же весьма далеко выходит за такие рамки. Об этом см. ниже.
Употребление терминов вектор и векторная величина в физике[ | ]
В целом в физике понятие вектора практически полностью совпадает с таковым в математике. Однако есть терминологическая специфика, связанная с тем, что в современной математике это понятие несколько излишне абстрактно (по отношению к нуждам физики).
В математике, произнося «вектор» понимают скорее вектор вообще, то есть любой вектор любого сколько угодно абстрактного линейного пространства любой размерности и природы, что, если не прилагать специальных усилий, может приводить даже к путанице (не столько, конечно, по существу, сколько по удобству словоупотребления). Если же необходимо конкретизировать, в математическом стиле приходится или говорить довольно длинно («вектор такого-то и такого-то пространства»), или иметь в виду подразумеваемое явно описанным контекстом.
В физике же практически всегда речь идёт не о математических объектах (обладающих теми или иными формальными свойствами) вообще, а об определённой их конкретной («физической») привязке. Учитывая эти соображения конкретности с соображениями краткости и удобства, можно понять, что терминологическая практика в физике заметно отличается от математической. Однако она не входит с последней в явное противоречие. Этого удаётся достичь несколькими простыми «приемами». Прежде всего, к ним относится соглашение об употребление термина по умолчанию (когда контекст особо не оговаривается). Так, в физике, в отличие от математики, под словом вектор без дополнительных уточнений обычно понимается не «какой-то вектор любого линейного пространства вообще», а прежде всего вектор, связанный с «обычным физическим пространством» (трёхмерным пространством классической физики или четырёхмерным пространством-временем[2] физики релятивистской). Для векторов же пространств, не связанных прямо и непосредственно с «физическим пространством» или «пространством-временем», как раз применяют специальные названия (иногда включающие слово «вектор», но с уточнением). Если вектор некоторого пространства, не связанного прямо и непосредственно с «физическим пространством» или «пространством-временем» (и которое трудно сразу как-то определённо охарактеризовать), вводится в теории, он часто специально описывается как «абстрактный вектор».
Всё сказанное ещё в большей степени, чем к термину «вектор», относится к термину «векторная величина». Умолчание в этом случае ещё жёстче подразумевает привязку к «обычному пространству» или пространству-времени, а употребление по отношению к элементам абстрактных векторных пространств скорее практически не встречается, по крайней мере, такое применение видится редчайшим исключением (если вообще не оговоркой).
В физике векторами чаще всего, а векторными величинами — практически всегда — называют векторы двух сходных между собою классов:
- в классической физике (классической механике, электродинамике в классической трёхмерной формулировке и в других областях физики, преимущественно сформировавшихся до начала XX века) векторными величинами или просто векторами называют, как правило, векторы обычного трёхмерного пространства — то есть обычные «геометрические» векторы или, быть может, отличающиеся от таковых на скалярный множитель (в том числе и на множитель размерный). Хотя в этих областях физики фактически и применялись разнообразные объекты, осознаваемые нынешней математикой как векторы — в физической терминологии это почти не получило отражения (так например, преобразование Фурье в классической электродинамике и классической теории сплошных сред весьма интенсивно применяется, но традиционно почти не рассматривается в контексте классической с использованием слова «вектор» применительно к функциям, хотя с математической точки зрения это было бы вполне законно[3]). Пожалуй, единственным явным исключением из правила является достаточно свободное векторами элементов фазового или конфигурационного пространств[4].
- в релятивистской физике[5] (начиная с Пуанкаре, Планка и Минковского) и, в значительной степени, в современной теоретической физике под векторами и векторными величинами понимаются прежде всего векторы четырёхмерного пространс
ru-wiki.ru
