В чем заключается физический смысл закона электромагнитной индукции – запишите формулу закона электромагнитной индукции в чем заключается физический смысл закона электромагнитной индукции?

Kvant. Правило потока — PhysBook

Лившиц М. Закон электромагнитной индукции или «правило потока»? //Квант. — 1998. — № 3. — С. 37-38.

По специальной договоренности с редколлегией и редакцией журнала “Квант”

В физике возможны (хотя и редко) ситуации, когда одна и та же формула допускает различное содержание, т.е. описывает разные по сути физические законы. Рассмотрим один такой случай, связанный со знаменитым законом электромагнитной индукции, открытым Фарадеем.

«Правило потока» как объединение двух законов

Физический смысл закона Фарадея заключается в том, что изменяющееся во времени магнитное поле порождает вихревое электрическое поле. А именно, при изменении во времени магнитного потока (Ф), пронизывающего поверхность, ограниченную замкнутым неподвижным проводником, в этом проводнике индуцируется ЭДС (ε_i), равная по величине и противоположная по знаку скорости изменения этого потока:

\(~\varepsilon_i = -\frac{\Delta \Phi}{\Delta t}\) . (*)

Это соотношение называют также «правилом потока».

Однако формулу (*), называя по-прежнему законом электромагнитной индукции, в ряде учебников, в том числе и школьных, понимают более широко, включая еще одну причину возникновения ЭДС в проводящем контуре. Этой причиной является сила Лоренца, т.е. сила, действующая на движущийся заряд в магнитном поле. Величина этой силы равна

\(~F_L = q \upsilon B \sin \alpha\) ,

где q – величина заряда, υ – скорость его движения, В — модуль вектора магнитной индукции поля, в котором движется заряд, α — угол между векторами \(~\vec \upsilon\) и \(~\vec B\). Направление силы Лоренца определяется известным правилом левой руки.

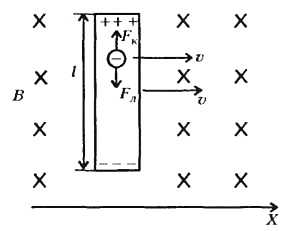
Рис. 1

Рассмотрим простейший случай движения проводника в магнитном поле, показанный на рисунке 1. Под действием силы Лоренца свободные электроны в проводнике (пластинке) перемещаются так, что нижний конец пластинки заряжается отрицательно, а верхний – положительно. Это происходит до тех пор, пока возникающее из-за смещения электронов электрическое поле не начнет действовать на электроны кулоновской силой, равной по величине и противоположной по направлению силе Лоренца. Таким образом действие силы Лоренца на свободные заряды проводника, движущегося в магнитном поле, приводит к возникновению ЭДС индукции. Хотя эта ЭДС не имеет никакого отношения к закону электромагнитной индукции Фарадея, оказывается, что ее можно описать точно такой же формулой. Действительно, напряженность наведенного в проводнике электрического поля равна

\(~E = -\frac{F_L}{q} = – \upsilon B\) ,

а ЭДС индукции –

\(~\varepsilon_i = El = – \upsilon Bl = -\frac{\Delta x}{\Delta t} Bl = -\frac{\Delta \Phi}{\Delta t}\) .

Но в данном случае под ΔФ понимается не величина изменения во времени магнитного потока, пронизывающего данный контур (как в законе Фарадея), а величина магнитного потока, пересекаемого движущимся проводником за время Δt. Для замкнутого контура, перемещающегося или деформируемого в магнитном поле, под Δ

Ф понимается происходящее при этом изменение магнитного потока через этот контур.

Обобщение формулы ЭДС электромагнитной индукции, или «правила потока», на движение проводника в магнитном поле (говорят еще – на явление пересечения проводником линий магнитной индукции) можно использовать при решении широкого круга задач – для сколь угодно сложной конфигурации проводящего контура и для любого характера движения его частей (надо только применить этот расчет к отдельным элементам сложного контура и просуммировать результат). Часто гораздо удобнее вычислять величину ЭДС, индуцируемой при движении проводника в магнитном поле, пользуясь «правилом потока», а не прямым вычислением работы силы Лоренца.

Итак, «правило потока» утверждает, что ЭДС в контуре равна взятой с обратным знаком скорости изменения магнитного потока через данный контур независимо от того, меняется ли величина потока из-за изменения магнитного поля во времени при неподвижном контуре, или в результате перемещения или деформации контура, или из-за того и другого вместе.

Парадоксы, парадоксы…

Так может быть, и не стоит различать причины возникновения ЭДС индукции и считать «правило потока» фундаментальным обобщением закона электромагнитной индукции? Оказывается, стоит, иначе такое отношение к «правилу потока» может вести к парадоксам. Вот несколько примеров.

1) Магнитный поток, пронизывающий контур, остается неизменным\[~\frac{\Delta \Phi}{\Delta t} = 0\], а ЭДС создается (рис.2)

.

Рис. 2

Когда медный диск вращается, контур тока, казалось бы, не изменяется, проходя в пространстве по диску от контакта К к его оси, следовательно, магнитный поток через контур остается постоянным. Но физически эта часть контура осуществляется меняющимися в процессе вращения участками диска, поэтому на свободные электроны в диске, обладающие из-за его вращения скоростью, действует сила Лоренца и возникает ЭДС индукции.

2) Изменение магнитного потока сквозь контур не приводит к возникновению ЭДС индукции (рис.3).

Рис. 3

При повороте металлических пластин с несколько изогнутыми поверхностями соприкосновения, помещенных в однородное магнитное поле, перпендикулярное их плоскости, на некоторый угол магнитный поток через цепь, замыкающуюся в пластинах по точечным линиям, изменяется на большую величину. Однако поворот пластин связан с незначительным их перемещением, при котором произведение

υB в формуле для силы Лоренца близко к нулю, поэтому ЭДС индукции практически отсутствует.

В чем же причина этих парадоксов?

В тех случаях, когда справедлив закон электромагнитной индукции, ЭДС существует вдоль данного геометрического контура независимо от того, материализуется этот контур или нет. В противоположность этому, для существования ЭДС индукции, порождаемой силой Лоренца, совершенно необходимо, чтобы контур был овеществлен, т.е. представлял собой проводник. Именно в этом и состоит принципиальное различие явлений возникновения ЭДС индукции, вызываемых действием двух разных законов, объединенных одной формулой «правила потока»-. Эта формула и оказывается именно правилом, а не законом. Но «нет правил без исключений». Вот мы и познакомились с исключениями из «правила потока».

А как избежать ошибок при использовании такого удобного правила и не наткнуться как раз на исключение?

Оказывается, имеется надежный ориентир: необходимо проверять, чтобы все время сохранялось точное соответствие между физическим контуром, состоящим из проводников, и геометрическим контуром, по которому вычисляется наводимая ЭДС. При нарушении такого соответствия необходимо вычисления производить раздельно: по закону Фарадея или непосредственно с помощью силы Лоренца. Иначе, как показывают приведенные выше примеры, возможны ошибки.

Примечание редактора

Тот факт, что две физически различные ситуации описываются одним и тем же законом, отнюдь не является случайным. Он находит полное объяснение в теории относительности Эйнштейна. Так, при равномерном приближении проводящего контура к неподвижному магниту возникновение тока в контуре объясняется действием силы Лоренца. Но если перейти в систему отсчета, связанную с контуром, то возникновение тока объясняется действием вихревого электрического поля. Подробнее об этом рассказывается, например, в статье А.Черноуцана «Электромагнитная индукция и принцип относительности», опубликованной в Приложении к журналу «Квант» №5/95.

www.physbook.ru

В чем заключается явление электромагнитной индукции

В различных электротехнических устройствах, например, в электрических машинах, используется явление, которое носит название электромагнитная индукция (ЭМИ). В чём же оно заключается?

Открытие

М. Фарадей также увлекался химическими экспериментами

ЭМИ была открыта в 1831 году англичанином М. Фарадеем.

В чем же заключается явление электромагнитной индукции? Смысл открытия состоял в обнаружении появления тока в проводнике при пересечении им магнитного поля (МП). Опыт Фарадея включал создание меняющегося МП в катушке с намотанным на ней проводом. В расположенной рядом с первой второй катушке появилась ЭДС, которая фиксировалась вольтметром.

Закон ЭМИ

Физик открыл, что возникающая в проводнике ЭДС пропорциональна скорости изменения МП, проходящего через проводник. Оказалось, что причина изменения потока не имеет значения. Он может изменяться при движении проводника в МП или при воздействии переменного МП на неподвижный проводник.

Проведя несколько опытой, учёный вывел закон электромагнитной индукции

Математически закон Фарадея имеет следующий вид:
е= -∆Ф/∆t,

где:

• е· – ЭДС;
• Ф — МП;
• t –время.

Знак минус соответствует правилу Ленца, по которому возникающий в результате индукции ток противодействует изменению основного МП.

Использование явления

На применении закона ЭМИ создано большое количество различных устройств и приборов. Наиболее распространенными и важными для промышленности являются электродвигатели, электрогенераторы, трансформаторы.

В статоре электродвигателя переменного тока, например, создается переменное магнитное поле, которое генерирует ток в роторе.

При взаимодействии МП статора и ротора возникает вращающий момент

В трансформаторе переменный ток создает изменяющееся МП, которое пронизывает вторичную обмотку. В результате этого во вторичной обмотке генерируется ЭДС. Изменяя соотношение числа витков обмоток можно получить повышающий или понижающий напряжение трансформатор.

Явление ЭМИ используется также в индукционных печах, различных электромагнитных датчиках. На основе этого явления создан магнитный газовый генератор, в котором в качестве замкнутой рамки используется токопроводящий газ.

ЭМИ, связанная с воздействием изменяющегося магнитного поля на проводник, была открыта Фарадеем еще в девятнадцатом веке. На использовании этого явления построены различные электротехнические устройства и приборы, которые широко применяются в современном мире.

Оцените статью: Поделитесь с друзьями!

elektro.guru

40) Явление электромагнитной индукции

Явление электромагнитной индукции заключается в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.

Особенности явления:

1. чем быстрее изменится число линий магнитной индукции, тем больше возникающий ток;

2. независимость явления возникновения индукционного тока от причины изменения числа линий магнитной индукции.

Практическое значение явления:

Фарадей первым сконструировал несовершенную модель генератора электрического тока, превращающего механическую энергию вращения в ток, состоящую из медного диска, вращающегося между полюсами сильного магнита. Зафиксированный гальванометром ток был слаб, но было сделано самое важное: найден принцип построения генераторов тока.

М. Фарадей (1791-1867) открыл явление электромагнитной индукции. Для раскрытия сущности этого явления введем понятие потока вектора магнитной индукции через поверхность площадью дельта S. Эта величина равна произведению модуля вектора магнитной индукции В на площадь AS и косинус угла амежду векторами В и n (нормалью к поверхности):

Произведение В • cos а= В_nпредставляет собой проекцию вектора магнитной индукции на нормаль к элементу площади. Поэтому дельта Ф = В_п• AS. Поток может быть как положительным, так и отрицательным в зависимости от угла а.

Если магнитное поле однородное, то поток через плоскую поверхность площадью S равен:

В замкнутом проводящем контуре возникает ток при изменении магнитного потока, пронизывающего поверхность, ограниченную этим контуром. Этот ток получил название индукционного тока, а само явление возникновения тока в проводящем контуре при изменении магнитного потока, пронизывающего поверхность, ограниченную контуром, назвали явлением электромагнитной индукции.

В электрической цепи появляется ток, если на свободные заряды действуют электрические силы. Следовательно, при изменении магнитного потока, пронизывающего поверхность, ограниченную контуром, в контуре возникает электродвижущая сила, ЭДС индукции е_iЗакон электромагнитной индукции утверждает, что ЭДС индукции в замкнутом контуре численно равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

Направление индукционного тока определяется правилом (законом) Э. X. Ленца (1804-1865), которое утверждает: возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, стремится препятствовать тому изменению потока, которое порождает данный ток. Закон Ленца есть следствие закона сохранения энергии.

Дж. Максвеллом было высказано следующее фундаментальное свойство магнитного поля: изменяясь во времени, магнитное поле порождает электрическое поле. Это электрическое поле имеет совсем другую структуру, чем электростатическое. Линии напряженности возникшего электрического поля представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Такое поле называют вихревым электрическим полем. Вихревое электрическое поле действует на электрические заряды, так же как и электростатическое F = q • Е, где E – напряженность вихревого поля. В отличие от статического или стационарного электрического поля работа вихревого поля на замкнутом пути не равна нулю. Вихревое электрическое поле, так же, как и магнитное, непотенциально.

Работа вихревого электрического поля по перемещению единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике.

Если проводник длиной lперемещать в магнитном поле с индукцией В, направленной перпендикулярно скорости перемещения, то магнитная сила Лоренца разделяет электрические заряды проводника и между его концами возникает ЭДС индукции, равная e_i=lvE.

Возникновение изменяющегося магнитного поля создает ЭДС индукции в том контуре, по которому течет ток, создающий это изменяющееся поле. Такое явление назвали самоиндукцией.

Магнитный поток, проходящий через контур, прямо пропорционален силе тока в контуре:

Физическая величина, равная отношению магнитного потока, проходящего через контур, к силе тока в контуре, называется индуктивностьюэтого контура:

ЭДС, возникающая в контуре, при изменении силы тока, протекающего по контуру, называется ЭДС самоиндукции.

По закону электромагнитной индукции ЭДС самоиндукции равна 

За единицу индуктивности в СИ принимается 1 генри (1 Гн), это индуктивность такого контура, в котором при равномерном изменении силы тока в цепи со скоростью 1 А за 1 с возникает ЭДС самоиндукции, равная 1 В:

studfiles.net

Явление электромагнитной индукции – курсовая работа

Описание.

Выдержка из работы.

 
 

Волжский  Институт Строительства и Технологий

(филиал) государственного образовательного  Учреждения

Высшего профессионального образования

«Волгоградский  Государственный Архитектурно-Строительный Университет» 
 
 
 
 
 
 

Курсовая работа 

по дисциплине 
 
 

« Физика» 
 

для студентов  специальности 

«Экономика  и управление на предприятии (строительство)»

сокращённой заочной формы обучения

группа  ЭУП -3-09 
 
 
 
 
 
 
 

                            Выполнил : студент группы ЭУП-3-09

                                                 Шатова Оксана Сергеевна

                                                 №  09341

                                                 Адрес: г. Волжский, ул. Мира, 94-9

                                                                         Вариант № 1

                           Проверил: _______________________

                                              ________________________________

                                                                         ________________________________ 
 
 
 
 

Вариант № 1  
 

План  курсовой работы: 

1. Теория : Явление электромагнитной индукции.
2. Практическая часть.

     Задачи №№ 11, 21, 31, 41, 51, 61, 71, 81, 91, 101. 
 
 
 
 

Литература. 

материалам  пособия “Физика – справочные материалы” Кабардин О.Ф. 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

1. Теоретическая часть.  Явление электромагнитной  индукции. 
 

      Если электрический ток, как показали опыты Эрстеда, создает магнитное поле, то не может ли в свою очередь магнитное поле вызывать электрический ток в проводнике? Многие ученые с помощью опытов пытались найти ответ на этот вопрос, но первым решил эту задачу Майкл Фарадей (1791 — 1867).  
   В 1831 г. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает электрический ток. Этот ток назвали индукционным током. 
   Индукционный ток в катушке из металлической проволоки возникает при вдвигании магнита внутрь катушки и при выдвигании магнита из катушки (рис. 192),

а также  при изменении силы тока во второй катушке, магнитное поле которой  пронизывает первую катушку (рис. 193).

Явление возникновения электрического тока в замкнутом проводящем контуре при изменениях магнитного поля, пронизывающего контур, называется электромагнитной индукцией..Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектростатической природы или о возникновении ЭДС индукции. Количественное описание явления электромагнитной индукции дается на основе установления связи между ЭДС индукции и физической величиной, называемой магнитным потоком. 
   Магнитный поток. Для плоского контура, расположенного в однородном магнитном поле (рис. 194), магнитным потоком Ф через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и на косинус угла между вектором и нормалью к поверхности:

. (54.1)  

Правило Ленца. Опыт показывает, что направление индукционного тока в контуре зависит от того, возрастает или убывает магнитный поток, пронизывающий контур, а также от направления вектора индукции магнитного поля относительно контура. Общее правило, позволяющее определить направление индукционного тока в контуре, было установлено в 1833 г. Э. X. Ленцем. 
   Правило Ленца можно наглядно показать с помощью легкого алюминиевого кольца (рис. 195).

Опыт  показывает, что при внесении постоянного  магнита кольцо отталкивается от него, а при удалении притягивается  к магниту. Результат опытов не зависит от полярности магнита.Отталкивание и притяжение сплошного кольца объясняется возникновением индукционного тока в кольце при изменениях магнитного потока через кольцо и действием на индукционный ток магнитного поля. Очевидно, что при вдвигании магнита в кольцо индукционный ток в нем имеет такое направление, что созданное этим током магнитное поле противодействует внешнему магнитному полю, а при выдвигании магнита индукционный ток в нем имеет такое направление, что вектор индукции его магнитного поля совпадает по направлению с вектором индукции внешнего поля. 
   Общая формулировка правила Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которым вызывается данный ток.  
   Закон электромагнитной индукции. Экспериментальное исследование зависимости ЭДС индукции от изменения магнитного потока привело к установлению закона электромагнитной индукции: ЭДС индукции в замкнутом контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром. 
   В СИ единица магнитного потока выбрана такой, чтобы коэффициент пропорциональности между ЭДС индукции и изменением магнитного потока был равен единице. При этом закон электромагнитной индукции формулируется следующим образом: ЭДС индукции в замкнутом контуре равна модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

.(54.2)

С учетом правила Ленца закон электромагнитной индукции записывается следующим образом:

.(54.3)   

ЭДС индукции в катушке. Если в последовательно соединенных контурах происходят одинаковые изменения магнитного потока, то ЭДС индукции в них равна сумме ЭДС индукции в каждом из контуров. Поэтому при изменении магнитного потока в катушке, состоящей из n одинаковых витков провода, общая ЭДС индукции в n раз больше ЭДС индукции в одиночном контуре:

.(54.4)

       Единица магнитного потока. Единица магнитного потока в Международной системе единиц называется вебером (Вб). Она определяется на основании использования закона электромагнитной индукции. Магнитный поток через площадь, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции 1 В:

, .

Для однородного магнитного поля на основании уравнения (54.1) следует, что его магнитная индукция равна 1 Тл, если магнитный поток через контур площадью 1 м² равен 1 Вб:

, 
 
   .

                Вихревое электрическое поле. Закон электромагнитной индукции (54.3) по известной скорости изменения магнитного потока позволяет найти значение ЭДС индукции в контуре и при известном значении электрического сопротивления контура вычислить силу тока в контуре. Однако при этом остается нераскрытым физический смысл явления электромагнитной индукции. Рассмотрим это явление подробнее.    

Возникновение электрического тока в замкнутом контуре свидетельствует о том, что при изменении магнитного потока, пронизывающего контур, на свободные электрические заряды в контуре действуют силы. Провод контура неподвижен, неподвижными можно считать свободные электрические заряды в нем. На неподвижные электрические заряды может действовать только электрическое поле. Следовательно, при любом изменении магнитного поля в окружающем пространстве возникает электрическое поле. Это электрическое поле и приводит в движение свободные электрические заряды в контуре, создавая индукционный электрический ток. Электрическое поле, возникающее при изменениях магнитного поля, называют вихревым электрическим полем.   

Работа  сил вихревого электрического поля по перемещению электрических зарядов и является работой сторонних сил, источником ЭДС индукции.   

Вихревое  электрическое поле отличается от электростатического  поля тем, что оно не связано с  электрическими зарядами, его линии  напряженности представляют собой  замкнутые линии. Работа сил вихревого электрического поля при движении электри ческого заряда по замкнутой линии может быть отлична от нуля.   

ЭДС индукции в движущихся проводниках. Явление электромагнитной индукции наблюдается и в тех случаях, когда магнитное поле не изменяется во времени, но магнитный поток через контур изменяется из-за движения проводников контура в магнитном поле. В этом случае причиной возникновения ЭДС индукции является не вихревое электрическое поле, а сила Лоренца.   

Рассмотрим  прямоугольный контур в однородном магнитном поле, вектор индукции которого перпендикулярен плоскости контура. Если провод скользит с постоянной скоростью по двум проводникам контура (рис. 196), то за время площадь контура изменяется на величину , а магнитый поток через контур — на .

Поэтому ЭДС индукции в контуре будет  равна 

.(54.5)

В проводнике, движущемся в магнитном  поле, на электрический заряд q действует сила Лоренца:

.

Вычислим  работу силы Лоренца, действующей на электрический заряд q во время полного обхода контура.На пути длиной l работа силы Лоренца равна

.(54.6)

В неподвижных частях контура сила Лоренца равна нулю, поэтому полная работа силы Лоренца при обходе контура зарядом q равна работе силы Лоренца на движущемся участке контура. Рассматривая работу силы Лоренца как работу сторонних сил в контуре, мы получим выражение для ЭДС сторонних сил:

.(54.7)

Совпадение  выражений (54.5). и (54.7) показывает, что  причиной возникновения ЭДС индукции в контуре в этом случае является действие силы Лоренца на заряды в  движущемся проводнике. 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

2. Практическая часть. 

Задача№11  

Точка движется по окружности радиусом  R= 10 см с постоянной тангенциальным ускорением. Найти тангенциальное ускорение точки, если известно, что к концу пятого оборота после начала движения скорость точки равна 79,2 см/с

Решение Тангенциальное  ускорение  а=, но т.к. a= const ,то =– линейная скорость ; =2– угловая скорость ; R- радиус окружности ; N- число оборотов ;   t- время этих оборотов  t= или a=

dipland.ru