В физике графики – .

Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении

Цели урока:

обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения за­дач закрепить полученные знания на практике;

развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;

воспитывающая: воспитание дисциплины и норм поведения, творческого от­ношения к изучаемому предмету; стимулировать активность учащихся.

Методы:

словесный — беседа;

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный (письменный) опрос, решение задач).

Связи:

межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;

внутрипредметные: равномерное и равноускоренное движение.

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

3. Объяснение нового материала.

Скачать этот видеоурок

Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.

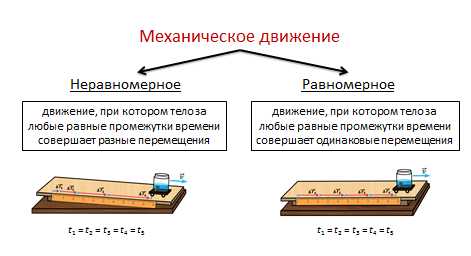
Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.

Если движение равномерное, то:

1. Скорость тела не меняется с течением времени;

2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;

3. Уравнение перемещения имеет вид:

4. И  — кинематическое уравнение равномерного движения.

Для равноускоренного:

1. Ускорение тела не изменяется с течением времени;

2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло

3. Уравнение скорости для равноускоренного движения имеет вид:

4.  — уравнение перемещения для равноускоренного движения;

5. — кинематическое уравнение равноускоренного движения.

Для большей наглядности движение можно описывать с помощью графиков.

Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.

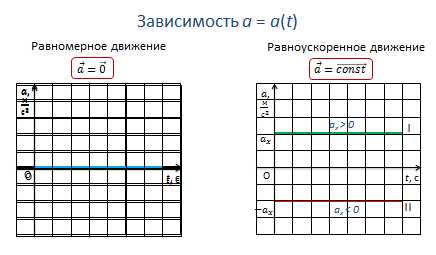
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.

Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.

Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.

Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.

Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.

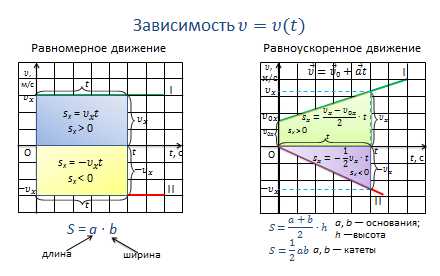
По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.

Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.

Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.

При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v₀ + at, т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.

По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.

При этом проекция перемещения для первого тела будет положительной.

Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.

Проекция перемещения — отрицательна.

Теперь рассмотрим зависимость пройденного пути от времени.

Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.

При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.

При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.

Теперь перейдем к рассмотрению зависимости перемещения от времени.

Рассмотрим равномерное движение.

Т.к. при равномерном движении перемещение линейно зависит от времени (s_x = υ_xt), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.

А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.

Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.

Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.

Для 2-го тела ускорение и начальная скорость тела больше нуля.

Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.

У 4-го тела начальная скорость и ускорение меньше нуля.

Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.

И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.

И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).

Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.

График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.

В случае прямолинейного движения тела графики дви­жения дают полное решение за­дачи механики, так как они позволяют найти поло­жение тела в любой момент времени, в том числе и в моменты времени, предшество­вавшие начальному моменту (если предполо­жить, что тело двигалось с такой же ско­ростью и до начала отсчета времени).

С помощью графика движения можно определить:

1. координаты тела в любой момент времени;

2. путь, пройденный телом за некоторый промежуток времени;

3. время, за которое пройден какой-то путь;

4. кратчайшее расстояние м/у телами в любой момент времени;

5. момент и место встречи и т. д.

По виду графиков зависи­мости координаты от времени можно судить и о скорости дви­жения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изме­нение координаты за одно и то же время).

При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

4. Этап обобщения и закрепления нового материала

И так, сделаем главный вывод.

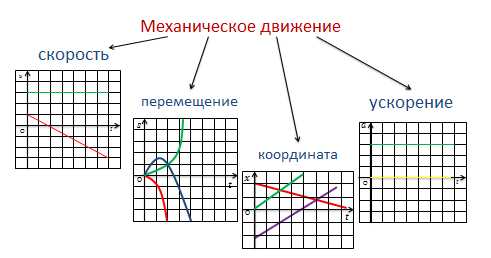
Механическое движение для большей наглядности можно описывать с помощью графиков:

1) Зависимости скорости от времени;

2) Зависимости ускорения от времени;

3) Зависимость координаты тела от времени;

4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

6. Домашнее задание.

videouroki.net

Интегрированный урок (физика + математика) по теме «Графики в физике и математике». 10-й класс

Разделы:
Математика, Физика

Тип урока: интегрированный урок
(математика + физика).

Форма урока: урок-практикум.

Цели урока:

1. Обобщение и систематизация знаний по теме
“Функции и их графики” (линейная, квадратичная,
тригонометрическая)

2. Применение математических знаний и умений в
физике.

3. Закрепление навыков построения графиков.

4. Решение задач графическим способом в физике.

5. Развитие творческих способностей.

6. Умение работать в группе.

Цвет карточки в системе работы на уроке:

• Карточка оранжевого цвета – выполнены все 4
  задания;
• Карточка желтого цвета – выполнены 3 задания;
• Карточка белого цвета – выполнено 2 или менее 2-х
  заданий.

Используемые технические средства: ноутбук,
интерактивная доска (мультимедийный проектор,
экран).

Эпиграф к уроку:

Вряд ли следует объяснять, что одна из
важнейших задач математики — помощь другим
наукам.

Морделл Л.(пишется на доске).

Ход урока

ПЕРВЫЙ УРОК начинается с
организационного момента: дети готовят тетради,
учебники, и класс разбивается на команды.

Математик: Наш урок начнется
сегодня с повторения теории и практики
преобразования графиков функций. Каждая группа
получает листы с заданиями и оценочные листы.
Каждый правильный ответ заносится в оценочный
лист. Вы будете работать в командах. Вам будут
предложены задания, которые необходимо
выполнить быстро и качественно. За каждое
выполненное задание вы будете получать 1 балл.
Баллы, полученные командой во всех заданиях,
суммируются, а по сумме баллов определяется
команда – победитель.

Вводное задание № 1 Разминка (работа с
презентацией): по одному баллу за правильный
ответ индивидуально, но в копилку своей команды.

Физик: Ребята, давайте вспомним: в
чём заключается основная задача механики?
(Определить положение тела в любой момент
времени). Сегодня на уроке мы посмотрим, как при
помощи функции можно решить основную задачу
механики.

Математик: Рассмотрим линейную
функцию и сопоставим математические переменные
с физическими величинами:

Физик: Теперь давайте посмотрим, как
линейная функция применяется в физике. В
кинематике мы с вами изучили два вида движения.
Каких? (Равномерное, равноускоренное). Что такое
равномерное движение? Что такое равноускоренное
движение?

Равномерное движение, если тело двигается с
постоянной скоростью.

Равноускоренное движение — если скорость тела
меняется за любые одинаковые промежутки времени
на одну и ту же величину.

Как определить скорость при таких движениях?

;

Вторая формула показывает, как изменяется
скорость тела в данный момент времени. Скажите,
является ли эта зависимость функцией? Какой?
(Линейной).

Давайте проведём аналогию между
математической записью линейной функции и
физической.

Задание №2. Учащиеся приступают к
выполнению задания в группах, распределив
задания между собой. (Время выполнения — 5 минут.)

По данным уравнениям построить график скорости
движения материальной точки, определить,
характер движения и начальную скорость тела:

;

;

;

;

Через 5 минут командой поднимается карточка
определенного цвета. Проверка со слайда:

Ответ к заданию высвечивается на экране. Каждая
группа проводит исследование своих графиков и
отвечает на вопрос: как двигается тело, быстро
или медленно? В какой момент времени покоится или
останавливается?

Максимально можно получить 5 баллов
(дополнительный балл дается команде, давшей
четкий правильный ответ без наводящих вопросов и
задержек по времени)

Выставление командой своих баллов в оценочный
лист.

Если есть время до звонка, предложить работу с
учебником “Алгебра 9” для повторения
квадратичной функции ко 2-му уроку.

ВТОРОЙ УРОК начинается с проблемной
ситуации: картинка с иллюстрацией свободного
падения тела плюс график зависимости координаты
свободно падающего тела от времени.

Физик: На графике представлена
зависимость координаты свободно падающего тела
от времени. Графиком какой функции она является?
(квадратичной)

Математик: По слайдам повторим
влияние коэффициентов в формуле на расположение
параболы в системе координат.

Физик: Запишем общий вид уравнения
движения тела вдоль прямой.

х = x₀+v₀t+0.5a_x t² с
пояснениями входящих в формулу обозначений.

Задание №3

Учащиеся приступают к выполнению задания (в
группах, распределив их между собой, 5 минут):

Построить график зависимости , если движение тела
описывается уравнением 1, 2, 3, 4;

• построить график функции х = х (t) для 2 и 3 случая,
• объяснить устно отличия этих графиков от
  графика функции :

1. ;

2. ;

3. ;

4. ;

Через 5 мин. поднимается карточка определенного
цвета. Проверка со слайда:

Дети работают по группам, и выполняют задание
№3.

Выполненное задание высвечивается на экране.
Каждая группа проводит исследование своих
графиков и отвечает на вопрос: как двигается
тело, быстро или медленно? В какой момент времени
покоится или остановится.

Выставление командой своих баллов в оценочный
лист.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ.
Презентация учащегося с его пояснениями и
подборкой тематических заданий из материалов
ГИА и ЕГЭ разных лет. Учащиеся отвечают на
вопросы заданий.

Домашнее задание. Перед самостоятельной
работой выдается дифференцированное домашнее
задание с пояснениями (включены 3-4 задания по
математике с физическим смыслом и по физике с
применением математических знаний и умений), и
собираются оценочные листы.

Самостоятельная работа. Учащимся предлагается
занять места за отдельными столами и выполнить
работу по индивидуальным карточкам, находящимся
в конвертах (10-15 минут).

Итог урока. Завершающий этап: учащиеся сдают
самостоятельную работу; объявляются результаты
урока: по результатам, приведенным в оценочных
листах, определяется команда – победитель. За
первое место всем участникам команды ставится
оценка “пять”. За второе — оценка “4”.

Физик: Итак, ребята, мы с вами
убедились на практике, что зависимость изменения
координаты материальной точки с течением
времени при равномерном движении и скорости при
равноускоренном (равнозамедленном) движении
задаются при помощи линейной функции.

Зависимость координаты тела при
равнопеременном движении задается при помощи
квадратичной функции. При гармонических
колебаниях, волновых процессах и в ряде иных
физических ситуаций характеристики процессов
могут задаваться тригонометрической функцией.

Если есть время до звонка, можно предложить
учащимся оценить свою работу на уроке по
пятибальной шкале и выбрать смайлик.

Спасибо всем за отличную работу. Урок окончен.

29.07.2013

xn--i1abbnckbmcl9fb.xn--p1ai

Графики равномерного прямолинейного движения (Ерюткин Е.С.)

На этом уроке мы изучим графики равномерного прямолинейного движения. С помощью графиков движения вы сможете более ясно представить себе картину происходящего с телом. Мы научимся строить графики, используя законы движения, и, наоборот, имея графики, определять по ним параметры движения. Кроме того, мы научимся определять путь, пройденный телом, используя график зависимости скорости тела от времени.

Графическое представление движения очень часто помогает наглядности и пониманию того, как движется тело. На графике удобно показывать, как можно выразить ту или иную величину. Обратите внимание, что для изображения движения необходимо правильно выбрать систему отсчета. Поскольку мы рассматриваем равномерное прямолинейное движение, то за ось абсцисс принимаем ось времени, ось ординат определяет координату тела (см. рис. 1).

Рис. 1. Система отсчета. Зависимость координаты тела от времени

Рассмотрим график движения тела вдоль прямой с положительной скоростью. На рис. 2 представлено две линии. Одна линия (голубого цвета) соответствует движению тела из начала координат . Уравнение этого графика можно записать в виде:  – линейная зависимость координаты от времени. Скорость в данном случае положительна.

Рис. 2. Графики движения тела вдоль прямой с положительной скоростью

Выше первого графика располагается график (зеленого цвета), который соответствует случаю, когда тело начинает свое движение уже не из начала координат, а из какой-либо точки . Данная линия может быть записана в виде: . Тело также будет двигаться пропорционально времени, но в этом случае существует ненулевая начальная координата тела.

Обратите внимание, что угол  характеризует скорость движения (см. рис. 3). Катет  соответствует изменению координаты . Второй катет соответствует расстоянию от  до точки . Тогда, записав определение тангенса угла, получим:

Чем больше угол наклона, тем, соответственно, больше скорость движения тела.

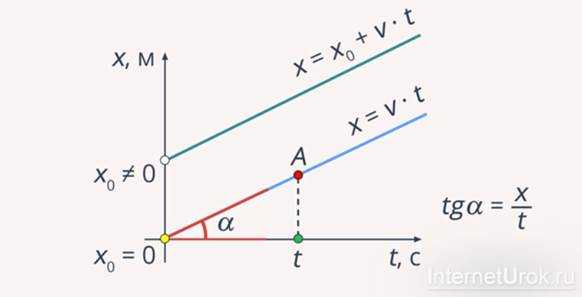
Рис. 3. Угол  характеризует скорость движения.

График движения тела позволяет определить модуль перемещения  (см. рис. 4). Между тем, по графику можно также определить пройденный телом путь: при равномерном движении он равен модулю перемещения тела.

Рис. 4. Модуль перемещения тела

Рассмотрев рис. 5, можем утверждать, что тело двигалось с отрицательной скоростью. Одна линия соответствует движению тела против оси Ох и выходит из начала координат . В данном случае уравнение движения будет иметь вид: . Вторая линия характеризует движение тела не из начала координат, а из какой-то точки . Уравнение движения будет иметь вид: .

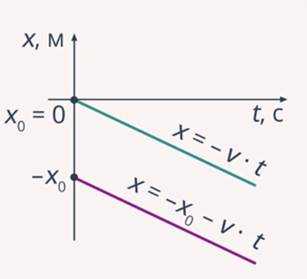
Рис. 5. Графики движения тела вдоль прямой с отрицательной скоростью

Рассмотрим график на рис. 6. В данном случае тело начинает свое движение из точки, которая находится выше начала координат , однако скорость при этом остается отрицательной. Уравнение движения тела будет иметь вид: .

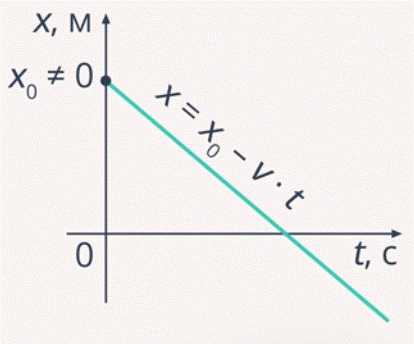
Рис. 6. График движения тела из начальной точки  с отрицательной скоростью

Рассмотрим еще один график движения тела (см. рис. 7).С течением времени, до значения времени , координата тела не меняется,  и только от красной точки график начинает подниматься вверх. Это означает, что за время, равное  тело находилось в состоянии покоя. Его координата в данной системе отсчета не изменялась. И только из точки, обозначенной на рисунке красным цветом, тело начинает двигаться, то есть появляется у тела скорость.

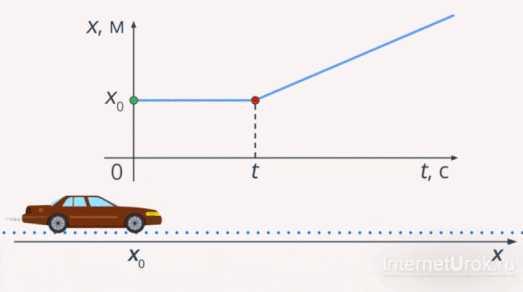
Рис. 7. Движение тела при

На рис. 8 приведен пример графика в системе отсчета с осью абсцисс – осью времени – и осью ординат – осью скорости. Для равномерного прямолинейного движения скорость остается величиной постоянной. Поэтому график скорости такого движения – прямая линия, параллельная оси времени.

Рис. 8. График зависимости скорости от времени при равномерном движении

В заключение урока отметим тот факт, что при помощи графиков очень удобно изобразить и определить пройденный телом путь. Дело в том, что геометрическое толкование пройденного пути – это площадь фигуры, ограниченной с одной стороны осью времени, а с другой стороны – графиком скорости.

Рассмотрим график скорости (см. рис. 9) для равномерного движения – прямая, параллельная оси времени. Возьмем отрезок времени от  до , тогда площадь фигуры  – пройденный телом путь.

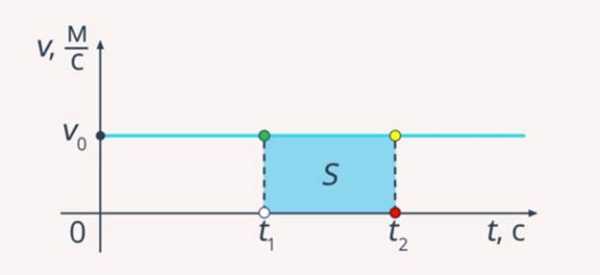
Рис. 9. Геометрический смысл пройденного пути

Заключение

На сегодняшнем уроке мы рассмотрели вопрос изображения движения при помощи графиков и как эти графики необходимо толковать. На следующем занятии мы познакомимся с другими видами движения, в частности с равнопеременным движением.

Список литературы

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
2. А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
3. О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
4. А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Физика для всех (Источник).
2. Википедия (Источник).

Домашнее задание

1. Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.
2. Задачи 21, 22, 24, 27 – сб. задач А.П. Рымкевич, изд. 10.
3. Парашютист спускается со скоростью 18 км/ч. На высоте 1000 метров из его кармана падает шарик от настольного тенниса и летит равномерно со скоростью 54 км/ч. Определите графически, какое время пройдет между приземлением шарика и парашютиста.

Рассмотрите следующие вопросы и ответы на них:

·                     Вопрос. Если измерить угол наклона графика транспортиром и вычислить его тангенс, будет ли это скоростью тела?

·                     Ответ. Нет! Оси времени и координаты несоизмеримы и имеют различные размерности, при этом тангенс угла, вычисленного как отношение катетов, имеет размерность скорости. Тангенс какого-либо определенного угла же, напротив, размерностью не обладает. Для полной ясности попробуйте поменять масштабы единиц на какой-либо из осей. Геометрический угол (измеряемый транспортиром) при этом изменится, а скорость тела – нет.

·                     Вопрос. Можно ли измерять площадь под графиком скорости палеткой?

·                     Ответ. Нет! В этом вопросе можно применить рассуждения, аналогичные предыдущим. При изменении масштабов осей площадь под графиком, определенная при помощи палетки, изменится, а путь, пройденный телом, – нет.

·                     Вопрос. Как определить место и время встречи двух тел?

·                     Ответ. Местом встречи двух тел является точка пересечения их графиков. Спроектировав эту точку на ось времени, вы определите время встречи тел, а на ось координаты – координату встречи двух тел.

·                     Вопрос. Что означает точка пересечения графика зависимости координаты от времени с осью времени?

·                     Ответ. Эта точка – момент времени, в который тело проходит начало отсчета.

interneturok.ru

графики в физике | EOR HELP

Автор конспекта:
Автор(ы): — Лишаева Надежда Александровна

Место работы, должность: —

МОУ — Лицей №2 г.Саратов

Регион: — Саратовская область

Характеристика конспекта:
Уровни образования: — основное общее образование
Уровни образования: — среднее (полное) общее образование

Класс(ы): — Все классы

Предмет(ы): — Физика

Целевая аудитория: — Учитель (преподаватель)

Тип ресурса: — методическая разработка

Краткое описание ресурса: —

методическая разработка занятий по физике. Темы физики рассматриваются через призму графиков: их описание, сравнение, чтение и построение. Графики можно выделить практически в любой теме курса. Соответственно один способ их прочтения дает возможность сравнить различные темы.

Программа курса разбита на блоки, соответствующие разделам механики, изучаемым в 9 классе, что приводит к более глубокому изучению материала. Каждый блок предполагает обобщение и систематизацию основного теоретического материала, практические занятия по решению графических задач.

Программа обеспечивает личностно-ориентированный подход в обучении.

Графический прием решения применим к тем качественным задачам, условия которых формулируются с помощью различных видов иллюстраций. Использование его позволяет получить ответ на вопрос задачи в процессе исследования соответствующего чертежа, графика, схемы, рисунка, фотографии и т.п.

Достоинство этого приема – наглядность и лаконичность решения. Он развивает функциональное мышление школьников, приучает их к точности, аккуратности.

Цели курса:

• Развить интерес к физике и решению физических задач
• Научить школьников рассуждать, сравнивать
• Научить школьников находить общие черты в рассматриваемых явлениях и изучаемых предметах

Задачи курса:

Файлы: графики в физике.docx
Размер файла: 13483 байт.

eorhelp.ru

Применение графических изображений в физике

Слайд 1

Применение графических изображений в физике Выполнил: Прошин Александр , курсант группы 11 Волгоградского техникума водного транспорта им. адмирала флота Н. Д. Сергеева Руководитель: Попова Н. Е., преподаватель математики Волгоградского техникума водного транспорта им. адмирала флота Н. Д. Сергеева

Слайд 2

Актуальность работы: Эту тему мы выбрали для того, чтобы показать связь математики с физикой. Ведь как в математике, так и в физике встречаются задачи, требующие построения графиков. Графики нужны для наглядного решения поставленной задачи. Ведь не всегда удобно решать задачу с помощью ее аналитической модели. В таких случаях строят график зависимости. С его помощью и решают задачу.

Слайд 3

Цели проекта: Обобщить и систематизировать учебный материал, в котором рассматриваются графики математических и физических функций Рассмотреть их применение в физике

Слайд 4

Задачи проекта: Рассмотреть разновидности графиков математических функций Выявить в каких областях физики применяются графики функций Изучить технологию решения прикладных задач по физике с применением графического метода

Слайд 5

1) линейные функции y = ax + b . При b = 0 она принимает вид у = ах. 2) квадратичные функции у= х 2 , 1) степенные функции y = x k , где k – любое действительное число; 2) показательные функции y = а х , где а – любое положительное число, отличное от единицы: а > 0, a  1; 3) логарифмические функции у = log a x , где а – любое положительное число, отличное от единицы: а > 0, a  1; 4) тригонометрические функции y = sin x , y = cos x , y = tg x , y = ctg x ; 5) обратные тригонометрические функции y = arcsin x , y = arccos x , y = arctg x , y = arcctg x . Функция – это зависимость одной переменной величины от другой . Другими словами, взаимосвязь между величинами. Основными элементарными функциями считаются следующие:

Слайд 6

Использование в изучении физики графиков, чертежей и рисунков не только способствует формированию связей учебного материала разных дисциплин курса обучения, но и помогает студентам понять основные факты и закономерности физики.

Слайд 7

Некоторые виды графиков, используемые в физике

Слайд 8

Применение графиков в термодинамике: Сейчас мы наглядно представим применение графиков в термодинамике. В качестве примера используем изопроцессы. Изопроцессы – процессы, протекающие при неизменном значении одного из параметров(температура, объем, давление). Изопроцессы мы будем рассматривать на основе уравнения Клапейрона: P 1 V 1 P 2 V 2 T 1 T 2 =

Слайд 9

Рассмотрим график зависимости P (давления) от T (температуры), при V( объеме) = const График-изохора Тогда уравнение P 1 V 1 P 2 V 2 примет вид P 1 P 2 T 1 T 2 = T 1 T 2 = T P 1 1 5

Слайд 10

Рассмотрим график зависимости V (объема) от T (температуры), при P( давлении) = const График -изобара Тогда уравнение P 1 V 1 P 2 V 2 примет вид V 1 V 2 T 2 T 1 T 2 = = T 1 1 V T 1 5 5

Слайд 11

Рассмотрим график зависимости V (объема) от P (давления), при T( температуре) = const График — изотерма Тогда уравнение P 1 V 1 P 2 V 2 примет вид P 1 V 1 = P 2 V 2 T 1 T 2 = P V 1 1 5 5

Слайд 12

Применение графиков в механике: Графики часто встречаются при описании механического движения. Чаще всего их используют, чтобы найти скорость или путь в определенный момент времени. Наглядным способом сделать это намного удобнее. Существует несколько видов механического движения. Сейчас мы их и рассмотрим.

Слайд 13

Равномерное движение V= S t V t 1 7 7 1 При равномерном движении скорость тела не меняется. На графике мы это видим. V=7 м/с t – изменяется от 0 до 7с

Слайд 14

Равноускоренное движение V= V 0 +at V t 1 5 5 1 Ускорение – это физическая величина, характеризующая быстроту изменения скорости. Ускорение задается формулой: V 0 =0 м/с a=1 м/с 2 a= V t

Слайд 15

Равнозамедленное движение: V= V 0 -at V t 1 5 10 10 5 1 V 0 =10 м/с a=1 м/с 2 t – изменяется от 0 до 10с

Слайд 16

S = V 0 t+ at 2 2 Пройденный путь: Возьмем произвольные значения скорости( V 0 ) и ускорения( a) , и построим график зависимости пути( S) от времени( t) Пусть V 0 =1м/с; a =1м/с 2 1 2 3 4 5 6 S t 24 17,5 12 7,5 4 1,5 1 Теперь рассмотрим пример, когда тело движется с ускорением. На графике мы видим зависимость пройденного пути от времени.

Слайд 17

графическое решение уравнений (ответ даётся точками пересечения кривых) графическое усреднение (определение среднего значения некоторой физической величины) графическая оценка наибольшего и наименьшего значения Типы заданий, решаемые графическим методом:

Слайд 18

В качестве примера решим задачу: Найти точку пересечения и время встречи 2-ух тел, если их движение задано уравнением: x 1 =x 0 +V 0 1 t 1 x 2 =V 0 2 t 2 + at 2 2 Решение x 1 = x 2 t 1 = t 2 так как тела встречаются, следовательно x 0 +V 0 1 t = V 0 2 t + at 2 2 Зададим переменные и построим график x 0 =5м V 0 1 =1м/с V 0 2 =5м/с a =2м/с 2 t=5 с

Слайд 19

x 1 =x 0 +V 0 1 t Принимает вид x 1 =5+ t (t изменяется от 0 до 5) x 2 =V 0 2 t+ Принимает вид x 2 = t 2 +5t x 0 =5м V 0 1 =1м/с V 0 2 =5м/с a =2м/с 2 t=5 с at 2 2 x t 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6

Слайд 20

Вывод: Графическое представление любого физического процесса делает его более наглядным и тем самым облегчает понимание рассматриваемого явления, способствует развитию абстрактного мышления, интуиции, умения анализировать и сравнивать, находить более рациональный способ решения задач. Кроме того, применение графического метода способствует укреплению связей физики с математикой, наполняет абстрактные математические закономерности конкретным физическим содержанием. При широком использовании графического метода привлекаются и развиваются не только мышление и память курсантов, но также зрение и моторные действия, формируются и развиваются навыки аккуратного и быстрого выполнения чертежа, пользования координатной сеткой, простейшими чертежными инструментами.

Слайд 21

Список использованных источников:

nsportal.ru

Статья: «Графики в курсе физики по теме «Основы кинематики»» — Другое — Физика и астрономия

Главным при обучении физике является создание единого представления о физике как науке, которая изучает окружающий нас мир. Физика без математики не была бы наукой. Учащимся надо дать понять, что любая физическая закономерность становится законом только в том случае, если она обличена в математическую формулу. Очень важно формулировку законов сопровождать видом графической зависимости. В этом плане само умение строить графики является очень важным. Построение графиков по результатам измерений – важнейшее из метапредметных  умений. В диагностических работах апробационного исследования ученики показали низкую грамотность при построении графиков. В большинстве случаев ученики испытывают трудности: как при построении, так и при интерпретации результатов.  Основные проблемы – это выбор масштабов (эти масштабы не обязательно должны быть одинаковы, как обычно бывает в заданиях по математике) , построение графика, учет нуля, конкретное использование графиков для обоснования выводов и др. Из всех разделов физики графики чаще всего встречаются при изучении кинематики и газовых законов. Однако есть и другие разделы, где построение графиков и умение их чтения открывает большие возможности для понимания учащимися сути явлений и законов, их проявления в природе и в технике.

Но я в данной работе хотела показать как на графических задачах по кинематике можно, применяя математические знания учащихся, не только решать качественные задачи, но и количественные задачи по определению кинематических величин( ускорения, скорости, перемещения и координаты  тела). При решении таких графических задач закрепляются понятие системы отсчета, расчетные формулы кинематических величин, геометрическая интерпретация понятий пути, перемещения и координаты тела. В связи с этим высвобождается время для решений задач повышенной сложности, повышается графическая грамотность и идет подготовка для дальнейшего применения графиков при изучении более сложных процессов( в разделах МКТ и термодинамики, электростатики, электродинамики, квантовой физики и т. д.).

В связи с тем, что к 9 классу в курсе математики получены  навыки построения графиков линейной  зависимости, обратной пропорциональности и параболы квадратного уравнения, нужно научить строить графики зависимости ускорения, скорости, пройденного пути, перемещения и координаты .   Начнем с примеров задач построения графиков кинематических величин.

Задача 1. Тело из состояния покоя увеличил свою скорость до 5 м/с за 10 секунд. Затем двигаясь в том же направлении увеличил скорость до 7 м/с за 2 секунду. Постройте график зависимости проекции скорости  и проекции ускорения ось Х от времени.

Задача 2. Тело, движущееся со скоростью 2 м/с, останавливается через 10 с, а затем движется к началу координат с таким же ускорением и увеличивает свою скорость до 3 м/с в течение 6 с.  Постройте график зависимости проекции скорости  и проекции ускорения ось Х от времени.

При построении первого графика обращаем внимание на разные уклоны графиков зависимости скорости на разных участках пути, при решении второй задачи на направления скорости и ускорения.

Построение графиков зависимости координаты и пройденного пути от времени носит качественный характер из- за нехватки достаточных умений по математике.

Задача 3. Тело на первом участке пути двигался равномерно прямолинейно , а потом оставшийся отрезок пути прошло равноускоренно. Постройте график зависимости пройденного пути от времени в течение всего движения. Начальная координата равна 0.

Задача 4. Дан график зависимости скорости тела от времени. Движение прямолинейное. Построить графики зависимости ускорения, координаты и пройденного пути от времени. Начальная координата равна 0.

Решая задачу 4 обращаем внимание учащихся на то, что движение является прямолинейным, и пока тело удаляется от начала координат, х(t), s(t) совпадают. При t Є[t₃;t₄] координата уменьшается, но пройденный путь продолжает возрастать( пройденный путь – неубывающая функция от времени). Так как a₁= tgα₁<|tgα₂| = |a₂|, то парабола на участке t Є[t₂;t₄] проходит более круто, чем на участке [0 ; t₁].

Задача 5. На рисунке представлен график зависимости координаты от времени для материальной точки, движущейся прямолинейно. Построить графики зависимостей  проекции ускорения на ось х, а также пройденного пути от времени. Все указанные интервалы времени равны.

[иллюстрации см. в скачиваемом файле]

При разборе данной задачи можно смело оперировать понятиями угловых коэффициентов и для парабол- старшими коэффициентами. Нужно показать, что СD, КL, NG – отрезки прямых с равными по модулю угловыми коэффициентами; ВС, DE, FK, LMN, GT – участки парабол с равными по модулю старшими коэффициентами; АВ и EF – отрезки прямых.

Задача 6. На рисунке представлен график зависимости проекции ускорения от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение скорости тела на каждом участке пути, если начальная скорость тела равна 2 м/с.

[иллюстрации см. в скачиваемом файле]

График Задача 7.  На рисунке представлен график зависимости проекции скорости от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение  движения тела на каждом участке пути, если начальная координата равна 500 м.

[иллюстрации см. в скачиваемом файле]

Задача 8.  На рисунке представлен график зависимости проекции координаты от времени для материальной точки, движущейся прямолинейно. А) Как тело двигалось на каждом участке пути? В) Написать уравнение  движения тела на каждом участке пути, если ускорение движения на всех участках пути одинаково и равно 3 м/с.

[иллюстрации см. в скачиваемом файле]

Решая данные графические задачи удается повторить и закрепить формулы расчета кинематических величин; ученики начинают понимать важность нахождения проекции векторов в разных осях ; одновременно оттачиваются вычислительные и графические навыки, что высвобождает время на изучение сути явлений, на экспериментальную деятельность.

При решении правильно подобранных графических задач обучающиеся овладевают  следующими метапредметными умениями:

• Выделение главного, существенных признаков понятий, обобщение понятий;

• Построение логических  рассуждений и выводов на основе текстовой информации, рисунков, графиков и схем;
• Сравнение объектов на основе известных характерных свойств;
• Сопоставление полученной информации из различных источников с жизненным опытом в соответствии с поставленными задачами. 

Полный текст материала Статья: «Графики в курсе физики по теме «Основы кинематики»» смотрите в скачиваемом файле.
На странице приведен фрагмент.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий

Оставить комментарий

pedsovet.su