Разветвленная электрическая цепь – Большая Энциклопедия Нефти и Газа, статья, страница 1
Разветвленная электрическая цепь
Cтраница 1
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей. [1]
Разветвленная электрическая цепь однофазного тока, питающаяся напряжением U 124B ( рис. 3.65, а), состоит из трех ветвей, соединенных параллельно, измерительных приборов и выключателей В – Вз. [2]
Если разветвленная электрическая цепь содержит источники в разных ветвях, то для расчета силы токов можно применить метод наложения. [3]
Если разветвленная электрическая цепь содержит один нелинейный элемент, то расчет и анализ такой цепи может быть значительно упрощен при использовании метода активного двухполюсника. [5]
В разветвленной электрической цепи
Расчет разветвленной электрической цепи с двумя параллельно соединенными нелинейными резисторами / и г2 ( рис. 32, а) с заданными соответственно ампер-вольтными характеристиками / i Fi ( U) и / 2 F % ( U), подключенной к напряжению U, сводится к построению ампер-вольтной характеристики / i / 2 F ( U) всей цепи ( рис. 32, б), отложению на оси абсцисс отрезка Ол, равного, в выбранном масштабе, величине напряжения U, проведению через точку А линии А А параллельно оси ординат и определению точек пересечения л2, Аг, А. [9]
В разветвленных электрических цепях вычисление токов, идущих по отдельным ветвям, представляет известные трудности. Для упрощения этих вычислений удобно воспользоваться двумя правилами Кирхгофа. [10]
В разветвленных электрических цепях вычисление токов, идущих по отдельным ветвям, представляет известные трудности. Для упрощения этих вычислений удобно воспользоваться двумя правилами Кирхгофа. [11]
Для расчета разветвленных электрических цепей разработан ряд специальных методов, базирующихся на тех же основных законах, но облегчающих в ряде случаев технику расчетов. [13]
Порядок расчета разветвленных электрических цепей при наличии взаимной индуктивности иллюстрирован ниже на примере схемы-рис. Предполагается, что элементы LI, L2 и L3, входящие в схему, связаны друг с другом индуктивно. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Ветвь – электрическая цепь – Большая Энциклопедия Нефти и Газа, статья, страница 3
Ветвь – электрическая цепь
Cтраница 3
На рис. 2 – 2 показаны четыре ветви электрической цепи. [31]
Таким образом, активную составляющую тока в рассматриваемой ветви электрической цепи можно представить в виде произведения напряжения на активную проводимость ветви, реактивную составляющую тока – в виде произведения напряжения на реактивную проводимость ветви, а ток в рассматриваемой ветви равен напряжению, действующему на зажимах цепи, помноженному на ее полную проводимость. [32]
Контур – замкнутый путь, проходящий по ветвям электрической цепи. [33]
Любой замкнутый путь, проходящий по нескольким ветвям электрической цепи, называется контуром. [35]
Итак сумма комплексных мощностей, потребляемых всеми ветвями электрической цепи, равна нулю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей. [36]
Определить токи 1 – / з в ветвях электрической цепи рис. 1.60 методом двух узлов. [37]
Определить токи l – / ч в ветвях электрической цепи переменного тока ( рис. 3.71), если ЭДС источников питания е, 60у2 – sincot; E2 60 В; активное и реактивные сопротивления: Rz 20 Ом; Л, Хг 30 Ом, Хл 20 Ом. [38]
Напоминаем, что узел – это место соединения ветвей электрической цепи. Сколько узлов в указанной электрической цепи. [40]
Результаты этих преобразований показывают, что полная проводимость ветви электрической цепи в комплексной форме выражается комплексным числом, действительная часть которого равна активной. [42]
Результаты этих преобразований показывают, что полная проводимость ветви электрической цепи в комплексной форме выражается комплексным числом, действительная часть которого равна активной проводимости, а мнимая часть равна реактивной проводимости этой ветви, причем индуктивная проводимость отрицательна, а емкостная – положительна. [43]
Итак, сумма комплексных мощностей, потребляемых всеми ветвями электрической цепи, равна нулю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей. [44]
Для правильного понимания того, как изменяется потенциал вдоль ветвей электрической цепи, полезно построить график, на котором по одной оси ( по вертикали) откладываются значения потенциала, а по другой – величины сопротивлений последовательно проходимых участков цепи выбранного контура. [45]
Страницы: 1 2 3 4
www.ngpedia.ru
Характеристики разветвленной электрической цепи
Процессы в любом электротехническом устройстве удобно рассматривать с помощью электрических схем, сформированных из идеализированных элементов, которые характеризуются схемой соединения элементов (геометрией, топографией). Основными характеристиками электрических схем являются ветвь, узел, контур. Для понятия основных характеристик электрических схем, рассмотрим электрическую цепь, приведенную на рисунке 1.18.
Ветвьюназывают часть схемы, состоящую из последовательно соединённых элементов.
Число ветвей электрической цепи принято обозначать « ». В приведенной схеме – . Вдоль каждой ветви протекают одинаковые токи , , , , , . Элементы, входящие в одну ветвь, рекомендуется обозначать одинаковыми индексами. Например, в третью ветвь входят резистивный элемент , индуктивность , емкость и источник напряжения .
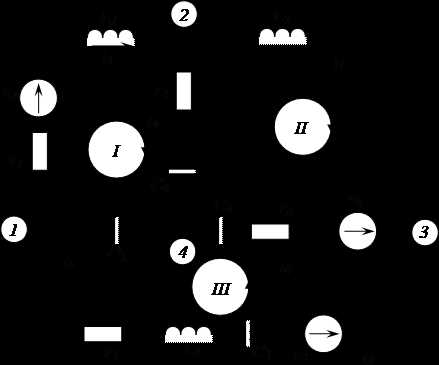
Рисунок 1.18 – Электрическая цепь
Узлом называется точка, в которой соединяются три или более ветвей.
Число узлов электрической цепи принято обозначать «y». В приведенной схеме – . Например, к первому узлу 1 подсоединены первая, третья и пятая ветви.
Несколько ветвей могут образовывать замкнутый контур. При обходе контура ветвь и узел встречаются один раз.
Выделяют (независимые) главные контуры. Число независимых контуров «m» равно . В приведенной схеме независимых контуров . Такими контурами могут быть: І контур, в который входят первая, четвертая и пятая ветви, ІІ контур – вторая, четвертая и шестая ветви, ІІІ контур – третья, пятая и шестая ветви.
На схеме указывают положительные направления токов в ветвях и направления обхода контуров. Эти направления выбираются произвольно.
Геометрию (топологию) электрических схем удобно оценивать с помощью графа электрической цепи. На рисунке 1.19 приведен граф электрической схемы, представленной на рисунке 1.18. Граф характеризуется ветвями, узлами, контурами. Ветви графа представляют собой отрезки линии.
Если в ветви указывают направление, то граф называют направленным. Направление графа характеризует положительное направление тока в ветви или напряжения.
Часть графа называют подграфом.
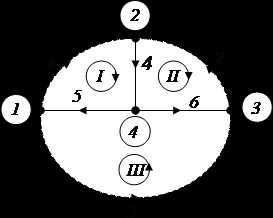
Рисунок 1.19 – Граф электрической цепи
Дерево – часть графа (подграф), состоящий из ветвей, соединяющих все узлы, но не образующих замкнутых контуров. Примеры деревьев графа представлены на рисунке 1.20.
Рисунок 1.20 – Примеры деревьев графа
Ветвями связи называют ветви графа, не вошедшие в состав дерева графа. Такими являются первая, вторая и третья ветви.
Для каждого дерева существуют свои ветви связи, но их число неизменно и равно числу независимых контуров. С помощью ветвей связи удобно выделять независимые (главные) контуры. Независимый контурвключает в себя только одну ветвь связи и дополняется ветвями дерева, поэтому ветви дерева могут входить в несколько контуров.
Похожие статьи:
poznayka.org
Узлом – электрическая цепь – Большая Энциклопедия Нефти и Газа, статья, страница 1
Узлом – электрическая цепь
Cтраница 1
Узлом электрической цепи и соответственно ее схемы называют место соединения ветвей. На схеме узел изображают точкой. [1]
Узлом электрической цепи и, соответственно, ее схемы называют место соединения ветвей. На схеме узел изображают точкой. [2]
Узлом электрической цепи и, соответственно, ее схемы, называют место соединения трех или большего числа ветвей. На схеме узел изображают точкой. [3]
Узлом электрической цепи и соответственно ее схемы называют место соединения ветвей. На схеме узел изображают точкой. [4]
Узлом электрической цепи называют точку, в которой соединены между собой более двух проводников. [5]
Узлом электрической цепи называют место соединения двух ветвей и более. Если в узле соединены только две ветви, то он – простой. Узел, который содержит хотя бы одну ветвь, не входящую в другие узлы, называют независимым. [6]
Место соединения ветвей называется узлом электрической цепи. Узел образуется при соединении в одной точке ке менее трех ветвей, например, на схеме рис. 3.6 к узлу 6 подключены четыре ветви. [7]
Место соединения ветвей называется узлом электрической цепи. [9]
Точка соединения трех или большего числа ветвей называется узлом электрической цепи. [10]
Ветвью электрической цепи называется такой ее участок, который состоит только из ( последовательно включенных источников напряжений и сопротивлений и вдоль которого в любой момент времени ток имеет одно и то же значение. Узлом электрической цепи называется место ( точка) соединения трех и более ветвей. [11]
В каком определении допущена смысловая ошибка. Весь участок электрической цепи, вдоль которого ток имеет одно и то же значение в любой момент времени, называется ветвью электрической цепи. Контур электрической цепи представляет собой любой замкнутый путь, проходящий по нескольким ветвям. Точка соединения трех или большего числа ветвей называется узлом электрической цепи. [13]
Страницы: 1
www.ngpedia.ru
Ветвь электрической цепи — с русского
См. также в других словарях:
Ветвь электрической цепи — участок электрической цепи, вдоль которого протекает один и тот же электрический ток… Источник: ЭЛЕКТРОТЕХНИКА . ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
ветвь электрической цепи — Участок электрической цепи, вдоль которого протекает один и тот же ток [ГОСТ 19880 74] [ОАО РАО “ЕЭС России” СТО 17330282.27.010.001 2008] Тематики электротехника, основные понятия EN circuit branchelectric circuit branch … Справочник технического переводчика
ветвь (электрической цепи) — 102 ветвь (электрической цепи) Участок электрической цепи, вдоль которого протекает один и тот же электрический ток Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа … Словарь-справочник терминов нормативно-технической документации
Ветвь электрической цепи — 93. Ветвь электрической цепи Участок электрической цепи, вдоль которого протекает один и тот же ток Источник: ГОСТ 19880 74: Электротехника. Основные понятия. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Ветвь электрической цепи — English: Circuit branch Участок электрической цепи, вдоль которого протекает один и тот же ток (по ГОСТ 19880 74) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
Ветвь (электрической цепи) — 1. Участок электрической цепи, вдоль которого протекает один и тот же электрический ток Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий … Телекоммуникационный словарь
ветвь электрической цепи — Весь участок электрической цепи, вдоль которого в любой момент времени ток имеет одно и то же значение … Политехнический терминологический толковый словарь
путь графа (электрической цепи) — 208 путь графа (электрической цепи) Непрерывная последовательность ветвей графа электрической цепи, в которой любая ветвь и любой узел встречаются только один раз Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий … Словарь-справочник терминов нормативно-технической документации
связь графа (электрической цепи) — 206 связь графа (электрической цепи) Ветвь графа электрической цепи, не принадлежащая его дереву Источник: ГОСТ Р 52002 2003: Электротехника. Термины и определения основных понятий оригинал документа … Словарь-справочник терминов нормативно-технической документации
Путь графа (электрической цепи) — 1. Непрерывная последовательность ветвей графа электрической цепи, в которой любая ветвь и любой узел встречаются только один раз Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий … Телекоммуникационный словарь
Связь графа (электрической цепи) — 1. Ветвь графа электрической цепи, не принадлежащая его дереву Употребляется в документе: ГОСТ Р 52002 2003 Электротехника. Термины и определения основных понятий … Телекоммуникационный словарь
translate.academic.ru
Электрическая цепь, ее элементы и параметры
Определение
Электрической цепью называется совокупность электротехнических устройств, создающих замкнутый путь электрическому току. Она состоит из источников (генераторов) энергии, приемников энергии (нагрузки) и соединительных проводов. В цепи могут быть также различные преобразователи (играют роль как роль источников, так и приемников), защитная и коммутационная аппаратура.
В источниках неэлектрические виды энергии преобразуются (в соответствии с законом сохранения энергии) в энергию электромагнитного поля. Так, например, на гидроэлектростанциях энергия падающей воды (энергия гравитационного поля) преобразуется в энергию электромагнитного поля. В приемниках энергия электромагнитного поля преобразуется в тепловую и другие виды энергии. Кроме того, некоторая часть энергии запасается в электрических и магнитных полях цепи.
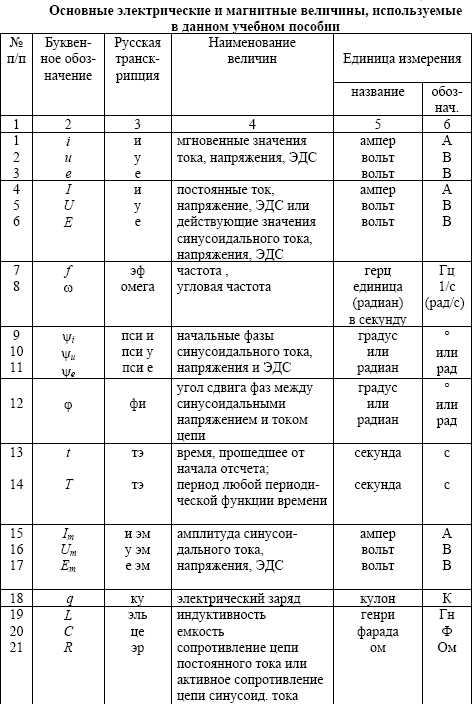
Электромагнитные процессы в электрической цепи описываются с помощью понятий о токе, напряжении, электродвижущей силе (ЭДС), сопротивлении, индуктивности и емкости. Буквенные обозначения этих, а также других величин, используемых в этом учебном пособии представлены в табл.1.1. Там же дана их русская транскрипция и единицы измерений. Заметим здесь, что ЭДС, токи и напряжения, изменяющиеся во времени, обозначаются строчными латинскими буквами е, i, u, а ЭДС, токи и напряжения, неизменные во времени, обозначаются заглавными латинскими буквами E, I, U.
Графическое изображение электрической цепи и ее элементов
Графическое изображение электрической цепи называется ее схемой. В схеме различают ветви, узлы и контуры. Ветвь – это часть схемы, состоящая только из последовательно соединенных источников и приемников. Узел – точка схемы, в которой сходятся не менее трех ветвей (ветви начинаются и заканчиваются на узлах цепи). Контур – часть схемы, образованная ветвями; число контуров определяется числом вариантов обходов по ветвям цепи. На рис.1.1 даны структурные схемы трех электрических цепей и указано количество ветвей узлов и контуров в каждой из них.
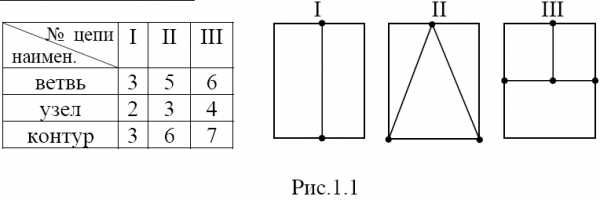
Принятые в настоящем учебном пособии графические обозначения основных элементов цепи, показаны на рис.1.2.
На этом рисунке : 1 – источник ЭДС; 2 – источник тока; 3 – соединительный провод; 4 – сопротивление R цепи; 5 – индуктивность L цепи; 6 – емкость С цепи; 7 – двухполюсник (цепь с неизвестной структурой, имеющая два входных зажима).
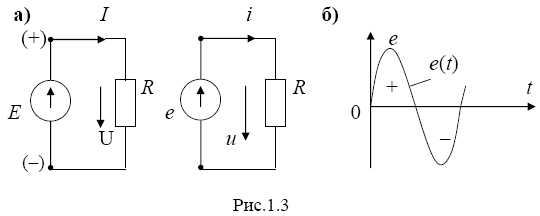
В цепях постоянного тока (рис.1.3,а) направление действия ЭДС источника принято указывать в сторону того зажима, на котором образуются положительные заряды. Направление тока во внешней цепи принято указывать от положительно заряженного полюса (зажима) источника к отрицательно заряженному. Направление действия напряжения в приемнике всегда указывают в ту же сторону, что и направление действия тока.
В цепях синусоидального тока (рис.1.3,б) принято обозначать направления ЭДС тока и напряжения, используя положительный полупериод тока, при котором ток не изменяет своего направления. При этом картина этих направлений получается аналогичной с цепью постоянного тока.

monitor.uxp.ru
Топология электрической цепи (Лекция N 2)
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.

Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.

Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
Рис.4
4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если граф содержит m узлов и n ветвей, то число ветвей любого дерева , а числа ветвей связи графа .
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.
Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 иS2 . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.
С понятием дерева связаны понятия главных контуров и сечений:
- главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
- главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Топологические матрицы
Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.
1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.
Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу АН , принимая, что элемент матрицы (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим
Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы АН путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим
Число строк матрицы А равно числу независимых уравнений для узлов , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
Первый закон Кирхгофа
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение
|
(1) |
где – вектор плотности тока; – нормаль к участку dS замкнутой поверхности S.
Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S2 графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать
.
Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:
|
(2) |
т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.
При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.
Введем столбцовую матрицу токов ветвей
| I= |
Тогда первый закон Кирхгофа в матричной форме записи имеет вид:
– где O – нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не АН, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.
В качестве примера запишем для схемы на рис. 3
Отсюда для первого узла получаем
,
что и должно иметь место.
2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы Всоответствуют контурам, а столбцы – ветвям схемы.
Элемент bijматрицы В равен 1, если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1, если не совпадает с направлением обхода контура, и 0, если ветвьj не входит в контурi.
Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.

Перейдем теперь ко второму закону Кирхгофа.
Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.
|
(4) |
Просуммируем напряжения на ветвях некоторого контура:
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.
Таким образом, второй закон Кирхгофа математически записывается, как:
|
(5) |
– и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
Введем столбцовую матрицу напряжений ветвей
|
U= |
Тогда второй закон Кирхгофа в матричной форме записи имеет вид
В качестве примера для схемы рис. 5 имеем
,
откуда, например, для первого контура получаем
,
что и должно иметь место.
Если ввести столбцовую матрицу узловых потенциалов
| = |
причем потенциал последнего узла , то матрица напряжений ветвей и узловых потенциалов связаны соотношением
| U=AТ |
(7) |
где AТ – транспонированная узловая матрица.
Для определения матрицы В по известной матрице А=АДАС , где АД – подматрица, соответствующая ветвям некоторого дерева, АС– подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-АТС А-1ТД1).
3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Матрица Q , составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Q равно числу независимых сечений.
Элемент qij матрицыQ равен 1, если ветвьвходит в i-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1, если ориентирована противоположно направлению сечения, и 0, если ветвьj не входит в i-е сечение.
В качестве примера составим матрицу Q главных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем
В заключение отметим, что для топологических матриц А, В и Q, составленных для одного и того же графа, выполняются соотношения
которые, в частности, можно использовать для проверки правильности составления этих матриц. Здесь 0 – нулевая матрица порядка .
Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.
Литература
1. Теоретические основы электротехники. Т.1. Основы теории линейных цепей./Под ред. П.А.Ионкина. Учебник для электротехн. вузов. Изд.2-е , перераб. и доп. –М.: Высш. шк., 1976.-544с.
2. Матханов Х.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. и радиотехн. спец. 3-е изд. переработ. и доп. –М.: Высш. шк., 1990. –400с.
3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- Сформулируйте основные топологические понятия для электрических цепей.
- Что такое узловая матрица?
- Что такое контурная матрица?
- Что такое матрица сечений?
- Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:
- Составить матрицу главных контуров для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5
- Решить задачу 5, используя соотношения (8) и (9).
.
Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв, что ветвям дерева присвоены первые номера.
Ответ:
| B= | |
| Q= |
Ответ:
| B= |
www.toehelp.ru
