Момент вращения и момент инерции: формулы, пример решения задачи
Тела, совершающие круговые движения, в физике принято описывать с помощью формул, включающих в себя угловую скорость и угловое ускорение, а также такие величины, как моменты вращения, сил и инерции. Рассмотрим подробнее эти понятия в статье.
Момент вращения относительно оси
Эту физическую величину также называют моментом импульса. Слово “момент” означает, что при определении соответствующей характеристики учитывается положение оси вращения. Так, момент импульса частицы массой m, которая вращается со скоростью v вокруг оси O и находится от последней на расстоянии r, описывается следующей формулой:
L¯ = r¯*m*v¯ = r¯*p¯, где p¯ – импульс частицы.
Знак “¯” указывает на векторный характер соответствующей величины. Направление вектора момента вращения L¯ определяется по правилу правой руки (четыре пальца направлены от конца вектора r¯ к концу p¯, и отставленный большой палец показывает, куда будет направлен L¯). Направления всех названных векторов можно посмотреть на главном фото статьи.
При решении практических задач пользуются формулой для момента импульса в форме скалярной. Кроме того, линейную скорость заменяют угловой. В этом случае формула для L будет выглядеть так:
L = m*r2*ω, где ω = v*r – угловая скорость.
Величина m*r2 обозначается буквой I и называется моментом инерции. Она характеризует инерционные свойства системы вращения. В общем виде выражение для L записывается так:
L = I*ω.
Эта формула справедлива не только для вращающейся частицы массой m, но и для любого тела произвольной формы, которое совершает круговые перемещения относительно некоторой оси.
Момент инерции I
В общем случае введенная в предыдущем пункте величина I рассчитывается по формуле:
I = ∑i(mi*ri2).
Здесь i указывает на номер элемента с массой mi, расположенном от оси вращения на расстоянии ri. Это выражение позволяет произвести расчет для неоднородного тела произвольной формы. Для большинства идеальных объемных геометрических фигур этот расчет уже произведен, и полученные значения момента инерции внесены в соответствующую таблицу. Например, для однородного диска, который совершает круговые движения вокруг оси, перпендикулярной его плоскости и проходящей через центр масс, I = m*r2/2.
Чтобы понять физический смысл момента инерции вращения I, следует ответить на вопрос, относительно какой оси легче раскрутить швабру: той, которая проходит вдоль швабры или той, которая ей перпендикулярна? Во втором случае придется приложить больше усилий, поскольку момент инерции для этого положения швабры имеет большую величину.

Закон сохранения величины L
Изменение момента вращения во времени описывается приведенной ниже формулой:
dL/dt = M, где M = r*F.
Здесь M – это момент результирующей внешней силы F, приложенной к плечу r относительно оси вращения.
Формула показывает, если M=0, тогда изменение момента импульса L не будет происходить, то есть он будет оставаться сколь угодно длительное время неизменным независимо от внутренних изменений в системе. Этот случай записывают в виде выражения:
I1*ω1 = I2*ω2.
То есть любые изменения внутри системы момента I будут приводить к изменениям угловой скорости ω таким образом, что их произведение будет оставаться постоянным.

Примером проявления этого закона является спортсмен в фигурном катании, который, выбрасывая руки и прижимая их к телу, меняет свой I, что отражается на изменении его скорости вращения ω.
Задача на вращение Земли вокруг Солнца
Решим одну интересную задачу: используя приведенные выше формулы, необходимо рассчитать момент вращения нашей планеты по своей орбите.

Поскольку притяжением остальных планет можно пренебречь, а также учитывая, что момент гравитационной силы, действующей со стороны Солнца на Землю, равен нулю (плечо r=0), то L=const. Для вычисления L воспользуемся следующими выражениями:
L = I*ω; I = m*r2; ω = 2*pi/T.
Здесь мы приняли, что Землю можно считать материальной точкой с массой m=5,972*1024 кг, поскольку ее размеры намного меньше расстояния до Солнца r=149,6 млн км. T = 365,256 дня – период обращения планеты вокруг своей звезды (1 год). Подставляя все данные в выражение выше, получаем :
L = I*ω = 5,972*1024*(149,6*109)2*2*3,14/(365,256*24*3600) = 2,66*1040 кг*м2/с.
Рассчитанное значение момента импульса является гигантским, что обусловлено большой массой планеты, высокой скоростью ее вращения по орбите и огромным астрономическим расстоянием.
fb.ru
Вращающий момент – это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Момент силы. Формула момента силы
В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции “момент силы”. В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.
Момент силы в физике
Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.
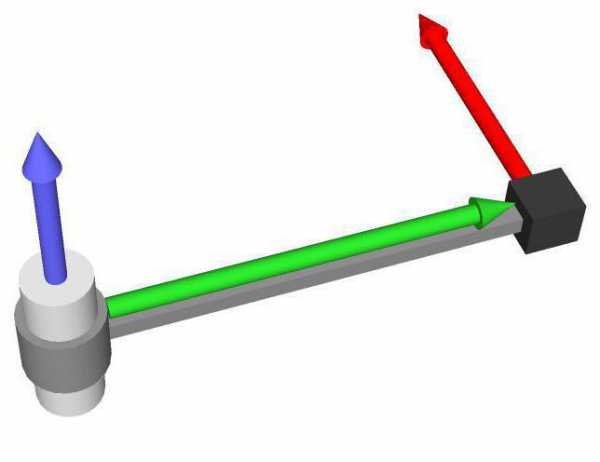
Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.
Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть формула момента силы относительно оси записывается следующим образом:
M¯ = r¯ * F¯
Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).
Скалярная форма записи M¯
На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90o. В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.

Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:
M = L * F * sin(Φ)
Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90o по отношению к L. Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).
При рассмотрении момента силы в скалярной форме часто пользуются понятием “рычага силы”. Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) – это рычаг силы (равенство следует из определения тригонометрической функции “синус”). Через рычаг силы формулу для момента M можно переписать так:
M = d * F
Физический смысл величины M
Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему. Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.
Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.
Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.
Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.

Несколько действующих сил в системе
Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов Mi¯, то есть:
M¯ = ∑i(Mi¯), где i – номер силы Fi
Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII – начала XVIII века – француза Пьера Вариньона. Она гласит: “Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке”. Математически теорему можно записать так:
∑i(Mi¯) = M¯ = d * ∑i(Fi¯)
Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.

Совершает ли работу момент силы?
Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M – это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы – это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:
A = M * θ
В этом выражении θ – это угол, на который было произведено вращение моментом силы M. В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.
Момент силы и момент импульса
Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название “момент импульса”. Его можно вычислить, применяя формулу:
L = I * ω
Здесь I – это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω – угловая скорость, она связана с линейной скоростью формулой ω = v/r.
Оба момента (импульса и силы) связаны друг с другом следующим выражением:
M = I * α, где α = dω / dt – угловое ускорение.
Приведем еще одну формулу, которая важна для решения задач на работу моментов сил. С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:
Ek = 1/2 * I * ω2
Далее приведем две задачи с решениями, где покажем, как пользоваться рассмотренными физическими формулами.
Равновесие нескольких тел
Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.
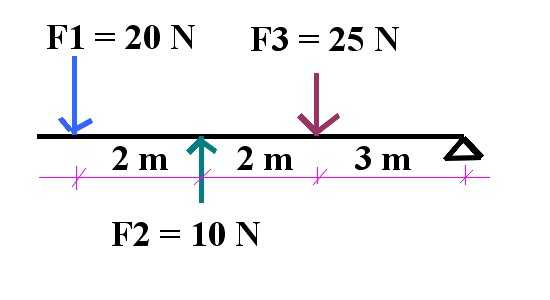
Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона. На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:
P = F1 – F2 + F3 = 20 – 10 + 25 = 35 Н
Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.
Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:
M1 – M2 + M3 = d * P = 7 * 20 – 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м
Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы. Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.
Задача с движущимся диском
Решение следующей задачи основано на использовании формулы момента силы трения и кинетической энергии тела вращения. Задача: дан диск радиуса r = 0,3 метра, который вращается со скоростью ω = 1 рад/с. Необходимо рассчитать, какое расстояние способен он пройти по поверхности, если коэффициент трения качения равен μ = 0,001.

Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:
I * ω2/2 = μ * N/r * r * θ
Первая часть формулы – это кинетическая энергия диска. Вторая часть – это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).
Учитывая, что N = m * g и I = 1/2m * r2, вычисляем θ:
θ = m * r2 * ω2/(4 * μ * m * g) = r2 * ω2/(4 * μ *g) = 0,32 * 12/(4 * 0,001 * 9,81) = 2,29358 рад
Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:
s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см
Отметим, что на данный результат масса диска никак не влияет.
fb.ru
15.Вращательное движение. Момент силы и момент импульса.
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
Кинетические характеристики:
Вращение твердого тела, как целого характеризуется углом , измеряющегося в угловых градусах или радианах, угловой скоростью (измеряется в рад/с)и угловым ускорением(единица измерения — рад/с²).
При равномерном вращении (T оборотов в секунду):
Частота вращения — число оборотов тела в единицу времени.-
,
Период вращения — время одного полного оборота. Период вращения T и его частота связаны соотношением .
Линейная скорость точки, находящейся на расстоянии R от оси вращения
Угловая скорость вращения тела
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса замкнутой системы сохраняется
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
16.Уравнение динамики вращательного движения. Момент инерции.
Основное уравнение динамики вращательного движения материальной точки – угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
М = E*J или E = M/J
Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Свойства момента инерции:
1.Момент инерции системы равен сумме момента инерции её частей.
2.Момент инерции тела является величиной, иманентно присущей этому телу.
Момент инерции твердого тела – это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.
Формула момента инерции:
Теорема Штейнера:
Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R – расстояние между осями.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Центральный момент инерции (или момент инерции относительно точки O) — это величина
.
studfiles.net
Вращательный момент – это… Что такое Вращательный момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
основные понятия, формулы, пример решения задачи
Когда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными размерами, вводя понятие материальной точки. Для другого типа задач, в которых рассматриваются покоящиеся или вращающиеся тела, важно знать их параметры и точки приложения внешних сил. В этом случае речь идет о моменте сил относительно оси вращения. Рассмотрим этот вопрос в статье.
Понятие о моменте силы
Перед тем как приводить формулу момента силы относительно оси вращения неподвижной, необходимо пояснить, о каком явлении пойдет речь. Ниже дан рисунок, на котором изображен гаечный ключ длиной d, к концу его приложена сила F. Нетрудно представить, что результатом ее воздействия будет вращение ключа против часовой стрелки и откручивание гайки.
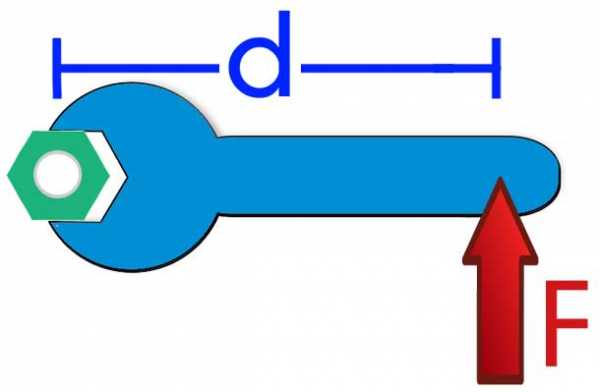
Согласно определению, момент силы относительно оси вращения представляет собой произведение плеча (d в данном случае) на силу (F), то есть можно записать следующее выражение: M = d*F. Сразу же следует оговориться, что приведенная формула записана в скалярном виде, то есть она позволяет рассчитать абсолютное значение момента M. Как видно из формулы, единицей измерения рассматриваемой величины являются ньютоны на метр (Н*м).
Как выше было оговорено, момент M в действительности представляет собой вектор. Для пояснения этого утверждения рассмотрим другой рисунок.
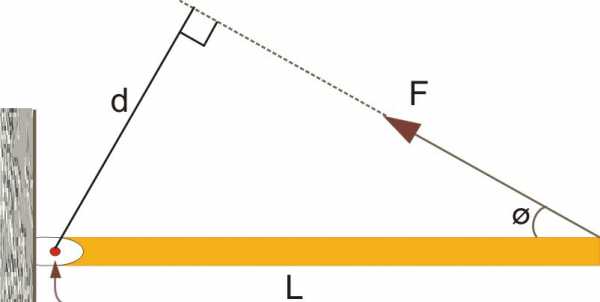
Здесь мы видим рычаг длиной L, который закреплен на оси (показано стрелкой). К его концу приложена сила F под углом Φ. Нетрудно себе представить, что эта сила будет вызывать подъем рычага. Формула для момента в векторной форме в этом случае запишется так: M¯ = L¯*F¯, здесь черта над символом означает, что рассматриваемая величина – это вектор. Следует пояснить, что L¯ направлен от оси вращения к точке приложения силы F¯.
Приведенное выражение является векторным произведением. Его результирующий вектор (M¯) будет направлен перпендикулярно плоскости, образованной L¯ и F¯. Для определения направления момента M¯ существуют несколько правил (правой руки, буравчика). Чтобы не заучивать их и не путаться в порядке умножения векторов L¯ и F¯ (от него зависит направление M¯), следует запомнить одну простую вещь: момент силы будет направлен таким образом, что если смотреть с конца его вектора, то воздействующая сила F¯ будет вращать рычаг против часовой стрелки. Это направление момента условно принято за положительное. Если же система совершает вращение по часовой стрелки, значит, результирующий момент сил имеет отрицательное значение.
Таким образом, в рассматриваемом случае с рычагом L величина M¯ направлена вверх (от рисунка к читателю).
В скалярной форме формула для момента запишется в виде: M = L*F*sin(180-Φ) или M = L*F*sin(Φ) (sin(180-Φ) = sin(Φ)). Согласно определению синуса, можно записать равенство: M = d*F, где d = L*sin(Φ) (см. рисунок и соответствующий прямоугольный треугольник). Последняя формула является аналогичной той, которая была приведена в предыдущем пункте.
Проведенные выше вычисления демонстрируют, как работать с векторными и скалярными величинами моментов сил, чтобы не допустить ошибок.
Физический смысл величины M¯
Поскольку два рассмотренных в предыдущих пунктах случая связаны с вращательным движением, то можно догадаться, какой смысл несет момент силы. Если сила, действующая на материальную точку, является мерой увеличения скорости линейного перемещения последней, то момент силы – это мера ее вращательной способности применительно к рассматриваемой системе.
Приведем наглядный пример. Любой человек открывает дверь, взявшись за ее ручку. Также это можно сделать, если толкнуть дверь в зоне ручки. Почему никто не открывает ее, толкая в области петель? Очень просто: чем ближе к петлям приложена сила, тем труднее открыть дверь, и наоборот. Вывод предыдущего предложения следует из формулы для момента (M = d*F), откуда видно, что при M = const величины d и F находятся в обратной зависимости.

Момент силы – аддитивная величина
Во всех рассмотренных выше случаях имела место лишь одна действующая сила. При решении же реальных задач дело обстоит гораздо сложнее. Обычно на системы, которые вращаются или находятся в равновесии, действуют несколько сил кручения, каждая из которых создает свой момент. В этом случае решение задач сводится к нахождению суммарного момента сил относительно оси вращения.
Суммарный момент находится путем обычной суммы отдельных моментов для каждой силы, однако, следует не забывать использовать правильный знак для каждого из них.
Пример решения задачи
Для закрепления полученных знаний предлагается решить следующую задачу: необходимо вычислить суммарный момент силы для системы, изображенной на рисунке ниже.
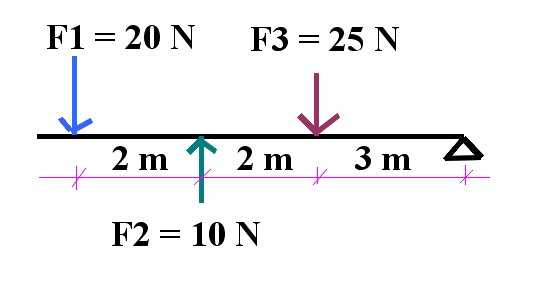
Мы видим, что на рычаг длиной 7 м действуют три силы (F1, F2, F3), причем они имеют разные точки приложения относительно оси вращения. Поскольку направление сил перпендикулярно рычагу, то нет необходимости применять векторное выражение для момента кручения. Можно рассчитать суммарный момент M, используя скалярную формулу и не забывая о постановке нужного знака. Поскольку силы F1 и F3 стремятся повернуть рычаг против часовой стрелки, а F2 – по часовой стрелке, то момент вращения для первых будет положительным, а для второй – отрицательным. Имеем: M = F1*7-F2*5+F3*3 = 140-50+75 = 165 Н*м. То есть суммарный момент является положительным и направлен вверх (на читателя).
fb.ru
Момент силы, формулы
Определение 1
Моментом силы представляется крутящий или вращательный момент, являясь при этом векторной физической величиной.
Она определяется как векторное произведение вектора силы, а также радиус-вектора, который проведен от оси вращения к точке приложения указанной силы.
Момент силы выступает характеристикой вращательного воздействия силы на твердое тело. Понятия «вращающий» и «крутящий» моменты не будут считаться при этом тождественными, поскольку в технике понятие «вращающий» момент рассматривают как внешнее, прикладываемое к объекту, усилие.
В то же время, понятие «крутящий» рассматривается в формате внутреннего усилия, возникающего в объекте под воздействием определенных приложенных нагрузок (подобным понятием оперируют при сопротивлении материалов).
Понятие момента силы
Момент силы в физике может рассматриваться в виде так называемой «вращающей силы». В СИ за единицу измерения принимают ньютон-метр. Момент силы также может называться «моментом пары сил», что отмечено в работах Архимеда над рычагами.
Замечание 1
В простых примерах, при приложении силы к рычагу в перпендикулярном отношении к нему, момент силы будет определяться в виде произведения величины указанной силы и расстояния до оси вращения рычага.
К примеру, сила в три ньютона, приложенная на двухметровом расстоянии от оси вращения рычага, создает момент, равнозначный силе в один ньютон, приложенной на 6-метровом расстоянии к рычагу. Более точно момент силы частицы определяют в формате векторного произведения:
$\vec {M}=\vec{r}\vec{F}$, где:
- $\vec {F}$ представляет силу, воздействующая на частицу,
- $\vec {r}$ является радиусом вектора частицы.
В физике следует понимать энергию как скалярную величину, в то время как момент силы будет считаться величиной (псевдо) векторной. Совпадение размерностей подобных величин не будет случайным: момент силы в 1 Н•м, который приложен через целый оборот, совершая механическую работу, сообщает энергию в 2 $\pi$ джоулей. Математически это выглядит так:
$E = M\theta $, где:
- $E$ представляет энергию;
- $M$ считается вращающимся моментом;
- $\theta $ будет углом в радианах.
Сегодня измерение момента силы осуществляют посредством задействования специальных датчиков нагрузки тензометрического, оптического и индуктивного типа.
Формулы расчета момента силы
Интересным в физике является вычисление момента силы в поле, производимого по формуле:
$\vec{M} = \vec{M_1}\vec{F}$, где:
- $\vec{M_1}$ считается моментом рычага;
- $\vec{F}$ представляет величину действующей силы.
Недостатком такого представления будет считаться тот факт, что оно не определяет направление момента силы, а только лишь его величину. При перпендикулярности силы вектору вектору $\vec{r}$ момент рычага будет равен расстоянию от центра до точки приложенной силы. При этом момент силы окажется максимальным:
$\vec{T}=\vec{r}\vec{F}$
При совершении силой определенного действия на каком-либо расстоянии, она совершит механическую работу. Точно также и момент силы (при выполнении действия через угловое расстояние) совершит работу.
$P = \vec {M}\omega $
В существующей международной системе измерений мощность $P$ будет измеряться в Ваттах, а непосредственно момент силы— в ньютон-метрах. При этом угловая скорость определяется в радианах в секунду.
Момент нескольких сил
Замечание 2
При воздействии на тело двух равных, а также противоположно направленных сил, не лежащих при этом на одной и той же прямой, наблюдается отсутствие пребывания этого тела в состоянии равновесия. Это объясняется тем, что результирующий момент указанных сил относительно любой из осей не имеет нулевого значения, поскольку обе представленные силы имеют направленные в одну сторону моменты (пара сил).
В ситуации, когда тело закрепляется на оси, произойдет его вращение под воздействием пары сил. Если пара сил будет приложенной в отношении свободного тела, оно в таком случае станет вращаться вокруг проходящей сквозь центр тяжести тела оси.
Момент пары сил считается одинаковым в отношении любой оси, которая перпендикулярна плоскости пары. При этом суммарный момент $М$ пары всегда будет равным произведению одной из сил $F$ на расстояние $l$ между силами (плечо пары) в независимости от типов отрезков, на которые оно разделяет положение оси.
$M={FL_1+FL-2} = F{L_1+L_2}=FL$
В ситуации, когда равнодействующая момента нескольких сил равнозначна нулю, он будет считаться одинаковым относительно всех параллельных друг другу осей. По этой причине воздействие на тело всех этих сил возможно заменить действием всего лишь одной пары сил с таким же моментом.
spravochnick.ru
