1.Кинематика. Перемещение, скорость, ускорение.
Кинематика – раздел механики, который описывает движение тел, не занимаясь исследованием причин этого движения.
Основные характеристики: траектория движения, перемещение точки, пройденный путь, координаты, скорость, ускорение.
Траектория – линия по которой движется матер. точка в пространстве.
Перемещение – изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Длина отрезка — это модуль перемещения, измеряется в метрах.
Можно определить перемещение, как изменение радиус-вектораточки:. Модуль перемещения совпадает с пройденным путёмв том и только в том случае, если при движении направление перемещения не изменяется. При этомтраекториейбудет отрезок прямой. В любом другом случае, например, при криволинейном движении, изнеравенства треугольникаследует, что путь строго больше.
Мгновенная скоростьточки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Более строго:
.
Ско́рость – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта .Скорость мат. точки представляет собой вектор, характеризующий направление и быстроту перемещения мат. точки относительно тела отсчета.
Вектор ускорения характеризует быстроту и направление изменения скорости мат. точки отн-но тела отсчета.
Скорость движения определяется как производная координат по времени:
,
где — единичные векторы, направленные вдоль соответствующих координат.
Ускоре́ние, производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).
Ускорение определяется как производная скорости по времени:
.
Ускорение бывает тангенциальным, центростремительным, угловым
2.Законы Ньютона
Зако́ны Ньюто́на — три эмпирических закона, лежащих в основе классической механики и позволяющих записать уравнения движения для любой механической системы исходя из известных силовых взаимодействий на составляющие её тела.
I з-н Ньютона: сущствуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Инерция— это явление сохранения телом скорости движения , когда на тело не действуют никакие силы. Тела обладают инертностью.Инертность— это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
II з-н Ньютона:
где — ускорение материальной точки;—сила, приложенная к материальной точке; m — масса материальной точки.
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.
где -импульсточки(где-скоростьточки)t -время;-производнаяимпульса по времени.
Когда на тело действуют несколько сил, с учётом принципа суперпозициивторой закон Ньютона записывается:
III з-н Ньютона
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникаетзакон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел, то возникаетзакон сохранения суммарной механической энергиивзаимодействующих тел:
Траектория путь перемещение скорость ускорение определение
Линию, вдоль которой движется материальная точка, называют траекторией. Длину траектории называют путем. Единица пути — метр.
Путь = скорость* время. S=v*t.
Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением (s). Перемещение — величина векторная. Единица перемещения — метр.
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка времени.
Формула скорости имеет вид v = s/t. Единица скорости — м/с
Составляющие ускорения тангенциальное и нормальное ускорения
Тангенциальное ускорение направлено по касательной к траектории
Нормальное ускорение направлено по нормали к траектории
Тангенциальное ускорение характеризует изменение скорости по величине. Если скорость по величине не изменяется, то тангенциальная составляющая равна нулю, а нормальная составляющая ускорения равна полному ускорению.
Нормальное ускорение характеризует изменение скорости по направлению. Если направление скорости не изменяется, движение происходит по прямолинейной траектории.
В общем случае полное ускорение:
Итак, нормальная составляющая вектора ускорения
быстрота изменения со временем направления касательной к траектории. Она тем больше ( ), чем больше искривлена траектория и чем быстрее перемещается частица по траектории.
4)Угловой путь
Угловой путь – это элементарный угол поворота:
, .
Радиан – это угол, который вырезает на окружности дугу, равную радиусу.
Направление углового пути определяется правилом правого винта: если головку винта вращать в направлении движения точки по окружности, то поступательное движение острия винта укажет направление .
Угловая скорость (средняя и мгновенная)
Средняя угловая скорость – это физическая величина, численно равная отношению углового пути к промежутку времени
, .
Мгновенная угловая скорость – это физическая величина, численно равная изменения пределу отношения углового пути к промежутку времени при стремлении данного промежутка к нулю, или является первой производной углового пути по времени:
, .
Угловое ускорение (среднее и мгновенное)
Среднее угловое ускорение – это физическая величина, численно равная отношению изменения угловой скорости к промежутку времени, за который это изменение произошло:
, .
Мгновенное угловое ускорение
, .
При ускоренном движении угловое ускорение совпадает по направлению с угловой скоростью. При замедленном вращении угловое ускорение направлено в противоположную относительно угловой скорости сторону.
Законы Ньютона
Первый закон Ньютона
- Инерциальной называется та система отсчёта, относительно которой любая, изолированная от внешних воздействий, материальная точка либо покоится, либо сохраняет состояние равномерного прямолинейного движения.
- Первый закон Ньютона гласит:
| Инерциальные системы отсчёта существуют. |
По сути, этот закон постулирует инерцию тел, что сегодня кажется очевидным. Но это было далеко не так на заре исследования природы. Аристотель вот утверждал, что причиной всякого движения является сила, т. е. движения по инерции для него не существовало. [источник?]
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и её ускорением.
Второй закон Ньютона утверждает, что
| в инерциальной системе отсчета (ИСО) ускорение, которое получает материальная точка, прямо пропорционально приложенной силе и обратно пропорционально массе. |
При подходящем выборе единиц измерения этот закон можно записать в виде формулы:
где — ускорение тела;
— сила, приложенная к телу;
m — масса тела.
Или в более известном виде:
Если на тело действуют несколько сил, то второй закон Ньютона записывается:
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется в общем виде: скорость изменения импульса точки равна действующей на неё силе.
где — импульс (количество движения) точки;
t — время;
— производная по времени.
Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.
Третий закон Ньютона
Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Сам закон:
| Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению: |
Выводы
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U( | r1 − r2 | ). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.
infopedia.su
I.1.3 СКОРОСТЬ. УСКОРЕНИЕ.
Для характеристики быстроты движения тел в механике вводится понятие скорости.
Различают: среднюю и мгновенную скорости.
Средней скоростью за промежуток времени называется физическая величина, равная отношению приращения радиус-вектора материальной точки к промежутку времени :
. (I.3)
Средняя скорость характеризует движение в течение всего того промежутка времени, для которого она определена.
Направление вектора средней скорости совпадает с направлением приращения радиус-вектора, т.е. направлен вдоль хорды, стягивающей соответствующий участок траектории точки (рис. 4 и 6).
Мгновенной скоростью (скоростью), называется физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени :
. (I.4)
Мгновенная скорость является первой производной по времени от радиус-вектора рассматриваемой точки:
. (I.5)
Вектор мгновенной скорости материальной точки направлен по касательной к траектории в сторону движения (рис. 6).
|
Для характеристики быстроты изменения скорости точки в механике вводится понятие ускорения.
Средним ускорением называется физическая величина, равная отношению изменения скорости материальной точки к длительности промежутка времени , в течение которого это изменение произошло:
. (I.6)
Направление векторов и совпадают (рис.7).
|
Мгновенным ускорением (ускорением) материальной точки в момент времени называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении промежутка времени :
. (I.7)
Мгновенное ускорение является первой производной по времени скорости рассматриваемой точки, или второй производной по времени от радиус-вектора этой точки:
. (I.8)
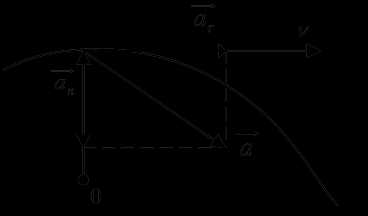
Вектор ускорения точки можно разложить на две составляющие: тангенциальную и нормальную .
Тангенциальная составляющая вектора ускорения направлена вдоль касательной к траектории в данной точке и называется тангенциальным (касательным) ускорением:
. (I.9)
Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор направлен в сторону движения точки при возрастании её скорости и в противоположную сторону – при убывании скорости.
Нормальная составляющая вектора ускорения, направлена по нормали к траектории к центру её кривизны в данной точке и называется нормальным (центростремительным) ускорением:
. (1.10)
Нормальное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении.
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.8):
. (I.11)
|
В зависимости от тангенциальной и нормальной составляющих ускорения, движение будет подразделяться на несколько видов (таблица 1.):
Таблица 1. Классификация движения в зависимости от составляющих ускорения: тангенциального ( ) и нормального ( ).
Похожие статьи:
poznayka.org
Ускорение | Физика
Мы выяснили, что движущийся по дороге автомобиль практически все время изменяет свою скорость. Так, если во время движения водитель нажимает на педаль тормоза, скорость автомобиля уменьшается. Если водитель нажимает на педаль газа, скорость автомобиля, наоборот, возрастает. При этом под словом «скорость» мы подразумеваем, как это было отмечено в предыдущем параграфе, мгновенную скорость.
Таким образом, если водитель нажмет на педаль тормоза сильно, скорость автомобиля начнет изменяться быстро, и вскоре он остановится. При слабом нажатии на тормоз скорость автомобиля будет уменьшаться медленно, и до момента остановки, когда скорость автомобиля станет равной нулю, пройдет больше времени (рис. 52). Можно сказать, что изменение скорости при этом происходит с разной быстротой.

Из приведенного примера ясно, что быстрота изменения скорости определяется начальным и конечным значениями скорости и промежутком времени, за который произошло изменение скорости.
Величину, характеризующую быстроту изменения скорости, называют ускорением.
При решении задач о прямолинейном движении тел используют понятие «значение ускорения».
Значением среднего ускорения тела за промежуток времени tк – t0 называют отношение изменения значения скорости тела за данный промежуток времени к длительности этого промежутка.
aср = (vк – v0) / (tк – t0)
Значение среднего ускорения в СИ измеряют в метрах на секунду в квадрате (м/с2), так как скорость измеряют в метрах в секунду, а время – в секундах.
Поясним сказанное на примерах.
Пусть автомобиль в некоторый начальный момент времени t0 = 0 двигался в положительном направлении оси X, как показано на рис. 53, а, со скоростью, имевшей значение v0 = 10 м/с. К моменту времени tк = 2 с значение его скорости увеличилось до vк = 16 м/с (автомобиль разгонялся), а направление движения осталось неизменным. Поэтому в соответствии с определением значение среднего ускорения автомобиля за эти две секунды
aср = (vк – v0) / (tк – t0) = (16 – 10) / (2 – 0) = 3 (м/с2).
Так как увеличение значения скорости происходило в положительном направлении оси X, то и изменение скорости, а следовательно, и значение среднего ускорения будут положительными.
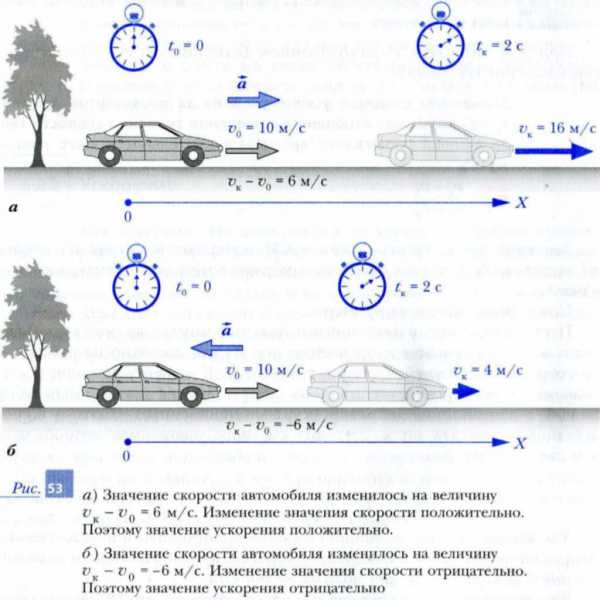
Значение среднего ускорения a = 3 м/с2 означает, что за каждую секунду скорость автомобиля увеличивалось в среднем на 3 м/с.
Пусть теперь автомобиль, который в начальный момент двигался в положительном направлении оси X со скоростью, имеющей значение v0 = 10 м/с, за две секунды уменьшил свою скорость до vк = 4 м/с (рис. 53, б). Тогда по определению значение среднего ускорения за эти две секунды будет таким же но модулю, как и в первом случае, но противоположным но знаку:
aср = (vк – v0) / (tк – t0) = (4 – 10) / (2 – 0) = -3 (м/с2).
Так как значение скорости уменьшается (vк < v0), то и изменение значения скорости Δv, и значение среднего ускорения получаются отрицательными.
Значение среднего ускорения a = -3 м/с2 означает, что за каждую секунду скорость автомобиля уменьшалась в среднем на 3 м/с (автомобиль тормозил).
Поскольку скорость является векторной величиной, то и изменение скорости – тоже вектор. Из рис. 53 следует, что, когда происходит разгон автомобиля, вектор изменения скорости направлен туда же, куда направлен вектор скорости.
Когда скорость автомобиля уменьшается (при торможении), вектор изменения скорости направлен противоположно вектору скорости.
Средним ускорением тела за промежуток времени Δt называют физическую величину, равную отношению изменения скорости этого тела за промежуток времени Δt к длительности этого промежутка.
aср = Δv/Δt
Из определения видно, что среднее ускорение является векторной величиной.
Направление среднего ускорения совпадает с направлением вектора изменения скорости за рассматриваемый промежуток времени.
Из определения следует, что среднее ускорение в СИ измеряют в метрах на секунду в квадрате (м/с2), так как скорость измеряют в метрах в секунду, а время – в секундах.
При уменьшении рассматриваемого промежутка времени до достаточно малого мы придем к понятию ускорения в данный момент времени.
Так же как и при определении мгновенной скорости, можно сказать, что
ускорение в данный момент времени t – это среднее ускорение за достаточно малый промежуток времени Δt, который начинается сразу после момента времени t.
Смысл словосочетания «достаточно малый промежуток времени» остается тем же самым, что и в предыдущем параграфе. Под этим промежутком подразумевается настолько малый промежуток времени, что его дальнейшее уменьшение не приводит к заметным изменениям определяемой нами величины (здесь — ускорения!).
Итоги
Величину, характеризующую быстроту изменения скорости, называют ускорением.
В СИ ускорение измеряют в метрах на секунду в квадрате (м/с2).
Значением среднего ускорения тела за промежуток времени Δt = tк – t0 называют отношение изменения значения скорости тела за данный промежуток времени к длительности этого промежутка.
aср = (vк – v0) / (tк – t0)
Вопросы
- Что такое ускорение тела? Приведите примеры движения тела с ускорением.
- Дайте определение значения среднего ускорения тела. Назовите единицу ускорения в СИ.
- Какой знак имеет значение ускорения при прямолинейном движении в положительном направлении оси X, если тело: а) разгоняется; б) тормозится? Куда при этом направлен вектор ускорения?
Упражнения
- Велосипедист, двигаясь в положительном направлении оси X, за 10 с увеличил свою скорость на 20 м/с. Определите значение среднего ускорения велосипедиста за этот промежуток времени.
- Мотоциклист, приближаясь к повороту, уменьшает модуль своей скорости от 108 до З6 км/ч. Определите значение среднего ускорения мотоциклиста, если он тормозил в течение 5 с. Считайте, что направление движения мотоциклиста совпадает с положительным направлением координатной оси.
phscs.ru
Координата, время, скорость, ускорение : Физика
Предыдущие ораторы всё правильно ответили. Особенно, учитывая школьный возраст ТС. А теперь я позволю себе несколько крамольных мыслей.Начнем с размерностей. Пусть у нас м.т. (материальная точка) совершает движение, зависимость ее скорости от времени известна, за время она приходит в какое-то конечное положение, которое можно рассчитать, проинтегрировав скорость по времени (с точностью до произвольной константы). Поделив теперь разность координат конечной и начальной точек (ака перемещение, если не ошибаюсь) на время движения мы получим вполне физически осмысленную характеристику – скорость, с которой надо было двигаться нашей точке прямолинейно и равномерно на всем интервале , чтобы прийти в ту же самую конечную точку. И размерность у этой характеристики – размерность скорости.
Проделаем то же самое для координаты. Проинтегрируем, получим некую характеристику с точностью до константы, посчитаем разность ее конечного и начального значений. Получим нечто размерности расстояние*время (пока не будем давать этому название), поделим его на наше , получим некую координату. Каков ее физический смысл? Это точка пространства, которой наша м.т. интегрально (в среднем) “уделяет больше всего времени”. Если положение этой точки в пространстве стационарно, то можно говорить о некоем “центре притяжения движения” (теперь меня точно в альты запишут), если нестационарно – то тоже интересная характеристика движения. Куда это можно практически применить? Например, некто ходит на работу, в бар и домой спать, причем, проводит в дороге не бесконечно малое время. Допустим, туалета негде нет, а наш некто испытывает регулярную в нем потребность, но мы можем поставить его только один. В какой точке нам надо его поставить “наиболее оптимально”, чтобы минимизировать (за большой промежуток времени) расстояние, которое наш некто будет преодолевать до туалета и обратно? Я подозреваю, что именно в “центре притяжения движения”.
dxdy.ru
