2 закон ньютона в общем виде?
Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению) , когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО) .
или
Первый закон Ньютона
* Первый закон Ньютона гласит: существуют системы отсчёта (называемые инерциальными) , в которых замкнутая система продолжает оставаться в состоянии покоя или прямолинейного равномерного движения. По сути, этот закон постулирует инертность тел. Это может казаться очевидным сейчас, но это не было очевидно на заре исследований природы. Так, например, Аристотель утверждал, что причиной всякого движения является сила, т. е. у него не было движения по инерции.
Инерциальная система отсчёта – это система отсчёта, связанная со свободным невращающимся телом. Свободное тело — тело, не взаимодействующее с другими телами.
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к телу силой и ускорением этого тела. Один из трех законов Ньютона.
Второй закон Ньютона утверждает, что ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела.
Этот закон записывается в виде формулы:
\vec a = \vec {F} / m
где \vec a — ускорение тела, \vec {F} — сила, приложенная к телу, а m — масса тела.
Или, в более известном виде:
\vec {F} = m\vec a
Если на тело действуют несколько сил, то во втором законе Ньютона под \vec {F} подразумевается равнодействующая всех сил.
В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в более общем виде:
\frac{d(m\vec \upsilon)}{dt} = \vec {F}
где m\vec \upsilon — импульс (количество движения) тела, t — время, а \frac{d}{dt} — производная по времени. Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. →
В данном законе как частный случай заключен первый закон Ньютона. Это можно видеть если \vec {F} = 0 (т. е. если на тело не действуют силы или равнодействующая сил равна нулю) при этом соответственно получаем что и \vec a = 0, а значит, тело сохраняет состояние покоя или равномерного прямолинейного движения.
otvet.mail.ru
9 Второй закон ньютона
1. Второй закон Ньютона отвечает на вопрос, каким будет движение тела относительно инерциальной системы отсчета при наличии сил.
Этот закон утверждает: тело под действием силы приобретает ускорение, пропорциональное этой силе.
Несмотря на то, что второй закон динамики является обобщением опытных фактов, проверить его со всей строгостью непосредственно на опыте, в реальных земных условиях невозможно. На опыте этот закон оправдывается лишь приближенно.
Почему?
Во-первых, потому, что во всех таких опытах неизбежно присутствуют дополнительные воздействия (трение, сопротивление среды и т.д.), учесть которые оказывается далеко не просто.
Во-вторых, потому, что опыты проводятся на Земле – в неинерциальной системе отсчета, в системе, которая сама
2.
Будем воздействовать на одно и то же
тело разными силами и всякий раз находить
отношение силы к соответствующему
ускорению –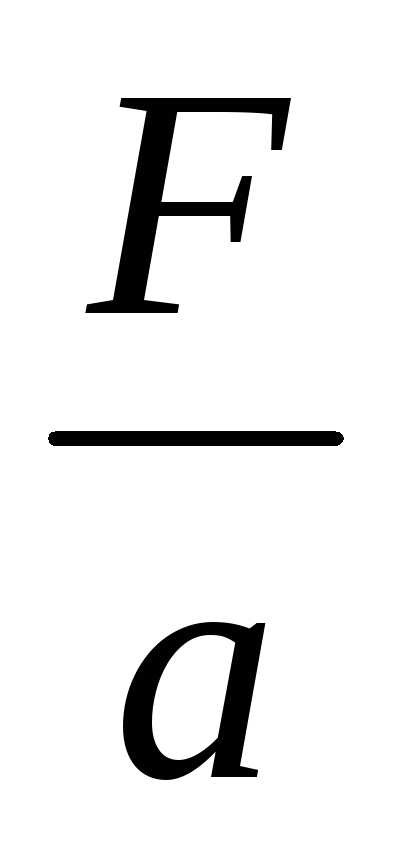 
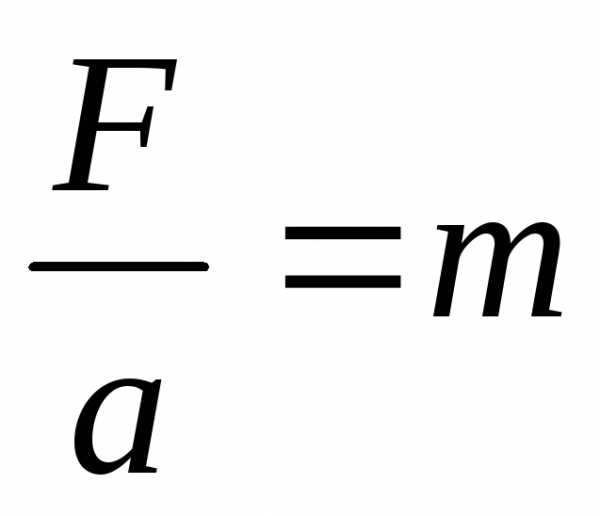(9.1)
Можно
убедиться в том, что отношение силы к
сообщаемому ею ускорению постоянно для
любых других тел (при этом величина его
может оказаться разной). Мы приходим к
выводу, что отношение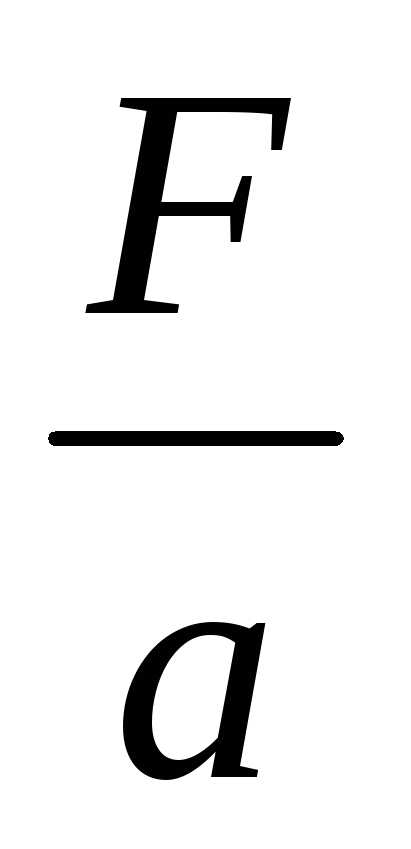 
зависит только от того,
к какому телу приложена сила. Следовательно,
величина 
Свойство тел изменять величину и направление скорости постепенно называется инерцией.
Можно сказать, таким образом, что масса есть количественная мера инерции материальных тел.
Чем больше масса тела, тем меньшее ускорение оно приобретает под действием данной силы, т.е. тем
Масса тела не зависит от температуры тела, его агрегатного состояния, химического состава, электрических, магнитных, упругих и иных свойств. В классической механике масса полагается величиной аддитивной (масса составного тела равна сумме масс отдельных его частей и не зависящей от скорости движения). Содержание массы, однако, не исчерпывается одними только динамическими проявлениями. В ряде физических явлений масса служит мерой иных свойств материальных объектов. Поэтому часто массу, фигурирующую во втором законе Ньютона и характеризующую инерционные свойства тел, называют «инертной».
3. Соотношение (9.1) позволяет по динамическому эффекту, обусловленному силой,- ускорению, найти массу тела.
Мы будем, однако, полагать, что масса измерена каким-либо другим способом (это возможно). Тогда соотношение (9.1) можно толковать как зависимость ускорения не только от силы, но и от массы:
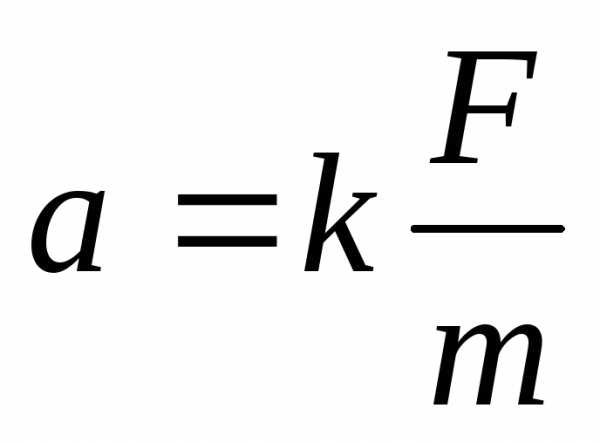, (9.2)
k – коэффициент пропорциональности, зависящий от выбора единиц измерения ускорения, силы и массы. Эти единицы выбирают таким образом, чтобы k = 1.
Тогда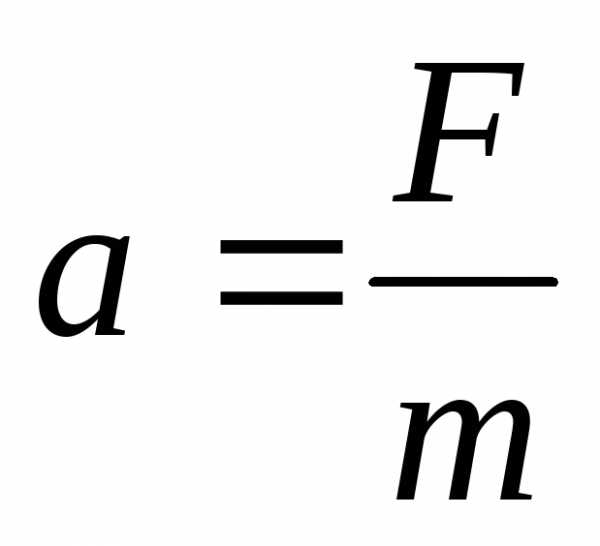 
(9.3)
Опыт
показывает, что направление ускорения
всегда совпадает с направлением силы,
вызвавшей это ускорение. Учитывая
направления 
и
,
получаем: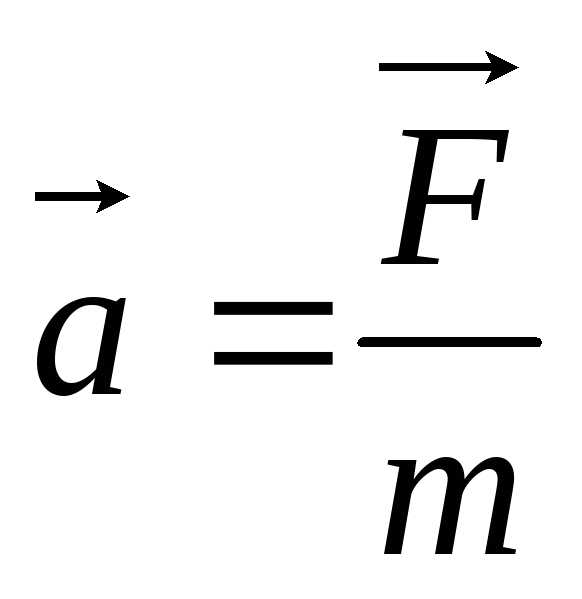 
. (9.4)
Это – одна из простейших формулировок второго закона Ньютона.
Ускорение, приобретаемое телом относительно инерциальной системы отсчета, прямо пропорционально силе, действующей на тело, зависит от массы тела и направлено в сторону силы.
4. Формулу (9.4) можно записать в виде
(9.5)
Это соотношение используется в качестве определяющего уравнения при установлении единиц измерения силы.
В
системе СИ масса измеряется в килограммах
(сокращенно кг),
ускорение – в метрах на секунду за
секунду (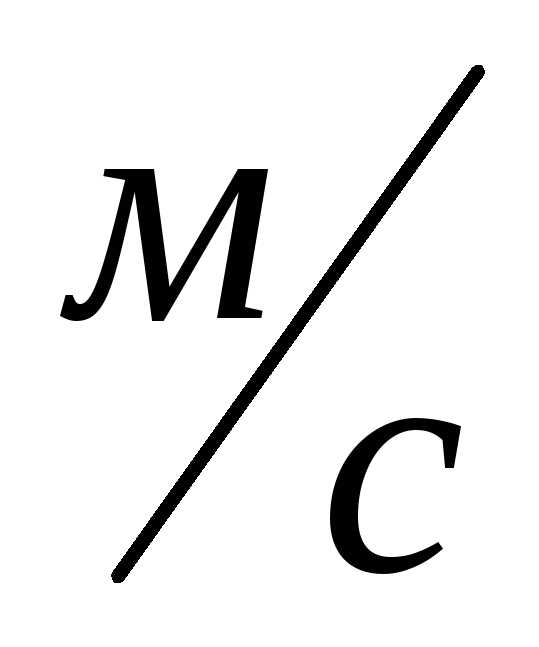
2).
Единицей силы в системе СИ является
ньютон (Н). Ньютон – это такая сила, под
действием которой тело массой в 1кг приобретает ускорение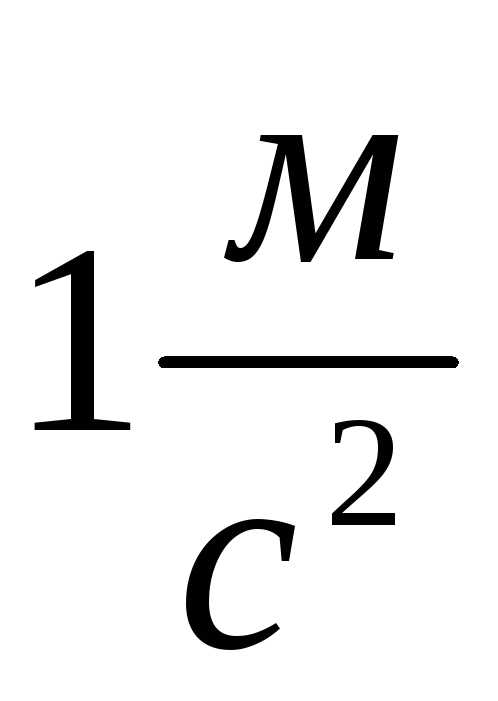 
:
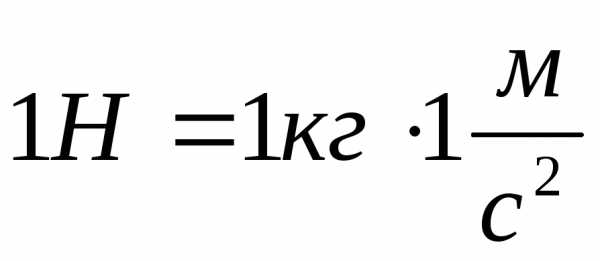
Силу
часто измеряют в килограммах (кГ).
Килограмм – это такая сила, которая
телу массой 1кг сообщает ускорение 9,8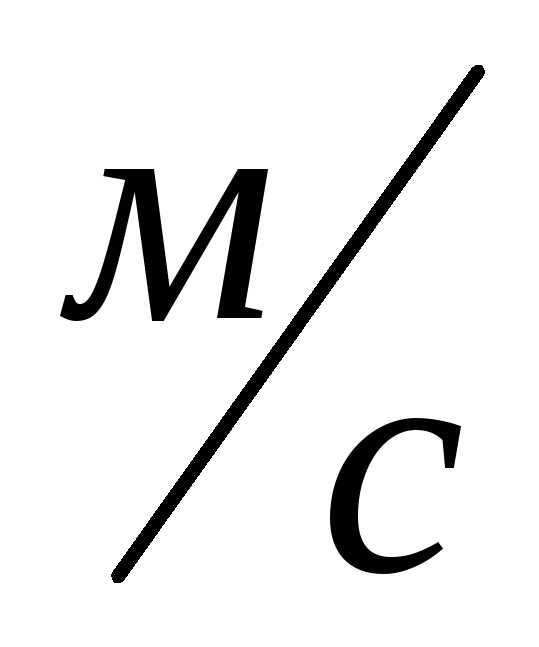 
2:
.
5. Чтобы перейти от векторной формы записи второго закона к скалярной, векторные величины соотношения (9.5) следует спроектировать на координатные оси выбранной системы координат:
тах = Fx;
таy = Fу ;
таz = Fz;
6. Опыт показывает, что при взаимодействии материальных тел выполняется принцип независимости действия сил (принцип суперпозиций): если на тело одновременно действует несколько сил, то действие каждой силы происходит независимо от других. Это значит, что
деформация или ускорение, обусловленные данной силой, будут тако-выми, как если бы других сил не было.
Следовательно,
в общем случае, когда на тело одновременно
действуют несколько сил, под 
— геометрическую сумму
всех действующих сил, а не какую-то
«особую» силу ускорения: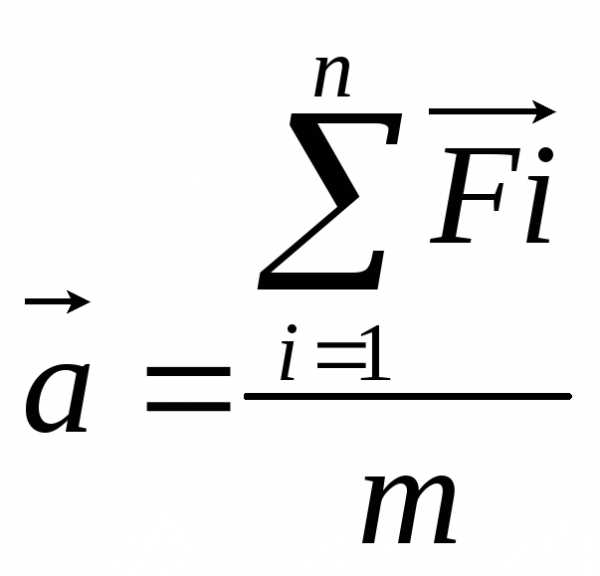 
. (9.7)
т.е. ускорение, приобретенное телом, прямо пропорционально результирующей всех действующих на тело сил и обратно пропорционально его массе.
7. Приведем теперь более общую формулировку второго закона Ньютона.
20 м/с; «запасы» механического движения этих тел различны, несмотря на одинаковую скорость. По-видимому, должна существовать единая мера механического движения, одинаковая для всех тел. Такая мера действительно существует и называется импульсом или количеством движения.
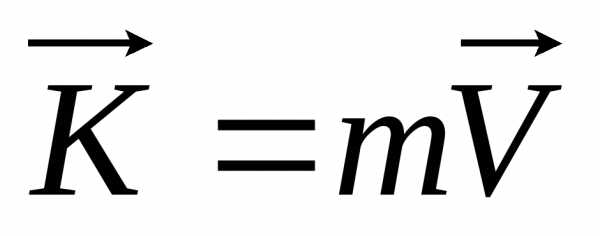(9.8)
Заметим, что численное значение импульса и его направление зависят от выбора системы отсчета, так как от системы отсчета зависит величина и направление скорости.
Опыт показывает, что изменение импульса тела однозначно связано с величиной и направлением силы, которая на него действует. Пусть в некоторый момент времени
.
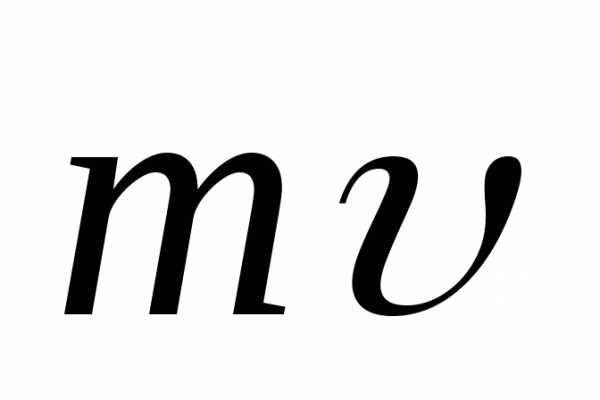Под действием силы
(она может быть переменной) за элементарный
проме-жуток времени
импульс
тела изменился на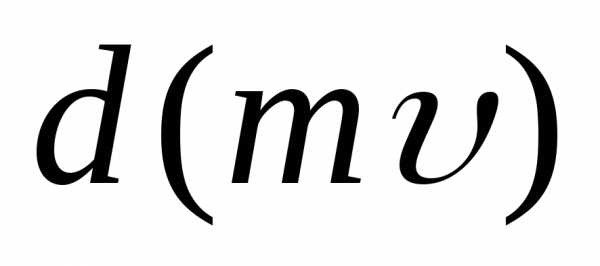
(в случае переменной силы промежуток
времени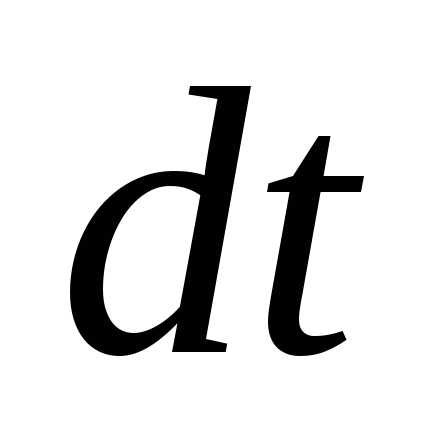
должен быть таким, чтобы сила в течение
этого промежутка времени практическине изменялась).
Разделив изменение импульса на промежуток
времени, в течение которого это изменение
произошло, мы рассчитаем, на сколько
изменился импульс за единицу времени
при условии, что во все последующие
интервалы времени движение будет
изменяться точно такими же темпами, что
и в течение промежутка
.
Отношение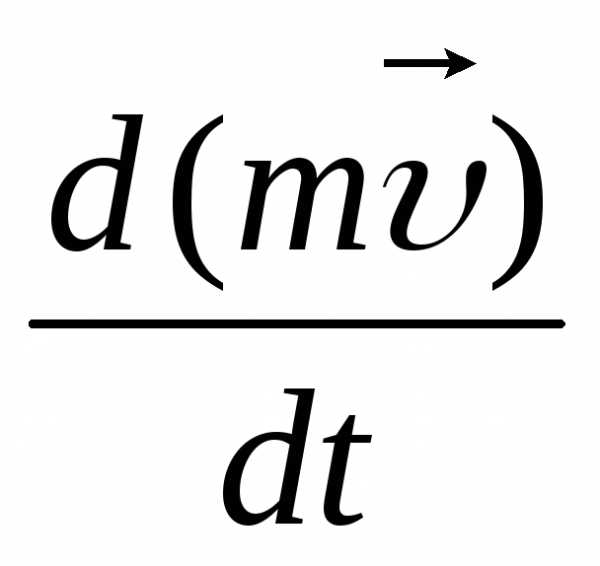
есть скорость
изменения импульса.Ньютон установил, что скорость изменения импульса тела (произ-водная от импульса по времени), равна по величине действующей силе и совпадает с ней по направлению:
(9.9)
Это соотношение и есть общая форма математической записи второго закона Ньютона. Из этой формулы можно получить тот частный вид математического выражения второго закона, который мы привели выше. Действительно, если масса не изменяется с течением времени, то ее можно вынести за знак производной:
,
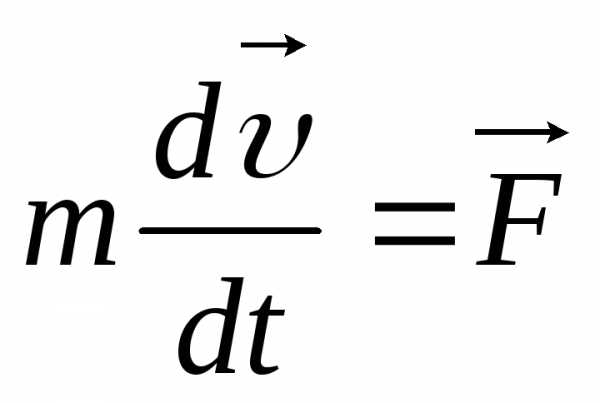но 
,
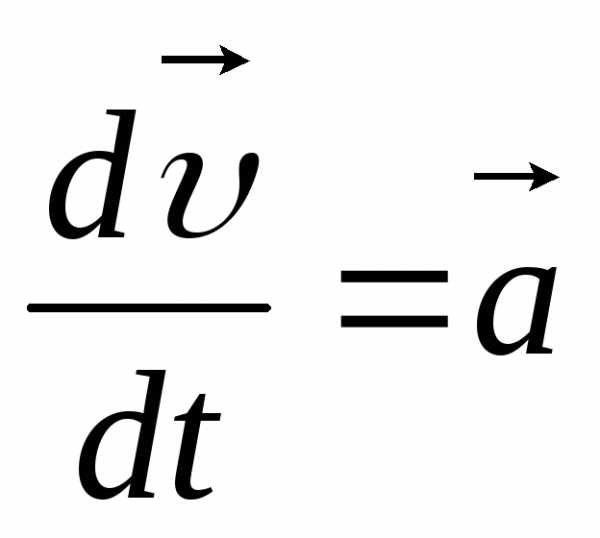следовательно,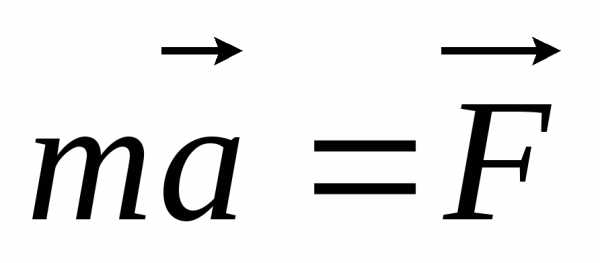
.
8. Создавая свою механику, Ньютон не подозревал, что масса, так же как и пространство, и время, – понятие относительное, зависящее от системы отсчета, от скорости движения. Поэтому предположение о неизменности массы без каких-либо специальных оговорок молчаливо положено в основу классической механики.
С точки зрения ньютоновской механики выражение второго закона динамик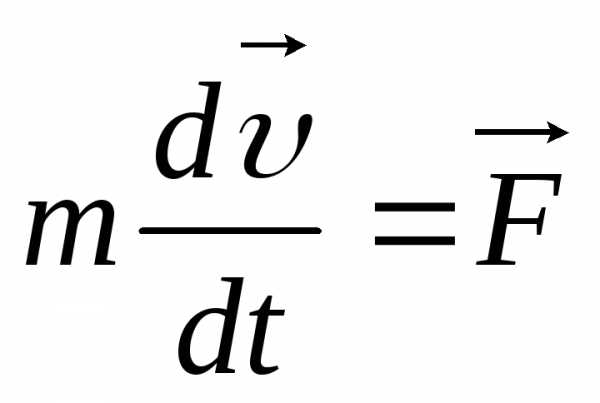и
,
и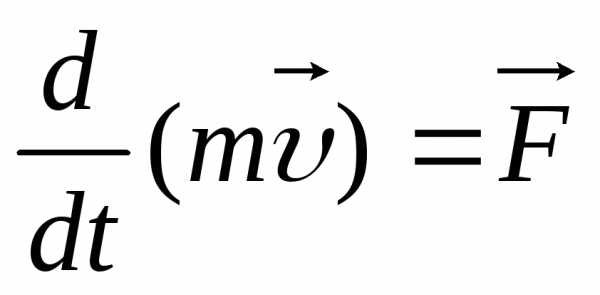 
тождественны.
С точки зрения современной физики эти формулы равноправны только для медленных (по сравнению со скоростью света) движений, когда изменением массы, обусловленным изменением скорости тела, можно пренебречь.
При скоростях, соизмеримых со скоростью света, эффект возрастания массы будет столь ощутим, что формула (9.5) оказывается непригодной. Для быстрых движений необходимо пользоваться формулой (9.9). Дифференцируя левую часть этого уравнения по правилам дифференцирования сложной функции, получим:
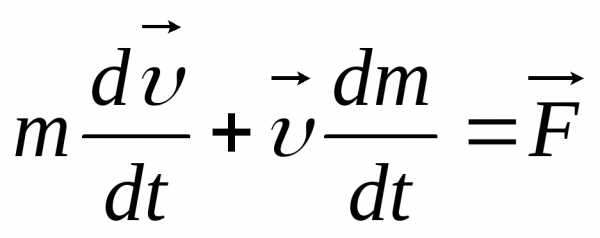. (9.10)
9. Соотношение (9.9) позволяет сделать вывод о том, что сила характеризует процесс передачи механического движения от одного тела к другому и численно равна импульсу, передаваемому за единицу времени.
10.
Математическое выражение второго закона
часто приводят еще в одном виде. Умножим
обе части уравнения (9.9) на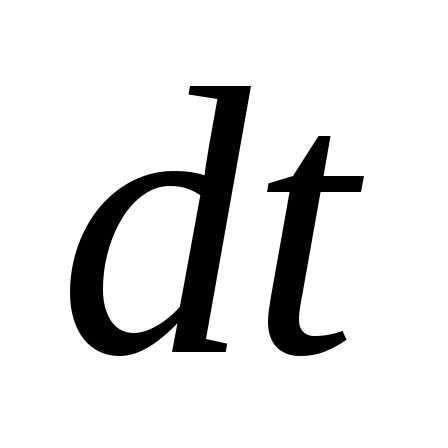
:
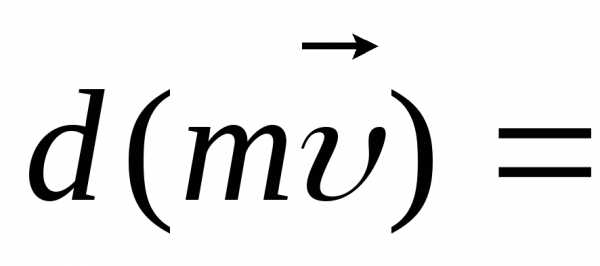
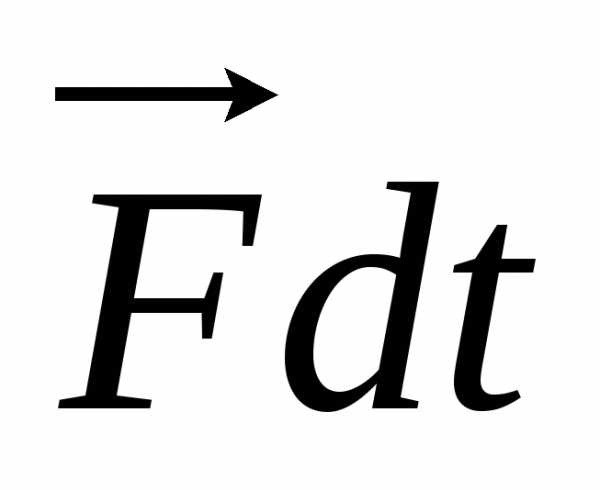. (9.11)
Величина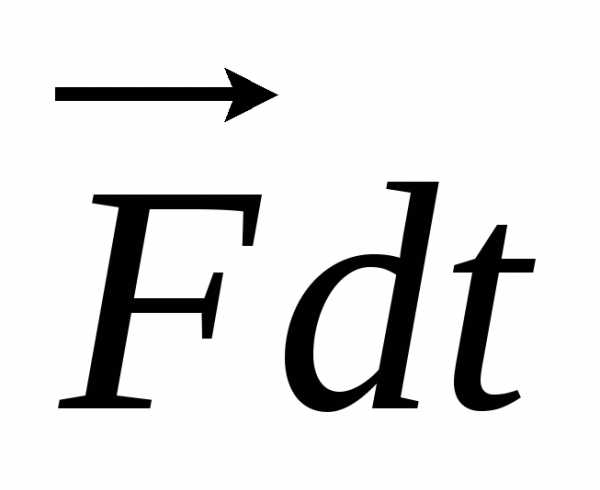 
описывает действие силы во времени и
называетсяимпульсом
силы.
Импульс силы – это вектор, численно равный произведению силы на время ее действия и совпадающий по направлению с направлением силы.
В
левой части соотношения (9.11) стоит
изменение импульса тела за элементарный
промежуток времени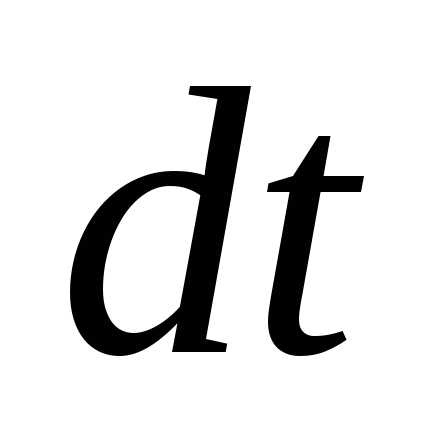 
.
Таким образом,изменение
импульса тела за время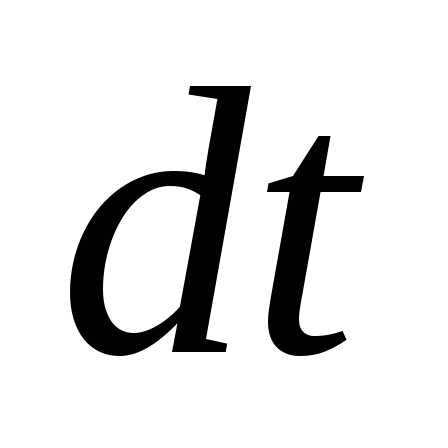 
равно импульсу действующей на него силы
за тот же промежуток.
Это еще одна из формулировок второго
закона Ньютона.
11.
Из формулы (9.11) видно, что второй закон
Ньютона – закон дифференциальный. Его
можно привести к интегральному виду.
Обозначим импульс буквой 
и перепишем формулу (9.11):
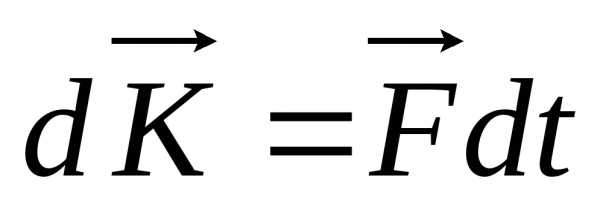(9.12)
Сложим все элементарные приращения импульса за конечный промежуток времени и одновременно подсчитаем импульс действующей силы за тот же промежуток. Для этого возьмем определенные интегралы от левой и правой частей соотношения (9.12):
. (9.13)
Если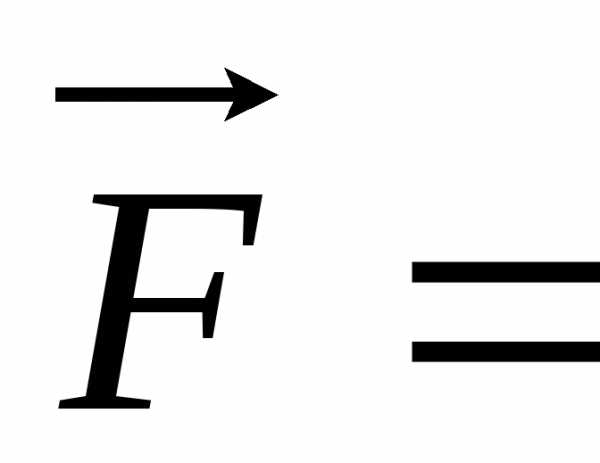 
const,
мы получим: 
2 – 
1 =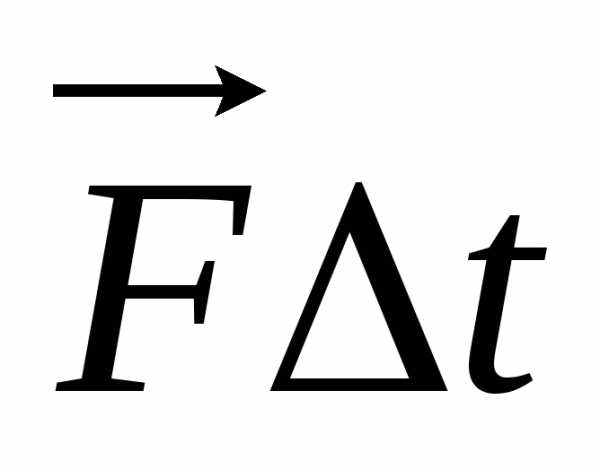 
(9.14)
Если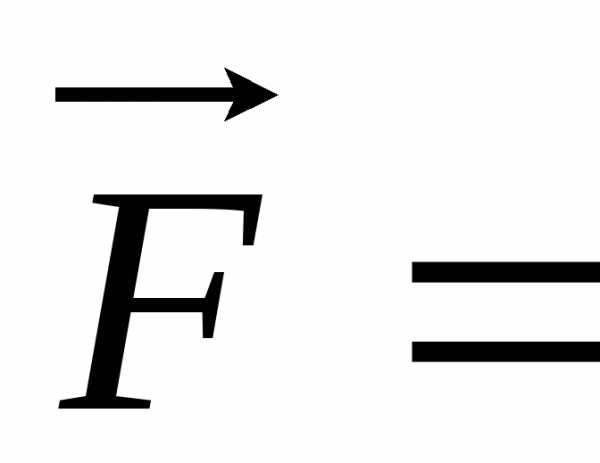 
,
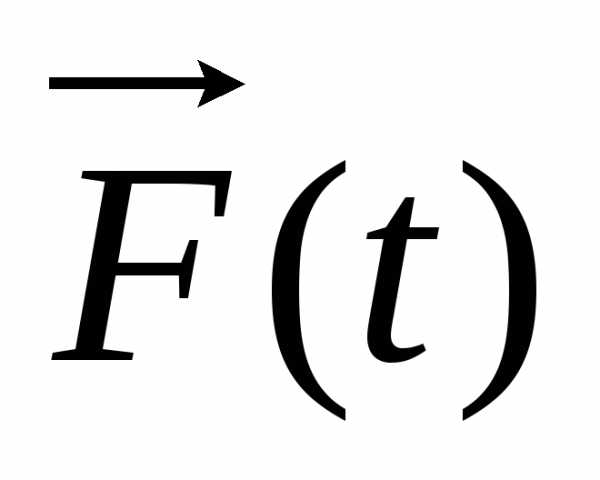то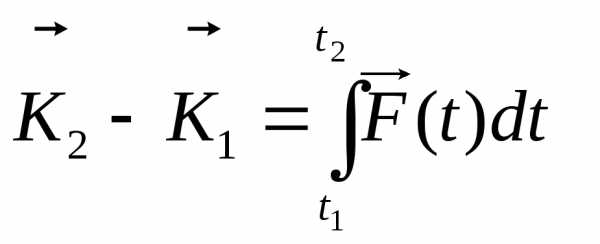
(9.15)
12. Обратимся к более подробному рассмотрению понятия инерции.
Инерция – важнейшее свойство, присущее всем материальным объектам (в том числе и полевой форме материи). Этим свойством тела обладают независимо от того, свободны они или взаимодействуют с другими телами, покоятся или движутся.
Необходимо чётко представлять, в чем проявляется инерция тел в различных условиях: в отсутствии внешнего воздействия и при наличии такового.
Ответ на этот вопрос дают первый и второй законы Ньютона.
В отсутствие внешнего воздействия инерция проявляется в том, что тело сохраняет неизменным свое состояние движения или покоя.
При наличии внешнего воздействия – сил, инерция проявляется не в том, что тело стремится сохранить свое состояние движения неизменным (ибо как только нескомпенсированая, даже сколь угодно малая сила начинает действовать, движение тела – величина и направление скорости – тотчас же изменяются, возникает ускорение), а в том, что изменения движения тела происходит постепенно.
Следовательно, инерция – это свойство тела сохранять имеющееся состояние движения или покоя (относительно инерциальной системы отсчета) неизменным при отсутствии воздействия и изменять это состояние постепенно при наличии воздействия.
С проявлениями инерции мы сталкиваемся очень часто. Но, к сожалению, объяснения этих проявлений иногда бывают ошибочными. Поэтому мы рассмотрим здесь один пример. Пусть на гладком, без бортиков столике движущегося вагона лежит предмет. При резком торможении поезда этот предмет может соскользнуть со столика. Почему? Потому, отвечают некоторые, «что предмет сохраняет свою первоначальную скорость», «продолжает двигаться по инерции». Такое объяснение, в сущности, ошибочно.
В самом деле, почему столик изменяет свою скорость, а предмет ее сохраняет? Могут ответить: «на столик действует тормозящая сила со стороны вагона (столик жестко скреплен с вагоном). Это верно, но разве на предмет не действует тормозящая сила? Действует! Тормозящей силой для предмета является сила трения, приложенная к нему со стороны столика (при торможении поезда эта сила направлена в сторону, противоположную движению). Так как на предмет действует неуравновешенная сила, скорость его (относительно полотна дороги) не может сохраняться, она изменяется! Вся суть в том, что изменение скорости столика и предмета происходят неодинаково быстро, иными словами, столик и предмет приобретают разные ускорения: столик большее, предмет меньшее. В результате предмет, опережая столик, начнет скользить по его поверхности в направлении по ходу поезда. Если же сила трения, действующая на предмет, достаточна для того, чтобы сообщить предмету такое же точно ускорение, какое имеет столик, – никаких относительных перемещений происходить не будет: столик и предмет будут тормозиться или ускоряться как единое целое.
Таким образом, инерционные эффекты объясняются не тем, что одни тела «сохраняют» свое движение (или покой) неизменным, а другие, напротив, изменяют, а тем, что изменение движения, изменение скорости всех взаимодействующих тел происходит неодинаково бы-стро: одни тела изменяют свое движение быстрее, другие медленнее. В результате мы наблюдаем относительные перемещения тел.
И еще одно обстоятельство не следует забывать. Изменение скорости тела зависит не от одной только инерции (читай: массы) тела. Оно зависит также от величины силы и времени ее воздействия.
studfiles.net
§2.2 Силы. 2-й закон Ньютона.
2-й закон Ньютона: Ускорение, которое приобретает тело прямо пропорционально результирующей всех сил, действующих на тело и обратно пропорционально массе.
,
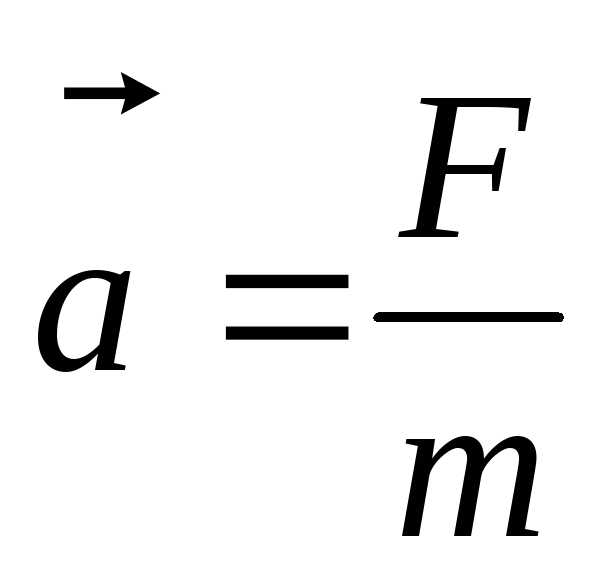Силой называется векторная физическая величина, которая характеризует действие одного тела на другое.
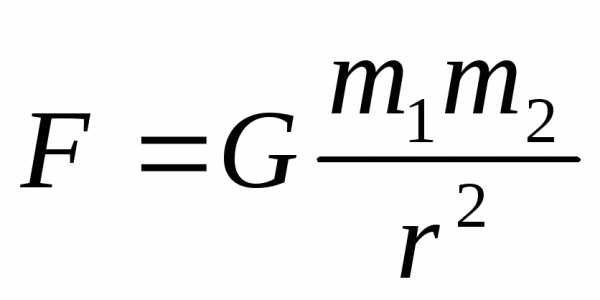
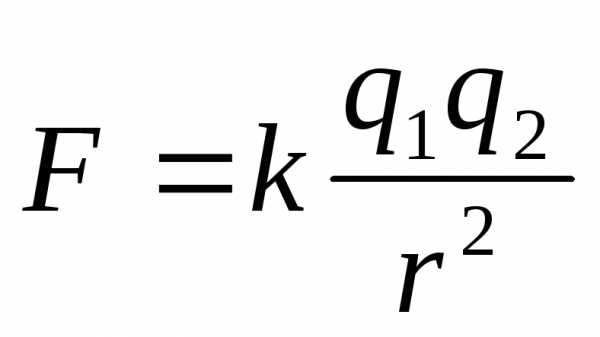
F=qυBsinα
§2.3 Импульсная форма 2-го закона Ньютона.
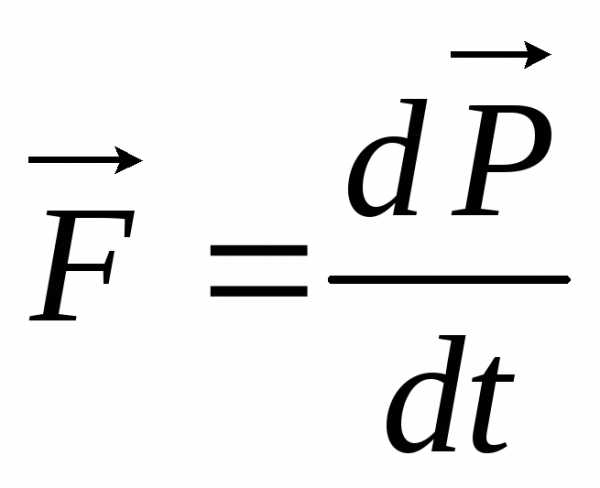– 2-й закон Ньютона – общая формулировка
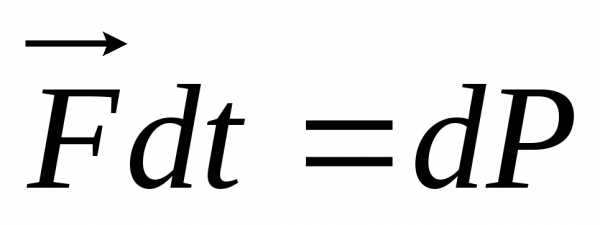
Действие
силы в течении tприводит к изменению импульса тела.
ЕслиF-const 
FΔt=ΔP
2.4 3-й закон Ньютона (Закон взаимодействия тел).
3-й закон Ньютона: два тела взаимодействуют друг с другом с силами, равными по величине и по модулю, но противоположными по направлению
Силы прилаженные к разным телам и никогда не могут компенсировать друг друга
Глава 3. Законы сохранения
Законы сохранения – носят всеобщий характер, они справедливы для всех видов движения (Механического, теплового, биологического). Закон сохранения импульса и энергии могут быть строго получены из таких свойств материи, как однородность пространства и однородность времени. Однородность пространства означает, что законы физики справедливы в любой точке пространства. Однородность времени означает, что законы физики с течением времени не изменяются. Совокупность тел, движение которых рассматривается совместно и одновременно называется системой тел. При этом силы, с которыми взаимодействуют тела, принадлежат данной системе, называются внутренние силы. Силы, которые создаются телами, не принадлежащими данной системе – внешние силы. Массой системы называют сумму масс всех тел системы.
Суммарный импульс – сумма импульсов тел системы.
§3.1 Закон сохранения импульса.
Пусть система состоит из 2-х тел. Согласно 3-у закону Ньютона
F1= -F2– равны и противоположны по направлению. Согласно 1-у закону Ньютона действие силы приводит к изменению импульса.
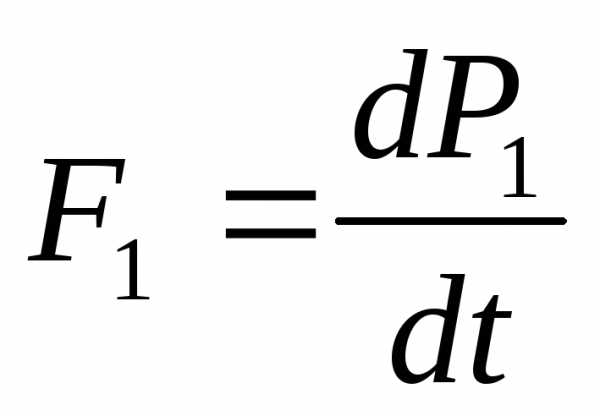
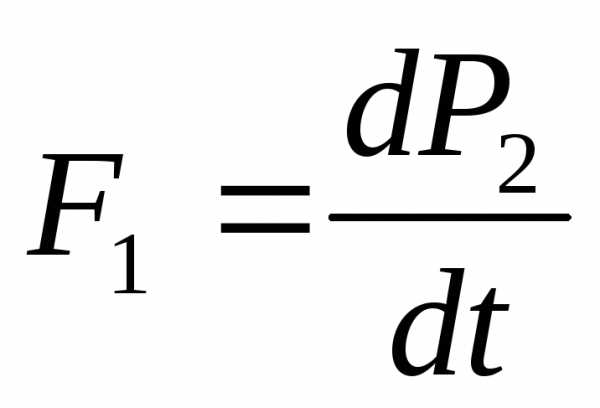
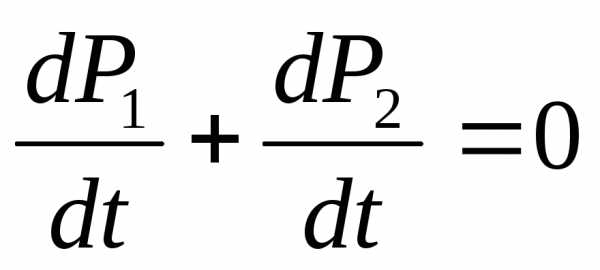
P1+ P2 =
P1`+
P2` =
const.
Движение системы тел может быть охарактеризовано понятием центром масс.
Центром масс любой системы тел называется вектор, который определяются соотношением:
,
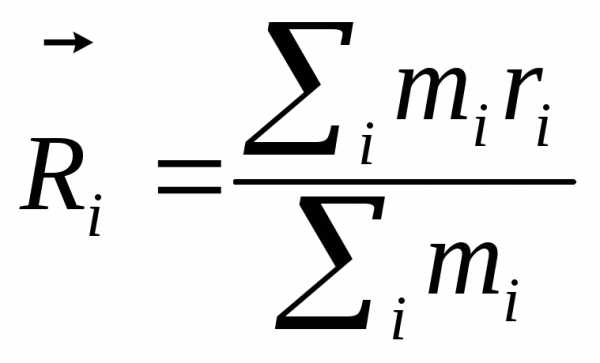
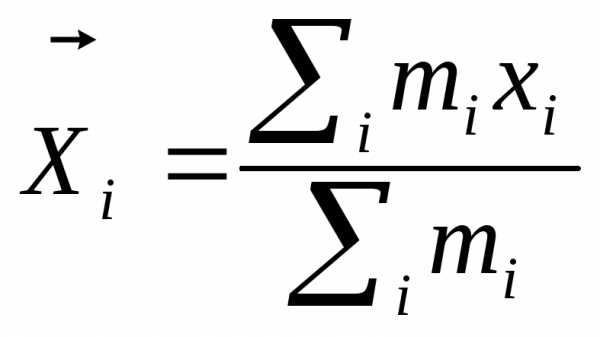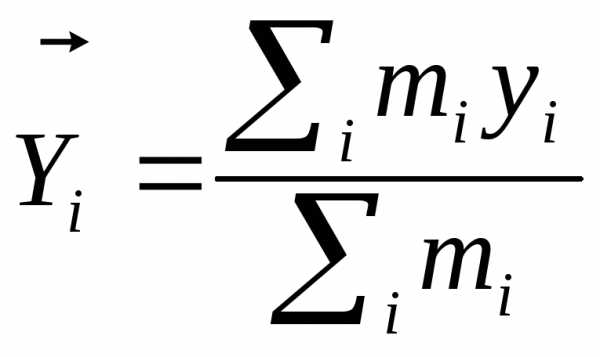
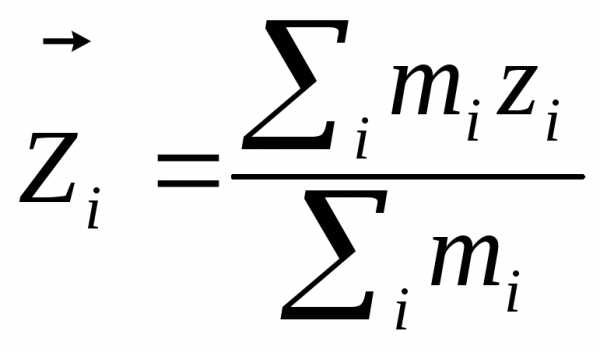
Скорость движения центра масс:
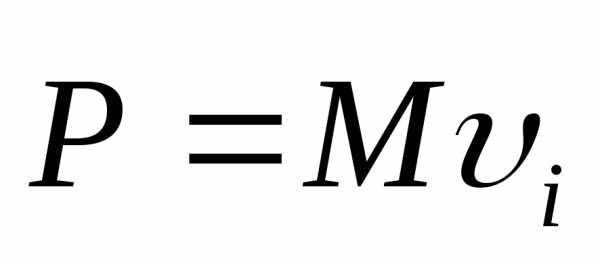
Центр массы системы тел, движущихся, как материальная точка в которой сосредоточена вся масса системы.
Особенности:
1) FВНЕШН.=0, тоdP=0P=const
2)Если dt0, то действие внешних сил очень малоdP=0, P=const
3) Fx =0, dPx=0, Px =const;
§3.2 Механическая работа и мощность.
Механическая работа – выражение, определяемое соотношением:
A=FScos=FS
Формула может быть использована только тогда, когда F-const,aперемещение прямолинейно. Если перемещение не прямолинейно, аF-неconst, то траекторию разбивают и считают что наSперемещение прямолинейно, аF-const
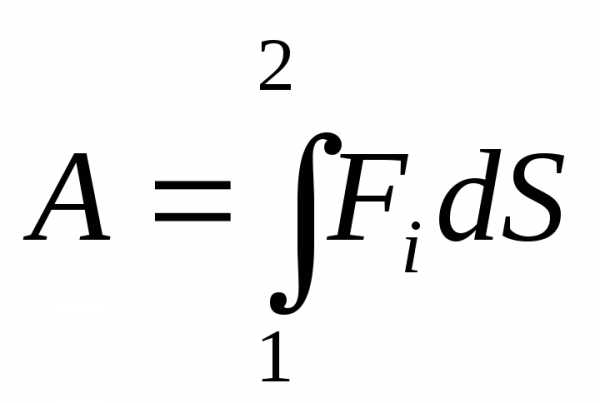
Примерыработы сил:
1) Работа сил упругости
2) Работа сил тяжести
dA=mgdh=mgdrcos=mgdh,
Работа сил тяжести не зависит от
траектории, а определяется уровнем над
поверхностью земли. Силы, работа которых
не зависит от траектории, а определяется
только начальным и конечным положением
наз. консервативные силами (Сила тяжести,
Гравитационная, Электростатическая,
). Если F=const,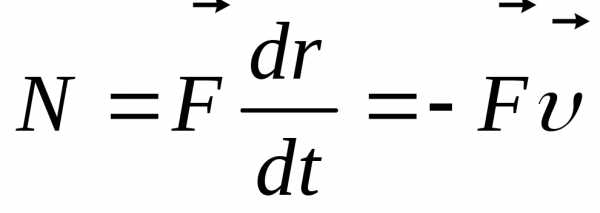
-мощность.
studfiles.net
II. Второй закон Ньютона.
Важнейшей мерой поступательного движения является его импульс или количество движения – это векторная физическая величина равная произведению массы материальной точки на её скорость.
Ускорение, приобретенное материальной точкой пропорционально вызывающей её силой, совпадает с её направлением и обратнопропорционально массе материальной точки.
– наиболее общая форма второго закона Ньютона.
Основное уравнение динамики, для поступательного движения.
Величина называетсяимпульсом силы – это векторная физическая величина, характеризующая действие силы во времени.
Формулы 3, 4, 5 – дифференциальная форма второго закона Ньютона.
– интегральная форма второго закона Ньютона.
При равноускоренном прямолинейном движении F=const.
III. Третий закон Ньютона.
Третий закон Ньютона: Всякое действие материальных точек друг на друга носит характер взаимодействия силы, с которой действуют друг на друга материальные точки – всегда равны по модулю, но противоположно направлены и действуют вдоль прямой соединяющей эти точки.
Особенности 3 закона Ньютона:
эти силы всегда одной природы,
возникают парами,
приложены к разным телам, поэтому не компенсируют друг друга.
Все законы Ньютона справедливы в инерциальных системах отсчета.
IV. Момент импульса материальной точки, момент силы, момент инерции
Моментом инерции материальной точки – называется физическая величина равная произведению массы материальной точки на квадрат расстояния от точки вращения до материальной точки.
J- аддитивная величина.
Моментом импульса относительно точки называется векторная физическая величина, равная векторному произведению радиус вектора r, проведённого из центра к данной точке, на импульс.
Если вращать буравчик от первого множителя векторного произведения ко второму, то направление его поступательного движения совпадает с направлением векторного произведения.
Моментом силы относительно точки, называется векторная физическая величина равная:
(направление определяется по правилу буравчика)
(4) – основное уравнение динамики для вращательного движения.
Второй закон Ньютона для вращательного движения.
Если тело (точка) вращается с постоянной угловой скоростью, то
При вращении точки с момент импульса остаётся постоянным.
Лекция 4 Работа силы и мощность. Кинетическая энергия. Консервативные и неконсервативные силы. Потенциальная энергия. Связь силы с потенциальной энергией.
План лекции
Работа
Механическая мощность
Кинетическая и потенциальная энергия.
Работа
Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую.
Элементарная работа, совершенная силой F равна скалярному произведению силы на элементарное перемещение точки приложения силы.
– элементарная работа, знак означает бесконечно малую порцию и заменяет знак d, для величин являющимися функциями процесса.
Работа на конечном перемещении из точки 1 в точку 2 – полная работа, определяющаяся интегралом:
Если на тело действует постоянная сила, её можно выносить за знак интеграла, перейдём к интегрированию по времени.
При прямолинейном движении
Работа может быть вычислена графически.
studfiles.net
Второй закон Ньютона — Традиция
Материал из свободной русской энциклопедии «Традиция»
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между равнодействующей всех приложенных к телу сил и ускорением этого тела. Один из трёх законов Ньютона.
Второй закон Ньютона утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Этот закон записывается в виде формулы:
\(\vec{a} = \frac{\vec{F}}{m}\) ,где \(\vec{a}\) — ускорение тела, \(\vec{F}\) — сила, приложенная к телу, а \(\ m\) — масса тела, причём \(\ m\) — константа.
Или, в более известном виде:
\(\vec{F} = m \vec{a}\)в тех же обозначениях.
В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в общем виде (в таком виде его написал сам Ньютон):
\(\vec{F} = \frac{d\vec{p}}{dt},\)где \(\vec{p}\) — импульс (количество движения) тела, \(\ t\) — время, а \(\frac{d}{dt}\) — производная по времени.
Второй закон Ньютона справедлив только для скоростей, меньших скорости света и в инерциальных системах отсчёта.
Вектора сил, массы и ускоренияУскорение тела определяется действующей на него силой . Но оно зависит и от свойств самого тела . Характер этой зависимости установил Второй Закон Ньютона.
Опыты показывают, что ускорение тела зависит не только от оказываемого на него воздействия, ( т.е. приложения силы) но и от свойств самого тела менять свою скорость под влиянием определённой силы. С увеличением массы тела, уменьшается получаемое телом ускорение при действии на него заданной силы. Величину, равную отношению модуля силы к модулю ускорения, называют массой (точнее, инертной массой) тела.
Масса — основная динамическая характеристика тела, количественная мера его инертности, т.е. способности тела приобретать определённое ускорение под действием силы. Для данного тела ускорение пропорционально силе, и коэффициентом пропорциональности является масса. Единица массы в СИ – 1 кг.[1]
traditio.wiki
Второй закон Ньютона. Импульс | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Второй закон Ньютона. Если на неподвижное тело с массой m начинает действовать сила F̅0, тело приобретает ускорение a̅, равное:
a̅ = (1 / m) • F̅0. [1]
Формула [1] предоставляет способ определения массы. Измеряются сила и ускорение, а масса выступает в качестве связывающего их коэффициента. Так, например, определяют массы атомных ядер (измеряется ускорение ядра при движении в известном магнитном поле).
В нерелятивистской (ньютоновской, классической) механике второй закон Ньютона формулируется в более общем виде: приведенная формула считается справедливой вообще, а не только при нулевой скорости тела. Однако в таком виде закон не согласуется с преобразованиями Лоренца, т. е. не удовлетворяет принципу относительности (хотя согласуется с преобразованиями Галилея).
При любом движении тела всегда можно выбрать инерциальную систему, в которой тело в данный момент покоится, и в этой системе второй закон Ньютона [1] будет справедлив. Переход в другую инерциальную систему отсчета, в которой тело будет иметь скорость v, осуществляется с помощью преобразований Лоренца. Преобразованная формула примет вид:
√((d / dt) • (mv / √(1 — (v / c)2))) = F̅. [2]
Система отсчета, связанная с космическим кораблем с выключенными двигателями, является инерциальной.
Производная по времени от величины mv / √(1 — (v / c)2) (изменение этой величины за единицу времени) равно силе, действующей на тело.
Выражение для силы также преобразуется, и величина F̅ однозначно выражается через F̅0.
Важная оговорка: формула [2] получается из формулы [1] лишь при m = const.
Если речь идет о протяженном теле, то под ускорением, о котором идет речь во втором законе Ньютона, понимают ускорение центра масс тела.
В терминах наблюдаемых величин вторым законом Ньютона утверждается следующее. Пусть в инерциальной системе имеется неподвижное тело, прикрепленное к пружине, и растяжение пружины свидетельствует о наличии силы F̅0. Тогда, если освободить тело от пружины, оно начнет двигаться с ускорением, определяемым формулой [1].
Ньютон формулировал свой закон для импульса, а не для ускорения. При постоянстве массы обе формулировки, очевидно, эквивалентны, но если масса тела меняется, второй закон в виде равенства [2], где под m понимают массу тела в данный момент времени, а под F̅ — действующую на это тело в этот же момент силу, остается верным.
Величина p̅ = mv̅ / √(1 — (v / c)2) называется импульсом частицы.
Второй закон Ньютона в форме уравнения [2] можно сформулировать в виде:
Δp̅ = F̅Δt. [3] Материал с сайта http://worldofschool.ru
Эта формула определяет малое изменение импульса частицы за малое время Δt.
Сила есть причина изменения импульса.
Если сила, действующая на частицу, равна нулю, импульс частицы не изменяется и ее скорость постоянна.
Скорость частицы, а стало быть, и импульс есть измеримая величина, и формула [3] может рассматриваться как определение силы, действующей на частицу. Задачей физики становится поиск соответствующих выражений для силы. Заслугой Ньютона было то, что он дал формулу для силы гравитационного взаимодействия двух тел и из формулы [4] вывел, что планеты движутся по эллиптическим орбитам, т. е. законы Кеплера.
На этой странице материал по темам:2 закон ньютона в импульсном виде
2 закон ньютона через импульс
Зарезонансная зона
Какая из формул выражает 2 закон ньютона при m=const
Закон ньютона шпора
worldofschool.ru
Второй закон Ньютона Википедия
| Классическая механика |
| d(mv→)dt=F→{\displaystyle {\frac {\mathrm {d} (m{\vec {v}})}{\mathrm {d} t}}={\vec {F}}}Второй закон Ньютона |
| История… |
Фундаментальные понятия Пространство · Время · Масса· Скорость · Сила · Механическая работа · Энергия · Импульс |
Формулировки Ньютоновская механика · Лагранжева механика · Гамильтонова механика · Формализм Гамильтона — Якоби · Уравнения Рауса · Уравнения Аппеля · Теория Купмана — фон Неймана |
Разделы Прикладная механика · Небесная механика · Механика сплошных сред · Геометрическая оптика · Статистическая механика |
Учёные Галилей · Кеплер · Ньютон · Эйлер · Лаплас · Д’Аламбер · Лагранж · Гамильтон · Коши |
| См. также: Портал:Физика |
Второ́й зако́н Нью́то́на — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона. Основной закон динамики[1][2][3].
Объектом (телом), о котором идёт речь во втором законе Ньютона, является материальная точка, обладающая неотъемлемым свойством — инерцией[4], величина которой характеризуется массой. В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами[5][6][7][8].
Второй закон Ньютона в его наиболее распространённой формулировке, справедливой для скоростей, много меньших скорости света, утверждает: в инерциальных системах отсчёта
ru-wiki.ru