Матрицы, сложения, вычитание, умножение
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
2) Действие второе. Умножение матрицы на число.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу: А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
3) Действие третье. Транспонирование матрицы.
Потом переписываем вторую строку во второй столбец:
4) Действие четвертое. Сумма (разность) матриц.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Действие пятое. Умножение матриц
Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицыравнялось числу строк матрицы.
– попытайтесь сразу уловить закономерность.
Умножить матрицу на матрицу
Формула:
Обратите внимание, что! Это почти всегда так!
Таким образом, при умножении переставлять матрицы нельзя!
Определители, свойства, алгебраические дополнения, вычисления
Обозначения: Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называетсяМИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
1. Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:
1) нулей побольше;
2) числа поменьше.
Из чего следует важный факт: строки и столбцы определителя равноправны.
2. Если две строки (или два столбца) определителя поменять местами,
то определитель сменит знак
То есть, любая парная перестановка строк (столбцов) влечёт изменение знака определителя на противоположный
3. Из строки (столбца) определителя можно вынести общий множитель
!!! Внимание!В правиле речь идёт обОДНОЙстроке или обОДНОМстолбце определителя. Пожалуйста, не путайте сматрицами, в матрице множитель выносится/вносится уВСЕХчисел сразу.
Справедливо и обратное правило – множитель можно не только вынести, но и внести, причём, в ЛЮБУЮ строку или в ЛЮБОЙ столбец определителя.
4. Если две строки (столбца) определителя пропорциональны
(как частный случай – одинаковы), то данный определитель равен нулю
Определитель с нулевой строкой (столбцом) равен нулю
Какие свойства определителей полезно знать?
1) Величина определителя не меняется при транспонировании. Свойство запоминаем.
2) Любая парная перестановка строк (столбцов) меняет знак определителя на противоположный. Свойство тоже запоминаем и стараемся не использовать во избежание путаницы.
3) Из строки (столбца) определителя можно вынести множитель (и внести его обратно). Используем там, где это выгодно.
Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.
Система линейных уравнений теорема Крамера
Запись систем линейных уравнений в матричной форме
infopedia.su
Вычитание матриц онлайн
www.matcabi.net позволяет найти вычитание матриц онлайн. Сайт производит вычитание матриц онлайн. За неколько секунд сервер выдаст точное решение. Вычитанием матриц будет являться матрица, каждый элемент которой вычисляется как разность соответствующих элементов вычитаемых матриц онлайн. При вычитании матриц, каждый элемент полученной матрицы будет результатом вычитания соответствующих элементов вычитаемых матриц онлайн. Найти онлайн разность двух матриц одинаковых размерностей сводится к нахождению матрицы этой же размерности. Операция вычитания онлайн двух матриц одинаковых размерностей сводится к нахождению матрицы этой же размерности. Элементы этой матрицы составляют алгебраическую разность элементов вычитаемых матриц, это результат вычитания матриц онлайн. Задача по нахождению разности матриц онлайн или операция вычитания матриц онлайн заключается в простом алгебраическом вычитании элементов матриц. www.matcabi.net находит разность матриц заданных размерностей в режиме онлайн. Вычитание матриц онлайн заданной размерности – это нахождение той же размерности матрицы, элементами которой будут разности чисел соответствующих элементов вычитаемых матриц. Относительно алгебраического вычитания матрицы образуют абелеву группу. Нахождение разности матриц онлайн широко распространено в теории матриц. Вычитание матриц онлайн используется для определения результирующей матрицы от вычитания заданных матриц. Для того, чтобы вычислить разность матриц или определить вычитание матриц онлайн, необходимо затратить не мало времени, в то время как наш сервер в считанные секунды найдет разность матриц онлайн от вычитания двух заданных матриц онлайн. При этом ответ по нахождению разности матриц будет правильным и с достаточной точностью, даже если числа при вычитании матриц онлайн будут иррациональными. На сайте www.matcabi.net допускаются символьные записи в элементах матриц, то есть разность матриц онлайн может быть представлена в общем символьном виде при вычитании матриц онлайн. Полезно проверить ответ, полученный при решении задачи на вычитание матриц онлайн, используя сайт www.matcabi.net. При совершении операции вычитания матриц онлайн необходимо быть внимательным и предельно сосредоточенным при решении задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему вычитание матриц онлайн. Если у Вас нет времени на долгие проверки решенных задач, то www.matcabi.net безусловно будет являться удобным инструментом для проверки вычитания матриц онлайн.
www.matcabi.net
Сумма (разность) матриц — Мегаобучалка
Сумма матриц – действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой.
– Такое действие не определено для этих матриц!
Определение: Для того чтобы получить матрицу, равную сумме (разности) двух исходных матриц, необходимо сложить (вычесть) их соответствующие элементы:
Пример:
Сложить матрицы и
В соответствии с определением, запишем:
.
Для разности матриц, аналогично, находим разность соответствующих элементов:
Пример:
Найти разность матриц и .
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу
Примечание: В теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
Умножение матриц.
Скажем сразу, правило умножения матриц (есть в любом учебнике по алгебре) выглядит очень странно для неподготовленного слушателя, но мы объясним это на конкретных примерах. Прежде всего: «Какие матрицы можно умножать?»
Пример:
Можно ли умножить матрицу
на матрицу ?
, значит, умножать данные матрицы можно.
А вот если, в данном случае, матрицы переставить местами, то умножение уже невозможно!
, значит, выполнить умножение нельзя, и, вообще, такая запись не имеет смысла:
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так, но с разным результатом, т. к. в общем случае KL ¹ LK. Например, для матриц
и существует как произведение , так и .
Как умножать матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Пример:
Умножить матрицу на матрицу
Мы будем сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность. Поэтому:
Пример сложнее:
Умножить матрицу на матрицу
Формула: . В таком случае произведение:
.
В результате мы получили так называемую нулевую матрицу.
Попробуйте самостоятельно выполнить умножение . Правильный ответ – .
Обратите внимание, что! Это почти всегда так!
Таким образом, переставлять матрицы в произведении нельзя!Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Умножить матрицу на матрицу .
Формула умножения очень похожа на предыдущие формулы:
.
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу на матрицу .
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
.
megaobuchalka.ru
Сложение и вычитание матриц, умножение матриц на число в MS EXCEL. Примеры и методы
В этой статье рассмотрены операции сложения и вычитания над матрицами одного порядка, а также операции умножения матрицы на число. Примеры решены в MS EXCEL.
Операция сложения определена только для матриц одного порядка. Т.е. нельзя говорить о сложении матриц разной размерности. Также неопределена операция сложения матрицы и числа. Напротив, операция умножения матрицы на число определена.
Сумма двух матриц А и В – это матрица, элементы которой равны сумме соответствующих элементов матриц А и В.

В MS EXCEL операцию сложения матриц реализовать элементарно.
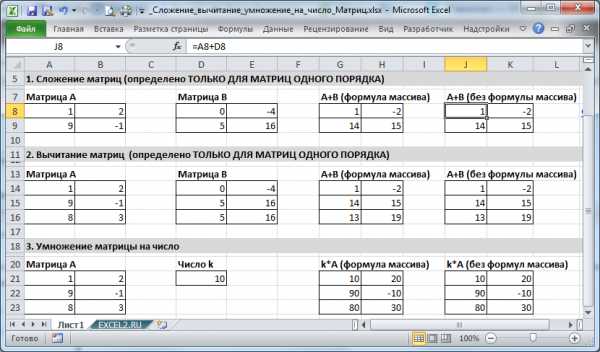
Поместив матрицу А размерности 2х2 в диапазон А8:В9, а матрицу B той же размерности 2х2 в диапазон D8:E9, в ячейке J8 введем формулу =A8+D8. Скопировав формулу в нужные ячейки, например, с помощью Маркера заполнения, получим матрицу А+В.
Аналогичного результата можно добиться с использованием формулы массива. Выделив диапазон G8:H9 в Строке формул введите формулу =A8:B9+D8:E9 и нажмите CTRL+SHIFT+ENTER. Преимущество формулы массива состоит в том, что невозможно удалить отдельные элементы матрицы А+В (появится окно Невозможно удалить часть массива).
Понятно, что операция вычитания матриц в MS EXCEL реализуется аналогично (см. файл примера).
Умножение матриц на число
Операция умножения матрицы на число определена для матриц любого порядка.
Произведение матрицы А и числа k – это матрица, элементы которой получаются умножением всех элементов исходной матрицы А на число k.
В MS EXCEL это реализовано с помощью формулы =A21*$D$21 (предполагается, что матрица находится в диапазоне А21:В23, а число в ячейке D21). Обратите внимание, что в формуле использована абсолютная адресация на ячейку с числом. Это позволяет при копировании формулы (для отображения всех элементов матрицы k*А) ссылаться на одну и ту же ячейку с числом.
excel2.ru
