§2. Методы вычисления определенных интегралов
Так как формула Ньютона–Лейбница сводит задачу вычисления определенного интеграла от непрерывной функции к нахождению первообразной, то все основные методы вычисления неопределенных интегралов переносятся и на задачу вычисления определенных интегралов. Сформулируем эти методы с учетом специфики определенных интегралов.
1. Непосредственное интегрирование
Типовой пример
Вычислить
определенный интеграл 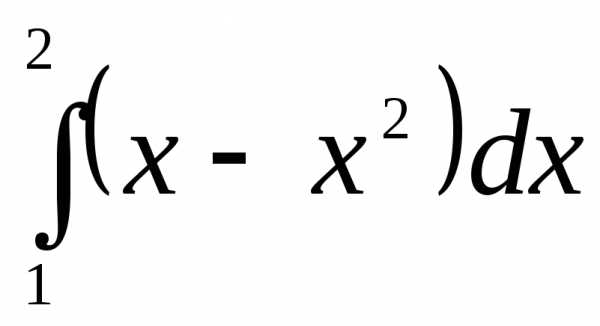 .
.
►Используя формулу Ньютона–Лейбница, получим:
.◄
2. Замена переменной в определённом интеграле
ТЕОРЕМА
Пусть:
для ;
.
Тогда .
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.
Типовые примеры
Вычислить интегралы.
1. 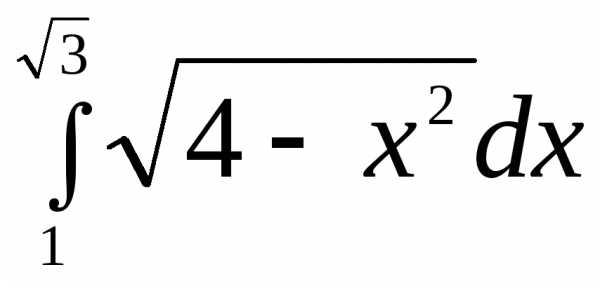 .
.
►
.◄
2. 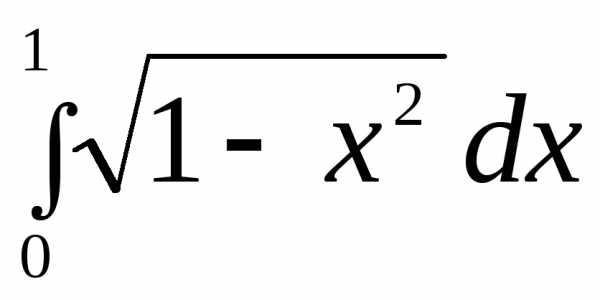 .
.
►
.◄
3. 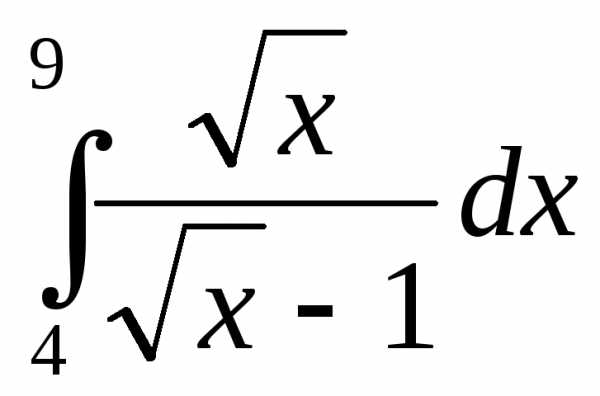
►Воспользуемся формулой замены переменной в определенном интеграле:
и
применим подстановку 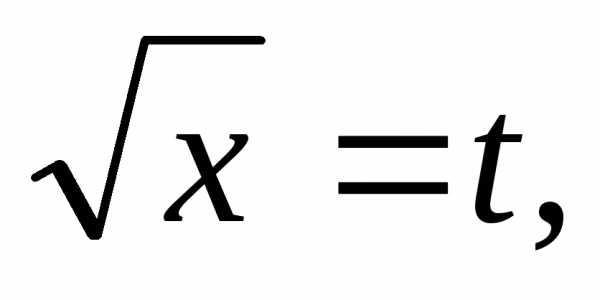 т.е.x = t².
Определим новый промежуток интегрирования: х = 4 при t = 2; х
= 9 при t = 3. Следовательно,
т.е.x = t².
Определим новый промежуток интегрирования: х = 4 при t = 2; х
= 9 при t = 3. Следовательно,
◄
3. Формула интегрирования по частям для определённого интеграла
ТЕОРЕМА
Пусть .Тогда
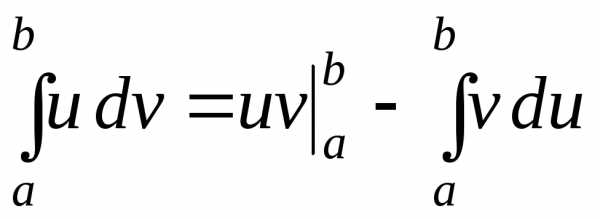 .
.
Типовые примеры
Вычислить интегралы.
1. 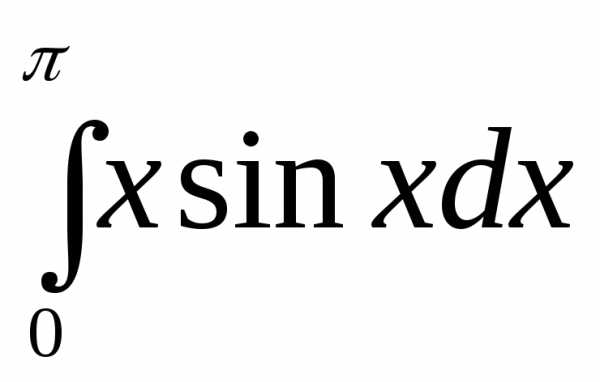 .
.
►Воспользуемся формулой интегрирования по частям в определенном интеграле. Имеем
. ◄
2. 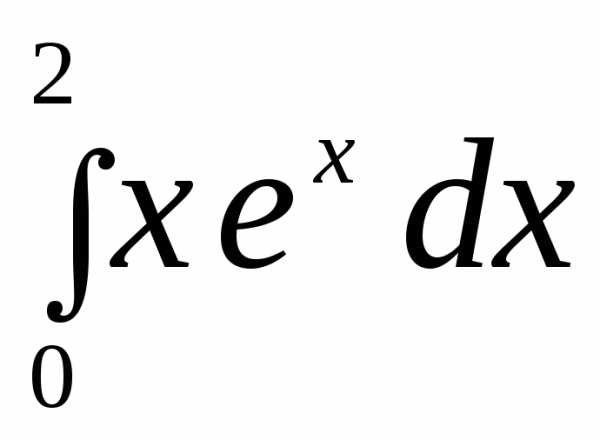 .
.
►
.◄
3. 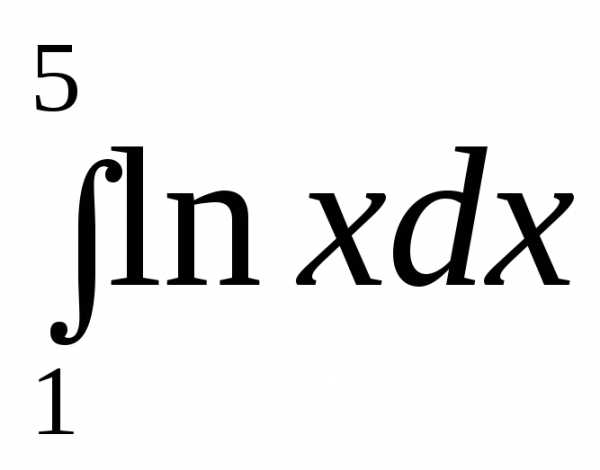 .
.
►.◄
§3. Геометрические приложения определенного интеграла
1.1. Декартовы координаты
Если 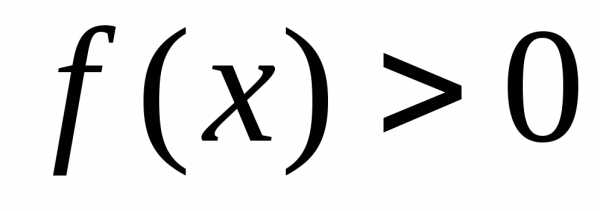 на отрезке
на отрезке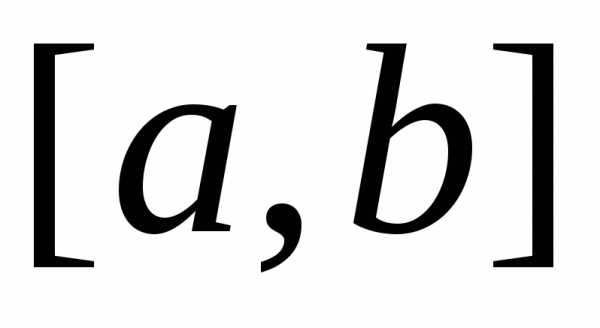 ,
то
,
то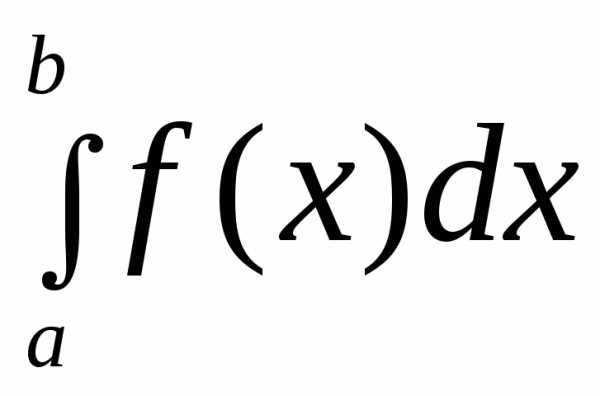 равен площади криволинейной трапеции
равен площади криволинейной трапеции ,
ограниченной снизу отрезком
,
ограниченной снизу отрезком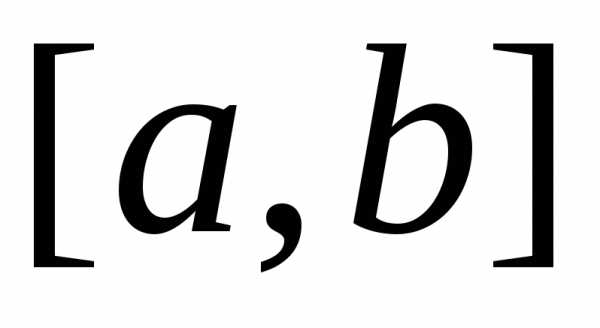 ,
слева и справа – прямыми
,
слева и справа – прямыми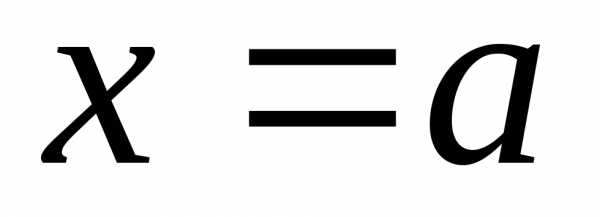
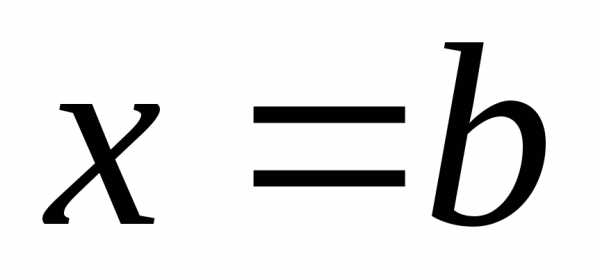 ,
сверху – функцией
,
сверху – функцией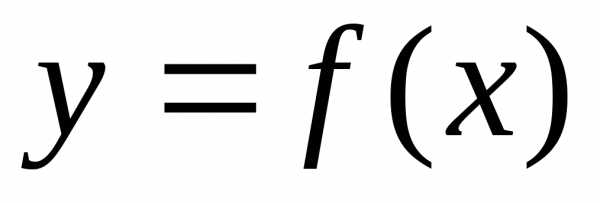 .
Следствие: если фигура ограничена сверху
кривой
.
Следствие: если фигура ограничена сверху
кривой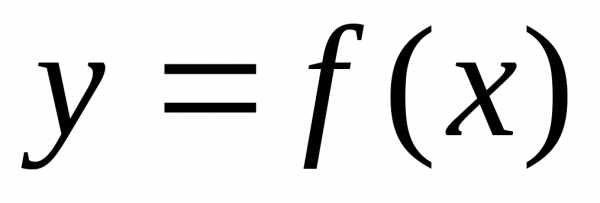 ,
снизу – кривой
,
снизу – кривой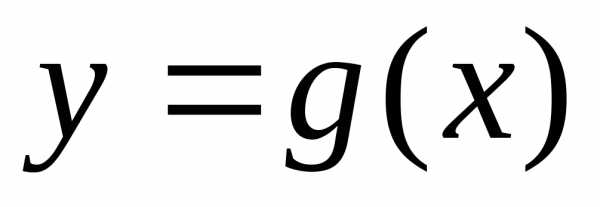 ,
слева и справа – отрезками прямых
,
слева и справа – отрезками прямых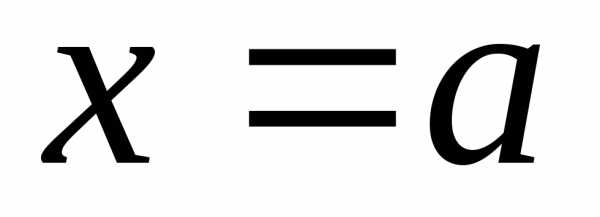 и
и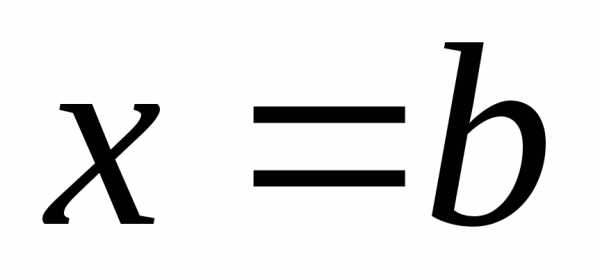 ,
то её площадь равна
,
то её площадь равна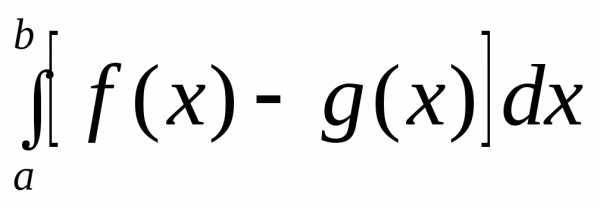 .
.Типовые примеры
1)
Найти площадь области  ,
ограниченной кривымипри
условии, что
,
ограниченной кривымипри
условии, что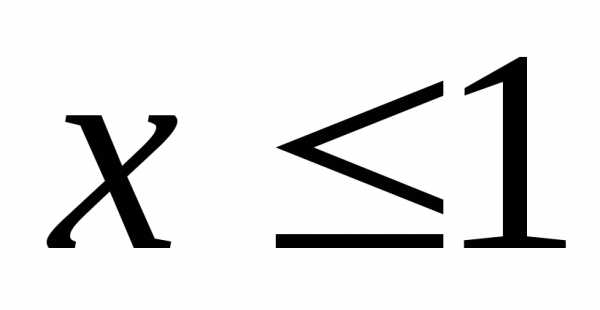 (дальше мы будем писать так:
(дальше мы будем писать так: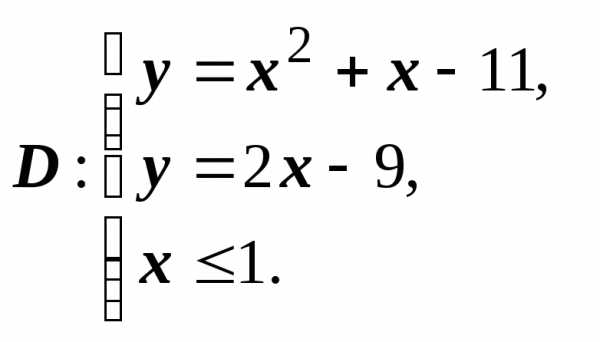 ).
).
►При
решении таких задач следует обязательно
изобразить исследуемый геометрический
объект. Для определения нижнего предела
интегрирования надо найти точку
пересечения кривых, уравнение
имеет два корня: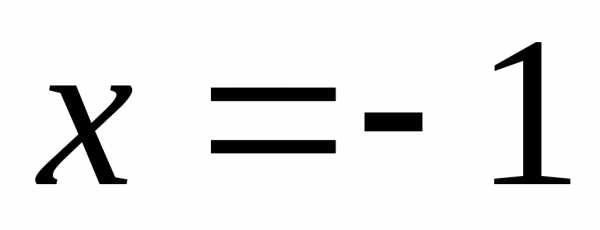 и
и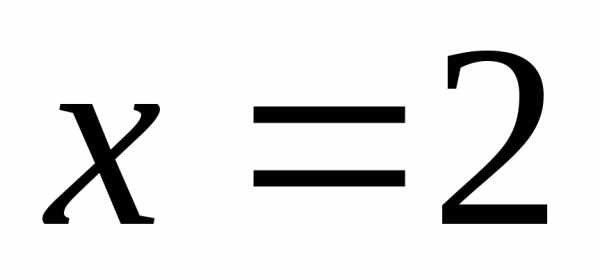
Подходящий
корень – 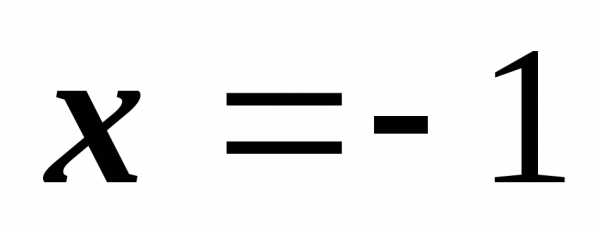 .
Область ограничена сверху параболой,
снизу – прямой, справа – прямой
.
Область ограничена сверху параболой,
снизу – прямой, справа – прямой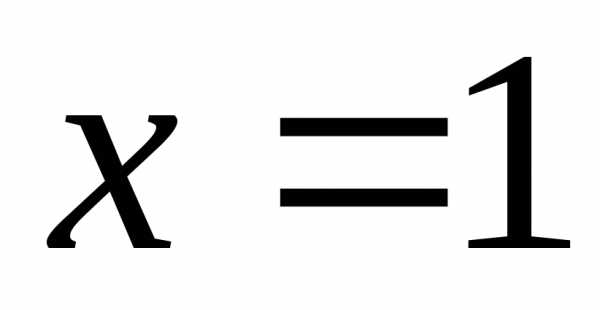 ,
крайняя левая точка –
,
крайняя левая точка –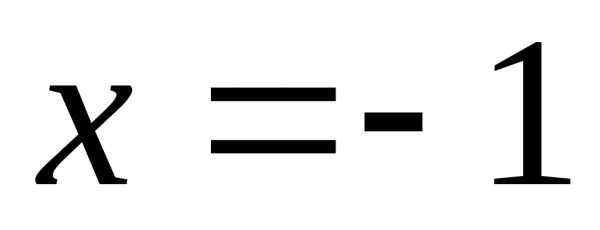 ,
поэтомуЕсли
область имеет более сложную структуру,
её следует разбить на простые части. ◄
,
поэтомуЕсли
область имеет более сложную структуру,
её следует разбить на простые части. ◄
2)
Вычислить площадь фигуры, ограниченной
графиками функций 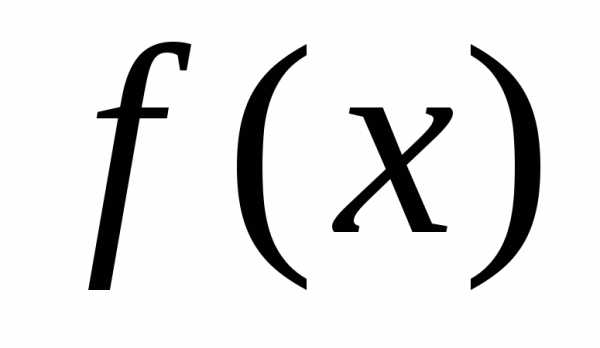 и
и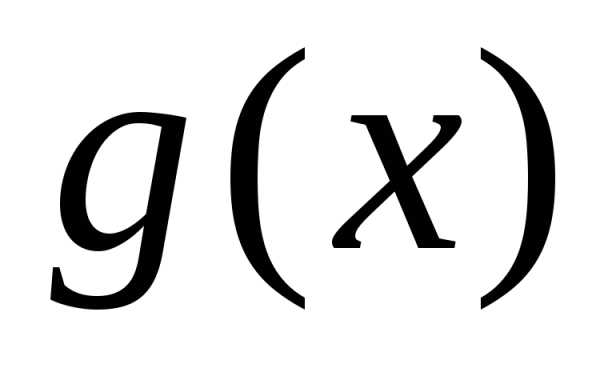
►Построим графики функций и найдем их точки пересечения. Точки пересечения: .Площадь фигуры, ограниченной линиями находится по формуле:
 ◄
◄
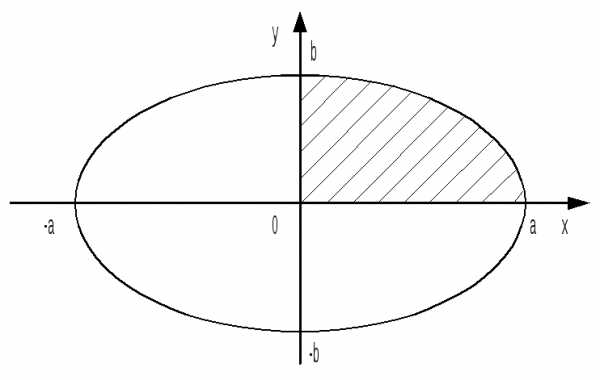
3)
Найти площадь фигуры, ограниченной
эллипсом 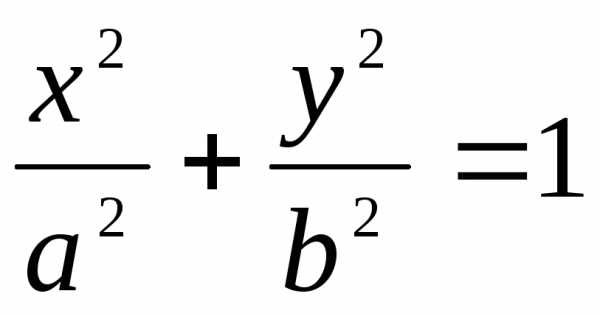 .
.
►Эллипс
имеет две оси симметрии: координатные
оси 0х и 0у. Поэтому площадь S
фигуры равна учетверённой площади S1 части (D1)
фигуры, расположенной в первой четверти
(заштриховано). Фигура (D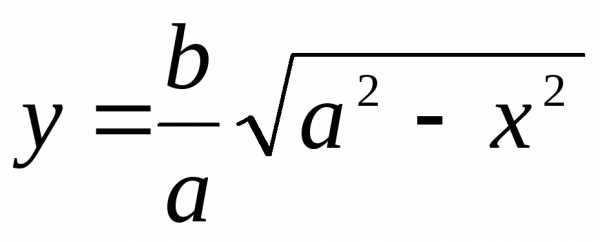 , снизу – осью 0х, слева – осью 0у. Поэтому
, снизу – осью 0х, слева – осью 0у. Поэтому
. Отсюда находим S = 4S1 = ab. ◄
1.2. Область задана в полярных координатах
Если
область  – сектор, ограниченный лучами
– сектор, ограниченный лучами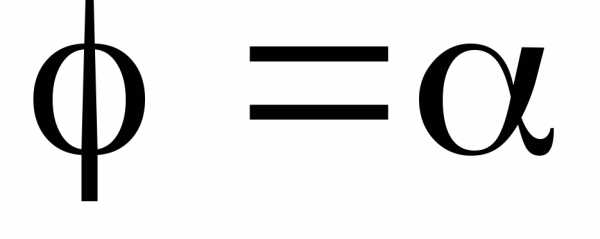 ,
,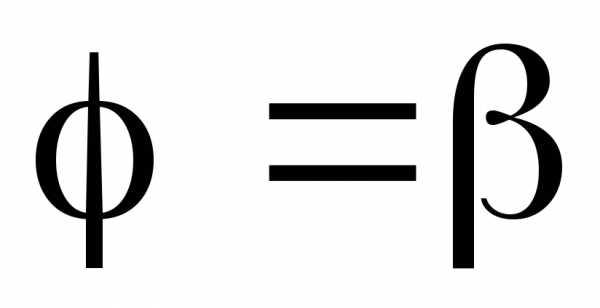 и кривой
и кривой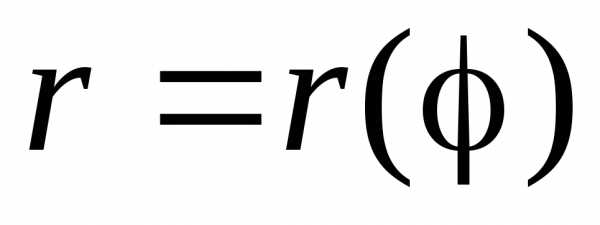 .
В Этом случае
.
В Этом случае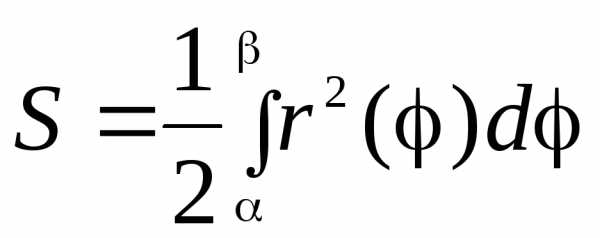
Типовые примеры
1. Найти площадь, ограниченную лемнискатой .
►Точки
лемнискаты расположены в секторах и
и ;
кроме того, при решении таких задаче
целесообразно использовать симметрию
фигуры, поэтому мы найдём площадь части,
расположенной в секторе
;
кроме того, при решении таких задаче
целесообразно использовать симметрию
фигуры, поэтому мы найдём площадь части,
расположенной в секторе и учетверим её:
и учетверим её:
◄
2. Найти площадь, лежащую внутри кардиоиды вне окружности.
►Найдём разность площадей, лежащих внутри кардиоиды и окружности. Для верхней части кардиоиды ; для верхней части окружности, поэтому◄
1.3.
Область ограничена кривыми, заданными
параметрически Если кривая, ограничивающая криволинейную
трапецию  задана в параметрическом виде,
то переход в интеграле
задана в параметрическом виде,
то переход в интеграле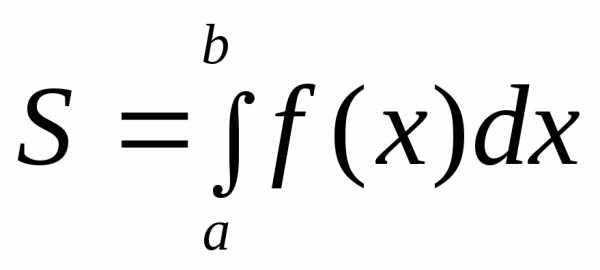 к переменной
к переменной приводит к формуле
приводит к формуле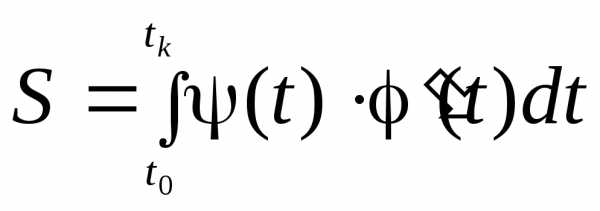 .
.
Найти
площадь, ограниченную астроидой 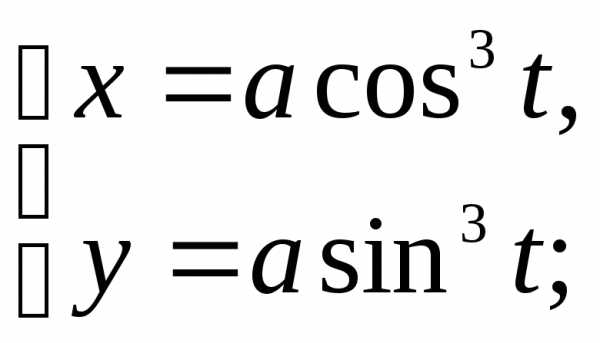 ().
().
►Используем
симметрию фигуры. Мы найдём площадь
части фигуры, расположенной в первом
квадранте (),
и учетверим её. Точка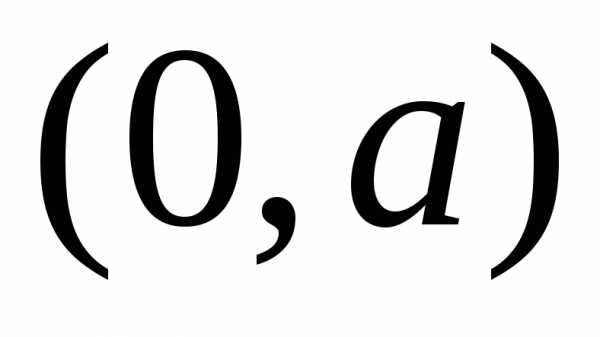 получается при,
точка
получается при,
точка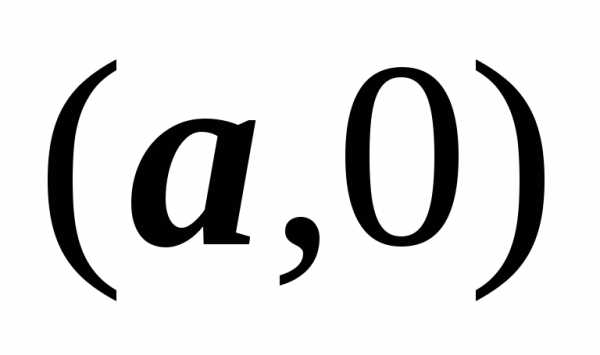 – при
– при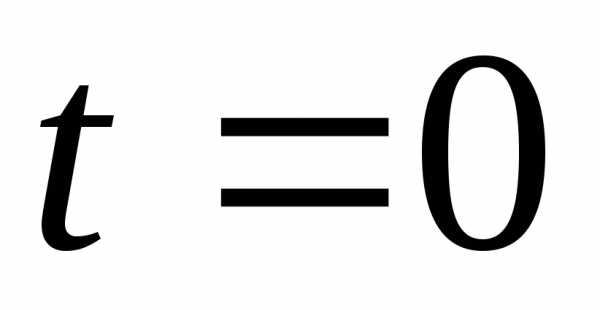 ,
поэтому◄
,
поэтому◄
studfiles.net
Тема 7. Теория
Тема 7. Определенные и несобственные интегралы Определенный интеграл
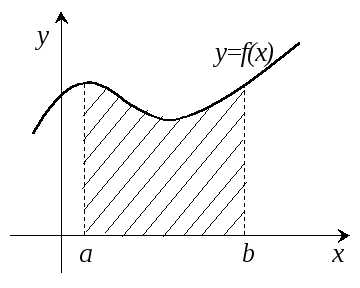
Задача, приводящая к понятию определенного интеграла – задача о вычислении площади криволинейной трапеции.
Пусть
на отрезке 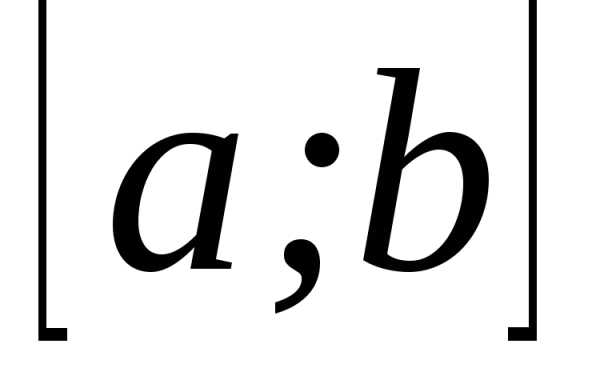 задана непрерывная функция
задана непрерывная функция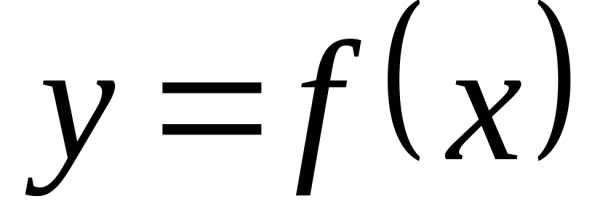 ,
для определенности
,
для определенности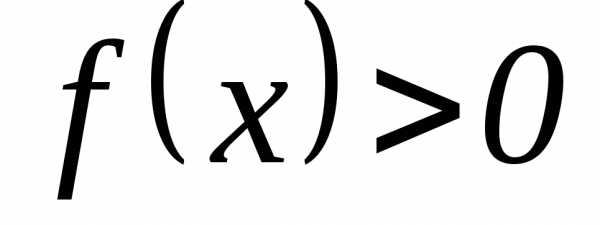 .
Найдем площадь, ограниченную осьюОХ,
прямыми
и линией
.
Найдем площадь, ограниченную осьюОХ,
прямыми
и линией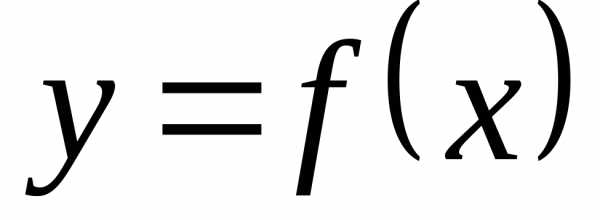 .
Можно также говорить о площадипод кривой
.
Можно также говорить о площадипод кривой 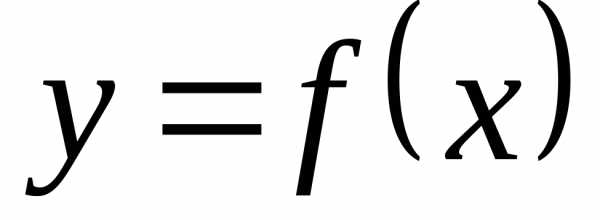 или о площади криволинейной трапеции.
или о площади криволинейной трапеции.
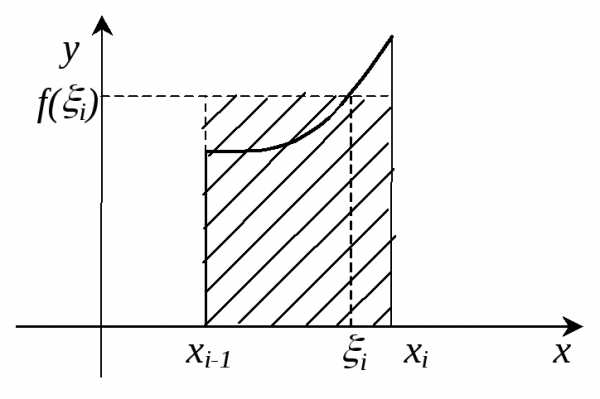
Для
этого разобьем трапецию произвольным
образом на частичные трапеции линиями, параллельными ОУ:
,
а затем заменим каждую прямоугольником
со сторонойи высотой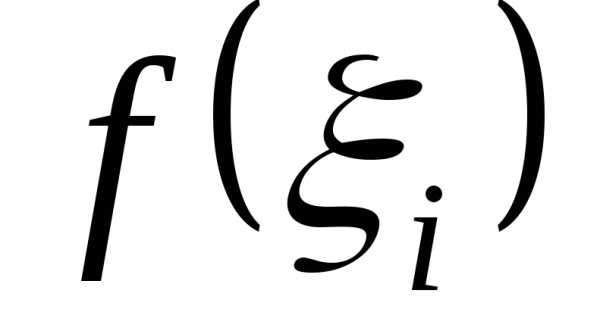 ,
где-произвольно
выбранная на
частичном отрезке точка.
,
где-произвольно
выбранная на
частичном отрезке точка.
Составим
сумму площадей всех прямоугольников,
она будет приближенно равна площади
всей криволинейной трапеции: 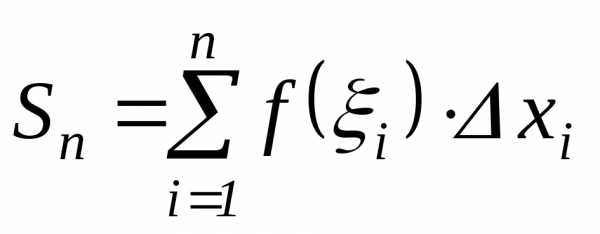 .
Такая сумма называетсяинтегральной.
Очевидно,
.
Такая сумма называетсяинтегральной.
Очевидно, 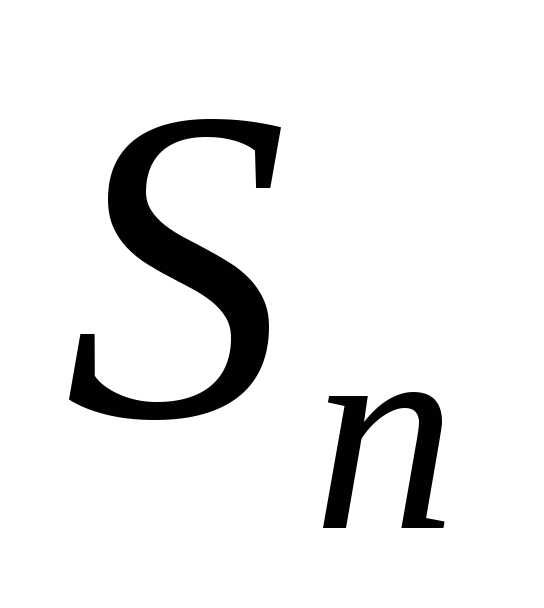 будет тем более точно определять площадь
криволинейной трапеции, чем на большее
число частичных трапеций будет разбита
исходная криволинейная трапеция. А при
будет тем более точно определять площадь
криволинейной трапеции, чем на большее
число частичных трапеций будет разбита
исходная криволинейная трапеция. А при или, что то же самое,эти площади совпадут.
или, что то же самое,эти площади совпадут.
Если
существует конечный предел интегральной
суммы 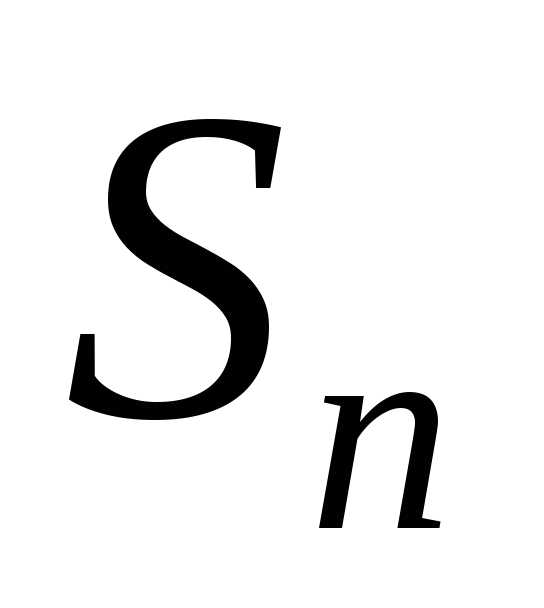 ,
при,
который не зависит от способа разбиения
области на частичные отрезки и выбора
точек
,
при,
который не зависит от способа разбиения
области на частичные отрезки и выбора
точек ,
то он называетсяопределенным
интегралом функции
,
то он называетсяопределенным
интегралом функции 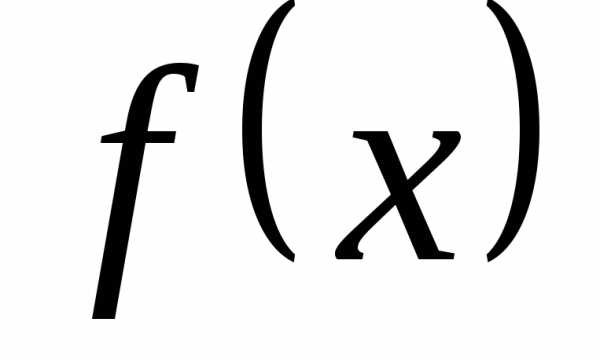 на отрезке
на отрезке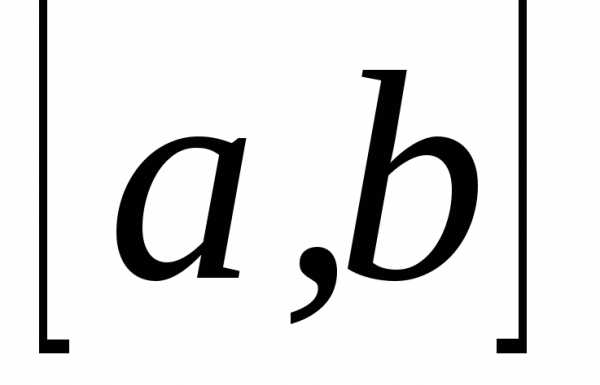 и обозначается
и обозначается
.
Здесь  – нижний ,
– нижний , – верхний пределы интегрирования.
– верхний пределы интегрирования.
– Несмотря на
сходство в обозначениях и терминологии,
определенный и неопределенный интегралы
существенно различные понятия: если
– представляет семейство функций, то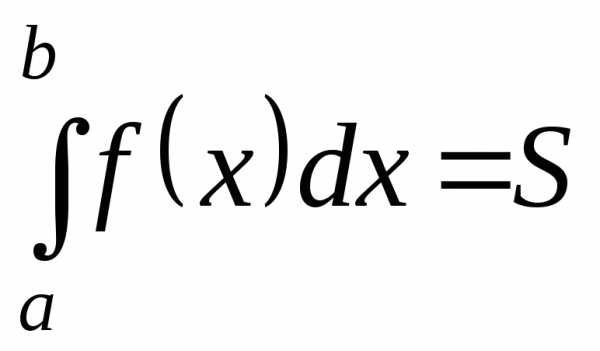 –
–
– определенное число.
– Заметим, что не имеет значения, какой буквой обозначена переменная интегрирования, т.к. смена обозначений не влияет на интегральную сумму.
Свойства определенного интеграла.
1 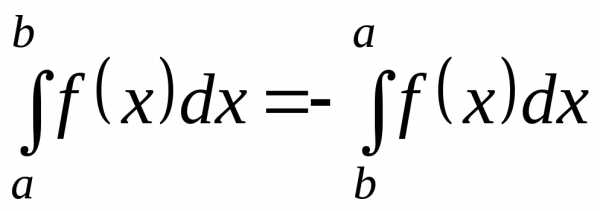 – если
поменять местами верхний и нижний
пределы интегрирования, определенный
интеграл поменяет знак.
– если
поменять местами верхний и нижний
пределы интегрирования, определенный
интеграл поменяет знак.
2 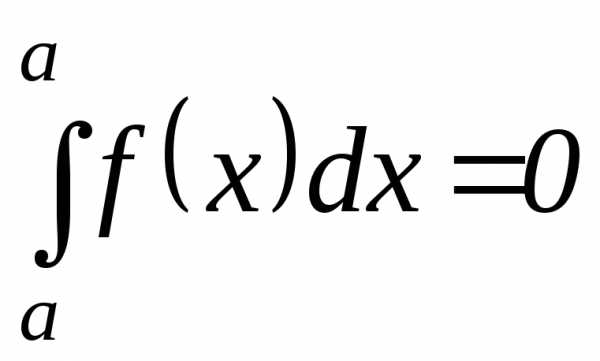 – интеграл с одинаковыми пределами
интегрирования равен нулю по определению.
– интеграл с одинаковыми пределами
интегрирования равен нулю по определению.
3 ;
.
Аналогичные свойства есть и у неопределенного интеграла. Они показывают, что интегрирование – линейная операция и может быть распространена на любое конечное число слагаемых: .
4
Свойство аддитивности.
Если 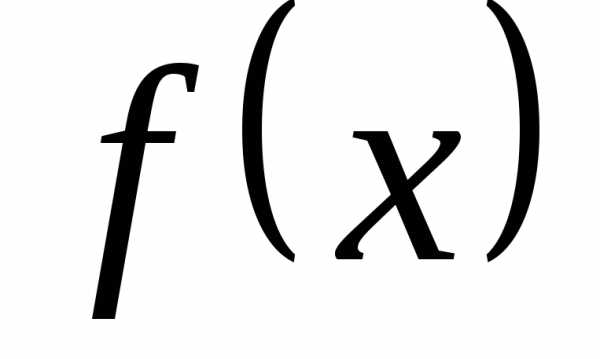 – функция, интегрируемая на
– функция, интегрируемая на
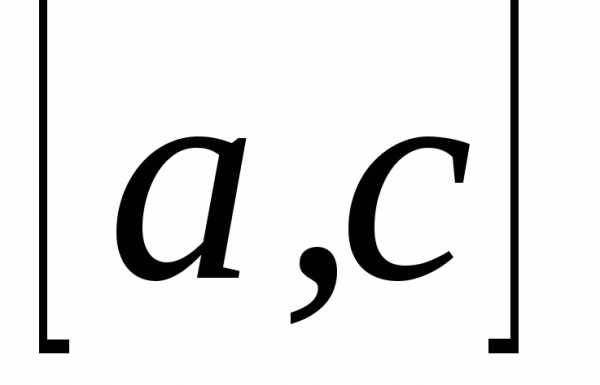 и
и 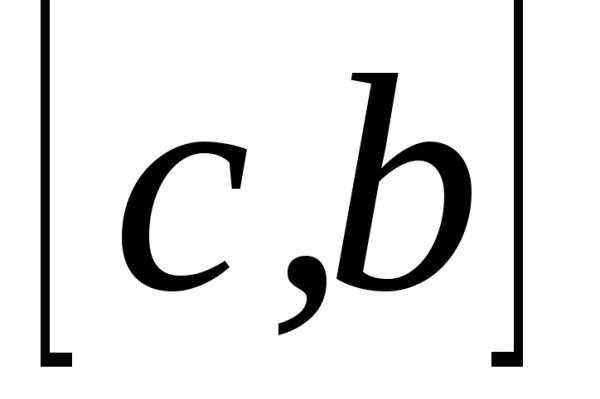 ,
где
,
где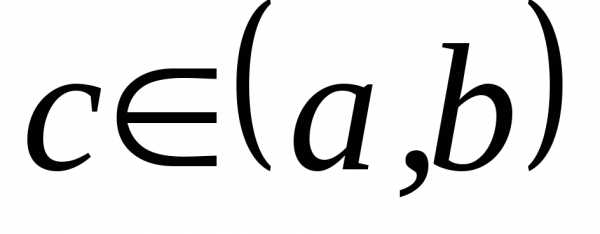 ,
то она интегрируема на
,
то она интегрируема на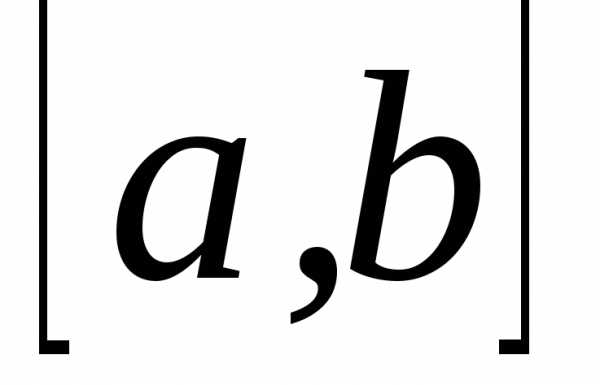 и
и
Иными словами, отрезок интегрирования можно разделить на части какой-либо точкой и интеграл по всему отрезку заменить суммой интегралов по двум полученным отрезкам.
5 Свойство алгебраической площади. Определенный интеграл есть число того же знака, что и подынтегральная функция. То есть при вычислении площадей с помощью определенного интеграла можно получить отрицательную площадь.
Теорема– о среднем значении функции на отрезке.
Если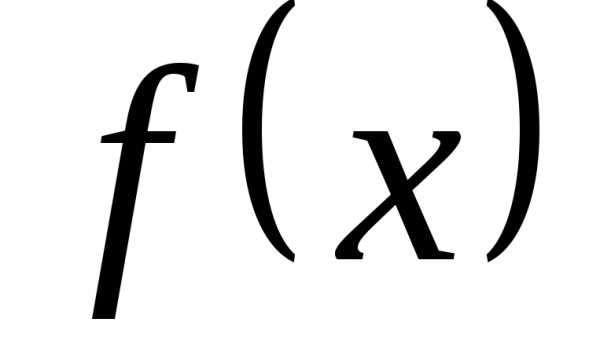 непрерывна на отрезке (),
то на этом отрезке существует хотя бы
одна точка (),
такая, что функция принимает в ней свое
непрерывна на отрезке (),
то на этом отрезке существует хотя бы
одна точка (),
такая, что функция принимает в ней свое
среднее значение: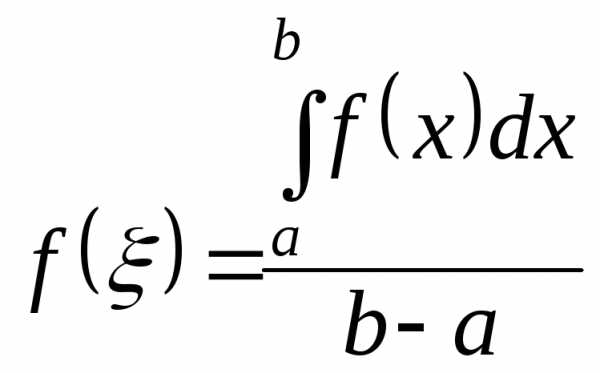 .
.
Г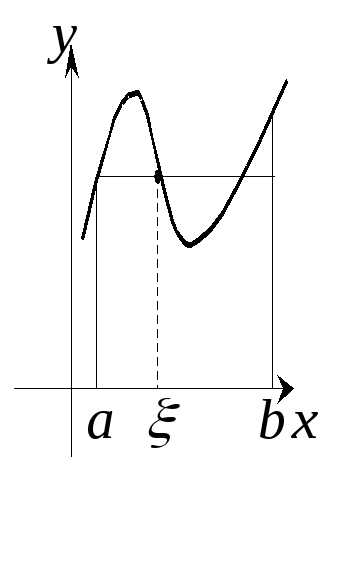 еометрический
смысл теоремы: пусть
еометрический
смысл теоремы: пусть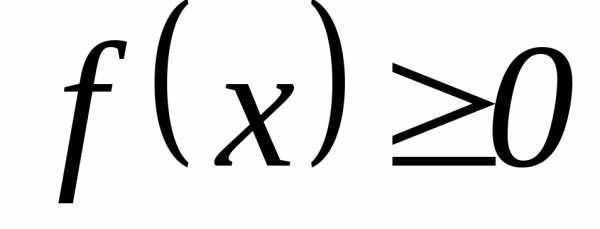 ,
тогда существует по крайней мере одна
точка
,
тогда существует по крайней мере одна
точка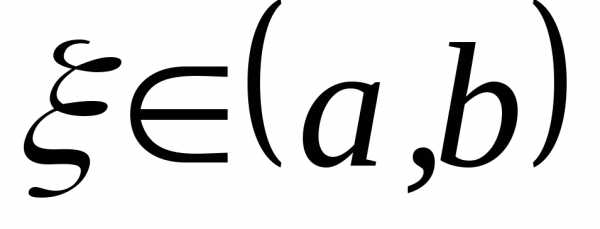 ,
такая, что площадь криволинейной
трапеции, ограниченной сверху непрерывной
кривойбудет равна площади прямоугольника с
тем же основанием и высотой, равной
,
такая, что площадь криволинейной
трапеции, ограниченной сверху непрерывной
кривойбудет равна площади прямоугольника с
тем же основанием и высотой, равной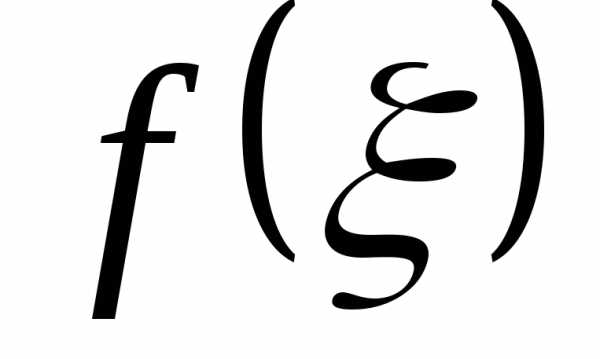 :
: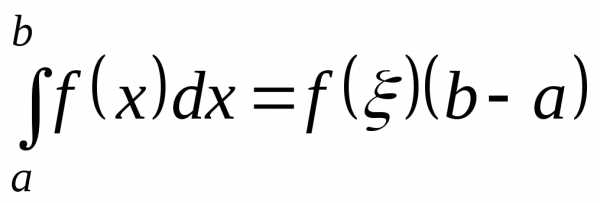 .
.
Вычисление определенных интегралов. Формула Ньютона-Лейбница
Если для подынтегральной функции можно найти первообразную, то определенный интеграл можно вычислить по формуле Ньютона-Лейбница.
–Формула Ньютона-Лейбница позволяет вычислить определенный интеграл как разность первообразных на верхнем и нижнем пределах интегрирования, не вычисляя предела интегральной суммы.
Можно выделить два этапа вычисления определенного интеграла.
Одним из методов интегрирования (см. тему 6) находят первообразную.
Вычисляют разность значений первообразной функции на верхнем и нижнем пределах интегрирования.
– Сначала в первообразную подставляют верхний предел.
studfiles.net
Примеры решения типовых задач неопределенный и определенный интегралы 1 ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ Метод непосредственного интегрирования
Примеры решения типовых задач
неопределенный и определенный интегралы
1. ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Методнепосредственного интегрирования связан с приведением подынтегрального выражения к табличной форме путём преобразований и применения свойств неопределённого интеграла.
Пример 1. Найти интеграл
.
Пример 2. Найти интеграл 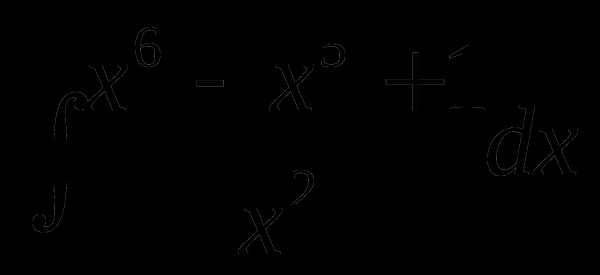
Пример 3..
Пример 4..
Пример 5. .
Метод замены переменной интегрирования.Пусть , где
, где 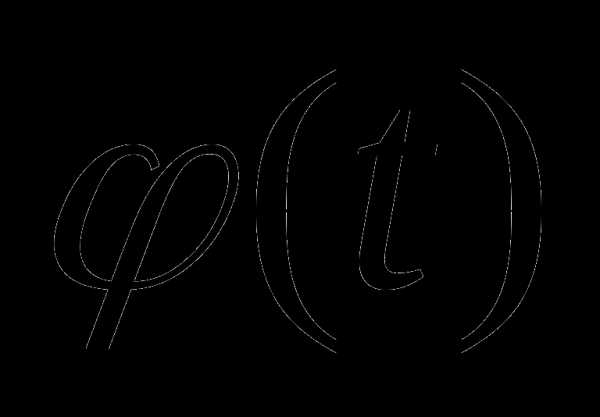 – функция, имеющая непрерывную производную. Тогда ; подставляя в интеграл, получим
– функция, имеющая непрерывную производную. Тогда ; подставляя в интеграл, получим
Пример 1. .
Пример 2.
Пример 3. Найти интеграл 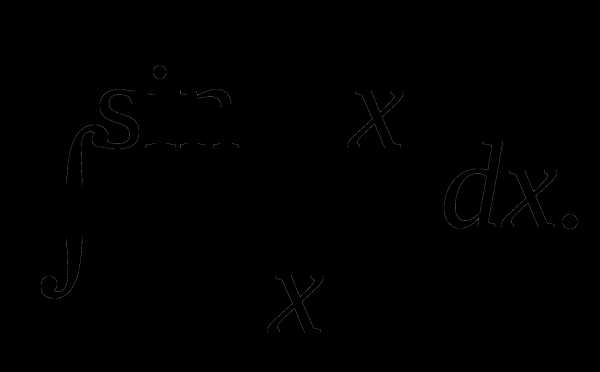
Воспользуемся подстановкой x = t2. Тогда , получим
Пример 4. .
Пример 5. .
Пример 6.
Пример 7.
Пример 8.
=
Пример 9.
=
Пример 10. Вычислить 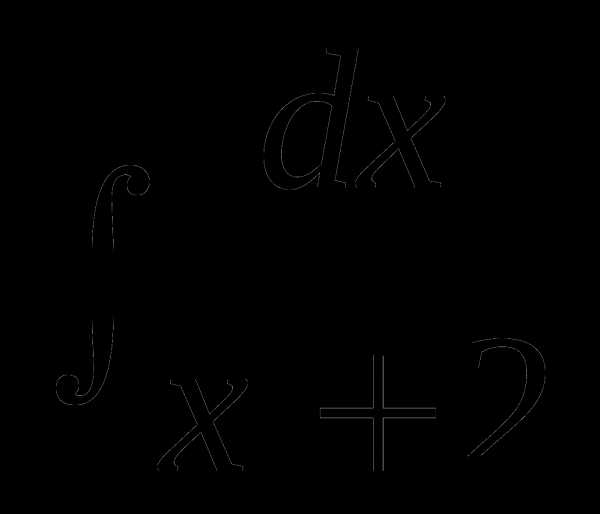 .
.
Решение. Обозначим t = x+2, тогда dx = dt, dx/(x+2) = dt/t = lnt+C =
= lnx+2+C.
Пример 11. Найти tg x dx.
Решение. tg x dx = sin x/cos x dx = – d(cos x)/ cos x. Пусть t = cos x, тогда tg x dx = – dt/t = – lnt+C = – lncos x+C.
Пример12. Вычислить 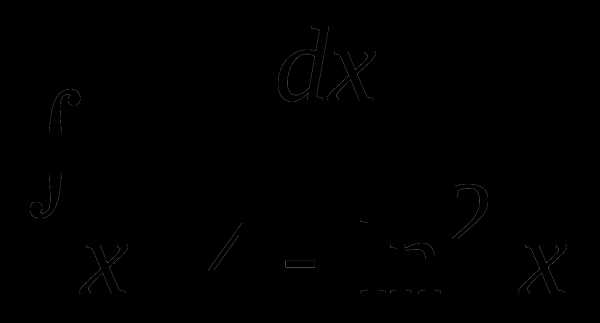 .
.
Решение. Учитывая, что = d(ln x), производим подстановку ln x = t. Тогда .
4. Определённый интеграл, его свойства и вычисление
Пример 1. Вычислить определенный интеграл 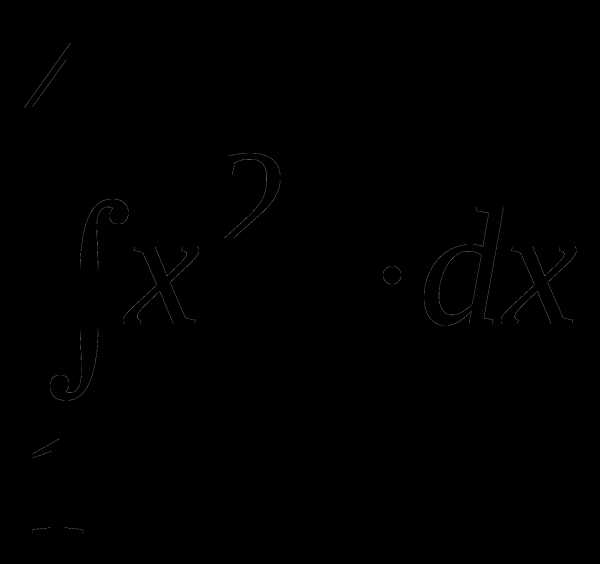 .
.
По формуле Ньютона-Лейбница имеем
.
Пример 2. Вычислить интеграл 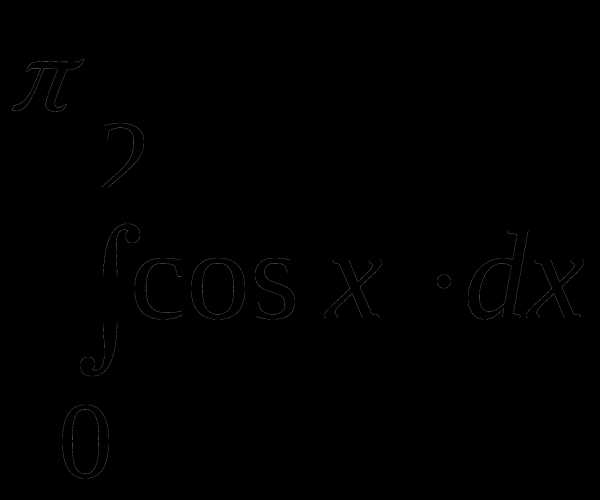 .
.
.
Пример 3. Вычислить интеграл 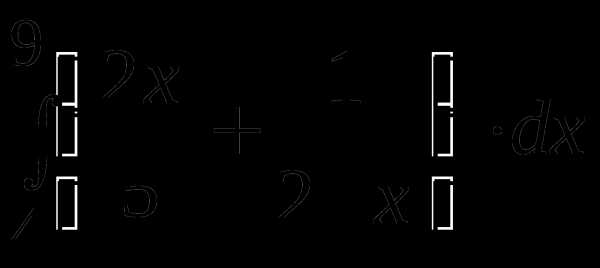 .
.
На основании свойств определенного интеграла и формулы Ньютона-Лейбница получаем
Пример 4. Вычислить интеграл 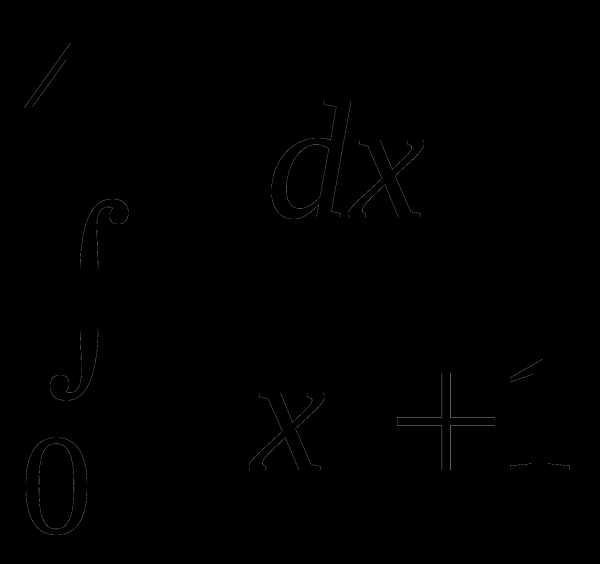 .
.
Обозначим , тогда 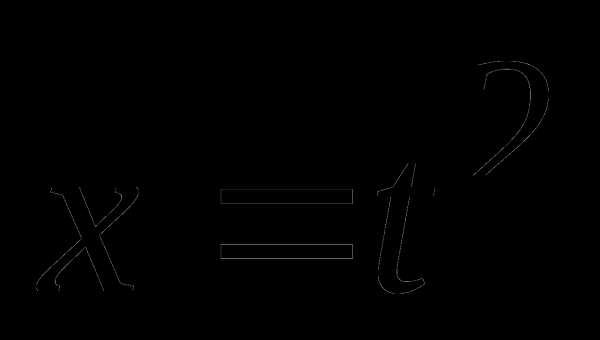 , . Подставим старые пределы интегрирования в формулу , получим новые пределы интегрирования
, . Подставим старые пределы интегрирования в формулу , получим новые пределы интегрирования 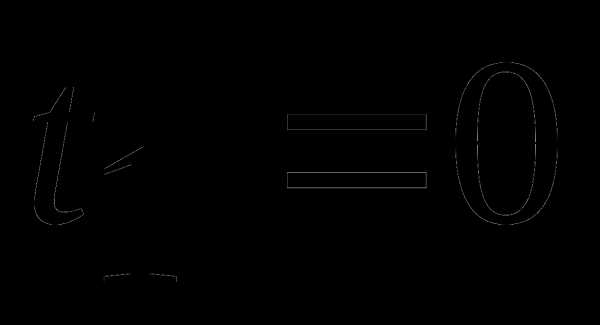 ,
, 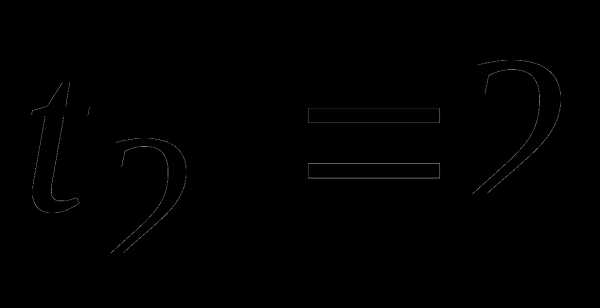 . Следовательно,
. Следовательно,
Пример 5. Вычислить интеграл 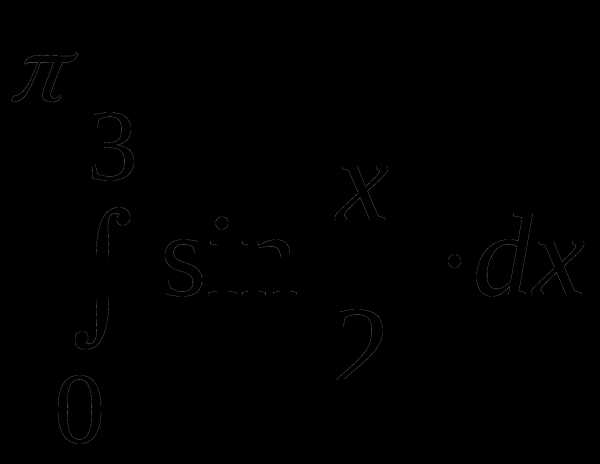 .
.
Представим дифференциал как 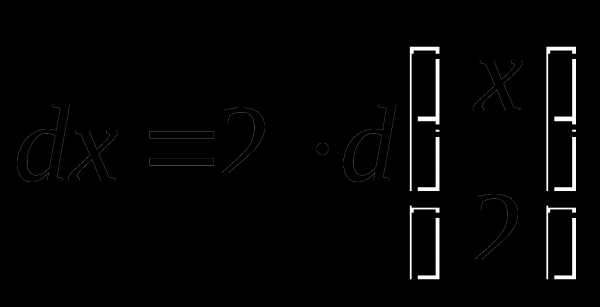 , тогда
, тогда
6. Вычисление площадей
Пример 1. Вычислить площадь фигуры, ограниченной графиками функций  ,
, 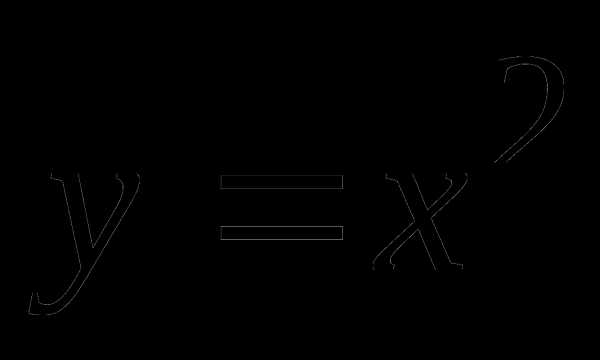 ,
,  ,
, 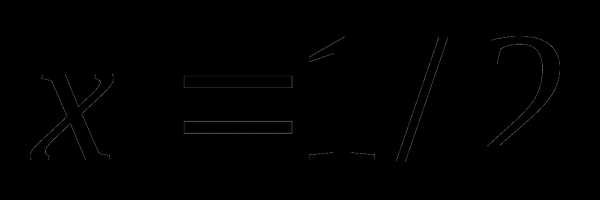 .
.
 ½ 1
½ 1 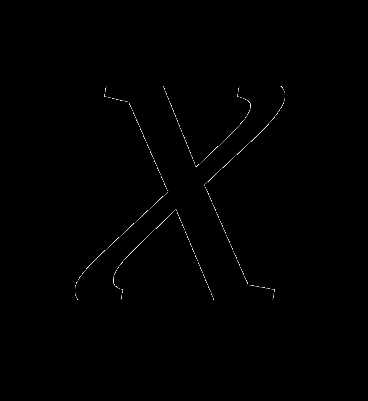
Пример 2. Найти площадь плоской фигуры, ограниченной графиком функции y = sinx и осью абсцисс при условии .
Разобьём отрезок 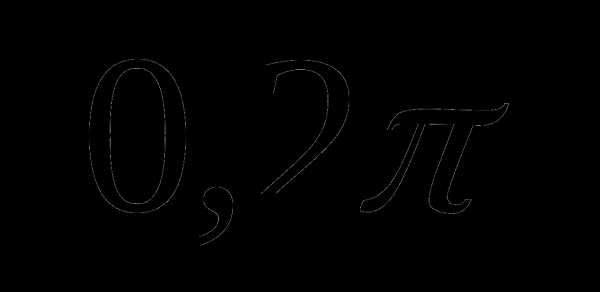 на два отрезка:
на два отрезка: 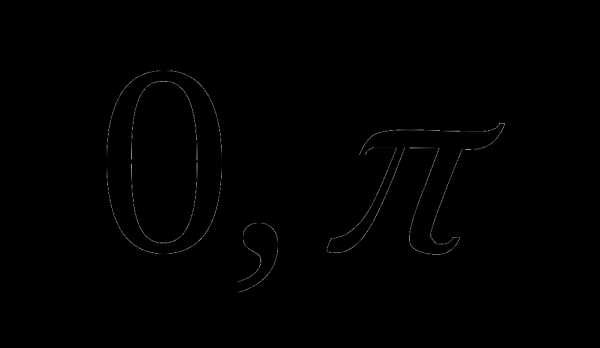 и
и 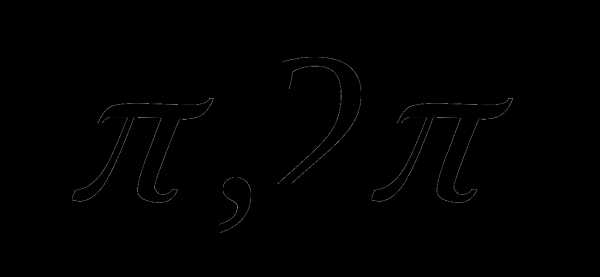 .
.
На первом из них sinx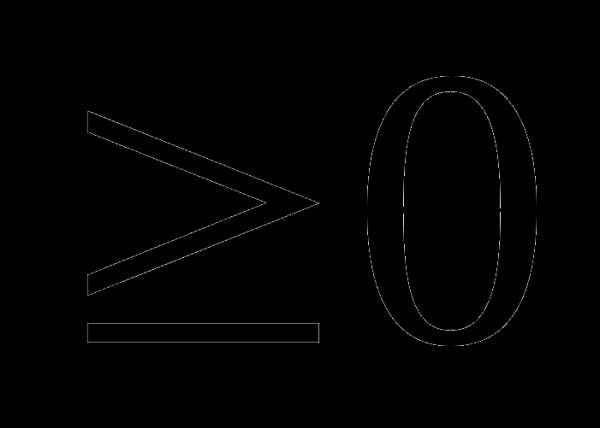 , на втором sinx
, на втором sinx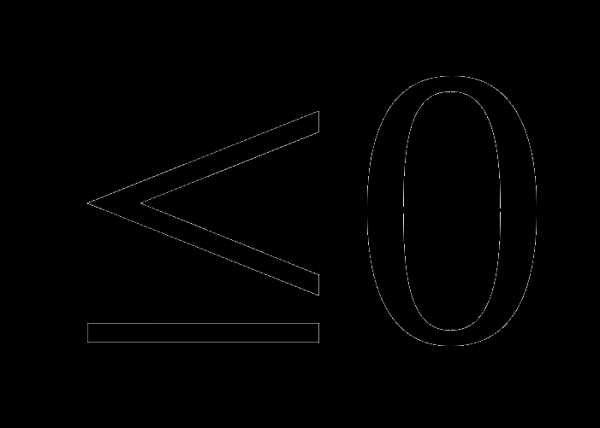 .
.
Тогда, используя формулы, находим искомую площадь:
textarchive.ru
Определенный интеграл
Определенный интеграл
Содержание
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
2. Геометрический смысл определенного интеграла
3. Основные свойства определенного интеграла
4. Формула Ньютона–Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям
Лекция 2. Применение определенных интегралов. несобственные интегралы
1. Площадь криволинейной трапеции
2. Объем тела вращения
3. Длина дуги плоской кривой
4. Несобственные интегралы с бесконечными пределами интегрирования
5. Несобственные интегралы от неограниченных функций
Литература
Лекция 1. Определенный интеграл
1. Понятие определенного интеграла
Пусть функция
определена на отрезке , . Выполним следующие операции:1) разобьем отрезок
точками на n частичных отрезков ;2) в каждом из частичных отрезков
, выберем произвольную точку и вычислим значение функции в этой точке: ;3) найдем произведения
, где – длина частичного отрезка , ;4) составим сумму
, (1)которая называется интегральной суммой функции y = f ( x ) на отрезке [ а, b ]. С геометрической точки зрения интегральная сумма
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки , а высоты равны соответственно (рис. 1). Обозначим через длину наибольшего частичного отрезка ;5) найдем предел интегральной суммы, когда
.Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка
на частичные отрезки, ни от выбора точек в них, то этот предел называется определенным интегралом от функции на отрезке и обозначается .Таким образом,
.В этом случае функция
называется интегрируемой на . Числа а и b называются соответственно нижним и верхним пределами интегрирования, – подынтегральной функцией, – подынтегральным выражением, – переменной интегрирования; отрезок называется промежутком интегрирования.Теорема 1. Если функция
непрерывна на отрезке , то она интегрируема на этом отрезке.2. Геометрический смысл определенного интеграла
Пусть на отрезке
задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f ( x ), снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).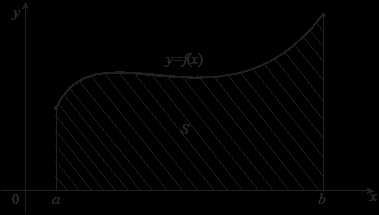
Рис. 2
Определенный интеграл
от неотрицательной функции с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа – отрезками прямых и , снизу – отрезком оси Ох.3. Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения переменной интегрирования:
.2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
3. Если
, то, по определению, полагаем4. Постоянный множитель можно выносить за знак определенного интеграла:
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:
.6. Если функция
интегрируема на и , то .7. ( теорема о среднем ). Если функция
непрерывна на отрезке , то на этом отрезке существует точка , такая, что .4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2. Если функция
непрерывна на отрезке и – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:, (2)
которая называется формулой Ньютона–Лейбница. Разность
принято записывать следующим образом: ,где символ
называется знаком двойной подстановки.Таким образом, формулу (2) можно записать в виде:
.Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную
для подынтегральной функции ; на втором – находится разность значений этой первообразной на концах отрезка .mirznanii.com
Определенный интеграл. Примеры решений
И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой .
Верхний предел интегрирования стандартно обозначается буквой .
Отрезок называется отрезком интегрирования.
Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.
Что такое определенный интеграл? Считаю немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность , то есть, находим число.
Готово.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.
Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывнана отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будетнесобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
– в таком виде интегрировать значительно удобнее.
Как и для неопределенного интеграла, для определенного интеграла справедливысвойства линейности:
– это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям:
Пример 1
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Пример 3
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: – первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: (в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная находится в одной скобке.
studopedya.ru