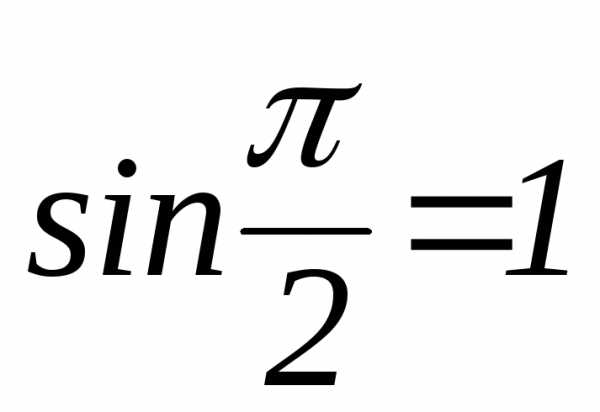Вычисление пределов по правилу Лопиталя
 – Правило Лопиталя для вычисления
пределов с неопределенными выражениями
вида
– Правило Лопиталя для вычисления
пределов с неопределенными выражениями
вида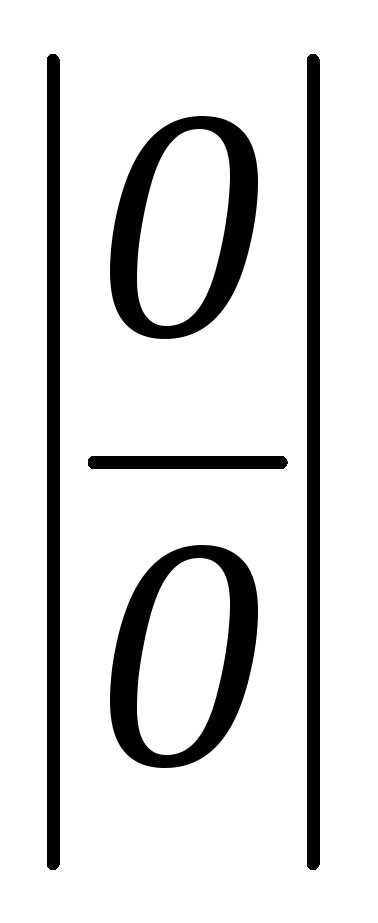 или
или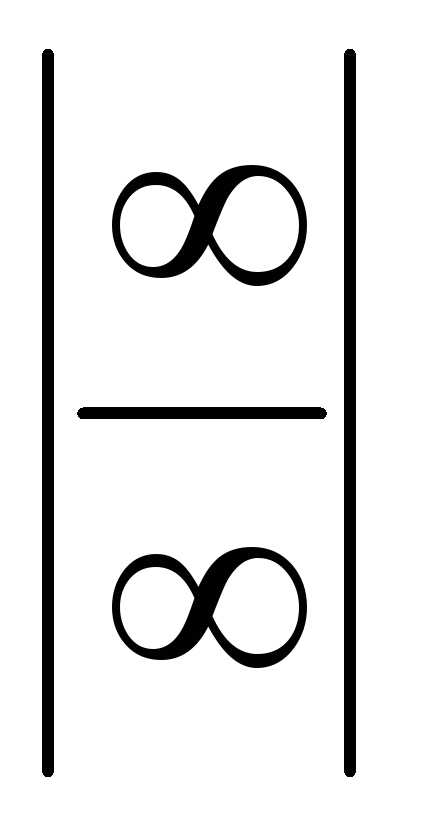 можно сформулировать в виде теоремы.
можно сформулировать в виде теоремы.
– Теорема. Пусть
однозначные функции 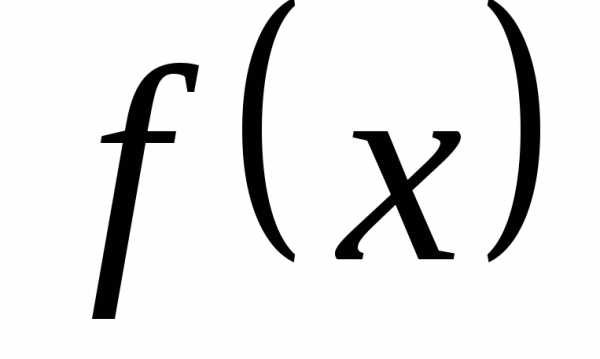 и
и дифференцируемы в некоторой окрестности
точки
дифференцируемы в некоторой окрестности
точки ,
причем
,
причем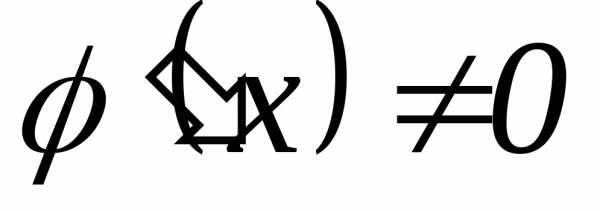 .
Тогда, если существует предел (конечный
или бесконечный) отношения производных
этих функций, то существует равный ему
предел отношения самих функций.
.
Тогда, если существует предел (конечный
или бесконечный) отношения производных
этих функций, то существует равный ему
предел отношения самих функций.
– Обратите внимание: именно существование предела отношений производных гарантирует существование предела отношения функций, но не наоборот! Предел отношения функций может существовать и при отсутствии предела отношения производных.
Однако на практике это правило применяют в обратном порядке: предел отношения функций приравнивают пределу отношения производных.
Пример – иллюстрирует случай неприменимости правила Лопиталя.
Пусть , найдем пределы отношения функций: ;
и их производных: – не существует.
Правило Лопиталя применять нельзя.
Правило Лопиталя можно применять несколько раз подряд, если неопределенность после очередного применения не раскрыта.
Неопределенные выражения вида с помощью тождественных преобразований приводят к виду
 и применяют правило Лопиталя.
и применяют правило Лопиталя.Желательно совмещать применение правила Лопиталя с применением эквивалентных бесконечно малых величин. При этом следует строго придерживаться теоремы: заменять эквивалентными можно только в произведении (частном) !
После каждого применения правила Лопиталя следует проверять, сохранилось ли неопределенное выражение. Если при проверке находятся
Примеры
Вычислить пределы по правилу Лопиталя.
| Применять
эквивалентные бесконечно малые
величины нельзя, т.к. |
= | Первое применение правила Лопиталя дает конечный предел. |
| Применять эквивалентные бесконечно малые величины нельзя, выполним тождественные |
= | |
но проверка пределов сомножителей показывает, что некоторые из них имеют конечные пределы, которыми они и заменяются. | |
Еще раз применяется правило Лопиталя. | |
Полученный в результате предел бесконечен. |
– При вычислении пределов сомножителей используются известные величины:
 – Раскрытие степенных неопределенных
выражений вида
– Раскрытие степенных неопределенных
выражений вида
.
Допустим,
существует конечный или бесконечный
предел степенно-показательной функции 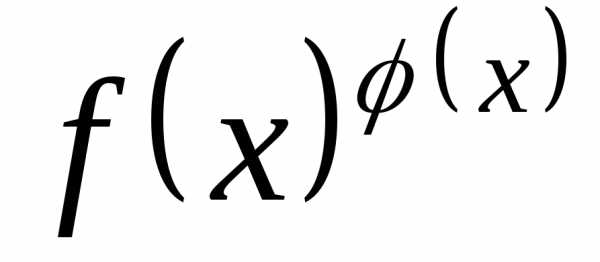 (см. раздел о логарифмическом
дифференцировании, тема 5). Обозначим
его
(см. раздел о логарифмическом
дифференцировании, тема 5). Обозначим
его
.
Прологарифмируем данное выражение и применим правило предельного перехода под знаком непрерывной функции (см. раздел о непрерывности функции, тема 4).
Логарифмируем по основанию е. | |||
| Используем свойства логарифмов (см. приложение) и правило предельного перехода. | ||
Степень числа е вычисляется как предел. | |||
, где | Окончательно получим формулы, по которым можно вычислять пределы степенно-показательных функций. | ||
– Часто при вычислении А применяют правило Лопиталя, поэтому полученные формулы для раскрытия степенно-показательной неопределенности иногда называют вторым правилом Лопиталя.
ПРИМЕР
Вычислить предел по второму правилу Лопиталя.
Допустим
нужный предел существует и обозначим
его | |||
Теперь вычислим показатель степени Преобразуем выражение под знаком предела, чтобы можно было применить правило Лопиталя. | |||
| Берем производные от числителя и знаменателя (отдельно!). | ||
Преобразуем полученное выражение и проверяем неопределенность. Она не устранена. | |||
Заменяем | |||
Окончательный ответ. | |||
Еще примеры вычисления пределов по правилу Лопиталя приведены в разделе “Примеры выполнения обязательных заданий по теме 5”.
57
studfiles.net
правило лопиталя
Правило Лопиталя | |||
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или. Пустьa является некоторым конечным действительным числом или равно бесконечности.
Правило Лопиталя можно также применять к неопределенностям типа . Первые две неопределенностиможно свести к типуилис помощью алгебраических преобразований. А неопределенностисводятся к типус помощью соотношения Правило Лопиталя справедливо также и для односторонних пределов. | |||
Пример 1 | |||
Вычислить предел . Решение. Дифференцируя числитель и знаменатель, находим значение предела:
| |||
Пример 2 | |||
Вычислить предел . Решение. Поскольку прямая подстановка приводит к неопределенности типа , применяем правило Лопиталя.
| |||
Пример 3 | |||
Вычислить предел . Решение. Здесь мы имеем дело с неопределенностью типа . После простых преобразований, получаем
| |||
Пример 4 | |||
Найти предел . Решение. Используя правило Лопиталя, можно записать
| |||
Пример 5 | |||
Найти предел . Решение. Здесь мы встречаемся с неопределенностью типа . Обозначим. После логарифмирования получаем
Далее, по правилу Лопиталя, находим
Соответственно,
| |||
Пример 6 |
15. Правила Лопиталя*
Швейцарский математик Иоганн I Бернулли (1667-1748) после успешного окончания Базельского университета, путешествуя по Европе, в 1690 году приезжает в Париж. В литературном салоне философа Никола Мальбранша (1638-1715) Иоганн знакомится с французским математиком маркизом Гийомом Франсуа Антуаном де Лопиталем (1661-1704). В ходе оживленной беседы Лопиталь удивился, как легко, “как бы играя”, юнец Бернулли решал трудные задачи по новому исчислению. Поэтому Лопиталь попросил прочитать ему несколько лекций. Устные беседы понравились Лопиталю, и он за приличный гонорар стал получать материалы в письменном виде. Заметим, что общеизвестное теперь “правило Лопиталя” для раскрытия неопределенностей также было передано ему Иоганном. Уже в 1696 году появился знаменитый трактат Лопиталя “Введение в анализ бесконечно малых для понимания кривых линий”. Вторая часть курса, изложенного Иоганном I Бернулли, была опубликована лишь в 1742 году и называлась “Математические лекции о методе интегралов и другие; написаны для знаменитого маркиза Госпиталия; годы 1691-1692”. В 1921 году были обнаружены рукописные копии лекций, написанные рукой Иоганна I Бернулли, оригиналы которых были переданы Лопиталю в 1691-1692 гг. Из них ученые неожиданно обнаружили, что Лопталь в своем “Анализе” почти не отступал от лекций своего молодого учителя.
Теорема (Коши). Пусть функции и непрерывны на , дифференцируемы на и . Тогда :
Доказательство. Рассмотрим функцию
выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .
По теореме Ролля существует :
Первое правило Лопиталя
Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Пусть конечно. По выберем : в интервале выполняется неравенство
Применим теорему Коши к отрезку , где . Существует :
и, значит,
Это и означает, что .
В случае, когда бесконечно, неравенство (1) заменяется на
или
в зависимости от знака . В остальном доказательство не меняется.
Второе правило Лопиталя
Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
то и
Доказательство. Пусть конечно. По выберем : в интервале выполняется неравенство
Определим функцию из условия
Имеем
при . Применим к отрезку теорему Коши. Получим, что существует :
Для тех , для которых
Так как произвольно мало, то
В случае, когда , неравенство (2) заменяется на
а неравенство (4) – на неравенство
имеющим место при , достаточно близких к a в силу (3).
Аналогично рассматривается случай .
studfiles.net
Правило Лопиталя | Математика | FANDOM powered by Wikia
В математическом анализе правилом Лопита́ля называют метод нахождения пределов функций, раскрывающий неопределённости вида $ 0/0 $ и $ \infty/\infty $. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Точная формулировка Править
Правило говорит, что если функции $ f(x) $ и $ g(x) $ обладают следующим набором условий:
- $ \lim_{x\to a+}{f(x)}=\lim_{x\to a+}{g(x)}=0 $ или $ \infty $;
- $ \exists \lim_{x\to a+}{\frac{f'(x)}{g'(x)}} $;
- $ g(x)\neq 0 $ в некоторой окрестности точки $ a $,
тогда существует $ \lim_{x\to a+}{\frac{f(x)}{g(x)}} = \lim_{x\to a+}{\frac{f'(x)}{g'(x)}} $. При этом теорема верна и для других баз (для указанной будет приведено доказательство).
Способ раскрытия такого рода неопределённостей был опубликован Лопиталем в его сочинении «Анализ бесконечно малых», изданном в 1696 году. В предисловии к этому сочинению Лопиталь указывает, что без всякого стеснения пользовался открытиями Лейбница и братьев Бернулли и «не имеет ничего против того, чтобы они предъявили свои авторские права на все, что им угодно». Иоганн Бернулли предъявил претензии на все сочинение Лопиталя целиком и в частности после смерти Лопиталя опубликовал работу под примечательным названием «Усовершенствование моего опубликованнного в „Анализе бесконечно малых“ метода для определения значения дроби, числитель и знаменатель которой иногда исчезают», 1704.
Доказательство Править
1. Докажем теорему для случая, когда пределы функций равны нулю (т. н. неопределённость вида $ \left(\frac{0}{0}\right) $).
Поскольку мы рассматриваем функции $ f $ и $ g $ только в правой проколотой полуокрестности точки $ a $, мы можем непрерывным образом их доопределить в этой точке: пусть $ f(a)=g(a)=0 $. Возьмём некоторый $ x $ из рассматриваемой полуокрестности и применим к отрезку $ [a,\;x] $ теорему Коши. По этой теореме получим:
- $ \exists c \in [a,x]\!:\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f'(c)}{g'(c)} $,
но $ f(a)=g(a)=0 $, поэтому $ \forall x\, \exists c \in [a,\;x]\!:\frac{f(x)}{g(x)}=\frac{f'(c)}{g'(c)} $.
Дальше, записав определение предела отношения производных и обозначив последний через $ A $, из полученного равенства выводим:
- $ \forall \varepsilon>0\, \exists \delta>0\, \forall x(x-a<\delta\Rightarrow \left|\frac{f(x)}{g(x)}-A\right|<\varepsilon) $ для конечного предела и
- $ \forall M > 0\, \exists \delta>0\, \forall x(x-a<\delta\Rightarrow \left|\frac{f(x)}{g(x)}\right| > M) $ для бесконечного,
что является определением предела отношения функций.
2. Докажем теорему для неопределённостей вида $ \left(\frac{\infty}{\infty}\right) $.
Пусть, для начала, предел отношения производных конечен и равен $ A $. Тогда, при стремлении $ x $ к $ a $ справа, это отношение можно записать как $ A+\alpha $, где $ \alpha $ — O(1). Запишем это условие:
- $ \forall\varepsilon_{1}\, \exists \delta_{1}\, \forall x(x-a<\delta_{1}\Rightarrow \alpha(x)<\varepsilon_{1}) $.
Зафиксируем $ t $ из отрезка $ [a,\;a+\delta_1] $ и применим теорему Коши ко всем $ x $ из отрезка $ [a,\;t] $:
- $ \forall x\in [a;t]\ \exists c\in [a;\;x]\!:\frac{f(x)-f(t)}{g(x)-g(t)}=\frac{f'(c)}{g'(c)} $, что можно привести к следующему виду:
- $ \frac{f(x)}{g(x)}=\frac{1-\frac{g(t)}{g(x)}}{1-\frac{f(t)}{f(x)}}\cdot\frac{f'(c)}{g'(c)} $.
Для $ x $, достаточно близких к $ a $, выражение имеет смысл; предел первого множителя правой части равен единице (так как $ f(t) $ и $ g(t) $ — константы, а $ f(x) $ и $ g(x) $ стремятся к бесконечности). Значит, этот множитель равен $ 1+\beta $, где $ \beta $ — бесконечно малая функция при стремлении $ x $ к $ a $ справа. Выпишем определение этого факта, используя то же значение $ \varepsilon $, что и в определении для $ \alpha $:
- $ \forall \varepsilon_{1}\, \exists \delta_{2}\, \forall x(x-a<\delta_{2}\Rightarrow \beta(x)<\varepsilon_{1}) $.
Получили, что отношение функций представимо в виде $ (1+\beta)(A+\alpha) $, и $ \left|\frac{f(x)}{g(x)}-A\right|<|A|\varepsilon_{1}+\varepsilon_{1}+\varepsilon_{1}^{2} $. По любому данному $ \varepsilon $ можно найти такое $ \varepsilon_{1} $, чтобы модуль разности отношения функций и $ A $ был меньше $ \varepsilon $, значит, предел отношения функций действительно равен $ A $.
Если же предел $ A $ бесконечен (допустим, он равен плюс бесконечности), то
- $ \forall M>0\, \exists \delta_{1}>0\, \forall x(x-a<\delta_{1}\Rightarrow\frac{f'(x)}{g'(x)}>2M) $.
В определении $ \beta $ будем брать $ \varepsilon_{1} < \frac{1}{2} $; первый множитель правой части будет больше 1/2 при $ x $, достаточно близких к $ a $, а тогда $ \frac{f(x)}{g(x)}>\frac{1}{2}\cdot 2M=M\Rightarrow \lim_{x\to a+}{\frac{f(x)}{g(x)}}=+\infty $.
Для других баз доказательства аналогичны приведённым.
- $ \lim_{x \to 0}\frac{x^2+5x} {3x} = \lim_{x \to 0}\frac{2x+5} {3} = \frac{5} {3}=1\frac{2}{3} $
- $ \lim_{x \to \infty}\frac{x^3+4x^2+7x+9} {x^3+3x^2} $
Здесь можно применить правило Лопиталя 3 раза, а можно поступить иначе. Можно разделить и числитель, и знаменатель на x в наибольшей степени(в нашем случае $ x^3 $). В этом примере получается:- $ \lim_{x \to \infty}\frac{1+4/x+7/x^2+9/x^3} {1+3/x} = \frac{1} {1} = 1 $
- $ \lim_{x\to+\infty}{\frac{e^{x}}{x^{a}}}=\lim_{x\to+\infty}{\frac{e^{x}}{a\cdot x^{a-1}}}=\ldots=\lim_{x\to+\infty}{\frac{e^{x}}{a!}}=+\infty $;
- $ \lim_{x\to+\infty}{\frac{x^{a}}{\ln{x}}}=\lim_{x\to+\infty}{\frac{ax^{a-1}}{\frac{1}{x}}}=a\cdot\lim_{x\to+\infty}{x^{a}}=+\infty $ при $ a>0 $.
ar:قاعدة اوبيتال
ca:Regla de L’Hôpital
cs:L’Hospitalovo pravidlo
da:L’Hôpitals regeleu:L’Hopitalen erregelahe:כלל לופיטל
hu:L’Hospital-szabály
is:Regla l’Hôpitalsla:Hospitalii regula
nl:Regel van L’Hôpital
pl:Reguła de l’Hospitalasl:L’Hôpitalovo pravilo
sr:Лопиталово правило
sv:L’Hôpitals regel
th:หลักเกณฑ์โลปีตาลправило Лопиталя
ru.math.wikia.com
Вычисление пределов по правилу лопиталя — Юридический статус
Предел функции, правило Лопиталя
Применение правила Лопиталя необходимо для вычисления пределов при получении неопределенностей вида » open=» 0 0 и » open=» ? ? .
Имеются неопределенности вида » open=» 0 · ? и » open=» ? — ? .
Самой важной частью правила Лопиталя является дифференцирование функции и нахождение ее производной.
Правило Лопиталя
Когда lim x > x 0 f ( x ) g ( x ) = » open=» 0 0 или » open=» ? ? и функции f ( x ) , g ( x ) являются дифференцируемыми в пределах точки х 0 , тогда lim x > x 0 f ( x ) g ( x ) = lim x > x 0 f ‘ ( x ) g ‘ ( x ) .
Если неопределенность нерешаема после применения правила Лопиталя, тогда необходимо снова его применить. Для полного понятия рассмотрим несколько примеров.
Произвести вычисления, применив правило Лопиталя lim x > 0 sin 2 ( 3 x ) x · cos ( x ) .
Для решения по правилу Лопиталя для начала необходимо произвести подстановку. Получаем, что lim x > 0 sin 2 ( 3 x ) x · cos ( x ) = sin 2 ( 3 · 0 ) 0 · cos ( 0 ) = » open=» 0 0 .
Теперь можно переходить к вычислению пределов, используя правило. Получаем, что
lim x > 0 sin 2 ( 3 x ) x · cos ( x ) = » open=» 0 0 = lim x > 0 sin 2 ( 3 x ) ‘ x · cos ( x ) ‘ = lim x > 0 2 sin ( 3 x ) ( sin ( 3 x ) ) ‘ x ‘ · cos ( x ) + x · ( cos ( x ) ) ‘ = = lim x > 0 6 sin ( 3 x ) cos ( 3 x ) cos ( x ) — x · sin ( x ) = 6 sin ( 3 · 0 ) cos ( 3 · 0 ) cos ( 0 ) — 0 · sin ( 0 ) = 0 1 = 0
Ответ: lim x > 0 sin 2 ( 3 x ) x · cos ( x ) = 0 .
Вычислить предел заданной функции lim x > ? ln ( x ) x .
Производим постановку бесконечностью. Получаем, что
lim x > ? ln ( x ) x = ln ( ? ) ? = » open=» ? ?
Полученная неопределенность указывает на то, что необходимо применить правило Лопиталя. Имеем, что
lim x > ? ln ( x ) x = » open=» ? ? = lim x > ? ln ( x ) ‘ x ‘ = lim x > ? 1 x 1 = 1 ? = 0
Ответ: lim x > ? ln ( x ) x = 0
Вычислить предел заданной функции lim x > 0 + 0 ( x 4 ln ( x ) )
Производим подстановку значения x . получаем, что
lim x > 0 + 0 ( x 4 ln ( x ) ) = ( 0 + 0 ) 4 · ln ( 0 + 0 ) = » open=» 0 · ( — ? )
Решение привело к неопределенности вида ноль умноженный на отрицательную бесконечность. Это указывает на то, что необходимо обратиться к таблице неопределенностей и принять решения для выбора метода нахождения этого предела. После преобразования применяем правило Лопиталя. Получаем, что
lim x > 0 + 0 ( x 4 ln ( x ) ) = » open=» 0 · ( — ? ) = lim x > 0 + 0 ln ( x ) x — 4 = ln ( 0 + 0 ) ( 0 + 0 ) — 4 = » open=» — ? + ?
Приход к неопределенности говорит о том, что необходимо повторное применение этого правила. Имеем, что
lim x > 0 + 0 ( x 4 ln ( x ) ) = » open=» 0 · ( — ? ) = lim x > 0 + 0 ln ( x ) x — 4 = » open=» — ? + ? = = lim x > 0 + 0 ( ln ( x ) ) ‘ ( x — 4 ) ‘ = lim x > 0 + 0 1 x — 4 — 5 = — 1 4 lim x > 0 + 0 1 x — 4 = — 1 4 · 1 ( 0 + 0 ) — 4 = = — 1 4 · ( 0 + 0 ) 4 = 0
Ответ: lim x > 0 + 0 ( x 4 ln ( x ) ) = 0
Выполнить вычисление предела функции lim x > 0 c t g 2 ( x ) — 1 x 2 .
После подстановки получаем
lim x > 0 c t g 2 ( x ) — 1 x 2 = » open=» ? — ?
Наличие неопределенности указывает на то, что следует использовать правило Лопиталя. Получаем, что
lim x > 0 c t g 2 ( x ) — 1 x 2 = » open=» ? — ? = lim x > 0 cos 2 ( x ) sin 2 ( x ) — 1 x 2 = = lim x > 0 x 2 cos 2 ( x ) — sin 2 ( x ) x 2 sin 2 ( x ) = lim x > 0 x cos x — sin x x cos x + sin x x 2 sin 2 ( x ) = = lim x > 0 x cos x — sin x x sin 2 ( x ) x cos x + sin x x = lim x > 0 x cos x — sin x x sin 2 ( x ) cos x + sin x x = = lim x > 0 cos x + sin x x lim x > 0 x cos x — sin x x sin 2 ( x ) = 2 lim x > 0 x cos x — sin x x sin 2 ( x ) = = 2 0 · cos ( 0 ) — sin ( 0 ) 0 · sin 2 ( 0 ) = » open=» 0 0
Для последнего перехода использовался первый замечательный предел. После чего приходим к решению по Лопиталю. Получим, что
2 lim x > 0 x cos x — sin x x sin 2 ( x ) = » open=» 0 0 = 2 lim x > 0 ( x cos x — sin x ) ‘ ( x sin 2 ( x ) ) ‘ = = 2 lim x > 0 cos x — x sin x — cos x sin 2 ( x ) + 2 x sin x cos x = 2 lim x > 0 — x sin ( x ) + 2 x cos x = » open=» 0 0
Так как неопределенность не ушла, необходимо еще одно применение правила Лопиталя. Получаем предел вида
2 lim x > 0 — x sin ( x ) + 2 x cos x = » open=» 0 0 = 2 lim x > 0 — x ‘ sin ( x ) + 2 x cos x ‘ = = 2 lim x > 0 1 cos x + 2 cos x — 2 x sin x = — 2 · 1 3 · cos ( 0 ) — 2 · 0 · sin ( 0 ) = — 2 3
Ответ: lim x > 0 c t g 2 ( x ) — 1 x 2 = — 2 3
www.zaochnik.com
Калькулятор для решения пределов
Данный онлайн калькулятор вычисляет предел функции. Программа не просто даёт ответ, она приводит пошаговое и подробное решение.
Как пользоваться калькулятором для решения пределов онлайн:
- Введите математическое выражение с переменной икс, в выражении используйте стандартные операции: + сложение, — вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции.
- Введите значение, к которому стремится переменная икс.
- Нажмите кнопку — Вычислить предел.
- Через несколько секунд внизу отобразится пошаговое решение с подробными комментариями.
В качестве тренировки, можете нажать на любой из 3-х примеров внизу и все поля заполнятся автоматически, затем нажмите на «Найти предел» и вы получите подробное решение и ответ. Также внизу страницы вы можете прочитать полные правила ввода данных, ответы на часто задаваемые вопросы и оставить свой комментарий.
www.webmath.ru
Вычисление пределов по правилу лопиталя
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ
- 2. Определение непрерывности функции в точке «на языке приращений».
- § 2. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ
- 2. Связь между непрерывностью и дифференцируемостью функции в точке.
- 3. Производная и дифференциал.
- 4. Односторонние и бесконечные производные.
- § 3. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧ
- 2. Геометрические приложения производной.
- 3. Применения производной в физических задачах. Механический смысл производной.
- § 4. ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАЦИЙ
- 2. Дифференцирование произведения.
- 3. Дифференцирование частного.
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ
- 2. Инвариантность формы записи дифференциала.
- § 6. ДИФФЕРЕНЦИРОВАНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Дифференцирование обратной функции.
- 3. Дифференцирование обратных тригонометрических функций.
- 4. Дифференцирование показательной и логарифмической функций.
- 5. Дифференцирование гиперболических функций.
- 6. Сводка правил и формул дифференцирования.
- 7. Логарифмическое дифференцирование.
- § 7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. Механический смысл второй производной.
- 3. Натуральная степень бинома (формула Ньютона).
- 4. Свойства производной n-го порядка.
- 5. Дифференциалы высшего порядка.
ГЛАВА 2. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ - 1. СВЯЗЬ МЕЖДУ ХОДОМ ИЗМЕНЕНИЯ ФУНКЦИИ И ЕЕ ПРОИЗВОДНОЙ
- 2. Экстремумы функции.
- § 2. ТЕОРЕМА ЛАГРАНЖА И ЕЕ СЛЕДСТВИЯ
- 2. Теорема 2 (теорема Ролля).
- 3. Теорема Лагранжа.
- 4. Условие постоянства функции.
- § 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ
- 2. Исследование функций на экстремум с помощью первой производной.
- 3. Использование второй производной для исследования функций на экстремум.
- 4. Нахождение наибольшего и наименьшего значений функции на данном отрезке.
- § 4. ВЫПУКЛЫЕ ФУНКЦИИ
- 2. Достаточные условия выпуклости.
- 3. Точки перегиба.
- § 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ И РЕШЕНИЮ УРАВНЕНИЙ
- 2. Приближенное решение уравнений.
- § 6. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ФУНКЦИЙ
- 2. Правило Лопиталя.
- § 7. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
- § 8. КРИВЫЕ НА ПЛОСКОСТИ
- 2. Жордановы кривые.
- 3. Связь между различными видами уравнений линий.
- 4. Дифференцирование параметрически заданных функций.
- 5. Полярное уравнение кривой.
- 6. Производная второго порядка для параметрически заданной функции.
- 7. Построение кривых, заданных параметрическими уравнениями.
- 8. Построение кривых, заданных полярными уравнениями.
- ОТВЕТЫ
© 2018 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
lib.alnam.ru
Правило Лопиталя для чайников: определение, примеры решения, формулы
Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.
Правило Лопиталя: история и определение
На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.
Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.
Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.
Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.
Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:
Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.
Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:
Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Раскрытие неопределенностей по правилу Лопиталя
В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:
Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.
Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:
Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:
Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:
Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:
Теперь перейдем к примерам.
Найти предел по правилу Лопиталя:
Вычислить с использованием правила Лопиталя:
Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.
Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:
Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
zaochnik.ru
Онлайн калькулятор. Решение пределов онлайн.
Используя этот онлайн калькулятор для вычисления пределов (лимитов), вы сможете очень просто и быстро найти предел функции.
Воспользовавшись онлайн калькулятором для вычисления пределов, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач и закрепить пройденный материал.
Найти предел
Для вычисления пределов онлайн выполните следующие действия
- введите значения функции f ( x ), используя стандартные математические операции и математические функции.
- Введите значение к которому стремится переменная x .
- Нажмите кнопку «Равно».
- Через несколько секунд вы увидите решение предела.
Данный калькулятор для решения пределов онлайн использует виджет на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
ru.onlinemschool.com
yurist-moscow.ru
Вычислите предел по правилу лопиталя
Правило Лопиталя обычно применяют, когда при вычислении пределов в результате получают неопределенность следующих видов: , , , .
Правило Лопиталя применяется наиболее часто. При случаях, когда, применив правило Лопиталя неопределенность не исчезнет, его можно применить еще.
Правило сводится к тому, что если в точке существуют производные от функций, которые стоят в числителе и знаменателе, то предел можно найти именно от частного этих функций, заменив ими заданные.
Рассмотрим на примере применение правила Лопиталя.
Пример 1.
Вычислим предел по правилу Лопиталя:
Решение.
Подставим значение х и получим:
В результате получилась неопределенность типа , которую можно решить с помощью правила Лопиталя:
Ответ. .
В данном примере правило сработало с первого раза. В случае, если после его применения опять получилась бы определенность одного из вышеупомянутых видов, то правило нужно было бы применить еще раз.
ru.solverbook.com
Найти пределы правилом лопиталя — Гармония
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x e e число, которое примерно равно 2.7 exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) pi Число — «Пи», которое примерно равно 3.14 sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) sign(x) Функция — Знак x erf(x) Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
Действительные числа вводить в виде 7.5, не 7,5 2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Нахождение предела функции, по правилу Лопиталя, раскрывающий неопределённости вида 0/0 и ∞/∞.
Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже.
Допустимые операции: + — / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точка в которой необходимо посчитать предел
Тогда существует предел отношения функций f(x) и g(x):
,
И он равен пределу отношения производной функции f(x) к производной функции g(x):
В формуле допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень
planetcalc.ru
Правило Лопиталя с примерами
Правило Лопиталя (п. Л.) облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций стремящихся к нулю. Т.е. отношение функций это неопределенность 0/0. Раскрыть ее поможет правило Лопиталя. В пределе отношение функций можно заменить отношением производных этих функций. Т.е. надо производную числителя разделить на производную знаменателя и от этой дроби взять предел.
1. Неопределенность 0/0. Первое п.Л.
Если = 0, то , если последний существует.
2. Неопределенность вида ∞/∞ Второе п. Л.
Нахождение пределов такого типа называется раскрытием неопределенностей.
Если = ∞, то , если последний существует.
3. Неопределенности 0⋅∞, ∞- ∞, 1 ∞ и 0 0 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности. Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.
Пример 1. В этом примере неопределенность 0/0
Пример 2. Здесь ∞/∞
В этих примерах производные числителя делим на производные знаменателя и подставляем предельное значение вместо х.
Пример 3. Вид неопределенности 0⋅∞ .
Неопределенность 0⋅∞ преобразуем к ∞/∞, для этого х переносим в знаменатель в виде дроби 1/x , в числителе пишем производную от числителя, а в знаменателе производную от знаменателя.
Пример 4 Вычислить предел функции
Здесь неопределенность вида ∞ 0 Сначала логарифмируем функцию, затем найдем от нее предел
Для получения ответа надо е возвести в степень -1, получим e -1 .
Пример 5. Вычислить предел от если x → 0
Решение. Вид неопределенности ∞ -∞ Приведя дробь к общему знаменателю перейдем от ∞-∞ к 0/0. Применим правило Лопиталя, однако снова получим неопределенность 0/0, поэтому п. Л. надо применить второй раз. Решение имеет вид:
= = = =
= =
Пример 6 Решить
Решение. Вид неопределенности ∞/∞, раскрыв ее получим
= = = 0.
В случаях 3), 4), 5) сначала логарифмируют функцию и находят предел логарифма, а затем искомый предел е возводим в полученную степень.
Пример 7. Вычислить предел
Решение. Здесь вид неопределенности 1 ∞ . Обозначим A =
Тогда lnA = = = = 2.
Основание логарифма е, поэтому для получения ответа надо е возвести в квадрат, получим e 2 .
Иногда бывают случаи, когда отношение функций имеет предел, в отличие от отношения производных, которое не имеет его.
Т.к. sinx ограничен, а х неограниченно растет, второй член равен 0.
Эта функция не имеет предела, т.к. она постоянно колеблется между 0 и 2, к этому примеру неприменимо п. Л.
www.mathelp.spb.ru
Правило Лопиталя: теория и примеры решений
Правило Лопиталя и раскрытие неопределённостей
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).
Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю
(),
то предел отношения этих функций равен пределу отношения их производных
().
Правило Лопиталя для случая предела двух бесконечно больших величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности
(),
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе — производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Пример 4. Вычислить
.
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида — ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Пример 9. Вычислить
.
Подсказка. Здесь придётся попыхтеть несколько больше обычного над преобразованием выражений под знаком предела.
Пример 10. Вычислить
.
Подсказка. Здесь правило Лопиталя придётся применять трижды.
Раскрытие неопределённостей вида «ноль умножить на бесконечность»
Пример 11. Вычислить
.
(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить
.
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя
.
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
.
Вычисляем предел выражения в показателе степени
 .
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
.
.
Раскрытие неопределённостей вида «бесконечность минус бесконечность»
Это случаи, когда вычисление предела разности функций приводит к неопределённости «бесконечность минус бесконечность»: .
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
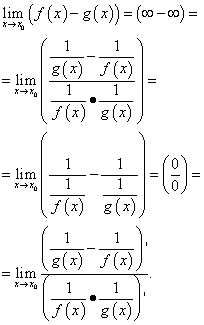
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.
Пример 16. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Пример 17. Вычислить, пользуясь правилом Лопиталя
.
function-x.ru
Правило Лопиталя для чайников: определение, примеры решения, формулы
Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.
Правило Лопиталя: история и определение
На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.
Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.
Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.
Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.
Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:
Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.
Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:
Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Раскрытие неопределенностей по правилу Лопиталя
В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:
Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.
Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:
Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:
Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:
Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:
Теперь перейдем к примерам.
Найти предел по правилу Лопиталя:
Вычислить с использованием правила Лопиталя:
Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.
Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:
Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
zaochnik.ru
42garmoniya.ru
2.4.3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ «Правило Лопиталя»
Задача 1.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Решение
Ответ:
Задача 2.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Если в результате вновь получится неопределенность, можно применять правило Лопиталя несколько раз.
Решение
Ответ: 3.
Задача 3.
Вычислить предел
Указание
Для того чтобы избавиться от неопределенности, примените правило Лопиталя:
Если в результате вновь получится неопределенность, можно применять правило Лопиталя несколько раз.
Решение
Ответ: 0.
Задача 4.
Вычислить предел
Указание
Преобразуйте функцию к виду
Тогда предел показателя степени можно вычислить по правилу Лопиталя.
Решение
Ответ: 1.
Задача 5.
Вычислить предел
Указание
Преобразуйте функцию, стоящую под знаком предела:
Решение
Ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua

 и применяют правило Лопиталя.
и применяют правило Лопиталя.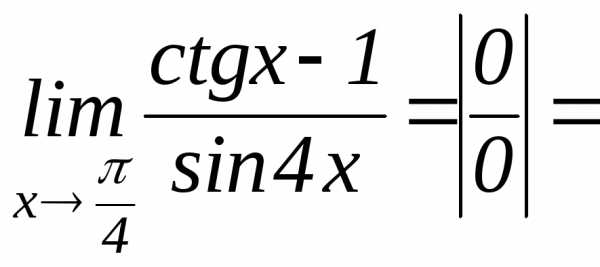
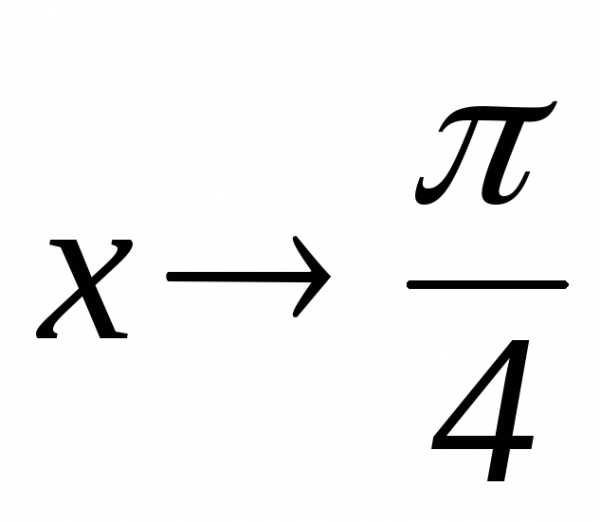 ,
а не к
,
а не к
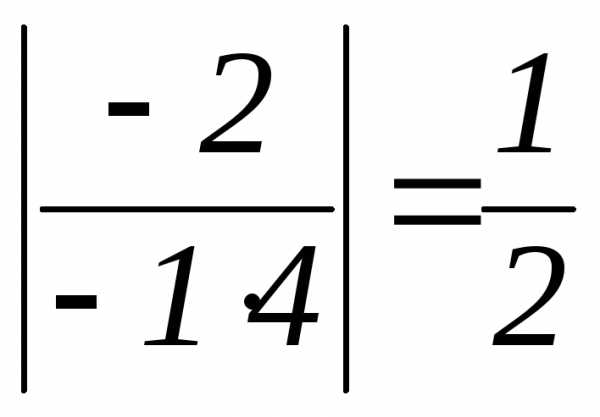

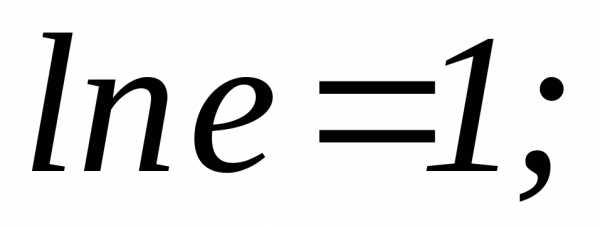
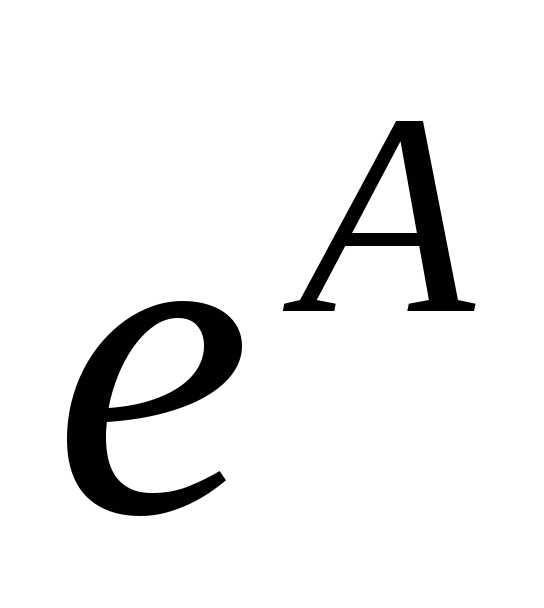 .
.