Вычислите значение производной функции – вычислите значение производной функции в точке х0=-1 у=(х-1)^2/x^2+1, математика

Найти значение производной функции в точке х0

Производная функции в точке

Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:

1) Необходимо найти производную.

2) Необходимо вычислить значение производной в заданной точке.

Пример 1

Вычислить производную функции 

 в точке 

Справка: Следующие способы обозначения функции эквивалентны:

В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».

Сначала находим производную:

Надеюсь, многие уже приноровились находить такие производные устно.

На втором шаге вычислим значение производной в точке 

:

Готово.

Небольшой разминочный пример для самостоятельного решения:

Пример 2

Вычислить производную функции 

 в точке 

Полное решение и ответ в конце урока.

Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), 

исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.

Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.

Пример 3

Вычислить производную функции 

 в точке . Сначала найдем производную:

Производная, в принципе, найдена, и можно подставлять требуемое значение 

. Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:

Ну вот, совсем другое дело. Вычислим значение производной в точке 

:

В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.

Пример 4

Вычислить производную функции 

 в точке .

Это пример для самостоятельного решения.

Уравнение касательной к графику функции

Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной кграфику функции

 в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.

Рассмотрим «демонстрационный» простейший пример.

Составить уравнение касательной к графику функции 

 в точке с абсциссой . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):

Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственной

точке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.

Применительно к нашему случаю: при 

 касательная  (стандартное обозначение) касается графика функции в единственной точке .

И наша задача состоит в том, чтобы найти уравнение прямой 

.

StudFiles.ru>

Производная функции в точке

Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:

1) Необходимо найти производную.

2) Необходимо вычислить значение производной в заданной точке.

Пример 1

Вычислить производную функции

в точке

Справка: Следующие способы обозначения функции эквивалентны:

В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».

Сначала находим производную:

Надеюсь, многие уже приноровились находить такие производные устно.

На втором шаге вычислим значение производной в точке

:

Готово.

Небольшой разминочный пример для самостоятельного решения:

Пример 2

Вычислить производную функции

в точке

Полное решение и ответ в конце урока.

Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика

, полное исследование функции и др.

Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.

Пример 3

Вычислить производную функции

в точке .
Сначала найдем производную:

Производная, в принципе, найдена, и можно подставлять требуемое значение

. Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:

Ну вот, совсем другое дело. Вычислим значение производной в точке

:

В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.

Пример 4

Вычислить производную функции

в точке .

Это пример для самостоятельного решения.

studopedia.ru>

Как найти значение производной функции F(x) в точке Хо? Как вообще это решать?

Sfash

Если формула задана, то найти производную и вместо Х подставить Х-нулевое. Посчитать

Если речь идет о б-8 ЕГЭ, график, то надо найти тангенс угла (острый или тупой) , который образует касательная с осью Х (с помощью мысленного построения прямоугольного треугольника и определения тангенса угла)

Тимур адильходжаев

Во-первых, надо определиться со знаком. Если точка х0 находится в нижней части координатной плоскости, то знак в ответе будет минус, а если выше, то +.
Во-вторых, надо знать что такое тангес в прямоугольном прямоугольнике. А это соотношение противолежащей стороны (катета) к прилежащей стороне (тоже катета) . На картине обычно есть несколько черных отметок. Из эти отметок составляешь прямоугольный треугольник и находишь тангес.

Как найти значение производной функции f x в точке x0?

нет конкретно поставленного вопроса — 3 года назад

Bk.Ru

В общем случае, что бы найти значение производной какой-либо функции по некоторой переменной в какой-либо точке, нужно продифференцировать заданную функцию по этой переменной. В вашем случае по переменной Х. В полученное выражение вместо Х поставить значение икса в той точке, для которой надо найти значение производной, т.е. в Вашем случае подставить нулевой Х и вычислить полученное выражение.

Ну а ваше стремление разобраться в этом вопросе, на мой взгляд, бесспорно заслуживает +, который ставлю с чистой совестью.

Lady v

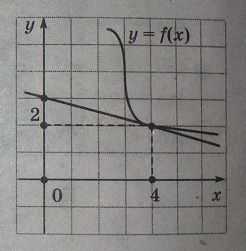
Такая постановка задачи на нахождение производной часто ставится для закрепления материала на геометрический смысл производной. Предлагается график некоей функции, совершенно произвольной и не заданной уравнением и требуется найти значение производной (не саму производную заметьте!) в указанной точке Х0. Для этого строится касательная к заданной функции и находится точки ее пересечения с осями координат. Потом составляется уравнение этой касательной в виде y=кx+b.

В этом уравнении коэффициент к и будет являться значением производной. остается лишь найти значение коэффициента b. Для этого находим значение у при х=о, пусть оно равно 3 – это и есть значение коэффициента b. Подставляем в исходное уравнение значения Х0 и У0 и находим к – нашу значение производной в этой точке.

bolshoyvopros.ru>

Читайте также

zna4enie.ru

Задача 7 — геометрический смысл производной

15 марта 2011

В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:

1. Значение производной в некоторой точке x₀,
2. Точки максимума или минимума (точки экстремума),
3. Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x

0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:

1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x₁; y₁) и B (x₂; y₂). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x₂ − x₁ и приращение функции Δy = y₂ − y₁.
3. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x₂ − x₁ = −1 − (−3) = 2; Δy = y₂ − y₁ = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x₂ − x₁ = 3 − 0 = 3; Δy = y₂ − y₁ = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x₂ − x₁ = 5 − 0 = 5; Δy = y₂ − y₁ = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x₀ называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≥ f(x).
2. Точка x₀ называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x₀) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x₀ известно, что f’(x₀) ≠ 0, то возможны лишь два варианта: f’(x₀) ≥ 0 или f’(x₀) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

1. Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≤ f(x₂). Другими словами, чем больше значение аргумента, тем больше значение функции.
2. Функция f(x) называется убывающей на отрезке [a; b] если для любых двух точек x₁ и x₂ из этого отрезка верно утверждение: x₁ ≤ x₂ ⇒ f(x₁) ≥ f(x₂). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

1. Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
2. Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
2. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
3. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l₁ = − 6 − (−8) = 2;
l₂ = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l₂ = 5.

Смотрите также:

1. Задача 7: касательная к графику функции
2. Задача 7: касательная к графику функции — 2
3. Пробный ЕГЭ-2011 по математике, вариант №4
4. Тест по теории вероятностей (1 вариант)
5. Специфика работы с логарифмами в задаче B15
6. Упрощаем решение задач с помощью замены переменной

www.berdov.com

Онлайн калькулятор: Производная функции

Данный калькулятор вычисляет производную функции и затем упрощает ее.
В поле функция введите математическое выражение с переменной x, в выражении используйте стандартные операции + сложение, – вычитание, / деление, * умножение, ^ — возведение в степень, а также математические функции. Полный синтаксис смотрите ниже.
Упрощение полученной производной может занять некоторое время, для сложных функций — весьма продолжительное. Если ждать до конца нет сил — нажмите кнопку остановить. У меня получался достаточно простой вариант уже после 10-15 секунд работы алгоритма упрощения.

Калькулятор производных

Допустимые операции: + – / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch

Производная функции

 

Показать детали вычисления

Показать шаги вычисления производной и упрощения формулы

Последовательность вычисления производной и упрощения формулы

Сохранить share extension

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, – — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

ГруппаКонстанты и переменныеОперацииТригонометрические функцииОбратные тригонометрические функцииГиперболические функции

Синтаксис математических выражений

planetcalc.ru

Производная функции от одной переменной f'(x) · Калькулятор Онлайн

Введите функцию, для которой необходимо вычислить производную

Сервис предоставляет ПОДРОБНОЕ решение производной.

Найдём производную функции f(x) – дифференциал функции.

Примеры

С применением степени
(квадрат и куб) и дроби

(x^2 - 1)/(x^3 + 1)

Квадратный корень

sqrt(x)/(x + 1)

Кубический корень

cbrt(x)/(3*x + 2)

С применением синуса и косинуса

2*sin(x)*cos(x)

Арксинус

x*arcsin(x)

Арккосинус

x*arccos(x)

Применение логарифма

x*log(x, 10)

Натуральный логарифм

ln(x)/x

Экспонента

exp(x)*x

Тангенс

tg(x)*sin(x)

Котангенс

ctg(x)*cos(x)

Иррациональне дроби

(sqrt(x) - 1)/sqrt(x^2 - x - 1)

Арктангенс

x*arctg(x)

Арккотангенс

x*arсctg(x)

Гиберболические синус и косинус

2*sh(x)*ch(x)

Гиберболические тангенс и котангенс

ctgh(x)/tgh(x)

Гиберболические арксинус и арккосинус

x^2*arcsinh(x)*arccosh(x)

Гиберболические арктангенс и арккотангенс

x^2*arctgh(x)*arcctgh(x)

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция – арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция – арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

e

e число, которое примерно равно 2.7

exp(x)

Функция – экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

pi

Число – “Пи”, которое примерно равно 3.14

sin(x)

Функция – Синус от x

cos(x)

Функция – Косинус от x

sinh(x)

Функция – Синус гиперболический от x

cosh(x)

Функция – Косинус гиперболический от x

sqrt(x)

Функция – квадратный корень из x

sqr(x) или x^2

Функция – Квадрат x

tg(x)

Функция – Тангенс от x

tgh(x)

Функция – Тангенс гиперболический от x

cbrt(x)

Функция – кубический корень из x

floor(x)

Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)

sign(x)

Функция – Знак x

erf(x)

Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7.5, не 7,5

2*x

– умножение

3/x

– деление

x^3

– возведение в степень

x + 7

– сложение

x – 6

– вычитание

www.kontrolnaya-rabota.ru

Вычисление производной функции онлайн | umath.ru

Калькулятор вычисляет производные всех элементарных функций, приводя подробное решение. Переменная дифференцирования определяется автоматически.

Вычислено WolframAlpha.

Производная функции — одно из важнейших понятий в математическом анализе. К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке.

Чаще всего производная функции определяется как предел отношения приращения функции к приращению аргумента, если он существует.

Определение. Пусть функция определена в некоторой окрестности точки . Тогда производной функции в точке называется предел, если он существует

   

Как вычислить производную функции?

Для того, чтобы научиться дифференцировать функции, нужно выучить и понять правила дифференцирования и научиться пользоваться таблицей производных.

Правила дифференцирования

Пусть и — произвольные дифференцируемые функции от вещественной переменной, — некоторая вещественная постоянная. Тогда

— правило дифференцирования произведения функций

— правило дифференцирования частного функций

— дифференцирование функции с переменным показателем степени

— правило дифференцирования сложной функции

— правило дифференцирования степенной функции

Производная функции онлайн

Наш калькулятор быстро и точно вычислит производную любой функции онлайн. Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку.

umath.ru

Производная онлайн с подробным решением

Калькулятор решает производные c описанием действий ПОДРОБНО бесплатно!

Это он-лайн сервис в один шаг:

• Ввести функцию, для которой надо найти производную

Перейти: Онлайн сервис “Производная функции” →

Это он-лайн сервис в один шаг:

• Ввести функцию, для которой надо найти частные производные

Перейти: Онлайн сервис “Частная производная функции” → Это он-лайн сервис в два шага:

• Ввести функцию, для которой надо найти производную
• Ввести найденную первую производную в форму

Перейти: Онлайн сервис “Вторая производная функции” → Это он-лайн сервис в три шага:

• Ввести функцию, для которой надо найти производную
• Ввести найденную первую производную в форму
• Ввести найденную вторую производную функции в форму

Перейти: Онлайн сервис “Третья производная функции” →

Введите функцию, заданную в неявном виде, вы получите соответствующую производную

Это он-лайн сервис в три шага:

• Ввести функцию x = x(t)
• Ввести функцию y = y(t)

Перейти: Онлайн сервис “Производной параметрической функции” →

Производная сложной функции

Производную сложной функции онлайн вы сможете вычислить с помощью калькулятора производных здесь

Таблица производных

Вы также можете воспользоваться таблицей производных, чтобы самостоятельно вычислить любую производную, перейти:

www.kontrolnaya-rabota.ru

Вычисление производной функции в точке

Вычисление производной функции в точке

Если вас интересуют общие вопросы и само понятие производной, вы можете посмотреть цикл демонстрационных видеороликов от автора данного сайта Максима Семенихина на тему «Понятие производной».

1. Понятие о скорости возрастания и убывания функции (6:01)
2. Вычисление скорости возрастающей функции (2:05)
3. Вычисление скорости убывающей функции (2:18)
4. На разных промежутках – разная скорость (4:15)
5. Средняя и мгновенная скорости (3:38)
6. Средняя скорость возрастания функции (1:59)
7. Определение производной как скорости (2:50)
8. Пример вычисления производной по определению (3:46)
9. Обозначение производной (1:41)

а также видеоурок

Вычисление производных сложных функций (14:51)

Для нахождения производной функции в общем случае необходимо знать следующее:

1. Таблицу производных элементарных функций.
2. Правила дифференцирования.
3. Как находить производную сложной функции.

Таблица производных элементарных функций представлена ниже:

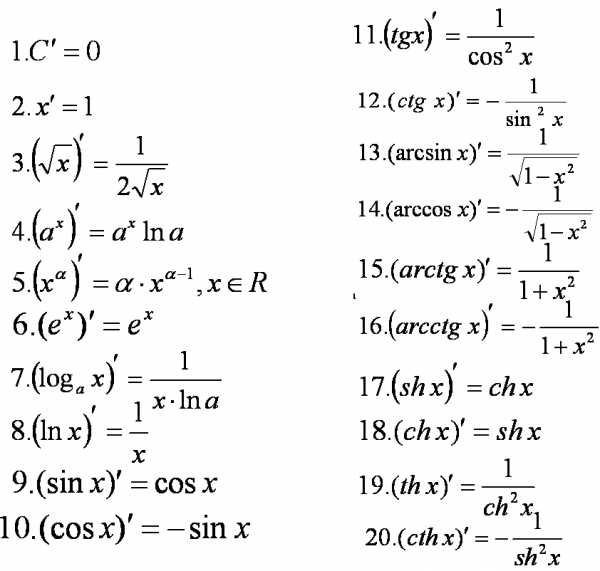
Для нахождения производной суммы, произведения и частного функций используются три правила дифференцирования:

Для нахождения производной сложной функции используется формула

f(g(x))’ = f ‘(g(x)) · g‘(x)

Нахождение производной сложной функции – вопрос, заслуживающий отдельного рассмотрения. Вы можете просмотреть видеоурок «Вычисление производных сложных функций».

Нахождение производной функции в точке

Для того, чтобы вычислить значение производной функции в точке, необходимо:

– найти производную функции;
– подставить в производную значение х точки, в которой необходимо найти производную.

Пример. Вычислить производную функции y = x² в точке х₀ = 3.
Решение. Производная функции: у‘ = (х²)’ = 2х;
подставляя в производную значение х₀ = 3, получим: у‘(3) = 2 ∙ 3 = 6.

Онлайн калькулятор
для вычисления значения производной функции в точке

Для того, чтобы вычислить значение производной функции в точке, можно воспользоваться калькулятором на данной странице. Просто введите саму функцию и точку, в которой необходимо вычислить производную. Калькулятор всё посчитает сам и выдаст ответ.

mathonline.um-razum.ru