Высшая математика уравнения дифференциальные уравнения – Дифференциальные уравнения | Высшая математика

Дифференциальные уравнения

Теорема (правило Лопиталя раскрытия неопределенностей вида
$\frac{0}{0}$ или $\frac{\infty}{\infty}$).

Пусть функции $f(x)$ и $g(x)$ :

а) дифференцируемы в окрестности точки $a,$ за исключением, быть
может, самой точки $a,$ причем $g'(x)\neq 0$ в этой окрестности;

б) функции $f(x)$ и $g(x)$ являются одновременно либо бесконечно
малыми либо бесконечно большими при $x\rightarrow a;$

в) существует конечный $\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$ 

Тогда существует  $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}$ и
выполняется равенство $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$   

Если функции $f(x)$ и $g(x)$ дифференцируемы в точке $a,$

$g(a)=f(a)=0,$ $ g'(a)\neq ,0$ то $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\frac{f'(a)}{g'(a)}.$

 Примеры:

1. $\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}$

Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:

$\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}=\lim\limits_{x\rightarrow 1}\frac{5x^4}{6x^2-1}=1.$

2. $\lim\limits_{x\rightarrow 0}\frac{x-arctg x}{x^3}$

Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:

$$\lim\limits_{x\rightarrow 0}\frac{x-arctg x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{1-\frac{1}{1+x^2}}{3x^2}=\lim\limits_{x\rightarrow 0}\frac{x^2}{3x^2(1+x^2)=\frac{1}{3}.}$$

3. $\lim\limits_{x\rightarrow 1}\frac{\ln x}{\sqrt{x}}$

Имеем неопределенность вида $\frac{\infty}{\infty}.$ Применяя правило Лопиталя, получим:

$$\lim\limits_{x\rightarrow +\infty}\frac{\ln x}{\sqrt{x}}=\lim\limits_{x\rightarrow +\infty}\frac{1/x}{1/(2\sqrt{x})}=\lim\limits_{x\rightarrow +\infty}\frac{2}{\sqrt{x}}=0.$$

4. $\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{\sin^3 x}.$

Имеем неопределенность вида $\frac{0}{0}.$ Замечая, что $\sin x\sim x$ при $x\rightarrow 0,$ по правилу Лопиталя находим

$\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{\sin^3 x}=\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{\cos x-\cos x+x\sin x}{3x^2}=$ $\frac{1}{3}\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}=\frac{1}{3}.$

 

5. $\lim\limits_{x\rightarrow 1}\frac{x^10-10x+9}{x^5-5x+4}.$

Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:

$\lim\limits_{x\rightarrow 1}\frac{x^10-10x+9}{x^5-5x+4}=\lim\limits_{x\rightarrow 1}\frac{10x^9-10}{5x^4-5}.$

Пользуясь еще раз правилом Лопиталя, находим

$\lim\limits_{x\rightarrow 1}\frac{10x^9-10}{5x^4-5}=2\lim\limits_{x\rightarrow 1}\frac{x^9-1}{x^4-1}=2\lim\limits_{x\rightarrow 1}\frac{9x^8}{4x^3}=\frac{9}{2}.$

 

6. $\lim\limits_{x\rightarrow+\infty}\frac{x^{\alpha}}{e^{\beta x}},$ где $\alpha>0,$ $\beta>0.$ 

Пусть $k=[\alpha]+1;$ тогда $\alpha-k<0.$ 

Применяя правило Лопиталя $k$ раз, получаем $\lim\limits_{x\rightarrow+\infty}\frac{x^{\alpha}}{e^{\beta x}}=\lim\limits_{x\rightarrow+\infty}\frac{\alpha x^{\alpha-1}}{\beta e^{\beta x}}=…=\lim\limits_{x\rightarrow+\infty}\frac{\alpha(\alpha-1)…(\alpha-k+1)x^{\alpha-k}}{\beta^k e^{\beta x}}=0.$

7. $\lim\limits_{x\rightarrow+\infty}\frac{\ln^{\alpha}x}{x^{\beta}},$ где $\alpha>0,$ $\beta>0.$ 

Пусть $\ln x =t;$ тогда $x=e^t$ и $\lim\limits_{x\rightarrow+\infty}\frac{\ln^{\alpha}x}{x^{\beta}}=\lim\limits_{t\rightarrow+\infty}\frac{t^{\alpha}}{e^{\beta t}}=0$ (пример 6).

Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:

8. $\lim\limits_{x\rightarrow +0}x\ln x$

Преобразуя неопределенность вида $0\cdot\infty$ к виду $\frac{\infty}{\infty}$ и применяя правило Лопиталя имеем

$$\lim\limits_{x\rightarrow +0}x\ln x=\lim\limits_{x\rightarrow +0}\frac{\ln x}{1/x}=\lim\limits_{x\rightarrow +0}\frac{1/x}{-1/x^2}=\lim\limits_{x\rightarrow +0}(-x)=0.$$

9. $\lim\limits_{x\rightarrow 1}\frac{1}{x^{50}}e^{-1/x^2}.$

Имеем неопределенность вида $\frac{0}{0}.$ Полагая $1/x^2=t,$ получаем

$$\lim\limits_{x\rightarrow 1}\frac{1}{x^{50}}e^{-1/x^2}=\lim\limits_{x\rightarrow 1}\frac{t^{25}}{e^t}=0.$$
10.  $\lim\limits_{x\rightarrow 0}\left(\frac{1}{x^2}-ctg^2 x\right).$ 

Преобразуя неопредленность вида $\infty-\infty$ к виду $\frac{0}{0}$ и используя асимптотическую формулу $\sin x \sim x$ при $x\rightarrow 0,$ получаем

$$\lim\limits_{x\rightarrow 0}\left(\frac{1}{x^2}-ctg^2 x\right)=\lim\limits_{x\rightarrow 0}\frac{\sin^2 x-x^2\cos^2 x}{x^2\sin^2 x}=$$ $$=\lim\limits_{x\rightarrow 0}\frac{(\sin x+x\cos x)(\sin x-x\cos x)}{x^2\sin^2 x}=$$ $$=\lim\limits_{x\rightarrow 0}\frac{\sin x+x\cos x}{x}\cdot\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}.$$ 

Так как

$$\lim\limits_{x\rightarrow 0}\frac{\sin x+x\cos x}{x}=\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}+\lim\limits_{x\rightarrow 0}\cos x=2,$$

а $\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}=\frac{1}{3}$  (см. пример 4), то искомый предел равен $2/3.$

mathportal.net

Дифференциальные уравнения

Дифференциальные уравнения

Общие сведения. 1

Дифференциальные уравнения первого порядка. 1

1. Уравнения с разделяющимися переменными. 1

2. Дифференциальные уравнения вида . 2

3. Однородные дифференциальные уравнения первого порядка. 2

4. Дифференциальные уравнения, приводимые к однородным.. 2

5. Линейные уравнения. 2

6. Уравнение Бернулли. 3

7. Особые точки и особые решения дифференциальных уравнений первого порядка 3

8. Уравнение в полных дифференциалах. 3

9. Метод введения интегрирующего множителя. 4

10. Уравнение Риккати. 4

11. Уравнения, неразрешенные относительно производной. 4

Дифференциальные уравнения второго порядка. 4

Основные определения. 4

24. Общее решение линейного однородного ДУ второго порядка с постоянными коэффициентами. 4

Характеристическое уравнение. 4

Линейные неоднородные дифференциальные уравнения второго порядка 5

Пример решения дифференциального уравнения второго порядка 5

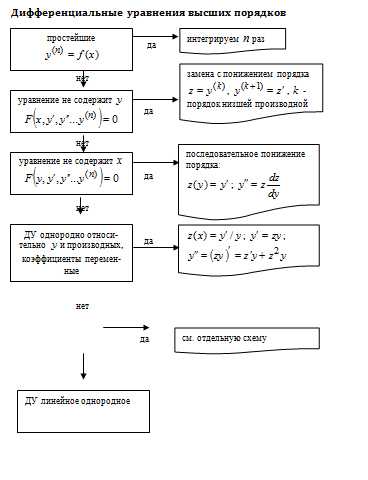
Дифференциальные уравнения высших порядков. 7

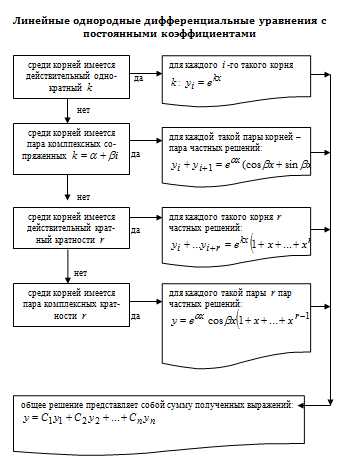
Линейные однородные дифференциальные уравнения с постоянными коэффициентами. 9

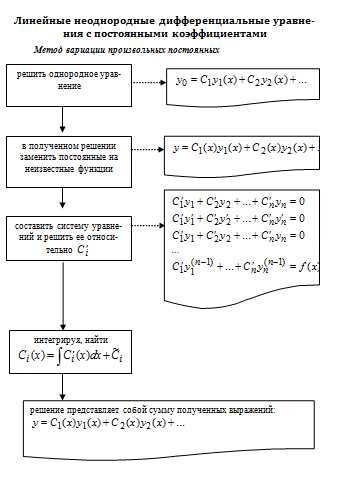
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. 10

Метод вариации произвольных постоянных. 10

Дифференциальным называют уравнение, содержащее независимую переменную, искомую функцию и ее производные различных порядков:

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Решением дифференциального уравнения называется всякая функция, которая при подстановке ее в уравнение превращает его в тождество.

/******************************

Пример. Решением уравнения

Есть функция , и вообще любая функция вида при любом выборе постоянных и .

/******************************

Общим решением дифференциального уравнения называется функция , которая зависит от произвольных постоянных и удовлетворяет заданному уравнению при любых конкретных значениях .

Общее решение дифференциального уравнения, не разрешенное относительно Y, часто называют также Общим интегралом.

Дифференциальное уравнение первого порядка имеет вид

Если это уравнение можно разрешить относительно У’, То его можно записать в виде

В этом случае мы говорим, что дифференциальное уравнение разрешено относительно производной. Для такого уравнения спра­ведлива следующая теорема, которая называется теоремой о суще­ствовании и единственности решения дифференциального уравнения.

Теорема. Если в уравнении Функция F (х, у) и ее частная производная по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку , то существует единственное решение этого урав­нения , Удовлетворяющее условию при .

1. Уравнения с разделяющимися переменными

Дифференциальное уравнение типа называют уравнением С разделенными переменными. Общий интеграл его есть

Уравнение вида

Называется уравнением С разделяющимися переменными. Оно может быть приведено к уравнению с разделенными переменными путем деления обеих частей на :

2. Дифференциальные уравнения вида

Такие уравнения решают подстановкой . Производная новой функции равна

Подставляя в исходное уравнение, получаем уравнение с разделяющимися переменными:

3. Однородные дифференциальные уравнения первого порядка

Это уравнения вида

Где – однородные функции одного измерения, или – однородная функция.

Такие уравнения решают заменой . Тогда

После подстановки в исходное уравнение получим уравнение с разделяющимися переменными.

4. Дифференциальные уравнения, приводимые к однородным

К однородному приводится уравнение

Подстановкой , при этом

H и K подбираются так, чтобы выполнялись равенства:

(необходимо решить систему уравнений)

Если определитель этой системы равен нулю, то после подстановки приходим к уравнению с разделяющимися переменными.

5. Линейные уравнения

Решение ищут в виде произведения функций: , тогда

Функцию V выбирают такой, чтобы выполнилось равенство:

отсюда ,

6. Уравнение Бернулли

Подстановка , приводит к линейному уравнению:

Это уравнение можно также решать предыдущим способом (в виде произведения двух функций).

7. Особые точки и особые решения дифференциальных уравнений первого порядка

Это решения, не входящие в семейство общих решений. График таких решений есть

Огибающая семейства интегральных кривых. Линия называется огибающей, если в каждой своей точке она касается той или иной линии семейства кривых.

См. Пискунов, стр.39, стр. 45

8. Уравнение в полных дифференциалах

– неоднородные функции, но соблюдается условие

(*)

Решение имеет вид , где функцию находят интегрированием любой части равенства (*):

А) ,

Полученное выражение дифференцируют по У , результат приравнивают к , находят и решают уравнение

Б)

Полученное выражение дифференцируют по Х , результат приравнивают к , находят и решают уравнение

9. Метод введения интегрирующего множителя

Если левая часть уравнения Не есть Полный дифференциал, то иногда удается найти

Интегрирующий множитель, так что левая часть становится полным дифференциалом:

,

10. Уравнение Риккати

В общем случае уравнение неразрешимо. Если известно одно частное решение , то заменой (z – новая переменная) уравнение сводится к линейному

11. Уравнения, неразрешенные относительно производной

Решение можно найти, только если из уравнения легко выражается Х или У. Тогда решение находится Методом введения параметра.

Основные определения

Дифференциальное уравнение второго порядка, разрешенное относительно старшей производной, имеет вид: .

Общее решение такого уравнения всегда содержит Две произвольные постоянные и . Частное решение (т. е. конкретные значения постоянных) находят из начальных условий вида ; (такое частное решение часто называют

Задачей Коши).

24. Общее решение линейного однородного ДУ второго порядка с постоянными коэффициентами

Уравнение вида называют Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. Если правая часть уравнения равна нулю, то уравнение называется Однородным.

Характеристическое уравнение

Для решения таких однородных уравнений вначале составляют так называемое Характеристическое уравнение, которое имеет вид:

Вид общего решения однородного уравнения определяется корнями характеристического уравнения. При этом возможны следующие случаи:

1. , т. е. корни характеристического уравнения , – действительные числа. Общее решение имеет вид: .

2. , т. е. корни характеристического уравнения – действительные числа, причем (обозначим кратный корень как K) . Общее решение имеет вид: .

3. , т. е. корни характеристического уравнения , – комплексные числа, причем , (). Общее решение имеет вид: .

Линейные неоднородные дифференциальные уравнения второго порядка

Общее решение неоднородного уравнения при правой части, не равной нулю, имеет вид: , где – общее решение соответствующего однородного уравнения (нахождение этого решения описано в предыдущем разделе), – некоторое частное решение неоднородного уравнения. Вид этого частного решения зависит от вида правой части уравнения.

1. Если имеет вид ( – полином степени

N), то частное решение имеет вид: , где – полином той же степени, что и . Число R равно нулю, если M не совпадает ни с одним корнем характеристического уравнения, в противном случае R равно кратности совпадений M с корнями характеристического уравнения.

2. Если имеет вид (А, В – действительные числа), то частное решение имеет вид: (M,N – неопределенные коэффициенты).

Пример решения дифференциального уравнения второго порядка

Найдем решение дифференциального уравнения

При начальных условиях:

Это линейное неоднородное уравнение второго порядка. Как уже говорилось, его решение имеет вид: , где – общее решение соответствующего однородного уравнения, а – частное решение неоднородного уравнения.

Составим характеристическое уравнение: . Корни этого уравнения равны: ; . Так как корни действительны и различны, то общее решение имеет вид:

Правая часть уравнения имеет вид , причем в данной задаче M = 4, . Число M не является корнем характеристического уравнения, Поэтому частное решение ищем в виде , где Q(X) =C – многочлен той же степени, что и P(x).

Константу многочлена C найдем с помощью метода неопределенных коэффициентов: ; . Подставляя эти значения в исходное уравнение, получим: , отсюда С= 1.

Следовательно, частное решение равно: , а решение уравнения в целом имеет вид:.

Значения констант находим из начальных условий:

, отсюда

отсюда

Решая систему уравнений, находим: С1 = 7; С2 = –6.

Окончательно получаем решение дифференциального уравнения:

Выполним проверку решения:

Следовательно, решение найдено верно.

 

 

 

po-teme.com.ua

Дифференциальные уравнения

Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. Научно-издательский центр “Регулярная и хаотическая динамика”. 2000.

 

Уравнения с разделяющимися переменными.

Уравнения с разделяющимися переменными могут быть записаны в виде $$y’=f(x)g(y),\qquad\qquad\qquad(1)$$ а также в виде  $$M(x)N(y)dx+P(x)Q(y)dy=0.\qquad\qquad\qquad(2)$$ Для решения этого уравнения его нужно преобразовать таким образом, чтобы в одну часть уравнения входило  только $x,$ а в другую только $y,$ а затем проинтегрировать обе части.

При делении обеих частей уравнения на выражение, содержащее неизвестные $x$ и $y,$ могут быть потеряны решения, обращающие это выражение в нуль.

Пример.  Решить уравнение $$x^2y^2y’+1=y.$$

Решение.

Преобразуем заданное уравнение к виду (2).

$$x^2y^2\frac{dx}{dy}=y-1;\qquad\qquad x^2y^2dy=(y-1)dx.$$

Делим обе части уравнения на $x^2(y-1):$

$$\frac{y^2}{y-1}dy=\frac{dx}{x^2}.$$

Переменные разделены. Интегрируем обе части уравнения:

$$\int\frac{y^2}{y-1}dy=\int\frac{dx}{x^2}.$$

$$\int\frac{y^2}{y-1}dy=\int\frac{y^2-1+1}{y-1}dy=\int\left(y+1+\frac{1}{y-1}\right)dy=\frac{y^2}{2}+y+\ln|y-1|+C.$$

$$\int\frac{dx}{x^2}=-\frac{1}{x}+C.$$

Таким образом,

$$\frac{y^2}{2}+y+\ln|y-1|=-\frac{1}{x}+C.$$

При делении на $x^2(y-1)$ могли быть потеряны решения $x=0$ и $y-1=0,$ то есть $y=1.$ Если подставить эти значения в условие, то становится очевидно, что $y=1$ – решение заданного уравнения, а  $x=0$ – нет.

Ответ: $\frac{y^2}{2}+y+\ln|y-1|=-\frac{1}{x}+C,$ $y=1.$

 

Уравнения сводящиеся к уравнениям с разделяющимися переменными.

Уравнения вида $y’=f(ax+by)$ приводится к уравнениям с разделяющейся переменной заменой $z=ax+by$ (или $z=ax+by+c,$ где $c- $ любое). 

Примеры.

65. $y’=\sqrt{4x+2y-1}.$

Решение.

Сделаем замену переменных.

$z=4x+2y-1.$ Отсюда $y=\frac{1}{2}(z-4x+1)\Rightarrow y’=\frac{1}{2}z’-2$

Получаем $$\frac{1}{2}z’-2=\sqrt{z}$$

Преобразуем данное уравнение к виду (2).

$$\frac{dz}{2dx}=\sqrt{z}+2\Rightarrow \frac{dz}{\sqrt z+2}=2dx$$

Интегрируем  обе части уравнения:

$$\int\frac{dz}{\sqrt z+2}=\int 2dx$$

$$\int\frac{dz}{\sqrt z+2}=[z=t^2\qquad dz=2tdt]=\int\frac{2tdt}{t+2}=2\int\frac{t+2-2}{t+2}dt=2(t-2\ln|t+2|)+C=$$ $$=2(\sqrt z-2\ln|\sqrt z+2|)+C=2(\sqrt{4x+2y-1}-2\ln|\sqrt{4x+2y-1}+2|)+С.$$

$$\int 2dx=2x+C.$$

Таким образом, получили 

$$2(\sqrt{4x+2y-1}-2\ln|\sqrt{4x+2y-1}+2|)=2x+C\Rightarrow \sqrt{4x+2y-1}-\ln(\sqrt{4x+2y-1}+2)=x+C.$$

Ответ: $$\sqrt{4x+2y-1}-\ln(\sqrt{4x+2y-1}+2)=x+C..$$

 

 

 

mathportal.net

Математический анализ и дифференциальные уравнения

Каплан И.А. Практические занятия по высшей математике. Часть 5: Численное решение алгебраических и трансцендентных уравнений, матричное исчисление, векторный анализ и интегрирование линейных дифференциальных уравнений первого порядка с частными производными. – Харьков: изд-во при Харьковском гос. университете, 1972. – 413с.
Книга содержит подробный разбор и решение типовых задач по таким разделам высшей математики: векторный анализ, алгебра матриц и их приложений к решению задач линейной алгебры, линейные дифференциальные у равнения с частными производными первого порядка, решение алгебраических и трансцендентных уравнений.
Книга рассчитана на студентов высших технических учебных заведений и может быть полезной также преподавателям, ведущим практические занятия.

Каплан И.А. Практические занятия по высшей математике. Часть 4: Кратные и криволинейные интегралы. – Харьков: изд-во при Харьковском гос. университете, 1971. – 133с.
Книга содержит разбор и подробное решение типовых задач по интегральному исчислению и интегрированию обыкновенных дифференциальных уравнений, кратным и криволинейным интегралам.
Большое количество задач, для упражнений снабжено указаниями, промежуточными результатами и ответами.
Книга соответствует новой программе по высшей математике. Она рассчитана на студентов высших технических учебных заведений, а также может быть полезна преподавателям, ведущим практические занятия.

Каплан И.А. Практические занятия по высшей математике (Аналитическая геометрия на плоскости и в пространстве. Дифференциальное исчисление функций одной и многих независимых переменных. Интегральное исчисление функций одной одной независимой переменной. Интегрирование дифференциальных уравнений). Часть I-III. – Харьков: изд-во при Харьковском гос. университете, 1967. – 947с.
В книге разобраны и подробно решены типовые задачи по аналитической геометрии на плоскости и в пространстве, дифференциальному и интегральному исчислениям и по интегрированию дифференциальных уравнений.
Из задач, помещенных для самостоятельного решения, многие снабжены указаниями, промежуточными результатами и ответами.
Книга рассчитана на студентов высших технических учебных заведений, может быть полезна также преподавателям, ведущим практические занятия.

Математический анализ в примерах и задачах, ч. 2. Ряды, функции нескольких переменных, кратные и криволинейные интегралы. Ляшко И. И., Боярчук А. К., Гай Я. Г., Головач Г. П. Издательское объединение «Вища школа», 1977, 672 с.
Пособие состоит из четырех глав. В начале каждого параграфа помещен соответствующий теоретический материал, а затем подробно рассмотрены примеры и контрпримеры. В нем содержится свыше 1140 решенных примеров и задач, имеются также примеры и задачи для самостоятельного решения.
Пособие предназначено для студентов механико-математических и физических факультетов, а также факультетов кибернетики университетов, физико-математических факультетов педагогических институтов и для студентов технических вузов.

Математический анализ в примерах и задачах, ч. 1. Введение в анализ, производная, интеграл. Ляшко И. И., Боярчук А. К., Гай Я. Г., Головач Г. П. Издательское объединение «Вища школа», 1974, 680 с.
Пособие состоит из четырех глав. В начале каждого параграфа помещен соответствующий теоретический материал, а затем подробно рассмотрены примеры и контрпримеры. Книга содержит свыше 1400 примеров и задач, к которым поданы подробные решения.
Пособие предназначено для студентов механико-математических и физических факультетов, а также факультетов кибернетики университетов, физико-математических факультетов педагогических институтов и для студентов технических вузов. Ил. 158.

Михайлова Л.М. Уникальные ряды «золотого сечения, золотой пропорции».- Авторская рукопись. – 32 с.
От автора:
“Считаю, что «Уникальный ряд «золотого сечения, золотой пропорции»» -это математический ряд Мироздания в обширнейшем диапазоне от Микромира (он может пригодиться в ядерной физике) до Макромира, причём под Макромиром надо подразумевать не только Солнечную Систему, но и другие Звёздные Системы, и Галактики.

Зоммерфельд А. Дифференциальные уравнения в частных производных физики. – М.: ИЛ, 1950.
В книге А. Зоммерфельда «Дифференциальные уравнения в частных производных физики», являющейся шестым томом его лекций по теоретической физике, последовательно изложен круг вопросов, входящих обычно в курс методов математической физики (ряды Фурье, проблемы, связанные с рассмотрением уравнений в частных производных второго порядка, цилиндрические и шаровые функции, уравнения колебаний мембран и т. д.).

edu-lib.com

Дифференциальные уравнения – Всё для чайников

• Главная
• Видеотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
  • Обществознание
    • Обществознание – как наука
    • Иностранные языки
    • История
    • Психология и педагогика
    • Русский язык и литература
    • Культурология
    • Экономика
    • Менеджмент
    • Логистика
    • Статистика
    • Философия
    • Бухгалтерский учет
  • Технические науки
    • Черчение
    • Материаловедение
    • Сварка
    • Электротехника
    • АСУТП и КИПИА
    • Технологии
    • Теоретическая механика и сопромат
    • САПР
    • Метрология, стандартизация и сертификация
    • Геодезия и маркшейдерия
  • Программирование и сеть
    • Информатика
    • Языки программирования
    • Алгоритмы и структуры данных
    • СУБД
    • Web разработки и технологии
    • Архитектура ЭВМ и основы ОС
    • Системное администрирование
    • Создание программ и приложений
    • Создание сайтов
    • Тестирование ПО
    • Теория информации и кодирования
    • Функциональное и логическое программирование
  • Программы
    • Редакторы и компиляторы
    • Офисные программы
    • Работа с аудио видео
    • Работа с компьютерной графикой и анимацией
    • Автоматизация бизнеса
  • Прочие
    • Музыка
    • Природное земледелие
    • Рисование и живопись
• Библиотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
    • Астрономия
  • Обществознание
    • Иностранные языки
  • Технические науки

forkettle.ru

Основные дифференциальные уравнения и их решения

Разделение переменных
f₁(x)g₁(y)dx + f₂(x)g₂(y)dy = 0

Решение
$\int\frac{f_1(x)}{f_2(x)}dx + \int\frac{g_2(y)}{g_1(y)}dy = c$

Линейное уравнение первого порядка
dx/dy + P(x)y = Q(x)

Решение
$y e^{\int P dx} = \int Q e^{\int P dx} dx + c$

Уравнение Бернулли
dy/dx + P(x)y = Q(x)yⁿ

Решение
$v e^{(1-n) \int P dx} = (1-n) \int Q e^{(1-n) \int P dx} dx + c$
, где v = y^1-n.
Если n = 1, решение имеет вид
$ln y = \int (Q – P ) dx + c$

Точное уравнение
M(x,y)dx + N(x,y)dy = 0, где ∂M/∂y = ∂N/∂x.

Решение
$\int M \partial x + \int (N – \frac{\partial}{\partial y}\int M \partial x) dy = c$
, где ∂x означает интегрирование по x при постоянной y.

Однородное уравнение
dy/dx = F(y/x).

Решение
$ln x = \int \frac{dv}{F(v) – v} + c$, где v = y/x. Если F(v) = v, решением будет y = cx.

yF(xy)dx + xG(xy)dy = 0

Решение
$ln x = \int \frac{G(v) dv}{v \{G(v) – F(v)\} } + c$, где v = xy. Если G(v) = F(v), решением будет xy = c.

Линейное однородное уравнение второго порядка
d²y/dx² + a(dy/dx) + by = 0 , a,b – действительные константы.

Решение
Пусть m₁, m₂ – корни уравнения m² + am + b = 0. Тогда возможны три варианта

Вариант 1.     m₁,m₂ действительные и несовпадающие:
$y = c_1 e^{m_1 x} + c_2 e^{m_2 x}$

Вариант 2.     m₁,m₂ действительные и равные:
$y = c_1 e^{m_1 x} + c_2 x e^{m_1 x}$

Вариант 3.     m₁ = p + qi,m₂ = p – qi:
$y = e^{px} (c_1 \cos qx + c_2 \sin qx)$

Линейное неоднородное уравнение второго порядка.
d²y/dx² + a(dy/dx) + by = R(x), a, b – действительные константы.

Решение
Аналогично предыдущему случаю, возможны три варианта.

Вариант 1

Вариант 2

Вариант 3

Уравнение Коши (или Эйлера).
x²d²y/dx² + a(dy/dx) + by = S(x) .

Решение
После замены x = e^t уравнение принимает вид
d²y/dt² + (a – 1)(dy/dt) + by = S(e^t)
, и теперь решение его сводится к вышеуказанным вариантам.

Уравнение Бесселя.
x²d²y/dx² + x(dy/dx) + (λ²x² – n²)y = 0.

Решение
y = c₁J_n(λx) + c₂Y_n(x).

Модифицированное уравнение Бесселя
x²d²y/dx² + (2p + 1)x(dy/dx) + (α²x^2r + β²)y = 0.

Решение
$y = x^{-p} \{c_1 J_{q/r} (\frac{\alpha}{\gamma}x^r) + c_2 Y_{q/r} (\frac{\alpha}{\gamma}x^r)\}$
, где q = √p² – β².

Уравнение Лежандра
(1 – x²)d²y/dx² – 2xdy/dx + n(n + 1)y = 0.

Решение
y = c₁P_n(x) + c₂Q_n(y).

www.math10.com

Дифференциальные уравнения и краевые задачи от НОУ ИНТУИТ

• Главная
• Видеотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
  • Обществознание
    • Обществознание – как наука
    • Иностранные языки
    • История
    • Психология и педагогика
    • Русский язык и литература
    • Культурология
    • Экономика
    • Менеджмент
    • Логистика
    • Статистика
    • Философия
    • Бухгалтерский учет
  • Технические науки
    • Черчение
    • Материаловедение
    • Сварка
    • Электротехника
    • АСУТП и КИПИА
    • Технологии
    • Теоретическая механика и сопромат
    • САПР
    • Метрология, стандартизация и сертификация
    • Геодезия и маркшейдерия
  • Программирование и сеть
    • Информатика
    • Языки программирования
    • Алгоритмы и структуры данных
    • СУБД
    • Web разработки и технологии
    • Архитектура ЭВМ и основы ОС
    • Системное администрирование
    • Создание программ и приложений
    • Создание сайтов
    • Тестирование ПО
    • Теория информации и кодирования
    • Функциональное и логическое программирование
  • Программы
    • Редакторы и компиляторы
    • Офисные программы
    • Работа с аудио видео
    • Работа с компьютерной графикой и анимацией
    • Автоматизация бизнеса
  • Прочие
    • Музыка
    • Природное земледелие
    • Рисование и живопись
• Библиотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
    • Астрономия
  • Обществознание

forkettle.ru