Часть 1. Химическая термодинамика
Министерство образования и науки Российской Федерации
Ростовский государственный университет
Сергей Иванович ЛЕВЧЕНКОВ
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов 3-гокурса вечернего отделения
биолого-почвенногофакультета РГУ
Часть 1. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
г. Ростов-на-Дону
2004 г.
|
|
| 2 |
|
| ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ | 3 | ||
1 ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА | 4 | ||
1.1 ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ | 4 | ||
1.2 ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ | 6 | ||
1.3 | ПРИЛОЖЕНИЯ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ | 9 | |
1.3.1 Закон Гесса | 8 | ||
1.3.2 | Зависимость теплового эффекта химической реакции от температуры | 12 | |
1.4 | ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНТРОПИЯ | 13 | |
1.4.1 | Статистическая интерпретация энтропии | 19 | |
1.5 | ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ | 19 | |
1.5.1 | Расчет абсолютной энтропии | 20 | |
1.6 | ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ | 21 | |
1.7 | ХИМИЧЕСКОЕ РАВНОВЕСИЕ | 24 | |
1.7.1 | Влияние внешних условий на химическое равновесие | 30 | |
1.7.2 | Влияние давления и концентрации | 30 | |
1.7.3 | Влияние температуры на положение равновесия | 31 | |
1.8 | ФАЗОВЫЕ РАВНОВЕСИЯ | 33 | |
Опубликовано по решению кафедры физической и коллоидной химии
Ростовского государственного университета.
Copyright © С. И. Левченков, 1996-2004
3
В В Е Д Е Н И Е
Предметом физической химии является объяснение химических явлений на основе более общих законов физики. Физическая химия рассматривает две
основные группы вопросов:
1.Изучение строения и свойств вещества и составляющих его частиц;
2.Изучение процессов взаимодействия веществ.
В курсе физической химии обычно выделяют несколько разделов.
Строение вещества. В этот раздел входят учение о строении атомов и молекул и учение об агрегатных состояниях вещества. Изучение строение вещества
необходимо для выяснения важнейших вопросов об образовании молекул из атомов, о природе химической связи, о строении и взаимодействии молекул. Именно
в этой своей части физическая химия очень тесно переплетается со всеми направлениями современной химии, поскольку изучение химических свойств
вещества вне связи со строением атомов и молекул на современном уровне невозможно.
Химическая термодинамика изучает энергетические эффекты химических процессов; позволяет определить возможность, направление и глубину протекания химического процесса в конкретных условиях.
Химическая кинетика. В этом разделе физической химии изучается скорость и механизм протекания химических процессов в различных средах при различных
условиях.
Учение о растворах рассматривает процессы образования растворов, их внутреннюю структуру и важнейшие свойства, зависимость структуры и свойств от
природы компонентов раствора.
Электрохимия изучает особенности свойств растворов электролитов,
явления электропроводности, электролиза, коррозии, работу гальванических элементов.
Коллоидная химия изучает поверхностные явления и свойства
мелкодисперсных гетерогенных систем.
Все разделы физической химии объединяет единая основа – общие законы
природы, которые применимы к любым процессам и любым системам, независимо
от их строения.
4
1 ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
Термодинамика – наука о взаимопревращениях различных форм энергии и законах этих превращений. Термодинамика базируется только на экспериментально
обнаруженных объективных закономерностях, выраженных в двух основных началах термодинамики.
Термодинамика изучает:
1.Переходы энергии из одной формы в другую, от одной части системы к другой;
2.Энергетические эффекты, сопровождающие различные физические и химические процессы и зависимость их от условий протекания данных процессов;
3.Возможность, направление и пределы самопроизвольного протекания процессов в рассматриваемых условиях.
Необходимо отметить, что классическая термодинамика имеет следующие
ограничения:
1.Термодинамика не рассматривает внутреннее строение тел и механизм протекающих в них процессов;
2.Классическая термодинамика изучает только макроскопические системы;
3.В термодинамике отсутствует понятие “время”.
1.1 ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ
Термодинамическая система – тело или группа тел, находящихся во взаимодействии, мысленно или реально обособленные от окружающей среды.
Гомогенная система – система, внутри которой нет поверхностей, разделяющих отличающиеся по свойствам части системы (фазы).
Гетерогенная система – система, внутри которой присутствуют поверхности, разделяющие отличающиеся по свойствам части системы.
Фаза – совокупность гомогенных частей гетерогенной системы, одинаковых по физическим и химическим свойствам, отделённая от других частей системы видимыми поверхностями раздела.
Изолированная система – система, которая не обменивается с окружающей средой ни веществом, ни энергией.
Закрытая система – система, которая обменивается с окружающей средой энергией, но не обменивается веществом.
Открытая система – система, которая обменивается с окружающей средой и веществом, и энергией.
5
Совокупность всех физических и химических свойств системы характеризует её термодинамическое состояние. Все величины, характеризующиекакое-либомакроскопическое свойство рассматриваемой системы –параметры состояния.
Опытным путем установлено, что для однозначной характеристики данной системы необходимо использовать некоторое число параметров, называемых независимыми;
все остальные параметры рассматриваются как функции независимых параметров. В качестве независимых параметров состояния обычно выбирают параметры, поддающиеся непосредственному измерению, например температуру, давление,
концентрацию и т.д. Всякое изменение термодинамического состояния системы (изменения хотя бы одного параметра состояния) есть термодинамический процесс.
Обратимый процесс – процесс, допускающий возможность возвращения системы в исходное состояние без того, чтобы в окружающей среде остались какие-
либо изменения.
Равновесный процесс – процесс, при котором система проходит через
непрерывный ряд равновесных состояний.
Энергия – мера способности системы совершать работу; общая качественная
мера движения и взаимодействия материи. Энергия является неотъемлемым
свойством материи. Различают потенциальную энергию, обусловленную положением тела в поле некоторых сил, икинетическую энергию, обусловленную изменением положения тела в пространстве.
Внутренняя энергия системы – сумма кинетической и потенциальной энергии
всех частиц, составляющих систему. Можно также определить внутреннюю энергию
системы как её полную энергию за вычетом кинетической и потенциальной энергии системы как целого.
Формы перехода энергии от одной системы к другой могут быть разбиты на
две группы. В первую группу входит только одна форма перехода движения путем
хаотических столкновений молекул двух соприкасающихся тел, т.е. путём
теплопроводности (и одновременно путём излучения). Мерой передаваемого таким способом движения является теплота. Теплота есть форма передачи энергии
путём неупорядоченного движения молекул. Во вторую группу включаются различные формы перехода движения, общей чертой которых является перемещение масс, охватывающих очень большие числа молекул (т.е. макроскопических масс), под действием каких-либо сил. Таковы поднятие тел в поле
тяготения, переход некоторого количества электричества от большего
6
электростатического потенциала к меньшему, расширение газа, находящегося под давлением и др. Общей мерой передаваемого такими способами движения является
работа – форма передачи энергии путём упорядоченного движения частиц.
Теплота и работа характеризуют качественно и количественно две различные формы передачи движения от данной части материального мира к другой. Теплота и
работа не могут содержаться в теле. Теплота и работа возникают только тогда, когда возникает процесс, и характеризуют только процесс. В статических условиях теплота и работа не существуют. Различие между теплотой и работой, принимаемое
термодинамикой как исходное положение, и противопоставление теплоты работе имеет смысл только для тел, состоящих из множества молекул, т.к. для одной
молекулы или для совокупности немногих молекул понятия теплоты и работы теряют смысл. Поэтому термодинамика рассматривает лишь тела, состоящие из большого числа молекул, т.е. так называемые макроскопические системы.
1.2 ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики представляет собой закон сохранения энергии, один из всеобщих законов природы (наряду с законами сохранения импульса,
заряда и симметрии):
Энергия неуничтожаема и несотворяема; она может только переходить из одной формы в другую в эквивалентных соотношениях.
Первое начало термодинамики представляет собой постулат – оно не может
быть доказано логическим путем или выведено из каких-либоболее общих положений. Истинность этого постулата подтверждается тем, что ни одно из его следствий не находится в противоречии с опытом. Приведем еще некоторые формулировки первого начала термодинамики:
Полная энергия изолированной системы постоянна;
Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).
Первое начало термодинамики устанавливает соотношение между теплотой
Q, работой А и изменением внутренней энергии системы ∆U:
Изменение внутренней энергии системы равно количеству сообщенной
системе теплоты минус количество работы, совершенной системой против внешних сил.
7
∆U =Q –А | (I.1) |
dU = δQ– δА | (I.2) |
Уравнение (I.1) является математической записью 1-гоначала термодинамики
для конечного, уравнение (I.2) – для бесконечно малого изменения состояния
системы.
Внутренняя энергия является функцией состояния; это означает, что
изменение внутренней энергии ∆U не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутренней энергии U2 и U1 в этих состояниях:
Следует отметить, что определить абсолютное значение внутренней энергии
системы невозможно; термодинамику интересует лишь изменение внутренней
энергии в ходе какого-либопроцесса.
Рассмотрим приложение первого начала термодинамики для определения
работы, совершаемой системой при различных термодинамических процессах (мы будем рассматривать простейший случай – работу расширения идеального газа).
Изохорный процесс (V = const;∆V= 0).
Поскольку работа расширения равна произведению давления и изменения
объема, для изохорного процесса получаем: |
|
∆U =Q –А | (I.1) |
А = Р∆V= 0 | (I.4) |
∆U =QV | (I.5) |
Изотермический процесс (Т = const ).
Из уравнения состояния одного моля идеального газа получаем:
Р = | RT | (I.6) | ||
| V |
| ||
Отсюда: |
|
|
| |
δА= PdV= RT | dV | (I.7) | ||
V | ||||
|
|
| ||
Проинтегрировав выражение (I.6) от V1 до V2, получим
8
V2 |
| =RT lnV2 | =RT lnP1 |
|
A = ∫RTdV | (I.8) | |||
V1 | V | V1 | P2 |
|
Изобарный процесс (Р = const). |
|
| ||
V2 |
|
|
|
|
A = ∫PdV= | Р∆V = R(T2 – T1) | (I.9) | ||
V1 |
|
|
|
|
Подставляя полученные выражения для работы различных процессов в уравнение (I.1), для тепловых эффектов этих процессов получим:
QV = ∆U |
| (I.10) | |
| V1 | P2 |
|
QT = A=RT ln |
| =RT lnP1 | (I.11) |
V2 | |||
QP = ∆U +P∆V |
| (I.12) | |
В уравнении (I.12) сгруппируем переменные с одинаковыми индексами. Получаем:
QP =U2 –U1 +P(V2 –V1) = (U2 +PV2) – (U1 +PV1) | (I.13) |
Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:H ≡U +PV. Тогда выражение (I.13) преобразуется к следующему виду:
QP =Н2 –Н1 = ∆Н | (I.14) |
Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.
Адиабатический процесс (Q = 0).
При адиабатическом процессе работа расширения совершается за счёт
уменьшения внутренней энергии газа:
2 | T1 |
|
A = – ∫dU= ∫CVdT | (I.15) | |
1T2
Вслучае если CV не зависит от температуры (что справедливо для многих
реальных газов), работа, произведённая газом при его адиабатическом расширении, прямо пропорциональна разности температур:
9
1.3ПРИЛОЖЕНИЯ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ
КХИМИЧЕСКИМ ПРОЦЕССАМ
1.3.1Закон Гесса
Как известно, большинство химических реакций сопровождаются выделением
(экзотермические реакции) либо поглощением (эндотермические реакции)
теплоты. Первое начало термодинамики дает возможность рассчитать тепловой
эффект химической реакции при различных условиях её проведения.
Тепловой эффект (теплота) химической реакции – количество теплоты,
выделившейся либо поглотившейся в ходе реакции. Тепловой эффект относят, как
правило, к числу молей прореагировавшего исходного вещества, стехиометрический коэффициент перед которым максимален.
Например, реакцию окисления водорода в химической термодинамике
записывают в виде:
Н2 +1/2 О2 = Н2О
и тепловой эффект рассчитывают на 1 моль водорода.
Тепловые эффекты, сопровождающие протекание химических реакций, являются предметом одного из разделов химической термодинамики – термохимии. Определим некоторые понятия термохимии.
Теплота образования вещества – тепловой эффект реакции образования 1
моля сложного вещества из простых. Теплоты образования простых веществ
принимаются равными нулю.
Теплота сгорания вещества – тепловой эффект реакции окисления 1 моля
вещества в избытке кислорода до высших устойчивых оксидов.
Теплота растворения – тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Теплота растворения складывается из двух составляющих: теплоты разрушения кристаллической решетки
(для твердого вещества) и теплоты сольватации:
∆Нраств= ∆Нкр.реш.+ ∆Нсольв
Поскольку ∆Нкр.реш всегда положительно (на разрушение кристаллической
решетки необходимо затратить энергию), а ∆Нсольв всегда отрицательно, знак ∆Нраств
определяется соотношением абсолютных величин ∆Нкр.реш. и ∆Нсольв:
∆Нраств= ∆Нкр.реш.– ∆Нсольв
10
Основным законом термохимии является закон Гесса, являющийся частным
случаем первого начала термодинамики:
Тепловой эффект химической реакции, проводимой в изобарноизотермических или изохорно-изотермическихусловиях, зависит только от вида и состояния исходных веществ и продуктов реакции и не
зависит от пути её протекания.
Выше было показано, что изменение энтальпии ∆Н (тепловой эффект изобарного процесса Qp) и изменение внутренней энергии ∆U (тепловой эффект
изохорного процесса Qv) не зависят от пути, по которому система переходит из
начального состояния в конечное.
Рассмотрим некоторый обобщенный химический процесс превращения
исходных веществ А1, А2, А3… в продукты реакции В1, В2, В3…, который может быть
осуществлен различными путями в одну или несколько стадий:
|
| ∆H5 |
|
|
|
|
∆h5 |
| ∆H6 |
|
| ||
A1,A2,A3… |
| ∆h2 |
| B | ,B ,B … | |
|
|
| ||||
|
|
| 1 | 2 | 3 | |
∆h3∆h4
Согласно закону Гесса, тепловые эффекты всех этих реакций связаны
следующим соотношением:
∆Н1 = ∆Н2 + ∆Н3 = ∆Н4 + ∆Н5 + ∆Н6 | (I.17) |
Практическое значение закона Гесса состоит в том, что он позволяет
рассчитывать тепловые эффекты химических процессов. В термохимических
расчетах обычно используют ряд следствий из закона Гесса:
1.Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции (закон Лавуазье-Лапласа).
2.Для двух реакций, имеющих одинаковые исходные, но разные конечные состояния, разность тепловых эффектов представляет собой тепловой эффект
перехода из одного конечного состояния в другое.
studfiles.net
Часть 1. Химическая термодинамика – Стр 3
21
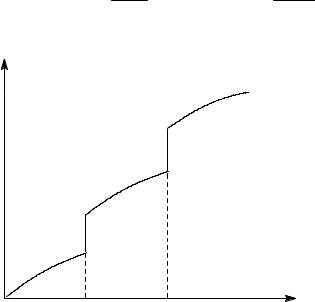
Таким образом, нагревание вещества без фазовых переходов
сопровождается непрерывным ростом энтропии; при фазовом переходе происходит
скачкообразное изменение энтропии. Графическая зависимость энтропии вещества от температуры приведена на рис. 1.3.
Учитывая это, рассчитать абсолютную энтропию любого вещества при любой
температуре можно следующим образом:
Тпл |
| ∆H | Ткип | ∆H |
| Т |
|
ST = ∫CP,тв d(lnT)+ | T пл+ | ∫CP,ж d(lnT)+ | T исп | + | ∫CP,газ d(lnT) | (I.66) | |
0 |
| пл | Тпл | кип |
| Ткип |
|
S |
|
|
|
|
|
|
|
| Tпл | Tкип | T |
|
|
| |
Рис. 1.3 | Зависимость энтропии вещества от температуры. |
| |||||
Поскольку энтропия есть функция состояния, изменение энтропии в ходе химического процесса определяется только видом и состоянием исходных веществ и продуктов реакции и не зависит от пути реакции; оно может быть рассчитано по уравнению (I.67):
∆S= ∑(νi Si )прод − ∑(νi Si )исх | (I.67) |
Для многих веществ величины абсолютной энтропии в стандартных условиях
приведены в справочной литературе.
1.6 ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных. На практике же большей частью приходится иметь дело с
22
системами, взаимодействующими с окружающей средой. Для характеристики процессов, протекающих в закрытых системах, были введены новые термодинамические функции состояния: изобарно-изотермический потенциал
(свободная энергия Гиббса) и изохорно-изотермическийпотенциал(свободная энергия Гельмгольца).
Поведение всякой термодинамической системы в общем случае определяется
одновременным действием двух факторов – энтальпийного, отражающего стремление системы к минимуму тепловой энергии, и энтропийного, отражающего
противоположную тенденцию – стремление системы к максимальной
неупорядоченности. Если для изолированных систем (∆Н = 0) направление и предел самопроизвольного протекания процесса однозначно определяется величиной
изменения энтропии системы ∆S, а для систем, находящихся при температурах, близких к абсолютному нулю (S = 0 либо S = const) критерием направленности
самопроизвольного процесса является изменение энтальпии ∆Н, то для закрытых систем при температурах, не равных нулю, необходимо одновременно учитывать оба фактора. Направлением и предел самопроизвольного протекания процесса в любых системах определяет более общий принцип минимума свободной энергии:
Самопроизвольно могут протекать только те процессы, которые
приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения.
Для закрытых систем, находящихся в изобарно-изотермическихлибоизохорно-изотермическихусловиях свободная энергия принимает вид изобарно-
изотермического либо изохорно-изотермическогопотенциалов (т.н. свободная
энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда
просто термодинамическими потенциалами, что не вполне строго, поскольку
термодинамическими потенциалами являются также внутренняя энергия (изохорноизэнтропный) и энтальпия (изобарно-изэнтропныйпотенциал).
Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме. Выразим работу данного процесса,
которую обозначим Amax (поскольку работа процесса, проводимого равновесно, максимальна), из уравнений (I.53, I.54):
|
| 23 |
Amax =T∆S – ∆U | (I.69) |
|
Преобразуем выражение (I.69), сгруппировав члены с одинаковыми | ||
индексами: |
|
|
Amax = T(S2 – S1)– (U2 – U1)= (U1 – TS1)– (U2 – TS2) | (I.70) | |
Введя обозначение: |
|
|
F ≡ U– TS, | (I.71) |
|
получаем: |
|
|
Amax =F1 –F2 = – ∆F | (I.72) |
|
∆F = ∆U –T∆S | (I.73) |
|
Функция F ≡ U – TS есть изохорно-изотермическийпотенциал (свободная
энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических
условиях.
Закрытую систему, находящуюся в изобарно-изотермическихусловиях, характеризуетизобарно-изотермическийпотенциал G:
G = U+ PV– TS= H– TS | (I.74) |
∆G = ∆H –T∆S | (I.75) |
Поскольку -∆F= Amax, можно записать: |
|
– ∆G =Amax –P∆V =A’max | (I.76) |
Величину А’max называютмаксимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах.
Условия самопроизвольного протекания процессов в закрытых системах:
Изобарно-изотермические(P = const, T = const):
∆G< 0, dG< 0
Изохорно-изотермические(V = const, T = const):
∆F< 0, dF< 0
24
Процессы, которые сопровождаются увеличением термодинамических
потенциалов, протекают лишь при совершении работы извне над системой. В химии
наиболее часто используется изобарно-изотермическийпотенциал, поскольку большинство химических (и биологических) процессов происходят при постоянном давлении. Для химических процессов величину ∆G можно рассчитать, зная ∆H и ∆S процесса, по уравнению (I.75), либо пользуясь таблицами стандартных термодинамических потенциалов образования веществ ∆G°обр; в этом случае ∆G°
реакции рассчитывается аналогично ∆Н° по уравнению (I.77):
∆Go = ∑(νi ∆Go обр )прод −∑(νi ∆Go обр )исх | (I.77) |
Величина стандартного изменения изобарно-изотермическогопотенциала в
ходе химической любой реакции ∆G°298 есть мера химического сродства исходных
веществ. Основываясь на уравнении (I.75), можно оценить вклад энтальпийного и
энтропийного факторов в величину ∆G и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов, основываясь на знаке величин ∆Н и ∆S.
1. Экзотермические реакции; ∆H < 0.
а) Если ∆S > 0, то ∆G всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно.
б) Если ∆S < 0, реакция будет идти самопроизвольно при ∆Н > T∆S (низкие температуры).
2. Эндотермические реакции; ∆H > 0.
а) Если ∆S > 0, процесс будет самопроизвольным при ∆Н < T∆S (высокие
температуры).
б) Если ∆S < 0, то ∆G всегда положительно; самопроизвольное протекание
эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно.
1.7 ХИМИЧЕСКОЕ РАВНОВЕСИЕ
Как было показано выше, протекание самопроизвольного процесса в
термодинамической системе сопровождается уменьшением свободной энергии системы (dG < 0, dF < 0). Очевидно, что рано или поздно (напомним, что понятие
“время” в термодинамике отсутствует) система достигнет минимума свободной энергии. Условием минимума некоторой функции Y = f(x) является равенство нулю
25
первой производной и положительный знак второй производной: dY = 0; d2Y > 0.
Таким образом, условием термодинамического равновесия в закрытой системе
является минимальное значение соответствующего термодинамического
потенциала:
Изобарно-изотермические(P = const, T = const):
∆G= 0 dG= 0, d2G> 0
Изохорно-изотермические(V = const, T = const):
∆F= 0 dF= 0, d2F> 0
Состояние системы с минимальной свободной энергией есть состояние
термодинамического равновесия:
Термодинамическим равновесием называется такое термодина-
мическое состояние системы, которое при постоянстве внешних условий не изменяется во времени, причем эта неизменяемость не обусловлена каким-либовнешним процессом.
Учение о равновесных состояниях – один из разделов термодинамики. Далее мы будем рассматривать частный случай термодинамического равновесного состояния – химическое равновесие. Как известно, многие химические реакции
являются обратимыми, т.е. могут одновременно протекать в обоих направлениях –
прямом и обратном. Если проводить обратимую реакцию в закрытой системе, то через некоторое время система придет в состояние химического равновесия – концентрации всех реагирующих веществ перестанут изменяться во времени. Необходимо отметить, что достижение системой состояния равновесия не означает
прекращения процесса; химическое равновесие является динамическим, т.е.
соответствует одновременному протеканию процесса в противоположных
направлениях с одинаковой скоростью. Химическое равновесие является подвижным – всякое бесконечно малое внешнее воздействие на равновесную
систему вызывает бесконечно малое изменение состояния системы; по прекращении внешнего воздействия система возвращается в исходное состояние. Ещё одним важным свойством химического равновесия является то, что система
может самопроизвольно прийти в состояние равновесия с двух противоположных
сторон. Иначе говоря, любое состояние, смежное с равновесным, является менее
26
устойчивым, и переход в него из состояния равновесия всегда связан с
необходимостью затраты работы извне.
Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации С,
парциальные давления P или мольные доли X реагирующих веществ. Для некоторой
реакции
aA + bB+ … mM+ nN+ …
соответствующие константы равновесия выражаются следующим образом:
K |
|
| CmCn | (I.78) | Kp= | PmPn | (I.79) | ||||
C | = | M | N | M | N | ||||||
Ca | Cb | PaPb | |||||||||
|
|
|
|
|
| ||||||
|
|
| A | B |
|
|
| A | B |
| |
|
|
|
|
| KX= | XmXn | (I.80) |
|
| ||
|
|
|
|
| M N |
|
| ||||
|
|
|
|
| XaAXBb |
|
| ||||
|
|
|
|
|
|
|
|
|
| ||
Константа равновесия есть характерная величина для каждой обратимой химической реакции; величина константы равновесия зависит только от природы реагирующих веществ и температуры. Выражение для константы равновесия для элементарной обратимой реакции может быть выведено из кинетических представлений.
Рассмотрим процесс установления равновесия в системе, в которой в начальный момент времени присутствуют только исходные вещества А и В. Скорость прямой реакции V1 в этот момент максимальна, а скорость обратной V2 равна нулю:
V1= k1САаСВb | (I.81) |
V2= k2CМmСNn | (I.82) |
По мере уменьшения концентрации исходных веществ растет концентрация продуктов реакции; соответственно, скорость прямой реакции уменьшается,
скорость обратной реакции увеличивается. Очевидно, что через некоторое время
скорости прямой и обратной реакции сравняются, после чего концентрации реагирующих веществ перестанут изменяться, т.е. установится химическое равновесие.
Приняв, что V1 = V2, можно записать:
k1САаСВb = k2CМmСNn | (I.83) |
27
k1 | m | n |
| |
= CMa | CbN=KC | (I.84) | ||
k2 | ||||
CACB |
| |||
Т.о., константа равновесия есть отношение констант скорости прямой и
обратной реакции. Отсюда вытекает физический смысл константы равновесия: она
показывает, во сколько раз скорость прямой реакции больше скорости обратной при
данной температуре и концентрациях всех реагирующих веществ, равных 1 моль/л.
Теперь рассмотрим (с некоторыми упрощениями) более строгий
термодинамический вывод выражения для константы равновесия. Для этого
необходимо ввести понятие химический потенциал. Очевидно, что величина
свободной энергии системы будет зависеть как от внешних условий (T, P или V), так и от природы и количества веществ, составляющих систему. В случае, если состав
системы изменяется во времени (т.е. в системе протекает химическая реакция),
необходимо учесть влияние изменения состава на величину свободной энергии
системы. Введем в некоторую систему бесконечно малое количество dni молейi-гокомпонента; это вызовет бесконечно малое изменение термодинамического потенциала системы. Отношение бесконечно малого изменения величины свободной энергии системы к бесконечно малому количеству компонента,
внесенному в систему, есть химический потенциал µi данного компонента в системе:
dG |
| |||
µi= | i |
| (I.85) | |
|
| |||
dn |
| |||
| i P,T,j≠i |
| ||
dF |
| |||
µi= | i |
| (I.86) | |
| ||||
dn |
| |||
| i V,T,j≠i |
| ||
Химический потенциал компонента связан с его парциальным давлением или | ||||
концентрацией следующими соотношениями: |
| |||
µi= µоi+ RTlnPi | (I.87) | |||
µi= µоi+ RTlnCi | (I.88) | |||
Здесь µоi – стандартный химический потенциал компонента (Pi = 1 атм., Сi = 1
моль/л.). Очевидно, что изменение свободной энергии системы можно связать с изменением состава системы следующим образом:
dG =µ1dn1 +µ2dn2 + … | = Σµidni | (I.89) |
dF =µ1dn1 +µ2dn2 + … | = Σµidni | (I.90) |
28
Поскольку условием равновесия является минимум свободной энергии
системы (dG = 0, dF = 0), можно записать:
В закрытой системе изменение числа молей одного компонента
сопровождается эквивалентным изменением числа молей остальных компонентов;
т.е., для приведенной выше химической реакции имеет место соотношение:
dnA | = | dnB | = | dnM | = | dnN | (I.92) | |
a | b | m | n | |||||
|
|
|
|
Отсюда можно получить следующее условие химического равновесия в
закрытой системе:
аµA+ bµB= mµM+ nµN | (I.93) |
В общем виде условие химического равновесия можно записать следующим
образом:
Выражение (I.94) носит название уравнения Гиббса-Дюгема.Подставив в него зависимость химического потенциала от концентрации, получаем:
о |
| о | CmCn |
| |
| M N |
| |||
Σniµi = Σniµ i + RTΣni lnCi = Σniµ i + RT ln |
|
| (I.95) | ||
CaACBb | |||||
Поскольку Σniµi = ∆F,Σniµоi = ∆F°, получаем: |
|
|
| ||
∆F= ∆F°+ RT ln | CMmCNn | (I.96) |
| ||
CaACBb |
|
| |||
Для изобарно-изотермическогопроцесса аналогичным образом можно получить:
PmPn
∆G = ∆G° +RT ln M N (I.97)
PAaPBb
Полученные нами выражения I.96 – I.97 есть изотерма химической реакции. Если система находится в состоянии химического равновесия, то изменение термодинамического потенциала равно нулю; получаем:
29
cmcn
∆F°= – RT lnM N = – RT ln KC (I.98)
caAcbB
pmpn
∆G°= – RT lnM N = – RT ln KP (I.99)
paApbB
Здесь сi и рi – равновесные концентрации и парциальные давления исходных
веществ и продуктов реакции (в отличие от неравновесных Сi и Рi в уравнениях I.96– I.97).
Поскольку для каждой химической реакции стандартное изменение термодинамического потенциала ∆F° и ∆G° есть строго определенная величина, то произведение равновесных парциальных давлений (концентраций), возведенных в степень, равную стехиометрическому коэффициенту при данном веществе в
уравнении химической реакции (стехиометрические коэффициенты при исходных веществах принято считать отрицательными) есть некоторая константа, называемая константой равновесия. Уравнения (I.98, I.99) показывают связь константы равновесия со стандартным изменением свободной энергии в ходе реакции.
Уравнение изотермы химической реакции связывает величины реальных
концентраций (давлений) реагентов в системе, стандартного изменения термодинамического потенциала в ходе реакции и изменения термодинамического потенциала при переходе из данного состояния системы в равновесное. Знак ∆G (∆F) определяет возможность самопроизвольного протекания процесса в системе.
При этом ∆G° (∆F°) равно изменению свободной энергии системы при переходе из стандартного состояния (Pi = 1 атм., Сi = 1 моль/л) в равновесное. Уравнение изотермы химической реакции позволяет рассчитать величину ∆G (∆F) при переходе из любого состояния системы в равновесное, т.е. ответить на вопрос, будет ли
химическая реакция протекать самопроизвольно при данных концентрациях Сi (давлениях Рi) реагентов:
∆F= ∆F°+ RT ln | CmCn | = RT ln |
| CmCn | – RT ln KC | (I.100) | ||||
| M N |
| M N | |||||||
CaACBb | CaACBb | |||||||||
|
|
|
|
| ||||||
∆G= ∆G°+ RT ln |
| PmPn | = RT ln | PmPn | – RT ln KP | (I.101) | ||||
| M N |
|
| M N |
| |||||
| PaPb |
| PaPb | |||||||
|
|
|
|
|
| |||||
|
| A B |
|
| A B |
|
| |||
Если изменение термодинамического потенциала меньше нуля, процесс в
данных условиях будет протекать самопроизвольно.
30
1.7.1 Влияние внешних условий на химическое равновесие
При постоянстве внешних условий система может находиться в состоянии
равновесия сколь угодно долго. Если изменить эти условия (т.е. оказать на систему
какое-либовнешнее воздействие), равновесие нарушается; в системе возникает
самопроизвольный процесс, который продолжается до тех пор, пока система опять
не достигнет состояния равновесия (уже при новых условиях). Рассмотрим, как
влияют на положение равновесия некоторые факторы.
1.7.2 Влияние давления и концентрации
Рассмотрим несколько возможных случаев смещения равновесия.
1. В систему добавлено исходное вещество. В этом случае
CmCn | < KC; | PmPn | < KP; | |
M N | M N | |||
| PaPb | |||
Ca | Cb |
|
| |
A | B |
| A B |
|
По уравнению изотермы химической реакции (I.100 – I.101) получаем: ∆F < 0;
∆G < 0. В системе возникнет самопроизвольный химический процесс, направленный в сторону расходования исходных веществ и образования продуктов реакции (химическое равновесие смещается вправо).
2. В систему добавлен продукт реакции. В этом случае
CmCn | > KC; | PmPn | > KP; | |
M N | M N | |||
| PaPb | |||
Ca | Cb |
|
| |
A | B |
| A B |
|
Согласно уравнению изотермы химической реакции, ∆F > 0; ∆G > 0 Химическое равновесие будет смещено влево (в сторону расходования продуктов реакции и образования исходных веществ).
3. Изменено общее давление (для реакций в газовой фазе).
Парциальные давления всех компонентов Рi в этом случае изменяются в одинаковой степени; направление смещения равновесия будет определяться
суммой стехиометрических коэффициентов ∆n.
Учитывая, что парциальное давление газа в смеси равно общему давлению, умноженному на мольную долю компонента в смеси (Рi = РХi), изотерму реакции можно переписать в следующем виде (здесь ∆n =Σ(ni)прод -Σ(ni)исх):
studfiles.net
Химическая термодинамика
Московский Авиационный Институт
(Технический Университет)
Кафедра физической химии
Курсовая работа
на тему:
“Химическая термодинамика”
Выполнил: Павлюк Д.В
Проверила: Селиванова С.И.
Содержание:
I. Теоретическая часть
1. Введение……………………………………………………………..3
2. Законы термохимии…………………………………………………3
3. Элементы термодинамики………………………………………….4
4. Первое начало термодинамики…………………………………….5
5. Элементы второго начала термодинамики………………………..9
6. Энтропия…………………………………………………………….11
II. Экспериментальная часть………………………………………16
III. Расчетная часть…………………………………………………17
Список используемой литературы……………………………………19
В результате химической реакции выделяется или поглощается энергия, так как реакция сопровождается перестройкой энергетических уровней атомов или молекул веществ, участвующих в ней, и веществ, образующихся в ходе реакции.
Реакции, при которых наблюдается выделение энергии, называются экзотермическими (Q>0).
Реакции, идущие с поглощением энергии, называются эндотермическими (Q<0). Выделение или поглощение энергии в результате процесса зависит от соотношения количеств энергии, затраченных на разрыв или возбуждение химических связей первоначально взятых веществ, и энергии, выделяющейся в результате образования новых химических связей в продуктах реакции.
Величина энергии отдельной химической связи очень мала. Её удобно выражать в электронвольтах на атом. Поскольку обычно в реакциях участвуют относительно большие количества веществ, то общие количества энергии получаются также большие. Так, элементарный расчет показывает:
на 1 атом: 1эВ=1,6·10-19 Кл∙1В = 1,6. 10-19 Дж,
на 1 моль: 1,6∙10-19 ∙6,02∙1023 =9,65∙104 Дж/моль = 96,5 кДж/моль.
Энергия, образующаяся в результате химических реакций, может выделяться в разных формах, но, конечно, в эквивалентных количествах. Так, например, фотохимические процессы при фотографии развиваются при поглощении квантов лучистой энергии галидами серебра и, наоборот, можно построить источник когерентного излучения—лазер, работающий на энергии химических реакций.
Затрачивая электрическую энергию, можно выделять нужные вещества из растворов или расплавов путем электролиза, с другой стороны, можно получить энергию за счет химических реакций, протекающих в гальванических элементах или аккумуляторах.
Чаще всего в, результате химических реакций выделяется или поглощается тепловая энергия. Поэтому раздел химии, изучающий энергию химических реакций, исторически стал называться термохимией, а изменение энергии называется тепловым эффектом химической реакции и измеряется в килоджоулях на моль образовавшегося или сгоревшего вещества. Так как в зависимости от условий, в которых протекает химическая реакция, возможно выделение или поглощение работы расширения газов (p=const), то различают тепловой эффект реакции при (p=const) Qp и тепловой эффект реакции при (v=const) Qv , хотя разница между ними обычно невелика.
ЗАКОНЫ ТЕРМОХИМИИ
Первый закон термохимии (Лавуазье и Лаплас, 1780—1784):
тепловой эффект образования данного соединения в точности равен, но обратен по знаку тепловому эффекту его разложения.
Из закона Лавуазье—Лапласа следует невозможность построить вечный двигатель I рода, использующий энергию химических реакций.
Второй закон термохимии (Г. И. Гесс, 1840):
тепловой эффект химической реакции не зависит от характера и последовательности отдельных ее стадий и определяется только начальными и конечными продуктами реакции и их физическим состоянием (при p=const или при v=const).
Г. И. Гесс первый принял во внимание физическое состояние реагирующих веществ, так как теплоты изменения агрегатных состояний веществ накладываются на тепловой эффект реакции, увеличивая или уменьшая его.
Утверждение закона Гесса о том, что тепловой эффект процесса не зависит от его отдельных стадий и их последовательности, дает возможность рассчитывать тепловые эффекты реакций для случаев, когда их определить экспериментально или очень трудно, или вообще невозможно.
Применение закона Гесса чрезвычайно расширило возможности термохимии, позволяя производить точные расчеты тепловых эффектов образования целого ряда веществ, опытные данные по которым получить было трудно.
Закон Гесса в наши дни применяют главным образом для расчета термодинамических функций—энтальпий, которые сейчас используются для термохимических расчетов. Термохимия, исторически сложившаяся раньше термодинамики, в настоящее время претерпела некоторые изменения и стала разделом химической термодинамики.
ЭЛЕМЕНТЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
Химическая термодинамика изучает изменения энергии в результате процессов в материальных системах, приводящих к изменению состава и свойств физических тел, из которых построена данная система.
Термодинамической системой называется комплекс взаимодействующих между собой физических тел, мысленно обособленный от окружающей среды.
Системы бывают изолированные, в которых энергообмен и массообмен с окружающей средой отсутствуют, и замкнутые, в которых возможен энергообмен с окружающей средой, но не возможен обмен веществом. Незамкнутые системырассматриваются в термодинамике необратимых процессов.
Системы можно разделить на гомогенные или однородные, не имеющие физических границ раздела между отдельными частями, так как во всех частях системы свойства одинаковы(например, ненасыщенный раствор), и системы гетерогенные, или неоднородные, разделяющиеся на отдельные части физическими границами раздела, на которых свойства системы резко изменяются. Часть гетерогенной системы, ограниченная физическими границами раздела, называется фазой. Например, насыщенный раствор, соприкасающийся с растворяемым веществом, представляет собой гетерогенную систему.
Состояние системы определяется физическими параметрами; в простейшем случае идеального газа — это давление и температура, так какv =f(p. Т).
Изменение параметров системы вызывает процесс. Если процесс заключается в последовательном изменении параметров, приводящих в конечном итоге систему в исходное состояние, то такой процесс называется циклом.
Химическая термодинамика, так же как и общая термодинамика, основана главным образом на двух законах (началах).
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики, окончательно сформулированное Джоулем в середине XIXв., представляет собой закон сохранения энергии. Для замкнутых систем, обменивающихся энергией с окружающей средой, уравнение первого закона термодинамики имеетвид:
(1)где Q — энергия, сообщенная системе; ΔU— приращение внутренней энергии системы; А — работа, совершенная системой.
Энергия, сообщенная системе (Q), может быть тепловой или другой формой энергии, так как первый закон термодинамики справедлив для любых процессов. Если система поглощает энергию, то Q принимает положительное значение, т. с. знак Q обратен знаку теплового эффекта реакции:
Q = ¾ Q (2)
Внутренняя энергия системы (U) включает все виды энергии, заключенные в веществах, составляющих систему, кроме энергии, созданной гравитационными, электрическими или магнитными нолями, а также кроме кинетической энергии системы в целом (для движущейся системы). Таким образом, U ¾ сумма всех видов тепловой энергии движения элементарных частиц, энергии связи и энергии агрегатных состояний. Это сложная термодинамическая функция, полностью определяемая состоянием системы или соответствующим сочетанием параметров (р и Т). Если система поглощает энергию, то запас внутренней энергии растет (ΔU>0).
Если работа совершается системой, то А — положительная величина; если же работа совершается над системой, то А отрицательна (например, сжатие газа).
Как Q, так и А в уравнении (1) характеризуют процесс и от состояний системы (начального и конечного) зависят неоднозначно, так как из начального состояния подойти к конечному состоянию можно разными путями и с различным поглощением энергии и различной величиной работы. Поэтому уравнение (1) мы не можем записать в дифференциальной форме, так как только одно приращение ΔU однозначно определяется параметрами состояния р, v, Т.
Если известен закон изменения параметров в данном процессе, то уравнение первого закона термодинамики можно записать в дифференциальной форме и исследовать математически. В области применения химических реакций наиболее часто встречаются процессы, протекающие при постоянном объеме (изохорический) и при постоянном давлении (изобарический).
1. Изохорический процесс: v = const. В этом случае параметры р и Т связаны между собой уравнением Гей-Люссака, р/Т = const . Уравнение (1) записывается в дифференциальной форме:
dQ=dU+dA. (3)
Но если объем постоянен, значит работа расширения или сжатия газа совершаться не может:dA==pdv=0 . Следовательно,dQ = – dU ;
приравниваем частные производные по температуре:
или
dU = Cv dT, (4)
где Сv — теплоемкость при постоянном объеме. Уравнение (4) позволяет вычислять изменение внутренней энергии системы приизменении температуры, если не происходит каких-либо изменений агрегатного или полиморфного состояния.
mirznanii.com
