Методы оптимальных решений – задачи с решением. Решение задач линейного программирования и других моделей
Рассмотрен графический метод решения задачи линейного программирования (ЗЛП) с двумя переменными. На примере задачи приведено подробное описание построения чертежа и нахождения решения.
На странице подробно разобрано решение задачи линейного программирования симплексным методом, кроме того, показано построение двойственной задачи линейного программирования и нахождение ее решения по решению прямой задачи.
Подробно рассмотрена транспортная задача, ее математическая модель и методы решения – нахождение опорного плана методом минимального элемента и поиск оптимального решения методом потенциалов.
На странице даются основные понятия теории игр – платежной матрицы, стратегии игроков, седловой точки, нижней и верхней цены игры. Приведена краткая теория и решены несколько простых задач на тему основных понятий матричных игр.
Содержит изложенные в краткой и доступной форме теоретические сведения о матричной игре без седловой точки и способе сведения такой задачи к задаче линейного программирования, для отыскания ее решения в смешанных стратегиях. Приведен пример решения задачи.
Рассмотрено решение статистической матричной игры в условиях неопределенности с помощью критериев Вальда, Сэвиджа, Гурвица, Лапласа, Байеса. На примере задачи подробно показано построение платежной матрицы и матрицы рисков.
На странице рассмотрено нахождение условного экстремума методом множителей Лагранжа. Показано построение функции Лагранжа на примере решения задачи нелинейного программирования. Решенную задачу предваряет краткая теория.
Приведен образец решения задачи квадратичного выпуклого программирования графическим методом.
Кратко изложены основные принципы динамического программирования (динамического планирования), рассмотрены уравнения Беллмана. Подробно решена задача оптимального распределения ресурсов между предприятиями.
На примере решения задачи рассмотрены вопросы построения сетевого графика работ, нахождение критического пути и критического времени. Также показано вычисление параметров и резервов событий и работ – ранних и поздних сроков, общих (полных) и частных резервов.
Приведены необходимые теоретические сведения, в частности формулы Эрланга, а также образец решения задачи по теме “Многоканальная система массового обслуживания с отказами”. Подробно рассмотрены показатели многоканальной системы массового обслуживания (СМО) с отказами – вероятность отказа и вероятность обслуживания, абсолютная пропускная способность системы и среднее число каналов, занятых обслуживанием заявки.
Приведены необходимые теоретические сведения и образец решения задачи по теме “Многоканальная система массового обслуживания с неограниченной очередью”, подробно рассмотрены показатели многоканальной системы массового обслуживания (СМО) с ожиданием обслуживания – среднее число каналов, занятых обслуживанием заявки, длина очереди, вероятность образования очереди, вероятность свободного состояния системы, среднее время ожидания в очереди.
На примере решения задачи рассмотрена основная модель управления запасами (модель Уилсона). Вычислены такие показатели модели как оптимальный размер партии заказа, годовые затраты на хранение, интервал между поставками и точка размещения заказа.
На примере решения задачи рассмотрена межотраслевая модель Леонтьева. Показано вычисление матрицы коэффициентов прямых материальных затрат, матрицы «затраты-выпуск», матрицы коэффициентов косвенных затрат, векторов конечного потребления и валового выпуска.
100task.ru
Методы оптимальных решений – Вариант 8
КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ:
«МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ»
Вариант № 8
1.Решить графическим методом задачу
линейного программирования. Найти
максимум и минимум функции 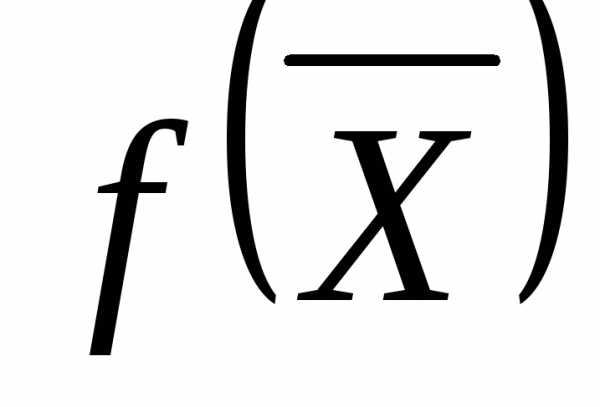 при заданных ограничениях:
при заданных ограничениях:
,

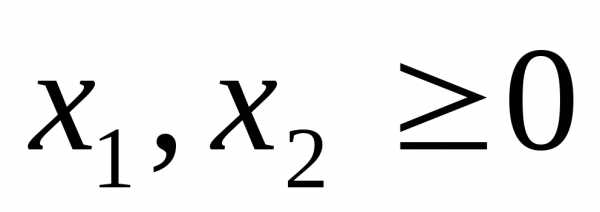 .
.
Решение
Необходимо найти минимальное значение целевой функции и максимальное, при системе ограничений:
9x1+3x2≥30, (1)
-x1+x2
x1+x2≤8, (3)
x1 ≥ 0, (4)
x2 ≥ 0, (5)
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
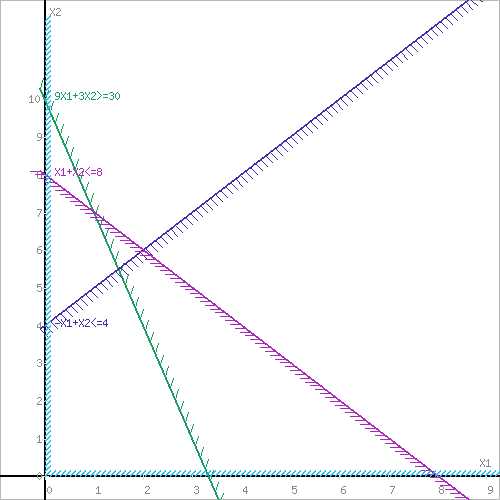
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений.

Рассмотрим целевую функцию задачи .
Построим прямую, отвечающую значению функции F = 0: F = 2x1+3x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0; 0), конец – точка (2; 3). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
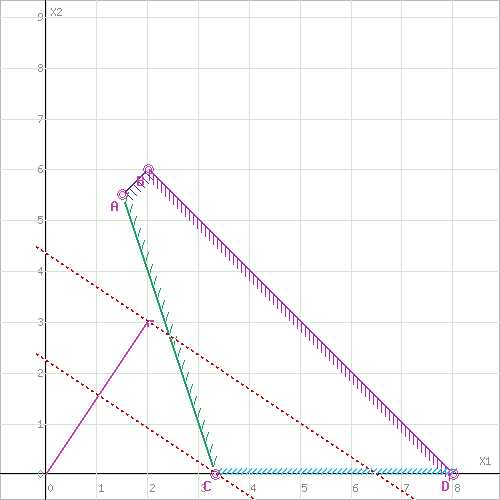
Прямая
пересекает область в точке C. Так как
точка C получена в результате пересечения
прямых (4) и (1), то ее координаты удовлетворяют
уравнениям этих прямых: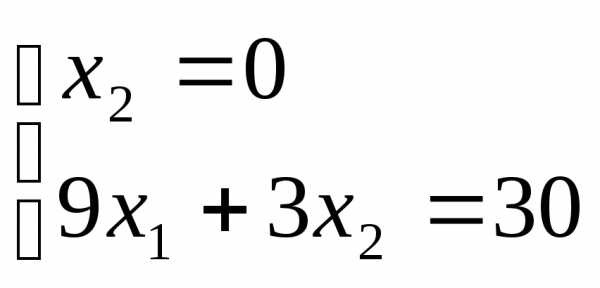 .
.
Решив систему уравнений, получим: x1 = 3.3333, x2 = 0.
Откуда найдем минимальное значение целевой функции: .
Рассмотрим целевую функцию задачи .
Построим прямую, отвечающую значению функции F = 0: F = 2x1+3x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (2; 3). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
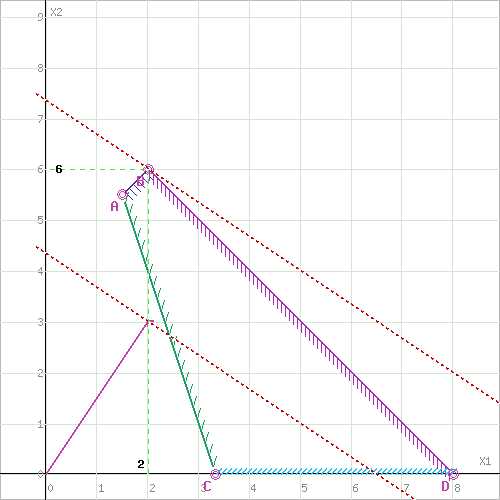
Прямая
пересекает область в точке B. Так как
точка B получена в результате пересечения
прямых (2) и (3), то ее координаты удовлетворяют
уравнениям этих прямых: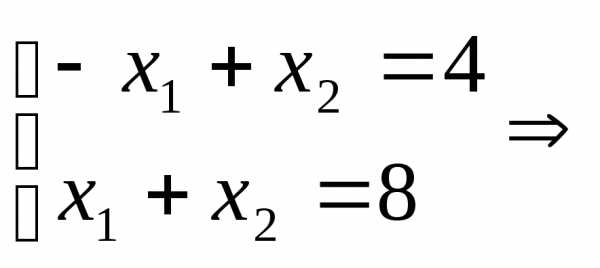
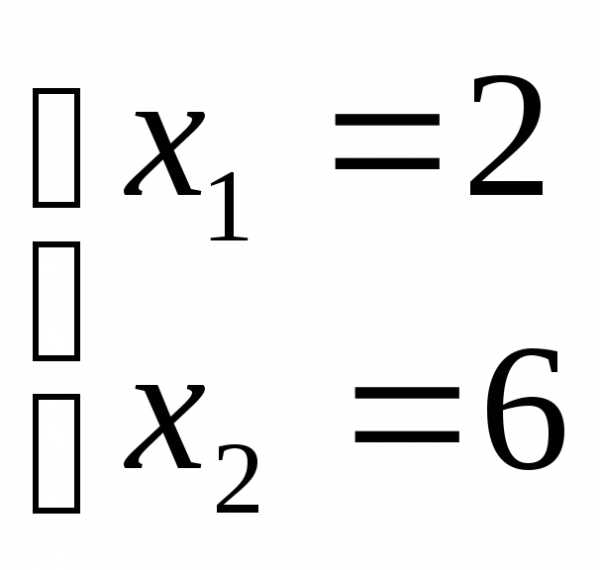
Откуда найдем максимальное значение целевой функции: .
Ответ:и.
2.Решитьзадачу линейного программирования симплекс-методом:
,

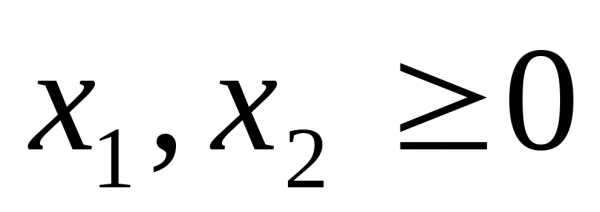 .
.
Решение
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим минимальное значение целевой
функции
при следующих условиях-ограничений: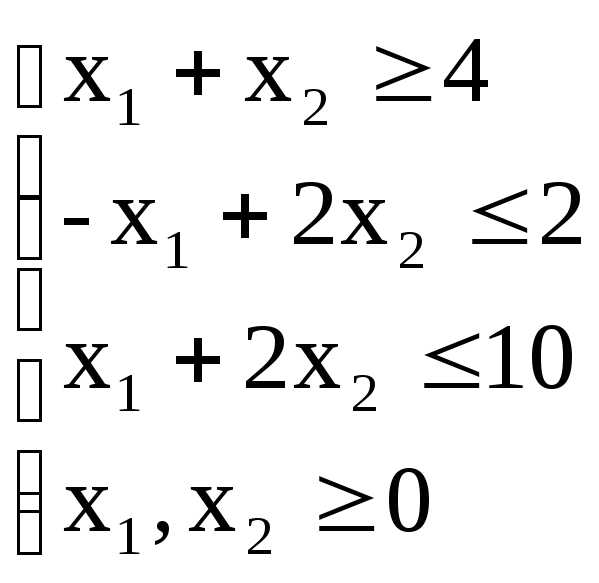
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных.
В 1-м неравенстве смысла (≥) вводим базисную переменную x3со знаком минус. В 2-м неравенстве смысла (≤) вводим базисную переменнуюx4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5.

Введем искусственные переменные  :
в 1-м равенстве вводим переменную
:
в 1-м равенстве вводим переменную
Для постановки задачи на минимум целевую функцию запишем так: .
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные: x6= 4-x1-x2+x3, которые подставим в целевую функцию: или.
Матрица коэффициентов 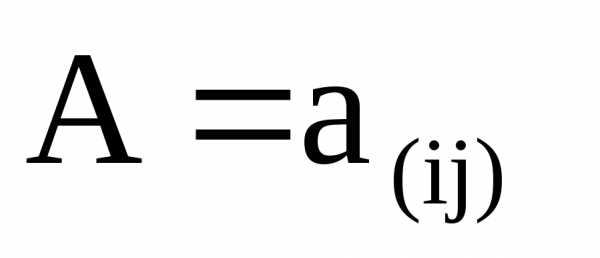 этой системы уравнений имеет вид:
этой системы уравнений имеет вид: .
.
Решим систему уравнений относительно базисных переменных: x6, x4, x5.
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,2,10,4)
Базисное решение называется допустимым, если оно неотрицательно.
Базис | B | x1 | x2 | x3 | x4 | x5 | x |
x6 | 4 | 1 | 1 | -1 | 0 | 0 | 1 |
x4 | 2 | -1 | 2 | 0 | 1 | 0 | 0 |
x | 10 | 1 | 2 | 0 | 0 | 1 | 0 |
F(X0) | 4M | -2+M | 1+M | -M | 0 | 0 | 0 |
Текущий опорный план не оптимален, так
как в индексной строке находятся
положительные коэффициенты. В качестве
ведущего выберем столбец, соответствующий
переменной x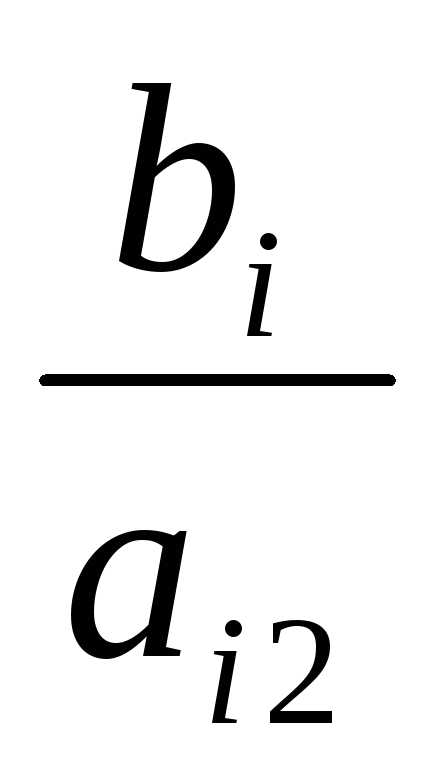 и из них выберем наименьшее: min(4: 1 , 2 : 2
, 10 : 2 ) = 1.
и из них выберем наименьшее: min(4: 1 , 2 : 2
, 10 : 2 ) = 1.
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
x6 | 4 | 1 | 1 | -1 | 0 | 0 | 1 | 4 |
x4 | 2 | -1 | 2 | 0 | 1 | 0 | 0 | 1 |
x5 | 10 | 1 | 2 | 0 | 0 | 1 | 0 | 5 |
F(X1) | 4M | -2+M | 1+M | -M | 0 | 0 | 0 | 0 |
.
Формируем следующую часть симплексной таблицы. Вместо переменной x4в план 1 войдет переменная x2.
Строка, соответствующая переменной x2в плане 1, получена в результате деления всех элементов строки x4плана 0 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2записываем нули.
Таким образом, в новом плане 1 заполнены строка x2и столбец x2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
x6 | 3 | 11/2 | 0 | -1 | -1/2 | 0 | 1 |
x2 | 1 | -1/2 | 1 | 0 | 1/2 | 0 | 0 |
x5 | 8 | 2 | 0 | 0 | -1 | 1 | 0 |
F(X1) | -1+3M | -11/2+11/2M | 0 | -M | -1/2-M | 0 | 0 |
Текущий опорный план неоптимален, так
как в индексной строке находятся
положительные коэффициенты. В качестве
ведущего выберем столбец, соответствующий
переменной x1, так как это наибольший
коэффициент . Вычислим значенияDiпо строкам как частное от деления: и из них выберем наименьшее: min (3: 11/2, – , 8 : 2 ) = 2.
и из них выберем наименьшее: min (3: 11/2, – , 8 : 2 ) = 2.
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (11/2) и находится на пересечении ведущего столбца и ведущей строки.
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | min |
x6 | 3 | 11/2 | 0 | -1 | -1/2 | 0 | 1 | 2 |
x2 | 1 | -1/2 | 1 | 0 | 1/2 | 0 | 0 | – |
x5 | 8 | 2 | 0 | 0 | -1 | 1 | 0 | 4 |
F(X2) | -1+3M | -11/2+11/2M | 0 | -M | -1/2-M | 0 | 0 | 0 |
Формируем следующую часть симплексной таблицы. Вместо переменной x6в план 2 войдет переменная x1.
Получаем новую симплекс-таблицу:
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
x1 | 2 | 1 | 0 | -2/3 | -1/3 | 0 | 2/3 |
x2 | 2 | 0 | 1 | -1/3 | 1/3 | 0 | 1/3 |
x5 | 4 | 0 | 0 | 11/3 | -1/3 | 1 | -11/3 |
F(X2) | 2 | 0 | 0 | -1 | -1 | 0 | 1-M |
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
Базис | B | x1 | x2 | x3 | x4 | x5 | x6 |
x1 | 2 | 1 | 0 | -2/3 | -1/3 | 0 | 2/3 |
x2 | 2 | 0 | 1 | -1/3 | 1/3 | 0 | 1/3 |
x5 | 4 | 0 | 0 | 11/3 | -1/3 | 1 | -11/3 |
F(X3) | 2 | 0 | 0 | -1 | -1 | 0 | 1-M |
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так: x1= 2, x2= 2:.
Ответ:,.
3.Фирма «Три толстяка» занимается доставкой мясных консервов с трёх складов, расположенных в разных точках города в три магазина. Запасы консервов, имеющиеся на складах, а также объёмы заказов магазинов и тарифы на доставку (в условных денежных единицах) представлены в транспортной таблице.
Склады | Магазины | Запасы, тыс. шт. | ||
№1 | №2 | №3 | ||
Склад №1 | 4 | 2 | 5 | 300 |
Склад №2 | 1 | 5 | 3 | 300 |
Склад №3 | 5 | 3 | 6 | 200 |
Заказы, тыс. шт. | 250 | 400 | 150 | |
Найти план перевозок, обеспечивающий наименьшие денежные затраты (первоначальный план перевозок выполнить по методу «северо-западного угла»).
Решение
Проверим необходимое и достаточное условие разрешимости задачи:
 =
300 + 300 + 200 = 800 .
=
300 + 300 + 200 = 800 .
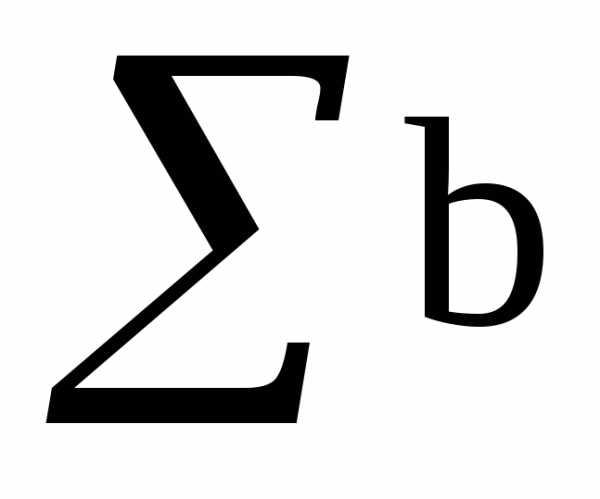 =
250 + 400 + 150 = 800.
=
250 + 400 + 150 = 800.
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.
1 | 2 | 3 | Запасы | |
1 | 4 | 2 | 5 | 300 |
2 | 1 | 5 | 3 | 300 |
3 | 5 | 3 | 6 | 200 |
Потребности | 250 | 400 | 150 |
Используя метод северо-западного угла, построим первый опорный план транспортной задачи.
План начинается заполняться с верхнего левого угла.
Искомый элемент равен 4. Для этого элемента запасы равны 300, потребности 250. Поскольку минимальным является 250, то вычитаем его: .
4 | 2 | 5 | 300 – 250 = 50 |
x | 5 | 3 | 300 |
x | 3 | 6 | 200 |
250 – 250 = 0 | 400 | 150 |
Искомый элемент равен 2. Для этого элемента запасы равны 50, потребности 400. Поскольку минимальным является 50, то вычитаем его: .
4 | 2 | x | 50 – 50 = 0 |
x | 5 | 3 | 300 |
x | 3 | 6 | 200 |
400 – 50 = 350 | 150 |
Искомый элемент равен 5. Для этого элемента запасы равны 300, потребности 350. Поскольку минимальным является 300, то вычитаем его:
4 | 2 | x | |
x | 5 | x | 300 – 300 = 0 |
x | 3 | 6 | 200 |
350 – 300 = 50 | 150 |
Искомый элемент равен 3. Для этого элемента запасы равны 200, потребности 50. Поскольку минимальным является 50, то вычитаем его:
4 | 2 | x | |
x | 5 | x | |
x | 3 | 6 | 200 – 50 = 150 |
50 – 50 = 0 | 150 |
Искомый элемент равен 6. Для этого элемента запасы равны 150, потребности 150. Поскольку минимальным является 150, то вычитаем его:
4 | 2 | x | |
x | 5 | x | |
x | 3 | 6 | 150 – 150 = 0 |
150 – 150 = 0 |
1 | 2 | 3 | Запасы | |
1 | 4[250] | 2[50] | 5 | 300 |
2 | 1 | 5[300] | 3 | 300 |
3 | 5 | 3[50] | 6[150] | 200 |
Потребности | 250 | 400 | 150 |
studfiles.net
3.Лекция . Линейное программирование.
3.1 Общая постановка задачи
Линейное программирование — наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.
Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.
Определение .
Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.
В общем виде математическая модель задачи линейного программирования (ЛП) записывается как
Z(x)=C1X1+C2X2 + . . . +СJXJ + . . . +СnXn _ max(min)
при ограничениях:

где Xi — неизвестные;a ij , bj , Ci — заданные постоянные величины.
Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.
Математическая модель в более краткой записи имеет вид
Z(x) = ∑Ci Xi max(min)
при ограничениях:
Определение Допустимым решением (планом) задачи линейного программирования называется вектор X = (х1, х2, ,…хn , ) , удовлетворяющий системе ограничений.
Множество допустимых решений образует область допустимых решений (ОДР).
Определение Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается Хопт.
Базисное допустимое решение
Является опорным решением, где r— ранг системы ограничений.
Виды математических моделей ЛП
Математическая модель задачи ЛП может быть канонической и неканонической.
Определение . Если все ограничения системы заданы уравнениями и переменные Xj неотрицательные, то такая модель задачи называется канонической.
Если хотя бы одно ограничение является неравенством, то модель задачи ЛП является неканонической. Чтобы перейти от неканонической модели к канонической, необходимо в каждое
неравенство ввести балансовую переменную хn+i .
Если знак неравенства < , то балансовая переменная вводится со знаком плюс, если знак неравенства >, то — минус. В целевую функцию балансовые переменные не вводятся.
Чтобы составить математическую модель задачи ЛП, необходимо:
— ввести обозначения переменных;
— исходя из цели экономических исследований, составить целевую функцию;
— учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений.
3. 2 Двойственность в задачах линейного программирования
Каждая задача линейного программирования, называемая прямой или исходной, тесно связана с другой задачей, ее называют двойственной.
Математические модели этих задач имеют следующий вид.
прямая задача: | двойственная задача: |
Эти задачи экономически могут быть сформулированы следующим образом.
Прямая задача: сколько и какой продукции хi(i-1, 2, … , n) надо произвести, чтобы при заданных стоимостях единицы продукции Сi, объемом имеющихся ресурсов bj (j=1,2,…, m) и нормах расхода ресурсов аij максимизировать выпуск продукции в стоимостном виде.
Двойственная задача: какова должна быть оценка единицы каждого ресурса yj (j=1, 2,…, m), чтобы при заданных bj, ci и аij минимизировать общую оценку затрат на все ресурсы.
Правила построения двойственной задачи по имеемой прямой задаче:
Если прямая задача решается на максимум, то двойственная задача решается на минимум; если прямая задача решается на минимум то двойственная на максимум;
В задаче на максимум ограничения неравенства имеют вид – ≤, а в задаче на минимум – ;
Каждому ограничению прямой задачи соответствует переменная двойственной задачи, в другой модели ограничению двойственной задачи соответствует переменная прямой задачи;
Матрица системы ограничений двойственной задачей получается из матрицы из матрицы систем ограничений прямой задачи транспонированием;
Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи и наоборот;
Если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, в противном случае – как ограничение равенство;
Если какое либо ограничение прямой задачи записано как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.
Пример:
Прямая задача: | Двойственная задача: |
В этой задаче – предельные оценки стоимости единицы каждого ресурса, целевая функция – оценка стоимости всех ресурсов, а каждое ограничение есть условие, что оценка ресурсов, идущих на производство продукции, не менее чем цена единицы продукции.
Взаимосвязь решений прямой и двойственной задач находится из трех теорем двойственности.
3. 3 Теоремы двойственности.
Первая теорема двойственности:
Если одна из двойственных задач имеет оптимальное решение, то и другая задача имеет оптимальное решение, причем экстремальные значения целевых функций совпадают Z(X)=Z'(Y). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание первой теоремы двойственности: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения и оценок ресурсов, при этом полная стоимость продукта, полученного в результате реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадения, значений целевых функций для соответствующих решений пары двойственных задач достаточно для того, чтобы эти решения были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными только тогда, когда полная стоимость произведенной продукции и суммарная оценка ресурсов совпадает.
Оценки выступают как инструмент сбалансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, т.е. равенство общей стоимости продукции и ресурсов обуславливает убыточность всякого другого плана отличающегося от оптимального. Двойственные оценки позволяют сопоставлять и сбалансировать затраты и результаты производства.
Вторая теорема двойственности:
Для того чтобы план Х* и Y* пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:
Эти условия называются условиями дополняющей нежесткости. Из них следует, что если какое-либо неравенство системы ограничений в одной из задач не обращается в строгое равенство оптимальным планом этой задачи, то соответствующий элемент оптимального плана двойственной задачи должен равняться нулю. Если какой-либо элемент оптимального плана одной из задач положителен, то соответствующее ограничение в двойственной задаче её оптимальным планом должно обращаться в строгое равенство, т.е.
если bj, то ;
если 0, то .
Аналогично,
если
если 0 то
Экономически это означает, что если по некоторому оптимальному плану X*= производства расход j-го ресурса меньше его запаса bj, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его j-й элемент больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс, т.е. полностью используемый по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, т.е. не используемый полностью имеет нулевую оценку.
Третья теорема двойственности:
Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи линейного программирования, т.е.
В последнем выражении дифференциалы заменим приращениями. Тогда получим выражение:
,
если , тогда, Экономическое содержание третьей теоремы двойственности: двойственная оценка численно равна изменению целевой функции при изменении соответствующего ресурса на единицу. Двойственные оценкиyjчасто называются скрытыми теневыми или маргинальными оценками ресурсов.
studfiles.net
Методы оптимальных решений Тесты с ответами ИММиФ Тема 4-5
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 4
Если число ресурсов, которые распределяются по работам равно числу работ и один ресурс назначаются только на одну работу, то задача линейного программирования, к которой сводится задача имеет основные ограничения…
+Все ограничения равенства
Все ограничения неравенства вида ≤
Все ограничения неравенства вида ≥
Ограничения могут быть как равенства, так и неравенства
Матрица эффективности задачи о назначениях при максимизации критерия имеет вид:
Какую матрицу нужно взять за исходную при решении задачи Венгерским методом?
+
Задача о назначениях с минимизацией критерия имеет матрицу затрат вида:
D E F
А 6 3 4
В 2 8 5
С 1 7 9
Ее решение будет:
+A-E, B-F, C-D
A-D, B-F, C-E
A-F, B-D, C-E
A-F, B-E, C-D
Суммарные затраты для предыдущей задачи равны…
Выберите один ответ.
7
6
+9
0
Какие компьютерные программы предназначены для помощи ЛПР в решении многокритериальных задач о назначении?
Системы управления базами данных
+Интеллектуальные информационные системы
Коммуникационные системы
Системы программирования
Тема 5
В выборах участвуют 3 кандидата: А, В и С. Предпочтения 30 избирателей распределились следующим образом:
Предпочтения Число голосов Предпочтение Число голосов
А→В→С 6 В→С→А 4
А→С→В 5 С→А→В 4
В→А→С 6 С→В→А 5
Кто победил по методу голосования Кондорсе?
Победил А
Победил В
Победил С
+Однозначно выявить победителя нельзя
Исходные данные о выборах приведены в задании 1. Кто победил по методу голосования Борда?
+Победил А
Победил В
Победил С
Однозначно выявить победителя нельзя
Исходные данные о выборах приведены в задании 1. Кто победил по методу большинства первых мест в одном туре?
+Победил А
Победил В
Победил С
Однозначно выявить победителя нельзя
Как называется принцип голосования «коллективный выбор в системе голосования должен повторять в точности единогласное мнение всех голосующих»?
Аксиома универсальности
+Аксиома единогласия
Аксиома полноты
Аксиома транзитивности
Из двух кандидатов каждый избиратель выбирает лучшего. Побеждает тот, который будет большее число раз выбран лучшим. Какая аксиома Эрроу не может быть проверена в данной системе голосования?
Аксиома универсальности
Аксиома единогласия
Аксиома полноты
Аксиома транзитивности
Несколько конкурентов, выпускающих аналогичный товар, пытаются договориться о объемах выпускаемого товара. Каждый производитель хочет увеличить свой объем выпуска за счет уменьшения выпуска у конкурентов. Какую математическую модель принятия решений целесообразно здесь использовать.
Организацию работы ГПР с помощью посредника
+Теорию игр
Принятие решений в условиях определенности
Метод голосования
Какой этап организации работы ГПР нужно выполнить в первую очередь?
Сбор информации
Разработка шкал оценки по критериям
+Определение списка критериев
Анализ информации
test-for-you.ru
Галкина М. Ю. Методы оптимальных решений (Лекции)
Галкина М. Ю. Методы оптимальных решений (Лекции) – страница №1/8
Галкина М.Ю.
Методы оптимальных решений
(Лекции)
2011 г.
Введение 3
1.1.Различные формы записи задачи линейного программирования. 4
1.2.Графический метод решения задачи линейного программирования 5
1.3.Графический способ метод решения ЗЛП, заданной в симметричной форме, в случае двух переменных 7
1.4.Использование надстройки Поиск решения MS Excel 12
1.5.Решение ЗЛП средствами MS Excel. 15
1.6.Двойственные задачи 16
Вопросы для самопроверки 22
2.1.Задача о назначениях 23
2.2.Теория игр 28
2.2.1.Основные понятия 28
2.2.2.Нижняя и верхняя цены игры. Принцип минимакса 31
2.2.3.Решение игр в смешанных стратегиях 32
2.2.4.Решение матричных игр 2х2 в смешанных стратегиях 33
2.2.5.Сведение матричной игры к задаче линейного программирования 40
2.2.6.Игры с природой 44
Вопросы для самопроверки 49
3.1.Множество Парето 50
3.2.Метод идеальной точки 51
Вопросы для самопроверки 54
4.1.Графическое решение задачи нелинейного программирования 55
4.2.Метод множителей Лагранжа 56
4.3.Решение задач выпуклого программирования 57
Вопросы для самопроверки 60
Введение
Несмотря на многообразие задач организационного управления, при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое исследование. Как правило, это:
1. Постановка задачи.
2. Построение содержательной модели рассматриваемого объекта (процесса). На данном этапе происходит формализация цели управления объектом, выделение возможных управляющих воздействий, влияющих на достижение сформулированной цели, а также описание системы ограничений на управляющие воздействия.
3. Построение математической модели, т. е. перевод сконструированной модели в ту форму, в которой для ее изучения может быть использован математический аппарат.
4. Решение задач, сформулированных на базе построенной математической модели.
5. Проверка полученных результатов на их адекватность природе изучаемой системы, включая исследование влияния так называемых внемодельных факторов, и возможная корректировка первоначальной модели.
6. Реализация полученного решения на практике.
В курсе методы оптимальных решений центральное место отведено вопросам, относящимся к четвертому пункту приведенной выше схемы. Это делается не потому, что он является самым важным, сложным или интересным, а потому, что остальные пункты существенно зависят от конкретной природы изучаемой системы, в силу чего для действий, которые должны производиться в их рамках, не могут быть сформулированы универсальные и содержательные рекомендации.
Для решения экономической задачи математическими методами составляют математическую модель задачи, т.е. записывают ее с помощью математических выражений: неравенств, уравнений и т.п. Для математического описания экономической задачи можно руководствоваться следующей общей схемой:
1) выбирают некоторое количество переменных , заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого экономического процесса;
2) выражают взаимосвязи исследуемого экономического процесса в виде математических соотношений (уравнений, неравенств). Эти соотношения образуют систему ограничений математической модели;
3) поиск наилучшего решения формулируют в терминах поиска оптимального (максимального или минимального) значения функции . Построенная функция называется целевой.
В зависимости от свойств целевой функции, математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач. Если – линейная функция и линейны функции, описывающие ограничения на переменные , то математическая модель представляет задачу линейного программирования. Если хотя бы одна из указанных функций нелинейная, то математическая модель является объектом исследования нелинейного программирования. Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач этого раздела разработан целый ряд эффективных алгоритмов и методов.
Математическое моделирование является, с одной стороны, очень важным и сложным, а с другой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся попытки выделить общие принципы создания математических моделей приводили либо к декларированию рекомендаций самого общего характера, трудноприложимых для решения конкретных проблем, либо, наоборот, к появлению рецептов, применимых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой математического моделирования на конкретных примерах.
Мощным инструментом решения задач, построенных на базе математической модели, является наука, которая называется математическое программирование. В данном случае понятие программирование употребляется в смысле планирование (в отличие от программирования для ЭВМ). В свою очередь, в зависимости от вида решаемых задач, в математическом программировании выделяют такие области, как линейное, нелинейное, дискретное, динамическое, стохастическое программирование.
Курс по методам оптимальных решений должен дать студентам достаточное представление о математическом аппарате, используемом при принятии решений в экономических задачах. Освоение этого материала придает студенту уверенность, которой обычно недостает, если он с самого начала направляет свои усилия на изучение философских аспектов и искусства принятия решений.
-
Линейное программированиеРазличные формы записи задачи линейного программирования.
Рассмотрим задачу линейного программирования (ЗЛП) в общем виде:
Задача линейного программирования задана в канонической форме, если требуется максимизировать целевую функцию, все ограничения системы – уравнения и на все переменные наложено условие неотрицательности.
Задача линейного программирования задана в симметричной форме, если требуется максимизировать целевую функцию, все ограничения системы – неравенства «» (или минимизировать целевую функцию, все ограничения системы – неравенства «») и на все переменные наложено условие неотрицательности.
Набор чисел называется допустимым решением (планом), если он удовлетворяет системе ограничений ЗЛП.
Множество всех допустимых решений называется областью допустимых решений (ОДР).
Допустимое решение , для которого достигается максимальное (минимальное) значение функции, называется оптимальным планом ЗЛП.
Термины «план» и «оптимальный план» возникли из экономических приложений.
Все три формы записи ЗЛП являются эквивалентными в том смысле, что имеются алгоритмы перехода от одной формы к другой. Таким образом, если имеется способ решения задачи в одной из форм, то всегда можно определить оптимальный план задачи, заданной в любой другой форме. Задача в симметричной форме решается графическим методом, а в канонической форме – симплекс–методом.
Рассмотрим алгоритмы перехода от одной формы к другой.
-
Симметричная каноническая. Переход осуществляется путем добавления в левую часть каждого неравенства дополнительной неотрицательной переменной. Если неравенство было «≤», то балансовая переменная добавляется в левую часть неравенства со знаком «+». Если неравенство было «», то балансовая переменная добавляется в левую часть неравенства со знаком «–». Вводимые новые переменные называются балансовыми. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) и используют, что min Z = –max (–Z). -
Каноническая симметричная. Для осуществления такого перехода находится общее решение системы уравнений – ограничений, целевая функция выражается через свободные переменные. Далее, воспользовавшись неотрицательностью базисных переменных, можно исключить их из задачи. Симметричная форма задачи будет содержать неравенства, связывающие только свободные переменные, и целевую функцию, зависящую только от свободных переменных. Значения базисных переменных находятся из общего решения исходной системы уравнений. -
Общая каноническая. Каждая переменная, на которую не было наложено условие неотрицательности, представляется в виде разности двух новых неотрицательных переменных. Неравенства преобразуются в уравнения путем введения в левую часть каждого неравенства балансовой переменной таким же образом, как это было описано при переходе от симметричной к канонической форме. Задачу минимизации функции Z заменяют на задачу максимизации функции (–Z) таким же образом, как это было описано при переходе от симметричной к канонической форме..
Графический метод решения задачи линейного программирования
Графический метод применяется для решения ЗЛП, заданной в симметричной форме. Этот метод наиболее эффективно применяется для решения задач с двумя переменными, т.к. требует графических построений. В случае трех переменных необходимы построения в R3, в случае четырех переменных необходимы построения в R4 и т.д.
Множество точек называется выпуклым, если для любых двух точек множества оно содержит отрезок, их соединяющий.
Пример 1
Следующие множества точек на плоскости являются выпуклыми:
Следующие множества точек на плоскости не являются выпуклыми:
Теорема 1 Пересечение любого количества выпуклых множеств является выпуклым множеством.
Теорема 2 Пусть имеются две произвольные точки и в пространстве Rn. Тогда для любой точки отрезка [PQ] должно выполняться: .где .
Гиперплоскостью в пространстве Rn называется множество точек, удовлетворяющее уравнению . Заметим, что в двумерном случае гиперплоскостью является прямая.
Полупространством называется множество точек, удовлетворяющее одному из неравенств или . Гиперплоскость делит точки пространства на два полупространства. В двумерном случае гиперплоскостью является полуплоскость.
Теорема 3 Полупространство является выпуклым множеством.
Следствие Пересечение любого количества полупространств является выпуклым множеством.
Многогранником называется пересечение одного или более полупространств. Многогранник в двумерном случае называется многоугольником.
Пример 2
Следующие множества являются многоугольниками.
Точка выпуклого множества называется угловой, если она не лежит внутри никакого отрезка, соединяющего две другие точки из множества.
Пример 3
Угловыми точками треугольника являются его вершины (их три). Угловыми точками круга являются точки окружности, которая его ограничивает (их бесконечное число).
Угловая точка многогранника называется его вершиной.
Рассмотрим ЗЛП, заданную в симметричной форме.
Теорема 4 Оптимальный план ЗЛП соответствует вершине многогранника решений, определяемого ее системой ограничений.
- следующая страница >>
umotnas.ru
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Индивидуальные задания к контрольной работе для студентов экономических специальностей очного и заочного обучения
Контрольная работа по курсу «Методы оптимальных решений» состоит из трех задач. Каждая задача должна быть решена по индивидуальному варианту, определяемому последними двумя цифрами номера зачётной книжки студента, полученное решение – выписано и проанализировано. Все вычисления по ходу решения задач должны быть записаны в тетради. Контрольная работа выполняется в тетради «в клетку», должна быть аккуратно оформлена, зарегистрирована на заочном факультете и сдана на кафедру экономической кибернетики для проверки до начала сессии. Проверенную работу студент должен исправить в соответствии со сделанными преподавателем замечаниями и защитить в процессе собеседования по вопросам, связанным с методикой решения задач.
ЗАДАЧА 1
Симплексный метод решения задач линейного программирования
Для изготовления различных видов продукции 1, 2, 3 и 4 предприятие использует три вида сырья А, В и С. Нормы расхода сырья на производство единицы продукции каждого вида, цена одного изделия, а также запас каждого вида ресурса известны и приведены в таблице 1.1.
Составить такой план производства продукции, при котором предприятие получит максимальную прибыль.
Исходные данные задачи выбрать в таблицах 1.1, 1.2 в соответствии с вариантом.
План решения задачи:
- выбрать из таблиц исходные данные своего варианта;
- обозначить неизвестные задачи;
- сформировать систему ограничений и целевую функцию задачи;
- привести систему ограничений к каноническому виду, обозначив и введя дополнительные переменные;
- вычертить симплексную таблицу и заполнить её первоначальным опорным планом;
- пользуясь алгоритмом симплексного метода, найти оптимальное решение задачи;
- выписать оптимальное решение и провести его экономический анализ.
Контрольные вопросы к зачёту по теме
«Симплексный метод решения задачи линейного программирования»
Страницы: 1 2 3 4 5
fpi-kubagro.ru
Метод оптимальных решений задачи с решениями
Дано: ?АВС, АС=12, ВМ-медиана. Найти: АМ Решение: ВМ-медиана ?АВС, следовательно АМ=МС=АС:2=12:2=6. Ответ: АМ=6. Комментарии; Отметить нарушение. 3.3. 3 оценки. 3 оценки. Оцени! Оцени! Спасибо. 11. Этот вопрос архивный. Добавить новый вопрос. Мозг; Помощник.
Методы оптимальных решений
В этом разделе вы найдете он-лайн учебник по методам оптимальных решений, в котором приведены краткие теоретические сведения, а также подробнейшим образом разобраны решения типовых задач.
Почему методы оптимальных решений для чайников? Потому что разобраны основные разделы, которые изучают студенты в курсе МОР: постановка задачи линейного программирования (в данном случае в форме задачи планирования и оптимизации производства), а также методы ее решения: симплексный, графический, программный с помощью Excel разных версий, а также решение методом Гомори.
Внимательно следите за расчетами и чертежами, повторяйте их для учебной задачи, а потом для своей, и вы научитесь решать задачи. Ниже вы найдете полезные ссылки на решенные примеры и контрольные по различным разделам оптимизации и математическому программированию, статьи. Удачи в учебе!
Мини-учебник по МОР
Глава 1. Задачи оптимизации
Глава 2. Производственная задача
Примеры с решением по МОР
Полезные статьи по методам оптимизации
МатБюро работает на рынке решения математических задач уже 11 лет. Все эти годы мы поддерживаем прекрасную репутацию и наилучшие условия «цена-качество».
Грамотное и подробное решение за разумную стоимость.
Метод оптимальных решений задачи с решениями
Методы оптимальных решений
Для изготовления различных видов продукции 1, 2, 3 и 4 предприятие использует три вида сырья А, В и С. Нормы расхода сырья на производство единицы продукции каждого вида, цена одного изделия, а также запас каждого вида ресурса известны и приведены в таблице 1.1.
Составить такой план производства продукции, при котором предприятие получит максимальную прибыль.
Исходные данные задачи выбрать в таблицах 1.1, 1.2 в соответствии с вариантом.
Таблица 1.1 – Нормативы затрат ресурсов на единицу продукции каждого вида (общие для всех вариантов)
Решение открытой транспортной задачи методом потенциалов
На оптовых складах А1, А2, А3, А4 имеются запасы некоторого продукта в известных количествах, который необходимо доставить в магазины В1, В2, В3, В4, В5. Известны также тарифы на перевозку единицы продукта из каждого склада в каждый магазин.
Найти такой вариант прикрепления магазинов к складам, при котором сумма затрат на перевозку была бы минимальной.
Исходные данные задачи выбрать в таблицах 2.1, 2.2 в соответствии с вариантом.
Таблица 2.1 – Матрица тарифов (общая для всех вариантов)
План решения задачи: Выбрать из таблиц исходные данные своего варианта. Проверить, является решаемая задача закрытой или открытой. Если задача открытая – выполнить действия, дающие возможность приступить к её решению. Вычертить матрицу транспортной задачи и записать в неё опорный план, пользуясь одним из известных вам способов построения опорного плана (способ северо-западного угла, наилучшего тарифа, двойного предпочтения). Проверить построенный опорный план на вырождение. Если надо, принять меры для преодоления вырождения опорного плана. Рассчитать значение целевой функции для опорного плана. По правилам метода потенциалов рассчитать потенциалы строк и столбцов. Используя найденные потенциалы, проверить построенный опорный план на оптимальность. Если решение оптимальное перейти к пункту 13. Если решение неоптимальное, его нужно улучшить. Для этого надо найти клетку матрицы транспортной задачи, подлежащую улучшению, построить для неё замкнутый цикл, определить объём ресурсов для перемещения по вершинам этого цикла. Выполнить перемещение ресурсов по вершинам цикла, не нарушая баланса по строкам и столбцам матрицы. Перейти к пункту 6. Выписать оптимальное решение и провести его экономический анализ.
ЗАДАЧА 3 . Оптимальное распределение ресурсов.
Совет директоров фирмы рассматривает предложение по наращиванию производственных мощностей для увеличения выпуска однородной продукции на четырех предприятиях, принадлежащих фирме.
Для модернизации предприятий совет директоров инвестирует средства в объеме 250 млн. р. с дискретностью 50 млн. р. Прирост выпуска продукции зависит от выделенной суммы, его значения предоставлены предприятиями и содержатся в таблице.
Найти предложение инвестиций между предприятиями, обеспечивающее фирме максимальный прирост выпуска продукции, причем на одно предприятие можно осуществить только одну инвестицию.
Исходные данные задачи выбрать в таблицах 3.1, 3.2 в соответствии с вариантом.
Таблица 3.1 – Значения параметров задачи
План решения задачи: Выбрать из таблиц исходные данные своего варианта. Разбить решение задачи на этапы по количеству предприятий, на которые предполагается осуществить инвестиции. Составить рекуррентные соотношения Провести первый этап расчета, когда инвестиции выделяются только первому предприятию Провести второй этап расчета, когда инвестиции выделяют первому и второму предприятиям Провести третий этап расчета, когда инвестиции выделяют 1-3-му предприятиям Провести четвертый этап расчета, когда инвестиции распределяются между четырьмя предприятиями Выписать оптимальное решение и провести его экономический анализ.
Правила ввода данных
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Метод оптимальных решений задачи с решениями
Методы оптимальных решений
В этом разделе вы найдете он-лайн учебник по методам оптимальных решений, в котором приведены краткие теоретические сведения, а также подробнейшим образом разобраны решения типовых задач.
Почему методы оптимальных решений для чайников? Потому что разобраны основные разделы, которые изучают студенты в курсе МОР: постановка задачи линейного программирования (в данном случае в форме задачи планирования и оптимизации производства), а также методы ее решения: симплексный, графический, программный с помощью Excel разных версий, а также решение методом Гомори.
Внимательно следите за расчетами и чертежами, повторяйте их для учебной задачи, а потом для своей, и вы научитесь решать задачи. Ниже вы найдете полезные ссылки на решенные примеры и контрольные по различным разделам оптимизации и математическому программированию, статьи. Удачи в учебе!
Мини-учебник по МОР
Глава 1. Задачи оптимизации
Глава 2. Производственная задача
Примеры с решением по МОР
Полезные статьи по методам оптимизации
МатБюро работает на рынке решения математических задач уже 11 лет. Все эти годы мы поддерживаем прекрасную репутацию и наилучшие условия «цена-качество».
Грамотное и подробное решение за разумную стоимость.

poiskvstavropole.ru
