2.3. Прямая и обратная (основная) задачи механики
Второй закон Ньютона (2.2), или, что то же самое, векторное уравнение движения, представляет собой три дифференциальных уравнения второго порядка по времени. Например, проектируя обе части (2.2) на оси декартовой системы координат, получим

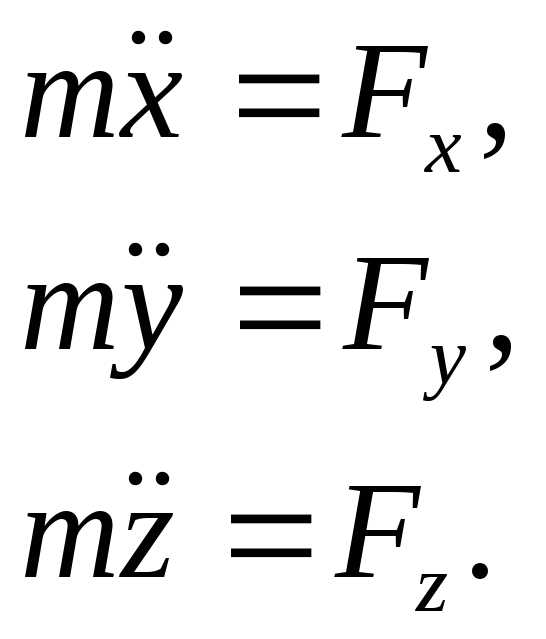 (9.2)
(9.2)
Различают
две задачи динамики: 1) по заданному
закону движения точки, т. е. по известному
как функция  векторному
соотношению
векторному
соотношению  находят
силу
находят
силу  ,
действующую на точку; это прямая задача
динамики
,
действующую на точку; это прямая задача
динамики
2)
по заданной силе 
 ;
это обратная (основная) задача динамики.
Поговорим об основной задаче динамики
более подробно. Для ее решения недостаточно
знать только силу. Следует задать также
механическое состояние в некоторый
момент времени
;
это обратная (основная) задача динамики.
Поговорим об основной задаче динамики
более подробно. Для ее решения недостаточно
знать только силу. Следует задать также
механическое состояние в некоторый
момент времени 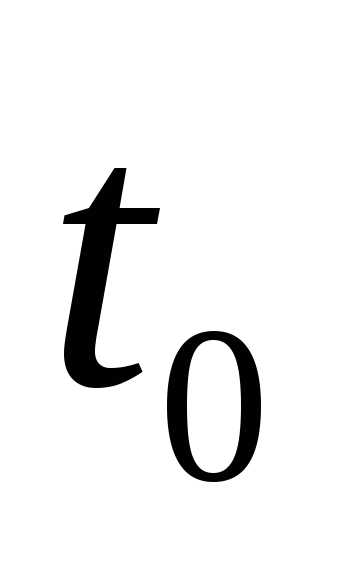 , т. е. начальные
условия . Механическое
состояние точки в момент
, т. е. начальные
условия . Механическое
состояние точки в момент  ,
т. е. однозначно
определяется ее начальным механическим
состоянием и условиями ее движения
(уравнениями движения). Это следует из
однозначности и единственности решения
дифференциальных уравнений (2.2),
удовлетворяющих данным начальным
условиям. Сформулированное предложение
о предсказуемости эволюции механической
системы во времени при заданных начальном
состоянии и условиях движения называется
принципом механической причинности,
или принципом механического детерминизма.
Его суть наиболее точно и полно выразил
Лаплас: «Разумное существо, которое в
каждый момент знало бы все движущие
силы природы и имело бы полную картину
состояния, в котором природа находится,
могло бы (если бы только его ум был в
состоянии проанализировать эти данные)
выразить одним уравнением как движение
мельчайших атомов, так и движение самых
больших тел мира. Ничто не осталось бы
для него неизвестным, и оно могло бы
обозреть одним взглядом как будущее,
так и прошлое», т. е. по начальным
состояниям и взаимодействиям состояние
системы в любой момент времени в будущем
определялось бы однозначно. Со времен
Лапласа появились новые важные идеи.
Вот одна из них.
,
т. е. однозначно
определяется ее начальным механическим
состоянием и условиями ее движения
(уравнениями движения). Это следует из
однозначности и единственности решения
дифференциальных уравнений (2.2),
удовлетворяющих данным начальным
условиям. Сформулированное предложение
о предсказуемости эволюции механической
системы во времени при заданных начальном
состоянии и условиях движения называется
принципом механической причинности,
или принципом механического детерминизма.
Его суть наиболее точно и полно выразил
Лаплас: «Разумное существо, которое в
каждый момент знало бы все движущие
силы природы и имело бы полную картину
состояния, в котором природа находится,
могло бы (если бы только его ум был в
состоянии проанализировать эти данные)
выразить одним уравнением как движение
мельчайших атомов, так и движение самых
больших тел мира. Ничто не осталось бы
для него неизвестным, и оно могло бы
обозреть одним взглядом как будущее,
так и прошлое», т. е. по начальным
состояниям и взаимодействиям состояние
системы в любой момент времени в будущем
определялось бы однозначно. Со времен
Лапласа появились новые важные идеи.
Вот одна из них.Хотя уравнения, описывающие эволюцию механической системы во времени, вполне детерминированы, ее развитие во времени может различаться своими маршрутами. Это связано с чувствительностью некоторых систем к начальным условиям, а точнее, к даже малому изменению начального состояния. В классической динамике в качестве примера можно привести шарик, падающий на острие лезвия бритвы, траектория которого после соприкосновения существенно зависит от положения шарика относительно острия в момент времени
 перед тем, как он касается лезвия.
перед тем, как он касается лезвия.Решение уравнения (2.2), которое удовлетворяет какому-либо конкретному начальному условию, называют частным решением. Более важно найти решение, удовлетворяющее произвольным условиям, это так называемое общее решение.
2.4. Интегралы движения
В
теории дифференциальных уравнений есть
понятие первых интегралов. Первыми
интегралами уравнений движения (9.2)
будем называть такие функции координат,
скоростей и времени, которые обращаются
в постоянные 
. (10.2)
Это означает, что система (9.2) может быть сведена к эквивалентной
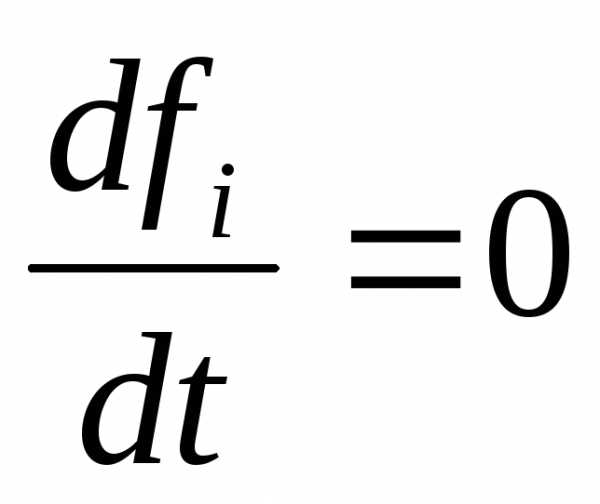 .
(11.2)
.
(11.2)
Условие функциональной независимости трех первых интегралов (рассматриваемых как функции скоростей) записывается виде неравенства нулю (функционального) определителя Якоби
 (12.2)
(12.2)
Если
(12.2) выполнено, то три первых интеграла
движения будут независимыми в смысле
разрешимости системы конечных уравнений
(10.2) относительно 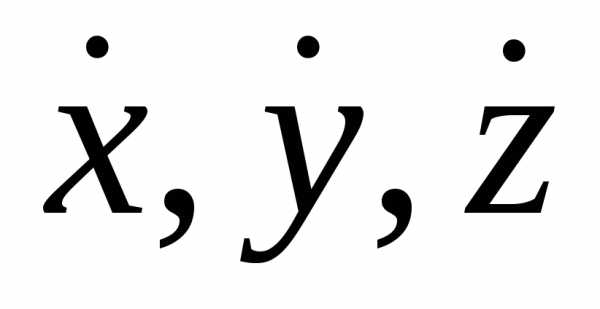
, (13.2)
т.
е. мы нашли  такие, что
такие, что
. (14.2)
 называют
вторыми интегралами движения. Они
являются независимыми, если уравнения
(14.2) разрешимы относительно координат
называют
вторыми интегралами движения. Они
являются независимыми, если уравнения
(14.2) разрешимы относительно координат
 . (15.2)
. (15.2)
Решение системы (14.2) представляется в виде
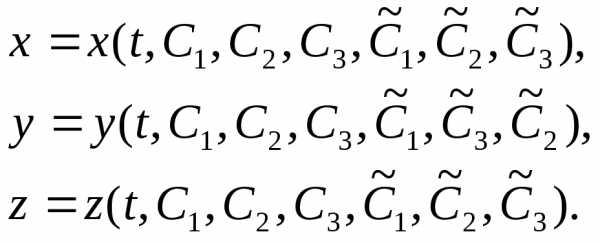 (16.2)
(16.2)
Найденные
таким образом функции (16.2), являющиеся
решением системы уравнений (9.2) и
содержащие шесть произвольных постоянных
интегрирования, называют общим решением,
так как, придавая определенные значения
постоянным  можно получить
функции (10.2) при любых начальных условиях.
Выражение постоянных
можно получить
функции (10.2) при любых начальных условиях.
Выражение постоянных 
1.
Из системы (10.2) при 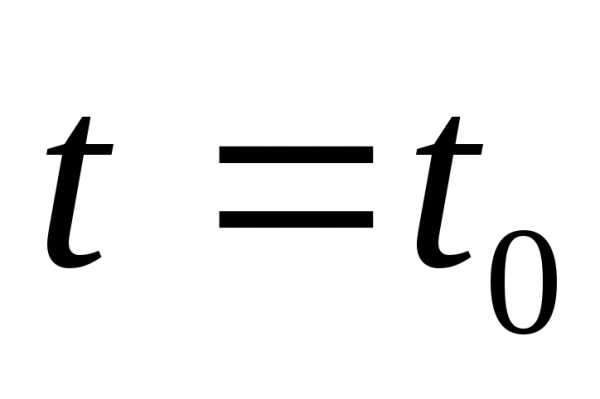 имеем
имеем
 (17.2)
(17.2)
2.
Подставляя в систему (14.2), взятую при  ,
,  из (17.2),
находим
из (17.2),
находим
(18.2)
Найти общее решение уравнений движения – это значит полностью решить обратную задачу динамики.
Пример. Найти общее решение векторного уравнения
движения (1.2), если сила зависит только
от времени  .
.
Интегрируя (1.2) один раз, получаем три первых независимых интеграла движения
 ,
,
где
постоянный вектор  – это начальная скорость
– это начальная скорость 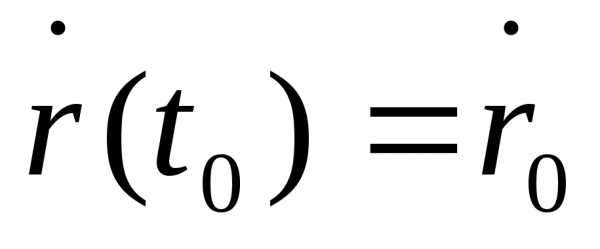 . Интегрируя
последнее уравнение, получаем три
независимых вторых интеграла движения
. Интегрируя
последнее уравнение, получаем три
независимых вторых интеграла движения 
.
Здесь 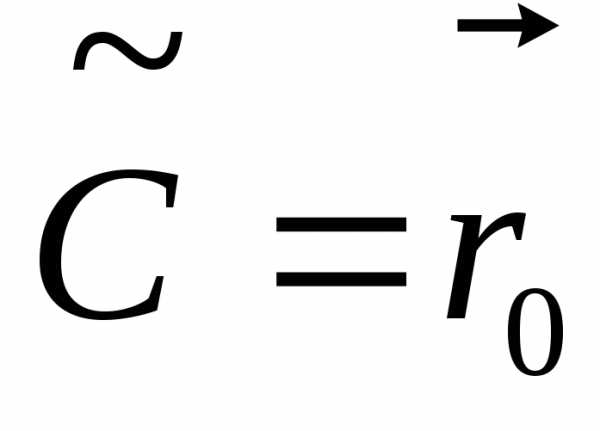 .
Общее решение имеет вид
.
Общее решение имеет вид
.
Пример. Пусть проекции силы в уравнениях (9.2) зависят только от соответствующих координат. Найти все первые интегралы движения в этом случае и общее решение (в квадратурах).
Введем обозначения . Тогда (9.2) можно переписать в виде . Последние уравнения, очевидно, имеют три первых интеграла
.
Откуда находим
.
Знак перед корнем нужно выбирать в соответствии с начальным состоянием. Разделяя переменные и интегрируя, найдем
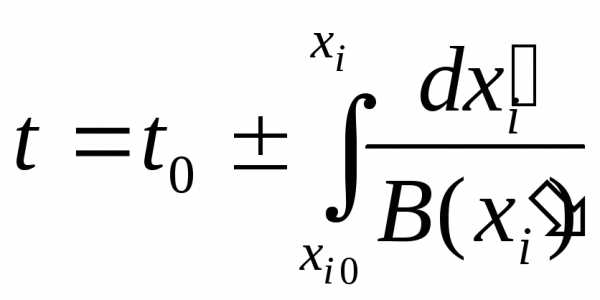 .
.
studfiles.net
Основная задача механики – характеристика
Основная задача механики. Основной задачей механики является описание механического движения тел, то есть установление закона (уравнения) движения тела на основе характеристик, описывают (координаты, перемещение, длина пройденного пути, угол поворота, скорость, ускорение и т.п.).
Иными словами, если с помощью составленного закона (уравнения) движения можно определить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от выбранных физических величин и методов решения основной задачи механики ее разделяют на кинематику, динамику и статику.
Кинематика – раздел механики, в котором изучается механическое движение без рассмотрения его причин. Кинематика дает ответ на вопрос, где будет тело в пространстве с течением времени, если известны его первоначальные характеристики.
Динамика – раздел механики, в котором изучают закономерности механического движения тел под действием приложенных к ним сил. Динамика дает ответ на вопрос, почему именно так движется тело.
Статика – раздел механики, изучающий условия равновесия материальных тел под действием приложенных к ним сил.
Следует также заметить, что законы классической механики не всегда могут быть применимы. Например, движение одной молекулы можно описать законами механического движения, а движение их совокупности в теле описывается уже другими – статистическими законами. Движение тела со скоростью, близкой к скорости света (скорость света обозначают буквой с. С = 300 000 км / с), описывается релятивистскими законами. Движение и взаимодействие элементарных частиц микромира описывают в квантовой механике.
Говоря «механика», мы будем понимать именно классическую механику, которая базируется на законах механического движения, сформулированных Ньютоном, которая стала толчком к созданию современной квантовой физики.
Изучение механики мы начинаем с ее первого раздела – кинематики.
worldofscience.ru
Прикладная механика и ее задачи
Прикладная механика: сущность понятия
Определение 1
Прикладной механикой называют такой раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений.
Данный термин очень близок к таким понятиям как «строительная» либо «техническая» механика. Он объединяет в себе дисциплины строительного направления, с которыми встречаются студенты при обучении, в «строительной механике», «сопротивлении материалов», «теоретической механике», принимая в расчет железобетонные, металлические, и многие другие виды конструкций.
Также прикладная механика является одной из главных учебных дисциплин всех инженерно-технических вузов. Очень широко она применяется именно в инженерной практике при проектировании различных инженерных конструкций, машин и приборов. При этом составной частью прикладной механики является сопротивление материалов, то есть раздел механики деформируемого твердого тела, и в котором рассматривают довольно упрощенные расчетные модели, а также изучают только общие методы расчета. Данные методы дают возможность применять самые ясные и простые подходы при оценивании прочностных возможностей разных конструктивных элементов только при внешних воздействиях.
В первую очередь, “прикладной механикой” называют дисциплину, которая представляет основу для общетехнической подготовки инженеров, но не машиностроительных направлений.
Существует отдел прикладной механики, который является разделом технической механики, рассматривающий основы конструирования и расчета узлов и деталей общего назначения, встречающихся в разных машинах, установках и механизмах.
В зависимости от физических свойств изучаемы объектов и их размеров механику делят на:
- Неклассическую или неньютоновую: это часть физики, исследующая объекты макромира и микромира, учитывая пространственно-временную зависимость.
- Классическую: она рассматривает объекты с обозримой протяженностью и при их изучении свойства времени и пространства считает постоянными.
При этом в зависимости от всех особенностей моделей реальных объектов классическую механику можно разделить на: теоретическую механику, то есть с моделью совершенно твердого тела; механику сплошной среды с моделью деформируемого тела.
Замечание 1
Главным методом при исследовании в механике можно назвать гипотетико-дедуктивный. Суть его заключена в выдвижении гипотезы, которая должна быть подтверждена или опровергнута опытом.
Цели и задачи прикладной механики
При освоении дисциплины «Прикладная механика» можно выделить следующие цели:
- Сформировать навыки проектно-конструкторской, организационно-управленческой и производственно-технологической деятельности.
- Освоить основы теории машин и механизмов, теорию расчета и конструирования, работы узлов и деталей общего назначения, которые широко применяются именно в пищевых оборудованиях и машинах.
- Приобретение новых знаний, формирование умений и навыков, изучая специальные дисциплины.
- Изучить общие принципы конструирования и проектирования, построение алгоритмов и моделей расчета типовых изделий машиностроения, учитывая главные критерии работоспособности, необходимые при оценке надежности действующего оборудования отрасли при эксплуатации.
- Изучить динамические, кинематические, силовые и структурные свойства основных видов механизмов, умение исследовать и проектировать данные схемы.
- Научить основам проектирования механизмов и машин, рациональному выбору необходимого типа привода машины и составляющих его узлов, довольно грамотному подходу при эксплуатации любых механизмов.
- Приобрести навыки конструирования и проектирования, обеспечивающих выбор форм, материалов, способов и размеров создания типовых изделий машиностроения.
- Изучить общие принципы всех расчетов для типовых изделий машиностроения.
Место прикладной механики в структуре профессиональной подготовки специалиста
Прикладную механику относят к циклу ОПД – С3. Также прикладная механика является основой общепрофессиональной подготовки (ОПД) инженеров. Именно как комплексная дисциплина «Прикладная механика» включает в себя положение курсов «Детали машин», «Теории машин и машинных механизмов». Весь курс «Прикладной механики» является завершающей и общепрофессиональной подготовкой студента. Существуют теоретические дисциплины, необходимые для изучения прикладной механики: сопротивление механизмов; инженерная графика и начертательная геометрия; прикладная математика и математика; физика; материаловедение; теоретическая механика.
Для того, чтоб изучать Прикладную механику необходимо знание вопросов предыдущих дисциплин: общей физики (то есть основы классической механики), еоретической механики, компьютерной и инженерной графики.
При этом теоретическая механика предшествует таким дисциплинам именно профессионального цикла: автоматизация технологических производств и процессов; производственное оборудование и его эксплуатация, робототехнические комплексы и системы высшей математики (то есть элементы аналитической геометрии, векторной алгебры, интегрального и дифференциального исчисления).
Можно выделить общие требования именно к содержанию и уровню освоения данной дисциплины (то есть умения и знания, владения и компетенции студентов, сформированные в итоге освоения дисциплины). В итоге приобретаемый, при освоении теоретической механики, весь комплекс навыков, умений и знаний необходим для научной базы при формировании компетенций, которые предусмотрены образовательной программой. То есть: овладеть полной системой научных знаний об окружающем мире; способность приобретать самостоятельно новые знания с применением современных информационных и образовательных технологий; способность применять базовые знания в области естественных, экономических, гуманитарных и математических наук в профессиональной деятельности.
spravochnick.ru
Что такое механика? Предмет, задачи, разделы :: SYL.ru
Окружающих мир состоит из материальных объектов, которые взаимодействуют между собой различными способами. Задачей естественных наук, в частности физики, является установление характера этих взаимодействий. Один из прикладных разделов физики называется механика. В статье речь пойдет о том, что такое механика, каков предмет и задачи данной науки, какие существуют отрасли механики.
Механика – это…
Слово “механика” переводится с греческого как “искусство построения машин”. Механика – это наука о движении объектов материального мира и их взаимодействии. Иными словами, любое материальное тело занимает какое-либо место в пространстве. Его перемещение называется механическим движением. Это движение, а также то, как тела при нем взаимодействуют друг с другом, и изучает механика.
Спектр исследований этой науки очень широк. Он включает изучение движения небесных тел, перемещения летательных аппаратов, машин, динамики жидкостей и газов.

Предмет и задачи
Понять, что такое механика, поможет изучение ее предмета и задач.
Главной задачей является описание механического перемещения объектов – выведение уравнения движения. Это делается с помощью системы координат, угла поворота, скорости и других категорий. Иначе говоря, выведенный закон движения позволяет высчитать положение тела в момент времени.
Предмет механики – это решение задач и вопросов, связанных с исследованием движения или равновесия тел и их взаимодействий при этом.
Разделы механики
Поскольку исследования механики касаются многих сфер науки, в ней выделяют несколько разделов:
- классическая (механика Ньютона) – изучает движения материальных дел;
- релятивистская (механика Эйнштейна) – базируется на постулатах теории относительности;
- квантовая – исследует движение элементарных частиц.
Классическая механика
Механика Ньютона включает следующие направления: кинематику, динамику и статику.

Кинематика исследует механическое движение тел без учета причин, его вызывающих. Иначе говоря, этот раздел исследует положение тела в пространстве по истечении определенного времени. В основном, законы и исследования кинематики применяются в расчетах движений механизмов и машин.
В области исследования динамической механики находится перемещение материальных объектов в результате воздействия, примененного к ним. Иными словами, эта наука объясняет, почему тело, к которому приложили силу, оказалось в той или иной точке пространства.
Статическая механика изучает равновесие тел под воздействием, приложенным к ним. Она делится на равновесную и неравновесную.
Разделы классической механики изучаются обычно в средней школе. Кроме них, существует еще несколько направлений этой науки:
- механика сплошных сред;
- статистическая;
- теоретическая;
- вычислительная и др.
Механика релятивистская
Что такое механика Эйнштейна? Если тела движутся с очень высокой скоростью, например, близкой к скорости света, то физические законы для них становятся иными. Время и пространство изменяют свои свойства по отношению к таким телам. Вопросы этих искажений и изучает релятивистская механика.
Слово “релятивистский” означает “относительный”. Поэтому постулаты эйнштейновский теории относительности играют здесь важную роль.
В классической механике существует три измерения: длина, ширина и высота. Релятивистская добавляет еще одно измерение – время. Таким образом, пространство считается четырехмерным, и перемещение тел и их характеристики будут зависеть не только от направления движения, но и от скорости.
Эйнштейн считал, что для движущихся наблюдателей время течет медленнее, чем для находящихся в состоянии покоя. Чем выше скорость – тем медленнее время. При достижении скорости света время совсем остановилось бы.
Квантовая механика
Эта наука является составляющей квантовой физики. Обе они исследуют законы мира элементарных частиц – нуклонов, электронов, кварков и т. д.
Классическая механика, описывающая явления макромира, не способна объяснить движения, происходящие на уровне элементарных частиц. Эти задачи взяла на себя квантовая механика. Эта наука является достаточно молодой, и в ее области еще много неисследованного.
Слово “квант” означает любую неделимую единицу чего-либо.
Примеры квантов:
- фотон – частица электромагнитного излучения;
- глюон – частица векторного поля;
- гравитон – квант гравитационного взаимодействия;
- фонон – квант колебаний кристаллов.

Итак, что такое механика? Данный раздел физики изучает материальные тела, их перемещения в пространстве, законы перемещений и взаимодействие движущихся тел между собой. Самые обширные ее разделы это классическая, релятивистская и квантовая.
www.syl.ru
Основная задача – механика – Большая Энциклопедия Нефти и Газа, статья, страница 1
Основная задача – механика
Cтраница 1
Основная задача механики состоит в определении положения тела в каждый момент времени. [1]
Основная задача механики состоит в определении положения тела в зависимости от времени. [2]
Основная задача механики о силах сохраняет свое значение и в динамике систем точек переменной массы и становится еще более сложной: в уравнения движения включаются реактивные силы. [3]
Основная задача механики и заключается в динамическом описании движения материальной точки, устанавливающем связь между силовым полем, в котором движется материальная точка, и кинематическим уравнением ее движения. [4]
Основная задача механики деформируемого твердого тела – описание процессов деформирования с учетом экспериментальных данных, определяющие соотношения которых могли бы быть использованы при решении конкретных технических задач. Поэтому развитие теории механики деформируемого твердого тела идет по пути постепенного усложнения и уточнения определяющих соотношений по мере накопления экспериментальных данных, В качестве основной исходной характеристики обычно принимают деформацию. [5]
Основной задачей механики является нахождение движения по заданным силам. Найти движение – это значит суметь указать, в каком месте пространства и в какой момент времени находится любая из материальных точек. Если же нас интересует сложная механическая система, то такие сведения нужны по отношению к каждой из материальных точек, на которые эта система мысленно разделена. [6]
Основной задачей механики является изучение движения тел в той или иной системе отсчета и причин, определяющих характер, этих движений. [7]
Основной задачей механики является изучение движения тел в той или иной системе отсчета и причин, определяющих характер этих движений. [8]
Основной задачей механики является нахождение движения по заданным силам. Найти движение – – это значит суметь указать, в каком месте пространства и в какой момент времени находится любая из материальных точек. Если же нас интересует сложная механическая система, то такие сведения нужны по отношению к каждой из материальных точек, на которые эта система мысленно разделена. [9]
Основной задачей механики является изучение движений тел в той или иной системе отсчета и причин, определяющих характер этих движений. Необходимо выяснить, при каких условиях тело движется по прямолинейной или криволинейной траектории, равномерно или неравномерно, ускоренно или замедленно. [10]
Одной из основных задач механики композитов является задача проектирования материалов с заранее заданными жесткост-ными и прочностными характеристиками. Если армированный ( композиционный) материал моделируется однородной анизотропной линейно упругой средой, то задача проектирования материала с заранее заданными жесткостными свойствами приводится к задаче теоретического определения модулей упругости ( податливости) композиционного материала ( так называемых эффективных модулей) по известным модулям упругости ( податливости) компонентов. [11]
Одна из основных задач механики разрушения состоит в следующем. Пусть в элементе конструкции имеется трещина и известны внешние нагрузки на этот элемент. [12]
Одной из основных задач механики композиционных материалов является расчет их упругих, реологических и прочностных характеристик по известным свойствам компонентов. При этом оказываются существенными не только механические свойства составляющих компонентов, но и топология их распределения, условия сопряжения на границе раздела фаз и взаимодействия между элементами неоднородностей. При использовании композиционных материалов в технике в одних случаях могут оказаться существенными прочностные, а в других – упругие свойства. Типичным примером выхода из строя конструкции намного раньше разрушения материала может быть потеря устойчивости листа стеклопластика, используемого в качестве несущей конструкции. Ниже основное внимание уделяется вычислению постоянных упругости и реологических характеристик структурно-неоднородных полимеров. [13]
Таким образом, основная задача механики хрупкого разрушения сводится к анализу напряжений в соответствующем теле с трещинами. [14]
В рассмотрении первой половины основной задачи механики мы не будем повторять исторического пути, который шел через последовательные обобщения постепенно накоплявшихся опытных фактов ( заметим только, что основные заслуги в установлении физических основ механики принадлежат Галилею и Ньютону, а в разработке ее математической формы – Лагранжу и Гамильтону), а сразу сформулируем чрезвычайно общий принцип, который называется принципом наименьшего действия и позволяет очень изящным и компактным образом выяснять, какие именно ограничения на вид уравнений движения налагают определенные физические требования. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Механика задачи – Энциклопедия по машиностроению XXL
Исключение из механики задач о движении электрически заряженных частиц приводит к тому, что из механики выпадают все вопросы о движениях со скоростями, не малыми по сравнению со скоростью света между тем именно с такими движениями приходится сталкиваться при рассмотрении многих вопросов в других разделах физики. Вместе с тем исключение из механики задач о движении со скоростями, сравнимыми со скоростью света, лишает конкретного содержания механику теории относительности. Вследствие этого приходится либо излагать механику как раздел физики, вовсе игнорируя теорию относительности (т. е. на уровне начала нашего века), либо излагать механику теории относительности совершенно формально, не опираясь на результаты экспериментов. Включив же в механику движения электрически заряженных частиц, мы устраняем не только ничем не оправданное ограничение рамок механики, но и указанные методические трудности, которые порождаются этим совершенно искусственным ограничением. [c.8]Рассмотрение в механике задач о быстрых движениях электрически заряженных частиц позволяет установить экспериментальный факт — зависимость массы от скорости и изложить механику быстрых движений, учитывая эту зависимость, но не пользуясь преобразованиями Лорентца — Эйнштейна. [c.8]
Конечно, изложение вопросов о движении электрически заряженных частиц, а тем более механики теории относительности связано с преодолением известных методических трудностей. Однако это — трудности естественные, обусловленные существом дела, и если не в разделе механики, то в разделе, посвященном электромагнитным явлениям, или в оптике эти трудности все равно преодолевать придется. Но эти трудности вполне преодолимы и в механике, поскольку элементарный курс физики дает знания, необходимые для того, чтобы ввести представление о силе Лорентца. Словом, включение в раздел механики задач о движении электрически заряженных частиц (в том числе и движущихся с большими скоростями) не создает никаких искусственных методических трудностей, а именно исключе- [c.8]
Как известно, многие законы механики, в частности механики сплошной среды, наряду с описанием их ди( еренциальными уравнениями сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать экстремума. В такой формулировке эти законы называются вариационными принципами механики. Задачи, в которых требуется исследовать функционал на экстремум, называются вариационными задачами. [c.96]
Книга представляет собой углубленный курс классической механики, написанный на современном уровне. Помимо краткого обзора элементарных принципов, в ней изложены вариационные принципы механики, задача двух тел, движение твердого тела, специальная теория относительности, уравнения Гамильтона, канонические преобразования, метод Гамильтона — Якоби, малые колебания и методы Лагранжа и Гамильтона для непрерывных систем и полей. Показывается связь между классическим развитием механики и его квантовым продолжением. Книга содержит большое число тщательно подобранных примеров и задач. [c.2]
Все остальное для конструктора — производные от этих наук. Возьмем, к примеру, в сопротивлении материалов задачу определения линии прогиба балок, а в строительной механике — задачи о фермах. А ведь в работе И, Подольского Универсальная формула упругой линии балки (ОНТИ, 1936) одной формулой [c.19]
Теория такого рода имеет и другие приложения. Во-первых, она включает в область теоретической механики задачи, которые неразрешимы методами статики или динамики твердого тела. Простейший пример такой задачи дан на рис. 1. Два жестких бруса А, В, соединенных тремя параллельными стержнями а, Ь, с, подвержены действию сил Р так, как показано на рисунке. Одни только теоремы статики не дают нам возможности сказать, как нагрузка распределится между стержнями. Ясно, что ответ зависит от относительной жесткости стержней. Основным требованием является равенство удлинений всех трех стержней. [c.8]
Помимо феноменологического подхода, были сделаны попытки микро-структурного описания механизма ползучести с помощью некоторого обобщения статической теории дислокаций. Однако пока нет оснований останавливаться на этих исследованиях, так как, по словам Ю. Н. Работнова, физические представления на современном уровне развития науки приносят механике скорее косвенную, чем прямую пользу . Эта точка зрения, разделяемая многими авторами, относится как к теории ползучести, так и к другим разделам механики твердого тела, поскольку пока редко удается получить решение стоящих перед механикой задач иначе, чем феноменологическим путем. [c.274]
В самостоятельный раздел теоретической механики кинематика выделилась сравнительно недавно (в первой половине XIX в.) в связи с развитием техники и машиностроения. Конструирование новых сложных машин и механизмов ставило перед механикой задачу исследования геометрических свойств движения твердого тела и тем самым способствовало развитию кинематики. Весьма [c.226]
В дальнейшем изложении, говоря об инерциальной, или условно неподвижной , системе отсчета, мы почти везде будем иметь в виду систему, связанную с Землей. В главе 24 мы рассмотрим с точки зрения классической механики задачу об относительном движении материальной точки, т. е. рассмотрим движение материальной точки относительно системы отсчета, которая сама движется по отношению к инерциальной системе. [c.384]
Диаграмма рассеяния может быть определена и с помощью другого варианта обобщенного метода собственных колебаний — 5-метода ( 13) это будет сделано в 20. Однородная задача 5-метода совпадает по существу с известной в квантовой механике задачей определения матрицы рассеяния. Для сферически-сим-метричного потенциала эта последняя задача может быть решена численно либо прямым интегрированием дифференциального уравнения, либо с помощью интегрального уравнения 5-метода. В 20 будет проведено сравнение численных результатов, полученных двумя методами, с целью иллюстрации точности приближенных формул. [c.67]
Как и другие задачи механики, задача об ударе абсолютно твердых тел приближенно описывает реальный физический процесс и имеет практическое значение при определенных условиях. Эти условия, состоящие в возможности пренебречь деформациями тел во время удара, выполняются во многих случаях инженерной практики (например, кузнечные молоты). [c.20]
В заключение рассмотрим задачу Чаплыгина из неголономной механики — задачу о качении без скольжения уравновешенного, но динамически несимметричного шара по горизонтальной плоскости. Динамика шара описывается в К = системой [c.42]
Механика тел переменной массы — новая широкая область исследований в современной теоретической механике. Главной задачей этого направления развития механики является изучение движения и равновесия тел, масса которых изменяется во время движения. Зарождение идей об изучении движения тел переменной массы относится к концу XIX столетия, когда развитие ракетной техники, наблюдательной астрономии и электродинамики привело к рассмотрению нового класса задач механики, задач, в которых масса движущегося тела является или функцией времени (ракетная техника, небесная механика), или функцией скорости (специальная теория относительности). Имея в виду необычайно быстрое развитие в XX в. новых отраслей промышленности ракетостроения и ядерной энергетики, для которых теория реактивного движения и теория относительности имеют фундаментальное значение, можно утверждать, что прогресс теоретической механики в XX столетии обусловлен в значительной степени совершенствованием методов механики тел переменной массы. [c.5]
Одна из классических задач небесной механики — задача о движении п материальных точек под действием ньютоновского тяготения, так называемая задача /г-тел , записывается системой дифференциальных уравнений вида [c.12]
Почти все решенные в механике задачи решаются с помощью следствия 2. [c.64]
В настоящем издании глава IV называется Задача неподвижных центров , где задача двух неподвижных центров отмечена как частный случай. В этой главе рассмотрена также классическая задача теоретической механики — задача о движении материальной точки, находящейся под действием одного неподвижного центра, куда относятся также задача Мещерского и одна задача, рассмотренная когда-то автором. [c.7]
Теперь полезно рассмотреть в качестве примера важную для небесной механики задачу об устойчивости какого-либо кеплеровского движения. [c.69]
В этой главе рассматривается простейшая ограниченная задача небесной механики — задача о движении материальной точки, притягиваемой (или отталкиваемой) несколькими неподвижными точечными центрами. Сама материальная точка не оказывает на эти центры никакого действия и называется, по этой причине, пассивно действующей. Каждый нз неподвижных центров обладает некоторой конечной массой, но не оказывает никакого действия на все другие неподвижные точечные массы. Сила, с которой каждый неподвижный точечный центр действует на свободную, пассивно действующую материальную точку, предполагается направленной по прямой, соединяющей обе точки. По величине эта сила предполагается пропорциональной произведению масс этих точек и некоторой функции от расстояния между ними. В более общем случае эта сила может также зависеть от первых двух производных по времени от упомянутого расстояния. [c.181]
Уже в первые десятилетия нашего века нелинейные проблемы обсуждались не только применительно к механике (задача трех тел, волны на воде и т. д.) и к акустике, но и в связи с исследованием свойств твердых тел (учет ангармоничности колебаний атомов в кристаллической решетке в теории теплопроводности). Нелинейные задачи ставились зарождающейся радиотехникой (детектирование и генерация колебании) они непрерывно появлялись в других разделах науки и техники. Однако нелинейные трудности в этих различных областях казались совершенно специфическими и не связанными друг с другом. И лишь в 20-30-е годы в значительной мере благодаря деятельности Леонида Исааковича Мандельштама — создателя советской школы нелинейных физиков — среди специалистов различных областей физики и техники начало вырабатываться нелинейное мышление , и они начали перенимать нелинейный опыт друг у друга. Общность нелинейных явлений различной природы и общность их моделей, образов и методов рассмотрения стали почти очевидными. Сформировался своеобразный нелинейный язык, оперирующий такими понятиями, как нелинейный резонанс, автоколебания, синхронизация, конкуренция, параметрическое взаимодействие и т. д. Этот язык сопутствовал формированию современной теории колебаний и волн. [c.13]
Тема Гейзенберговская картина квантовой механики. Задача 1. Докажите, что [c.167]
I. Общая форма уравнений небесной механики. В 143 гл. VII этой книги были выведены диференциальные уравнения основной задачи небесной механики — задачи о многих телах. [c.377]
Одна из основных задач небесной механики, в которой рассматриваются три свободные материальные точки, взаимодействующие по закону тяготения Ньютона, носит название задача трех тел ). Система, состоящая из трех свободных материальных точек, представляет собой замкнутую (изолированную) систему, поскольку внешние силы не принимаются во внимание. Аналитическое исследование движения каждой точки в задаче трех тел, несмотря на очень простую структуру самой системы, связано с огромными математическими трудностями и общее решение в приемлемом виде еще не найдено ). Со времен Эйлера, Лагранжа, Лапласа и до наших дней задача трех тел привлекает внимание многих исследователей, среди которых немало крупнейших математиков и механиков. Задаче трех тел посвящено много сотен работ и монографий. [c.160]
Задача № 199 (И. М. Б е л е и ь j и и. Введение в аналитическую механику, задача № 2). В условии задачи 195 вместо жесткого соединения невесомого стержня Л-1 А с диском сделано HiapiiHpiioe соеди]]ение в точке А, остальные условия не измепепы (рис. 243). [c.444]
В небесной механике задача о движении двух материгипьных точек под действием сил всемирного тяготения называется задачей двух тел. Полученный результат можно сформулировать следующим образом. В задаче двух тел относительное движение точек описывается уравнением движения, справедливым для одной материальной точки в поле центргичьной ньютонианской силы (теорема 3.11.2), когда в неподвижном центре помещена притягивающая масса, равная сумме масс взаимодействующих тел. [c.258]
Книга состоит из десяти глав. По охватываемому материалу I Vi главы соответствуют в целом традиционным курсам механики. Задачи остальных четырех глав связаны с тематикой спецкурса Методы интегрирования канонических систем . В отличие от лагранжева формализма гамильтонов подход позволяет в принципе найти решение как каноническое преобразование начальных данных, не обращаясь непосредственно к уравнениям. В этом аспекте канонический формализм является мощным рабочим методом, позволяющим получить приближенное решение широкого круга физических и математических задач [1]. Рассмотрены проблемы, относящиеся к интегр ированию нелинейных уравнений, преобразованиям Дарбу и Фрелиха, ВКБ-приближению, определению собственных векторов и собственных значений, гамильтоновой теории специальных функций. Дополнительные преимущества дает метод удвоения переменных, позволяющий использовать канонический формализм для решения нового класса задач алгебраических и трансцендентных уравнений, сингулярио-возму-щенных уравнений, построению Паде-аппроксимантов, обращению интегралов и т. д. Широта диапазона рассматриваемых проблем обусловлена возможностью приведения к гамильтоновой форме нелинейных систем общего вида и универсальностью используемых методов интегрирования. [c.3]
Как было указано в предыдущем параграфе, в квантовой механике задача о состоянии двух электронов в поле ядра ставится таким образом, что квадрат модуля собственной функции обобщенного уравнения Шредин-гера, умноженной на произведение элементов объема и должен давать вероятность обнаружения 1-го электрона в пределах объема dx , а 2-го электрона в пределах объема dx2- При этом необходимо иметь в виду, что с точки зрения квантовой механики одинаковые частицы неотличимы друг от друга состояние, в котором 1-й электрон находится в объеме dx , а 2-й — в объеме dx не отличимо от состояния, в котором 1-й электрон находится в объеме dx2, а 2-й — в объеме dx они оба представляют собой одно и то же состояние. [c.154]
Рассмотрим, как ставится в квантовой механике задача о рассеянии элек тронов частицами. Пусть имеется пучок параллельно движущихся электронов с кинетической энергией 47 и рассеивающая частица А (рис. 257). [c.466]
Последний пример — вариац. принцип Р и т ц а в квантовой механике. Задачу о решении ур-ння Шрё-дингера Н р q) = (q) можно сформулировать как задачу о минимизации функционала/= dg при [c.246]
Нестационарная В. т. Рассмотрим теперь важный случай, когда воамущения зависят от времени. Осн. задачей здесь является вычисление вероятностей квантовых переходов между состояниями невозмущённой системы, происходящих под влиянием возмухцеяия. В, т. в зтом случае основывается на методе вариации постоянных, так же как и в классич. механике. Задача состоит в решении ур-ния ТПрёдингсра [c.304]
Классическая теория рассеяния. Согласно законам классич. нерелятивистской механики, задачу расшяния двух частиц массами тп1 и можно свести путём перехода к системе центра инерции (с. ц. и.) сталкивающихся частиц к задаче рассеяния одной частицы с приведённой массой р = П1 т2/(т1 + т,) на неподвижном силовом центре. Траектория частицы, проходящей через силовое поле (с центром О), искривляется — происходит рассеяние. Угол 0 между начальным (Рдач) конеч-вым (Ркон) импульсами рассеиваемой частицы наз. углом рассеяния. Угол рассеяния зависит от взаимодействия. между частицами и от прицельного параметра р — расстояния, на к-ром частица пролетала бы от силового центра, если бы взаимодействие отсутствовало (рис. 1). [c.271]
При чтении курса мною были подготовлены для иллюстрации простейших законов и теорем механики задачи-примеры, в которых экстремальные свойства движения снова были изюминкой , т. е. главной целью исследования. Не приводя здесь этих задач-приме-ров, хочу только указать, что большинство их было заимствовано из курса теоретической механики Г Лэмба (русское издание. Динамика, т. 2, 1935) и хорошо известных преподавателям сборников задач по теоретической механике Ф. Виттенбауэра и Н. Бухгольца, И. Воронкова и А. Минакова. [c.206]
Общая теория малых колебаний материальной точки приводится во всех курсах теоретической механики. Задача обычно сводится к отысканию решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Наибольшие затруднения, по-видимому, представляют вопросы, связанные с определением сил,, создающих колебательное движение, а также составление дифференциальных уравнений, определяющих малые колебания. В простейших задачах линейные дифференциальные уравнения в точности описывают механический процесс. В общем же случае эти уравнения являются лишь приближенными и остаются справедливыми только для достаточно малых колебаний. Методы линеаризации уравнений движения остаются и в настоящее время наиболее простым и эффективным средством решения бТ)льшей части технических задач. [c.48]
Сам Ляпунов уже рассматривал некоторые приложения своей теории к задачам небесной механики (задача об устойчивости кеплеровых движений в системе двух и трех тел), но оказалось, что такие задачи могут быть просто решены только по первому приближению, а дальнейшее продвижение оказывается здесь недоступным. [c.332]
В квантовой механике задача о рассеянии двух частиц сводится к вычислению вероятности изменения направления относит, имнульса за время от о = — со до 1 = + со. Амнлитуда такого перехода и связывает. значение волновых ф-ций г з в эти моменты вре-менн [c.358]
Действительно, для главной задачи небесной механики— задачи о движении больших планет солнечной системы, где число плапет равно девяти ), первоначальный порядок уравнений абсолютного движения есть 6-9 + 6 = 60. Если выполнить псе возможные понижения порядка, то мы получим систему уравнений 6-9—6 = 48, для которой мы пе знаем никаких интегралов, а поэтому можем решать ее только приближенными методами. [c.342]
mash-xxl.info
В чем состоит основная задача механики?
Дата публикации
В развитии естествознания ведущую роль сыграла и до сих пор играет классическая механика, или механика Ньютона. В ее рамки укладывается объяснение множества физических явлений и процессов, проходящих в земных и внеземных условиях. Многие методы научных исследований сформированы именно на ее основе. Суть механистического мировоззрения, господствовавшего в науке практически до начала ХХ века, сводится к объяснению всех физических процессов движением и взаимодействием тел и частиц. То есть механика – это наука о движении тел.
Концепция Ньютона, кратко выраженная Энштейном, гласила: физическая реальность определяется факторами времени, пространства, материальной точки и силой, т. е. взаимодействием материальных точек. Основная задача механики, таким образом, сводилась к изучению физических событий, под которыми понималось движение и взаимодействие в пространстве материальных точек, происходящее по неизменным законам.
В современной трактовке область применения классической механики – взаимодействие тел с относительно медленным движением (многократно меньше скорости света). «Классические» понятия пространства, времени, силы, массы и т. п. остались неизменными, основные законы механики действуют и не будут опровергнуты, пока существует наука.
Давайте вспомним главные понятия механики. Это механическое движение – так называется изменение положения данного тела по отношению к другим телам в пространстве и во времени (примером может служить движение транспорта, часовой стрелки, небесного тела, молекулы), относительность движения – тело движется относительно одних тел и может быть неподвижным относительно других. Пример – водитель автомобиля движется относительно пешеходов и неподвижен относительно корпуса машины. Поэтому существует понятие тела отсчета – так называется тело, относительно которого происходит движение.
Система координат определяет расположение тела или точки в пространстве. Движение может происходить по прямой, в плоскости или в пространстве. Соответственно изменяются одна, две или три его координаты. Основная задача механики сводится к определению координаты тела в определенный (любой) момент. При этом под координатой понимается расстояние от точки отсчета по соответствующей оси. Кроме того, следует учитывать, что движение осуществляется в определенном временном промежутке, т. е время является также одной из исходных величин.
Таким образом, систему отсчета, в которой решается основная задача механики, составляют система координат и часы. Любое движение происходит не само по себе, а относительно выбранной нами системы отсчета. Зная, как изменяется координата тела во времени, можем узнать положение данного тела (точки) в любой нужный нам момент.
Основная задача механики сводится, таким образом, к определению положения тела (его координаты) в любой нужный нам момент времени.
Каждое тело имеет свои определенные размеры. При поступательном движении все его точки движутся по одной траектории, и нет нужды описывать движение всех точек. Как же определить его координаты? В определенных условиях (если размеры тела многократно меньше проходимого им расстояния) его размерами можно пренебречь и считать тело материальной точкой. Например, при движении Земли по орбите наша планета может быть принята за материальную точку. При изучении же процессов, происходящих на поверхности Земли, ее никак нельзя считать таковой. Т. е. в механике под материальной точкой подразумевается тело, размерами которого можно пренебречь.
Путь – это расстояние, которое проходит точка вдоль траектории. Перемещение – вектор (направленный отрезок), соединяющий два положения тела, начальное и конечное.
Кроме того, движение не всегда бывает поступательным. Если части тела движутся по разным траекториям, такое движение можно рассматривать как вращение вокруг определенной оси. Любое движение в механике является совокупностью поступательных и вращательных движений.
Опубликовано в Образование и наука
Добавить комментарий
www.vigivanie.com
