Задачи Первый закон Ньютона. Инерциальные системы отсчета. Масса тел. Сила. Равнодействующая сил
Нашли ошибку? Сообщите в комментариях (внизу страницы)
Действия каких тел компенсируются в следующих случаях: а) подводная лодка покоится в толще воды; б) подводная лодка лежит на твердом днеРЕШЕНИЕ
Парашютист спускается, двигаясь равномерно и прямолинейно. Действия каких тел компенсируются при этом?
РЕШЕНИЕ
Мальчик держит на нити шарик, наполненный водородом. Действия каких тел взаимно компенсируются, если шарик находится в состоянии покоя? Мальчик выпустил нить. Почему шарик пришел в ускоренное движение
РЕШЕНИЕ
Может ли автомобиль двигаться равномерно по горизонтальному шоссе с выключенным двигателем
РЕШЕНИЕ
На горизонтальном участке пути маневровый тепловоз толкнул вагон. Какие тела действуют на вагон во время и после толчка? Как будет двигаться вагон под влиянием этих тел?
РЕШЕНИЕ
Система отсчета жестко связана с лифтом. В каких из приведенных ниже случаев систему отсчета можно считать инерциальной? Лифт: а) свободно падает; б) движется равномерно вверх; в) движется ускоренно вверх; г) движется замедленно вверх; д) движется равномерно вниз
РЕШЕНИЕ
Система отсчета связана с автомобилем. Будет ли она инерциальной, если автомобиль движется: а) равномерно и прямолинейно по горизонтальному шоссе; б) ускоренно по горизонтальному шоссе; в) равномерно, поворачивая на улицу, расположенную под прямым углом; г) равномерно в гору; д) равномерно с горы; е) ускоренно с горы
РЕШЕНИЕ
Как движется поезд, если яблоко, упавшее со столика вагона в системе отсчета Вагон: а) движется по вертикали; б) отклоняется при падении вперед; в) отклоняется назад; г) отклоняется в сторону
РЕШЕНИЕ
На стержне (рис. 22), вращающемся с некоторой частотой, два стальных шарика разных размеров, связанные нерастяжимой нитью, не скользят вдоль стержня при определенном соотношении радиусов R1 и R2. Каково соотношение масс шариков, если R2 = 2R1?
РЕШЕНИЕ
Маневровый тепловоз массой 100 т толкнул покоящийся вагон. Во время взаимодействия ускорение вагона было в 5 раз больше ускорения тепловоза. Какова масса вагона
РЕШЕНИЕ
Найти отношение модулей ускорений двух стальных шаров во время столкновения, если радиус первого шара в 2 раза больше радиуса второго. Зависит ли ответ задачи от начальных скоростей шаров
РЕШЕНИЕ
Найти отношение модулей ускорений двух шаров одинакового радиуса во время взаимодействия, если первый шар сделан из стали, а второй из свинца
РЕШЕНИЕ
При столкновении двух тележек, движущихся по горизонтальной плоскости, проекция вектора скорости первой тележки на ось X изменилась от 3 до 1 м/с, а проекция вектора скорости второй тележки на ту же ось изменилась от -1 до +1 м/с. Ось X связана с землей, расположена горизонтально, и ее положительное направление совпадает с направлением вектора начальной скорости первой тележки. Описать движения тележек до и после взаимодействия. Сравнить массы тележек
РЕШЕНИЕ
Два тела массами 400 и 600 г двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью 3 м/с?
РЕШЕНИЕ
Вагон массой 60 т подходит к неподвижной платформе со скоростью 0,3 м/с и ударяет ее буферами, после чего платформа получает скорость 0,4 м/с. Какова масса платформы, если после удара скорость вагона уменьшилась до 0,2 м/с
РЕШЕНИЕ
Мяч после удара футболиста летит вертикально вверх. Указать и сравнить силы, действующие на мяч: а) в момент удара; б) во время полета мяча вверх; в) во время полета мяча вниз; г) при ударе о землю
РЕШЕНИЕ
Указать и сравнить силы, действующие на шарик в следующих случаях: а) шарик лежит на горизонтальном столе; б) шарик получает толчок от руки; в) шарик катится по столу; г) шарик летит со стола
РЕШЕНИЕ
Человек стоит в лифте. Указать и сравнить силы, действующие на человека в следующих случаях: а) лифт неподвижен; б) лифт начинает движение вверх; в) лифт движется равномерно; г) лифт замедляет движение до остановки
РЕШЕНИЕ
Указать и сравнить силы, действующие на автомобиль, когда он: а) стоит неподвижно на горизонтальном участке дороги; б) трогается с места; в) движется равномерно и прямолинейно по горизонтальному участку; г) двигаясь равномерно, проходит середину выпуклого моста; д) двигаясь равномерно, поворачивает; е) тормозит на горизонтальной дороге
РЕШЕНИЕ
На рисунке 23 показаны силы, действующие на самолет, и направление вектора скорости в некоторый момент времени (F — сила тяги, Fc — сила лобового сопротивления, Fт— сила тяжести, Fп — подъемная сила). Как движется самолет, если: a) Fт = Fп, F = Fс; 6) Fт = Fп F > Fc; в) Fт > Fп, F = Fc; г )Fт < Fп, F = Fc?
РЕШЕНИЕ
При каком соотношении сил, действующих на пузырек воздуха, поднимающийся со дна водоема, движение пузырька становится равномерным
РЕШЕНИЕ
Может ли равнодействующая двух сил 10 и 14 Н, приложенных к одной точке, быть равной 2, 4, 10, 24, 30 Н?
РЕШЕНИЕ
Может ли равнодействующая трех равных по модулю сил, приложенных к одной точке, быть равной нулю
РЕШЕНИЕ
Найти равнодействующую трех сил по 200 Н каждая, если углы между первой и второй силами и между второй и третьей силами равны 60°
РЕШЕНИЕ
На парашютиста массой 90 кг в начале прыжка действует сила сопротивления воздуха, проекции которой на оси координат X и У равны 300 и 500 Н. (Ось У направлена вверх.) Найти равнодействующую всех сил, действующих на парашютиста
РЕШЕНИЕ
На реактивный самолет действуют в вертикальном направлении сила тяжести 550 кН и подъемная сила 555 кН, а в горизонтальном направлении — сила тяги 162 кН и сила сопротивления воздуха 150 кН. Найти модуль и направление равнодействующей
РЕШЕНИЕ
Нить, на которой висит груз массой 1,6 кг, отводится в новое положение силой 12 Н, действующей в горизонтальном направлении. Найти силу натяжения нити.
РЕШЕНИЕ
bambookes.ru
Решение задач по теме “Законы Ньютона”

Решение задач по теме “Законы Ньютона”
9 класс
Коваленко И. В.

Фронтальный опрос по вопросам:
- 1 закон Ньютона
- 2 закон Ньютона
- 3 закон ньютона

Система отсчёта связана с автомобилем. Будет ли она инерциальной, если автомобиль движется:
А. Равномерно и прямолинейно по горизонтальному шоссе;
В. Ускоренно по горизонтальному шоссе;
C. Равномерно, поворачивая на улицу, расположенную под прямым углом;
D. Равномерно в гору;
E. Равномерно с горы;
F. Ускоренно с горы.
Ответ: в случаях A, D, E.

от t 1 до t 2 и
от t 3 до t 4 R=0;
от 0 до t 1 и
от t 2 до t 3 R 0

Второй закон Ньютона
F = a m
F = ∆ /∆t m

Какую скорость приобретает тело массой 3 кг под действием силы, равной 9 Н, по истечении 5 с?
F = ∆ /∆t m
∆ = (F ∆t)/m
∆ = (9 5)/ 3 = 15 (м/с)
Ответ: 15 м/c.

Задача 1.
- Как объяснить, что бегущий человек, споткнувшись, падает в направлении своего движения, а поскользнувшись, падает в направлении, противоположном направлению своего движения?

Решение:
- Первое и второе явление легко объясняется на основании первого закона Ньютона. Бегущий человек, споткнувшись, падает в направлении своего движения потому, что ноги человека замедляют движение, а туловище сохраняет прежнее состояние движения по инерции.
- Человек падает назад потому, что в то время, как ноги начинают быстрее скользить вперед, туловище ещё движется по инерции.

Задача 2.
Парашютист падает с постоянной по модулю скоростью.
Чему равен модуль силы сопротивления воздуха при этом движении?

Решение:
- Движение парашютиста равномерное и прямолинейное, поэтому, на основании 1 закона Ньютона, все силы, действующие на парашютиста, компенсируются. Так как парашютист движется под действием силы тяжести, то сила сопротивления воздуха по модулю равна силе тяжести парашютиста и противоположно направлена.

Задача 3.
- Как направлено ускорение самолета, если на него действует 4 силы: по вертикали – сила тяжести 200 кН и подъемная сила 210 кН. По горизонтали: сила тяжести мотора 20 кН и сила лобового сопротивления воздуха 10 кН.
- Чему равна равнодействующая всех сил?
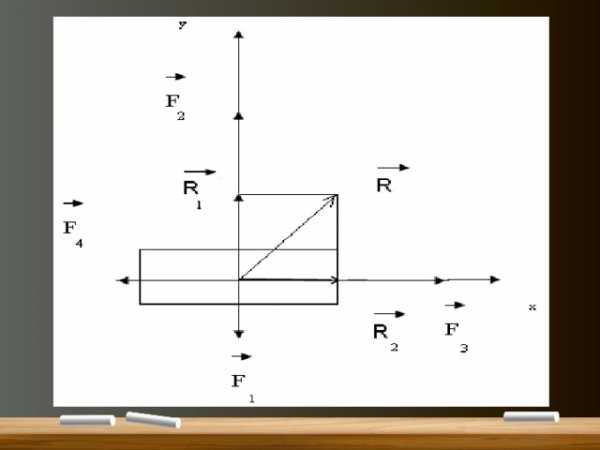

Дано:
Решение:
F 1 = 2 10 5 H
R 1 = F 2 + F 1
F 2 = 2,1 10 5 H
F 3 = 2 10 4 H
R 1 = F 2 – F 1 , (по вертикали)
R 1 = 2,1 10 5 – 2 10 5 = 0,1 10 5 =
F 4 =10 4 H
= 10 4 (Н)
Найти:
R 2 = F 3 + F 4
R-?
R 2 = F 3 – F 4 , (по горизонтали)
R 2 = 2 10 4 – 10 4 = 10 4 (H)

Найдем равнодействующую всех сил, пользуясь правилом параллелограмма:
= +
Так как катеты равны, то равнодействующая всех сил направлена под углом 45° к горизонту. Модуль силы R вычислим с помощью теоремы Пифагора: R =
R = =1, 4 10 4 (Н)
Ответ : Равнодействующая всех сил направлена под углом 45° к горизонту и равна 1,4

Задача 4.
- Под действием силы в 20 Н материальная точка движется с ускорением а = 0,4 м/с 2 .
- С каким ускорением будет двигаться точка под действием силы в 50 Н?

Дано:
F 1 = 20 H
Решение:
Движение материальной точки является равноускоренным.
a 1 = 0, 4 м/с
F 2 = 50 H
По второму закону Ньютона можно определить массу материальной точки.
m = ; m = =
Найти:
а 2 -?
а 2 = ;
а 2 = (0,4 50)/20 = 1 (м/с 2 ).
Ответ : а 2 = 1 м/с 2 .

Задача 5.
- К пристани причаливают две одинаковые лодки. Лодочники подтягиваются к берегу с помощью веревок. Противоположный конец первой веревки привязан к столбу на пристани; за противоположный конец второй веревки тянет матрос, стоящий на пристани. Все трое прилагают одинаковые усилия. Какая лодка причалит раньше?

Решение
- Обе лодки причалят одновременно. По третьему закону Ньютона каждому действию есть равное противодействие. С какой силой лодочники тянут за один конец веревки, с такой же силой второй конец веревки действует на столб и на матроса.
- Другими словами, столб “тянет” конец веревки с такой же силой, с какой ее тянет матрос, стоящий на пристани.

Задача 6.
- На тело массой 2160 кг, лежащее на горизонтальной дороге, действует сила, под действием которой тело за 30 секунд пройдет расстояние 500 метров. Найти величину этой силы.

;
Дано:
Решение:
m = 2160 кг
F = ma
t = 30 c
;
S = 500 м
,
Найти:
F-?
Ответ : 2400 Н.

Самостоятельная работа
Вариант 1.
№ 1. Действие на тело сил компенсируется в том случае, когда: Воздушный шар, поднявшись на максимальную высоту, покоится
№ 2. К бруску, находящемуся на горизонтальной плоскости, приложено несколько сил, как показано на рисунке. Скорость движения тела: Не изменяется Возрастает Убывает Вскоре тело остановится и будет двигаться в обратном направлении Правильного ответа нет.
№ 3. Шар массой m сталкивается с шаром массой 4m. В момент столкновения действуют силы: На шар 4m большая по модулю сила На шар m меньшая по модулю сила
№ 4. Автомобиль массой 3 т за 15 с от начала движения развил скорость 9 м/с. Определите силу, сообщающую ускорение автомобилю. 1 кН 180 Н 1,8 кН 1,8 Н 18 Н.
№ 5. Электровоз развивает силу тяги 180 кН. Масса поезда 1200 т. На каком участке пути скорость поезда возрастает от 18 км/ч до 36 км/ч? 150 м 175 м 200 м 225 м Правильного ответа нет.
Вариант 2.
№ 1. Если действие на тело всех сил компенсируется, то тело:
№ 2. На рисунке изображены силы, действующие на тело, движущееся
по горизонтальной поверхности. Скорость движения тела: Не изменяется Возрастает Убывает Вскоре тело остановится и будет двигаться в обратном направлении Правильного ответа нет.
№ 3. К двум тележкам приложены одинаковые по модулю силы, направленные вдоль одной прямой в противоположные стороны. Тела движутся: С одинаковыми по модулю и противоположно направленными скоростями Отношение модулей скоростей равно отношению их масс С ускорениями, направленными в противоположные стороны; отношение модулей ускорений равно обратному отношению масс тел С одинаковыми по модулю ускорениями Правильного ответа нет.
№ 4. Поезд массой 1500 т увеличил скорость от 5 м/с до 10 м/с за 3 мин. Определите силу, сообщающую поезду ускорение. 4170 Н 417 кН 41,7 кН 4,17 кН 417 Н.
№ 5. Автомобиль массой 1000 кг останавливается при торможении за 5 с, пройдя путь 50 м. Определите начальную скорость автомобиля и силу торможения. 2 м/с; 40 кН 10 м/с; 4 кН 5 м/с; 2 кН 20 м/с; 4 кН Правильного ответа нет.

Домашнее задание
Оформить самостоятельную работу в тетрадях.
multiurok.ru
|
9 Задач в теме 9 Решений в теме |
0 Подписчиков |
| Ширина | b | 3,6 | м |
|---|---|---|---|
| Скорость вагона | υ_{в} | 15 | м/c |
| Смещение отверстий от пули (путь вагона) | S_{в} | 0,18 | м |
| Пуля летит перпендикулярно направлению движения вагона | |||
| Скорость движения пули | υ_{п} | ? |
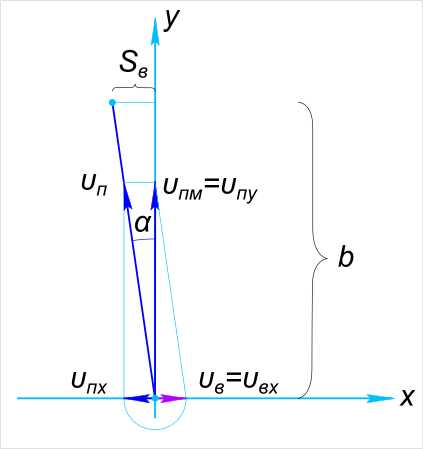
Изобразим на рисунке условия задачи
Согласно закону прямолинейного равномерного поступательного движения составляем уравнение
$ \frac{S_{в}}{υ_{в}} =\frac{S_{п}}{υ_{п}}= t $
Путь пули
$ S_{п}=\sqrt{b^{2}+(S_{в})^{2}}=\sqrt{(3,6)^{2}+(0,18)^{2}}=3,6045 м $
Из уравнения находим
$ υ_{п} = \frac{S_{п}υ_{в}}{S_{в}}=\frac{3,6045×15}{0,18}=300,375 \frac{м}{с} $
Ответ:
$ Скорость движения пули 300,375 \frac{м}{с} $
Определить скорость лодки и скорость течения рекиДанные задачи: лодка переплывает реку
| Ширина реки | b | 100 | м |
|---|---|---|---|
| Смещение лодки | a | 25 | м |
| Время в пути | t | 100 | с |
| Скорость лодки | υ_л | ? | |
| Скорость реки | υ_р | ? |
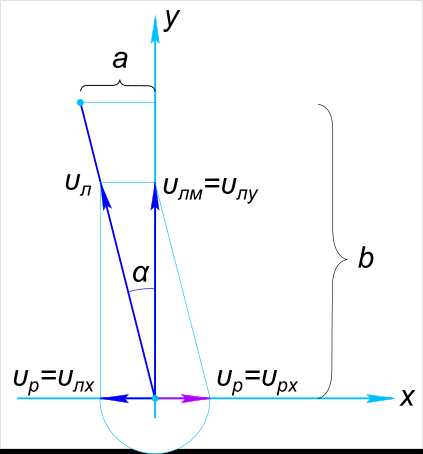
Изобразим на рисунке условие задачи
За время пути перемещение лодки складывается из двух взаимно перпендикулярных перемещений – поперек реки и вдоль реки
$ \vect{S_{л}} = \vect{S_{x}}+\vect{S_{y}} $
Согласно закону прямолинейного равномерного поступательного движения составляем уравнение
$ \frac{b}}{υ_{лм}}= \frac{S_{x}}{υ_{р}}=t $
Откуда находим
$ υ_{р} = \frac{S_{a}}{t}=\frac{25}{100}=0,25 \frac{м}{с} $
и
$ υ_{лм} = \frac{b}{t}=\frac{100}{100}=1 \frac{м}{с} $
Тогда
$ υ_{л} = \sqrt{(υ_{лм})^{2}+(υ_{р})^{2}}=\sqrt{(1)^{2}+(0,25})^{2}}=1,03 \frac{м}{с} $
Ответ:
$ Скорость реки 1 \frac{м}{с}, а скорость лодки 1,03 \frac{м}{с} $
Определить положения центра тяжести стержняДанные задачи: Стержень одинакового поперечного сечения, состоящий из двух равных частей – железной и свинцовой
| Длина стержня | L | 0,4 | м |
|---|---|---|---|
| Положения центра тяжести стержня | ? |
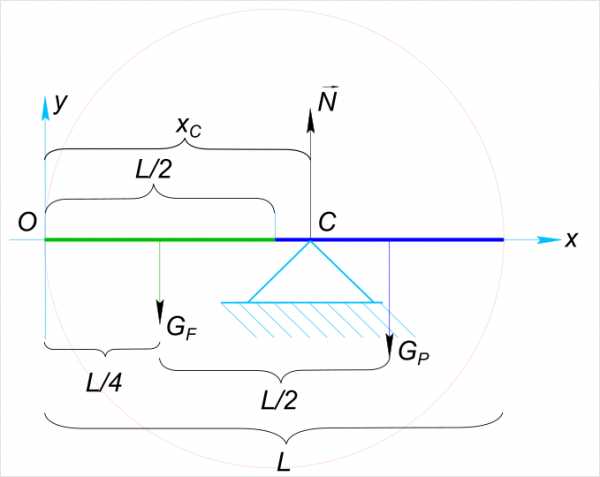
Изобразим на рисунке условия задачи
Лестница находится в равновесии, тогда для сил лежащих в одной плоскости (изображенных на рисунке) должны выполняться следующие условия:
$ Σ\vect{F_{x}} = 0 $
$ Σ\vect{F_{y}} = 0 $
$ M\vect{F_{y}} = 0 $
Откуда:
$ G_{F}+G_{P} = N $
Где вес железной половины стержня
$ G_{F} = ρ_{F}\frac{L}{2}Sg $
Где вес свинцовой половины стержня
$ G_{P} = ρ_{P}\frac{L}{2}Sg $
Моменты относительно начала координат
$ M_{G_{F}}+M_{G_{P}} = M_{N} $
или
$ ρ_{F}\frac{L}{2}Sg\frac{L}{4}+ρ_{F}\frac{L}{2}Sg\frac{3L}{4} = (ρ_{F}\frac{L}{2}Sg+ρ_{P}\frac{L}{2}Sg)x_{C} $
Откуда
$ x_{C} = \frac{(ρ_{F}\frac{1}{4}+ρ_{P}\frac{3}{4})L}{ρ_{F}+ρ_{P}}=\frac{(7,9\frac{1}{4}+11,3\frac{3}{4})0,4}{7,9+11,3}=0,218 м $
Ответ:
От свинцового конца до центра тяжести 0,182 м $
Найти жёсткость пружиныПример текста
Данные задачи: Брусок с помощью горизонтальной пружины тянут равномерно по доске, расположенной горизонтально
| Масса бруска | m | 3 | кг |
|---|---|---|---|
| Коэффициент трения | f | 0,25. | |
| Удлинение пружины | s | 0,05 | м |
| Какова жесткость пружины | ? | Н/м |
Анализируем условие задачи: – брусок движется равномерно; – на брусок действует сила трения и сила натяжения пружины. Для решения задачи применяем Первый закон Ньютона – тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю.
Составляем уравнение
$ Fпр – Fтр = sD – fmg =0 $
Откуда находим жесткость пружины
$ D = \frac{fmg}{s} = \frac{0,25×3×9,81}{0,05} = 147,15 \frac{Н}{м} $
Ответ: жесткость пружины равна
$ D = 147,15 \frac{Н}{м} $
С какой скоростью и по какому курсу должен лететь самолетДанные задачи: прокладка курса самолета
| Время в полете | $t$ | 2 | ч |
|---|---|---|---|
| Пройденный путь | $S$ | 500 | км |
| Ветер северо-западный под углом к меридиану | $β$ | 30 | град. |
| По какому курсу должен лететь самолет | $α$ | ? | |
| С какой скоростью должен лететь самолет | $ν_{с}$ | ? |

Изобразим на рисунке условия задачи
Уравнение пройденного пути при равномерном поступательном движении
$ S = (ν_{сy}-ν_{вy})t $
Откуда находим скрость
$ ν_{сy} = ν_{см}+ν_{вy}=\frac{S}{t}+ν_{в}cos(β)=\frac{500}{2}+30×0,866=276 \frac{км}{ч}$
Проекция скорости на ось x
$ ν_{сx} = ν_{вx}=ν_{в}sin(β)=30×sin(\frac{π}{6})=15 \frac{км}{ч}$
Скорость самолета
$ν_{с}=\sqrt{(ν_{сy})^{2}+(ν_{сx})^{2}}=\sqrt{76176+225}=276,41 \frac{км}{ч} $
Находим курс самолета
$ sin(α) = \frac{ν_{сx}}{ν_{с}}=\frac{15}}{276,41}=0.054 $
определяем угол α
$ arcsin(α) = arcsin(0.054)=0.054 рад $
Переводим в градусы
$ α = \frac{0.054×180}{π}=\frac{0.054×180}{3,14}=3,1 град $
Ответ:
$ Скорость самолета 276 \frac{км}{ч}, а курс 3,1° на С_З $
phys.fxyz.ru
Задачи. Третий закон Ньютона — PhysBook
Уровень А
1. Два тела взаимодействуют друг с другом. На рис. 1 указаны силы \(~\vec F_{A1}\) , \(~\vec F_{A2}\) , \(~\vec F_{A3}\) и \(~\vec F_{A4}\) , действующие на тело A, и указаны силы \(~\vec F_{B1}\) , \(~\vec F_{B2}\) , \(~\vec F_{B3}\) и \(~\vec F_{B4}\) , действующие на тело B. Определите, какие из сил могли возникнуть из-за взаимодействия двух этих тел.
Рис. 1
Решение
2. Человек массой 50 кг, стоя на коньках, отталкивает от себя шар массой 2 кг с силой 20 Н. Какие ускорения получат при этом человек и шар? Трением пренебречь.
Решение
3. Шар массой 1 кг сталкивается с шаром неизвестной массы. Полученные ими ускорения равны 0,2 и 0,4 м/с2 соответственно. Определите значение силы их взаимодействия и массу второго шара. Трением пренебречь.
Решение
4. Шар массой 1 кг сталкивается с шаром массы 2 кг, при этом второй шар получил ускорение равное 0,2 м/с2. Определите значение силы их взаимодействия и ускорение первого шара. Трением пренебречь.
Решение
Уровень B
1. При перетягивании каната возникают силы, равные по величине, но противоположные по направлению. Почему тогда часто удается перетянуть канат к себе?
Решение
2. Найдите ошибку в рассуждении: «при взаимодействии двух тел возникают силы равные по величине, но противоположные по направлению, поэтому равнодействующая этих сил равна нулю (\(~\vec F_1 = -\vec F_2 , \vec F_1 + \vec F_2 = 0\))».
Решение
3. Можно ли:
а) человеку подняться вверх, ухватившись за конец веревки, перекинутой через закрепленный неподвижный блок и привязанной вторым концом к поясу;
б) сдвинуть лодку с места, когда человек, находящийся в ней, давит на борт;
в) вытащить самого себя из болота за волосы?
Решение
4. Сравните модули ускорений двух стальных шаров во время столкновения, если радиус первого шара в 2 раза больше радиуса второго.
Решение
5. Сравните модули ускорений двух шаров одинакового радиуса во время взаимодействия, если первый шар сделан из стали, а второй – из свинца.
Решение
6. Тележки связанны нитью и вращаются не смещаясь на центробежной машине (рис. 2). Определите массу второй тележки, если r1 = 30 см; r2 = 10 см, а масса первой тележки равна 300 г.
Рис. 2
Решение
7. Два цилиндра, связанные нитью, вращаются не смещаясь на центробежной машине. При этом оказалось, что первый цилиндр при вращении расположился на расстоянии 9 см от оси вращения. Какова длина нити, если масса второго цилиндра в три раза больше первого?
Решение
8. Груз массой m лежит на полу неподвижного лифта массой М. Изобразите силы взаимодействия между следующими телами: Земля, груз, лифт, подвес лифта. Весом подвеса можно пренебречь.
Решение
9. На нити, перекинутой через неподвижный блок массой М, подвешены два груза массами m1 и m2 (m1 > m2). Изобразите силы взаимодействия между следующими телами: Земля, груз массой m1, груз массой m2, нить, блок, подвес блока. Массами нити и подвеса, силой трения можно пренебречь.
Решение
www.physbook.ru
Задачи на тему Законы механики Ньютона
Нашли ошибку? Сообщите в комментариях (внизу страницы)
20.1 В чем состоит основное утверждение механики. Подтвердите его примерами, не упомянутыми в текстеРЕШЕНИЕ
20.2 При каких условиях тело движется с постоянной скоростью
РЕШЕНИЕ
21.1 Что называется материальной точкой
РЕШЕНИЕ
21.2 Материальных точек в природе нет. Зачем же мы используем это понятие
РЕШЕНИЕ
21.3 Можно ли считать материальной точкой камень, брошенный вверх
РЕШЕНИЕ
22.1 Какое утверждение содержится в первом законе Ньютона
РЕШЕНИЕ
22.2 Какая система отсчета называется инерциальной
РЕШЕНИЕ
22.3 Каким образом можно установить, что данная система отсчета является инерциальной
РЕШЕНИЕ
23.1 Дайте определение силы
РЕШЕНИЕ
23.2 Какие две силы считаются в механике равными
РЕШЕНИЕ
23.3 Как складываются силы, действующие на тело
РЕШЕНИЕ
24.1 Как связано ускорение тела с силой
РЕШЕНИЕ
24.2 Что такое инерция? Приведите примеры, демонстрирующие инерцию тел, не указанные в тексте
РЕШЕНИЕ
24.3 В каких случаях направление скорости совпадает с направлением силы
РЕШЕНИЕ
25.1 Что такое инертность тела? Дайте определение массы
РЕШЕНИЕ
25.2 Можно ли утверждать, что первый закон Ньютона является следствием второго
РЕШЕНИЕ
25.3 Справедлив ли второй закон Ньютона для произвольного тела или только для материальной точки
РЕШЕНИЕ
25.4 При каких условиях материальная точка движется равномерно и прямолинейно
РЕШЕНИЕ
25.5 Какие условия необходимы для того, чтобы тело двигалось с постоянным ускорением
РЕШЕНИЕ
26.1 Правильна ли следующая запись третьего закона Ньютона a) F1,2=F2,1; 6) |F1,2| = |F2,1|
РЕШЕНИЕ
26.2 Лошадь тянет телегу, а телега действует на лошадь с такой же по модулю силой, направленной в противоположную сторону. Почему же лошадь везет телегу, а не наоборот
РЕШЕНИЕ
27.1 Чем отличаются основные единицы измерения физических величин от производных единиц
РЕШЕНИЕ
27.2 Единица какой величины-силы или массы-является в СИ основной
РЕШЕНИЕ
1 К центру однородного шарика массой m=0,2 кг приложена сила F=1,5 Н. Определите модуль и направление силы F1, которую необходимо приложить к центру шарика, помимо силы F, чтобы шарик двигался с ускорением a = 5 м/с2, направленным так же, как и сила F
РЕШЕНИЕ
2 В результате полученного толчка брусок начал скользить вверх по наклонной плоскости из точки O с начальной скоростью v0=4,4 м/с. Определите положение бруска относительно точки O через промежуток времени t1 = 2 с после начала его движения, если угол наклона плоскости к горизонту α=30. Трение не учитывать.
РЕШЕНИЕ
3 Два тела массами m1=10 г и m2=15 г связаны нерастяжимой и невесомой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости. Плоскость образует с горизонтом угол α= 30. Определите ускорение, с которым будут двигаться эти тела. Трением пренебречь.
РЕШЕНИЕ
4 Автомобиль массой m=1000 кг движется со скоростью v=36 км/ч по выпуклому мосту, имеющему радиус кривизны R=50 м. С какой силой F давит автомобиль на мост в его середине? С какой минимальной скоростью vmin должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост
РЕШЕНИЕ
6.1 К центру шара приложена сила F (рис. 3.23). Куда направлено ускорение шара? В каком направлении движется шар
РЕШЕНИЕ
6.2 На динамометре опускают по вертикали груз массой 5 кг так, что его скорость за 2 с изменяется от 2 до 8 м/с. Определите показание динамометра.
РЕШЕНИЕ
6.3 На полу лифта находится тело массой 50 кг. Лифт поднимается так, что за 3 с его скорость изменяется от 8 до 2 м/с. Определите силу давления тела на пол лифта.
РЕШЕНИЕ
6.4 Тепловоз на горизонтальном участке пути длиной 600 м развивает постоянную силу тяги 147 кН. Скорость поезда возрастает при этом от 36 до 54 км/ч. Определите силу сопротивления движению, считая ее постоянной. Масса поезда 1000 т.
РЕШЕНИЕ
6.5 Жесткий стержень длиной 1 м с прикрепленным к нему шариком массой 100 г вращается равномерно в вертикальной плоскости. Определите модуль и направление силы, с которой стержень действует на шарик в верхней точке, при скоростях шарика 2 м/с и 4 м/с.
РЕШЕНИЕ
6.6 Два груза массами 2 кг и 4 кг, связанные нерастяжимой нитью, поднимают по вертикали силой 84 Н, приложенной к первому грузу. Определите ускорение, с которым движутся грузы, и силу натяжения нити.
РЕШЕНИЕ
bambookes.ru
Решение задач по теме “Законы Ньютона”

Решение задач по теме «Законы Ньютона»
- Цель урока:
- 1. Знать алгоритм решения задач на законы Ньютона.
- 2. Уметь применять алгоритм к решению задач на законы Ньютона.

Повторим теорию
- Сформулируйте первый закон Ньютона. Приведите примеры, объясняющие данную формулировку.
- Какие системы отсчета называются инерциальными? Неинерциальными? Привести примеры.
- Что в физике понимают под термином «сила»?
- Приведите примеры, показывающие связь сила и ускорения, с которым движется тело.
- Сформулируйте второй закон Ньютона и запишите его математическое выражение.
- В чем состоит третий закон Ньютона? Запишите его математическое выражение. Поясните на примерах смысл этого закона. Каковы особенности сил, о которых идет речь в третьем законе Ньютона?

Алгоритм решения задач
- 1. Прочитать внимательно условие задачи.
- 2. Выделить заданные условием тела.
- 3. Выполнить анализ взаимодействия тел.
- 4. Кратко записать условие задачи.
- 5. Сделать рисунок, изобразить на нем векторы сил, действующие на каждое из тел, показать направление векторов перемещения, ускорения.
- 6. Записать в векторной форме уравнение для равнодействующей силы.
- 7. Выбрать наиболее рациональное в данных условиях задачи направление координатных осей в ИСО.
- 8. Определить проекции векторов на координатные оси.
- 9. Записать дополнительные уравнения кинематики (если необходимо).
- 10. Решить в общем виде полученные уравнения относительно искомой величины.
- 11. Сделать проверку размерности.
- 12. Вычислить.
- 13. Оценить полученные значения искомых вели чин.

Задачи по темам: «Второй закон Ньютона». «Третий закон Ньютона» из учебника Степанова
- № 118. Сила 50 Н сообщает телу ускорение 0,1 м/с 2 . Какая сила сообщает этому телу ускорение 0,01 м/с 2 ?

Решение:
- F = ma; F 1 = ma 1 ; F 2 = ma 2
- m = F1/a1 m = F2/a2
- F1/a1 = F2/a2
- F2 = F1*a2 /a1
- 50 Н*0,01 м/с2
F2 = = 5 Н
0,1 м/с2

- № 119. Тело массой 2 кг приобретает под действием некоторой силы ускорение 2 м/с2. Какое ускорение приобретет под действием этой силы тело массой 5 кг?

- Решение задачи: F =m 1 a 1 ; F = m 2 a 2 ; m 1 a 1 = m 2 a 2

- № 121. Тело, движущееся под действием постоянной силы, прошло в первую секунду путь 25 см. Определите силу, если масса тела 25 г.

Решение:

- № 122. Снаряд массой 2 кг вылетает из ствола орудия горизонтально со скоростью 1000 м/с. Определите силу давления пороховых газов, считая ее постоянной, если длина ствола равна 3,5 м.

Решение:

- № 130. Птица в клетке-ящике сидит на дне. Ящик с ней уравновешен на весах. Нарушится ли равновесие весов, если птица взлетит?

- Решение задачи: В момент взлета да, затем весы опять придут в равновесие, т. к. клетка является замкнутой системой.

- № 133. Два мальчика тянут веревку в разные стороны, прилагая силы 100 Н каждый. Веревка может выдержать, не разрываясь, груз весом 150 Н. Разорвется ли веревка?

- Решение задачи: Нет. Так как растягивание каната мальчиком с силой 100Н эквивалентно тому, что один конец каната закреплен, а к другому подвешен груз 100Н.
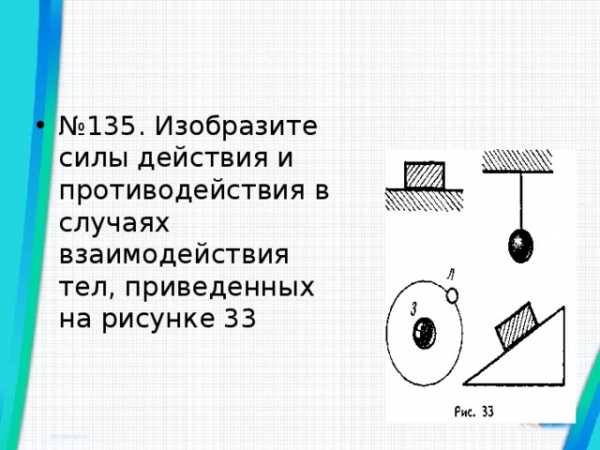
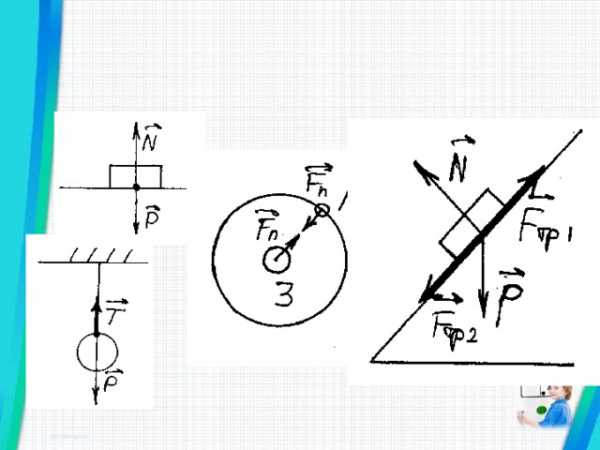
- № 135. Изобразите силы действия и противодействия в случаях взаимодействия тел, приведенных на рисунке 33

- № 136. Нарушится ли равновесие весов (рис. 34), если удлинить нить так, чтобы гиря оказалась полностью погруженной в воду, но не касалась дна? А если обрезать нить и положить гирю на дно?

- Решение задачи: не нарушится, т. к. система замкнута, т. е. сумма внутренних сил равна 0, а сумма внешних сил в обоих случаях не изменяется.

Задание на дом:
- П. 10 – 12 повторить
- Упр.11 (1,3)
- Упр.13 (1,3)

Использованные материалы:
- http://davay5.com/z.php?theme=vtoroy-zakon-nyutona-tretiy-zakon-nyutona&a=stepanova_9_10_11_klass&g=osnovy-dinamiki
- http://easyen.ru/load/shablony_prezentacij/498
multiurok.ru
Как решать задачи на применение законов Ньютона
Как решать задачи на применение законов Ньютона.
Внимательно прочитайте условие задачи (если бы вы знали, сколько ошибок происходит от невнимательного прочтения условия задачи!). Выясните, какие силы действуют на тела, движением которых мы интересуемся. Все известные силы надо изобразить на рисунке. При этом надо отчетливо представлять себе, со стороны каких тел действуют рассматриваемые силы.
Не следует забывать, что действие одного тела на другое является взаимным. Следует говорить не о действии тел, а о взаимодействии их, подчиняющемуся третьему закону Ньютона.
Выберите систему отсчета, относительно которой будете рассматривать движение тел. Выбор системы отсчета не влияет на ответ задачи, но удачно выбранное направление осей может облегчить решение задачи. В случае прямолинейного движения удобно одну из осей направить вдоль направления ускорения, а другую перпендикулярно ей.
Для
каждого тела записывается второй закон
Ньютона в векторной форме (будем считать,
что непонятные значки над векторами
обозначают стрелки):
После этого второй закон Ньютона переписывается для проекций ускорений и сил на оси выбранной системы координат:
В случаях, когда движение тел не являются свободными, а ограничено твердыми поверхностями, нерастяжимыми нитями, жесткими стержнями и т. п., эти ограничения необходимо выразить в виде специальных уравнений, которые мы будем называть “кинематической связью”. Этому вопросу будет посвящен специальный урок.
Массой нитей, связывающих тела, в подавляющем числе задач пренебрегают. Лишь в этом случае натяжение нити одинаково во сех сечениях и одинаковы по модулю силы, действующие на нить со стороны прикрепленных к ней тел.
Действительно, пусть на нить действуют силы и . Согласно второму закону Ньютона . Так как масса нити считается равной нулю, то и .
По третьему закону Ньютона одинаковы и силы, с которыми нить действует на прикрепленные к ней тела.
Массой всех блоков, встречающихся в условиях, также будем пренебрегать. В этом случае натяжение перекинутой через блок нити можно считать одинаковым по обе стороны блока. В противном случае натяжение нити по обе стороны блока будет различным. За счет различия в натяжении угловая скорость блока, обладающего массой, будет изменяться.
На этом заканчивается этап постановки задачи. Мы выполнили работу физика. Теперь необходимо перейти в состояние математика и решить полученную нами систему уравнений. Это второй этап, математический. Получив решение задачи в общем виде, необходимо перейти в состояние физик и заняться анализом решения. Прежде всего, необходимо проверить размерность. Такая проверка поможет обнаружить возможную ошибку в расчетах.
Полезно проследить, как будут меняться найденные величины при варьировании величин, заданных в условии задачи. Если, к примеру, окажется, что при некоторых значениях заданных в условиях величин искомая величина обращается в бесконечность, то это указывает обычно на ошибку в решении или на неприменимость использованной физической модели. Это третий этап, анализ решения. Видно, что наиболее сложным и ответственным является первый этап, этап постановки задачи. На этом этапе в основном и требуются ваши способности физика.
В начале, когда вы только обучаетесь решению задач, необходимо осознанно выполнять каждый пункт этого алгоритма. В дальнейшем, когда вы станете мастерами в решении задач, отдельные пункты можно будет не писать на бумаге, держа их в подсознании. Вспомним слова Р. Фейнмана: “Физик – это тот, кто видит решение задачи, не решая ее”. К этому можно прийти, прорешав несколько тысяч задач. Это немного, 3 – 4 задачника.
Рассмотрим задачу, которая проиллюстрирует нам пятый пункт стадии “Постановка задачи”.
Задача
1. Однородный стержень длиной L и массой
m движется по гладкой горизонтальной
плоскости под действием силы ,
приложенной к торцу стержня и направленной
вдоль оси стержня (рис. 1). Определите
натяжение стержня в сечении, отстоящем
от этого торца на l.
Сила является
единственной горизонтальной силой,
действующей на стержень. Под действием
этой силы стержень движется с ускорением ,
которое легко найти, используя второй
закон Ньютона. Направим координатную
ось Х вдоль оси стержня в сторону действия
силы. В проекциях на эту ось второй закон
Ньютона имеет вид
. (1)
Мысленно отсечем от стержня переднюю часть длиной l. Оставшаяся часть имеет длину и массу . Эта часть стержня движется с тем же ускорением , что и весь стержень, под действием искомой силы натяжения . Запишем для нее второй закон Ньютона в проекциях на ось Х:
(2)
На этом стадия постановки задачи заканчивается. Соединим, в знак этого, уравнения (1) и (2), фигурной скобкой. Переходим из состояния физик в состояние математик и приступаем к решению полученной системы уравнений. В результате получаем
. (3)
Приступаем к третьему этапу – анализ решения. Переходим в состояние физик.
Видно, что размерность в уравнении (3) слева и справа имеет размерность силы, т.е. в системе СИ – ньютон. Это хороший довод в пользу того, что мы не ошиблись при решении.
Далее,
из уравнения (3) видно, что натяжение
линейно убывает от максимального
значения F до нуля с увеличением расстояния
lот нуля до L (рис. 2).
Таким образом, если речь в задаче будет идти о нити или тросе, масса которых не является пренебрежимо малой, то необходимо учитывать изменение натяжения при переходе от одного сечения к другому.
Задача 2. Человек везет двое связанных саней, прикладывая силу под углом 300 к горизонту. Найдите эту силу, если известно, что сани движутся равномерно. Массы саней по 40 кг. Коэффициент трения 0,3.
Читаем условие задачи. В задаче не указано, движутся ли сани равномерно или ускоренно. Так как эту задачу не решить без знания величины ускорения, примем, что ускорение равно нулю, т.е. сани движутся равномерно. Далее, не указано, направлена ли веревка вверх или вниз. При заданном в задаче значении коэффициента трения это несущественно, если бы угол или были больше, то возможно явление заклинивания, если сила направлена вниз, и этого явления нет, если сила направлена вверх. Примем, что сила направлена вверх. Если подобная ситуация возникнет на экзамене или олимпиаде и вы увидите, что условие задачи толкуется неоднозначно, то следует обсудить и решить все возможные варианты.
Делаем
рисунок. Так как мы принимаем, что
веревка, связывающая сани, невесома и
нерастяжима, то мы сразу рисуем одинаковые
силы натяжения Т, приложенные к саням
от натянутой веревки. 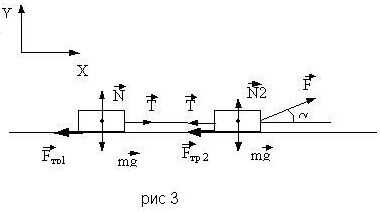
Так
как сани движутся с постоянной скоростью,
то по первому закону Ньютона сумма сил,
действующих на сани, равна нулю. Запишем
первый закон Ньютона для каждого тела
сразу в проекции на оси:
Мы добавили к уравнениям первого закона Ньютона уравнения Кулона для сухого трения, так как известно, что сани скользят.
На этом мы закончили этап постановки задачи, переходим из состояния физик в состояние математик и решаем полученную систему уравнений.
Получаем
.
Если бы мы направим силу F вниз, то в знаменателе перед появится минус, и при знаменатель обращается в нуль. Это означает, что тело не может сдвинуться при любой величине силы F.
Эта задача решалась в задачнике Черноуцана, задача №10, глава 2, “Динамика”. Задачка решалась неверно, предполагалось, что сила F приложена сразу к двум связанным в одно тело санкам. Но ответ получился такой же, как и у нас. Подумайте, почему это произошло. Может быть, стоит доказать теорему: если тело разделить на n тел, связанных между собой нитями, то сила трения, возникающая при движении этого тела равна сумме сил трения, действующих на связку n движущихся тел?
Задача 3. На гладкой горизонтальной поверхности расположены три тела массами m1, m2 и m3, связанные нерастяжимыми нитями друг с другом (рис 4а). К телу массой m1 прикреплена перекинутая через блок нить, на конце которой находится груз массой m4.. Найдите модули ускорений тел системы и натяжений всех нитей. Массами нитей и блока пренебречь.
Изобразим все силы, действующие на тела (рис 4б). Силы, действующие по вертикали на тела массами m1, m2 и m3 взаимно уравновешиваются, и их рассмотрение не требуется для решения задачи. Если бы в задаче действовали силы трения, то нам потребовалось бы написать уравнения проекций этих сил на осьY, чтобы получить N1, N2, N3, нужные нам для определения сил трения.
Ось Х направим горизонтально слева направо, а ось Y – вертикально вверх.
Уравнения движения для проекций ускорений и сил (второй закон Ньютона) на оси Х и Y для всех четырех тел будут иметь вид:
Нити нерастяжимы, поэтому . Так как массами нитей и блока пренебрегаем, то с учетом направления осей Х и Y имеем
Тогда уравнения движения запишутся следующим образом:
На этом заканчивается этап постановки задачи, мы становимся математиками и решаем полученную систему уравнений. Такую систему можно решать методом подстановки, но изящнее было бы сложить первые три уравнения и отнять четвертое. Тогда сразу получим
Подставляя найденное значение ускорения поочередно во все уравнения движения, начиная с последнего, получим
На этом заканчивается математический этап, и мы приступаем к анализу решения. Первым делом проверяем размерности. Видно, что размерность a совпадает с размерностью g. Размерности Т имеют размерность mg, т.е. размерность силы. Порядок.
Обратим внимание, что натяжение Т1 первой нити не равно , как это было бы для покоящегося тела, а меньше в отношении
Как и следовало ожидать, , так как нити сообщают одинаковые ускорения разным массам.
Задача
4. Найдите натяжения Т1 и Т2 нитей abcd и ce
в устройстве с подвижным блоком,
изображенном на рис 5а. Массы тел
соответственно равны m1 = 3 кг и m2 = 2 кг.
Так как массой нитей и блоков можно пренебречь, то натяжение нитей одинаково во всех сечениях. Нить abcd, огибающая блоки, действует на тело m1 и на левую и правую стороны подвижного блока с одинаковой силой (рис 5б). Нить ce, соединяющая тело массой m2 с подвижным блоком, действует на них с одинаковыми по модулю силами .
Координатную ось Y направим вверх. Учитывая, что получим следующую систему уравнений:
Последнее уравнение написано для подвижного блока с учетом того, что его масса равна нулю.
Система трех уравнений содержит четыре неизвестных: . Необходимо добавить уравнение кинематической связи
.
Мы получили систему из четырех уравнений для четырех неизвестных. На этом стадия постановки задачи заканчивается. Дальше мы, став на время математиками, решаем эту систему уравнений и получаем:
Учитывая, что получим Т2 = 25,2 Н. Так как то ускорение направлено вверх.
Проекция ускорения первого тела Знак минус у проекции ускорения показывает, что ускорение первого тела направлено противоположно оси , т.е. вниз.
Домашнее задание:
Из базового задачника: с 2.1 до 2.27 нечетные.
Задание для физиков:
Задача 1. На горизонтальной доске длиной l лежит груз массой m. Коэффициент трения между грузом и доской равен . Через какое время груз соскользнет с доски, если доска движется с ускорением (рис 6).
Ответ:.
Задача 2. Какую силу F должен приложить человек массой m, чтобы сдвинуть с места ящик массой M? Коэффициент трения о пол человека и ящика одинаковы и равны . Считать M m.
Ответ:
Задача 3. Мальчик вращает в вертикальной плоскости камень на нити длиной 1,2 м. После обрыва нити камень летит вертикально вверх. На какую максимальную высоту поднимется камень, если в момент отрыва полное ускорение камня было направлено под углом 450 к вертикали?
Ответ:
Задача 4. На подставке лежит тело, подвешенное к потолку с помощью пружины. В начальный момент пружина не растянута. Подставку начинают опускать вниз с ускорением а. Через какое время t тело оторвется от подставки? Жесткость пружины k, масса тела m.
Ответ:
gigabaza.ru
