Векторная алгебра | Решение задач по математике и другим предметам!!! |
Решение типового варианта контрольной работы. Векторная алгебра.
Задание 1: Коллинеарны ли векторы и , разложенные по векторам и , где
Решение:
1. Вычислим проекции векторов на оси координат:
2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:
не коллинеарны.
Задание 2: Перпендикулярны ли векторы ?
Решение: Два вектора перпендикулярны, если их скалярное произведение равно 0,скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле:, где вычислим скалярное произведение:
Векторы не перпендикулярны.
Задание 3: Компланарны ли векторы ?
Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле: , гдеВычислим смешанное произведение векторов:
Векторы не компланарны.
Задание 4: При каком значении векторы где , перпендикулярны?
Решение:
1) Для определения , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) мы сможем найти из условия: , для этого найдем проекции векторов и на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора
Итак: векторы и перпендикулярны при и при
Задание 5: Даны точки:
Найти:
1. пр;
2. ;
3. ;
4. орт вектора ;
5. ;
6. ;
7.
Решение:
1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: пр где скалярное произведение векторов вычисляется по формуле: Где и длина вектора: итак ,в нашем случае, формула принимает вид: для нахождения необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:

на основании формулы, выше написанной, получим :
Пр;
2. Для нахождения длины вектора воспользуемся формулой:, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:
;
Итак:
3. Угол между векторами можно найти из определения скалярного произведения: в нашем случае формула принимает вид: находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:
Итак
4. Направление вектора Определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам: Направляющие косинусы вектора связаны соотношением Мы имеем вектор единичной длины, такой вектор называется ортом для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину Орт вектора .
Итак: орт вектора
5. Скалярное произведение векторов вычисляем по формуле:
(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :
Итак:
6. Векторное произведение векторов вычисляется по формуле:
, где
Находим проекции векторов на оси координат:

Итак:
7. Смешанное произведение векторов вычисляется по формуле:
, где Итак:
Задание 6: Даны координаты вершин пирамиды:
Вычислить:
1. объем пирамиды;
2. длину ребра ;
3. площадь грани ;
Решение:
1. Объем пирамиды равен объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения объем
Параллелипипеда, построенного на векторах как на ребрах равен:
Найдем проекции соответствующих векторов на оси координат:
Тогда объем пирамиды равен:
Вычислим объем по указанной формуле:
;
2. Длина ребра
; (смотри пункт 5,3)
3. Площадь грани вычисляется по формуле:
так как грань треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения найдем проекции векторов на оси координат:
;
| < Предыдущая | Следующая > |
|---|
matica.org.ua
1. Основные понятия векторной алгебры; примеры решения задач.
Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.
Пример 1. Задание. Разложить вектор по векторам
Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.
Рассмотрим систему векторов и составим равенство вида:
–постоянные величины.
Если это равенство выполняется только
при одновременном равенстве нулю всех 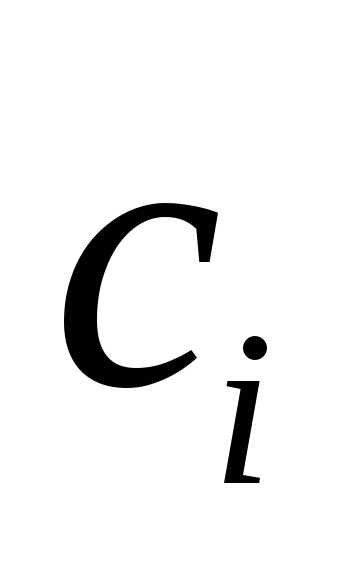
, тогда система векторов называется линейно независимой , в противном случае – система векторов линейно зависима, то есть один вектор можно представить в виде линейной комбинации других векторов.
.
Разделим левую и правую части равенства
на  ,
получим:
,
получим:
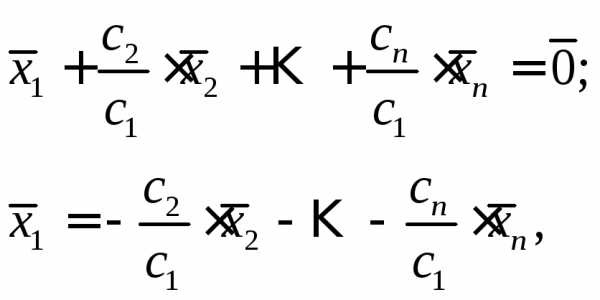
то есть вектор 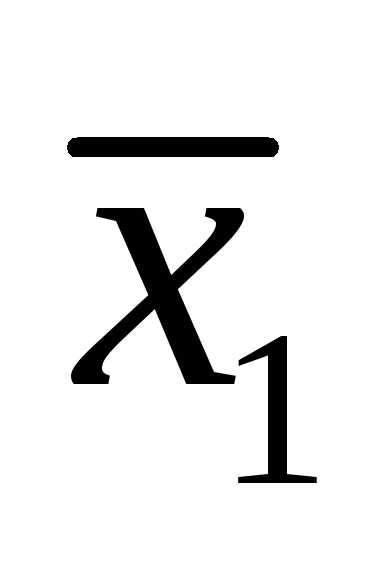 представлен в виде линейной комбинации.
представлен в виде линейной комбинации.
Решение.
 по векторам
по векторам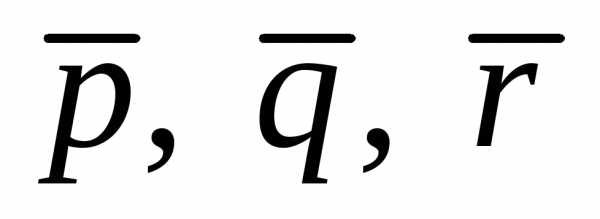 это значит представить его в виде
линейной комбинации– искомые числа.
это значит представить его в виде
линейной комбинации– искомые числа.Представим линейную комбинацию в координатной форме
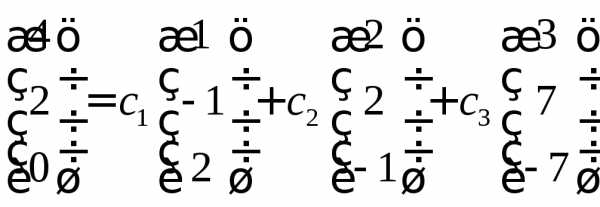
И получим систему линейных уравнений
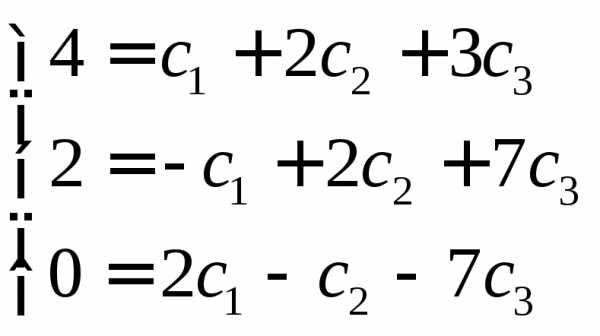
Решение системы имеет вид:
Следовательно:
Пример 2.
Напомним понятие длины вектора (модуля вектора)
Если , то
–называется длиной вектора.
Рассмотрим свойство
скалярного произведения:
,
то есть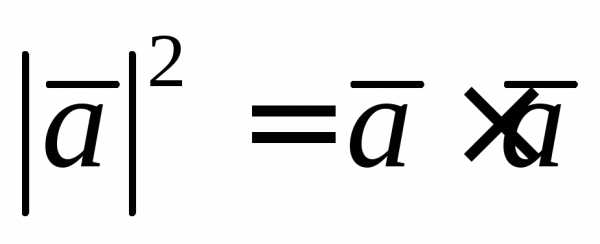 .
.
Задание.
Найти длину вектора 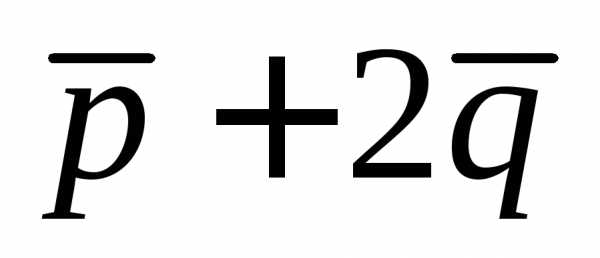 ,
если
,
если
Решение. Имеем

Пример 3.
Напомним определение
коллинеарности двух векторов 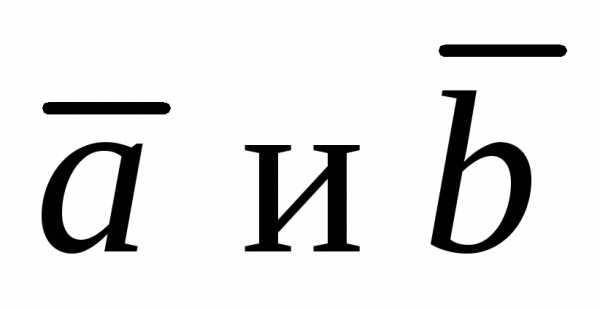 отличных от нуля: два вектора
отличных от нуля: два вектора называются коллинеарными, если
называются коллинеарными, если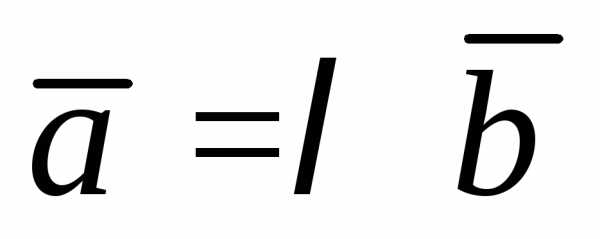
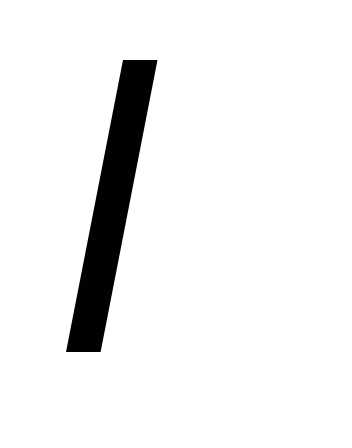 – некоторый постоянный множитель.
– некоторый постоянный множитель.Задание.
Найти вектор  ,
коллинеарный векторуи
удовлетворяющий условию: скалярное
произведение векторов.
,
коллинеарный векторуи
удовлетворяющий условию: скалярное
произведение векторов.
Решение.
Запишем условие
коллинеарности двух векторов
и полученный вектор подставим в условие
подставим в условие
Следовательно .
Пример 4.
Напомним определение скалярного произведения векторов:
Задание.
Вычислить проекцию
вектора  на направление вектора
на направление вектора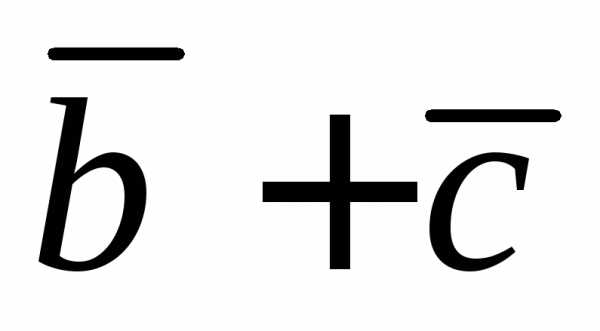 ,
если
,
если
Решение.
Обозначим , тогда
, отсюда
Ответ: 
Пример 5.
Пусть
.
Напомним, что векторное произведение
двух векторов и
и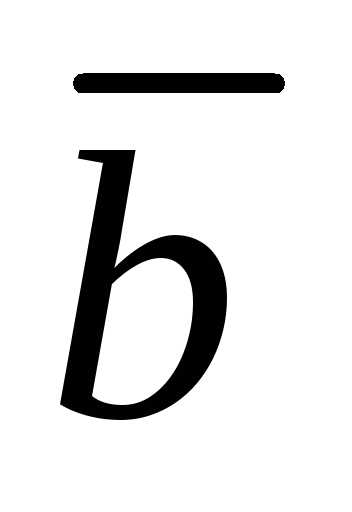 равно:
равно: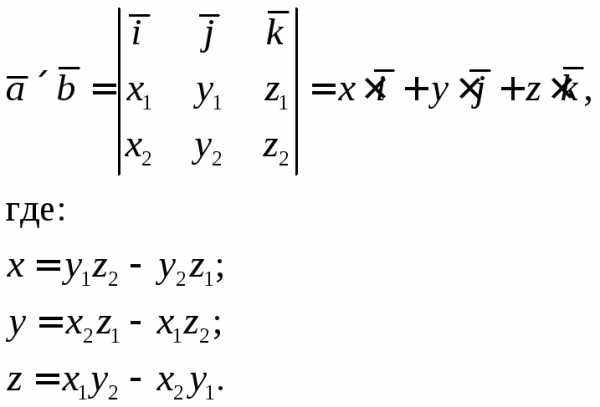
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.
Задание.
Найти площадь треугольника
Решение.
Построим
параллелограмм  на векторах(рис. 1):
на векторах(рис. 1):
рис. 1 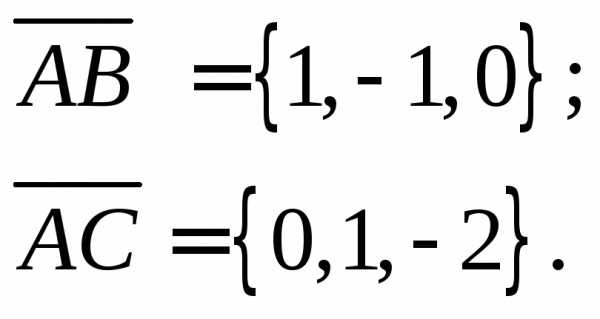

Пример 6.
Задание.
Найти вектор 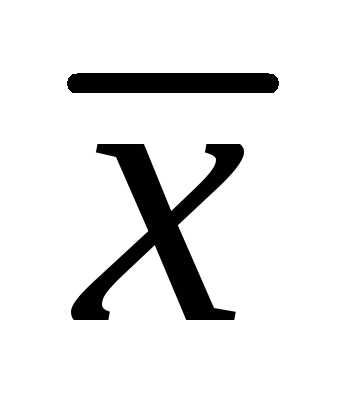 ,
перпендикулярный векторами образующий с осью
,
перпендикулярный векторами образующий с осью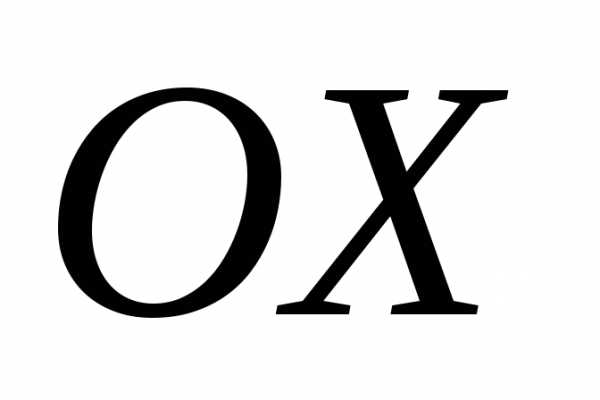 тупой угол, если
тупой угол, если .
.
Решение.
Если
,
тогда вектор перпендикулярен векторам
перпендикулярен векторам .
.
Найдем вектор  :
: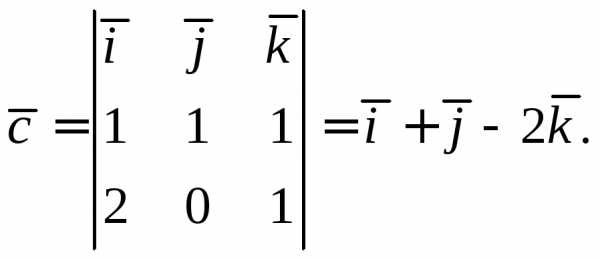
Так как 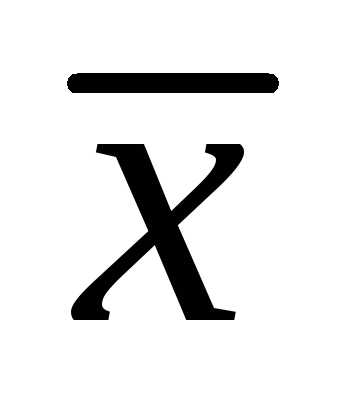 тоже перпендикулярен
тоже перпендикулярен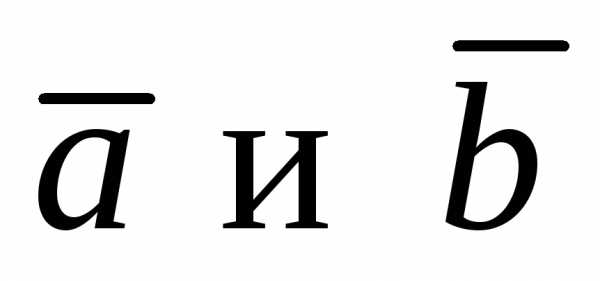 ,
следовательно вектора
,
следовательно вектора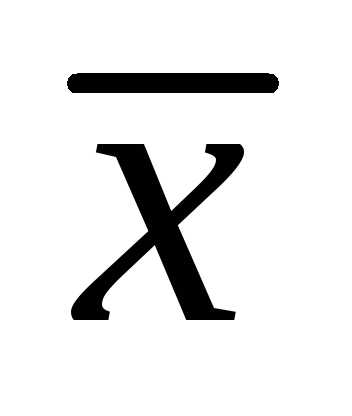 и
и – коллинеарны. Запишем условие
коллинеарности векторов:
– коллинеарны. Запишем условие
коллинеарности векторов: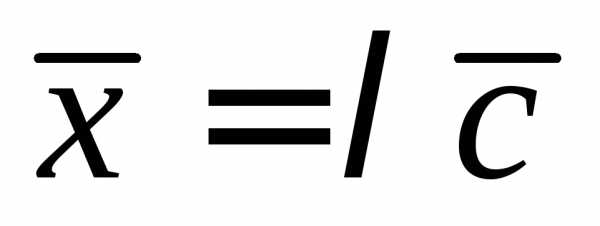 ,
,
По условию 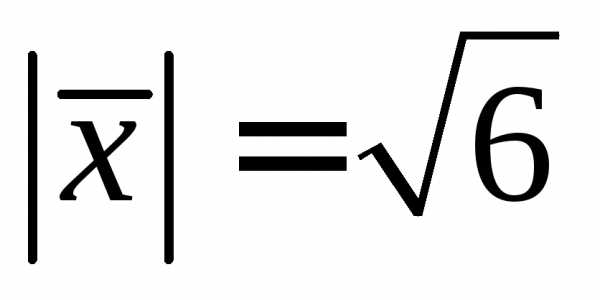 ,
то есть
,
то есть
Так как вектор  образует с осью
образует с осью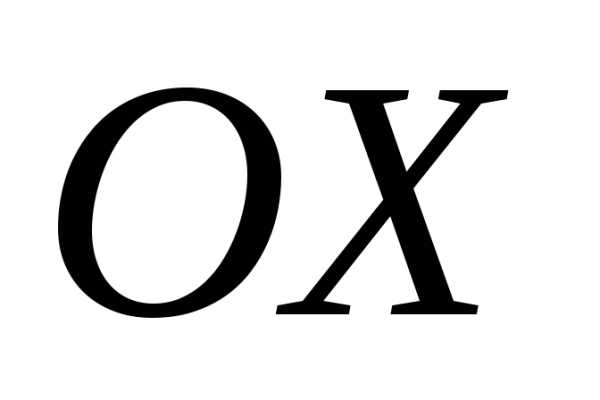 тупой угол, то его проекция на ось
тупой угол, то его проекция на ось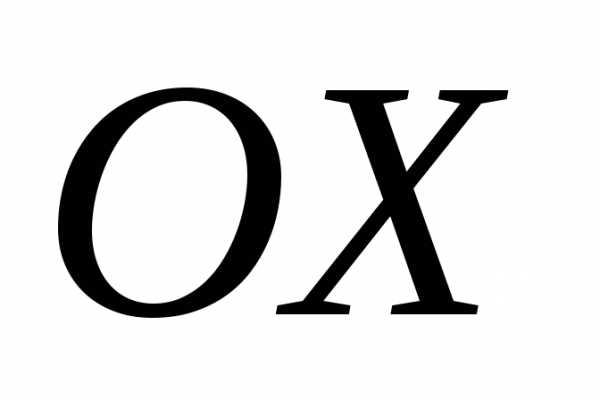 должна быть отрицательной.
должна быть отрицательной.
Отсюда
Пример 7.
Рассмотрим вектор
.
Вектор образует с осями координат углы
образует с осями координат углы ,
аназываются направляющими косинусами,
при этом
,
аназываются направляющими косинусами,
при этом
Задание.
Найти направляющие
косинусы вектора силы
,
приложенной в точке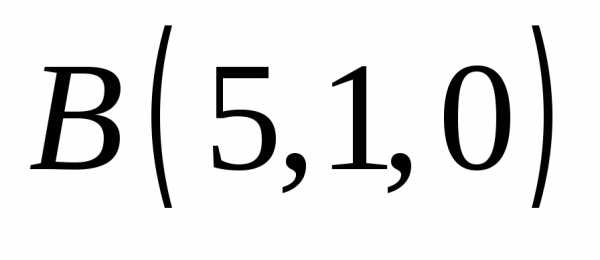 ,
и момент этой силы относительно точки
,
и момент этой силы относительно точки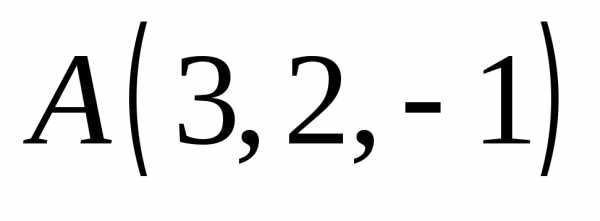 .
.
Решение.
Найдем направляющие косинусы вектора силы:
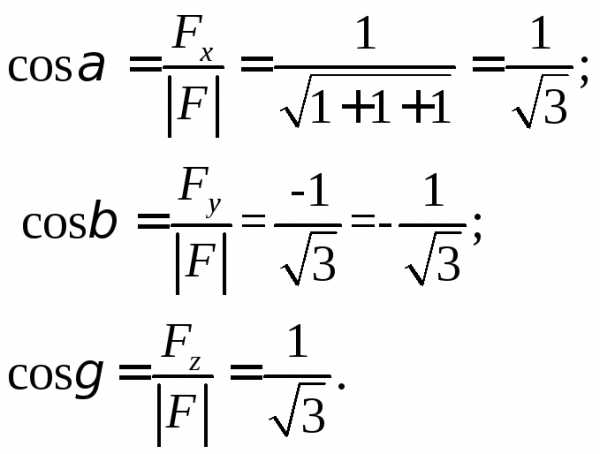
Момент силы
определим как векторное произведение
вектора 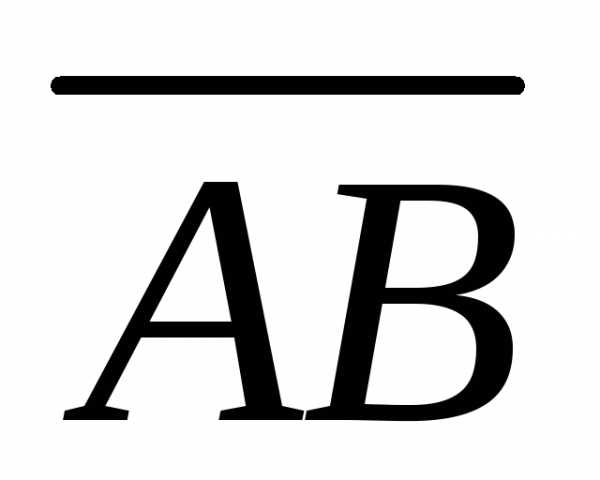 на вектор
на вектор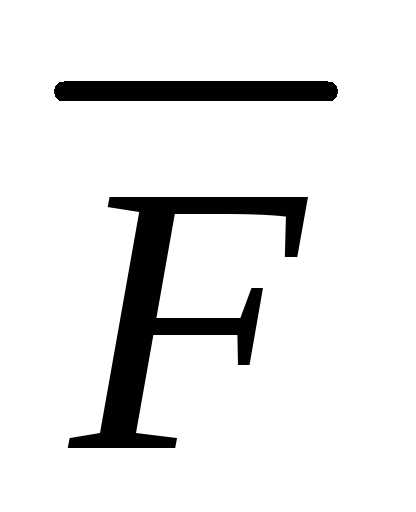 .
Имеем
.
Имеем

Пример 8.
Напомним формулу смешанного произведения трех векторов
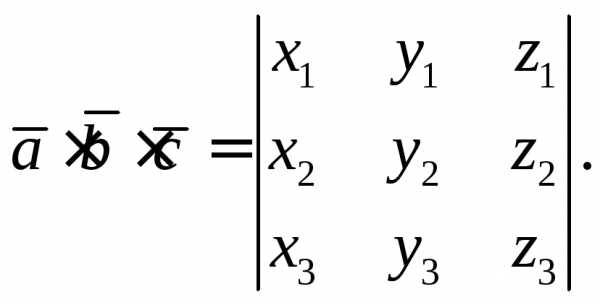
Известно, что
модуль смешанного произведения  равен объему параллелепипеда, построенного
на этих векторах.
равен объему параллелепипеда, построенного
на этих векторах.
Задача.
Найти длину высоты
пирамиды, опущенной из вершины 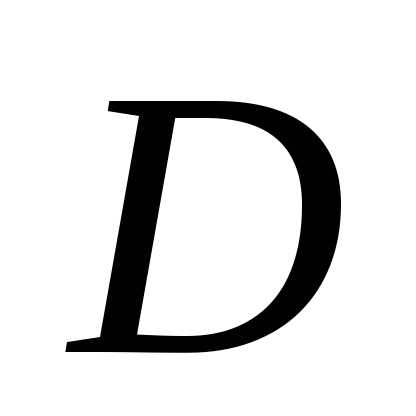 (рис. 2), если ее вершины
(рис. 2), если ее вершины
Решение.
рис. 2
Найдем векторы:
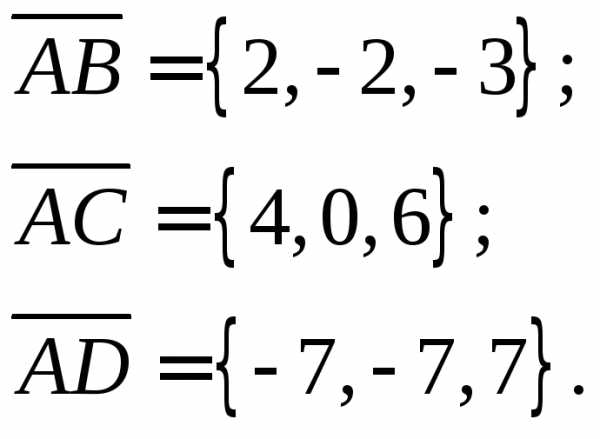
Объем пирамиды, построенной на векторах , равен одной шестой модуля смешанного произведения этих векторов.
, где  – высота пирамиды, а площадь прямоугольника,
построенного на векторах
– высота пирамиды, а площадь прямоугольника,
построенного на векторах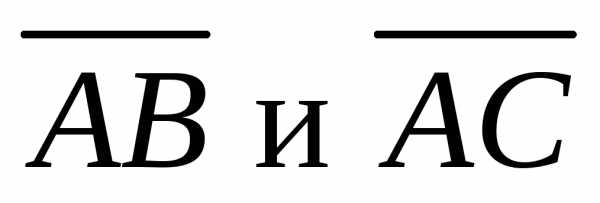 равна одной второй векторного произведения.
равна одной второй векторного произведения.
Вычислим смешанное произведение векторов
Отсюда  пирамиды
пирамиды
Вычислим векторное произведение векторов:
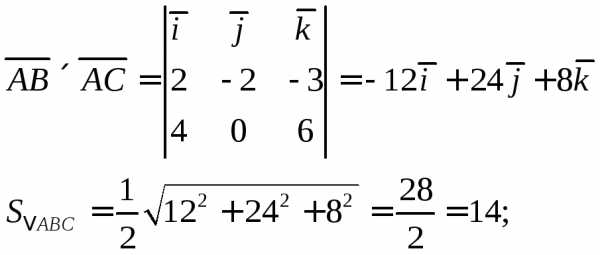
Найдем высоту пирамиды:
studfiles.net
Примеры решения задач с векторами
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме – координаты вектора.
Пример
Запись означает, что векторимеет следующие координаты: абсцисса равна 5, ордината равна -2.
Пример
Задание. Заданы векторы и. Найти координаты вектора
Решение.
Пример
Задание. Вектор . Найти координаты вектора
Решение.
Пример
Задание. Найти координаты вектора , если
Решение.
Длина (модуль) вектора
Теоретический материал по теме – длина вектора.
Пример
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Пример
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Угол между векторами
Теоретический материал по теме – угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов , а их длины. Найти угол между векторамии.
Решение. Косинус искомого угла:
Пример
Задание. Найти угол между векторами и
Решение. Косинус искомого угла
Пример
Задание. Найти угол между векторами и
Решение. Косинус искомого угла:
Разложение вектора по ортам координатных осей
Теоретический материал по теме – разложение вектора по ортам.
Пример
Задание. Зная разложения вектора по базисной системе векторов:, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , получаем, что
Пример
Задание. Вектор задан своими координатами:. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора – это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
Скалярное произведение векторов
Теоретический материал по теме – скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов и, если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия ,, а, то
Пример
Задание. Найти скалярное произведение векторов и
Решение. Скалярное произведение
Векторное произведение векторов
Теоретический материал по теме – векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов и
Решение. Составляем определитель и вычисляем его:
Смешанное произведение векторов
Теоретический материал по теме – смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной на векторах ,,
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов ,и:
studfiles.net
1. Основные понятия векторной алгебры; примеры решения задач.
Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.
Пример 1. Задание. Разложить вектор по векторам
Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.
Рассмотрим систему векторов и составим равенство вида:
–постоянные величины.
Если это равенство выполняется только
при одновременном равенстве нулю всех  ,
,
, тогда система векторов называется линейно независимой , в противном случае – система векторов линейно зависима, то есть один вектор можно представить в виде линейной комбинации других векторов.
.
Разделим левую и правую части равенства
на  ,
получим:
,
получим:
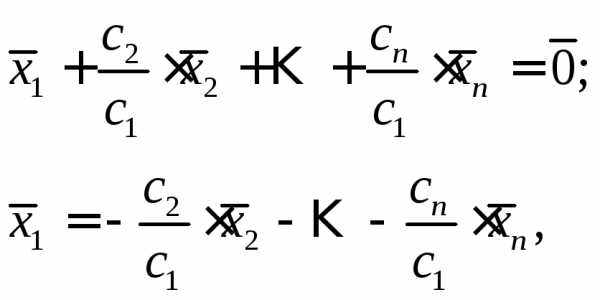
то есть вектор 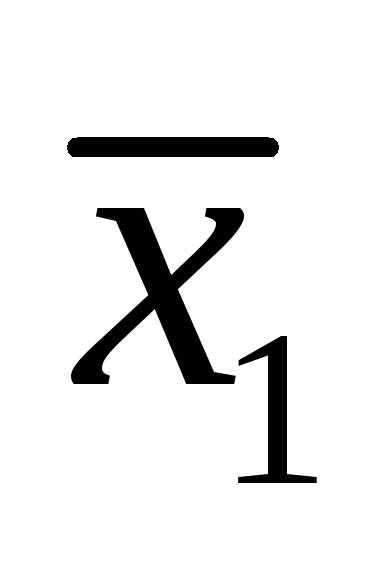 представлен в виде линейной комбинации.
представлен в виде линейной комбинации.
Решение.
Разложить вектор  по векторам
по векторам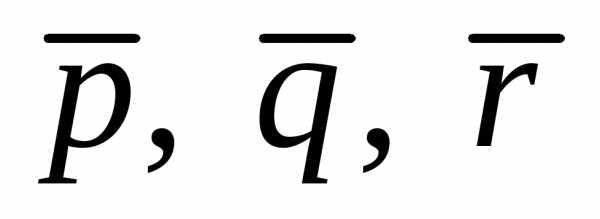 это значит представить его в виде
линейной комбинации– искомые числа.
это значит представить его в виде
линейной комбинации– искомые числа.
Представим линейную комбинацию в координатной форме
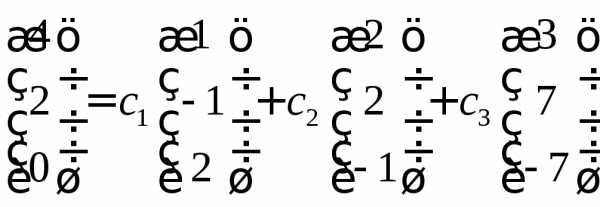
И получим систему линейных уравнений
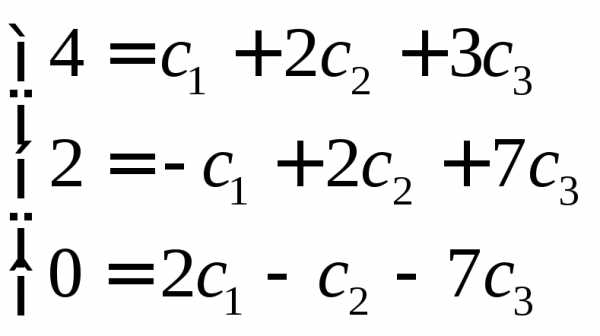
Решение системы имеет вид:
Следовательно:
Пример 2.
Напомним понятие длины вектора (модуля вектора)
Если , то
–называется длиной вектора.
Рассмотрим свойство
скалярного произведения:
,
то есть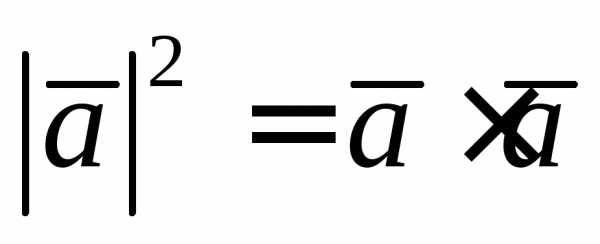 .
.
Задание.
Найти длину вектора 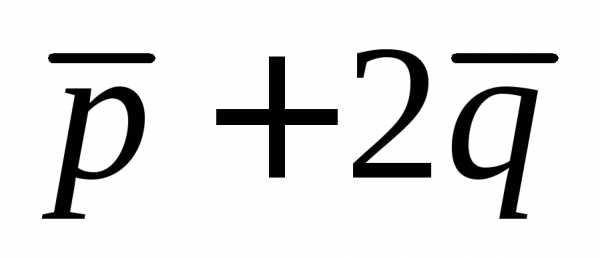 ,
если
,
если
Решение. Имеем
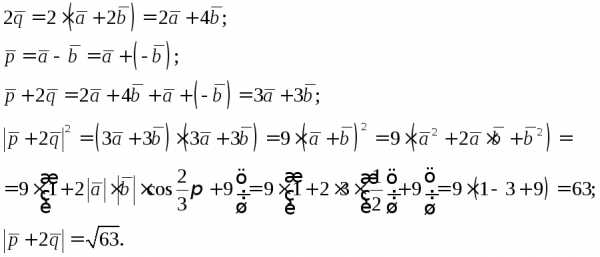
Пример 3.
Напомним определение
коллинеарности двух векторов 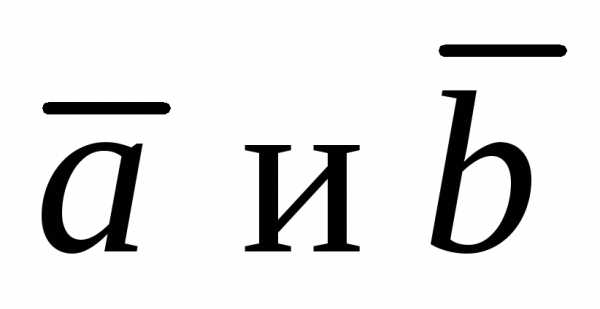 отличных от нуля: два вектора
отличных от нуля: два вектора называются коллинеарными, если
называются коллинеарными, если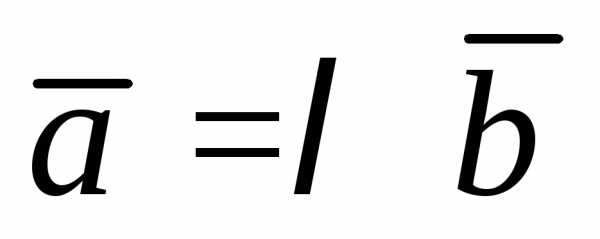 ,
где
,
где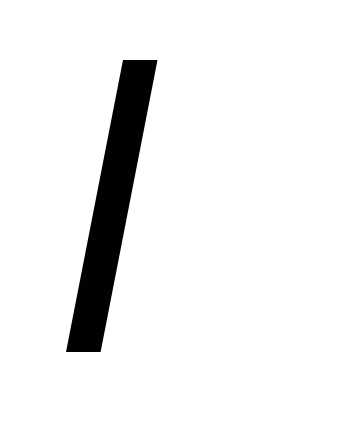 – некоторый постоянный множитель.
– некоторый постоянный множитель.
Задание.
Найти вектор  ,
коллинеарный векторуи
удовлетворяющий условию: скалярное
произведение векторов.
,
коллинеарный векторуи
удовлетворяющий условию: скалярное
произведение векторов.
Решение.
Запишем условие
коллинеарности двух векторов
и полученный вектор подставим в условие
подставим в условие
Следовательно .
Пример 4.
Напомним определение скалярного произведения векторов:
.
Задание.
Вычислить проекцию
вектора  на направление вектора
на направление вектора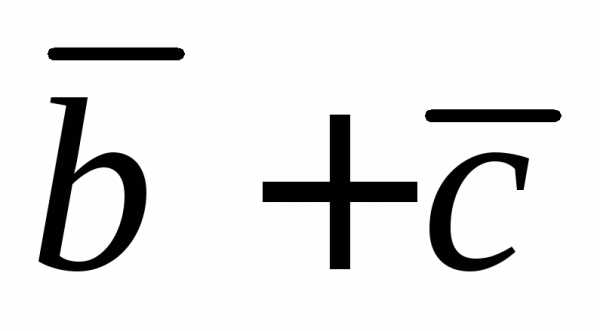 ,
если
,
если
Решение.
Обозначим , тогда
, отсюда
Ответ: 
Пример 5.
Пусть
.
Напомним, что векторное произведение
двух векторов и
и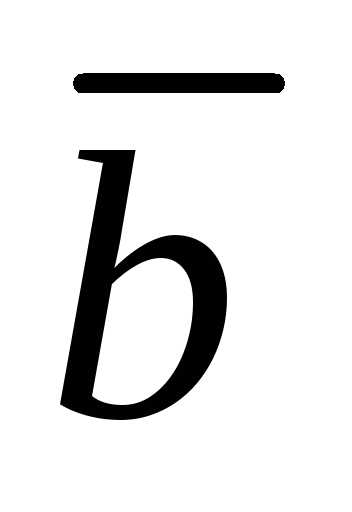 равно:
равно: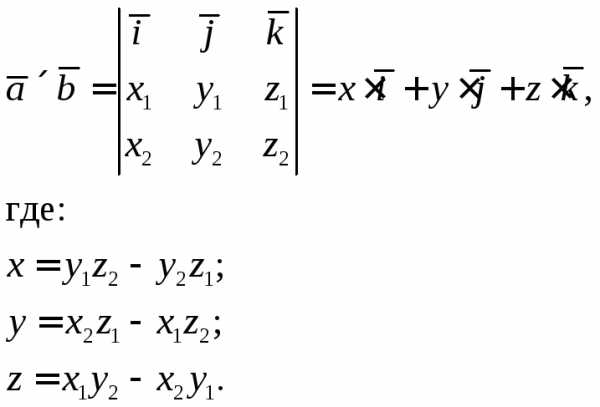
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.
Задание.
Найти площадь треугольника
Решение.
Построим
параллелограмм 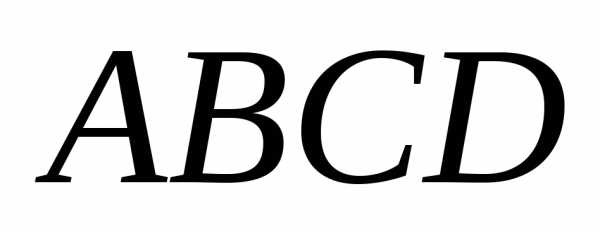 на векторах(рис. 1):
на векторах(рис. 1):
рис. 1 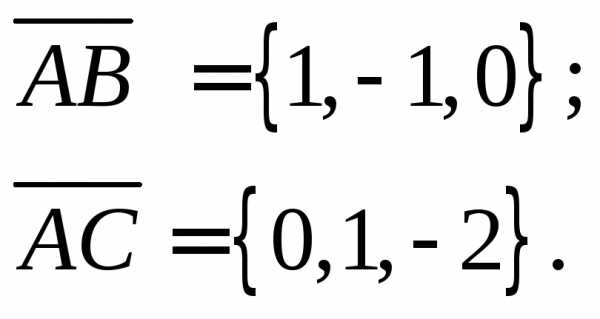

Пример 6.
Задание.
Найти вектор 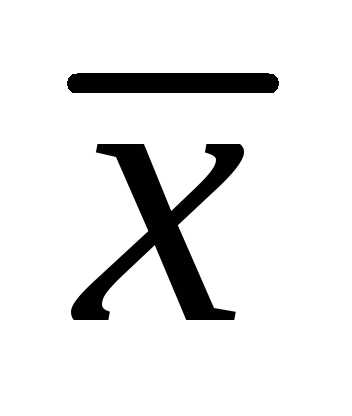 ,
перпендикулярный векторами образующий с осью
,
перпендикулярный векторами образующий с осью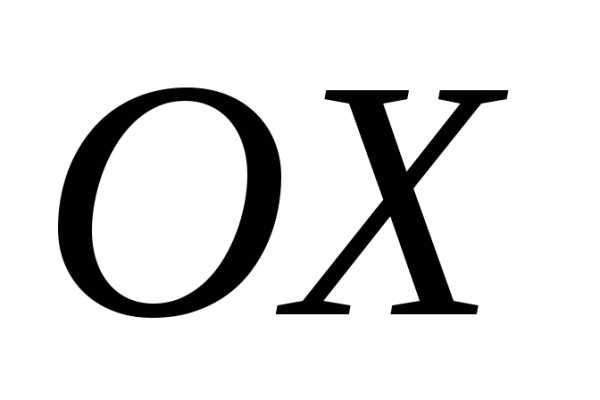 тупой угол, если
тупой угол, если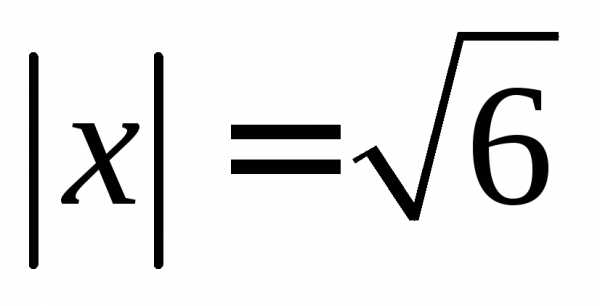 .
.
Решение.
Если
,
тогда вектор перпендикулярен векторам
перпендикулярен векторам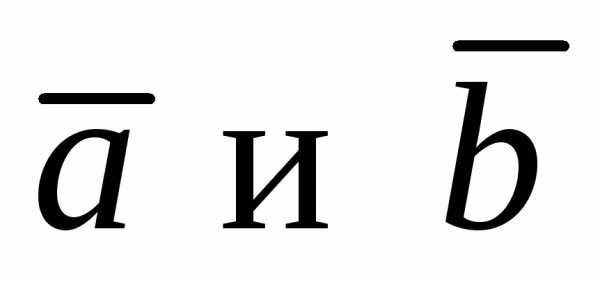 .
.
Найдем вектор  :
: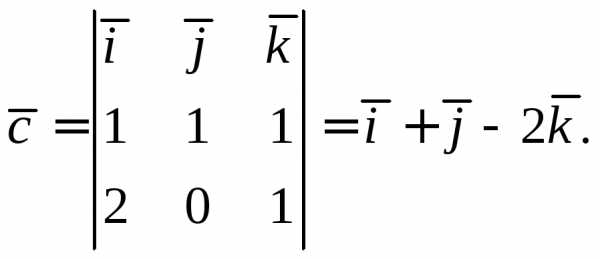
Так как 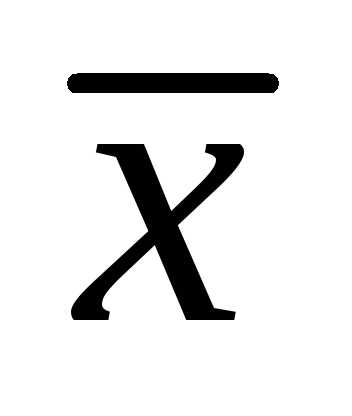 тоже перпендикулярен
тоже перпендикулярен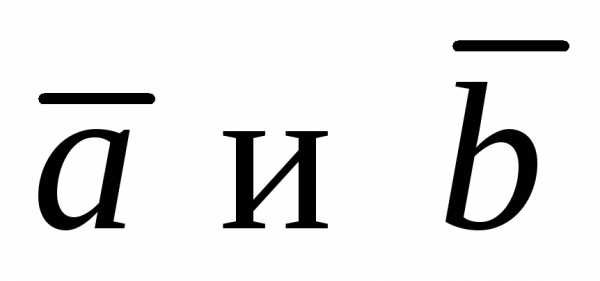 ,
следовательно вектора
,
следовательно вектора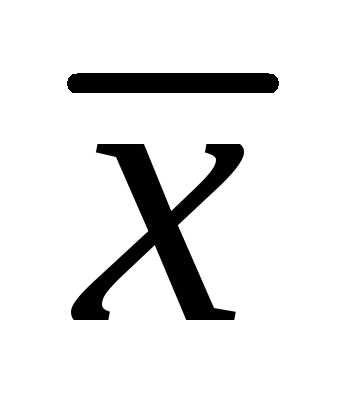 и
и – коллинеарны. Запишем условие
коллинеарности векторов:
– коллинеарны. Запишем условие
коллинеарности векторов: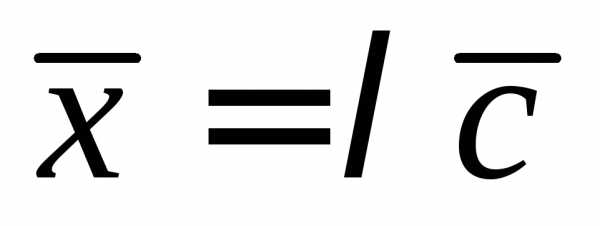 ,
,
По условию 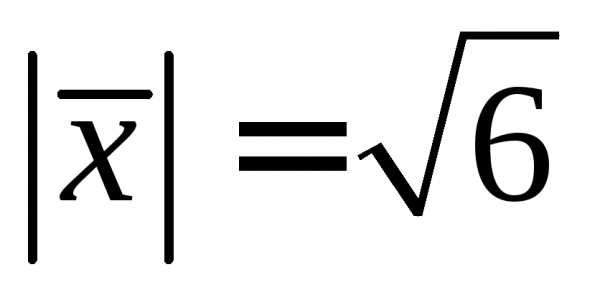 ,
то есть
,
то есть
Так как вектор  образует с осью
образует с осью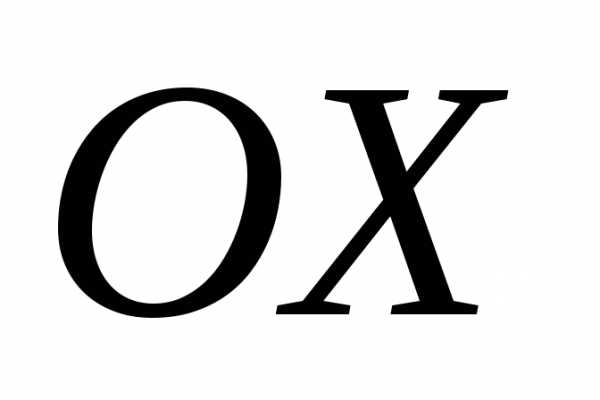 тупой угол, то его проекция на ось
тупой угол, то его проекция на ось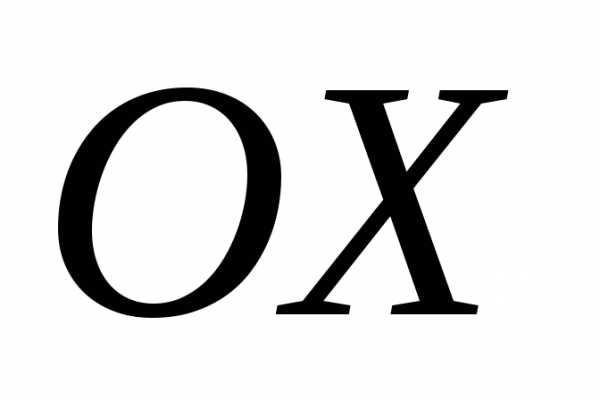 должна быть отрицательной.
должна быть отрицательной.
Отсюда
Пример 7.
Рассмотрим вектор
.
Вектор образует с осями координат углы
образует с осями координат углы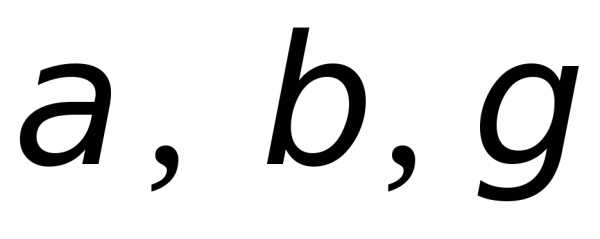 ,
аназываются направляющими косинусами,
при этом
,
аназываются направляющими косинусами,
при этом
Задание.
Найти направляющие
косинусы вектора силы
,
приложенной в точке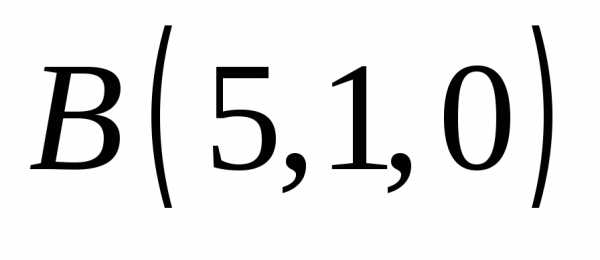 ,
и момент этой силы относительно точки
,
и момент этой силы относительно точки .
.
Решение.
Найдем направляющие косинусы вектора силы:

Момент силы
определим как векторное произведение
вектора 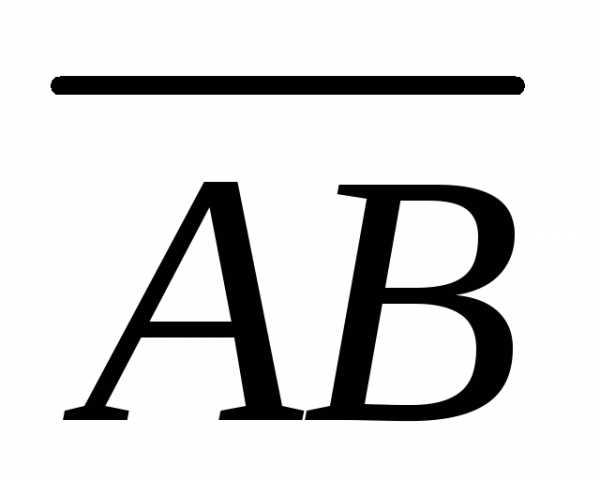 на вектор
на вектор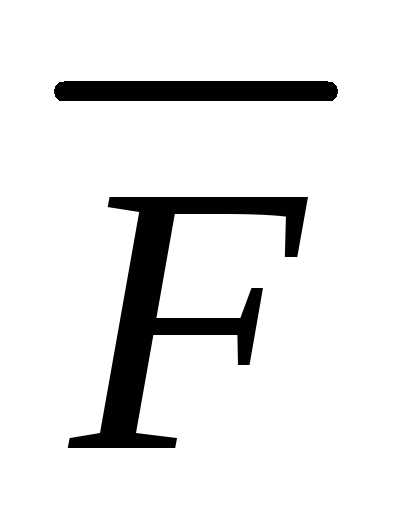 .
Имеем
.
Имеем
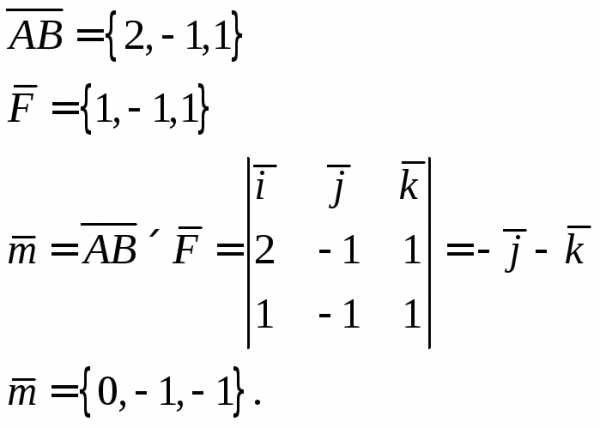
Пример 8.
Напомним формулу смешанного произведения трех векторов
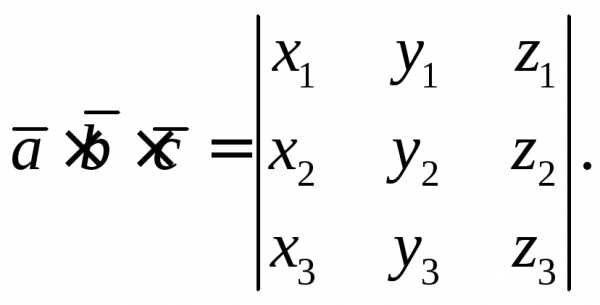
Известно, что
модуль смешанного произведения  равен объему параллелепипеда, построенного
на этих векторах.
равен объему параллелепипеда, построенного
на этих векторах.
Задача.
Найти длину высоты
пирамиды, опущенной из вершины 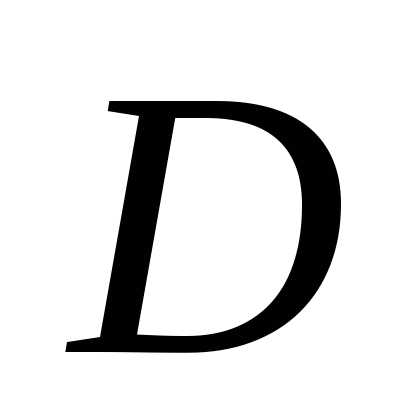 (рис. 2), если ее вершины
(рис. 2), если ее вершины
Решение.
рис. 2
Найдем векторы:
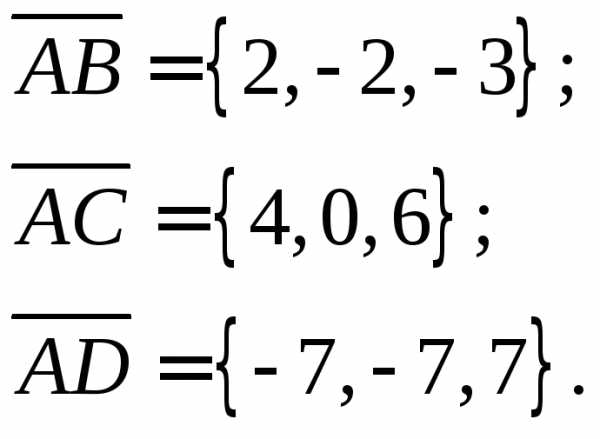
Объем пирамиды, построенной на векторах , равен одной шестой модуля смешанного произведения этих векторов.
, где 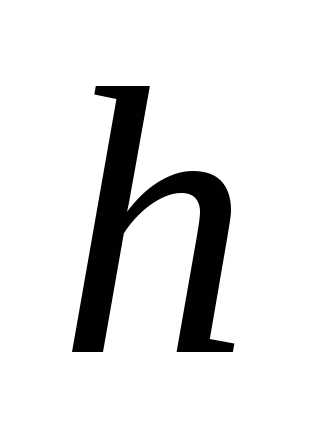 – высота пирамиды, а площадь прямоугольника,
построенного на векторах
– высота пирамиды, а площадь прямоугольника,
построенного на векторах равна одной второй векторного произведения.
равна одной второй векторного произведения.
Вычислим смешанное произведение векторов
Отсюда  пирамиды
пирамиды
Вычислим векторное произведение векторов:

Найдем высоту пирамиды:
studfiles.net
Векторная алгебра | Высшая математика
Векторная алгебра | Высшая математика- Основные определения.
- Вектор (геометрический вектор) — это направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).
На чертеже вектор обозначается стрелкой
над буквенным обозначением вектора также ставится стрелка .
Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора. - Закрепленный вектор — это направленный отрезок АВ, началом которого является точка А, а концом — точка В.
Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается .
Если же точка приложения вектора (точка A для вектора ) может быть выбрана произвольно, вектор называется свободным.
Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов. - Нулевой вектор — это вектор, у которого начало и конец совпадают:
- Коллинеарные векторы — это векторы, которые лежат на одной прямой, либо на параллельных прямых.
Нулевой вектор коллинеарен любому вектору. - Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны. - Длина вектора (модуль) — это расстояние между началом и концом вектора. Обозначение: или
- Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Например,
- Алгебраические операции над векторами.
- Операция сложения.
Суммой двух свободных векторов и называется свободный вектор , начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора и начало вектора .
Сумма двух векторов и () — это вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора (правило треугольника).
Свойства операции сложения векторов:
1) Переместительное свойство: (коммутативность).
2) Сочетательное свойство: (ассоциативность).
3) Существует нулевой вектор , такой, что для любого вектора (особая роль нулевого вектора).
Нулевой вектор порождается нулевым закрепленным вектором, то есть точкой.
4) Для каждого вектора существует противоположный ему вектор , такой, что . Вектор называется вектором, противоположным вектору .
Правило параллелограмма (правило сложения векторов): если векторы и приложены к общему началу и на них построен параллелограмм, то сумма этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов и
Вычитание векторов определяется через сложение: .
Другими словами, если векторы и приложены к общему началу, то разностью векторов и будет вектор , идущий из конца вектора к концу вектора . - Операция умножения вектора на число.
Произведением вектора на число называется вектор такой, что:
1) если λ > 0, ≠ , то получается из растяжением в λ раз: ;
2) если λ < 0, ≠ , то получается из растяжением в |λ| раз и последующим отражением: ;
3) если λ = 0 или , то .
Свойства операции умножения:
1) Распределительное свойство относительно суммы чисел: для любых действительных и всех (дистрибутивность).
2) Распределительное свойство относительно суммы векторов: (дистрибутивность).
3) Сочетательное свойство числовых сомножителей: (ассоциативность).
4) Существование единицы: .
- Ортонормированный базис. Декартова прямоугольная система координат.
- Ортонормированный базис (ОНБ) — это три взаимно перпендикулярных вектора с длинами, равными единице.
Обозначения: - Базисные орты — это векторы .
- Зафиксированная точка О – это начало координат.
Отложим от точки O векторы .
Полученная система координат — это прямоугольная декартова система координат. - Декартовы координаты вектора — это координаты любого вектора в этом базисе:
Пример 11. - Координатные оси — это прямые линии, проведенные через начало координат (точку O) по направлениям базисных векторов:
– порождает Ox;
– порождает Oy;
– порождает Oz. - Абсцисса — это координата точки M (вектора в декартовой системе координат по оси Ox.
Ордината — это координата точки M (вектора в декартовой системе координат по оси Oy.
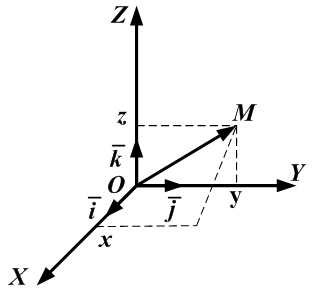
Аппликата — это координата точки M (вектора ) в декартовой системе координат по оси Oz. - Декартовы прямоугольные координаты x, y, z вектора равны проекциям этого вектора на оси Ox, Oy, Oz, соответственно. Иначе:
где α, β, γ – углы, которые составляет вектор с координатными осями Ox, Oy, Oz, соответственно, при этом cosα, cosβ, cosγ называются направляющими косинусами вектора . Пример 12.
Для направляющих косинусов справедливо соотношение: - Орт направления — это вектор единичной длины данного направления.
Формулы, уравнения, теоремы, примеры решения задач
matematika.electrichelp.ru
Примеры решения задач по теме: «Векторная алгебра».
Задача 1. Разложить вектор по векторам
Решение.
Разложить вектор  по векторам
по векторам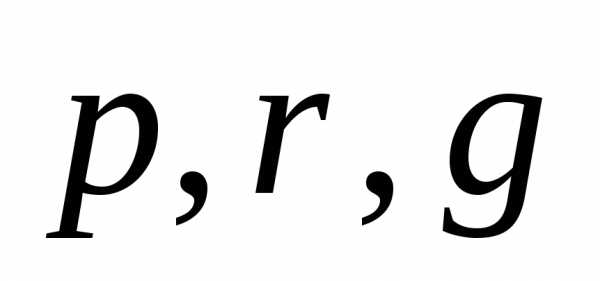 – значит представить его в виде
– значит представить его в виде
(1)
где 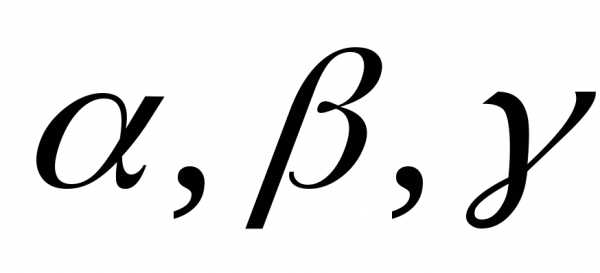 – неизвестные пока числа. Переходя в
равенстве (1) к координатам векторов,
получим
– неизвестные пока числа. Переходя в
равенстве (1) к координатам векторов,
получим
Как известно у равных векторов равны соответствующие координаты,
 (2)
(2)
Решив систему (2), найдём . Следовательно,.
Задача
2. Найти
вектор 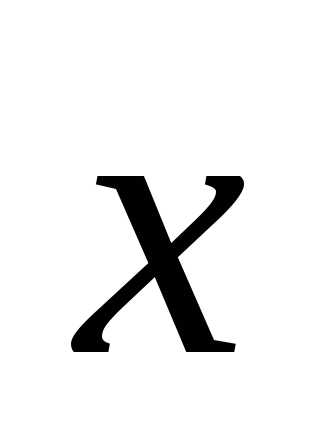 коллинеарный векторуи удовлетворяющий условию.
коллинеарный векторуи удовлетворяющий условию.
Решение. В силу коллинеарности векторов  и
и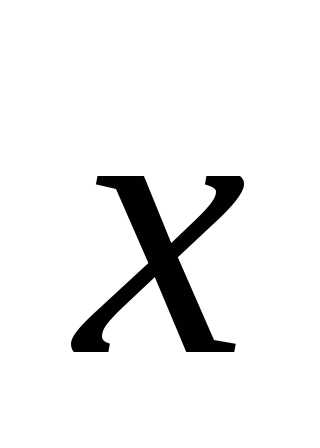 вектор
вектор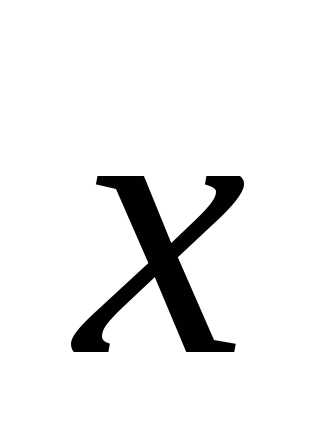 можно представить в виде
можно представить в виде где
где – пока неизвестный множитель. Для его
определения используем второе условие:
– пока неизвестный множитель. Для его
определения используем второе условие:
.
Отсюда 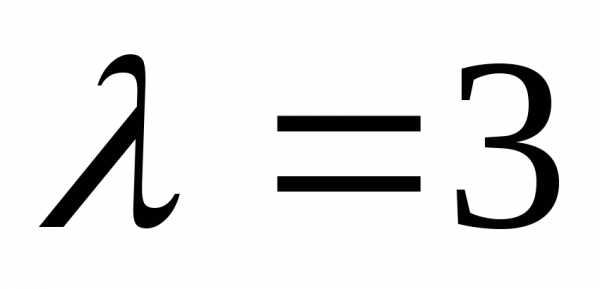 ,
поэтому.
,
поэтому.
Задача
3. Найти
вектор 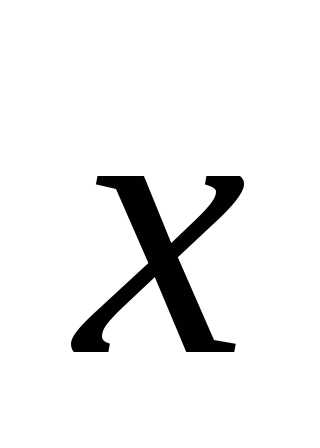 ,
перпендикулярный векторамии образующий с осью Ох тупой угол, если
,
перпендикулярный векторамии образующий с осью Ох тупой угол, если .
.
Решение.
Найдём вектор 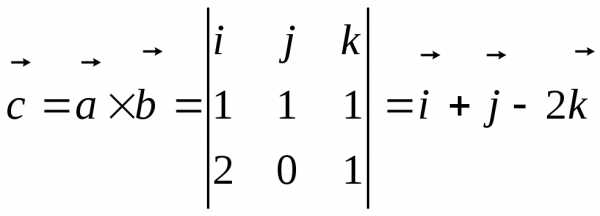 .
.
Так
как 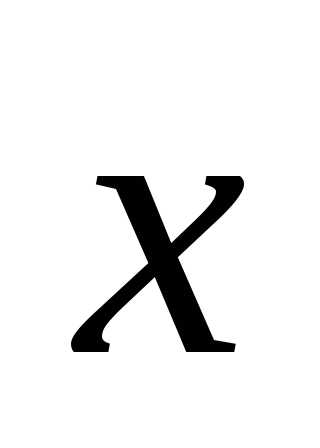 перпендикулярен векторам
перпендикулярен векторам и
и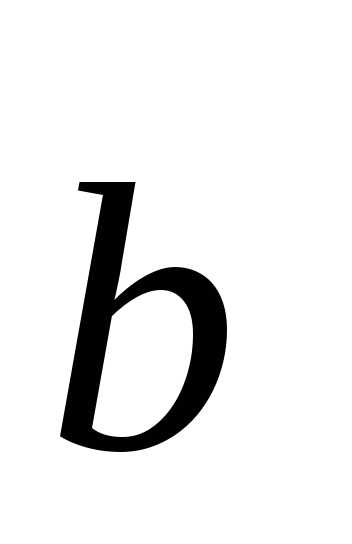 ,
то он коллинеарен вектору
,
то он коллинеарен вектору .
Следовательно,.
.
Следовательно,.
По
условию 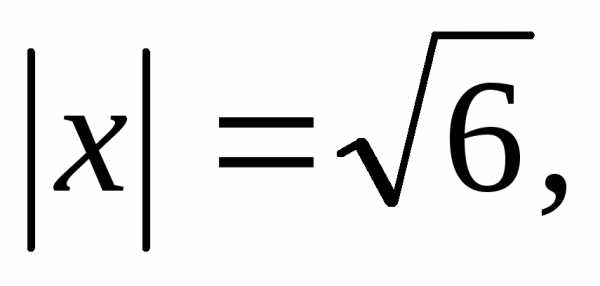 т.е.или
т.е.или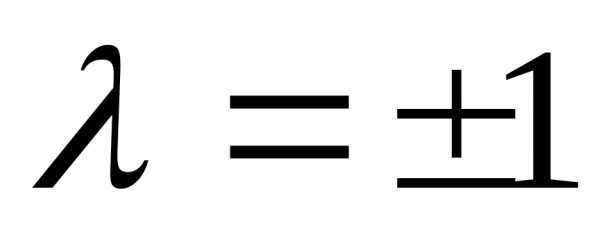 .
Вектор
.
Вектор образует тупой угол с осью Ох, поэтому
его проекция на эту ось должна быть
отрицательной, отсюда
образует тупой угол с осью Ох, поэтому
его проекция на эту ось должна быть
отрицательной, отсюда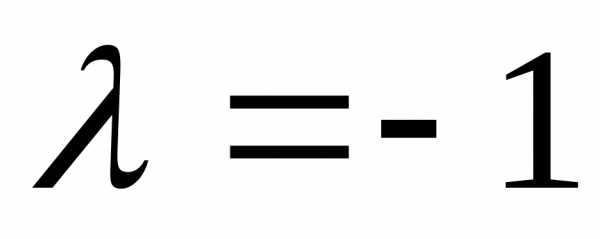 и.
и.
Системы координат 3
Линии на плоскости 8
Линии первого порядка. Прямые на плоскости. 10
Угол между прямыми 12
Общее уравнение прямой 13
Неполное уравнение первой степени 14
Уравнение прямой “в отрезках” 14
Совместное исследование уравнений двух прямых 15
Нормаль к прямой 15
Угол между двумя прямыми 16
Каноническое уравнение прямой 16
Параметрические уравнения прямой 17
Нормальное (нормированное) уравнение прямой 18
Расстояние от точки до прямой 19
Уравнение пучка прямых 20
Примеры задач на тему «прямая на плоскости» 22
Векторное произведение векторов 24
Свойства векторного произведения 24
Геометрические свойства 24
Алгебраические свойства 25
Выражение векторного произведения через координаты сомножителей 26
Смешанное произведение трёх векторов 28
Геометрический смысл смешанного произведения 28
Выражение смешанного произведения через координаты векторов 29
Примеры решения задач по теме: «Векторная алгебра». 30
Поверхности в пространстве 33
Плоскость 33
Неполные уравнения плоскости 35
Уравнение плоскости в «отрезках» 35
Угол между плоскостями 36
Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой 37
Нормальное уравнение плоскости. Расстояние от точки до плоскости. 38
Расстояние от точки до плоскости 39
Приведение общего уравнения плоскости к нормальному виду 40
Примеры задач на тему «Плоскость». 40
Линии в пространстве. Прямая в пространстве 45
Канонические уравнения прямой в пространстве 46
Параметрические уравнения прямой 47
Уравнения прямой, проходящей через две заданные точки 47
Угол между двумя прямыми в пространстве 48
Угол между прямой и плоскостью 48
Условие принадлежности двух прямых одной плоскости 49
Некоторые задачи на построение прямых и плоскостей 49
Примеры решения задач по теме «Аналитическая геометрия» 54
Кривые второго порядка 58
Пример приведения общего уравнения линии второго порядка к каноническому виду 58
Эллипс 61
Вывод уравнения эллипса 61
Гипербола 63
Парабола 64
Примеры решения задач на тему «Кривые второго порядка». 65
Поверхности в пространстве
Пусть 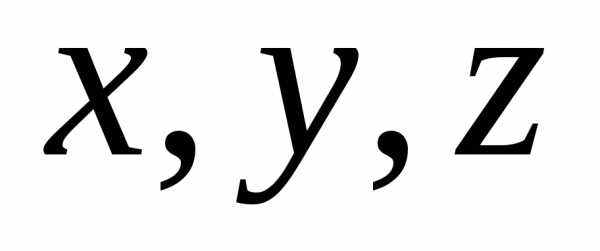 – переменные.
– переменные.
Выражение
называется уравнением, если оно
выполняется не для любых значений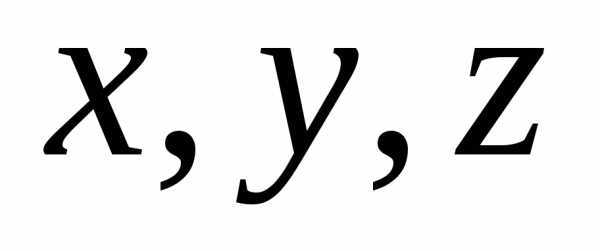 .
.
Уравнению поверхности удовлетворяют только точки поверхности и никакие другие точки пространства.
Определение. Поверхность – это геометрическое место точек, координаты которых удовлетворяют данному уравнению .
Пример: уравнениезадает сферу с центром в точке (
уравнениезадает сферу с центром в точке (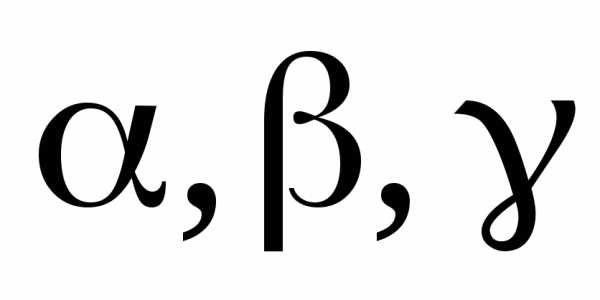 ),
радиусом
),
радиусом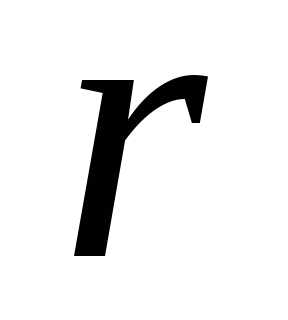 .
.
Алгебраические поверхности определяются в декартовой системе координат алгебраическими уравнениями вида:
Уравнение – общее уравнение первой степени.
studfiles.net
Примеры решения задач по векторной алгебре
. Примеры решения задач по векторной алгебре
Пример 1. Найти длину вектора и его направляющие косинусы.
Решение:
 =
=
Пример 2. Найти скалярное произведение векторов ,.
Решение: Находим
Так как и,
то
и,
то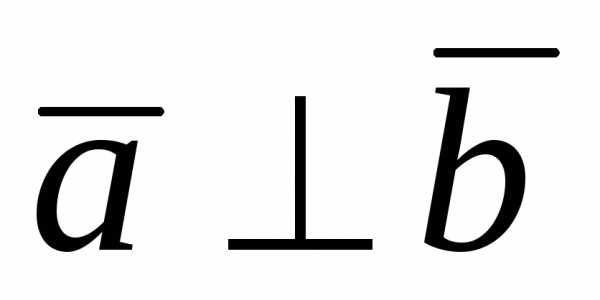 .
.
Пример 3. Определить,
при каком значении m векторы 3 + m
+ m  и
и  –
2
–
2 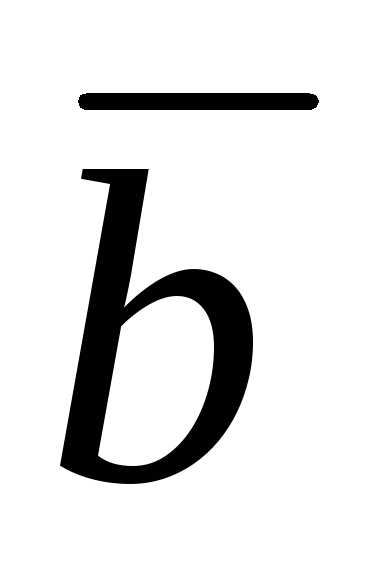 будут взаимно перпендикулярны, если
будут взаимно перпендикулярны, если
 = 7
= 7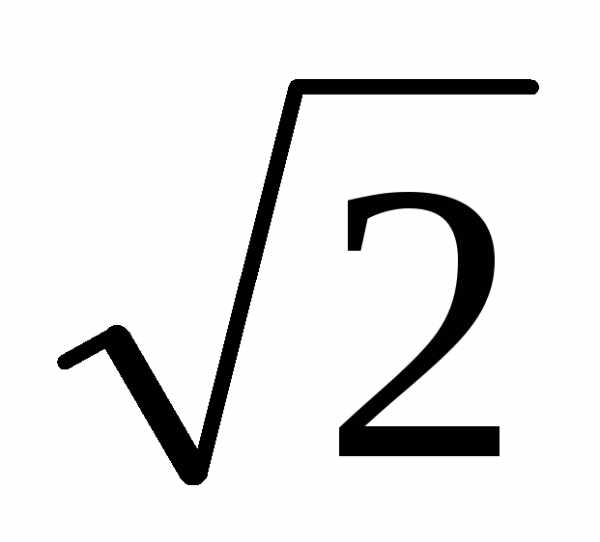 ;
;
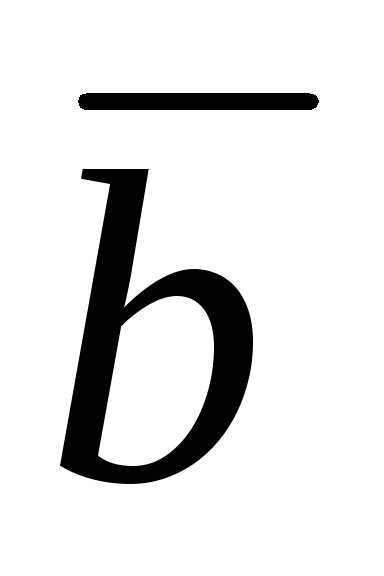 = 4;
(
= 4;
(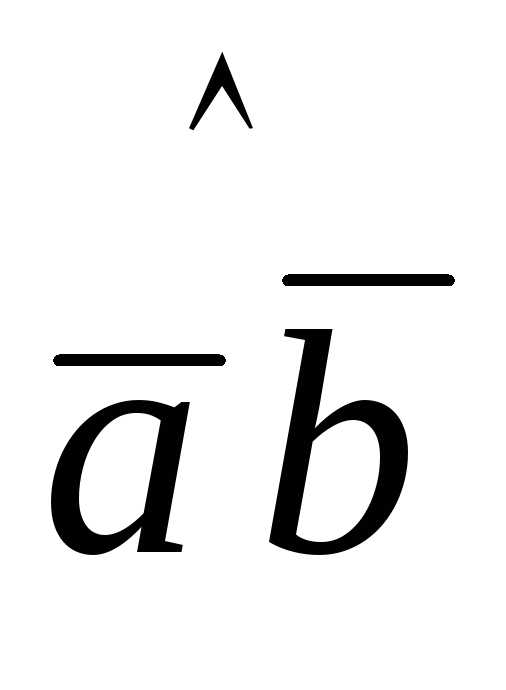 ) =
) = 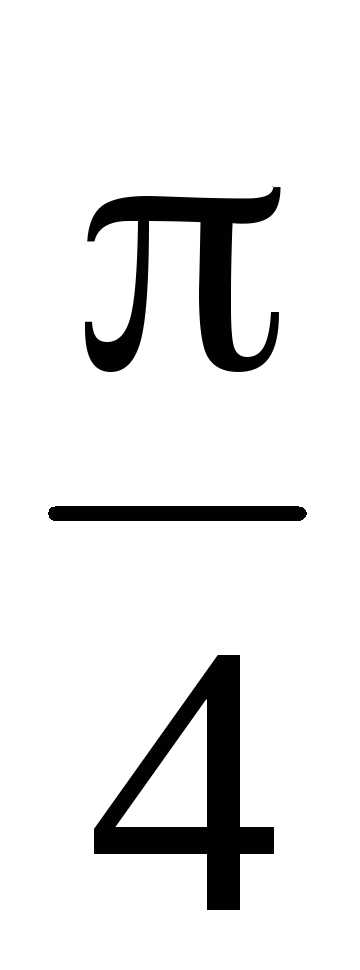 .
.
Решение:
Если два вектора взаимно перпендикулярны, то их скалярное произведение равно нулю.
Возьмем скалярное
произведение векторов 3 + m
+ m 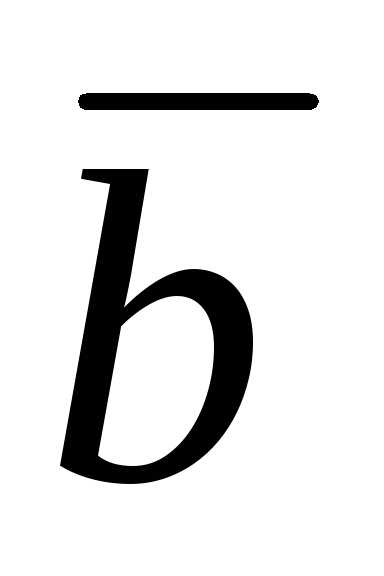 и
и  – 2
– 2 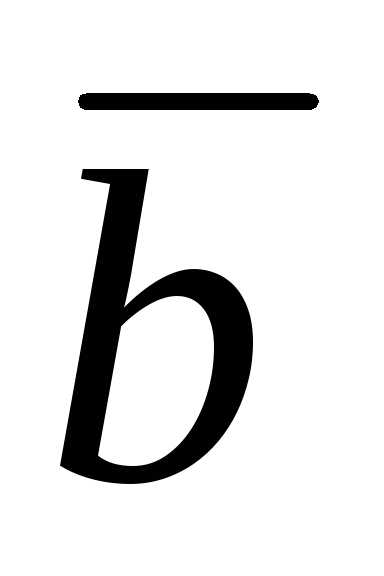 и, приравняв его нулю, найдем m:
и, приравняв его нулю, найдем m:
(3 + m
+ m 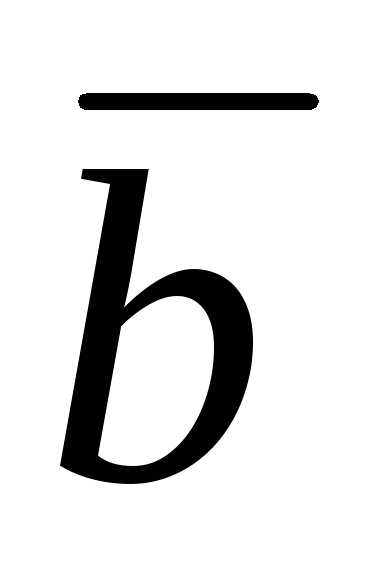 )(
)( – 2
– 2 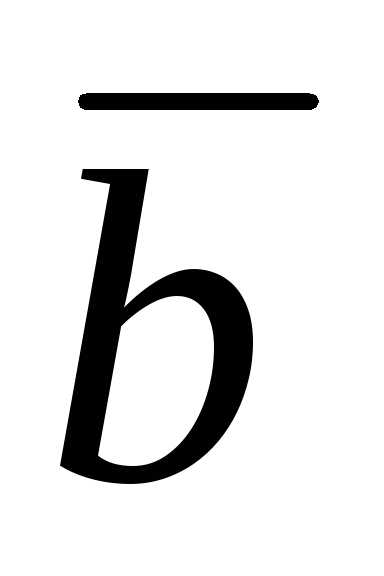 ) = 0;
) = 0;
3  2– 6
2– 6 
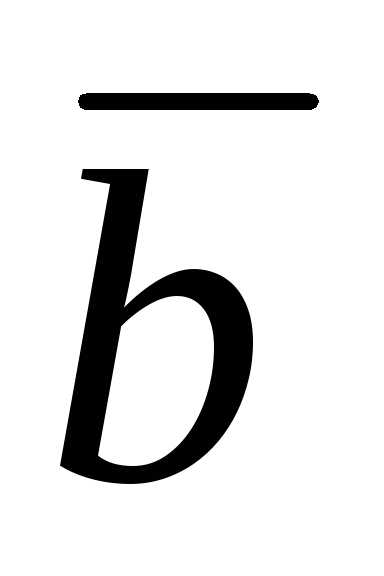 cos +m
cos +m
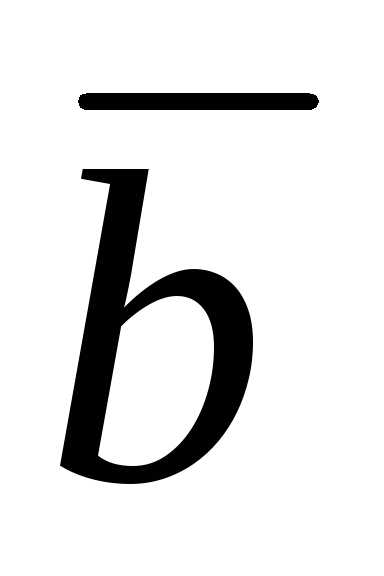 cos
cos 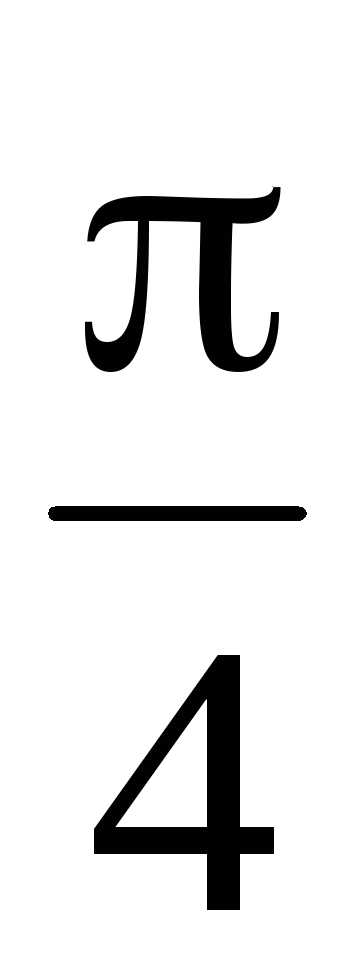 – 2m
– 2m 2 = 0;
2 = 0;
3 49 2 – 6 7 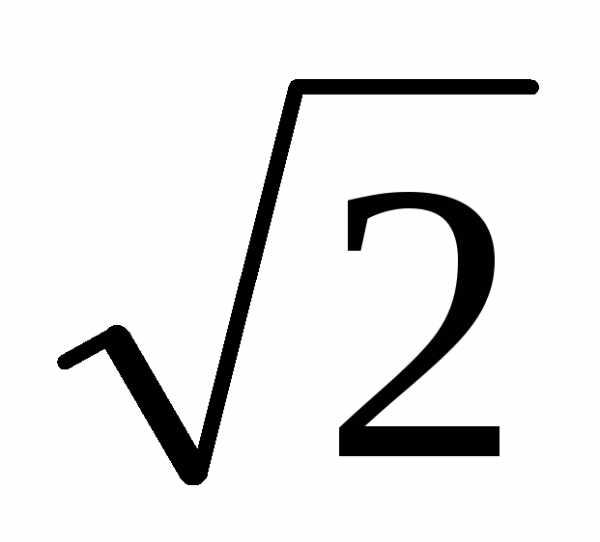 4
4 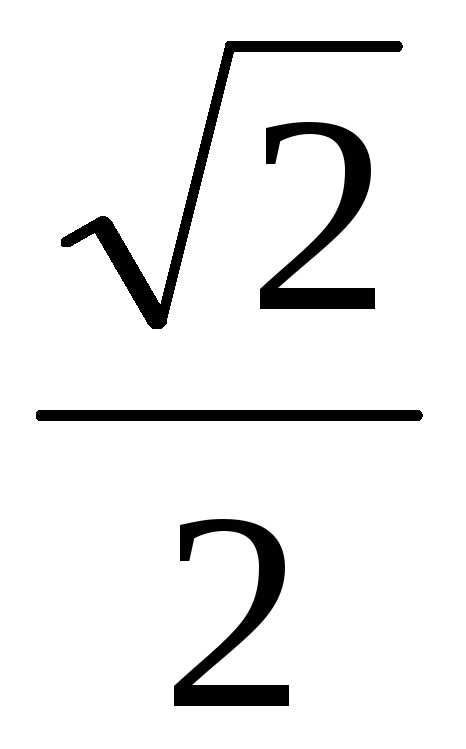 +m 7
+m 7 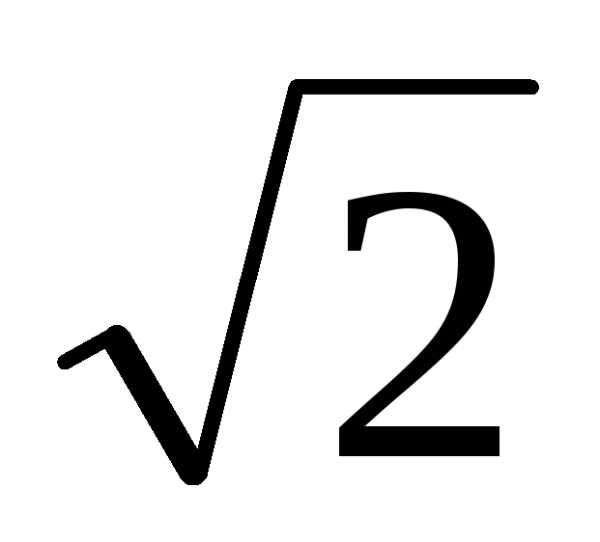 4
4 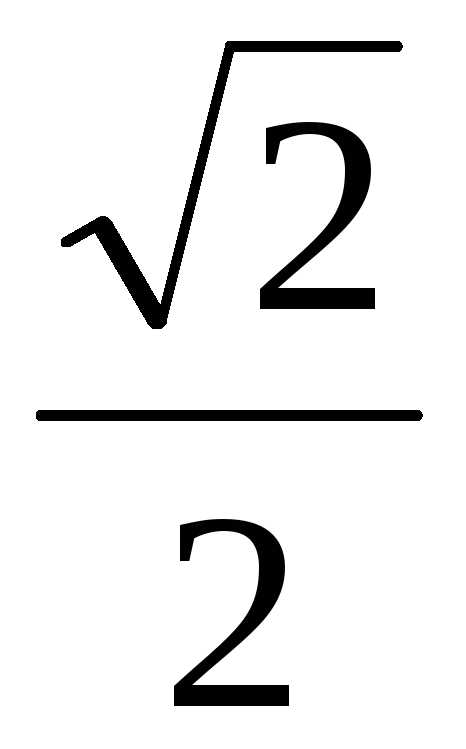 –
2 m 16 = 0;
–
2 m 16 = 0;
294 –
168 + 28 m – 32 m = 0,
4 m =126, m = = 31,5.
= 31,5.
Пример 4. Определить угол между векторами и.
Решение:
Так как 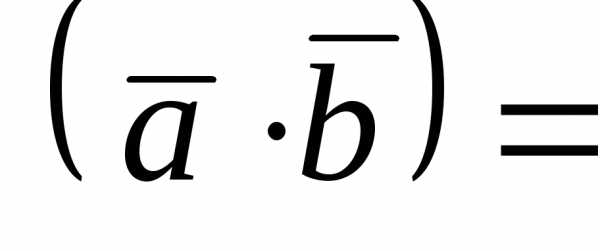

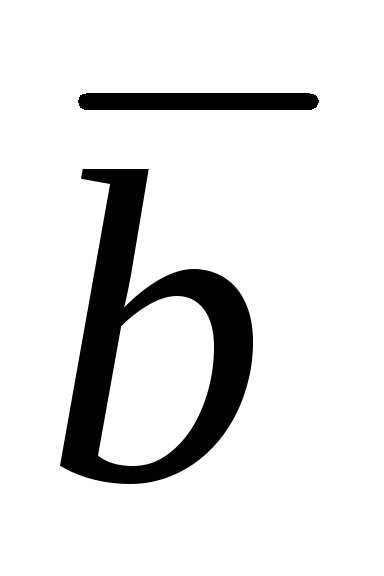 cos ,
то cos =
cos ,
то cos =  .
Имеем
.
Имеем
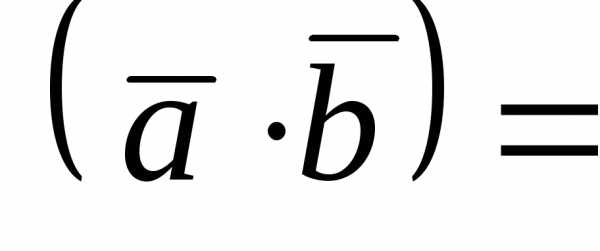 2 4 + 1 6 – 3 7
= –7;
2 4 + 1 6 – 3 7
= –7;
 =;
=;
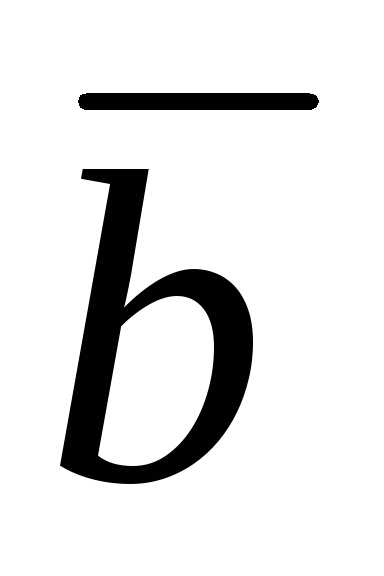 =.
=.
Следовательно,
cos = , = arccos 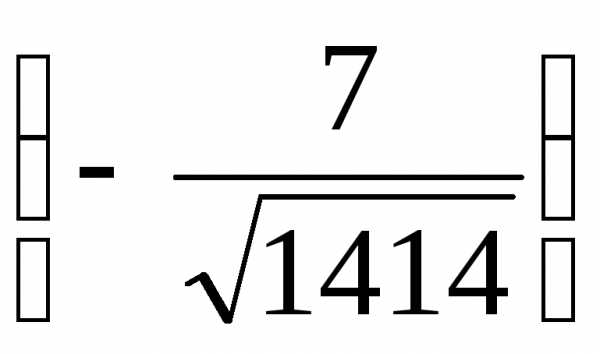 .
.
Пример 5. Найти векторное произведение векторов и.
Решение:
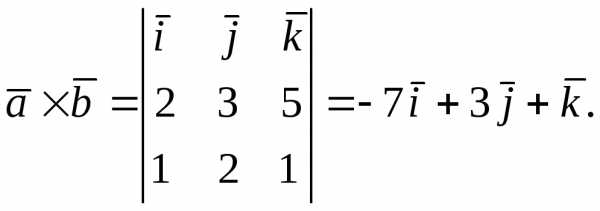
Пример 6. Вычислить площадь параллелограмма, построенного на векторах и
Решение:
Находим векторное
произведение  на
на 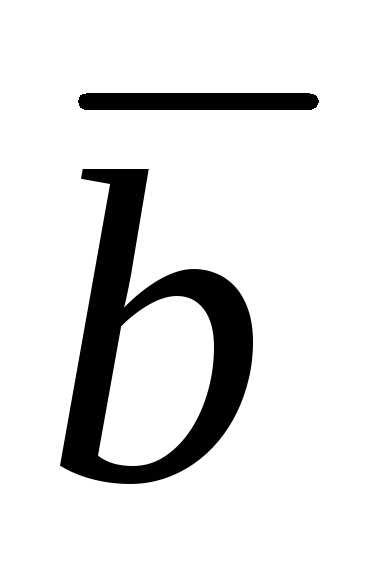 :
:
Так
как модуль векторного произведения
двух векторов равен площади построенного
на них параллелограмма, то S =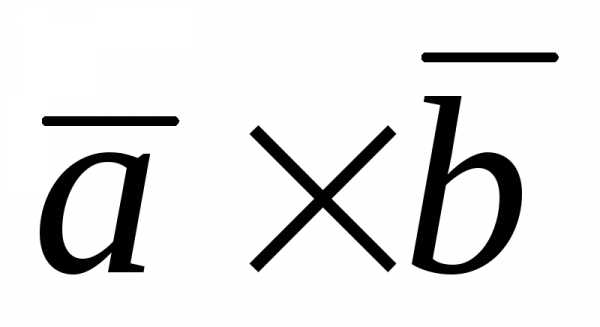 ==
49 (кв. ед.).
==
49 (кв. ед.).
Пример 7. Найти площадь треугольника ABC с вершинами A (1, 2, 0), B (3, 0, –3) и C (5, 2, 6).
Решение:
Площадь треугольника ABC равна половине площади параллелограмма,
построенного на векторах 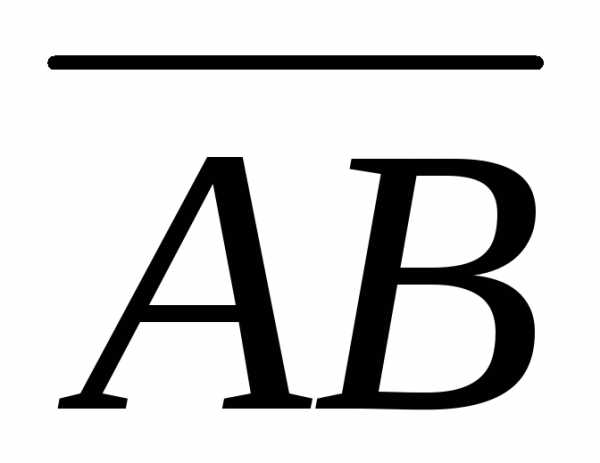 и
и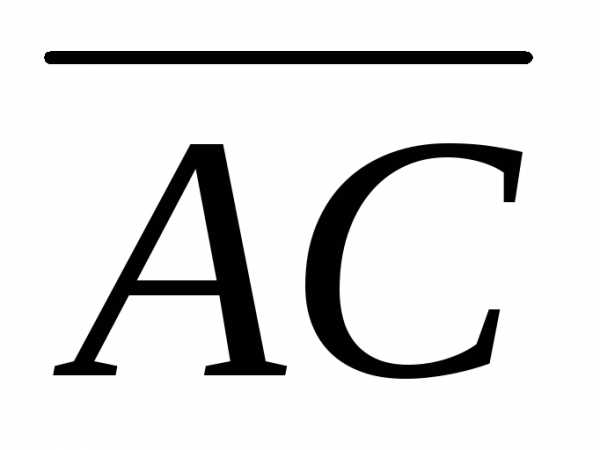 :S =
:S = 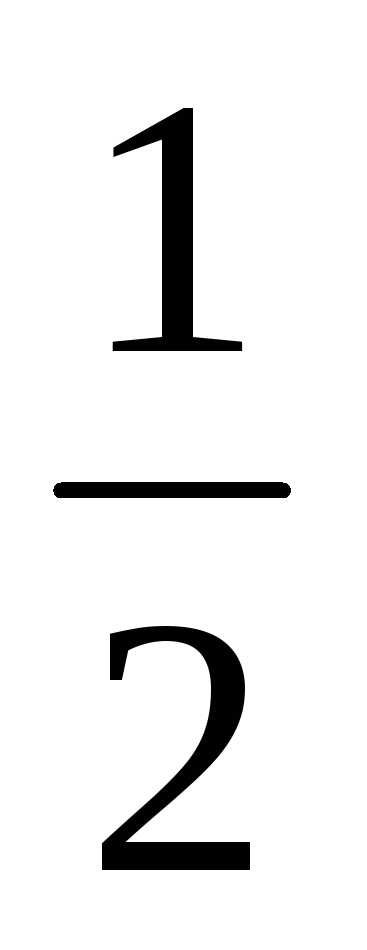
 .
Найдем векторы
.
Найдем векторы 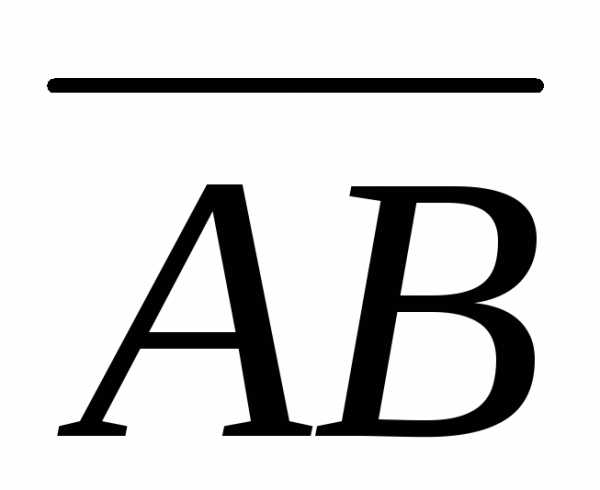 и
и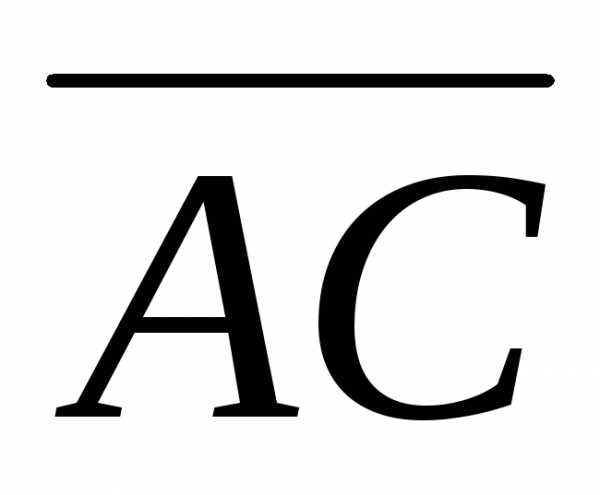 :
: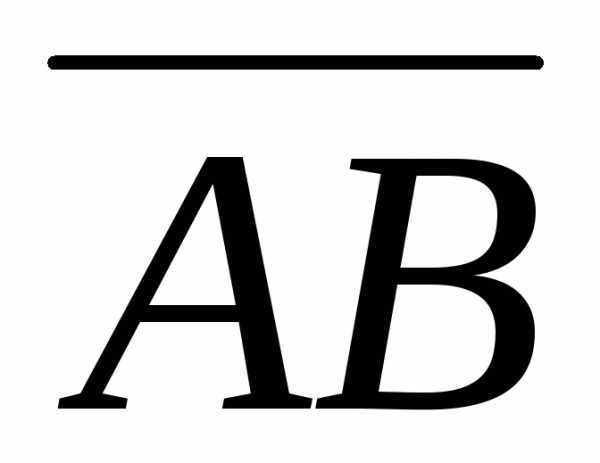 =;=
=;=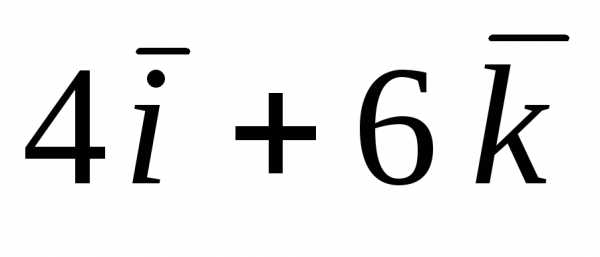 .
.
Их векторное произведение
,
поэтому
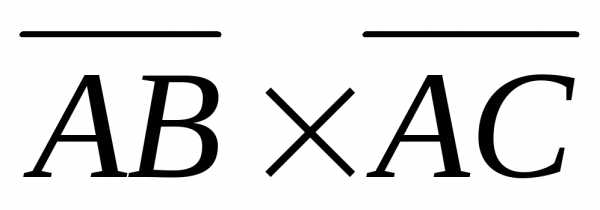 = 4 = 4 = 28,
и следовательно, S = 14 (кв.
ед.)
= 4 = 4 = 28,
и следовательно, S = 14 (кв.
ед.)
Пример 8. Вычислить
площадь параллелограмма, построенного
на векторах  =
6
=
6 – 3
– 3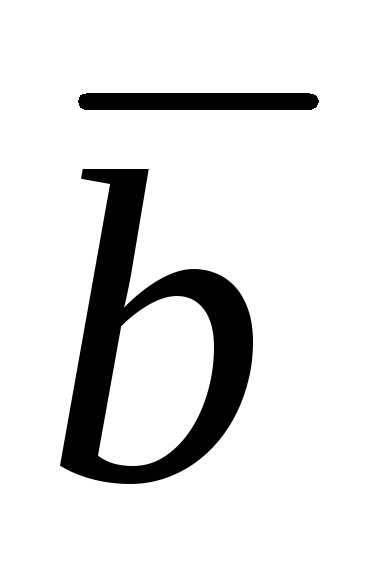 и
и  = 3
= 3  + 2
+ 2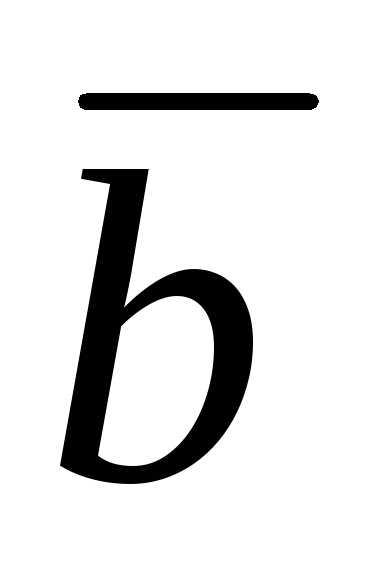 , если
, если  = 3;
= 3;
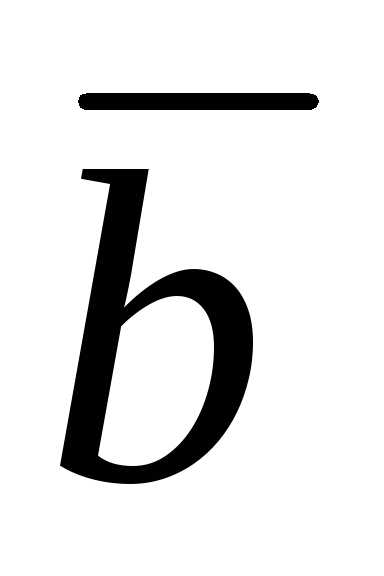 = 5;
(
= 5;
(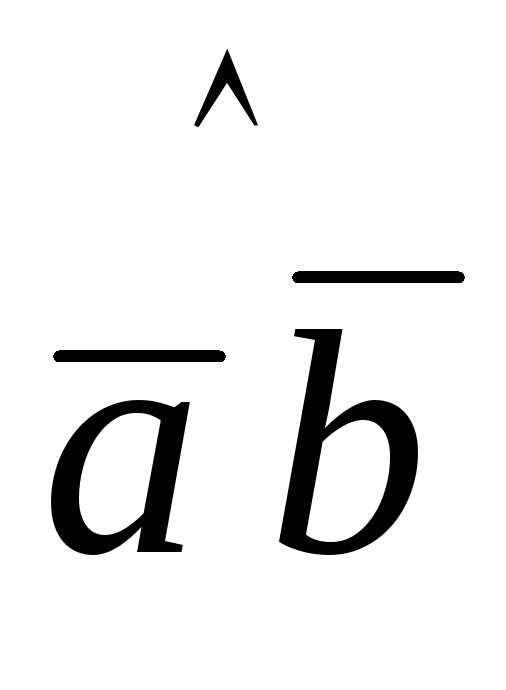 )=
)= 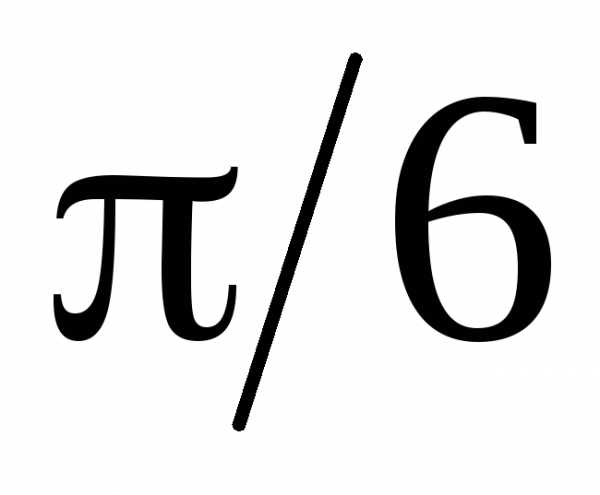 .
.
Решение:
Имеем 18 (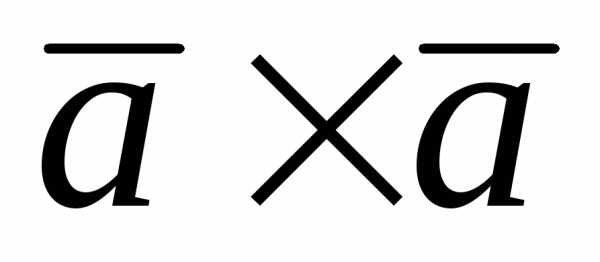 )
–9 (
)
–9 (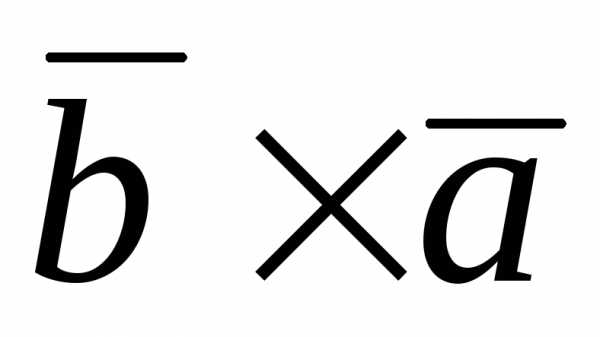 ) +12 (
) +12 (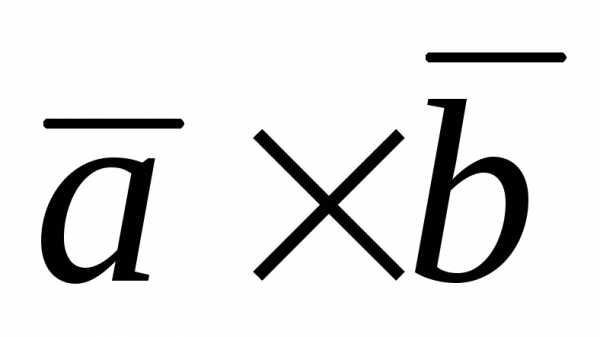 ) – 6 (
) – 6 (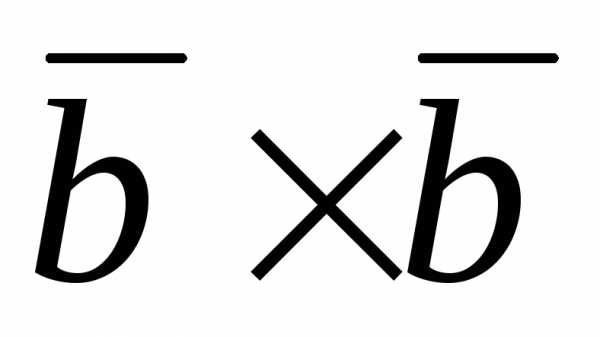 ) = 21(
) = 21(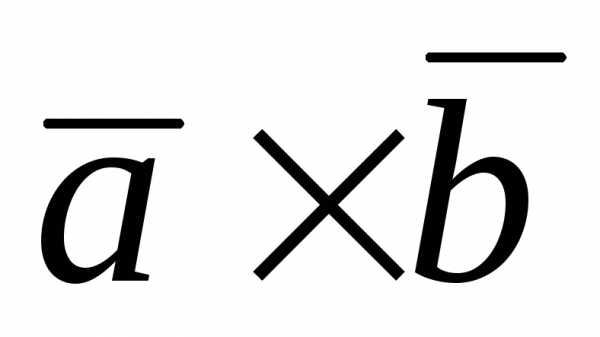 ),
где
),
где
.
Итак, S = = 21 3 5
= 21 3 5 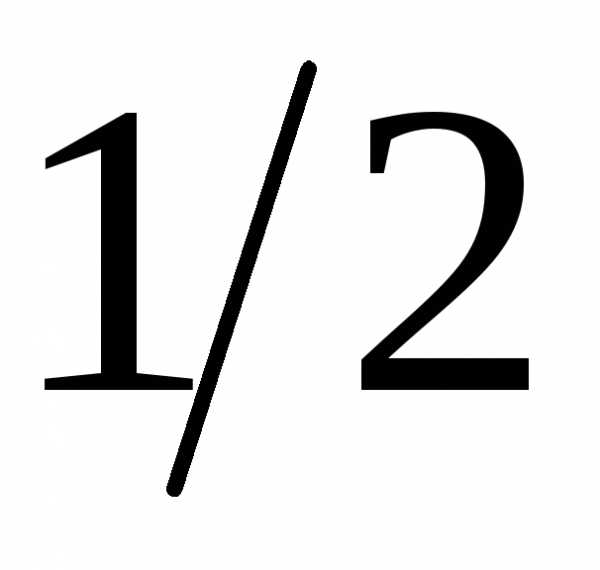 = 157,5
(кв. ед.)
= 157,5
(кв. ед.)
Пример 9. Найти смешанное произведение векторов ,и.
Решение:
Пример 10. Показать, что векторы ,икомпланарны.
Решение:
Так как 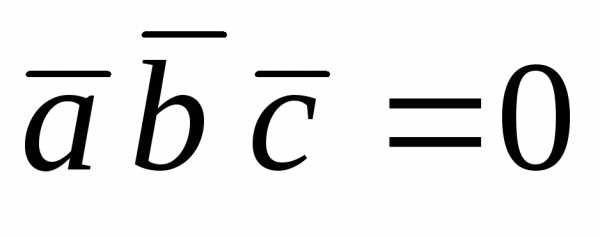 ,
то заданные векторы компланарны.
,
то заданные векторы компланарны.
Пример 11. Найти объем треугольной пирамиды с вершинами A (2, 2, 2), B (4, 3, 3), C (4, 5, 4) и D (5, 5, 6).
Решение:
Найдем векторы 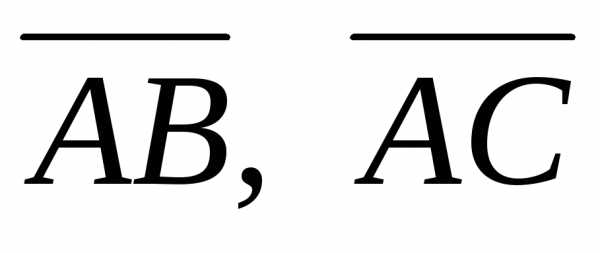 и
и ,
совпадающие с ребрами пирамиды,
сходящимися в вершинеA:
,,.
,
совпадающие с ребрами пирамиды,
сходящимися в вершинеA:
,,.
Находим смешанное произведение этих векторов:
Так как объем
пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах 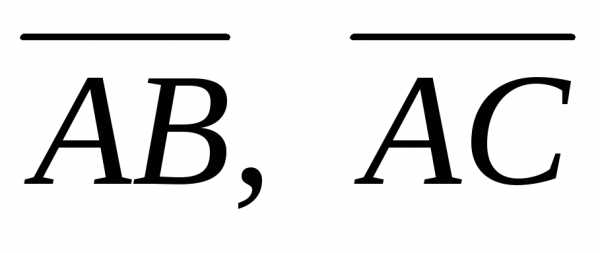 и
и ,
тоVпир =
,
тоVпир =  (куб. ед.).
(куб. ед.).
studfiles.net
